测震台网记录的事件中包含很多非天然地震事件,如爆破、塌陷等[1]。这些非天然地震事件会造成地震台网失误触发识别报警,影响地震速报的时效性和准确性[2]。因此,识别天然地震与非天然地震事件对地震速报有重要意义。
20世纪50年代以来,天然地震与人工爆破的识别取得一定的研究成果。刘强希等[3]利用小波变换能量线性度方法识别天然地震与爆破、塌方事件;边银菊[4]将遗传算法(GA)和反向传播算法(BP算法)相结合,建立遗传BP神经网络;沈萍等[5]基于非稳态WD理论,利用地下核爆和天然地震的瞬态谱、瞬时频率随时间的变化等特征来识别天然地震与地下核爆事件;杨选辉等[6]利用小波变换理论,以小波包分量比作为识别天然地震与核爆的判据;和雪松[7]利用小波包识别地震和矿震;安镇文等[8]总结了核爆炸与地震识别的研究进展。
天然地震与人工爆破事件最本质的不同在于震源性质:天然地震震源较深,为非对称剪切源;人工爆破大多发生于地表,为膨胀源。天然地震发震持续时间较长,能量衰减较慢,各地震台测震台网记录到的地震波频率复杂;而人工爆破持续时间较短,能量衰减较快,各地震台测震台网记录到的地震波高频成分较多。由于两者产生波形的物理性质存在差异,相对应的震幅大小、频谱成分、能量高低也不同,导致提取的能量比、香农熵、能量熵等均会存在较大偏差,支持向量机方法可利用两者的差异对天然地震和人工爆破事件进行分类。利用小波分析原理提取天然地震与人工爆破的特征向量,对其进行软件自动识别,通过实验分析和研究对比,确定影响分类准确度的因素,从而获得可靠的识别特征参数,实现对天然地震和人工爆破事件的自动识别。
1 研究方法 1.1 小波变换小波变换是一种分析信号时间-频率的算法,具有多分辨率的特点,在时域和频域上均能较好地表现信号的局部特征。小波变换在信号低频部分具有高频率分辨率和低时间分辨率,在高频部分具有高时间分辨率和低频率分辨率,因此被称为信号分析的显微镜[9]。小波变换分为一维小波变换、二维小波变换等,可根据实际问题选择不同的变换类型。
1) 离散小波(DWT)变换可表示为:
| $ \begin{array}{c} {\rm{W}}{{\rm{T}}_f}\left( {m, \mathit{k}} \right) = < f\left( t \right), {\mathit{\Psi }_{m, k}}\left( t \right) > = \\ {2^{ - \frac{m}{2}}}\int_R {f\left( t \right)\mathit{\Psi }} \left( {{2^{ - m}}t - k} \right){\rm{d}}t \end{array} $ | (1) |
式中,
2) 静态小波变换(SWT)是程序设计语言Matlab中用来实现ε-采样离散小波变换的算法[10]。与离散小波变换不同的是,静态小波变换不对信号进行下采样,因此用SWT变换得到的近似系数和细节系数的长度与原始信号长度一致。
3) 小波包变换(WPT)可对频带部分进行多层次划分,对多分辨率未细分的高频部分进一步分解,而且能够根据被分析信号的特征自动选择相应的频带,与信号频谱相匹配,由此提高视频分辨率。
1.2 特征参数 1.2.1 能量比(Ewt)设S为原始信号,长度为l,Sj为S分解后的第j个小波系数,经过DWT、SWT分析变换后将近似系数、细节系数按顺序排列。对于WPT分解,将最后一层分解后的系数按小波树节点顺序排列,其长度为c,则能量比(Ewt)可表示为:
| $ {E_{{\rm{wt}}}}\left( j \right) = 100\sum\limits_{k = 1}^c {S_{\left( {j, k} \right)}^2/\sum\limits_{i = 1}^l {S_i^2} } $ | (2) |
熵可以用来衡量信息规律。假设S为原始信号,Si为信号在任意一组正交基上的第i项系数。用E表示熵,则E为每个正交基系数某种变换的叠加值,即
假设S为原始信号,Si为信号S分解后的第i个小波系数,其长度为c,则小波系数的香农熵和能量熵可表示为:
| $ {E_{{\rm{shannon}}}}\left( i \right) = - \sum\limits_{j = 1}^c {S_{\left( {i.j} \right)}^2\lg \left[ {S_{\left( {i, j} \right)}^2} \right]} $ | (3) |
| $ {E_{\lg }}\left( i \right) = \sum\limits_{j = 1}^c {\lg S_{\left( {i.j} \right)}^2} $ | (4) |
支持向量机(SVM)是一种对不同类别已知样本的特征值进行训练,来预测未知样本类别的机器学习方法[11]。SVM在解决高维、小样本、非线性问题的模式识别上具有很大优势[3]。对于非线性情形,SVM利用核函数将多维空间向量映射到高维空间上,从而把问题转换为高维空间下的线性可分类问题。支持向量机分类算法C-SVC是指使用一个常数C来调节模型复杂程度与训练样本误差大小之间的平衡[12]。由于该常数受人为因素影响较大,研究人员通过引入一个0~1的参数υ来调节算法误差,即υ-SVC算法。在支持向量机的分类方法中,核函数的选择具有重要意义,合适的核函数可以将二维空间中线性不可分问题转化为高维空间中线性可分问题,因此只需要在低维空间对核函数进行运算即可进行分类。常用的核函数有线性核、多项式核、径向基核、Sigmoid核。
2 实验 2.1 数据选取选取2016~2021年内蒙古地区测震台网人工记录的内蒙古境内及其周边(96°~126°E, 36°~54°N)信噪比较高、记录清晰的BHZ分量地震事件(M≥1.5)和爆破事件(M≥1.0)共计200次,其中地震事件100次,爆破事件100次。从中随机选取各80次事件数据作为训练样本,其余20次事件数据作为测试样本。
2.2 小波变换对事件进行分解利用小波变换对事件进行分解的步骤为:1)使用msdp软件将seed格式事件转换成ASCⅡ码格式;2)利用小波变换分解程序,实现对天然地震事件和爆破事件DWT、SWT、WPT的4层小波分解。图 1为DWT对爆破和地震事件的5个分解系数结果,图 2为SWT对爆破和地震事件的8个分解系数结果,图 3为WPT对爆破和地震事件的16个分解系数结果。

|
图 1 DWT对爆破和天然地震事件的分解(db4) Fig. 1 Decomposition of blasting and natural earthquake events by DWT (db4) |
|
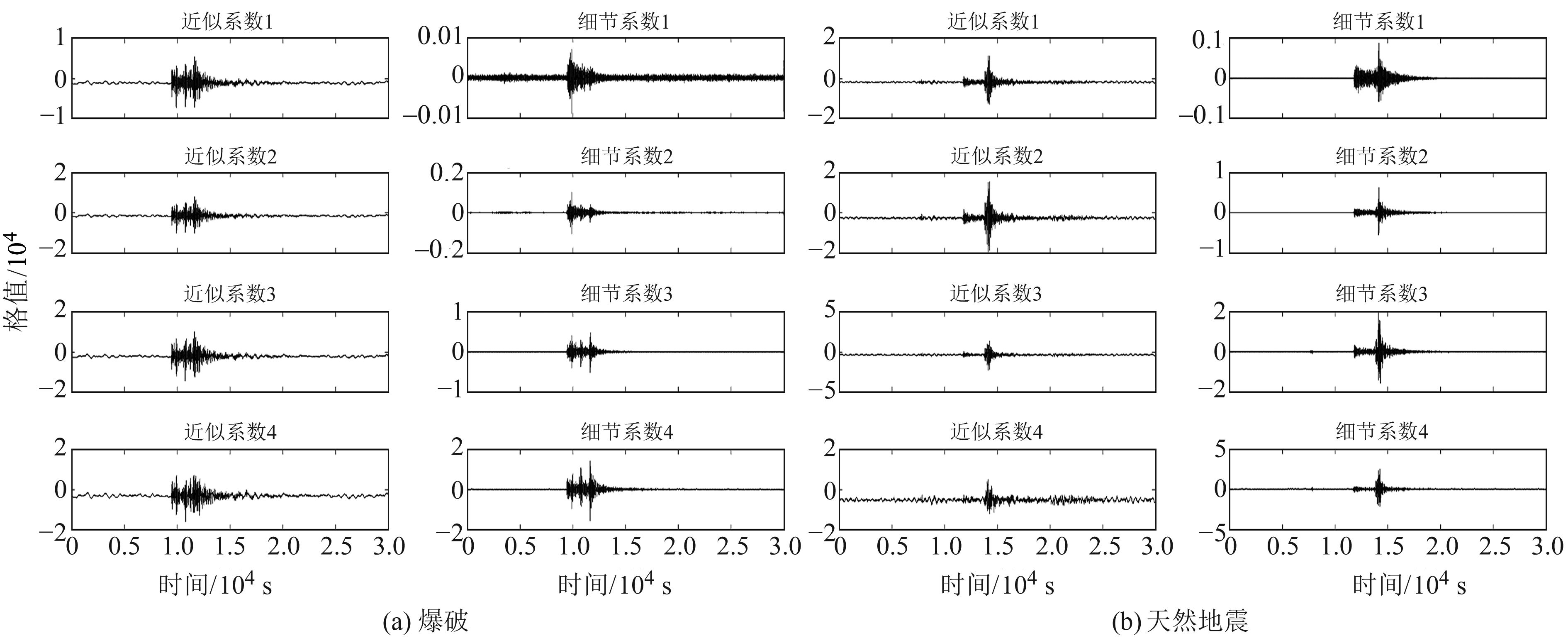
图 2 SWT对爆破和天然地震事件的分解(db4) Fig. 2 Decomposition of blasting and natural earthquake events by SWT (db4) |

|
图 3 WPT对爆破和天然地震事件的分解(db4) Fig. 3 Decomposition of blasting and natural earthquake events by WPT (db4) |
特征参数的提取是指在DWT、SWT、WPT采用db7、rbio1.5、sym6小波基分析的基础上对事件进行4层分解,得到小波低频系数和高频系数,然后分别计算其能量比、香浓熵、能量熵,最后采用不同的核函数和支持向量机按照随机组合的方式作为特征参数进行实验。
2.4 波形分类及检验效果为研究经过小波变换后提取的特征向量对天然地震和人工爆破的影响,设定具体实验参数如下:1)小波基函数为db7小波、sym6小波、rbio1.5小波;2)支持向量机类型为C-SVC和υ-SVC;3)核函数为线性核、多项式核、径向基核、Sigmoid核。
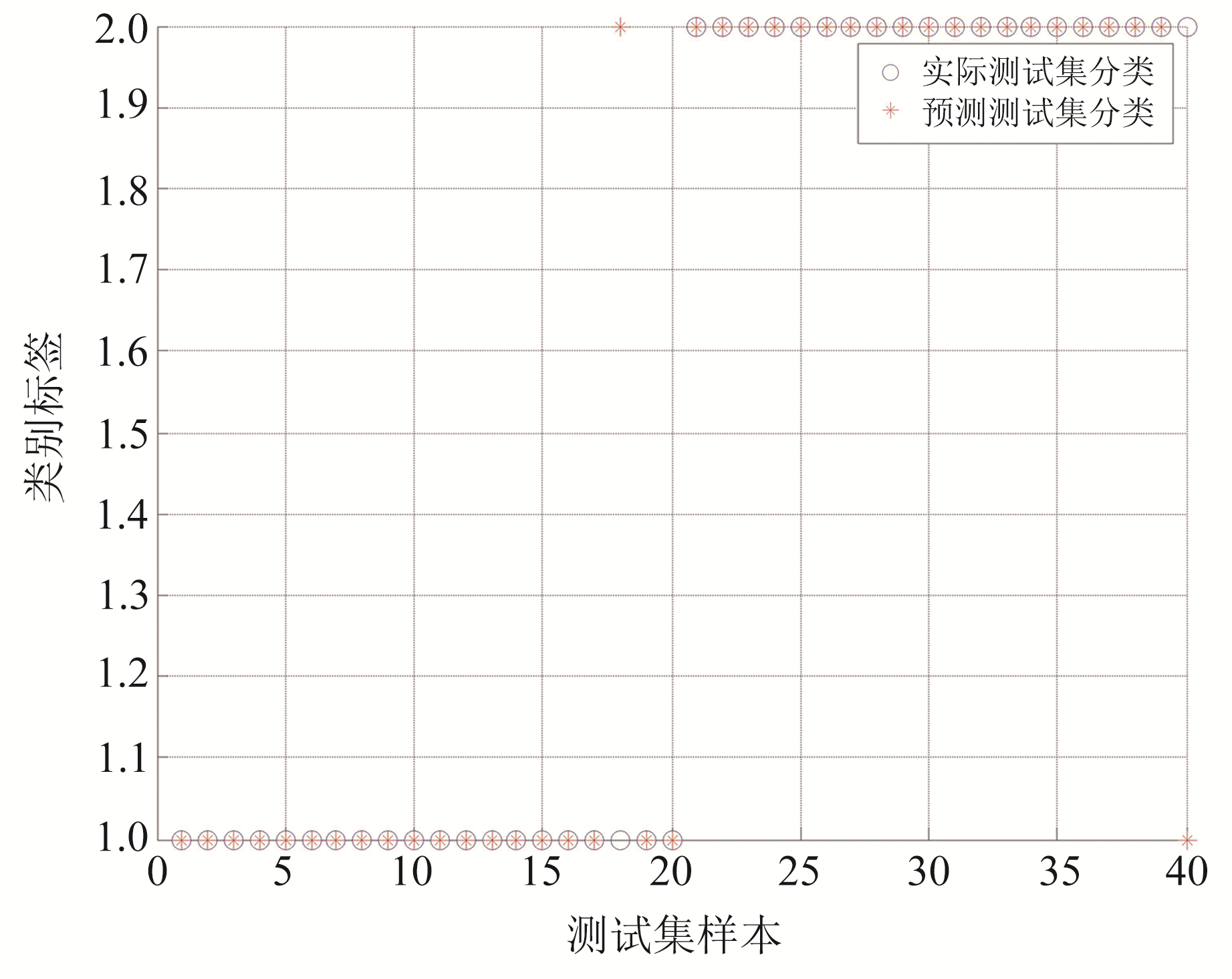
利用不同的小波分解方式、小波基函数提取特征参数能量比、香农熵、能量熵,采用2种支持向量机和4种核函数的随机组合,共进行288组识别实验,表 1为4种最优识别结果。结果表明,“DWT+υ-SVC+db7+线性核+能量比+香农熵+能量熵”识别率最高为95%,图 4为该组合的效果图。
|
|
表 1 最优识别结果 Tab. 1 The best recognition results |
|
图 4 识别效果 Fig. 4 Identification effect |
采用支持向量机方法对内蒙古地区天然地震和爆破事件进行识别,得到以下结论:
1) 将特征参数能量比、香农熵、能量熵与小波分解方式、小波基类型、支持向量机类型、核函数类型进行随机组合,识别结果表明,“DWT +υ-SVC+db7+线性核+能量比+香农熵+能量熵”识别率最高为95%,表明该方法更适合内蒙古地区。
2) 内蒙古地区非天然地震数据量较少,无法达到数据训练与测试的要求,故只对天然地震和爆破事件进行自动识别。尽管“DWT+υ-SVC+db7+线性核+能量比+香农熵+能量熵”识别率高达95%,但还需要继续使用其他机器学习算法,不断提高事件类型的识别率,为日常地震台网工作提供辅助决策支持。
3) 内蒙古地区测震台网可以监测记录到境内及周边省份一定范围内的所有爆破事件,如山西省朔州市和陕西省榆林市爆破。距离较近的台网记录到的爆破事件地表面波特征较为明显,但随着震中距的增加,爆破事件面波的波形会趋向于天然地震事件记录波形,从而造成地震与爆破事件的误识别。因此,需要尽量选择离震中位置最近的台站。
4) 天然地震与爆破事件的识别原则上属于二分类问题,从表 1可以看出,线性核能更好地对两类事件进行识别,识别率均在80%以上。
5) 目前自动编目软件还未将天然地震与非天然地震事件进行有效区分,部分无需处理的非天然事件还需进行人工核实,必然会增加编目的工作量。在后续研究中,可将本文支持向量机方法与自动编目软件进行对接,将天然地震和非天然地震事件进行区分,以便更好地服务测震台网编目工作。
| [1] |
卢世军. 天然地震与人工爆破波形特征提取与识别算法研究[D]. 桂林: 广西师范大学, 2009 (Lu Shjun. Research of Seismic Wave Features Extraction and Recognition Algorithm of Earthquake and Explosion[D]. Guilin: Guangxi Normal University, 2009)
(  0) 0) |
| [2] |
范晓易, 曲均浩, 刘方斌, 等. 使用支持向量机识别地震类型的影响因素分析[J]. 大地测量与地球动力学, 2020, 40(10): 1034-1038 (Fan Xiaoyi, Qu Junhao, Liu Fangbin, et al. Analysis of Influencing Factors in Use of Support Vector Machine Method to Identify Earthquake Types[J]. Journal of Geodesy and Geodynamics, 2020, 40(10): 1034-1038)
(  0) 0) |
| [3] |
刘希强, 沈萍, 张玲, 等. 用小波变换能量线性度方法识别天然地震与爆破或塌方[J]. 西北地震学报, 2003, 25(3): 204-209 (Liu Xiqiang, Shen Ping, Zhang Ling, et al. Using Method of Energy Linearity in Wavelet Transform to Distinguish Explosion or Collapse from Nature Earthquake[J]. Northwestern Seismological Journal, 2003, 25(3): 204-209)
(  0) 0) |
| [4] |
边银菊. 遗传BP网络在地震和爆破识别中的应用[J]. 地震学报, 2002, 24(5): 516-524 (Bian Yinju. Application of Genetic BP Network to Discriminating Earthquakes and Explosions[J]. Acta Seismologica Sinica, 2002, 24(5): 516-524 DOI:10.3321/j.issn:0253-3782.2002.05.009)
(  0) 0) |
| [5] |
沈萍, 郑治真. 瞬态谱在地震与核爆识别中的应用[J]. 地球物理学报, 1999, 42(2): 233-240 (Shen Ping, Zheng Zhizhen. Application of Transient Spectrum to Discrimination of Nuclear Explosions and Earthquakes[J]. Chinese Journal of Geophysics, 1999, 42(2): 233-240 DOI:10.3321/j.issn:0001-5733.1999.02.011)
(  0) 0) |
| [6] |
杨选辉, 沈萍, 刘希强, 等. 地震与核爆识别的小波包分量比方法[J]. 地球物理学报, 2005, 48(1): 148-156 (Yang Xuanhui, Shen Ping, Liu Xiqiang, et al. Application of Method of Spectral Component Ratio of Wavelet-Packets to Discrimination between Earthquakes and Nuclear Explosions[J]. Chinese Journal of Geophysics, 2005, 48(1): 148-156)
(  0) 0) |
| [7] |
和雪松. 用小波包识别地震和矿震[D]. 北京: 中国地震局地球物理研究所, 2005 (He Xuesong. A Wavelet Packet Approach to Earthquake and Mining Shocks Wave Classification[D]. Beijing: Institute of Geophysics, CEA, 2005)
(  0) 0) |
| [8] |
安镇文, 郭祥云, 边银菊, 等. 核爆炸与地震识别研究进展[J]. 国际地震动态, 2008, 38(8): 22-31 (An Zhenwen, Guo Xiangyun, Bian Yinju, et al. Recent Advances in Discrimination of Nuclear Explosion and Earthquake[J]. Recent Developments in World Seismology, 2008, 38(8): 22-31)
(  0) 0) |
| [9] |
卢世军, 黄汉明. 基于能量比的天然地震与人工爆破自动识别算法研究[J]. 华南地震, 2010, 30(1): 34-39 (Lu Shijun, Huang Hanming. Research on Automatic Recognition of Natural Earthquake and Artificial Explosion Based on Energy Ratio[J]. South China Journal of Seismology, 2010, 30(1): 34-39)
(  0) 0) |
| [10] |
高成, 董长虹, 郭磊, 等. Matlab小波分析与应用[M]. 北京: 国防工业出版社, 2007 (Gao Cheng, Dong Changhong, Guo Lei, et al. Wavelet Analysis and Application of Matlab[M]. Beijing: National Defense Industry Press, 2007)
(  0) 0) |
| [11] |
边肇祺, 张学工. 模式识别[M]. 北京: 清华大学出版社, 2000 (Bian Zhaoqi, Zhang Xuegong. Pattern Recognition[M]. Beijing: Tsinghua University Press, 2000)
(  0) 0) |
| [12] |
郝红艳. 基于支持向量机的可靠性优化设计方法研究[D]. 武汉: 华中科技大学, 2013 (Hao Hongyan. Research on RBDO Methods Based on SVM[D]. Wuhan: Huazhong University of Science and Technology, 2013)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


