2. 青海省地震局,西宁市柴达木路242号,810017
地震孕育的过程是应力应变在局部地区(震源体及附近)缓慢积累的过程,而岩石破裂实验表明,岩石电导率与应力应变关系密切[1-4],因此地震在孕育过程中必然伴随着岩石电导率的变化。地磁场的内场强度既和外场强弱有关,又和地下物质电导率的大小有关,所以由应力累积引起的地下物质电导率的变化必然会导致外场和内场比值发生改变,这种改变是可以通过地磁日变化的谐波振幅比反映出来的[5]。冯志生等[6-8]对不同地震震前地磁谐波振幅比异常变化特征进行研究发现,地磁谐波振幅比异常特征与地电阻率趋势性异常特征具有相似性。
随着观测数据的累积和地磁谐波振幅比方法的推广,研究发现,地磁谐波振幅在地震前确实存在异常[9-14]。但该方法应用于日常震情跟踪工作时存在以下2个问题:1)目前分析主要采用分钟值采样数据,不能反映浅层介质的性质变化;2)无定量化指标。近年来,速率累加方法在跨断层水准观测资料的前兆异常识别中已经得到应用,该方法可以使某时段内较为频繁的速率异常变化更加直观和突出,更易于判定异常和提取异常指标[15]。
本文利用谐波振幅比法分析青海地区磁通门秒采样观测资料,利用速率累加方法分析连续数据的逐日变化速率,再根据需要对分析时段进行累加计算,识别数据资料的异常变化,进一步分析异常变化与强震的关系,梳理总结青海地区磁通门秒值谐波振幅比方法的异常指标,并将研究结果应用于青海地区的震情跟踪中。
1 主要方法与计算数据 1.1 方法与计算步骤 1.1.1 地磁谐波振幅比方法地磁谐波振幅比YZHx(NS) 和YZHy(EW)的定义为:
| $ \begin{array}{*{20}{c}} {{Y_{ZHx}}({\rm{NS}}) = \left| {\frac{{Z(\omega )}}{{{H_x}(\omega )}}} \right|}\\ {{Y_{ZHy}}({\rm{WE}}) = \left| {\frac{{Z(\omega )}}{{{H_y}(\omega )}}} \right|} \end{array} $ | (1) |
式中,Z(ω)、Hx(ω)、Hy(ω)分别为地磁场的垂直分量、水平NS向分量和WE向分量的振幅谱,可利用地磁三分量的min采样数据计算获得。对于随时间发生周期变化的不均匀场源,在地球介质为均匀各向同性平面导体的条件下,有:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{Z(\omega )}}{{{H_x}(\omega )}} = \frac{{Z(\omega )}}{{{H_y}(\omega )}} = {\rm{i}}\frac{\lambda }{\theta }}\\ {{\theta ^2} = \sigma \mu \omega {\rm{i}} + {\lambda ^2}} \end{array}} \right. $ | (2) |
式中,μ为磁导率,σ为电导率,ω为圆频率,λ为变化磁场的波数。
| $ \left[ {\frac{{Z(\omega )}}{{{H_x}(\omega )}}/\frac{{Z(\omega )}}{{{H_y}(\omega )}}} \right] = \frac{{{H_x}(\omega )}}{{{H_y}(\omega )}} $ | (3) |
式中,
地磁谐波振幅比可以表达为磁测深视电阻率:
| $ \begin{array}{*{20}{c}} {{\rho _{ax}} = \frac{{\bar \omega }}{{\mu {\lambda ^2}}}\left| {\frac{{{H_z}}}{{{H_x}}}} \right| = \frac{{\bar \omega }}{{\mu {\lambda ^2}}}\left| {{Y_{ZHx}}({\rm{NS}})} \right|}\\ {{\rho _{ay}} = \frac{{\bar \omega }}{{\mu {\lambda ^2}}}\left| {\frac{{{H_z}}}{{{H_y}}}} \right| = \frac{{\bar \omega }}{{\mu {\lambda ^2}}}\left| {{Y_{ZHx}}({\rm{EW}})} \right|} \end{array} $ | (4) |
由式(4)可知,YZHx(NS)和YZHy(EW)与地下介质电阻率ρ呈正比。具体计算步骤为:1)计算每天地磁三分量采样数据谱幅度,计算各段各周期谐波振幅比(复数余);2)按照虚实部分别计算各周期的谐波振幅比96段的均值及相位;3)读入逐频值文件,按照指定频带分别计算谐波振幅比虚实部均值和幅度;4)读入谐波振幅比逐日值文件,按一定窗长逐日滑动平均,消除噪声;5)读入消除噪声的谐波比逐日值文件,按365 d窗长逐日滑动平均,消除年变。
1.1.2 速率累加方法速率累加方法是对地磁谐波振幅比计算结果进行二次计算的数学方法,其目的是通过二次计算的结果图像更加直观地反映地磁谐波振幅比异常,同时能够获得清晰的地磁谐波振幅比异常特征[11]。具体计算步骤为:1)计算地磁谐波振幅比南北向和东西向各周期逐日值的一阶差分,获得各周期一阶差分序列,该序列可反映其变化速率;2)对一阶差分序列进行正负判断,大于0取值为1,小于0取值为-1,0取值不变,形成归一化序列;3)将南北向与东西向各周期归一化序列对应数值相乘,形成归一化序列的积序列;4)将各周期积序列进行累加计算,获得各周期速率累加序列,该序列可用于判断对应周期是否存在不同步异常;5)将所有周期累加序列对应数值求和,得到所有周期速率累加和,用于分析不同步异常的起始时间。
1.2 计算数据2015年前青海地区共有5个地磁观测点,分别为格尔木、都兰、德令哈、大武和西宁,“十二五”背景场项目新增设金银滩、贵德和玉树巴塘3个观测点,8个地磁观测点共有16套地磁三分量观测仪器(其中磁通门秒采样观测仪14套),已积累至少5 a的分钟值采样及秒采样连续观测资料。分析研究区5级以上地震与地磁谐波振幅比曲线变化特征的关系,针对不同方向或不同周期出现的不同步变化进行科学总结,从时间、空间、强度方面总结规律特征。
2 结果分析格尔木台FHDZ-M15[1]谐波振幅比曲线自2016-05起部分速率累加曲线出现转平或连续波动变化,170 s和260 s的周期曲线首先出现异常变化,自2016-05开始曲线转为平稳的波动变化;随后,290 s的周期曲线在2017年出现转平变化,50 s的周期曲线在2017-10转为平稳变化。异常出现24个月后发生称多5.3级地震,异常出现27个月后发生治多5.1级地震,具体见图 1(a)。

|
图 1 格尔木台地磁谐波振幅比 Fig. 1 Geomagnetic harmonic amplitude ratio at Golmud station |
格尔木台GM4[B]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,20 s的周期曲线在2016年初出现下降趋势,同时260 s和290 s的周期曲线在2016年初转为平稳的波动变化。随后,80 s的周期曲线在2017年转平,并呈小幅度下降趋势;230 s的周期曲线在2017-08转平并呈下降趋势。异常出现29个月后发生称多5.3级地震,异常出现32个月后发生治多5.1级地震,具体见图 1(b)。
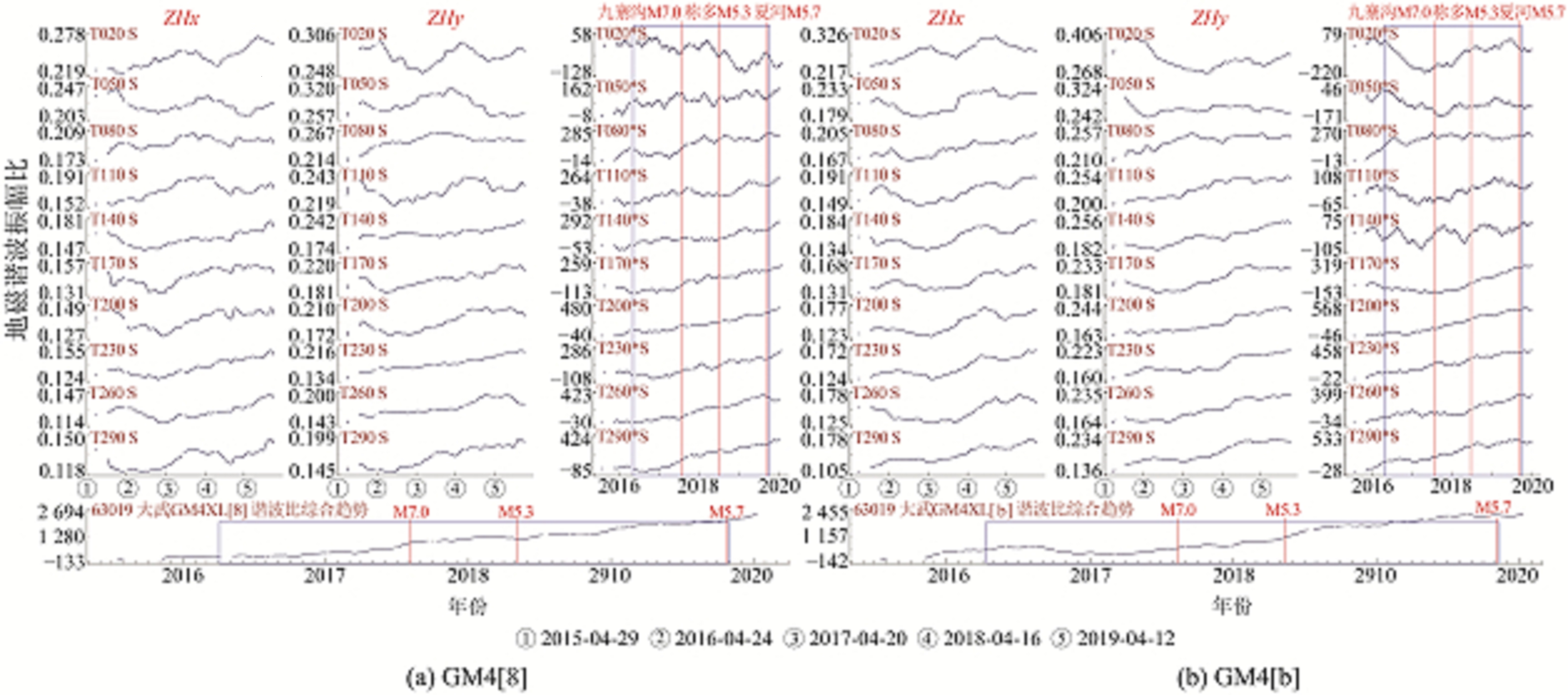
大武台GM4[8]谐波振幅比曲线自2016-04起部分速率累加曲线出现转平或连续波动变化,九寨沟7.0级地震前20 s、50 s、80 s、170 s周期曲线均在震前出现转平变化,持续时间为1.5 a;称多5.3级地震前20 s、50 s、80 s、110 s、140 s和170 s周期曲线波动变化平稳,持续时间为1 a左右;夏河5.7级地震前20 s、50 s、80 s、110 s、140 s和260 s周期曲线出现转折和下降变化。上述曲线变化的共同特征为周期较小的曲线波动变化更明显。异常出现16个月后发生九寨沟7.0级地震,异常出现25个月后发生称多5.3级地震,异常出现42个月后发生夏河5.7级地震,具体见图 2(a)。
|
图 2 大武台地磁谐波振幅比 Fig. 2 Geomagnetic harmonic amplitude ratio at Dawu station |
大武台GM4[b]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,九寨沟7.0级地震前20 s、50 s、110 s周期曲线出现显著转折下降变化,持续时间为1.5 a左右;80 s、170 s的周期曲线波动变化平稳,持续时间近1 a。称多5.3级地震前50 s、80 s、110 s、140 s周期曲线变化平稳,持续时间为1 a左右;夏河5.7级地震前20 s、50 s、80 s、110 s、140 s周期曲线出现转折和下降变化,且周期较小曲线波动变化更明显。异常出现20个月后发生九寨沟7.0级地震,异常出现29个月后发生称多5.3级地震,异常出现46个月后发生夏河5.7级地震,具体见图 2(b)。
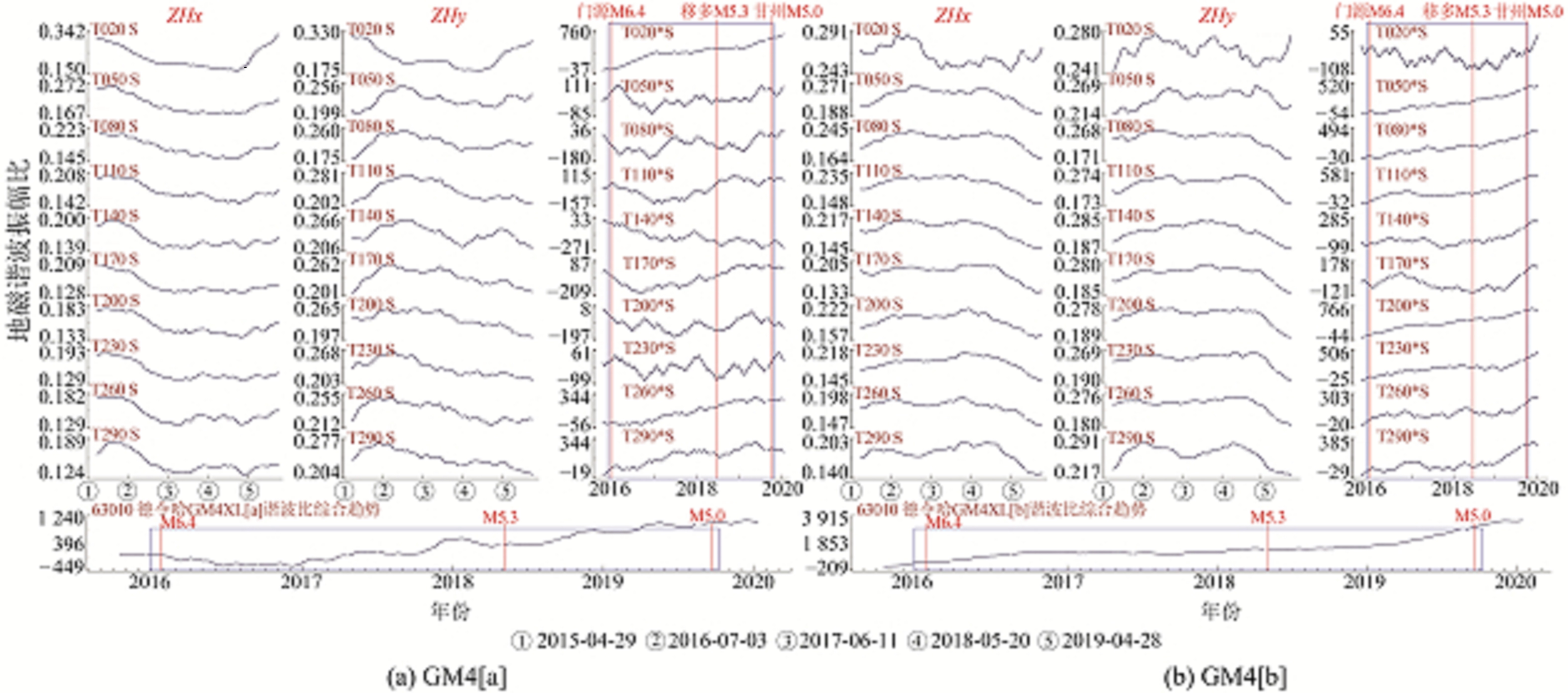
德令哈台GM4[a]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,门源6.4级地震前80 s、140 s、170 s、200 s、260 s周期曲线出现显著转折下降变化;称多5.3级地震前20 s、50 s、80 s、110 s、140 s、170 s、200 s、230 s周期曲线变化平稳,持续时间为1 a左右,在此基础上前50 s、80 s、200 s和230 s周期曲线还出现小幅度的波动变化;甘州5.0级地震前20 s、50 s、80 s、110 s、140 s、200 s、230 s周期曲线波动变化平稳,持续时间为1a,另外290 s周期曲线在震前4个月(2019-05)出现快速下降变化。异常出现29个月后发生称多5.3级地震,异常出现45个月后发生甘州5.0级地震,具体见图 3(a)。
|
图 3 德令哈台地磁谐波振幅比 Fig. 3 Geomagnetic harmonic amplitude ratio at Delhi station |
德令哈台GM4[b]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,门源6.4级地震前20 s、140 s、170 s周期曲线出现显著转折下降变化,震前50 s、80 s周期曲线均处于平稳变化阶段,地震发生在曲线转折拐点处;称多5.3级地震前20 s、110 s、140 s、170 s、230 s、260 s、290 s周期曲线变化平稳,持续时间1.5 a,其中震前20 s周期曲线波动变化显著;甘州5.0级地震前20 s周期曲线波动变化平稳,此外震前110 s、140 s、170 s、230 s、260 s周期曲线震前4个月(2019-05)异常形态恢复至正常状态。异常出现29个月后发生称多5.3级地震,异常出现45个月后发生甘州5.0级地震,具体见图 3(b)。
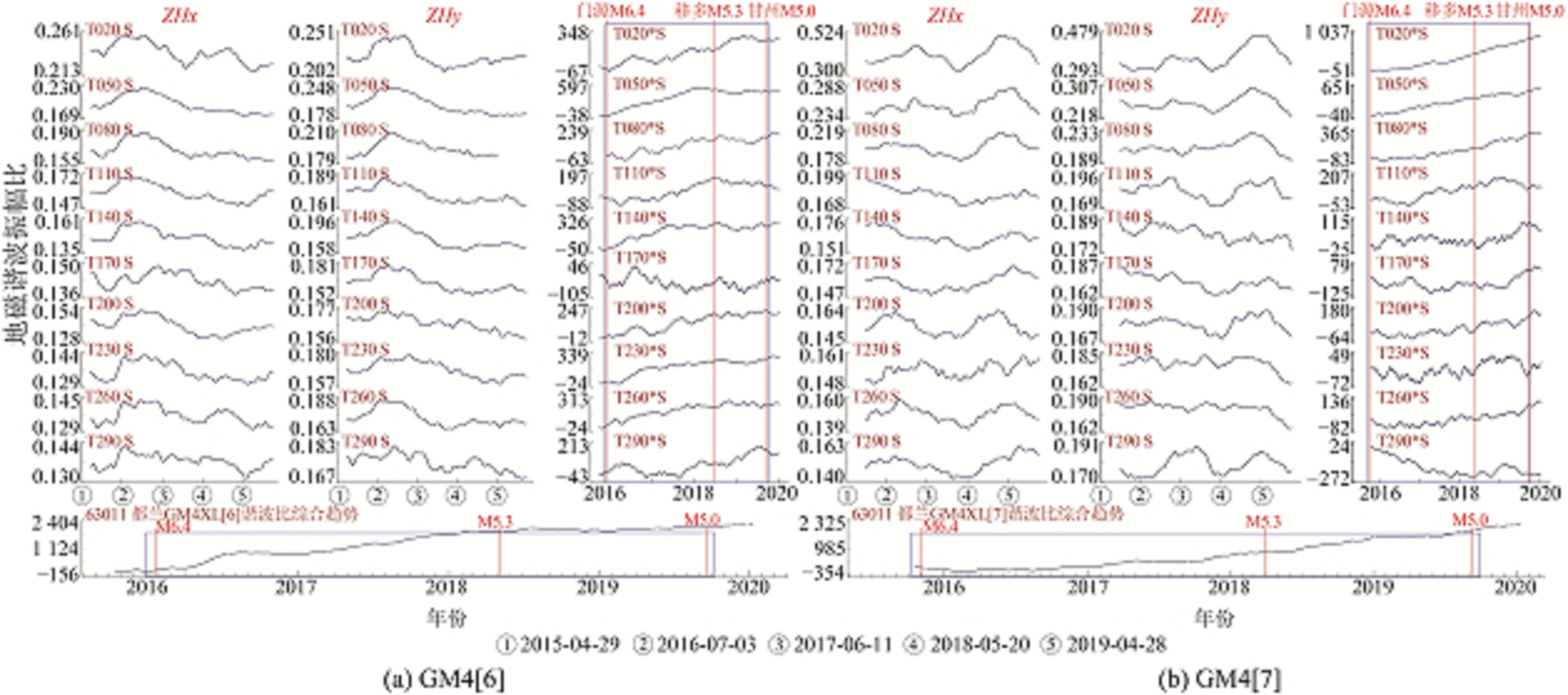
都兰台GM4[6]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,门源6.4级地震前20 s、110 s、170 s周期曲线出现显著转折下降变化,地震发生在曲线转折拐点处;称多5.3级地震前140 s、170 s、200 s、290 s周期曲线变化平稳,持续时间为1.5 a,其中震前170 s与260 s周期曲线波动变化显著;甘州5.0级地震前20 s、50 s、80 s、110 s、140 s、170 s、200 s、290 s周期曲线波动变化平稳,时间持续1 a以上。异常出现29个月后发生称多5.3级地震,异常出现45个月后发生甘州5.0级地震,具体见图 4(a)。
|
图 4 都兰台地磁谐波振幅比 Fig. 4 Geomagnetic harmonic amplitude ratio at Dulan station |
都兰台GM4[7]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,门源6.4级地震前170 s、230 s、260 s、290 s周期曲线出现显著转折下降变化,地震发生在曲线趋势下降过程中;称多5.3级地震前140 s、170 s、200 s、230 s、290 s周期曲线变化平稳,持续时间为1.5 a,其中震前170 s、200 s与230 s周期曲线波动变化显著;甘州5.0级地震前110 s、170 s、200 s、230 s、290 s周期曲线波动变化平稳,大部分持续时间1 a以上。异常出现29个月后发生称多5.3级地震,异常出现45个月后发生甘州5.0级地震,具体见图 4(b)。
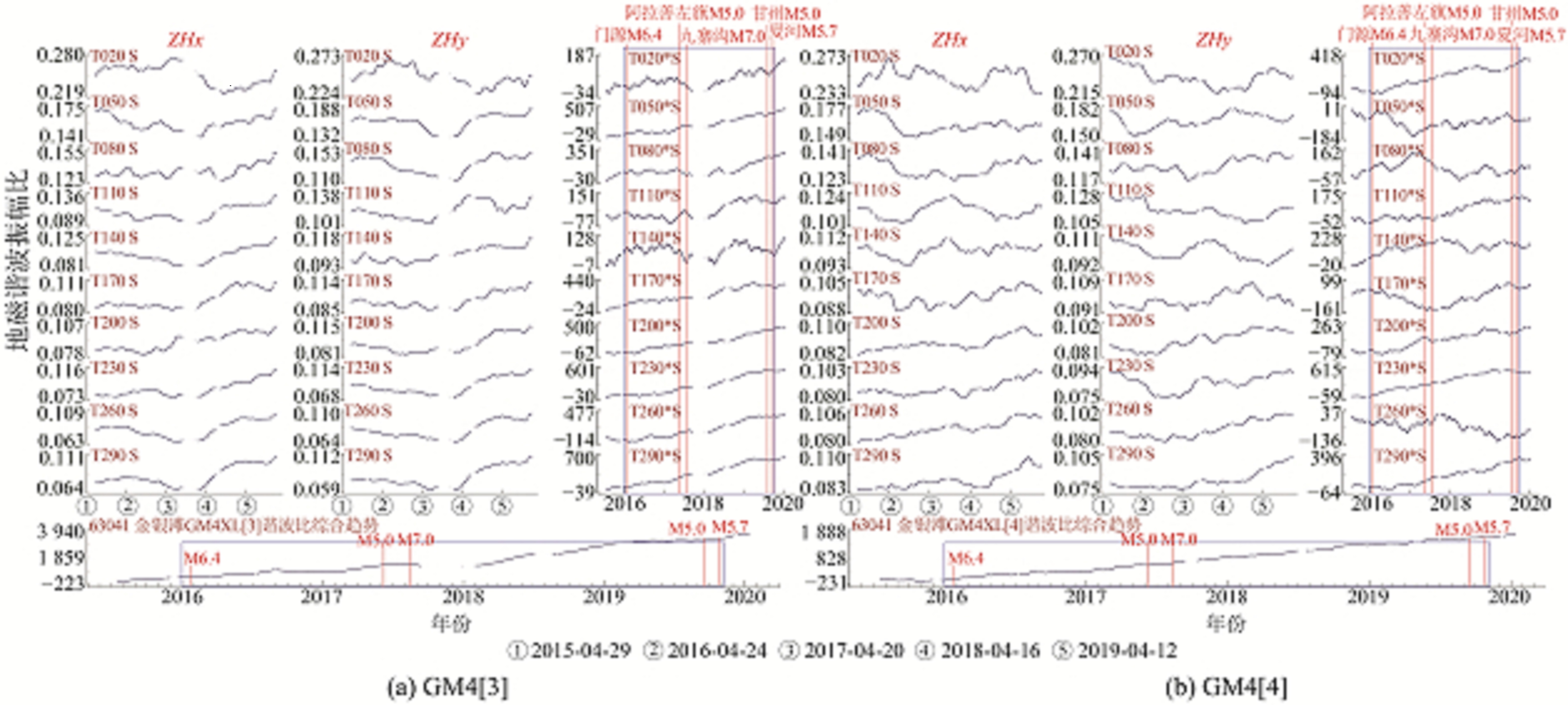
金银滩台GM4[3]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,门源6.4级地震前无显著异常出现;阿左旗5.0级和九寨沟7.0级地震前20 s、80 s、110 s、140 s周期曲线变化平稳,持续时间为1.5 a,其中震前20 s与140 s周期曲线小幅度波动变化显著;甘州5.0级和夏河5.7级地震前异常形态不显著,仅110 s和140 s的周期曲线波动变化平稳,持续时间1 a左右。异常出现18~20个月后发生阿左旗5.0级和九寨沟7.0级地震,异常出现45~46个月后发生甘州5.0级和夏河5.7级地震,具体见图 5(a)。
|
图 5 金银滩台地磁谐波振幅比 Fig. 5 Geomagnetic harmonic amplitude ratio at Jinyintan station |
金银滩台GM4[4]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,门源6.4级地震前仅50 s、260 s周期曲线出现明显下降趋势;阿左旗5.0级和九寨沟7.0级地震前50 s、80 s、110 s、170 s、260 s周期曲线变化平稳,持续时间为1.5 a,其中震前50 s与170 s周期曲线在变化初期还伴随着下降趋势;甘州5.0级和夏河5.7级地震前20 s、80 s、140 s和260 s周期曲线波动变化平稳,持续时间1.5 a左右,且200 s周期曲线在震前10个月转折变平。异常出现18~20个月后发生阿左旗5.0级和九寨沟7.0级地震,异常出现45~46个月后发生甘州5.0级和夏河5.7级地震,具体见图 5(b)。
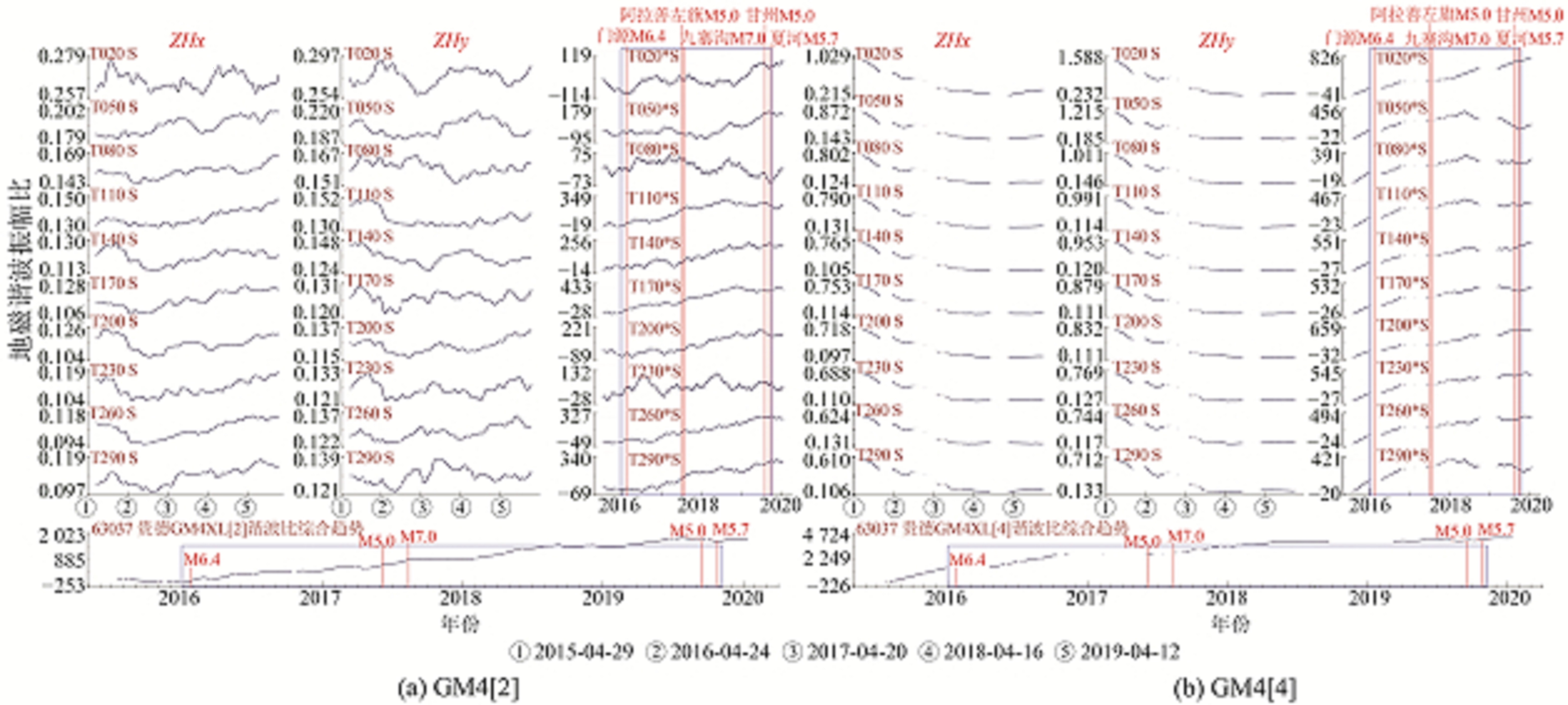
贵德台GM4[2]谐波振幅比曲线自2016年起部分速率累加曲线出现转平或连续波动变化,门源6.4级地震前仅20 s、50 s、80 s、200 s周期曲线出现明显下降趋势;阿左旗5.0级和九寨沟7.0级地震前20 s、50 s、80 s、230 s周期曲线变化平稳,持续时间为1.5 a,其中20 s、80 s与230 s周期曲线在变化初期还伴随着波动变化;甘州5.0级和夏河5.7级地震前20 s、50 s、80 s、110 s和230 s周期曲线变化平稳,持续时间1.5 a左右,且170
s周期曲线在震前10个月转折变平。异常出现18~20个月后发生阿左旗5.0级和九寨沟7.0级地震,异常出现45~46个月后发生甘州5.0级和夏河5.7级地震,具体见图 6(a)。
|
图 6 贵德台地磁谐波振幅比 Fig. 6 Geomagnetic harmonic amplitude ratio at Guide station |
贵德台GM4[4]谐波振幅比曲线在门源6.4级、阿左旗5.0级和九寨沟7.0级地震前未出现显著异常;甘州5.0级和夏河5.7级地震前速率累加曲线50 s、80 s、110 s、170 s和290 s波动变化平稳,持续时间1.5 a左右,且50 s周期曲线在异常出现初期伴随着快速下降变化。异常出现17~18个月后发生甘州5.0级和夏河5.7级地震,具体见图 6(b)。
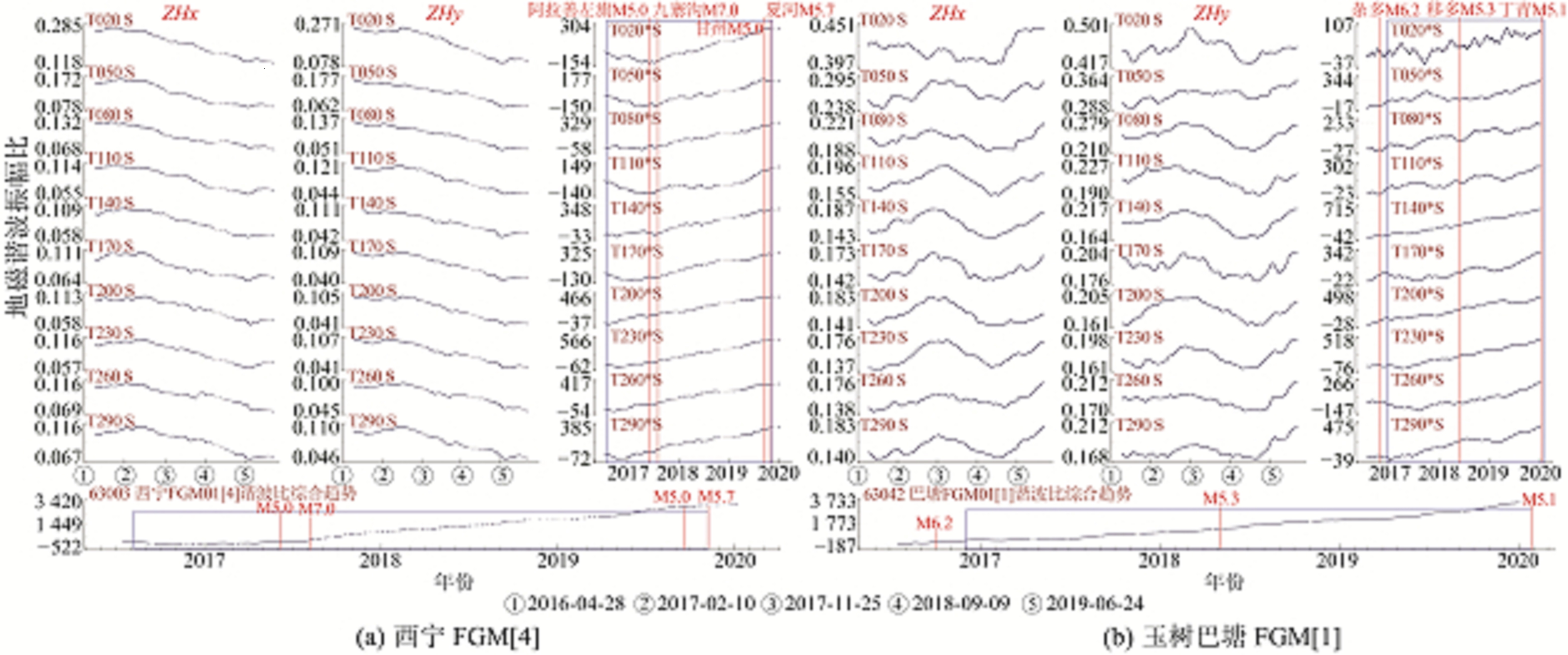
西宁台FGM[4]谐波振幅比曲线在甘州5.0级和夏河5.7级地震前未出现显著异常;阿左旗5.0级和九寨沟7.0级地震前速率累加曲线20 s、50 s、80 s、110 s、140 s、170 s自2016-04保持平稳变化,其中20 s、50 s和110 s周期曲线还伴随着小幅下降变化。异常出现14~16个月后发生阿左旗5.0级和九寨沟7.0级地震,具体见图 7(a)。
|
图 7 西宁台和巴塘台地磁谐波振幅比 Fig. 7 Geomagnetic harmonic amplitude ratio at Xi'ning and Batang station |
玉树巴塘台FGM[1]谐波振幅比曲线在杂多6.2级地震前未出现显著异常;称多5.3级地震前20 s、80 s、170 s和260 s周期曲线转平,持续时间1.5 a,期间50 s周期曲线于2018-09出现转折变化;丁青5.1级地震前仅20 s周期曲线波动变化平稳,其他周期曲线均保持正常上升趋势。异常出现17个月后发生称多5.3级地震,异常出现37个月后发生丁青5.1级地震,具体见图 7(b)。
统计地震前9组异常的基本参数信息可知,除2015年杂多6.2级地震前无异常外,其他地震震前均提取到异常信息,且异常与地磁暴无关。由于门源地震发生在观测时段1 a后,无法记录到异常开始时间,因此未统计异常持续时间,其他震例中异常持续时间最短为14个月,最长为46个月,异常周期数量较多,详细参数信息见表 1。
|
|
表 1 2015~2020年青海磁通门地磁谐波振幅比异常参数与地震对应统计 Tab. 1 Anomalous parameters and seismic statistics of geomagnetic harmonic amplitude ratio of magnetic fluxgate in Qinghai from 2015 to 2020 |
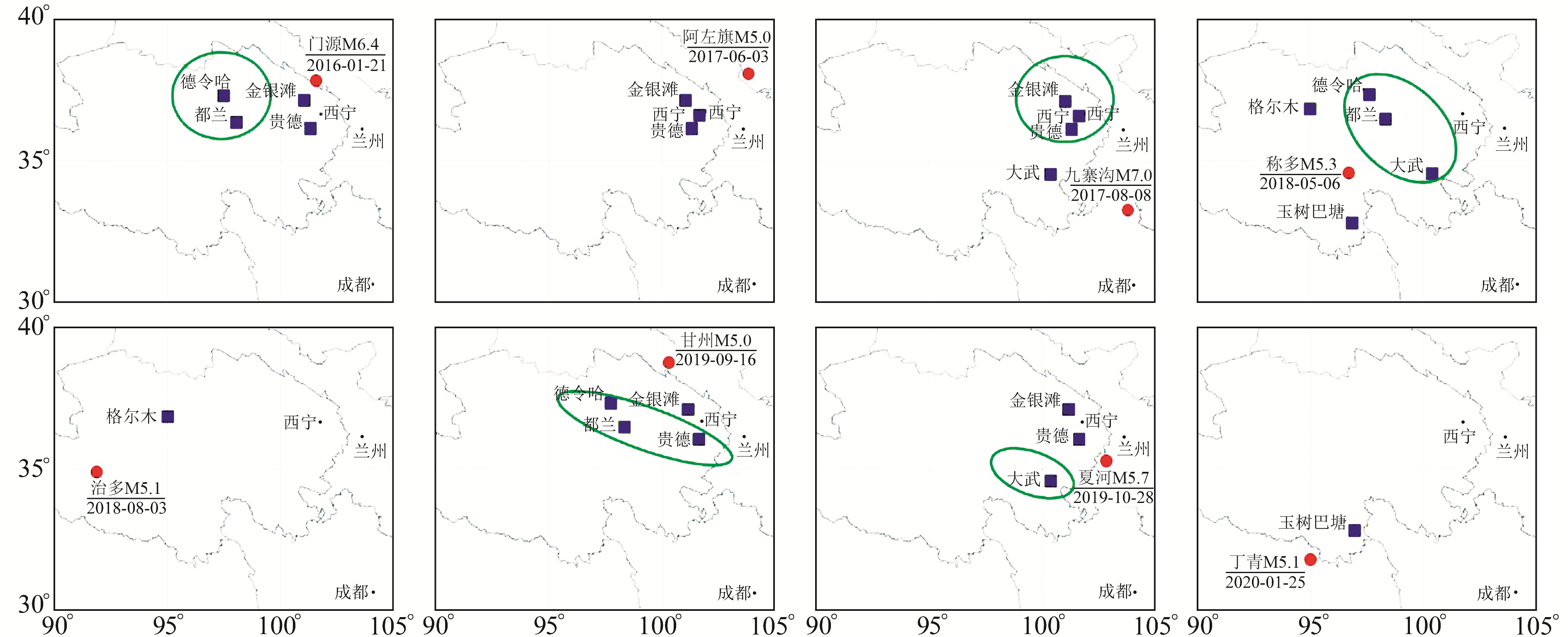
本文在总结异常的过程中发现如下规律:1)震中距较远的台站异常曲线数量较多,异常形态显著,如门源6.4级、九寨沟7.0级、称多5.3级、甘州5.0级及夏河5.7级地震震前表现出的异常特征,具体见图 8。2)异常出现后2 a内发震的频次较高(图 9(a)),对应地震中异常曲线数量超过1/2(图 9(b)),大部分分布在20~170 s周期内(图 9(c)),且震级与震中距成正比,即震级越高震中距越远(图 9 (d))。但由于样本数量有限,无法给出定量化的描述,且震级与异常曲线数量、震级与异常持续时间及震中距与异常持续时间之间并没有发现明显相关性,均比较离散。
|
图 8 异常台站与震中分布 Fig. 8 Distribution of anomalous stations and epicenters |

|
图 9 异常参数统计 Fig. 9 Statistical table of abnormal parameters |
对2015年以来青海地区14套磁通门观测资料进行地磁谐波振幅比计算,并利用速率累加法提取异常信息,从8组震例信息中总结异常规律,确定青海地区的异常判别指标和预测规则。
1) 判别指标。速率累加曲线持续上升为正常,持续下降和水平波动为异常,异常时间大于1 a,10条周期曲线中至少5条出现异常,且大部分分布在20~170 s周期范围内为异常成立。
2) 预测规则。时间:速率累加异常出现后2 a内发震概率较高;地点:震中距与震级成正比,即震中距越大震级越高;强度:M≥5。
4 结语针对当前研究中地磁谐波振幅比的成果主要为分钟值采样数据及无定量化指标2个关键问题,重新分析青海地区磁通门秒采样观测资料,并利用速率累加方法分析连续数据的逐日变化速率,再根据需要对分析时段进行累加计算,使原有异常变化更加直观和突出,异常变化幅度显著,更易于定量判定和异常指标提取。在此基础上进一步分析异常变化与强震的关系,总结青海地区磁通门秒值谐波振幅比方法的异常指标,并将研究结果应用于青海地区的震情跟踪中。需要强调的是,本文结果仅基于5 a数据计算得出,因为统计样本数量有限,不能完全反映客观规律。随着数据资料的进一步积累,异常指标将会得到完善。
| [1] |
Yanagihara K, Nagano T. Time Change of Transfer Function in the Central Japan Anomayl of Conductivity with Special Reference to Earthquake Occurrences[J]. Journal of Geomagnetism and Geoelectricity, 1976, 28(2): 157-163 DOI:10.5636/jgg.28.157
(  0) 0) |
| [2] |
陈绍明, 谢美娟, 杜锡武. 地磁短周期变化预报方法的研究[J]. 地震, 1991, 11(5): 19-25 (Chen Shaoming, Xie Meijuan, Du Xiwu. Research on Earthquake Prediction Method with Geomagnetic Short Period Variations[J]. Earthquake, 1991, 11(5): 19-25)
(  0) 0) |
| [3] |
国家地震局科技监测司. 地震预报方法实用化文集——地磁地电专集[M]. 北京: 学术期刊出版社, 1990 (Science and Technology Monitoring Department, CEA. Corpus of Practical Earthquake Prediction Methods: Electromagnetic Album[M]. Beijing: Academic Journal Press, 1990)
(  0) 0) |
| [4] |
郝锦绮, 黄平章, 张天中, 等. 岩石剩余磁化强度的应力效应[J]. 地震学报, 1989, 11(4): 381-391 (Hao Jinqi, Huang Pingzhang, Zhang Tianzhong, et al. The Stress Effect on Remanent Magnetization of Rocks[J]. Acta Seismologica Sinica, 1989, 11(4): 381-391)
(  0) 0) |
| [5] |
丁鉴海, 黄雪香, 戴淑玲. 地震活动的月相效应[J]. 地震, 1994, 14(4): 7-13 (Ding Jianhai, Huang Xuexiang, Dai Shuling. The Effect of Lunar Phase on Seismicity[J]. Earthquake, 1994, 14(4): 7-13)
(  0) 0) |
| [6] |
冯志生, 梅卫萍, 张秀霞, 等. 中强震前地磁谐波振幅比的趋势性变化特征初步研究[J]. 西北地震学报, 2004, 26(1): 50-56 (Feng Zhisheng, Mei Weiping, Zhang Xiuxia, et al. Preliminary Study on the Characteristics of Long and Medium Term Variation for the Amplitude Ratio of Geomagnetic Humorous Wave before Moderate-Strong Earthquakes[J]. Northwestern Seismological Journal, 2004, 26(1): 50-56)
(  0) 0) |
| [7] |
冯志生, 居海华, 李鸿宇, 等. 地磁谐波振幅比异常特征的进一步研究及定性解释[J]. 华南地震, 2009, 29(1): 17-23 (Feng Zhisheng, Ju Haihua, Li Hongyu, et al. Further Study on Characteristics of Long-Term and Medium-Term Variations of Geomagnetic Harmonic Wave Amplitude Ratios before Moderate or Strong Earthquakes[J]. South China Journal of Seismology, 2009, 29(1): 17-23 DOI:10.3969/j.issn.1001-8662.2009.01.003)
(  0) 0) |
| [8] |
冯志生, 李鸿宇, 张秀霞, 等. 地磁谐波振幅比异常与强地震[J]. 华南地震, 2013, 33(3): 9-15 (Feng Zhisheng, Li Hongyu, Zhang Xiuxia, et al. The Relationship between Strong Earthquake and Geomagnetic Harmonic Wave Amplitude Ratio[J]. South China Journal of Seismology, 2013, 33(3): 9-15 DOI:10.3969/j.issn.1001-8662.2013.03.002)
(  0) 0) |
| [9] |
蒋延林, 袁桂平, 李鸿宇, 等. 高邮-宝应4.9级地震地磁谐波振幅比异常特征初步分析[J]. 中国地震, 2016, 32(1): 143-150 (Jiang Yanlin, Yuan Guiping, Li Hongyu, et al. The Preliminary Analysis on the Characteristics of Geomagnetic Harmonic Wave Amplitude Ratios before the Gaoyou-Baoying MS4.9 Earthquake[J]. Earthquake Research in China, 2016, 32(1): 143-150 DOI:10.3969/j.issn.1001-4683.2016.01.014)
(  0) 0) |
| [10] |
李鸿宇, 朱培育, 王维, 等. 2013年前郭5.8级震群的地磁多方法异常分析[J]. 地震研究, 2018, 41(1): 111-117 (Li Hongyu, Zhu Peiyu, Wang Wei, et al. Geomagnetic Anomaly Analysis of Qianguo M5.8 Earthquake Swarm by Multiple Methods[J]. Journal of Seismological Research, 2018, 41(1): 111-117 DOI:10.3969/j.issn.1000-0666.2018.01.014)
(  0) 0) |
| [11] |
李鸿宇, 袁桂平, 杨云, 等. 基于速率累加算法的地磁谐波振幅比异常分析[J]. 防灾减灾工程学报, 2019, 39(6): 1010-1015 (Li Hongyu, Yuan Guiping, Yang Yun, et al. The Anomaly Analysis on Geomagnetism Harmonic Amplitude Ratio Based on Rate Accumulation Algorithm[J]. Journal of Disaster Prevention and Mitigation Engineering, 2019, 39(6): 1010-1015)
(  0) 0) |
| [12] |
倪晓寅, 陈莹. 强震前短周期地磁谐波振幅比变化特征[J]. 地震研究, 2017, 40(3): 431-436 (Ni Xiaoyin, Chen Ying. The Variation Characteristics of Short-Period Geomagnetic Harmonic Wave Amplitude Ratio before Strong Earthquakes[J]. Journal of Seismological Research, 2017, 40(3): 431-436 DOI:10.3969/j.issn.1000-0666.2017.03.019)
(  0) 0) |
| [13] |
刘素珍, 李自红, 刘瑞春. 2016年3月12日运城MS4.4地震地磁谐波振幅比异常分析[J]. 地震地磁观测与研究, 2018, 39(2): 50-56 (Liu Suzhen, Li Zihong, Liu Ruichun. Anomaly Analysis of the Amplitude Ratio of Geomagnetic Humorous for MS4.4 Yuncheng Earthquake in 2016[J]. Seismological and Geomagnetic Observation and Research, 2018, 39(2): 50-56 DOI:10.3969/j.issn.1003-3246.2018.02.007)
(  0) 0) |
| [14] |
李霞, 冯丽丽, 赵玉红, 等. 2016年门源6.4级地震地磁谐波振幅比异常特征分析[J]. 地震地磁观测与研究, 2018, 39(3): 81-88 (Li Xia, Feng Lili, Zhao Yuhong, et al. Analysis on the Magnetic Harmonic Wave Amplitude Ratio Characteristics before Menyuan MS6.4 Earthquake in 2016[J]. Seismological and Geomagnetic Observation and Research, 2018, 39(3): 81-88 DOI:10.3969/j.issn.1003-3246.2018.03.012)
(  0) 0) |
| [15] |
刘冠中, 蒋靖祥, 王建军, 等. 跨断层定点形变观测资料"速率累加分析"及其异常初步提取方法[J]. 内陆地震, 2007, 21(3): 230-237 (Liu Guanzhong, Jiang Jingxiang, Wang Jianjun, et al. "Rate Cumulation Analysis" on Cross-Fault Fixed Deformation Data and Anomaly Extraction Method[J]. Inland Earthquake, 2007, 21(3): 230-237)
(  0) 0) |
2. Qinghai Earthquake Agency, 242 Tsaidam Road, Xi'ning 810017, China
 2022, Vol. 42
2022, Vol. 42

