在观测信号质量不佳的情况下,RTK精度往往会受到观测冗余度低、中断失锁、周跳、粗差等异常问题的影响,导致模糊度难以固定,对此科技工作者开展了大量研究[1-7]。Li等[6]指出,正确求解整周模糊度的关键是观测模型的强度和偏差。国内多普勒重构研究大部分仅限于周跳检测,蔡成林等[8]提出用多普勒重构与STPIR联合探测周跳,比较载波相位计算值与观测值以检测更小的周跳;张炘等[9]通过多普勒值拟合再积分计算连续载波相位。多普勒重构依据速度与多普勒频移、多普勒频移与载波相位的关系,获得连续载波相位用于定位,能够避免受到异常观测信号的影响,得到稳定和精确的定位。
多普勒重构所需设备为全天候工作的速度计,因此重构多普勒能精确地反映载波相位的变化趋势,且不受环境影响。目前速度测量基本是以GPS组合INS惯导加速度计为主流,能够满足低速测量的要求。多普勒重构方法在理论上可以解决观测信号质量不佳的问题,简化定位步骤,结合垂直仰角选择的互差加权法降低问题信号在定位中的权重,保证单历元整周模糊度的可解算性及其正确率。
本文首先介绍基于多普勒频移重构的GNSS定位算法以及相关基础理论,阐述该算法采用的宽巷(wide-lane, WL)组合双差分技术,然后从单历元模糊度解的角度对该算法进行性能分析与评定。
1 算法基本原理 1.1 多普勒重构方法接收机实时定位数据一般不包含多普勒频移信息,而是需要通过流动站的速度测量重构多普勒频移值。重构多普勒反映出的载波相位变化量,与载波相位的计算关系如下:
| ${\varphi _t} = - \int_{ - \infty }^t {D\left( t \right)dt - {N_t}} $ | (1) |
式中,t为历元时刻,φt为t历元时刻的载波相位估计值,D(t)为重构多普勒频移值,Nt为整周模糊度。重构多普勒频移值可通过式(2)得到:
| $D\left( t \right) = \frac{{\left( {v - {v_s}} \right)\mathit{\boldsymbol{l}}}}{\lambda }$ | (2) |
式中,v为测量的接收机速度;vs为卫星速度;l为单位观测向量,l= ρ /| ρ |,ρ为方向坐标[xr-xs, yr-ys, zr-zs],(xr, yr, zr)为伪距定位坐标,(xs, ys, zs)为卫星坐标;重构多普勒频移的对应频段由波长λ决定。
此时重构值包含指数化缩小的测距码噪声和微小的测速噪声。将可视卫星与接收机的相对距离变化量看作是3次多项式的线性表达,则按照式(3)消减重构多普勒频移拟合噪声,其中a0、a1、a2、a3是拟合系数:
| $\begin{array}{l} D\left( t \right) = {a_0} + {a_1}\left( {t - {t_0}} \right) + \\ {a_2}{\left( {t - {t_0}} \right)^2} + {a_3}{\left( {t - {t_0}} \right)^3} \end{array}$ | (3) |
建立载波相位计算模型,将卫星位置、卫星速度和接收机速度等三维向量全部置于地心地固坐标系框架内,能够忽略地球自转的影响。以北斗卫星系统中B1(频率fB1=1 561.098 mHz)、B2(频率fB2=1 207.14 mHz) 两个频段的宽频组合信号为例,组合波长为λw=c/(fB1-fB2)=1.024 7 m,代入式(2)可得宽巷多普勒重构值。随着历元数的增加,可通过式(3)得到拟合去噪的多普勒重构值Dw(t)。假设接收机从某时段观测到无异常载波相位φ0, w开始,每经过一个历元间隔ΔT,便计算出对应接收机与北斗卫星的距离变化量S,经过连续的一段时间后即可得到载波相位值φt, w。
代表可视卫星与接收机相对位移的距离变化量为:
| $ \begin{array}{l} {{\rm{S}}_{t - 1}} = {\lambda _w}\int_t^{t + 1} {\nabla \Delta {D_{\rm{w}}}\left( t \right){\rm{d}}t = \frac{1}{2}{\lambda _{\rm{w}}}\Delta T\left( {\nabla \Delta {D_{t + 1, {\rm{w}}}} + } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\nabla \Delta {D_{t, {\rm{w}}}}} \right) = {\lambda _{\rm{w}}}\left( {\nabla \Delta {\varphi _{t + 1, {\rm{w}}}} - \nabla \Delta {\varphi _{t, {\rm{w}}}}} \right) \end{array} $ | (4) |
在得到每个时刻的距离变化量后,计算宽巷双差载波相位:
| $ \begin{array}{l} {\lambda _{\rm{w}}}\nabla \Delta {\varphi _{t, {\rm{w}}}} = {\lambda _{\rm{w}}}\nabla \Delta {\phi _{0, {\rm{w}}}} + {\lambda _{\rm{w}}}\mathop \smallint \limits_0^t \nabla \Delta {D_{\rm{w}}}\left( t \right){\rm{d}}t = \\ \;\;\;\;\;\;\;\;\;\;{\lambda _{\rm{w}}}\nabla \Delta {\varphi _{0, {\rm{w}}}} + {{\rm{S}}_0} + {{\rm{S}}_1} + \cdots + {{\rm{S}}_{t - 1}} \end{array} $ | (5) |
式中,▽Δ为星间单差和站间单差的双差算子,下标w为宽巷组合。
宽巷双差观测方程y=Hx的矩阵形式为:
| $ \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\beta _1}}\\ {{\beta _2}}\\ {\begin{array}{*{20}{c}} \vdots \\ {{\beta _n}} \end{array}} \end{array}}\\ {\begin{array}{*{20}{c}} {{\alpha _1}}\\ {{\alpha _2}}\\ {\begin{array}{*{20}{c}} \vdots \\ {{\alpha _n}} \end{array}} \end{array}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{B}}&\mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{B}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{X}}\\ {{\mathit{\boldsymbol{N}}_{\rm{w}}}{\lambda _{\rm{w}}}} \end{array}} \right] $ | (6) |
式中,β为宽巷双差载波相位计算值与几何距离之差,α为宽巷双差测距码观测值与几何距离之差,n为单历元可视卫星个数,B为泰勒级数展开的n×3线性系数矩阵,I为n×n单位矩阵,X为流动站坐标向量,Nw为宽巷模糊度向量。
得到宽巷双差载波相位后,采用垂直仰角选择的互差加权法估计观测方程y=Hx中的整周模糊度和坐标。向量β=[β1 β2 … βn]和α=[α1 α2 … αn]所对应的接收机与可视卫星间垂直仰角的向量为γ=[γ1 γ2 … γn],从中选出最小垂直仰角γmin≤[γ1 γ2 … γn]、对应元素γ(min)的位置以及对应垂直仰角最小的卫星;选出βSTD=β(min)和αSTD=α(min)作为互差标准量,式(7)中其余向量元素与互差标准量相减可得权重向量w:
| $ \mathit{\boldsymbol{w = }}\left\{ \begin{array}{l} {w_1} = \left| {{\beta _1} - {\beta _{{\rm{STD}}}}} \right|\\ {w_2} = \left| {{\beta _2} - {\beta _{{\rm{STD}}}}} \right|\\ \;\;\;\;\;\;\;\;\; \vdots \\ {w_n} = \left| {{\beta _n} - {\beta _{{\rm{STD}}}}} \right|\\ {w_{n + 1}} = \left| {{\alpha _1} - {\alpha _{{\rm{STD}}}}} \right|\\ {w_{n + 2}} = \left| {{\alpha _2} - {\alpha _{{\rm{STD}}}}} \right|\\ \;\;\;\;\;\;\;\;\;\; \vdots \\ {w_{2n}} = \left| {{\alpha _n} - {\alpha _{{\rm{STD}}}}} \right| \end{array} \right. $ | (7) |
此时向量w中会出现0元素wmin,将wmin设置为0.001的经验值。这是因为选择将垂直仰角最小的卫星αSTD作为互差标准量,意味着将垂直仰角最小的那颗卫星的权重设为最大值。对于两旁有遮挡物道路上的移动接收机,最佳GNSS信号接收方向只有U向。随着垂直仰角的增大,接收信号受遮挡的可能性增大,权重减小,这样才可以保证在联合伪距的组合定位中将有问题测距码的影响最小化。
互差加权矩阵为:
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{w_1}}}}&0& \ldots &0\\ 0&{\frac{1}{{{w_2}}}}& \ldots &0\\ \vdots & \vdots & \ddots &0\\ 0&0&0&{\frac{1}{{{w_{2n}}}}} \end{array}} \right] $ | (8) |
加权最小二乘为:
| $ \begin{array}{l} \hat x = x + {\rm{\Delta }}x = x + {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{W}}^{ - 1}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}*\\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{W}}^{ - 1}}\mathit{\boldsymbol{y}}, \left\| {{\rm{\Delta }}x} \right\| < \tau \end{array} $ | (9) |
式中,τ为设置的阈值,Δx为坐标改变量。当几何变化距离‖Δx‖小于阈值时,停止式(9)的迭代,解算出接收机坐标
实验使用湘潭大学智能导航实验室两台三频GNSS接收机(PANDA PD318型号和BDSTAR M66型号),天线安装在信息楼楼顶,已通过标准测绘仪器得到两个天线的地心地固(ECEF)坐标,采样率为1 s。给出不同的单历元定位精度作为对照,以验证本文算法的优越性。
基于多普勒频移重构的GNSS定位算法步骤如下:1)实时获取基站和流动站测距码观测值,测量流动站速度;2)实时预处理,包括拟合去噪、宽巷组合、双差、计算载波相位等;3)采用互差加权法估计式(6)获得协方差矩阵和浮点解;4)采用Lambda算法依据协方差矩阵搜索宽巷整周模糊度;5)将宽巷整周模糊度还原成L1单频载波相位的整周模糊度;6)利用以单频整周模糊度为约束的互差加权法解算出流动站坐标固定解。
2.1 重构多普勒频移与多普勒频移观测量的比较以重构B1、B2双频的多普勒频移为例,在静止状态下通过前后历元频移值相减的方式计算其中的噪声变化。对比图 1(a)、(b)可以看出重构多普勒与多普勒观测值的区别:拟合过的重构多普勒频移是线性无噪的,单调线性增长曲线可反映卫星与接收机的相对运动轨迹,两个频段的多普勒值明显分离,符合多普勒效应受传播信号频率高低影响的特性;而多普勒观测值掺杂观测噪声,两个频段的多普勒值因近似重合而无法得到精确值,这也是多普勒观测值仅用于大周跳探测而多普勒重构值可用于小周跳探测的原因[8]。

|
图 1 重构多普勒频移与多普勒频移观测量的对比 Fig. 1 Difference between reconstructed Doppler shift and Doppler shift observation |
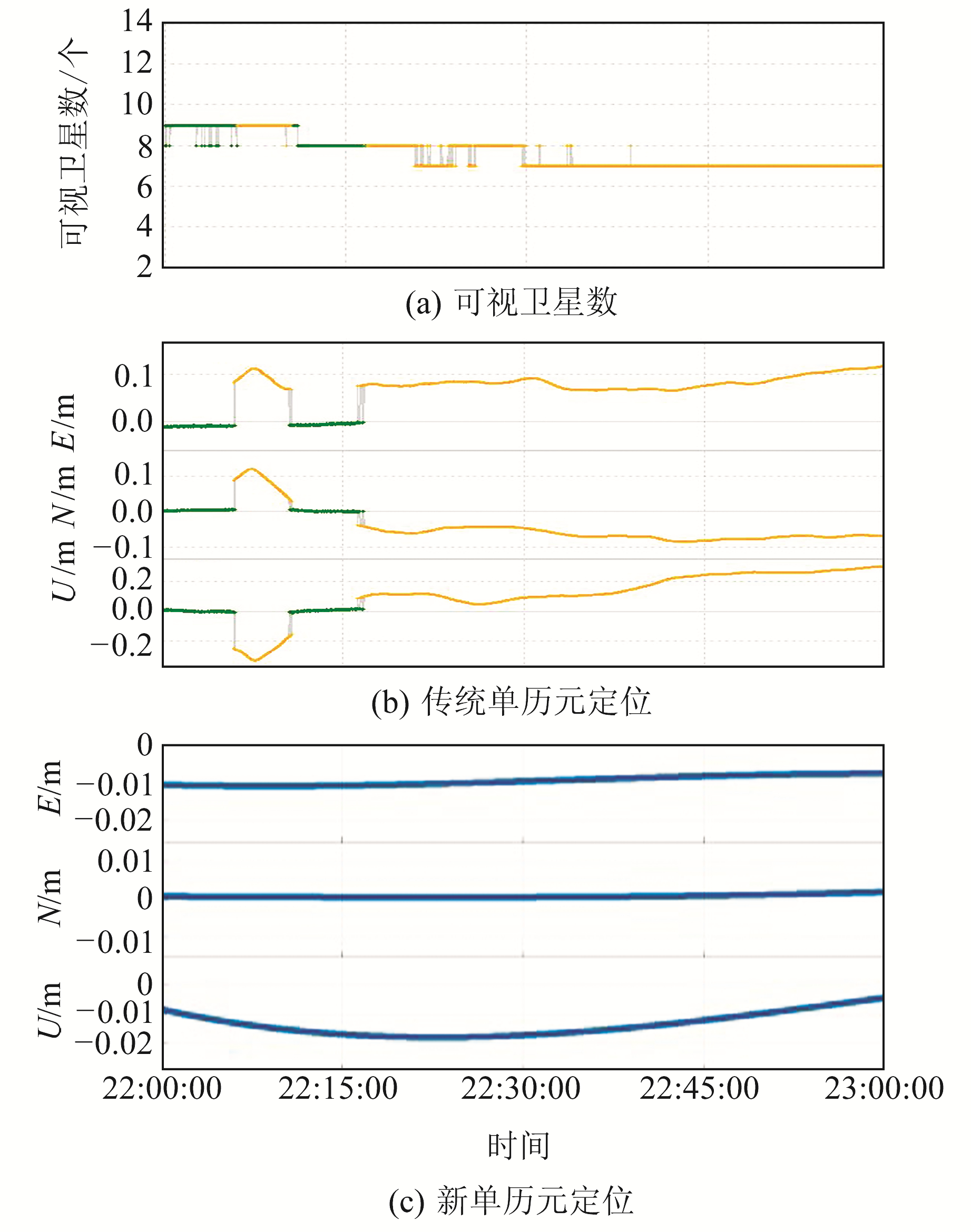
静态实验选取2021-06-03~04 22:00~23:00时段的单GPS双频(fL1=1 575.42 mHz、fL2=1 227.6 mHz)观测值作为实验数据。使用传统单历元定位算法与本文算法进行比较,解算出的坐标以标准坐标为基准转换成E、N、U坐标(图 2),见表 1(单位cm)。可以看出,在可视卫星数少于9个的情况下,观测信号冗余程度低,传统的单历元定位的整周模糊度很难固定,结果基本上是浮点解;而本文算法在全部历元内解出了流动站的精确坐标。
|
图 2 传统单历元定位和新单历元定位的E、N、U方向定位精度比较 Fig. 2 Comparison of positioning accuracy of E, E, U directions between traditional single epoch positioning and new single epoch positioning |
|
|
表 1 两种单历元定位的平均精度统计 Tab. 1 Average accuracy statistics of two single-epoch positioning methods |
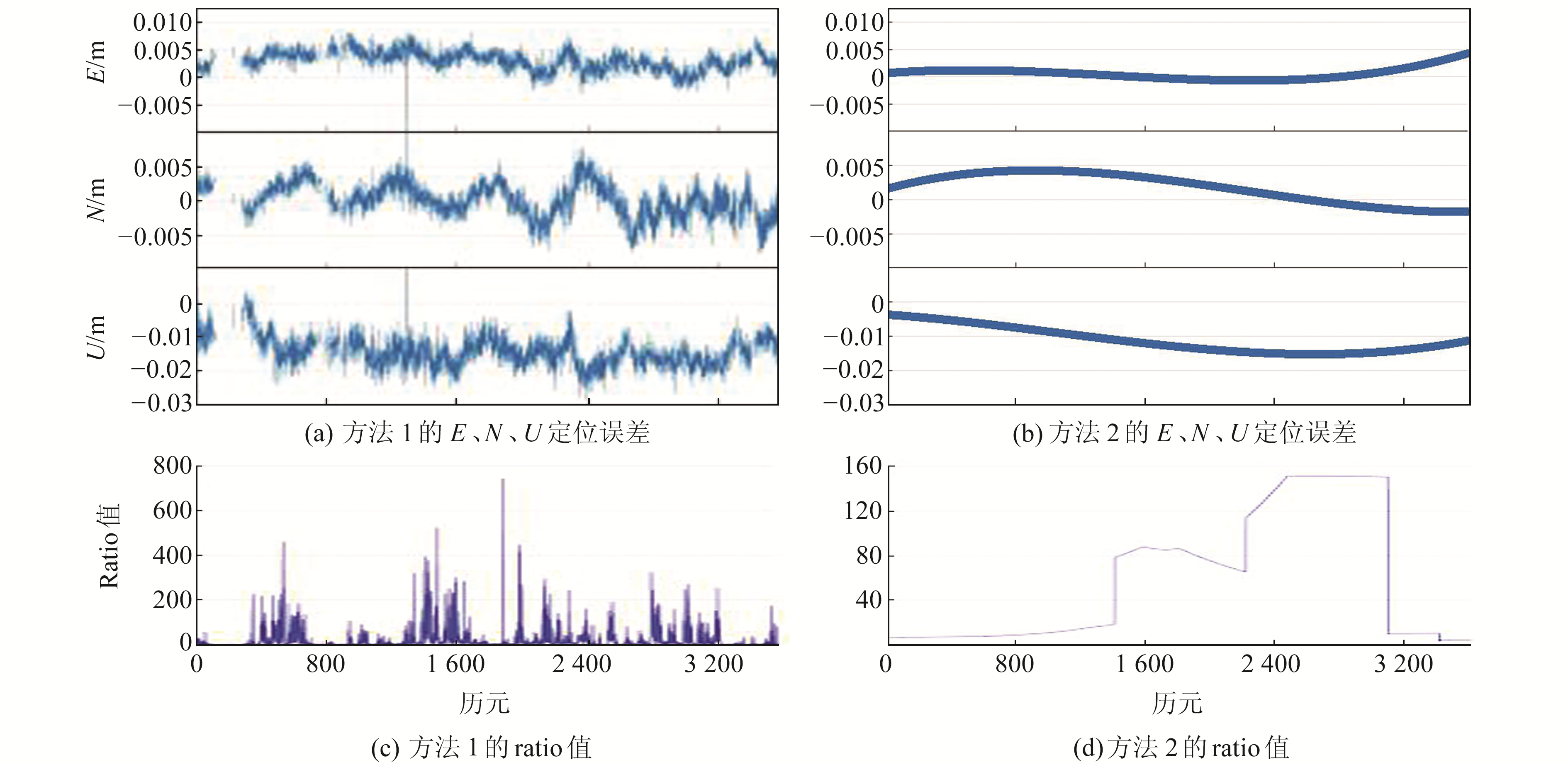
再取17:00~18:00时段单GPS观测数据用于基于互差加权的定位算法(方法1)和本文算法(方法2)的定位比较,实验结果如图 3所示,数据见表 2(单位cm),两种方法的ratio经验阈值分别取2和3。
|
图 3 两种定位方法的误差比较 Fig. 3 Error comparison of two positioning methods |
|
|
表 2 两种定位实验的统计结果 Tab. 2 Statistical results of two positioning experiments |
由表 2可知,两种方法定位误差的RMS值和均值均在cm级;方法2的标准差偏小且最大值和最小值没有出现较大偏离,表明方法2的定位结果更加稳定;反观方法1的E方向和U方向都存在较大偏差,影响整体定位的稳定性。比较图 3(c)、(d)可以看出,方法2的ratio值偏小且基本稳定在200以下,方法1有些ratio值的极值比方法2的极值高出1~5倍,但方法2的平均ratio值更大,说明方法2具有低ratio值高精度的特性,更容易固定模糊度,因此方法2的模糊度固定率能达到100%。综上所述,本文算法能在观测信号冗余程度低的情况下提供较高的整周模糊度固定率和正确率。
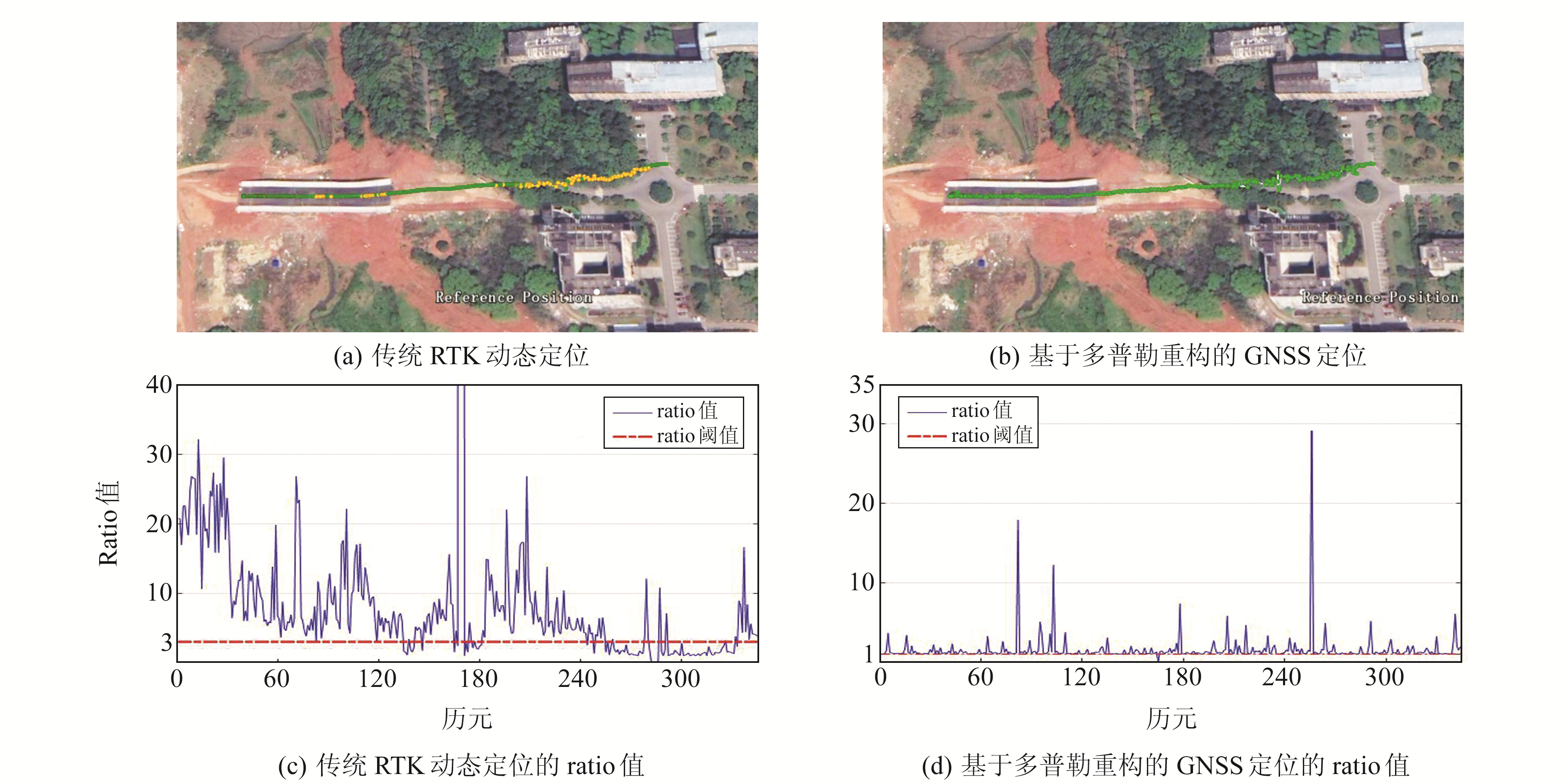
2.2.2 动态实验动态实验于2021-06-08展开,将信息楼顶部所架设的PANDA接收机天线作为参考站。如图 4所示,流动站从左边大桥位置开始采集GPS、北斗双系统观测数据,沿着直线道路以平均1 m/s的低速移动,采集时间约为6 min30 s,采样间隔为1 s,截止高度角设置为10°。图 4(a)、(b)中黄色节点代表浮点解、绿色节点代表固定解。由图 4(a)可见,当流动站经过不能很好地接收观测信号的路段时,传统RTK定位无固定整周模糊度解,依靠浮点解定位。图 4(c)、(d)中本文算法的动态经验阈值设置为1,传统RTK动态定位的阈值设置为3。表 3中传统RTK动态定位通过阈值的模糊度固定率为73.62%,本文算法通过阈值的模糊度固定率为100%,两者的定位精度基本一致,展示了本文算法在动态情形下的定位精度和固定率。
|
图 4 动态定位结果比较 Fig. 4 Comparison of dynamic positioning results |
|
|
表 3 动态定位结果统计 Tab. 3 Statistical results of dynamic positioning |
本文研究多普勒频移重构的GNSS定位算法在静、动态定位中的应用。实验结果表明,相较于无垂直仰角选择加权、无多普勒重构的传统定位方法,本文算法在冗余程度低的静态实验中保证了至少cm级精度和100%模糊度固定率;在动态实验中本文算法精度与传统RTK定位精度基本持平,固定率也达到了100%。表明在接收观测信号质量不佳的情况下,本文算法依旧能够保持较高的精度和模糊度固定率。
| [1] |
Chang G B, Xu T H, Yao Y F, et al. Adaptive Kalman Filter Based on Variance Component Estimation for the Prediction of Ionospheric Delay in Aiding the Cycle Slip Repair of GNSS Triple-Frequency Signals[J]. Journal of Geodesy, 2018, 92(11): 1 241-1 253 DOI:10.1007/s00190-018-1116-4
(  0) 0) |
| [2] |
Zhou Z B, Li B F. Optimal Doppler-Aided Smoothing Strategy for GNSS Navigation[J]. GPS Solutions, 2017, 21(1): 197-210 DOI:10.1007/s10291-015-0512-y
(  0) 0) |
| [3] |
潘树国, 王庆, 彭慧. 基于伪距宽巷组合的GPS模糊度固定方法[J]. 中国惯性技术学报, 2008, 16(6): 699-702 (Pan Shuguo, Wang Qing, Peng Hui. GPS Baseline Ambiguity Fixing Method Based on Pseudorange Widelane Combination Observation[J]. Journal of Chinese Inertial Technology, 2008, 16(6): 699-702)
(  0) 0) |
| [4] |
Corbett S J, Cross P A. GPS Single Epoch Ambiguity Resolution[J]. Survey Review, 1995, 33(257): 149-160 DOI:10.1179/sre.1995.33.257.149
(  0) 0) |
| [5] |
Duong V, Harima K, Choy S, et al. An Assessment of Wide-Lane Ambiguity Resolution Methods for Multi-Frequency Multi-GNSS Precise Point Positioning[J]. Survey Review, 2020, 52(374): 442-453 DOI:10.1080/00396265.2019.1634339
(  0) 0) |
| [6] |
Li B F, Verhagen S, Teunissen P J G. Robustness of GNSS Integer Ambiguity Resolution in the Presence of Atmospheric Biases[J]. GPS Solutions, 2014, 18(2): 283-296 DOI:10.1007/s10291-013-0329-5
(  0) 0) |
| [7] |
李昕, 郭际明, 章迪, 等. 基于多普勒测速的GPS单历元动态定位算法[J]. 武汉大学学报: 信息科学版, 2018, 43(7): 1 036-1 041 (Li Xin, Guo Jiming, Zhang Di, et al. An Algorithm of GPS Single-Epoch Kinematic Positioning Based on Doppler Velocimetry[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7): 1 036-1 041)
(  0) 0) |
| [8] |
蔡成林, 沈文波, 曾武陵, 等. 多普勒积分重构与STPIR联合周跳探测与修复[J]. 测绘学报, 2021, 50(2): 160-168 (Cai Chenglin, Shen Wenbo, Zeng Wuling, et al. Detect and Repair Cycle-Slip by Reconstruction Doppler Integral Algorithm and STPIR[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(2): 160-168)
(  0) 0) |
| [9] |
张炘, 蔡成林, 唐振辉, 等. 一种基于多普勒改进的BDS单频观测值周跳探测与修复法[J]. 天文学报, 2017, 58(2): 42-48 (Zhang Xin, Cai Chenglin, Tang Zhenhui, et al. A Method of Detecting and Repairing Cycle-Slip Based on Doppler Improved BDS Single-Frequency Observations[J]. Acta Astronomica Sinica, 2017, 58(2): 42-48)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


