重力辅助惯性导航具有自主性强、隐蔽性好、抗干扰性强、不受地域和时域限制以及定位精度高等诸多优点,是目前水下潜器实现长时间安全航行的重要手段之一[1-2]。惯性导航(下文简称惯导)的解算精度会极大地影响重力辅助导航的精度,其解算核心是姿态更新,姿态的精度又会直接影响速度、位置以及重力匹配的精度[3-5],因此需要对各种姿态算法的精度和适用性进行研究。最常用的姿态求解方法为经典多子样算法和多子样优化算法,但经典多子样算法只考虑了Bortz方程[6]的二阶项,存在原理误差,会出现高子样算法精度低于低子样算法精度的现象[3-4];多子样优化算法只适用于小角度锥角和低动态载体的姿态求解[7-8]。宋敏[9]提出适用于大机动环境下载体姿态求解的扩展圆锥误差补偿算法,但只考虑了Bortz方程的二阶项,仍存在原理误差;严恭敏等[4]基于四元数微分方程给出了姿态更新的迭代算法,算法在推导过程中未作任何假设,有效避免了原理误差。本文以圆锥运动作为姿态算法的测试输入,通过仿真实验分析经典多子样算法、多子样优化算法、扩展圆锥误差补偿算法以及基于迭代的姿态更新算法的精度、计算量和适用范围,给出适用于水下工作环境的惯导姿态求解算法。
1 姿态更新算法与测试 1.1 经典多子样算法与多子样优化算法假设陀螺在姿态更新周期[0, T]内进行了N次等间隔角增量采样(N子样),则等效旋转矢量φ(T)的经典多子样算法计算公式为[10]:
| $\mathit{\boldsymbol{\varphi }}\left( T \right) = \mathop \sum \limits_{i = 1}^N \Delta {\mathit{\boldsymbol{\theta }}_i} + \mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = i + 1}^N {k_{ij}}\Delta {\mathit{\boldsymbol{\theta }}_i} \times \Delta {\mathit{\boldsymbol{\theta }}_j}$ | (1) |
式中,Δθi为姿态更新周期内的N个角增量,kij为各子样对应的不可交换的误差补偿系数,具体数值见文献[10]。
等效旋转矢量φ(T)的多子样优化算法为[8]:
| $\mathit{\boldsymbol{\varphi }}\left( T \right) = \mathop \sum \limits_{i = 1}^N \Delta {\mathit{\boldsymbol{\theta }}_i} + \mathop \sum \limits_{j = 1}^{N - 1} {k_{N - i}}\Delta {\mathit{\boldsymbol{\theta }}_j} \times \Delta {\mathit{\boldsymbol{\theta }}_N}$ | (2) |
式中,kN-i为各子样对应的圆锥误差补偿系数,具体数值见文献[8]。
1.2 扩展圆锥误差补偿算法与基于四元数微分方程迭代的姿态更新算法为使大机动环境下的载体姿态求解具有较高精度,宋敏[9]提出扩展的圆锥误差补偿算法及其优化方法,具体步骤见文献[9]。严恭敏等[4]提出基于四元数微分方程迭代的姿态更新算法,通过迭代计算给出姿态更新的精确数值解,推导过程见文献[4]。由于迭代算法在原理上未作任何假设,因此可获得等效旋转矢量的精确数值解,具有良好的环境适应性,但缺点是计算量较大[4]。
1.3 圆锥运动假设圆锥运动的锥轴为x轴,半锥角为φ,圆锥运动频率为f,振动角频率为Ω(Ω=2πf)。当t>0时,动坐标系(b系)相对于参考坐标系(i系)的变换四元数Q(t)、角速度ω(t)、等效旋转矢量φ(t)分别为[11]:
| $\begin{array}{l} \mathit{\boldsymbol{Q}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} {\cos (\varphi /2)}\\ 0\\ {\sin (\varphi /2)\cos \mathit{\Omega }t}\\ {\sin (\varphi /2)\sin \mathit{\Omega }t} \end{array}} \right]\\ \mathit{\boldsymbol{\omega }}\left( t \right) = \mathit{\Omega }\sin \varphi \left[ {\begin{array}{*{20}{c}} { - \tan (\varphi /2)}\\ { - \sin \mathit{\Omega }t}\\ {\cos \mathit{\Omega }t} \end{array}} \right]\\ \mathit{\boldsymbol{\varphi }}\left( t \right) = \mathit{\boldsymbol{\varphi }}\left[ {\begin{array}{*{20}{c}} 0\\ {\cos \mathit{\Omega }t}\\ {\sin \mathit{\Omega }t} \end{array}} \right] \end{array}$ | (3) |
根据式(3)可计算出任意时刻圆锥运动的姿态,并作为参考姿态与姿态更新算法解算出的姿态作差获得失准角误差,从而实现对姿态算法的精度评定。
2 仿真实验与分析水下潜器上搭载的惯导会受到周期性机械振动噪声、螺旋桨噪声和水动力噪声的影响[12],容易激发出圆锥角运动。但由于水下潜器质量巨大且航行过程较为平稳,潜器不会出现大角度的机动,且圆锥运动的半锥角也不会过大。因此,半锥角为5°的圆锥运动与潜器的实际运动情况较为相符。
以圆锥运动作为测试输入对经典多子样算法、多子样优化算法、扩展圆锥补偿算法、迭代更新算法进行仿真实验。设置圆锥运动频率f=1 Hz,角增量采样间隔为0.01 s,半锥角φ分别取1′和5°,子样数分别取2~6(扩展圆锥算法最高为5子样),仿真时长为1 h。以锥轴方向姿态每小时的漂移角度作为衡量算法精度的指标(通常要求算法漂移的角度误差小于1″/h),以各种算法的运行时间作为算法的计算量。算法运行环境为Windows 10 64 bit,MATLAB R2018a。
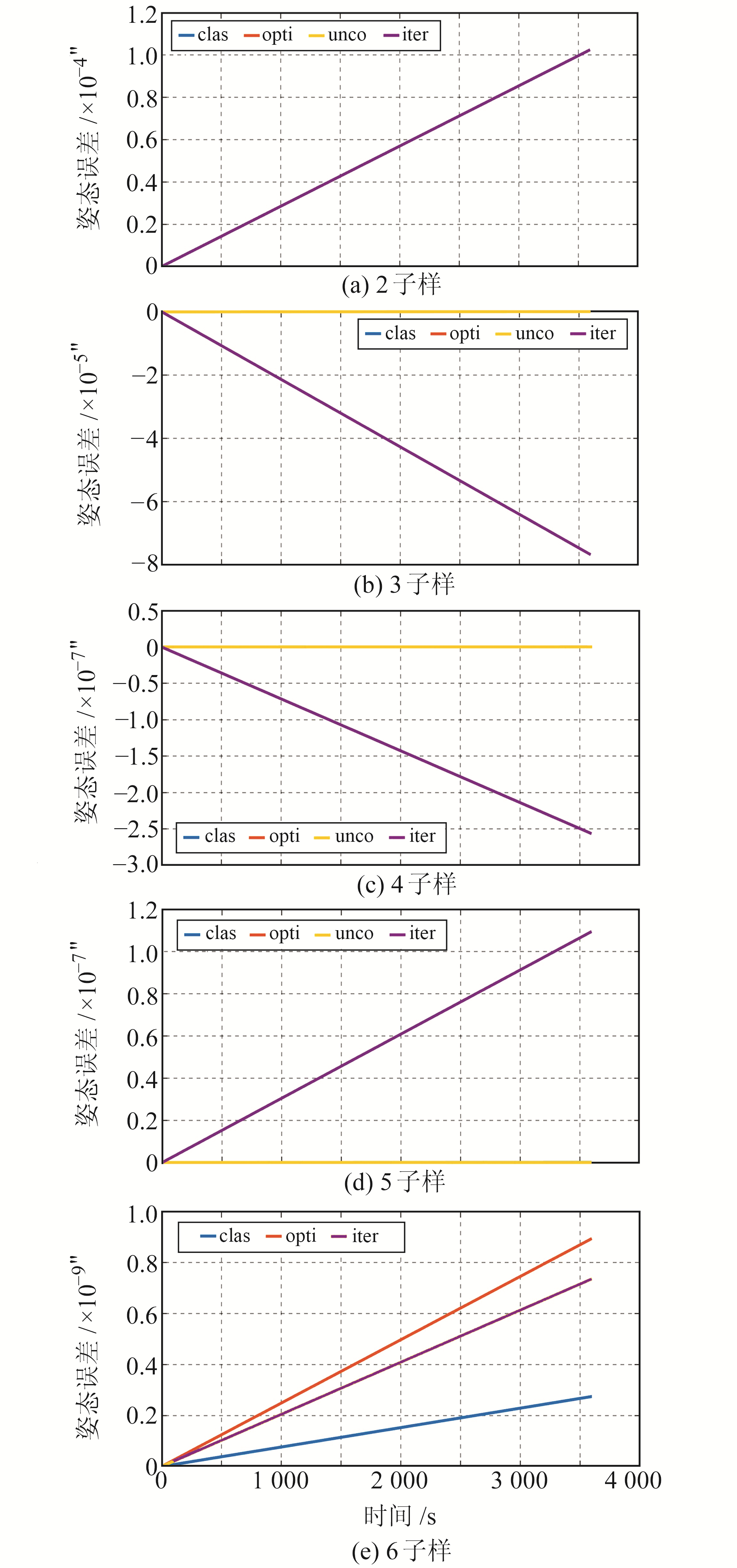
2.1 仿真实验1为考察载体在小角度半锥角低动态环境下各算法的求解精度和计算量,取半锥角φ为1′,子样数为2~6。不同子样数下各算法锥轴方向的姿态漂移角度如图 1所示,各方向误差最大值的绝对值如表 1、表 2和表 3所示(单位″/h)。不同子样数下各姿态更新算法的运行时间如表 4所示(单位s),其中clas为经典多子样算法,opti为多子样优化算法,unco为扩展圆锥误差补偿算法,iter为姿态更新迭代算法。
|
图 1 2~6子样数下锥轴方向姿态漂移角度 Fig. 1 Attitude drift angle of cone axis under two to six sub-samples |
|
|
表 1 X轴(锥轴)误差最大值 Tab. 1 Maximum error of X axis (cone axis) |
|
|
表 2 Y轴误差最大值 Tab. 2 Maximum error of Y axis |
|
|
表 3 Z轴误差最大值 Tab. 3 Maximum error of Z axis |
|
|
表 4 运行时间 Tab. 4 Running time |
由表 1可见,当半锥角为小角度时,各算法各子样的姿态误差量级最大为10-4″/h,均满足姿态求解的精度要求。随着子样数的增加,各算法姿态求解的精度逐渐提高,在相同子样数下,unco精度最高、opti次之、clas最低,这与理论上3种算法在同一子样数下的精度大小是一致的。当子样数为2时,各算法精度相当且均满足解算精度要求,因此为提高解算频率,建议采用2子样进行解算。由表 2和表 3可见,除锥轴方向外,各算法在其他两个轴向上姿态漂移角度的量级均为10-9″/h,可忽略不计。由表 4可见,unco、opti和clas运行时间大致相同,而iter的运行时间较长。
2.2 仿真实验2为考察潜器在实际运动情况下各算法的求解精度和计算量,取半锥角φ为5°,子样数为2~6。不同子样数下各算法锥轴方向的姿态漂移角度如图 2所示,各方向误差最大值的绝对值如表 5、表 6和表 7所示(单位″/h),不同子样数下各算法的运行时间如表 8所示(单位s)。

|
图 2 2~6子样数下锥轴方向姿态漂移角度 Fig. 2 Attitude drift angle of cone axis under two to six sub-sample |
|
|
表 5 X轴(锥轴)误差最大值 Tab. 5 Maximum error of X axis(cone axis) |
|
|
表 6 Y轴误差最大值 Tab. 6 Maximum error of Y axis |
|
|
表 7 Z轴误差最大值 Tab. 7 Maximum error of Z axis |
|
|
表 8 运行时间 Tab. 8 Running time |
由表 5可见,当半锥角为5°、子样数大于3时clas、opti、unco的精度会随子样数的增加而降低,这与严恭敏等[4]的结论相同。当姿态角不满足小角度条件时,clas会有部分子样数精度低于1″/h,难以满足姿态解算的精度要求。而iter的精度会随子样数的增加而逐渐升高,当子样数大于3时,角度漂移量小于0.03″/h,能够满足姿态求解精度的要求。由表 6和表 7可见,除锥轴方向外各算法在其他两个轴向上的姿态误差可以忽略不计,clas、opti、unco的漂移角度均随子样数的增加而逐渐增大,而iter的漂移角度却随子样数的增加而逐渐减小。对比同一子样数下各算法在其他两个轴向上的姿态漂移角度可知,iter的漂移角度最小,clas与unco大致相当,opti漂移最为严重(最大值接近0.11″/h),这是由于推导圆锥误差补偿系数时未对其他两个方向上的分量进行补偿所致。由表 8可见,unco、opti和clas运行时间大致相同,而iter的运行时间较长。
3 结语本文以圆锥运动作为姿态更新算法的测试输入,对现有姿态更新算法进行仿真研究,对比分析各种算法的精度、计算量以及适用范围,得出如下结论:
1) 当载体处于小角度低动态环境时,多子样优化算法、经典多子样算法、扩展圆锥误差补偿算法和迭代算法均能满足姿态解算的精度要求。为获得更高的姿态解算频率,建议采用2子样解算。
2) 当载体处于大角度低动态或高动态环境时,迭代算法具有明显的优势,能够更好地适应环境,在锥轴或非锥轴方向上均具有较高的补偿精度,可以精确地进行姿态求解。其缺点在于计算量较大,但现代导航计算机的高性能处理能力能够满足导航实时计算的要求。
3) 综合考虑水下潜器实际所处环境、姿态求解精度以及计算量后,建议选择子样数大于3的迭代算法进行水下重力辅助惯性导航姿态的求解。
| [1] |
张驰, 李姗姗, 邢志斌, 等. 多特征值分析的重力辅助导航适配区选择方法[J]. 测绘科学技术学报, 2019, 36(1): 28-33 (Zhang Chi, Li Shanshan, Xing Zhibin, et al. Methods for Selecting Gravity Assisted Navigation Adaptation Zone Based on Multi-Eigenvalue Analysis[J]. Journal of Geomatics Science and Technology, 2019, 36(1): 28-33)
(  0) 0) |
| [2] |
邹嘉盛, 肖云, 孟宁, 等. 一种基于约束条件的重力匹配导航算法[J]. 武汉大学学报: 信息科学版, 2020, 45(10): 1 570-1 577 (Zou Jiasheng, Xiao Yun, Meng Ning, et al. A Gravity Matching Navigation Algorithm Based on Constraint[J]. Geomatics and Information Science of Wuhan University, 2020, 45(10): 1 570-1 577)
(  0) 0) |
| [3] |
严恭敏, 杨小康, 翁浚, 等. 一种无误差的捷联惯导数值更新新算法[J]. 导航定位学报, 2018, 6(2): 20-22 (Yan Gongmin, Yang Xiaokang, Weng Jun, et al. A New Error Free Algorithm for SINS Numerical Updating[J]. Journal of Navigation and Positioning, 2018, 6(2): 20-22)
(  0) 0) |
| [4] |
严恭敏, 翁浚, 杨小康, 等. 基于毕卡迭代的捷联姿态更新精确数值解法[J]. 宇航学报, 2017, 38(12): 1 307-1 313 (Yan Gongmin, Weng Jun, Yang Xiaokang, et al. An Accurate Numerical Solution for Strapdown Attitude Algorithm Based on Picard Iteration[J]. Journal of Astronautics, 2017, 38(12): 1 307-1 313)
(  0) 0) |
| [5] |
李姗姗. 水下重力辅助惯性导航的理论与方法研究[D]. 郑州: 信息工程大学, 2010 (Li Shanshan. Research on the Theory and Method of Underwater Gravity-Aided Inertial Navigation[D]. Zhengzhou: Information Engineering University, 2010)
(  0) 0) |
| [6] |
BortzJ E. A New Mathematical Formulation for Strapdown Inertial Navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1971, 7(1): 61-66
(  0) 0) |
| [7] |
Ignagni M B. Efficient Class of Optimized Coning Compensation Algorithms[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(2): 424-429 DOI:10.2514/3.21635
(  0) 0) |
| [8] |
Park C G, Kim K J, Lee J G, et al. Formalized Approach to Obtaining Optimal Coefficients for Coning Algorithms[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(1): 165-168 DOI:10.2514/2.7620
(  0) 0) |
| [9] |
宋敏. 高动态下捷联惯性导航算法误差分析与优化方法研究[D]. 长沙: 国防科学技术大学, 2012 (Song Min. Research on Error Analysis and Optimization Methods for Strapdown Inertial Navigation Algorithm under Highly Dynamic Environment[D]. Changsha: National University of Defense Technology, 2012)
(  0) 0) |
| [10] |
严恭敏, 杨小康, 翁浚, 等. 一种求解姿态不可交换误差补偿系数的通用方法[J]. 宇航学报, 2017, 38(7): 723-727 (Yan Gongmin, Yang Xiaokang, Weng Jun, et al. A General Method to Obtain Noncommutativity Error Compensation Coefficients for Strapdown Attitude Algorithm[J]. Journal of Astronautics, 2017, 38(7): 723-727)
(  0) 0) |
| [11] |
严恭敏, 严卫生, 徐德民. 经典圆锥误差补偿算法中剩余误差估计的局限性研究[J]. 中国惯性技术学报, 2008, 16(4): 379-385 (Yan Gongmin, Yan Weisheng, Xu Demin. Limitations of Error Estimation for Classic Coning Compensation Algorithm[J]. Journal of Chinese Inertial Technology, 2008, 16(4): 379-385)
(  0) 0) |
| [12] |
冯亮, 刘宝柱, 刘明. 潜艇流噪声与流激噪声有限元仿真建模研究[J]. 声学与电子工程, 2019(3): 20-23 (Feng Liang, Liu Baozhu, Liu Ming. Research on Finite Element Simulation Modeling of Submarine Flow Noise and Flow-Induced Noise[J]. Acoustics and Electronics Engineering, 2019(3): 20-23)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


