连续、稳定、可靠的位置信息是车辆执行任务和实现自动驾驶的基础,但在复杂环境下,任何单一的导航定位技术都有可能存在风险,只有冗余信息才能够保障载体导航定位的可靠性和稳健性[1]。全球卫星导航系统(GNSS)具有全天候、高精度等优点,但缺点是信号易被遮挡、干扰和欺骗;而低成本惯性导航系统(INS)信息丰富、动态特性好且完全自主,但导航误差会随时间积累;里程计(odometer,ODO)能自主测量车辆行驶的速度信息,可以结合非完整性约束构成车载导航的重要辅助。由GNSS、INS和ODO优势互补形成的组合导航系统,是导航、定位与授时(PNT)体系建设发展的重要一环,广泛应用于各项高精度位置估计。
目前,GNSS高精度定位技术包括实时动态定位(RTK)和精密单点定位(PPP)。选择两台或多台接收机信号进行差分的卫星导航系统需要确保接收机间距不能太远,这极大限制了复杂环境下的长距离作业。PPP不受作业距离影响,无需接收机同步观测,只需利用单台接收机即可实现高精度定位[2]。同时,GFZ和WUM提供BDS-3系统精密星历钟差产品,为BDS-3 PPP的高精度动态导航提供了条件[3]。然而复杂动态环境下,单系统PPP存在部分卫星失锁导致定位精度和连续性显著下降的风险。徐宗秋等[4]讨论复杂环境下GPS+BDS-3组合PPP的定位性能,但选用静态数据进行分析,不能完全反映实际情况。本文采用GPS+BDS-3观测数据进行PPP/INS组合,可有效提高可用卫星数量,改善定位几何强度。
多传感器的一体化集成需要顾及各传感器测量中心的几何和物理关系。在基于GPS+BDS-3的PPP/INS/ODO组合系统中,为得到高精度的融合定位解,需要考虑3个系统间的时间同步和空间杆臂。严恭敏等[5]指出,事先对不同系统间的杆臂或时间不同步误差进行精确测量并作相应补偿,有利于避免杆臂和时间不同步对其他状态的干扰。本文采用朱锋[6]的方法,在原始观测值层面进行补偿。
本文详细介绍了复杂环境下GPS+BDS-3双系统的PPP/INS/ODO组合车载导航方案。采用松组合模型来融合PPP、INS和ODO的位置和速度信息,利用静态数据分析GPS+BDS-3的PPP定位性能,利用车载实验数据分析PPP/INS/ODO组合方案的定位性能。
1 函数模型 1.1 基于GPS+BDS-3的PPP函数模型精密单点定位中的观测值主要包含伪距和载波相位两种,观测方程可表示为[7-8]:
| $\left\{ {\begin{array}{*{20}{l}} {{P_i} = \rho + c\left( {{\rm{d}}{t_r} - {\rm{d}}{t^{\rm{s}}}} \right) + T + {I_i} + {\varepsilon _P}}\\ {{\mathit{\Phi }_i} = \rho + c\left( {{\rm{d}}{t_r} - {\rm{d}}{t^{\rm{s}}}} \right) + T - {I_i} + {\lambda _i}{N_i} + {\varepsilon _\mathit{\Phi }}} \end{array}} \right.$ | (1) |
式中,s、r、i分别为观测卫星、接收机和观测值的频率号,λi为第i个频率载波的波长,Pi、Φi分别为伪距和载波相位观测值,ρ为几何距离,c为光速,Ni为整周模糊度,dtr、dts分别为接收机钟差和卫星钟差,T为对流层延迟,Ii为第i个频率上的电离层延迟,εP为伪距观测值噪声,εΦ为载波相位观测值噪声。
无电离层组合模型利用电离层延迟与信号频率之间的相关性,将两个频率上的观测值进行线性组合来消除电离层延迟的影响。GPS+BDS-3无电离层组合模型为[9]:
| $ \begin{array}{l} {P_{{\rm{if}}}} = \frac{{f_1^2}}{{f_1^2 - f_2^2}}{P_1} - \frac{{f_2^2}}{{f_1^2 - f_2^2}}{P_2} = \\ = \rho + c\left( {{\rm{d}}{t_r} - {\rm{d}}{t^{\rm{s}}}} \right) + {\rm{isb}}_{\rm{G}}^{\rm{C}} + \mathit{T} + {\varepsilon _{{P_{{\rm{if}}}}}} \end{array} $ | (2) |
| $\begin{array}{l} \;\;\;\;\;{\Phi _{{\rm{if}}}} = \frac{{f_1^2}}{{f_1^2 - f_2^2}}{\mathit{\Phi }_1} - \frac{{f_2^2}}{{f_1^2 - f_2^2}}{\mathit{\Phi }_2} = \\ \rho + c\left( {{\rm{d}}{t_r} - {\rm{d}}{t^{\rm{s}}}} \right) + {\rm{isb}}_{\rm{G}}^{\rm{C}} + T + {\lambda _{{\rm{if}}}}{N_{{\rm{if}}}} + {\varepsilon _{{\mathit{\Phi }_{{\rm{if}}}}}} \end{array}$ | (3) |
其中,
| ${\lambda _{{\rm{if}}}}{N_{{\rm{if}}}} = \frac{{f_1^2}}{{f_1^2 - f_2^2}}{\lambda _1}{N_1} - \frac{{f_2^2}}{{f_1^2 - f_2^2}}{\lambda _1}{N_2}$ | (4) |
式中,Pif、Φif分别为伪距和载波相位的无电离层组合观测值,Nif、λif分别为无电离层组合的模糊度及其波长,isbGC为GPS与BDS-3间的系统偏差,εPif、εΦif分别为无电离层组合的伪距和载波相位观测噪声,其余符号定义与式(1)相同。
采用精密星历和钟差产品时卫星轨道误差和钟差可以不作考虑,将接收机钟差和对流层湿延迟作为未知参数进行估计。利用随机模型降低多路径效应以及观测噪声的影响,其余误差可用模型进行精确改正。待估参数X为:
| $\mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{l}} x&y&z&{{\rm{d}}{t_r}}&{{\rm{isb}}_{\rm{G}}^{\rm{C}}}&\mathit{T}&{{N_{{\rm{if}}}}} \end{array}} \right]^{\rm{T}}}$ | (5) |
为了更加准确地描述PPP/INS/ODO组合导航的各项误差和改正,建立22维导航系统的状态参数x:
| $\mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{l}} {\delta {\mathit{\boldsymbol{r}}^e}}&{\delta {\mathit{\boldsymbol{v}}^e}}&\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}&{{\mathit{\boldsymbol{b}}_g}}&{{\mathit{\boldsymbol{b}}_a}}&{{\mathit{\boldsymbol{s}}_g}}&{{\mathit{\boldsymbol{s}}_a}}&{\delta k} \end{array}} \right]^{\rm{T}}}$ | (6) |
式中,上标e为该矢量所投影的地心地固坐标系,包括9维导航解误差参数(位置误差δre、速度误差δve和姿态误差Ψ)、6维加速度误差模型参数(加速度计零偏ba和比例因子sa)、6维陀螺误差模型参数(陀螺零偏bg和比例因子sg)以及1维里程计刻度系数误差δk。其中,惯性测量单元(inertial measurement unit,IMU)的零偏和比例因子被建模为1阶高斯-马尔可夫过程,里程计刻度系数误差被建模为随机常数。同时考虑空间杆臂和时间同步的影响,以GPS+BDS-3的PPP位置解算pg获得位置误差,以里程计速度解算vO获得速度误差。作为量测量的PPP/INS/ODO组合系统的函数模型为[10-11]:
| $\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{x}}_{k - 1}} + {\mathit{\boldsymbol{G}}_{k/k - 1}}{\mathit{\boldsymbol{w}}_{k - 1}}}\\ {{\mathit{\boldsymbol{z}}_k} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_g} - {\mathit{\boldsymbol{p}}_{\rm{I}}}}\\ {\mathit{\boldsymbol{v}}_{\rm{O}}^e - \mathit{\boldsymbol{v}}_{\rm{I}}^e} \end{array}} \right] = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{\eta }}_k}} \end{array}} \right.$ | (7) |
式中,Φk, k-1、Gk/k-1和Hk为系统结构参数,分别为状态转移矩阵、噪声投影矩阵和量测矩阵;zk为量测新息向量,具体表达式参考文献[11];wk-1为系统噪声向量;ηk为量测噪声向量。
对于里程计辅助的车载导航系统,通常需要考虑刻度系数误差和安装角的影响。将刻度系数误差建模成随机常数,记载体坐标系为b系,车体坐标系为b′系。由于在实际应用中很难确保IMU的轴向与车体轴向平行,故用Cbb′表示二者间的姿态转换矩阵。b系和b′系间的安装角被假设为小角度,里程计的速度输出量在INS坐标系下可表达为:
| $\begin{array}{l} \mathit{\boldsymbol{v}}_{\rm{O}}^b = {\left( {\mathit{\boldsymbol{C}}_b^{b'}} \right)^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} 0\\ {1 + \delta k}\\ 0 \end{array}} \right]{\mathit{\boldsymbol{v}}_{\rm{O}}} = \\ \left( {1 + \delta k} \right)\left[ {\begin{array}{*{20}{c}} { - {\rm{cos}}\;\theta {\rm{sin}}\;\varphi }\\ {{\rm{cos}}\;\theta {\rm{cos}}\;\varphi }\\ {{\rm{sin}}\;\theta } \end{array}} \right]{\mathit{\boldsymbol{v}}_{\rm{O}}} \end{array}$ | (8) |
式中,θ和φ分别为安装误差角的俯仰角和航向角。速度误差新息为:
| $\mathit{\boldsymbol{z}} = \mathit{\boldsymbol{v}}_{\rm{O}}^e - \mathit{\boldsymbol{v}}_{\rm{I}}^e = \mathit{\boldsymbol{C}}_b^e\mathit{\boldsymbol{v}}_{\rm{O}}^b - \mathit{\boldsymbol{v}}_{\rm{I}}^e$ | (9) |
式中,Cbe为e系和b系间的姿态转换矩阵。复杂环境下,采用位置新息和速度新息构造量测方程,通过Kalman滤波进行参数解算,达到对INS累积误差进行修正的目的。
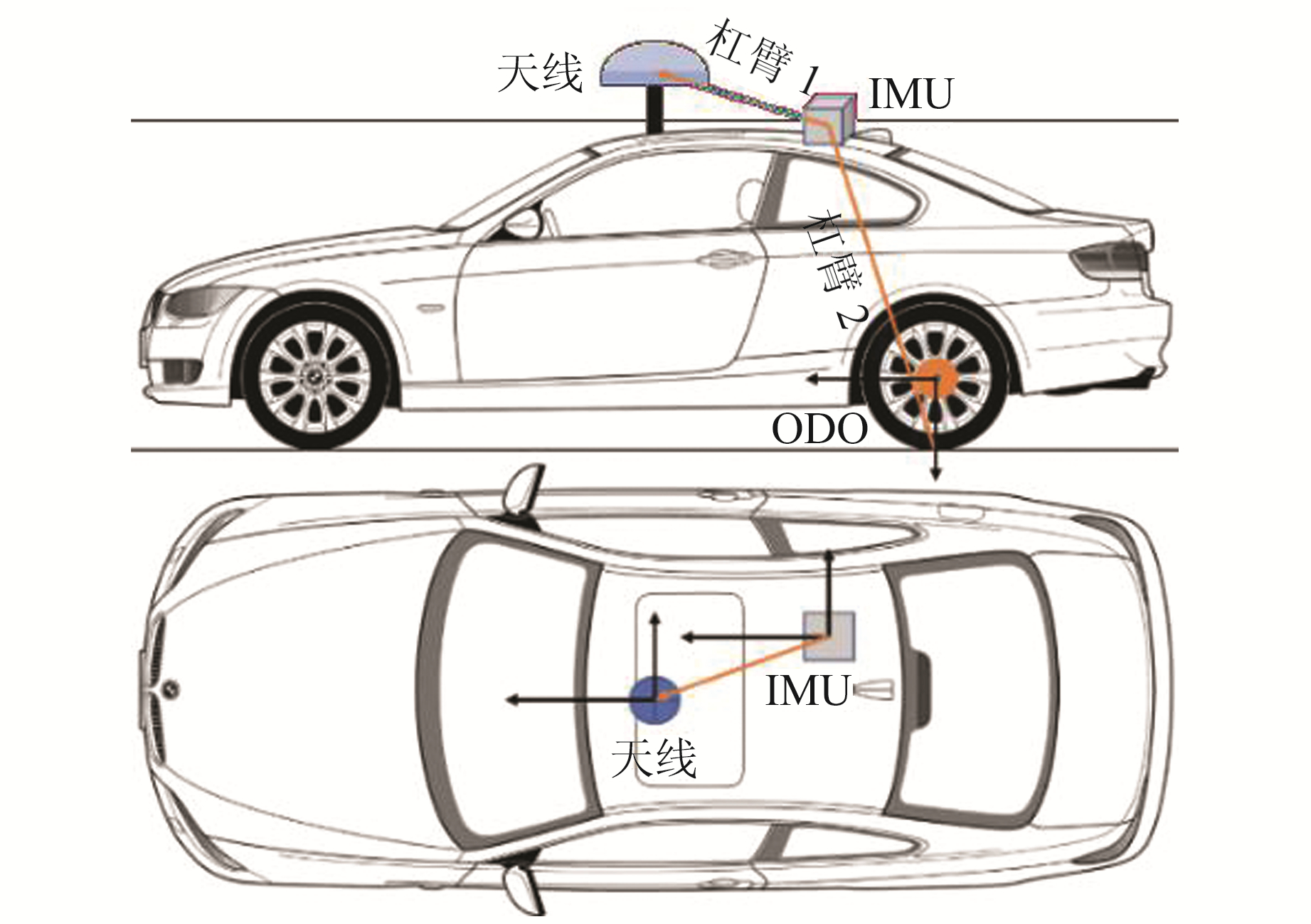
1.3 PPP/INS/ODO组合系统中杆臂、异步函数模型PPP/INS/ODO的一体化集成需要顾及GNSS天线、INS和里程计相位中心的几何关系。一般情况下,INS以IMU的测量中心为固定参考点,GNSS以接收机天线的相位中心为参考点,车载里程计一般固定在后车轮上(图 1)。假设里程计测量的速度方向沿车轮与地面的切线,则GNSS天线的相位中心、IMU固定参考点和里程计的参考点不重合,解算时需要将3者归算到同一参考点上。IMU和GNSS之间的矢量在b系下的投影为杆臂lg,杆臂矢量可通过全站仪测得。
|
图 1 车载杆臂 Fig. 1 Vehicle lever arm |
由INS位置解算结果推算GNSS天线中心处位置转换关系为:
| $\mathit{\boldsymbol{p}}_g^e = \mathit{\boldsymbol{p}}_{\rm{I}}^e + \mathit{\boldsymbol{C}}_b^e{\mathit{\boldsymbol{l}}_g}$ | (10) |
式中,Cbe为地心地固坐标系e系和b系间的姿态转换矩阵。假设lg为定值,二者间速度转换关系为:
| $\mathit{\boldsymbol{v}}_g^e = \mathit{\boldsymbol{v}}_{\rm{I}}^e - \left( {\mathit{\boldsymbol{\omega }}_{ie}^e \times } \right)\mathit{\boldsymbol{C}}_b^e{\mathit{\boldsymbol{l}}_g} - \mathit{\boldsymbol{C}}_b^e\left( {{\mathit{\boldsymbol{l}}_g} \times } \right)\mathit{\boldsymbol{\omega }}_{ib}^b$ | (11) |
式中,ωiee表示e系相对i系的角速度在e系下的投影,ωibb表示b系相对i系的角速度在b系下的投影,(ωiee×)为矢量ωiee的反对称阵,(lg×)为矢量lg的反对称阵。
为得到车载PPP/INS/ODO组合导航系统的高精度解算结果,需要同步来自各系统不同时间的数据。通常情况下,组合导航系统的时钟与GNSS接收机的秒脉冲同步,但INS的采样时刻并不与GNSS系统和ODO系统采样时刻同步(图 2)。为准确计算Kalman滤波的量测量,通常常用两种方法:一是将INS系统的递推结果内插或外插到GNSS观测时刻上[12],二是在INS的原始观测值层面进行内插或外插[6]。第一种方法在车载剧烈运动时容易造成样本点内插出的插值点与实际运动特性不相符;第二种方法容易实现,且在剧烈运动下误差更小。

|
图 2 组合系统采样异步 Fig. 2 Asynchronous sampling of coupled system |
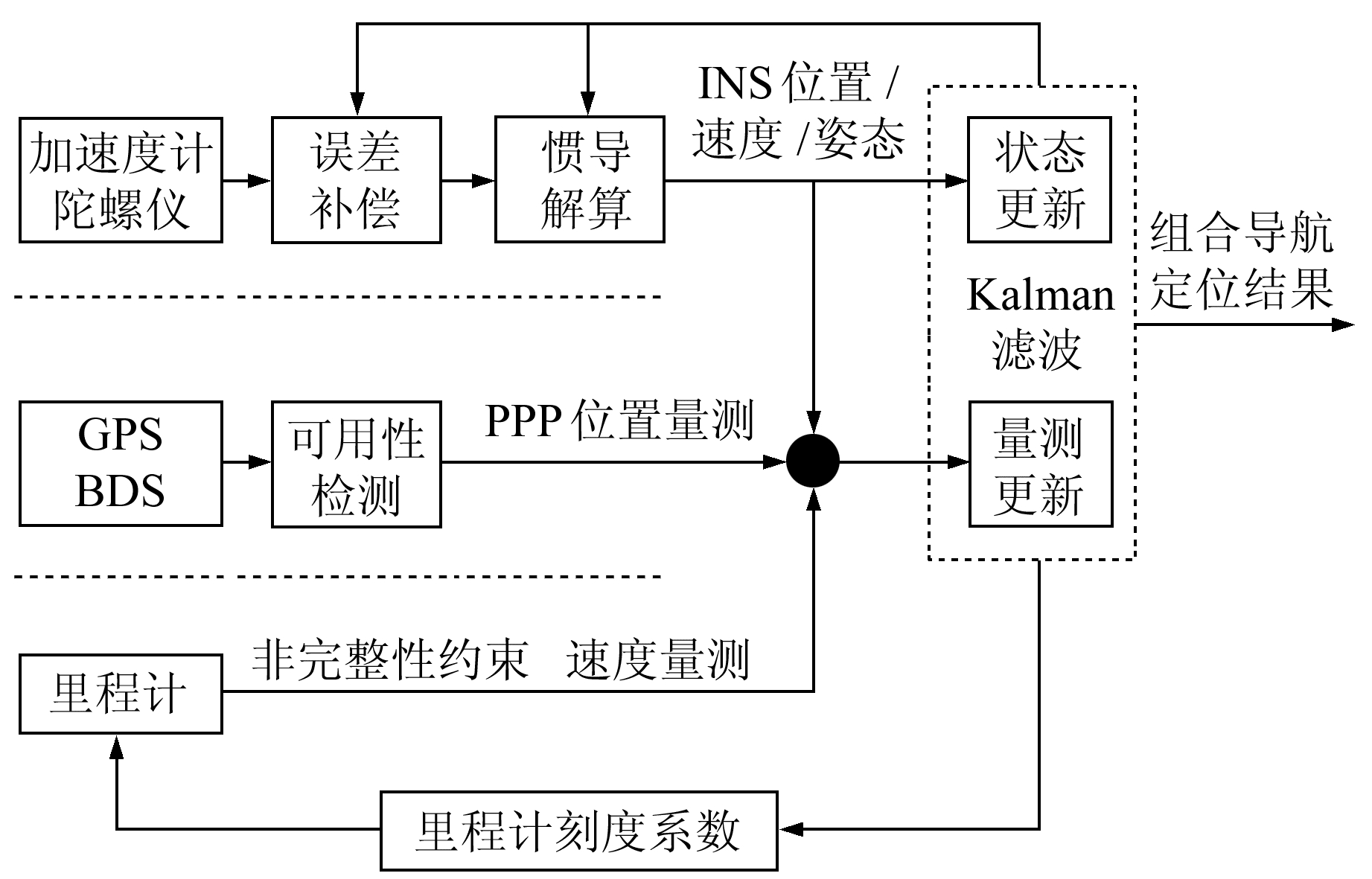
基于GAMP开源软件开发并实现GPS+BDS-3的PPP/INS/ODO组合导航功能[8],采用GPS+BDS-3无电离层组合的PPP/INS/ODO松组合算法得到组合框架如图 3所示。首先通过误差补偿对IMU的原始输出进行惯性导航机械编排,得到位置、速度和姿态;然后与GPS+BDS-3的PPP解算位置结果以及顾及非完整性约束的里程计速度信息一起进行Kalman滤波;最后分别进行状态更新和时间更新。该组合系统在启动前需要进行必要的配置和操作,包括Kalman滤波初始化配置和IMU性能参数配置,如状态向量初始化及其对应的先验方差、量测噪声方差参数配置等。对于初始对准,低成本IMU可以利用加速度计求得横滚角和俯仰角,利用实测车载数据(平稳路面作直线加速运动)的PPP位置矢量求得航向角。由于IMU的采样率远高于GNSS和ODO,因此IMU只在有量测信息时进行量测更新,否则只进行状态更新。将解算后的位置、速度和IMU传感器的误差参数反馈给INS,完成闭环修正。
|
图 3 基于GPS+BDS-3的PPP/INS/ODO组合框架 Fig. 3 Frame of PPP/INS/ODO integrated navigation based on GPS+BDS-3 |
首先对MGEX跟踪站的GPS+BDS-3数据进行仿动态PPP性能分析,然后利用实测车载数据分析和验证复杂环境下基于GPS+BDS-3的PPP/INS/ODO组合导航性能。
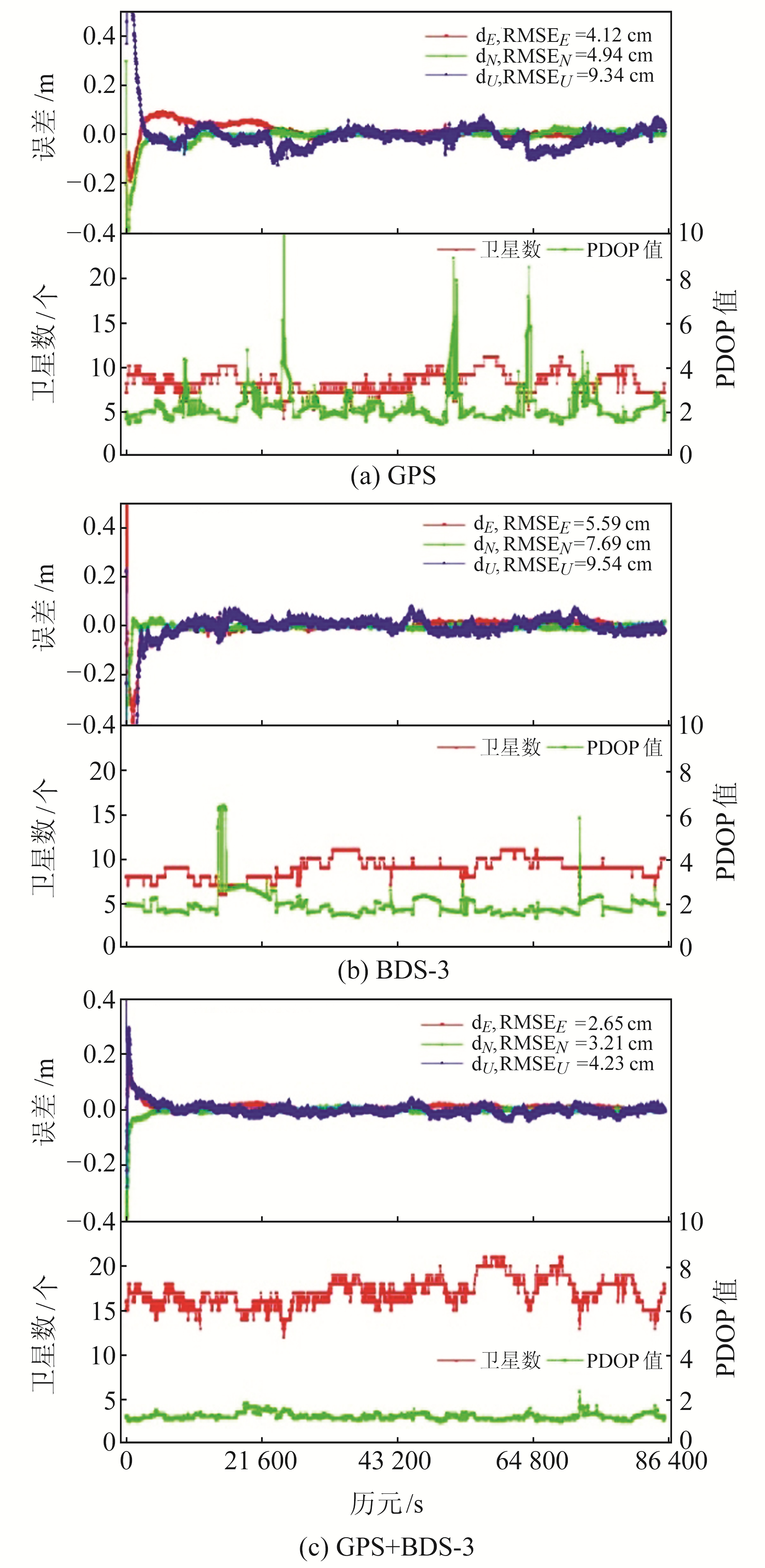
2.1 仿动态GPS+BDS-3的PPP可行性分析选取MGEX观测网的3个国内测站JFNG、WUH2和URUM,连续观测时间为2020年年积日(doy)345~351(2020-12-10~16),数据采样率为30 s,分别对测站进行GPS、BDS-3和GPS/BDS-3组合仿动态定位处理。数据采用GFZ分析中心的多系统精密星历(5 min)、钟差(30 s)产品,精确坐标采用IGS周解结果,处理策略如表 1所示。JFNG测站doy 345的PPP和观测卫星数、PDOP结果如图 4所示。将解算结果与IGS周解进行对比,得到E、N、U方向的位置偏差,并统计doy 345~351在E、N、U方向位置偏差的RMSE,如表 2所示(单位cm)。
|
|
表 1 PPP解算策略 Tab. 1 PPP solution strategy |
|
图 4 JFNG测站doy 345的PPP和观测卫星数、PDOP结果 Fig. 4 PPP, number of observation satellites and PDOP results on doy 345 at JFNG station |
|
|
表 2 动态PPP doy 345~351定位结果RMSE统计值 Tab. 2 RMSE statistics of dynamic PPP positioning results during doy 345-351 |
由图 4可见,单GPS会受有效观测卫星数影响而导致PDOP值产生较大波动,最终导致PPP定位结果出现较大偏差,单GPS动态PPP的RMSE分别为4.12 cm、4.94 cm和9.34 cm;单BDS-3的有效观测卫星数略多于单GPS,动态PPP的RMSE分别为5.59 cm、7.69 cm和9.54 cm;GPS+BDS-3组合可以增加观测卫星数量、改善观测几何结构以及显著提高定位精度。由表 2可见,相比于单GPS,GPS+BDS-3在E、N、U方向的RMSE分别减少29.5%、23.1%和38.0%;相比于单BDS-3,GPS+BDS-3在E、N、U方向的RMSE分别减少45.6%、43.7%和41.8%。可以看出,GPS+BDS-3组合能够显著提高定位精度,BDS-3的定位精度提高最明显。
2.2 复杂环境下的定位性能分析为验证GPS+BDS-3的PPP/INS/ODO组合系统在复杂环境下的定位性能,分别选择荷兰Xsens公司生产的MTi-G-710(表 3)、Trimble R9接收机以及车辆后轮搭载的Sicke Encoder DFS60里程计作为测试设备,利用NovAtel公司生产的高精度SPAN-FSAS分体式组合导航系统作为参考真值进行验证。测试地点为徐州市郊区,包括林荫道、城市峡谷和高架桥等3种典型复杂环境。本次测试的杆臂向量由全站仪测得,天线杆臂矢量为[0.45,-0.08,-1.21](单位m),里程计辅助杆臂矢量为[0.543,0.629,0.586] (单位m)。
|
|
表 3 惯性传感器性能参数 Tab. 3 Performance parameters of inertial sensors |
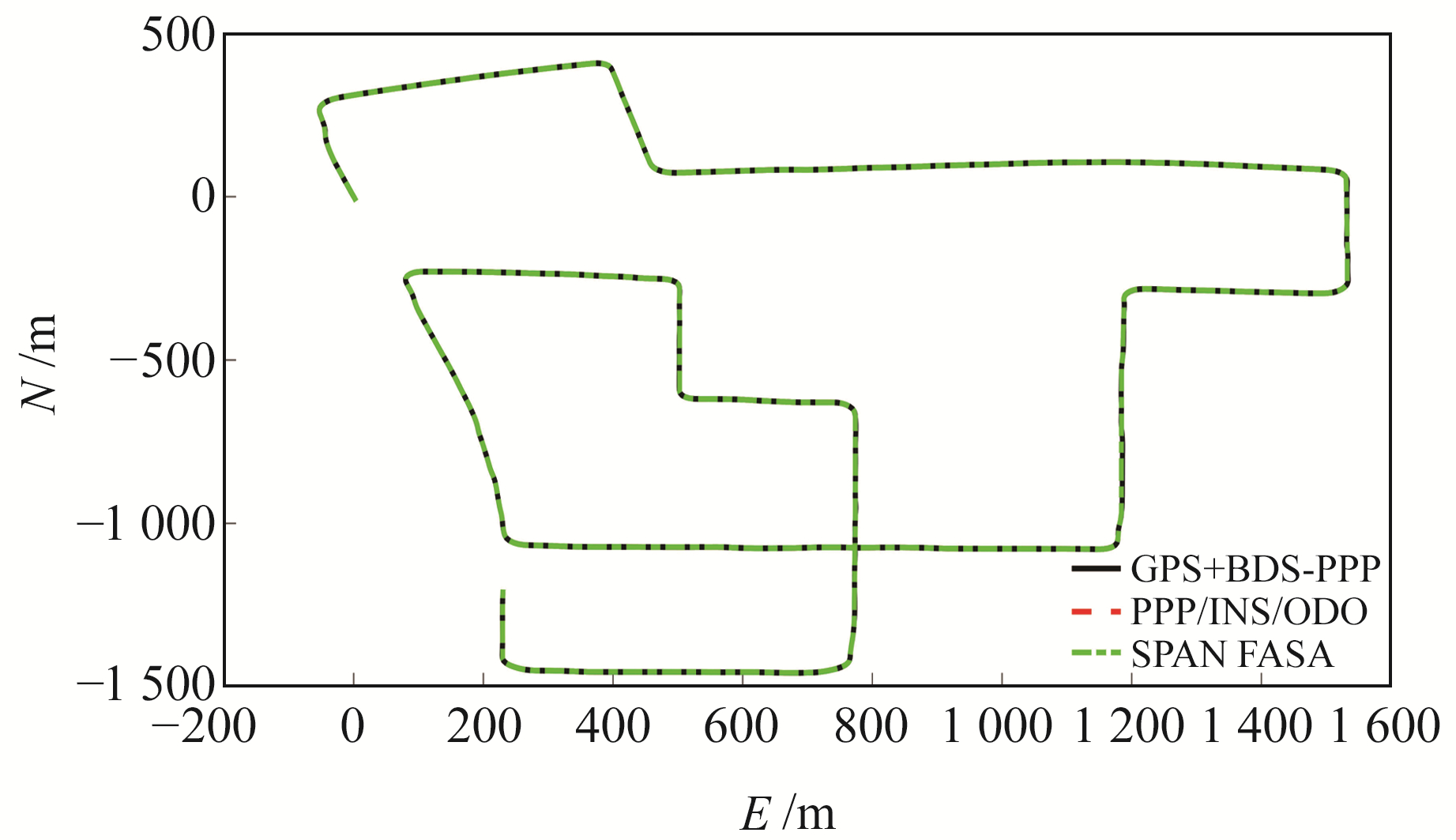
采用图 3的技术方案对跑车数据进行分析。将Kalman滤波更新频率设置为1 Hz,滤波过程中状态协方差根据先验知识和IMU的技术参数设置,与PPP有关的量测噪声协方差设置为0.01 m2,与里程计有关的量测噪声协方差设置为0.01(m/s)2,初始状态向量均设置为0。随着Kalman滤波进入循环,初始状态对系统的影响会迅速减小。分别比较GPS+BDS-3导航结果、PPP/INS/ODO组合导航结果和高精度组合导航系统SPAN FASA参考值,三者轨迹计算值的二维平面图如图 5所示。
|
图 5 行驶轨迹对比 Fig. 5 Comparison of driving trajectories |
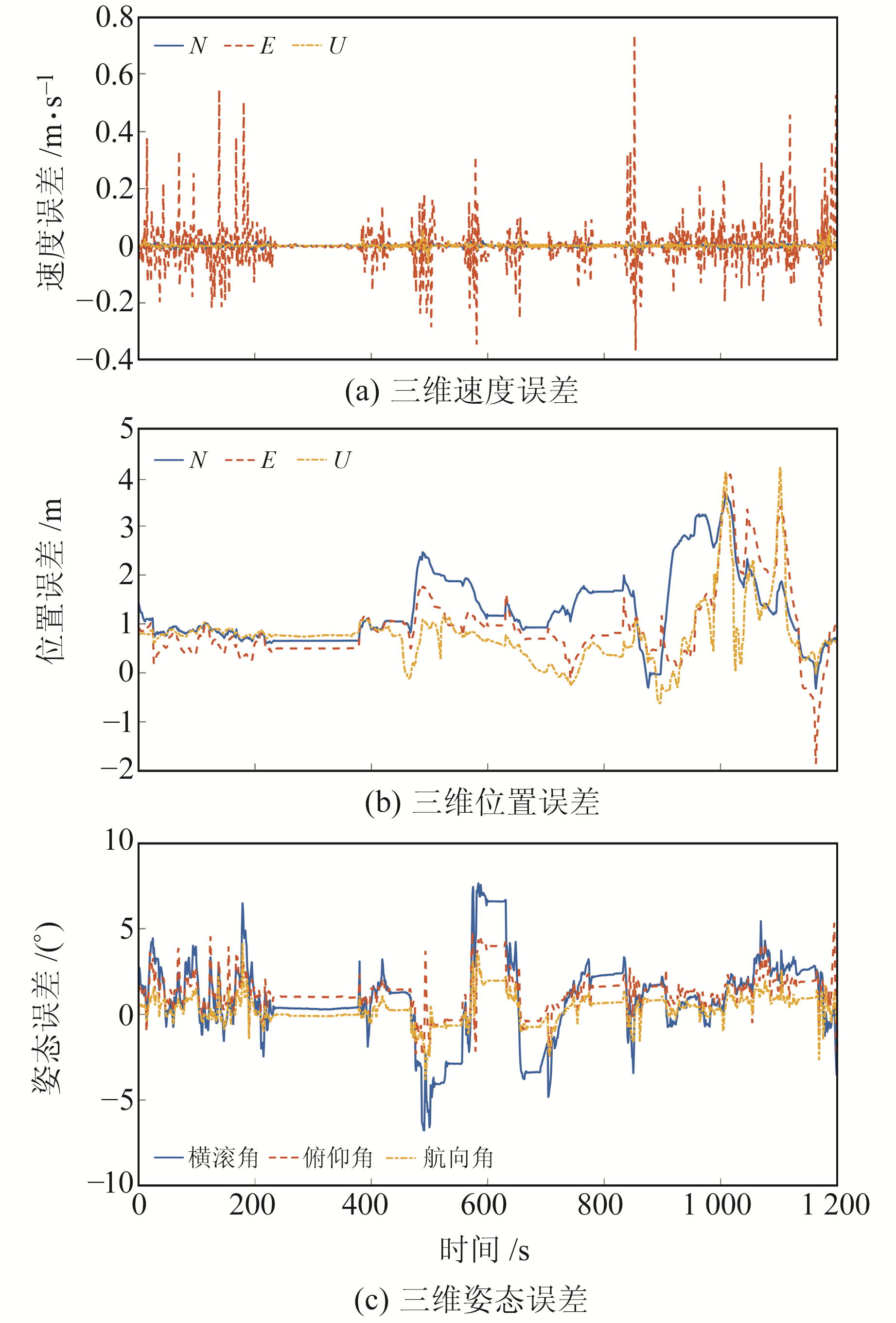
由图 5可见,GPS+BDS-3、PPP/INS/ODO和SPAN FASA三者在E和N方向上具有很好的吻合性,证明了技术方案的有效性。为更加客观地评价PPP/INS/ODO方案的性能,计算其相对参考值的三维速度误差、三维位置误差和三维姿态误差(图 6)。
|
图 6 PPP/INS/ODO的误差值 Fig. 6 Error of PPP/INS/ODO |
由图 6可知,组合系统的位置解算值在前400 s表现良好,800 ~1 200 s位置误差波动较大,极少数点的最大误差值接近4 m,这与实际跑车复杂环境的变化情况基本一致。由于有里程计和非完整性约束进行辅助,组合系统的速度与高精度组合系统的输出结果一致性较好。3个方向上速度误差的RMSE分别为0.005 8 m/s、0.078 4 m/s和0.006 7 m/s;3个方向上位置误差的RMSE分别为0.754 7 m、0.791 1 m和0.622 2 m;3个方向上姿态误差的RMSE分别为2.378 0°、1.156 0°、0.837 4°,该结果可为复杂环境下的车载导航提供技术支撑。
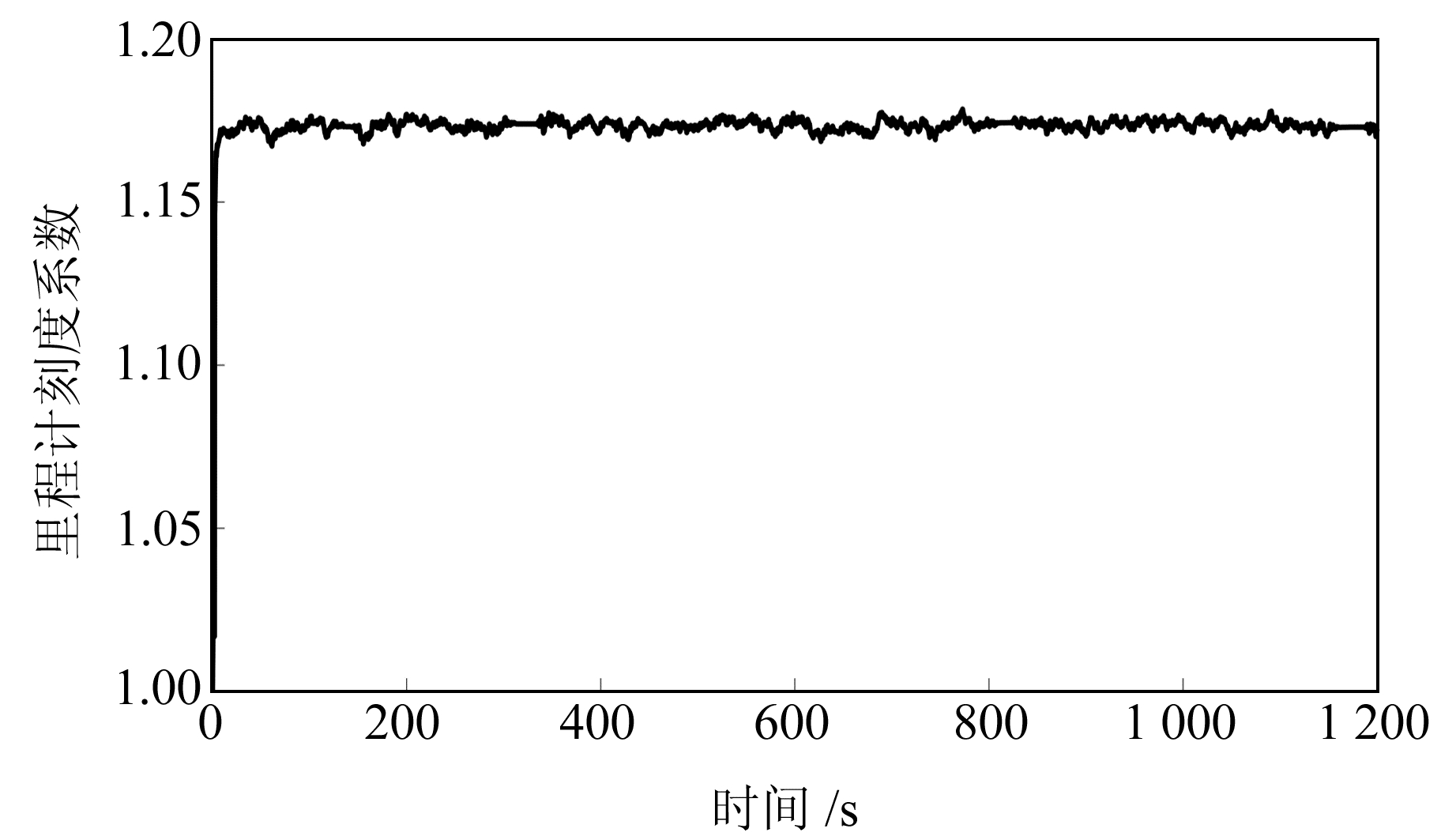
里程计的刻度系数误差被建模为随机常数,随着Kalman滤波逐渐趋于稳定,刻度系数也得到较好的收敛。里程计刻度系数随时间变化曲线如图 7所示,可以看出,里程计的刻度系数从一开始就迅速收敛到1.16~1.18之间,证明了该滤波的稳定性与有效性。
|
图 7 里程计刻度系数变化曲线 Fig. 7 Variation curve of odometer scale coefficient |
采用GPS+BDS-3双系统推导无电离层组合PPP模型和PPP/INS/ODO组合模型。通过仿动态和动态跑车实测数据分析GPS+BDS-3无电离层组合PPP和PPP/INS/ODO组合系统的定位性能。实验结果表明,该系统具有稳定性和有效性,可为复杂环境下的车载导航提供技术支撑。在当前室内外高精度位置服务的需求推动下,建立更加高效的组合模型将会成为下一步研究的重点。
| [1] |
杨元喜. 弹性PNT基本框架[J]. 测绘学报, 2018, 47(7): 893-898 (Yang Yuanxi. Resilient PNT Concept Frame[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 893-898)
(  0) 0) |
| [2] |
Deng Z, Fritsche M, Uhlemann M, et al. Reprocessing of GFZ Multi-GNSS Product GBM[C]. IGS Workshop 2016, Sydney, 2016
(  0) 0) |
| [3] |
Kouba J, Héroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28 DOI:10.1007/PL00012883
(  0) 0) |
| [4] |
徐宗秋, 韩澎涛, 丁新展, 等. 复杂环境下GPS/BDS组合PPP定位性能分析[J]. 导航定位学报, 2019, 7(4): 56-59 (Xu Zongqiu, Han Pengtao, Ding Xinzhan, et al. Performance Analysis of GPS/BDS Combined PPP Positioning under Complex Environment[J]. Journal of Navigation and Positioning, 2019, 7(4): 56-59)
(  0) 0) |
| [5] |
严恭敏, 邓瑀. 传统组合导航中的实用Kalman滤波技术评述[J]. 导航定位与授时, 2020, 7(2): 50-64 (Yan Gongmin, Deng Yu. Review on Practical Kalman Filtering Techniques in Traditional Integrated Navigation System[J]. Navigation Positioning and Timing, 2020, 7(2): 50-64)
(  0) 0) |
| [6] |
朱锋. PPP/SINS组合导航关键技术与算法实现[D]. 武汉: 武汉大学, 2015 (Zhu Feng. The Key Technology Algorithm of PPP/SINS Integration[D]. Wuhan: Wuhan University, 2015)
(  0) 0) |
| [7] |
Li X, Zhang X, Ren X, et al. Precise Positioning with Current Multi-Constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and Beidou[J]. Scientific Reports, 2015(5): 8 328
(  0) 0) |
| [8] |
Liu Z, Li Y Y, Li F, et al. Near Real-Time PPP-Based Monitoring of the Ionosphere Using Dual-Frequency GPS/BDS/Galileo Data[J]. Advances in Space Research, 2018, 61(6): 1 435-1 443 DOI:10.1016/j.asr.2017.12.038
(  0) 0) |
| [9] |
Zhou F, Dong D N, Li W W, et al. GAMP: An Open-Source Software of Multi-GNSS Precise Point Positioning Using Undifferenced and Uncombined Observations[J]. GPS Solutions, 2018, 22(2): 1-10
(  0) 0) |
| [10] |
李增科, 王坚, 高井祥. 精密单点定位在GPS/INS组合导航中的应用[J]. 武汉大学学报: 信息科学版, 2013, 38(1): 48-51 (Li Zengke, Wang Jian, Gao Jingxiang. The Apply of Precise Point Positioning in GPS/INS Integrated Navigation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 48-51)
(  0) 0) |
| [11] |
Lu J Z, Lei C H, Yang Y Q, et al. In-Motion Initial Alignment and Positioning with INS/CNS/ODO Integrated Navigation System for Lunar Rovers[J]. Advances in Space Research, 2017, 59(12): 3 070-3 079
(  0) 0) |
| [12] |
Shin E H. Accuracy Improvement of Low-Cost INS/GPS for Land Applications[D]. Calgary: University of Calgary, 2001
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

