2. 昆明冶金高等专科学校测绘学院,昆明市学府路388号,650033
随着科技发展及实际需要,对坐标定位精度的要求越来越高,电离层高阶项延迟也备受重视[1-2]。取消SA(selective availability)后,电离层延迟误差成为制约GPS定位精度的主要因素之一[3]。在经典相对定位中,大部分GNSS用户采用双频技术来削弱电离层一阶项延迟的影响,但往往忽视电离层高阶项延迟的干扰。研究证实,电离层二阶项延迟的影响在GPS动态单点定位中可达2~3 cm,在极端情况下甚至达到7 cm[4];对静态定位亦能造成mm级的系统性偏差[5-6]。近年来,国内外学者通过对高精度GPS观测站实测数据进行处理,深入研究电离层二阶项延迟对GPS定位结果的影响。大量实验结果表明,电离层二阶项延迟对一定区域范围内GPS定位结果的影响具有规律性[7],如何有效控制、改正、消除这一影响是GPS技术实现高精度定位必须解决的关键问题之一。
电离层高阶项延迟的影响通常采用由IGS分析中心CODE提供的最终GIMs产品进行计算,而采用由GPS自身观测计算的TEC进行改正的研究较少,地磁模型与TEC间的匹配也鲜有探讨。本文从影响电离层高阶项延迟的因素出发,分析地磁模型、TEC、频率、测站纬度等因素引起的电离层高阶项延迟,在此基础上设计相关实验,验证不同处理策略下电离层高阶项延迟对基线的影响,并进一步讨论太阳活动剧烈时段电离层高阶项延迟对基线规律的影响。
1 电离层高阶项延迟模型电离层高阶项效应的载波相位和伪距观测方程可表示为[8]:
| $ \begin{array}{l} {\varphi _{Li}} = \rho ' - I_g^1 - \frac{1}{2}I_g^2 - \frac{1}{3}I_g^3 + {N_i} + {v_{{\varphi _{{\rm{L}}i}}}}\\ \;\;\;\;\;{\rm{P}}{{\rm{R}}_{{\rm{Li}}}} = \rho ' + I_g^1 + I_g^2 + I_g^3 + {v_{{P_{{\rm{L}}i}}}} \end{array} $ | (1) |
式中,ρ′为卫星到接收机之间的几何距离,Ig1、Ig2及Ig3分别为电离层一阶项、二阶项和三阶项效应,Ni为载波相位观测的整周模糊度,vφLi及vPLi分别为相位和伪距的残差效应。
由式(1)可知,电离层效应在相位和范围上是相似的,电离层二阶项及三阶项效应的因子分别为1/2和1/3。频率fLi(i=1, 2)的电离层延迟计算公式为[8]:
| $ \left\{ \begin{array}{l} I_g^{(1)} = 40.28\frac{{{\rm{TEC}}}}{{{f^2}}}\\ I_g^{(2)} = (\frac{{eA}}{{f_{{\rm{L}}i}^32\pi {m_e}}}) \cdot \left\| {\;\mathit{\boldsymbol{B}}\;} \right\|\;\;\left| {\cos \theta } \right|\;{\rm{TEC = }}\\ \;\;\;\;(\frac{{{\lambda ^3}eA}}{{{c^3}2\pi {m_e}}}) \cdot \left\| {\;\mathit{\boldsymbol{B}}\;} \right\|\;\;\left| {\cos \theta } \right|\;{\rm{TEC}}\\ I_g^{(3)} = (\frac{{3{A^2}}}{{8f_{Li}^4}}) \cdot \eta {N_{{\rm{e}}, \max }}{\rm{TEC}} \end{array} \right. $ | (2) |
式中,
| $ \left\| {\;\mathit{\boldsymbol{B}}\;} \right\|\left| {\cos \theta } \right| = \left\| {\;\mathit{\boldsymbol{B}}\;} \right\|\;\;\left\| {\;\mathit{\boldsymbol{J}}\;} \right\|\left| {\cos \theta } \right| = {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{J}} $ | (3) |
式中,内积BTJ可由偶极地磁模型(dipolar geomagnetic model)、参数化电离层模型(parameterized ionosphere model, PIM)修改的地磁模型(CGM)及国际地磁参考场模型(IGRF)等获取。一般来说,Dipolar模型的精度近似为75%[9],但计算过程中需要先将接收机的大地坐标转换为地磁坐标,再转换为地磁局域系统。通常,内积BTJ可用接收机和卫星间的位置函数表示[10]:
| $ \begin{array}{l} {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{J}}{\rm{ = }}(\cos \varphi _{\rm{m}}^{'}\sin {z_{\rm{m}}}\cos {a_{\rm{m}}} - \sin \varphi _{\rm{m}}^{'}\cos {z_{\rm{m}}})\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{(\frac{{{R_{\rm{e}}}}}{{{R_{\rm{e}}} + {h_{{\rm{ion}}}}}})^3}{B_{{\rm{eq}}}} \end{array} $ | (4) |
式中,φm′为穿透点的地磁纬度,αm与zm分别为卫星在局域地磁系统中的地磁方位角和天顶角,Re为地球赤道半径,hion为电离层高度,Beq为赤道处的地磁感应。式(2)的电离层三阶项延迟计算公式中,η为函数因子,常近似取0.66。Ne, max的计算公式为[11]:
| $ {N_{{\rm{e}}, \max }}({m^{ - 3}}) = \frac{{(20 - 6) \times {{10}^{12}}}}{{(4.55 - 1.38) \times {{10}^{18}}}}{\rm{TEC}} $ | (5) |
式中, TEC可以由卫星接收机方向的伪距计算得到:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{\rm{TEC}} = \frac{{f_{{\rm{L}}1}^2f_{{\rm{L}}2}^2}}{{40.3(f_{{\rm{L}}1}^2 - f_{{\rm{L}}2}^2)}} \cdot \\ [{\rm{P}}{{\rm{R}}_{{\rm{L}}1}} - {\rm{P}}{{\rm{R}}_{{\rm{L}}2}} - c({\rm{DC}}{{\rm{B}}_{\rm{r}}} + {\rm{DC}}{{\rm{B}}_{\rm{s}}}) + {\varepsilon _{{\rm{L}}1{\rm{L}}2}}] \end{array} $ | (6) |
式中,DCBr与DCBs分别为接收机和卫星的差分码偏差,即两个频率间的硬件延迟;c为真空中的光速;εL1L2为所有未建模的残余效应。由式(2)~(6)可知,电离层高阶项延迟的影响因素主要与TEC、地磁模型及频率或波长有关。TEC可通过伪距及相位平滑伪距得到,也可通过全球电离层图(GIMs)进行内插得到。
在计算电离层高阶项延迟过程中,需对计算参数进行配置。实验采用RINEX_HO软件进行分析。
电离层高阶项延迟处理策略和约束条件主要包括卫星差分码偏差、TEC计算方式及地磁模型的选取等。为避免多路径误差对电离层高阶项延迟的干扰,文中所有实验的卫星截止高度角均设置为15°,所需电离层图(GIMs)及DCB产品可分别在美国地壳动力数据信息系统(CDDIS)及欧洲定轨中心(CODE)官网下载。因电离层高阶项延迟的影响极其复杂,为分析几种因素的不同影响,本文采用约束相关参数计算其他参数的策略对电离层高阶项延迟进行讨论。
2 算例及结果分析 2.1 地磁模型对载波观测值的电离层二阶项延迟为分析不同地磁模型对载波相位观测值电离层二阶项延迟的贡献,采用由CDDIS提供的GIMs产品获取的TEC作为实验前提,分别采用Dipolar、CGM及IGRF13模型进行计算。实验数据为位于赤道附近的IGS站中BAKO站点2016-07-19的单日数据。采用TEQC软件对观测文件进行预处理,使观测文件中的观测量仅含有C1、P1、L1、S1、D1及C2、P2、L2、S2、D2等类型数据,同时删除不健康的卫星,避免因观测数据类型不一致或其他不利因素对实验结果造成干扰。实验分析采用载波观测量的L2为对象,电离层二阶项延迟的实验结果如图 1所示。
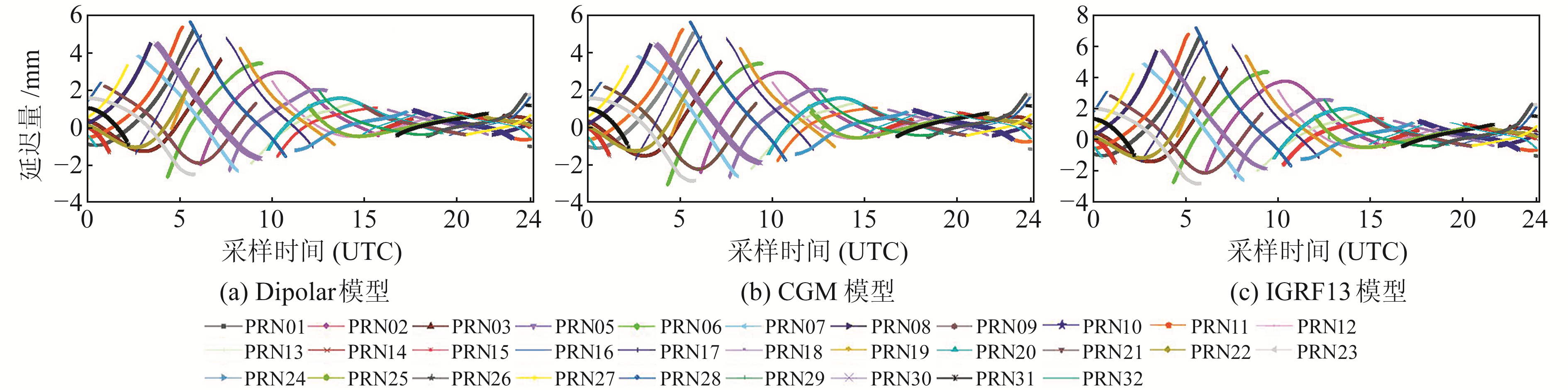
|
图 1 3种模型计算的L2载波相位观测电离层二阶项延迟 Fig. 1 Second-order ionospheric delay calculated by three models of L2 carrier observation |
由图 1可见,随着卫星的运动,各卫星载波相位观测值中电离层二阶项延迟的大小及符号均出现不同变化。由式(2)及式(4)可知,影响其变化的因素为卫星信号的方向与地磁强度矢量B方向间的夹角及穿刺点纬度。在采用GIMs方式获取TEC数据的前提下,利用Dipolar模型计算出的电离层二阶项延迟最大值为5.6 mm、最小值为-2.6 mm;利用CGM模型计算出的电离层二阶项延迟最大值为5.6 mm、最小值为-3.1 mm;采用IGRF13模型计算出的电离层二阶项延迟最大值为7.2 mm、最小值为-2.9 mm。对比3种地磁模型计算的电离层二阶项延迟可以发现,BAKO站至观测卫星的距离差异在2.0 mm以内,差异大小约为IGRF13模型的30%。图 1显示,BAKO站电离层二阶项延迟在UTC时间00:00~13:00之间变化较大,表明此时段该站上空电离层较活跃;在其他电离层不活跃时段,各卫星的电离层高阶项延迟总体趋于常数。
2.2 TEC对载波观测值的电离层二阶项延迟由式(2)可知,计算电离层二阶项延迟必须有TEC数据,可采用原始伪距、相位平滑伪距或国际电离层模型等方法获取TEC数据。为分析由不同模式获取的TEC对电离层二阶项延迟的贡献,采用IGRF13模型为实验前提,分别采用原始伪距、相位平滑伪距及GIMs计算的TEC进行实验。实验删除了相位平滑伪距周跳较大的观测时段或卫星观测数据,约占观测量的5%,此比例随观测质量变化。实验结果见表 1(单位mm)、图 2(a)、(b)(图例同图 1)。为直观表达3种TEC计算结果的差异,选择典型的PRN27卫星对3种电离层二阶项延迟结果进行比较(图 2(c))。
|
|
表 1 不同方式获取TEC计算的电离层二阶项延迟 Tab. 1 Second-order ionospheric delay calculated by different ways to compute TEC |

|
图 2 不同方式获取TEC计算的L2载波相位观测电离层二阶项延迟 Fig. 2 Second-order ionospheric delay calculated by TEC from different ways of L2 carrier observation |
由表 1可见,在IGRF13模式下,分别采用原始伪距、相位平滑伪距及GIMs计算TEC,其对应的电离层二阶项延迟最大值分别为10.0 mm、8.0 mm和7.2 mm,最小值分别为-4.6 mm、-3.5 mm和-0.4 mm。由图 2(a)可见,直接采用原始伪距获得的TEC计算电离层二阶项延迟,其延迟量走势具有一定的跳跃性,可能受到广播星历精度的影响;由图 2(b)可见,采用相位平滑伪距获取TEC计算的电离层二阶项延迟存在周跳现象,主要由观测不连续或信号干扰导致;由图 2(c)可见,采用原始伪距TEC计算的电离层延迟有一定的跳跃性,而相位平滑伪距和GIMs计算的电离层二阶项延迟则更为平滑(噪声更少),这是因为处理过程中发现相位平滑伪距周跳严重而采用了滤波平滑策略。但实验中发现,部分相位平滑伪距计算的电离层二阶项延迟仍有小部分不连续;GIMs计算的电离层二阶项延迟最为平滑,且其最大值和最小值的绝对值均比其他两种方式的绝对值大。
2.3 不同频率的电离层二阶项延迟由式(2)可知,电离层二阶项延迟与GPS频率有关。为比较不同频率间的电离层二阶项延迟差异,采用由GIMs获取的TEC及地磁模型IGRF13作为实验前提,对BAKO站进行电离层二阶项延迟计算。L1与L2频段计算的站星间电离层二阶项延迟结果见图 3(图例同图 1)和图 1(c)。
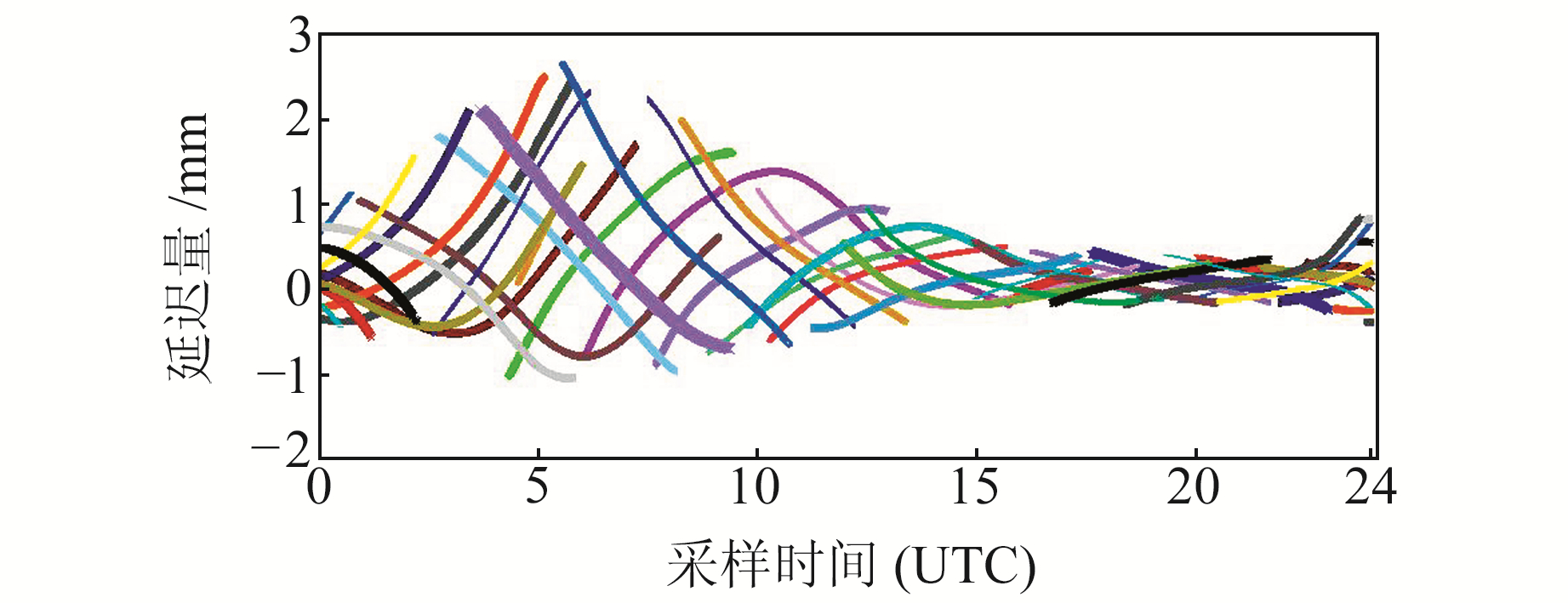
|
图 3 L1载波相位观测的电离层二阶项延迟 Fig. 3 Second-order ionospheric delay by L1 carrier observation |
由图 3和图 1(c)可知,L1频段的电离层二阶项延迟最大值为2.6 mm,最小值为-1.1 mm,L1频段的电离层二阶项延迟约为L2频段的1/3。由式(2)可知,电离层二阶项延迟的大小与频率的立方成反比,与波长的立方成正比。因此,在相同情况下,L2频段的电离层二阶项延迟比L1频段的大。
2.4 不同纬度的电离层二阶项延迟电离层的活跃程度与太阳辐射密切相关,因此不同区域、不同季节、不同时间的电离层活跃程度会呈现一定的差异。为比较不同纬度区域电离层高阶项延迟的差异,选择赤道附近的BAKO站、北半球中纬度的BJFS站及南半球中纬度的PERT站2016-07-19的观测数据进行实验,并采用L2频段进行分析。实验在GIMs计算得到的TEC和采用IGRF13模型的前提下进行,图 1(c)、图 4(图例同图 1)显示了不同纬度下电离层二阶项延迟的差异及其时间序列特性。
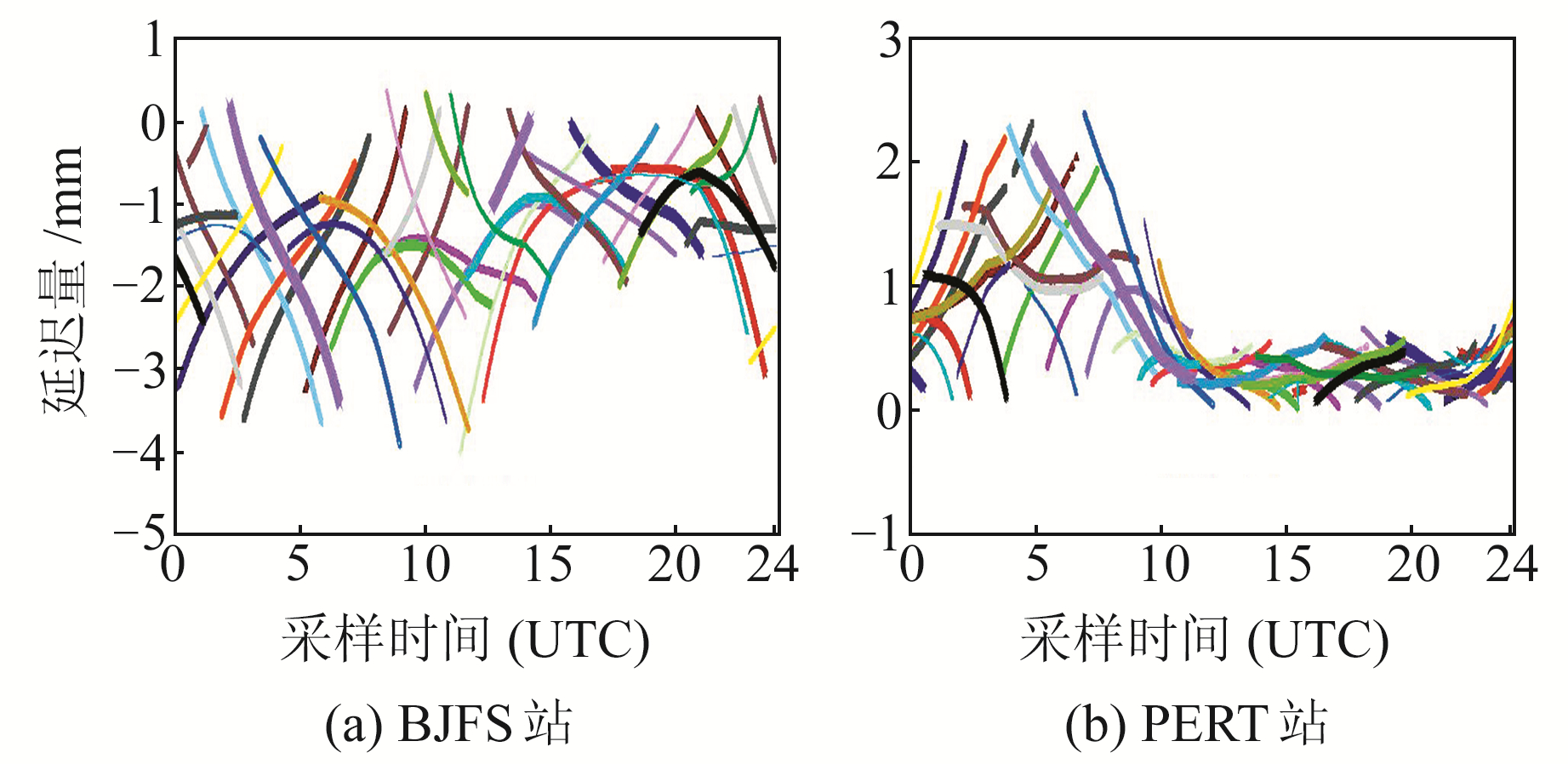
|
图 4 两个测站L2载波相位观测值中的电离层二阶项延迟 Fig. 4 Second-order ionospheric effect for two stations of L2 carrier observation |
由图 1(c)、图 4可见,L2频率下BAKO站的电离层二阶项延迟最大达7.2 mm;BJFS站的电离层二阶项延迟居中,最大为0.4 mm,最小为-4.0 mm;PERT站的电离层二阶项延迟最大为2.4 mm,最小为0 mm。由图 4可见,BJFS及PERT两个测站的电离层二阶项延迟均呈现系统性变化,其中BJFS站的电离层延迟主要为负值,而PERT站的电离层延迟主要为正值。BAKO站的延迟量除电离层活跃期正值偏大外,其他时段则呈现偶然性,其平均值近似为一个常数。实验结果表明,电离层高阶项延迟的大小和穿刺点的位置密切相关。
2.5 电离层三阶项延迟电离层高阶项延迟包含二阶项和三阶项。由前文实验可知,电离层二阶项延迟对站星间的影响最大可达10.0 mm。为探讨电离层三阶项延迟,采用§2.3的实验方案与数据计算电离层三阶项延迟的大小。图 5(图例同图 1)显示了电离层三阶项延迟中L2频段的时间序列。
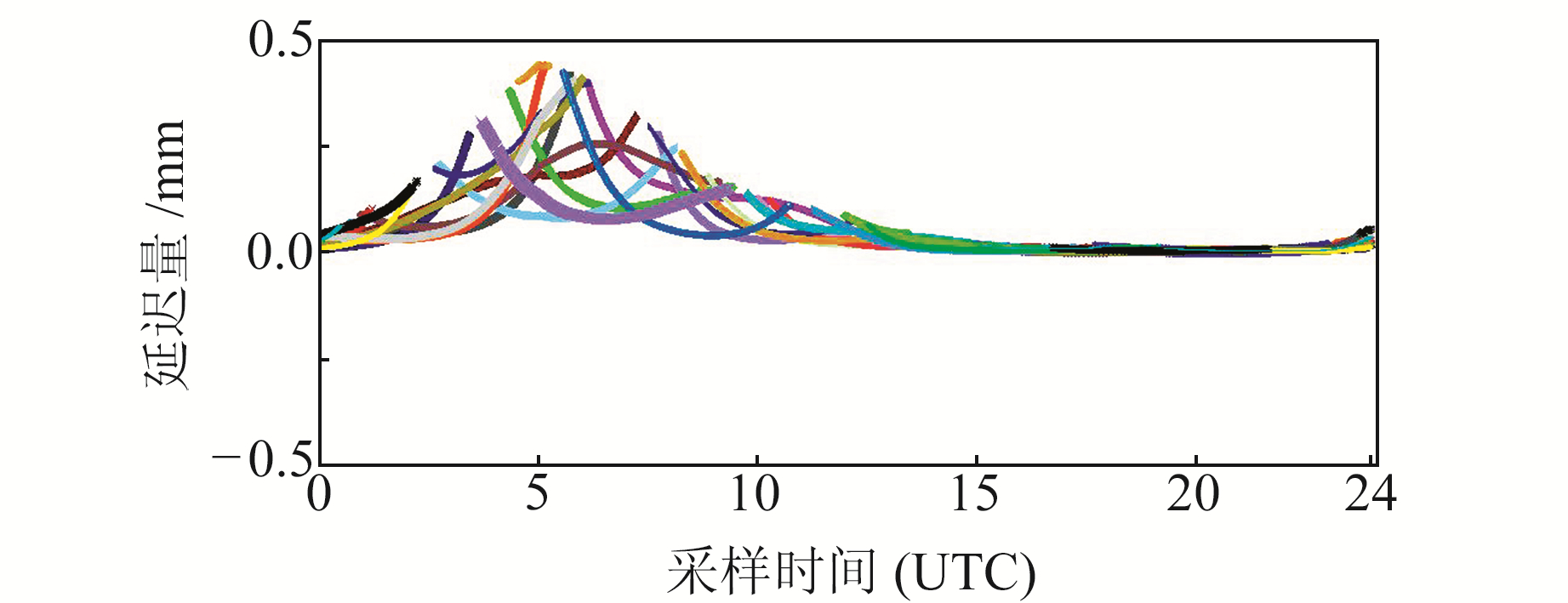
|
图 5 L2载波相位观测的电离层三阶项延迟 Fig. 5 Third-order ionospheric delay by L2 carrier observation |
由图 5可知,L2频段的电离层三阶项延迟均为正值,且最大值在1.0 mm以内。实验结果表明,电离层三阶项延迟通常情况下几乎可以忽略不计。
3 电离层高阶项延迟对高精度基线的影响电离层高阶项延迟对站星间可以产生mm级甚至cm级的影响,因此也会对长距离精密定位产生影响。为研究电离层高阶项延迟对精密相对定位的影响,分别选择不同间距的IGS站进行基线处理。本文选取BJFS-SUWN、WUHN-SHAO、SUWN-DAEJ及BJFS-WUHN四条不同长度和走向的基线在GAMIT10.71软件中进行解算。实验以CODE提供的GIMs产品计算的TEC及IGRF13模型为前提,为降低实验过程中其他因素的干扰,采用§2.1中的方法进行数据预处理,实验结果见表 2。
|
|
表 2 不同长度基线受电离层高阶项延迟的影响 Tab. 2 High-order ionospheric delay effected by different length baselines |
由表 2可知,在基线长度约为100~1 000 km的范围内,电离层高阶项延迟影响较仅一阶项影响的基线最大偏差(指包含一阶项、二阶项及三阶项的电离层延迟计算的基线与仅含有电离层一阶项延迟计算的基线差值)在3.0 mm左右,其中U方向的影响整体上比N、E方向大。南北走向的基线N方向与E、U方向的偏移方向相反;而东西走向的基线N、E、U方向的偏移方向一致并具有系统性,表明在精密相对定位的基线处理中,电离层高阶项延迟误差不可忽略。
为了分析电离层高阶项延迟处理策略的差异性,选择不同的处理方案对BJFS-SUWN基线进行实验。实验采用由不同方式获取的TEC和地磁模型计算的电离层高阶项延迟进行改正后的观测数据进行基线解算,解算结果和仅采用电离层一阶项延迟改正的基线结果进行比较,统计结果见表 3(单位mm)。
|
|
表 3 不同地磁模型及TEC对电离层高阶项延迟的影响 Tab. 3 High-order ionosphere delay effected by different geomagnetic models and TEC |
由表 3可知,在TEC相同的前提下,采用Dipolar、CGM及IGRF地磁模型计算出的电离层高阶项延迟对基线的影响差异在0.5 mm左右。相位平滑伪距获得的TEC比原始伪距及GIMs计算出的TEC对基线的影响更大,采用相位平滑伪距获得的TEC计算的基线长度较电离层一阶项延迟计算出的基线长度偏差大多在2.0 mm之内,但U方向达10.7 mm;GIMs模型获得的TEC较原始伪距获得的TEC计算的基线长度偏差约为1.0 mm,且两者基线长度比电离层一阶项延迟计算的基线长度短约4.0 mm。
电离层剧烈变化程度通常和太阳活动水平密切相关。表 4(单位mm)列出BJFS-SUWN基线8:30~14:30时段采用不同TEC和地磁模型计算的电离层高阶项延迟获得的基线与电离层一阶项延迟计算的基线偏差。
|
|
表 4 太阳活动高水平时段电离层高阶项延迟对基线的影响 Tab. 4 Effect of High-order ionosphere delay on baseline during high solar activity |
由表 4可以看出,在太阳活动高水平时段,采用相位平滑伪距获得的TEC计算的电离层高阶项延迟较一阶项计算的基线长度偏差达40.3 mm,且在E方向和U方向均呈现负值;其他两种TEC方式计算的基线较电离层一阶项延迟计算的基线长度差值在2.0 mm以内。对比表 3可以发现,在太阳活动高水平时段,电离层高阶项延迟在原始伪距和GIMs模式下对基线的影响并未出现太大的变化,主要原因可能是在此时段内单个卫星的影响有正有负,电离层高阶项延迟的改正可以相互抵消。
4 结语本文采用由不同方式获取的TEC及不同地磁模型计算GPS载波相位观测值中的电离层高阶项延迟,继而讨论站点位置及基线电离层高阶项延迟大小的差异性,分析电离层活跃时段对基线的影响。主要结论如下:
1) 电离层高阶项延迟大小及方向主要取决于卫星信号方向与地磁矢量间的夹角、太阳活动水平及穿刺点纬度;3种地磁模型计算的电离层二阶项延迟中,Dipolar及CGM模型计算出的电离层延迟量约为IGRF13模型的70%;GIMs获得的电离层二阶项延迟较另外两种方法结果更为平滑;通常情况下电离层三阶项延迟可以忽略不计。
2) 由原始伪距获取的TEC计算的电离层二阶项延迟最大可达10.0 mm,会出现严重的跳跃现象,这是否与广播星历的精度有关,有待进一步研究;CDDIS提供的最终GIMs产品较为平滑和稳定。
3) 电离层高阶项延迟的大小与载波相位观测值的频率有关,频率越大,电离层高阶项延迟越小。其在中纬度区域的延迟量呈系统性偏差,在北半球的中纬度区域,载波相位观测值的电离层高阶项延迟多为负值,在南半球的中纬度区域多为正值,赤道附近则呈现偶然性。其对基线向量的影响具有一定的可统计性,南北向基线N方向与E、U方向偏移量方向相反,U方向偏差量较大;东西向基线则表现出N、E、U三个方向的一致性偏移。
4) TEC在电离层高阶项延迟计算中起关键性作用,采用由平滑伪距获得的TEC计算基线时,电离层高阶项延迟比一阶项计算的基线长度更长;而采用由原始伪距及GIMs获得的TEC计算基线时,电离层高阶项延迟比一阶项计算的基线长度更短。
| [1] |
Strangeways H J, Ioannides R T. Rigorous Calculation of Ionospheric Effects on GPS Earth-Satellite Paths Using a Precise Path Determination Method[J]. Acta Geodaetica et Geophysica Hungarica, 2002, 37(2-3): 281-292 DOI:10.1556/AGeod.37.2002.2-3.17
(  0) 0) |
| [2] |
Deng L S, Jiang W P, Li Z, et al. Assessment of Second-and Third-Order Ionospheric Effects on Regional Networks: Case Study in China with Longer CMONOC GPS Coordinate Time Series[J]. Journal of Geodesy, 2016, 91(2): 207-227
(  0) 0) |
| [3] |
刘西凤, 袁运斌, 霍星亮, 等. 电离层二阶项延迟对GPS定位影响的分析模型与方法[J]. 科学通报, 2010, 55(12): 1 162-1 167 (Liu Xifeng, Yuan Yunbin, Huo Xingliang, et al. Model Analysis Method(MAM)on the Effect of the Second-Order Ionospheric Delay on GPS Positioning Solution[J]. Chinese Science Bulletin, 2010, 55(12): 1 162-1 167)
(  0) 0) |
| [4] |
张绍成, 王鑫哲, 黄龙强, 等. 电离层二阶项延迟对GPS动态精密单点定位的影响[J]. 测绘学报, 2018, 47(增1): 45-53 (Zhang Shaocheng, Wang Xinzhe, Huang Longqiang, et al. Impact of Second Order Ionosphere Delays for GPS Kinematic Precise Point Positioning Applications[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(S1): 45-53)
(  0) 0) |
| [5] |
Datta-Barua S, Walter T, Blanch J, et al. Bounding Higher-Order Ionosphere Errors for the Dual-Frequency GPS User[J]. Radio Science, 2008, 43(5): 1-15
(  0) 0) |
| [6] |
Hadas T, Gregorczyk A K, Pajares M H, et al. Impact and Implementation of Higher-Order Ionospheric Effects on Precise GNSS Applications[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(11): 9 420-9 436 DOI:10.1002/2017JB014750
(  0) 0) |
| [7] |
Munekane H. A Semi-Analytical Estimation of the Effect of Second-Order Ionospheric Correction on the GPS Positioning[J]. Geophysical Journal International, 2005, 163(1): 10-17 DOI:10.1111/j.1365-246X.2005.02723.x
(  0) 0) |
| [8] |
Kedar S, Hajj G A, Wilson B D, et al. The Effect of the Second Order GPS Ionospheric Correction on Receiver Positions[J]. Geophysical Research Letters, 2003, 30(16): 1 829
(  0) 0) |
| [9] |
Marques H A, Monico J F G, Aquino M. RINEX_HO: Second-and Third-Order Ionospheric Corrections for RINEX Observation Files[J]. GPS Solutions, 2011, 15(3): 305-314 DOI:10.1007/s10291-011-0220-1
(  0) 0) |
| [10] |
Marques H A, Monico J F G, Rosa G P S, et al. Second and Third Order Ionospheric Effects on GNSS Positioning: A Case Study in Brazil[C]. Geodesy for Planet Earth, International Association of Geodesy Symposia, Berlin, 2012
(  0) 0) |
| [11] |
Fritsche M, Dietrich R, Knöfel C, et al. Impact of Higher-Order Ionospheric Terms on GPS Estimates[J]. Geophysical Research Letters, 2005, 32(23)
(  0) 0) |
2. Faculty of Surveying and Mapping, Kunming Metallurgy College, 338 Xuefu Road, Kunming 650033, China
 2022, Vol. 42
2022, Vol. 42


