日长(length-of-day, LOD)是地球自转参数之一,获取LOD时存在着时延问题,因此,对日长变化进行高精度预报具有重要的科学意义和应用价值[1]。传统的日长变化预报采用最小二乘拟合外推与其他残差修正的组合模型[2-4]方法。然而,最小二乘法是线性拟合方法,不能很好地拟合日长变化序列中实际存在的非线性特征,从而影响最终的预报精度。研究表明,大气活动与日长变化密切相关,甚至部分日长变化年际尺度信号可以完全由大气激发来解释[5-6]。文献[7-8]在预报日长变化时,在误差修正模型中引入轴向大气角动量(atmospheric angular momentum, AAM)序列,结果表明,顾及大气角动量能够有效提高日长变化的预报精度。
本文提出应用于日长变化预测的Prophet与向量自回归(VAR)组合模型。Prophet模型适用于拟合信号的非线性特征,VAR模型本质上是自回归模型(AR)在多元变量时间序列领域的推广。首先,利用Prophet模型代替最小二乘法,分别对日长变化参数序列及大气角动量序列进行趋势项及周期项拟合外推;然后,针对所得的两种时序残差,利用VAR模型再次进行拟合;最后,将两种模型预报结果相加,即可得到日长变化的最终预报结果。
1 预报原理 1.1 模型介绍Prophet模型是由Facebook在2017年构建的一种用于时序分析的新模型,该模型算法将时间序列y(t)分解为长期趋势项、季节周期项以及节假日效应项等特征,并通过贝叶斯曲线拟合分别对各特征序列进行建模及预测,最后根据如下广义加法模型对特征序列进行累加,以此得到完整的拟合及预测结果[9]:
| $y\left( t \right) = g\left( t \right) + s\left( t \right) + h\left( t \right) + \varepsilon \left( t \right)$ | (1) |
式中,y(t)为完整时间序列,g(t)、s(t)、h(t)分别为趋势项、周期项及节日项,ε(t)为误差项。趋势项g(t)的逻辑回归函数为[9]:
| $g\left( t \right) = \frac{C}{{1 + {{\rm{e}}^{ - k\left( {t - m} \right)}}}}$ | (2) |
式中,C为趋势上限,k为增长率,m为偏移量。随着时间t的延续,曲线以增长率k非线性增加,最后趋于上限值C[10]。周期项s(t)的模型为[11]:
| $s\left( t \right) = \mathop \sum \limits_{n = 1}^N \left( {{a_n}\cos \left( {\frac{{2{\rm{ \mathsf{ π} }}nt}}{T}} \right) + {b_n}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}nt}}{T}} \right)} \right)$ | (3) |
式中,T为周期,N为频谱个数。
p阶的VAR(p)模型可以表达为[12]:
| ${\mathit{\boldsymbol{y}}_t} = \mathit{\boldsymbol{c}} + {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{y}}_{t - 1}} + \ldots + {\mathit{\boldsymbol{A}}_p}{\mathit{\boldsymbol{y}}_{t - p}} + {\mathit{\boldsymbol{\varepsilon }}_t}$ | (4) |
式中,c为n×1阶待估常数向量;Ai为n×n阶待估系数矩阵;yi为n维内生变量组成的向量;εt为随机扰动项,与自身滞后项及等式右边各变量严格无关[12]。构建VAR模型最关键的步骤是通过不同的筛选准则确定最优滞后阶数p。以最终预测误差(FPE)为例,其表达式为:
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{FPE}}\left( p \right) = \\ \left( {1 + \frac{p}{M}} \right){\left( {1 - \frac{p}{M}} \right)^{ - 1}}\left( {{{\hat y}_0} - \mathop \sum \limits_{i = 1}^p {a_i}{{\hat y}_i}} \right) \end{array}$ | (5) |
式中,M为序列长度,
预报流程如下:1)在原始LOD时序中去除固体潮影响,得到LODR序列;2)利用Prophet算法将LODR序列进行特征分解,得到基于Prophet的拟合序列;3)利用LODR拟合的残差序列,以及经过Prophet拟合的AAM残差序列,共同建立VAR模型,从而得到顾及大气角动量的残差修正模型预测结果;4)将Prophet拟合序列和VAR拟合序列的预测结果相加,得到最终的LODR预测值。采用平均绝对误差(MAE)作为预测精度的评价指标,其计算公式为[15]:
| $ {\rm{MA}}{{\rm{E}}_i} = \frac{1}{N}\sum\limits_{j = 1}^N {\left| {P_j^i - Q_j^i} \right|} $ | (6) |
式中,N为预报期数,Pji、Qji分别为当预报跨度为i时第j期的预报值及真实值。
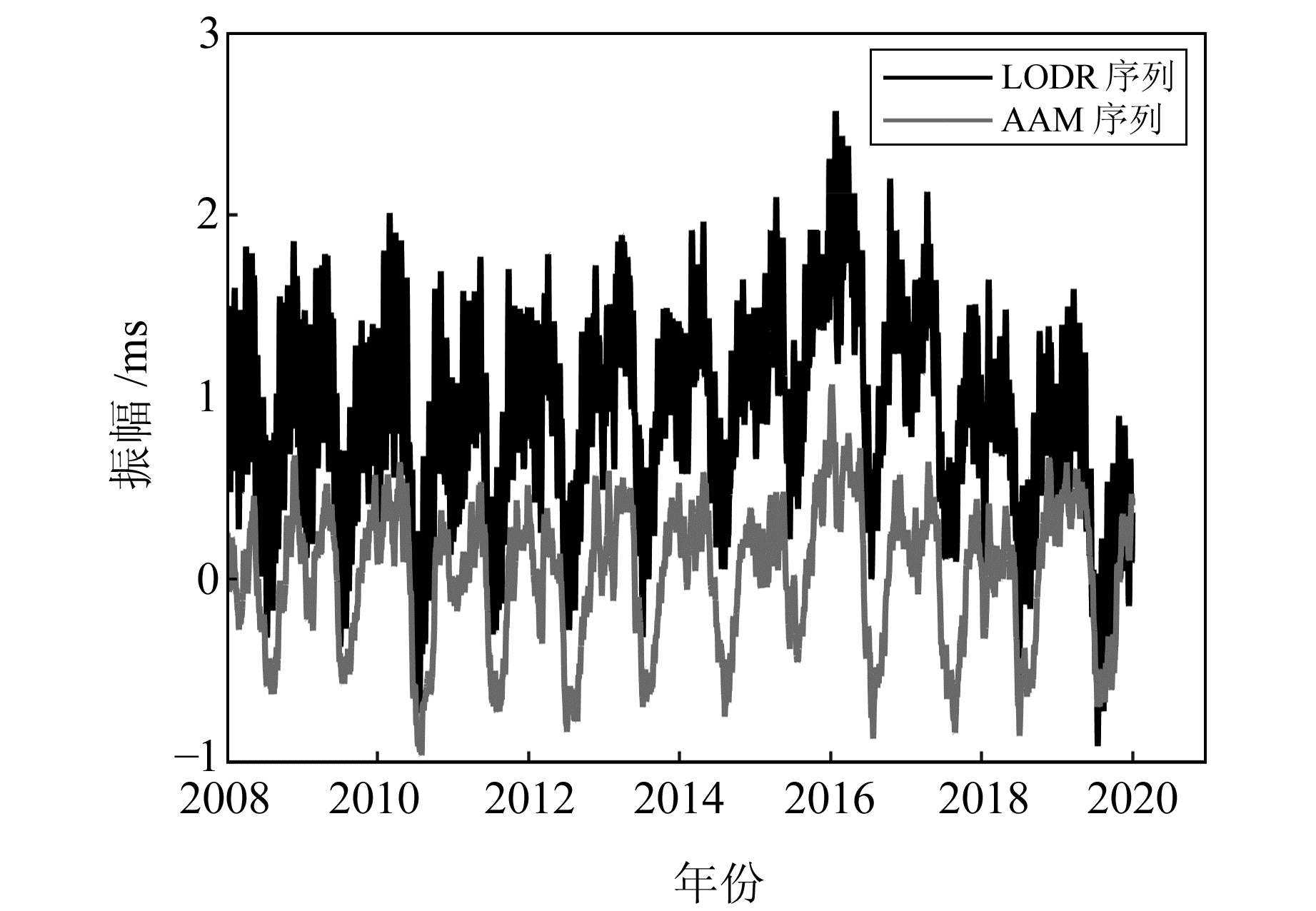
2 实验分析 2.1 数据日长变化数据为IERS发布的EOP14 C04地球自转参数序列(http://hpiers.obspm.fr/iers/eop),大气角动量序列来源于由欧洲中期气候预报中心(ECMWF)发布的轴向分量χ3序列(http://rz-vm115.gfz-potsdam.de:8080/repository)。序列区间为2008-01-01~2020-12-31,区间内序列保持连续,其中2008-01-01~2019-12-31为初始建模序列,预报跨度为150 d。每进行一次预报后将序列整体进行隔天前推,从而在维持预报序列总长度为12 a的情况下进行第二次预报。以此类推,总预报期数为217组,统计所有组1~150 d预报期间的平均绝对误差进行分析。图 1为去除潮汐项后的LODR序列及原始AAM序列,可以看出,两个序列之间存在明显的同向运动规律,对其进行皮尔逊相关性分析,得到二者的相关系数为0.751,呈强相关,因此完全可以引入大气角动量序列来预报日长变化。
|
图 1 去除潮汐项后的LODR序列及原始AAM序列 Fig. 1 LODR sequence after deducting tidal term and original AAM sequence |
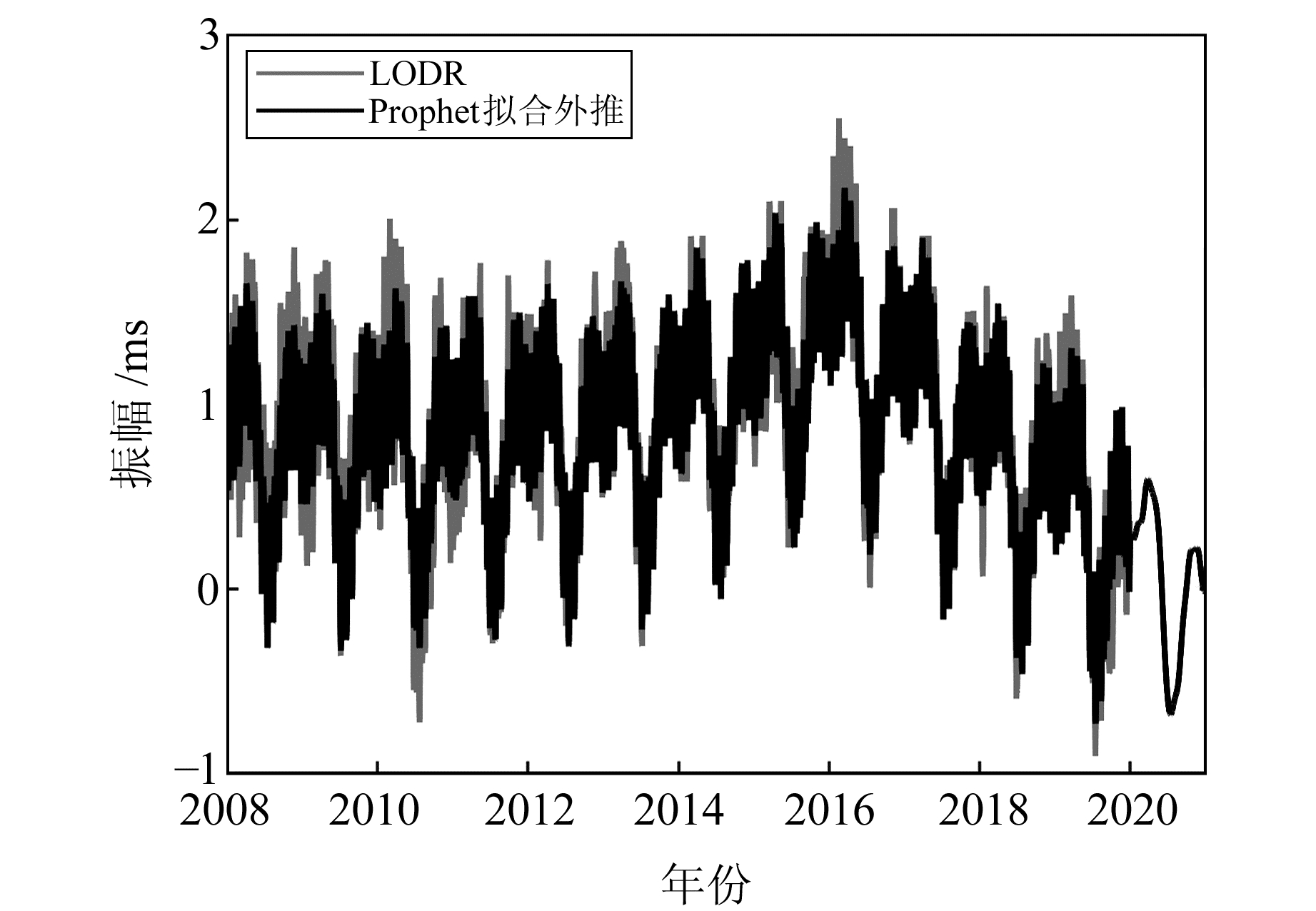
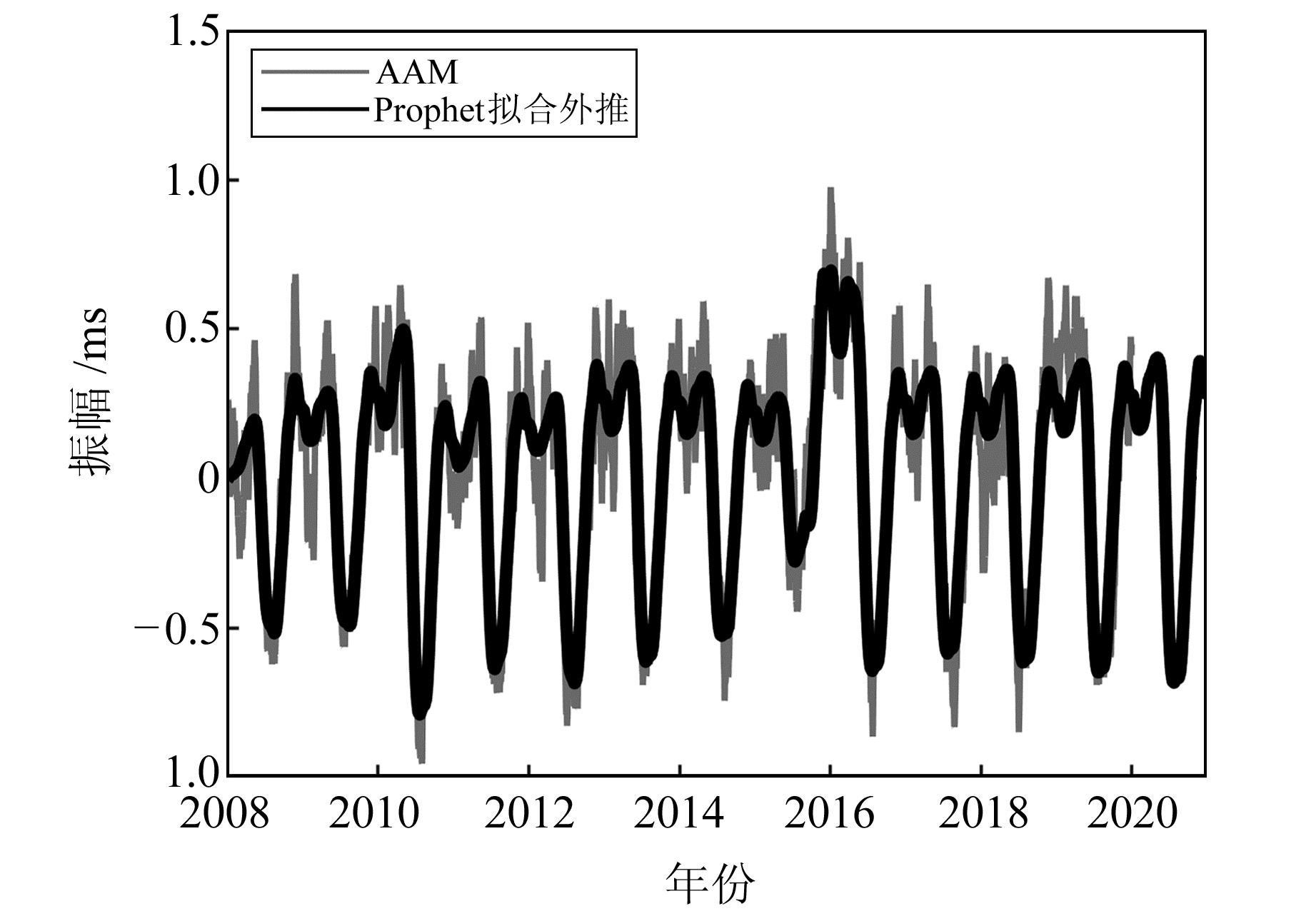
采用Prophet算法分别对LODR和AAM序列进行拟合,并预测2020年数值,结果如图 2和图 3所示。由图可见,经过Prophet算法拟合后,拟合曲线可以较好地反映相应原始序列的发展趋势。为更好地显示拟合效果,对LODR序列与其拟合序列作差,并统计残差序列的分布情况,将统计结果与经过最小二乘拟合去除趋势项及周期项的残差统计信息进行对比。表 1(单位ms)给出了LODR序列分别经过Prophet、LS拟合后残差序列的均方根误差(RMSE)、平均值、最大值及最小值信息。统计发现,采用Prophet算法来拟合外推LODR序列更为有效。
|
图 2 Prophet模型拟合预报LODR效果 Fig. 2 The results of fitting and predicting LODR by Prophet model |
|
图 3 Prophet模型拟合预报AAM效果 Fig. 3 The results of fitting and predicting AAM by Prophet model |
|
|
表 1 LODR残差序列的统计信息 Tab. 1 Statistical information of LODR residual sequence |
图 4为拟合后的LODR及AAM残差序列,二者之间的相关系数为0.815。这说明残差序列之间依然存在着较强的相关性,并且两个残差序列均为平稳序列。因此,可以考虑建立联合LODR残差序列及AAM残差序列的VAR误差补偿模型,再次对Prophet模型的LODR预测误差进行拟合修正。

|
图 4 LODR及AAM残差序列 Fig. 4 Residual sequences of LODR and AAM |
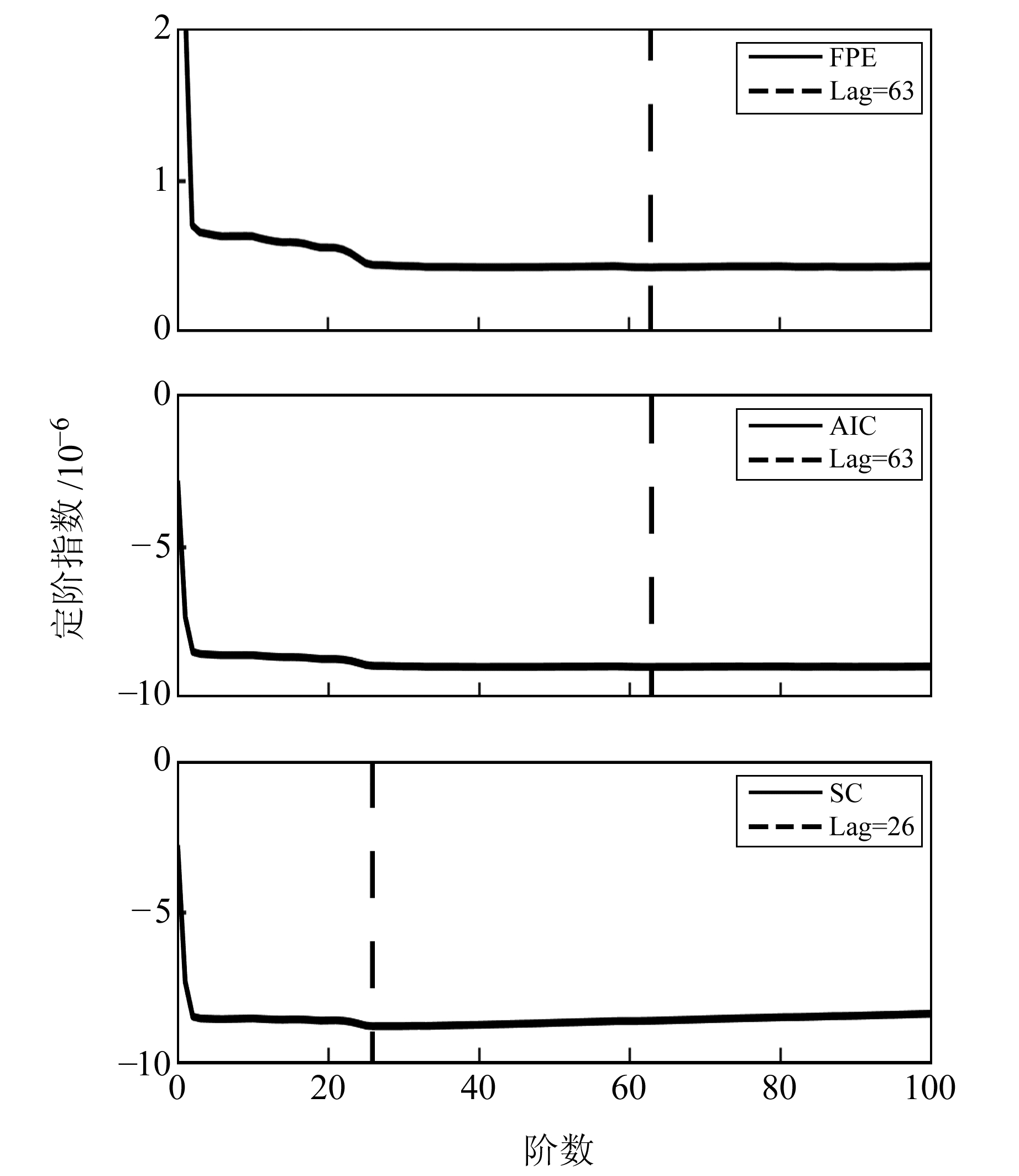
建立VAR模型的关键是确定模型的阶数q。利用初始残差序列,分别计算其1~100阶内的FPE、AIC及SC指数,结果如图 5所示。图中虚线代表序列最小值处的阶数,分别为63、63、26。根据多数原则,本文选取p值为63作为VAR模型的阶数,从而构建VAR(63)模型用于拟合预测。值得注意的是,这仅仅是初始残差建模序列所构造的预报模型,当完成一期预报后,第二期的建模序列会整体向前推移1 d,此时需要重新构造VAR模型。
|
图 5 3种定阶准则指数信息 Fig. 5 Index information of three order determination criteria |
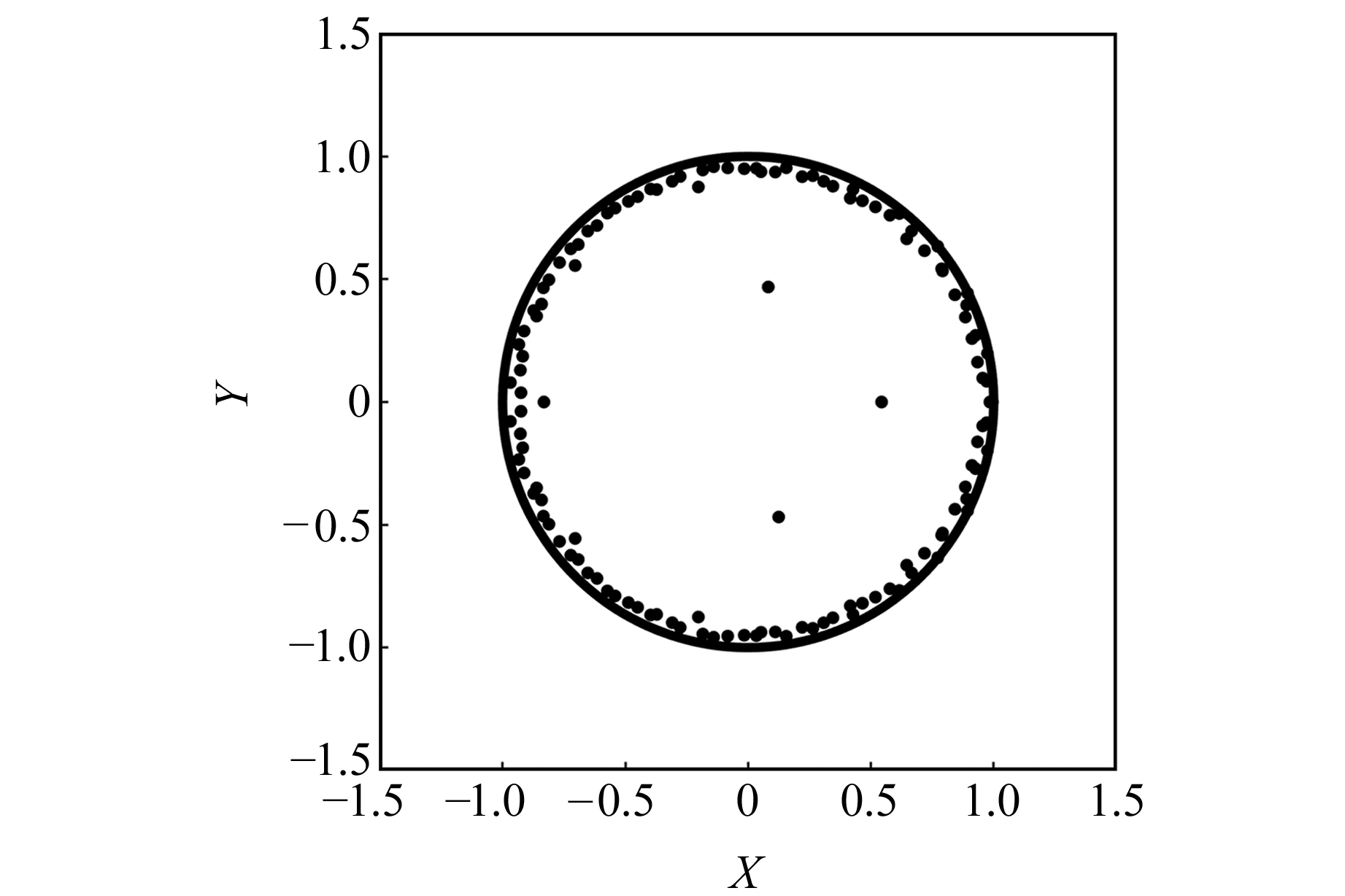
构建好VAR模型后,需要检验模型是否稳定,判断的准则是模型特征根倒数的模均小于1。检验结果如图 6所示,图中点表示特征根的倒数。如果没有点落在单位圆外,就认为通过了平稳检验,VAR误差补偿模型有效。
|
图 6 特征根检验 Fig. 6 Eigenvalues test |
利用Prophet和VAR模型,可得到每期最终的LODR预测序列。将EOP14 C04序列作为真值序列,在217组预报全部完成以后,计算1~150 d跨度的MAE值,并将其作为精度评价指标。为了更好地分析预报效果,本文设计另外两种方案作为对比:
1) Prophet-AR模型。不考虑AAM序列,仅依据LODR序列进行日长预测。此时,VAR模型变为单变量的AR模型。将此方法与本文方法进行对比,可分析顾及大气角动量对预报效果的影响。
2) LS-AR模型。提取原始序列趋势项,选用传统的LS算法来代替Prophet算法。将此方法与本文方法及方案1进行对比,可分析Prophet算法与LS算法的优劣。
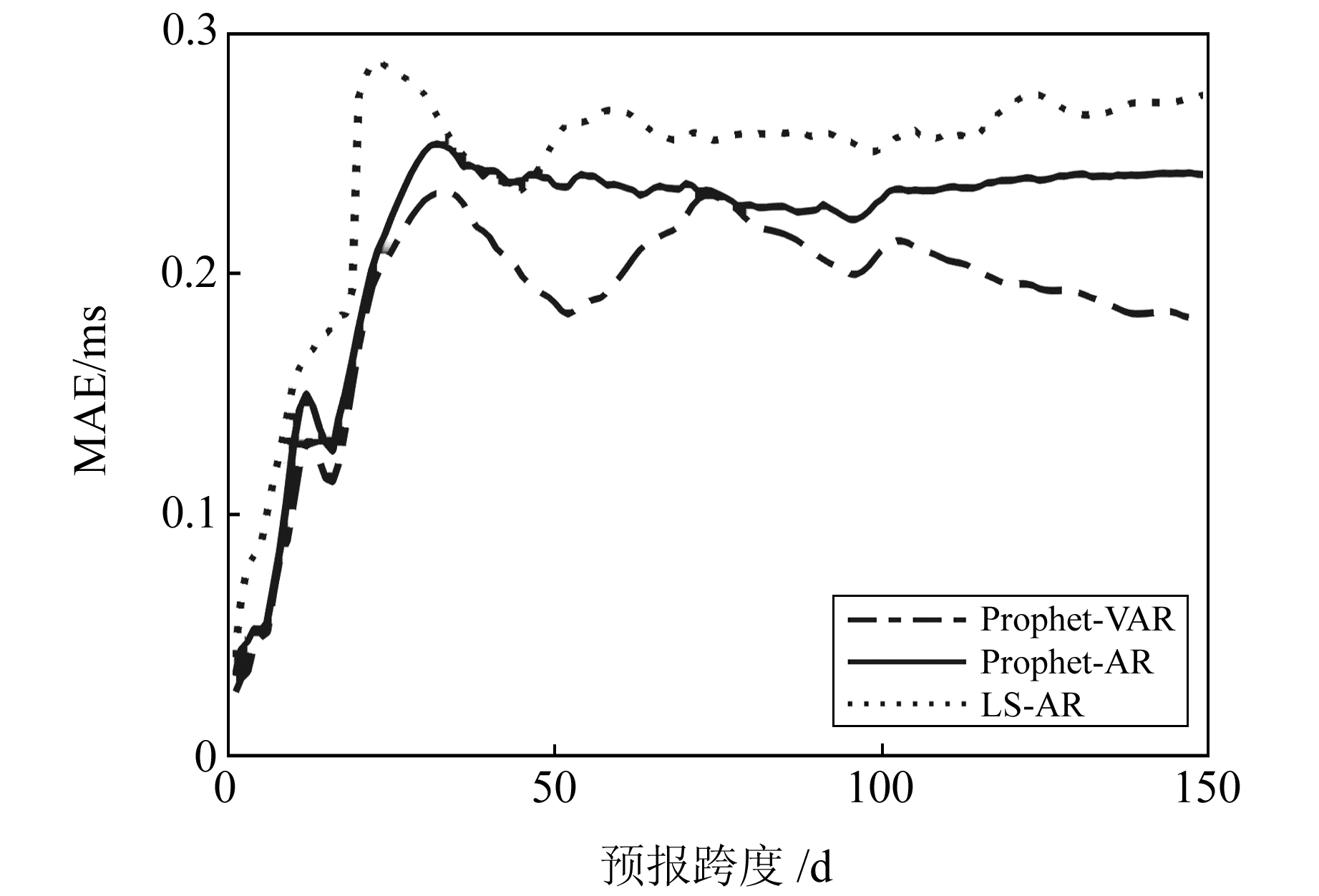
3种方案采用同样的预报流程,最终的MAE序列如图 7所示。由图可见,在1~150 d的预报跨度内,本文给出的Prophet-VAR预报模型最优。为定量分析预报效果,表 2(单位ms)列出3种方案在1~150 d预报跨度的MAE值,并分别计算Prophet-AR模型及Prophet-VAR模型相对于LS-AR模型的精度改善百分比。
|
图 7 3种预报模型的MAE曲线 Fig. 7 The MAE curves of three prediction models |
|
|
表 2 3种预报模型的MAE值及对比LS-AR的改善程度 Tab. 2 The MAE value of three prediction models and the improvement compared to LS-AR |
由表 2可见,Prophet-AR与LS-AR相比,精度提升8%~40%,尤其是在超短期预报(1~10 d)中精度改善幅度更大。Prophet-VAR与LS-AR相比,精度提升16%~57%,在任意预报跨度内的精度提升都非常明显,且显著高于同时段Prophet-AR方法的改善精度,表明在日长变化参数预报中加入大气角动量序列,对预报精度有明显的提升作用。综上所述,顾及大气角动量的Prophet-VAR模型是一种非常有效的日长变化预报方法。
3 结语本文提出一种顾及大气角动量的Prophet-VAR日长变化参数预报模型,利用2008-01-01~2020-12-31期间的日长变化序列进行实验,以1~150 d的预报跨度来分析该模型的预报效果。为便于比较,同时设计了传统的LS-AR及不顾及大气角动量的Prophet-AR两种预报方案与本文方法进行对比分析,评价指标采用平均绝对误差。结果表明,Prophet算法代替LS算法来结合AR模型在预报日长变化参数时更有优势,这种优势在超短期预报时最为明显,且加入大气角动量序列对提高预报精度有显著的提升效果。由此说明,在预报日长变化参数时顾及大气角动量的Prophet-VAR模型是一种更有优势的高精度预报模型。
本文在分析过程中发现,尽管Prophet算法相较于LS算法能够更加有效地拟合LODR原始序列中的趋势项,从而提取出更多真实的非线性长期趋势项信号,但在提取周期项时,其与LS算法一样,仍然是提取振幅固定的周期信号,这并不符合日长变化序列的周期振幅时变特征。因此下一步的工作可以从该角度出发,探索如何通过提取更准确的周期项信号来提升日长变化参数预报的效果。
| [1] |
许雪晴, 周永宏. 地球定向参数高精度预报方法研究[J]. 飞行器测控学报, 2010, 29(2): 70-76 (Xu Xueqing, Zhou Yonghong. High Precision Prediction Method of Earth Orientation Parameters[J]. Journal of Spacecraft TT & C Technology, 2010, 29(2): 70-76)
(  0) 0) |
| [2] |
Kosek W, Kalarus M, Johnson T J, et al. A Comparison of LOD and UT1-UTC Forecasts by Different Combined Prediction Techniques[J]. Artificial Satellites, 2005, 40(2): 119-125
(  0) 0) |
| [3] |
Lei Y, Zhao D N, Cai H B. Prediction of Length-of-Day Using Extreme Learning Machine[J]. Geodesy and Geodynamics, 2015, 6(2): 151-159 DOI:10.1016/j.geog.2014.12.007
(  0) 0) |
| [4] |
孙张振, 徐天河. 基于LS+AR模型的LOD预报及其周期项影响分析[J]. 大地测量与地球动力学, 2013, 33(4): 69-72 (Sun Zhangzhen, Xu Tianhe. Prediction of Length of Day Based on LS + AR Model and Accuracy Analysis of Different Cycle Term[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 69-72)
(  0) 0) |
| [5] |
Zotov L, Sidorenkov N S, Bizouard C, et al. Multichannel Singular Spectrum Analysis of the Axial Atmospheric Angular Momentum[J]. Geodesy and Geodynamics, 2017, 8(6): 433-442 DOI:10.1016/j.geog.2017.02.010
(  0) 0) |
| [6] |
张欣峰, 刘根友. 日长年际信号提取及其与大气相关性分析[J]. 大地测量与地球动力学, 2020, 40(11): 1 188-1 193 (Zhang Xinfeng, Liu Genyou. Extraction of Interannual Signals in the Length-of-Day Variation and Correlation Analysis with the Atmosphere[J]. Journal of Geodesy and Geodynamics, 2020, 40(11): 1 188-1 193)
(  0) 0) |
| [7] |
Niedzielski T, Kosek W. Prediction of UT1-UTC, LOD and AAM χ3 by Combination of Least-Squares and Multivariate Stochastic Methods[J]. Journal of Geodesy, 2008, 82(2): 83-92 DOI:10.1007/s00190-007-0158-9
(  0) 0) |
| [8] |
王琪洁, 廖德春, 周永宏, 等. 大气角动量函数在日长变化非线性预报中的重要作用[J]. 天文学报, 2008, 49(1): 93-100 (Wang Qijie, Liao Dechun, Zhou Yonghong, et al. Importance of Atmospheric Angular Momentum Function in Non-Linear Prediction of Length of Day Variation[J]. Acta Astronomica Sinica, 2008, 49(1): 93-100 DOI:10.3321/j.issn:0001-5245.2008.01.009)
(  0) 0) |
| [9] |
Taylor S J, Letham B. Forecasting at Scale[J]. The American Statistician, 2018, 72(1): 37-45 DOI:10.1080/00031305.2017.1380080
(  0) 0) |
| [10] |
李威, 鲁铁定, 贺小星, 等. 基于Prophet-RF模型的GNSS高程坐标时间序列预测分析[J]. 大地测量与地球动力学, 2021, 41(2): 116-121 (Li Wei, Lu Tieding, He Xiaoxing, et al. Prediction and Analysis of GNSS Vertical Coordinate Time Series Based on Prophet-RF Model[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 116-121)
(  0) 0) |
| [11] |
翟笃林, 张学民, 熊攀, 等. Prophet时序预测模型在电离层TEC异常探测中的应用[J]. 地震, 2019, 39(2): 46-62 (Zhai Dulin, Zhang Xuemin, Xiong Pan, et al. Detection of Ionospheric TEC Anomalies Based on Prophet Time-Series Forecasting Model[J]. Earthquake, 2019, 39(2): 46-62)
(  0) 0) |
| [12] |
李双, 李哲, 杜建括, 等. 陕西省水资源利用与经济增长动态关系的VAR模型分析[J]. 生态经济, 2020, 36(10): 146-154 (Li Shuang, Li Zhe, Du Jiankuo, et al. Study on the Dynamic Relationship between Water Resources Utilization and Economic Growth in Shaanxi Province Based on the VAR Model[J]. Ecological Economy, 2020, 36(10): 146-154)
(  0) 0) |
| [13] |
Hatemi-J A. A New Method to Choose Optimal Lag Order in Stable and Unstable VAR Models[J]. Applied Economics Letters, 2003, 10(3): 135-137 DOI:10.1080/1350485022000041050
(  0) 0) |
| [14] |
李艺珍, 毛建刚, 张明, 等. 基于VAR模型的新疆金沟河气象要素与径流关系分析[J]. 水资源与水工程学报, 2020, 31(5): 80-86 (Li Yizhen, Mao Jiangang, Zhang Ming, et al. Relationship between Meteorological Elements and Runoff in Jingou River Basin of Xinjiang Based on the VAR Model[J]. Journal of Water Resources and Water Engineering, 2020, 31(5): 80-86)
(  0) 0) |
| [15] |
严凤, 姚宜斌. 地球自转参数短期预报方法及其实现[J]. 大地测量与地球动力学, 2012, 32(4): 71-75 (Yan Feng, Yao Yibin. Short-Term Prediction Methods and Realization of Earth Rotation Parameters[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 71-75)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

