2. 江西理工大学土木与测绘工程学院,江西省赣州市红旗大道86号,341000;
3. 南昌航空大学校长办公室,南昌市丰和南大道696号,330063
以GNSS为主的卫星导航定位基准站网近年来发展迅速,为大地测量的应用提供了高精度的空间基准基础设施[1]。GNSS坐标时间序列蕴含丰富的物理信息,包括测站长期受区域内构造应力影响产生的线性变化以及地球物理效应与其他外部环境等导致的非线性变化[2]。由于测站会受到电离层延迟、多路径效应、环境负载、轨道异常等多种误差影响[3],GNSS坐标时间序列在呈现非线性变化的同时也存在异常值[4]。这些异常值在整体或局部数据中表现出较大的波动,无法准确反映出时间序列的变化特征,对数据分析与应用产生较大的负面影响。
经典的粗差探测法有3σ法[5]和MAD(median absolute deviation)法[6-7]。3σ法的原理是利用最小二乘法求得观测序列的残差,再对残差序列进行粗差探测。由于最小二乘法本身含有粗差,因此3σ法的残差中误差估计值不够准确,从而影响粗差探测的可靠性[8-11]。MAD方法的运算崩溃污染率可达50%,其异常值探测相比于3σ法更加稳健,但MAD法需要满足样本对称分布的条件[12-13]。基于上述讨论,诸多学者在此基础上引入新的准则和方法以提高粗差探测的效率和准确率。明锋等[8]提出L1范数与IQR组合探测方法,使模型化后的残差探测准确率更高;吴浩等[5]提出一种利用小波改进的3σ粗差探测方法,既能准确提取变形趋势,也能提高3σ在坐标数据中的适用性;Wang等[14]发现有效提取趋势项和周期项至关重要,SSA在这方面具有一定优势,能准确提取出残差项;蔡晓军等[15]研究表明,在提取趋势项和周期项方面SSA优于小波分析法。
综合以上异常值探测方法的优势与不足并结合GNSS坐标时间序列的数据特征,建立一种SSA与Sn估计量[14]相结合的异常值探测方法。选用模拟的时间序列数据以及中国部分IGS站的实测数据进行实验,结果表明,在粗差探测方面SSA-Sn法的探测效果优于3σ法和MAD法。
1 原理及方法 1.1 SSA数学模型将时间序列X =(x1, x2, x3, …, xN)中心化后,根据窗口长度L构造维度为L×(N-L+1)的轨迹矩阵
| $\mathit{\boldsymbol{\tilde X}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_{i + 1}}}& \cdots &{{x_{N - L + 1}}}\\ {{x_2}}&{{x_3}}& \cdots &{{x_{i + 2}}}& \cdots &{{x_{N - L + 2}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{x_L}}&{{x_{L + 1}}}& \cdots &{{x_{i + L}}}& \cdots &{{x_N}} \end{array}} \right]$ | (1) |
滞后协方差矩阵为
| $\mathit{\boldsymbol{C}} = \mathit{\boldsymbol{V \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}$ | (2) |
将C的特征值进行降序排列,得到λk,Λ为λk构成的对角矩阵,正交矩阵V的行向量为vk。主成分矩阵为:
| $\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{V\tilde X}}$ | (3) |
A的第k行ak为第k个主成分,其中ak, i为:
| ${a_{k, i}} = \mathop \sum \limits_{j = 1}^L {x_{i + j - 1}}{v_{k, j}}, 1 \le i \le N - L + 1$ | (4) |
式中,vk, j是vk的第j个元素。时间序列中第k个重构分量为:
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{x}_i^k = \\ \left\{ \begin{array}{l} \frac{1}{i}\mathop \sum \limits_{j = 1}^i {a_{k, i - j + 1}}{v_{k, j}}, 1 \le i \le L - 1\\ \frac{1}{L}\mathop \sum \limits_{j = 1}^L {a_{k, i - j + 1}}{v_{k, j}}, L \le i \le N - L + 1\\ \frac{1}{{N - i + 1}}\mathop \sum \limits_{j = i - N + L}^L {a_{k, i - j + 1}}{v_{k, j}}, N - L + 2 \le i \le N \end{array} \right. \end{array}$ | (5) |
将所有的重构序列进行累加即可得到原始的时间序列,因此选取合适的主成分个数P可有效提取序列中的主要特征,其他成分将视为噪声,即有q个主成分的重构序列
| $\mathit{\hat x} = \mathop \sum \limits_{k = 1}^q x_i^k, i = 1, 2, \cdots , N$ | (6) |
采用交叉验证法确定SSA需要的窗口长度L与主成分个数P两个参数。首先给出两个参数的初始值,并在原始数据中随机挑选部分数据用于验证,验证数据处用0填充,即可得到训练数据。随后将训练数据进行奇异谱分析,计算验证部分模型导出值与参考值的均方根误差RMSE,RMSE最小时的窗口长度L与主成分个数P即为最优参数。Wang等[14]表明,2~3 a的窗口长度适合提取年周期及半年周期分量,因此本文采用2 a作为窗口长度的初值。
1.3 Sn尺度估计量Sn是一个由Rousseeuw和Croux提出的稳健统计量,Sn估计量具有与MAD法相同的稳健性,并且不依赖于对称分布。假设一组数据为{x1, x2, …, xn},则Sn估计量被定义为:
| ${S_n} = c{\rm{me}}{{\rm{d}}_i}\left\{ {{\rm{me}}{{\rm{d}}_i}\left| {{x_i} - {x_j}} \right|} \right\}$ | (7) |
式中,常数c是为了满足Fisher一致性的调节因子,其值为1.192 6;外中位数是一个秩为[(n+1)/2]阶的顺序统计量,而内中位数是一个秩为[n/2]+1的顺序统计量。
1.4 SSA-Sn粗差探测原理在对GNSS坐标时间序列进行粗差探测时,可将时间序列数据视为一组被噪声和粗差污染的趋势信号。SSA相较于小波分析能够更加准确地提取趋势项、周期项等主要的时间序列特征,从而分离出残差项;Sn与MAD法对异常值探测的稳健性相同且都优于3σ法,估计量崩溃点均为50%,不易受到粗差的污染,但Sn无需依赖数据的对称分布,因此本文采用SSA-Sn法进行粗差探测。具体步骤如下:
1) 输入坐标时间序列原始数据集X(t),使用交叉验证法确定最优的窗口长度L与主成分个数P;
2) 根据确定的窗口长度L以及主成分个数P对原始数据X(t)进行奇异谱分解,得到时间序列数据的趋势项、周期项等主要特征,重构数据
3) 原始数据与重构数据作差,得到含有噪声以及粗差的残差序列:
| $\mathit{v} = \mathit{X}\left( t \right) - \mathit{\tilde X}\left( t \right)$ | (8) |
式中,v为残差项;
4) 采用Sn估计量对残差序列v进行粗差探测,判别式为:
| $\left| {{v_i} - {\rm{median}}\left( v \right)} \right| > 3{S_n}$ | (9) |
式中,median(v)为残差序列的中值。
2 实验结果与分析 2.1 模拟GNSS站坐标时间序列为检验粗差探测方法的有效性,根据GNSS单站、单分量坐标时间序列函数模型和随机模型构造包含趋势项、周期项和噪声项的模拟时间序列,其函数表达式为:
| $\begin{array}{l} y\left( {{t_i}} \right) = a + \frac{{b{t_i}}}{T} + c\sin (\frac{{2{\rm{ \mathsf{ π} }}{t_i}}}{T}) + d\cos (\frac{{2{\rm{ \mathsf{ π} }}{t_i}}}{T}) + \\ \;\;\;\;\;\;\;\;\;\;e\sin \frac{{(4{\rm{ \mathsf{ π} }}{t_i}}}{T}) + f\cos (\frac{{4{\rm{ \mathsf{ π} }}{t_i}}}{T}) + {v_i} \end{array}$ | (10) |
式中,ti为观测时间,a为测站时间序列的起始位置,b为测站运动的线性速度,c、d、e、f分别为测站周年运动和半周年运动的振幅,vi为GPS坐标时间序列中的噪声。为更加真实地模拟GPS时间序列噪声,采用式(11)生成白噪声和有色噪声:
| $ \left\{ \begin{array}{l} \mathit{v}\left( {{t_i}} \right) = \mathit{w}\left( {{t_i}} \right), i \le 2\\ \mathit{v}\left( {{t_i}} \right) = {f_1}\mathit{v}\left( {{t_{i - 1}}} \right) + {f_2}\mathit{v}\left( {{t_{i - 2}}} \right) + \mathit{w}\left( {{t_i}} \right), i \ge 3 \end{array} \right. $ | (11) |
式中,w(ti)是均值为0、方差为1的白噪声,f1和f2均为0.2。
根据式(10)和式(11),模拟长度为1 826、不含粗差的时间序列数据y(t)。在模拟粗差数据过程中,考虑到实际时间序列数据具有粗差分布广泛、随机等特点,首先采用均值为0、标准差为10σ的正态分布,模拟得到一组误差序列,然后将大于3σ的数据任意地添加到不含粗差的原始序列中,从而得到一组被粗差污染的模拟坐标时间序列
|
|
表 1 模拟数据统计 Tab. 1 Simulation data statistics |
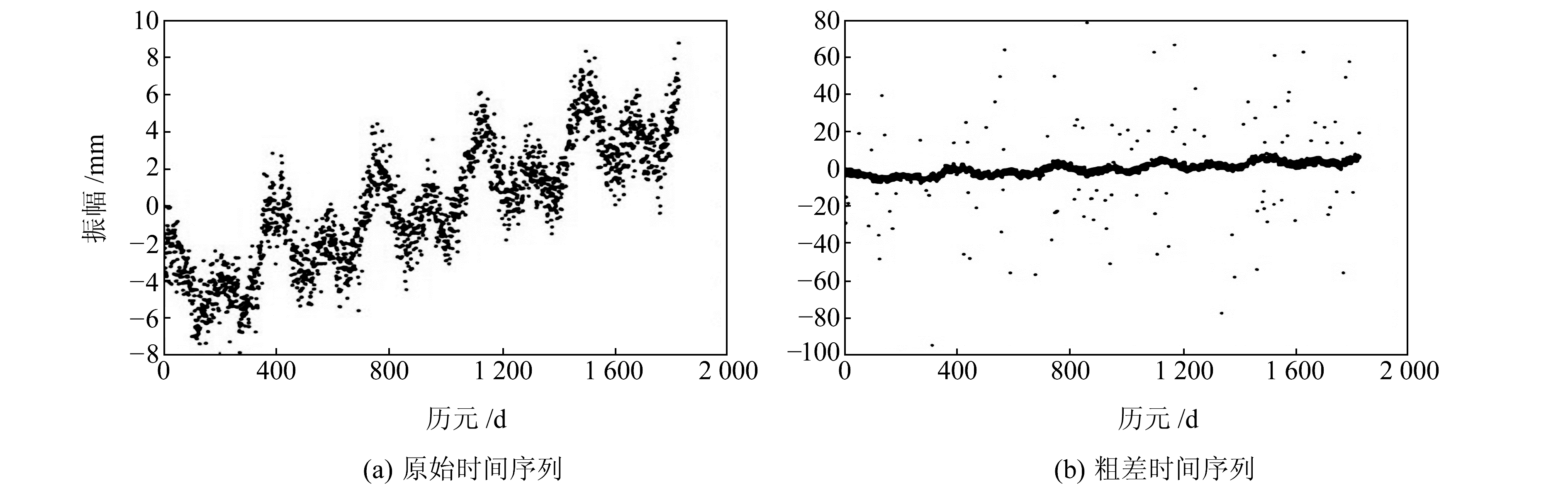
|
图 1 模拟时间序列 Fig. 1 Simulated time series |
利用交叉验证法对含有粗差的模拟时间序列
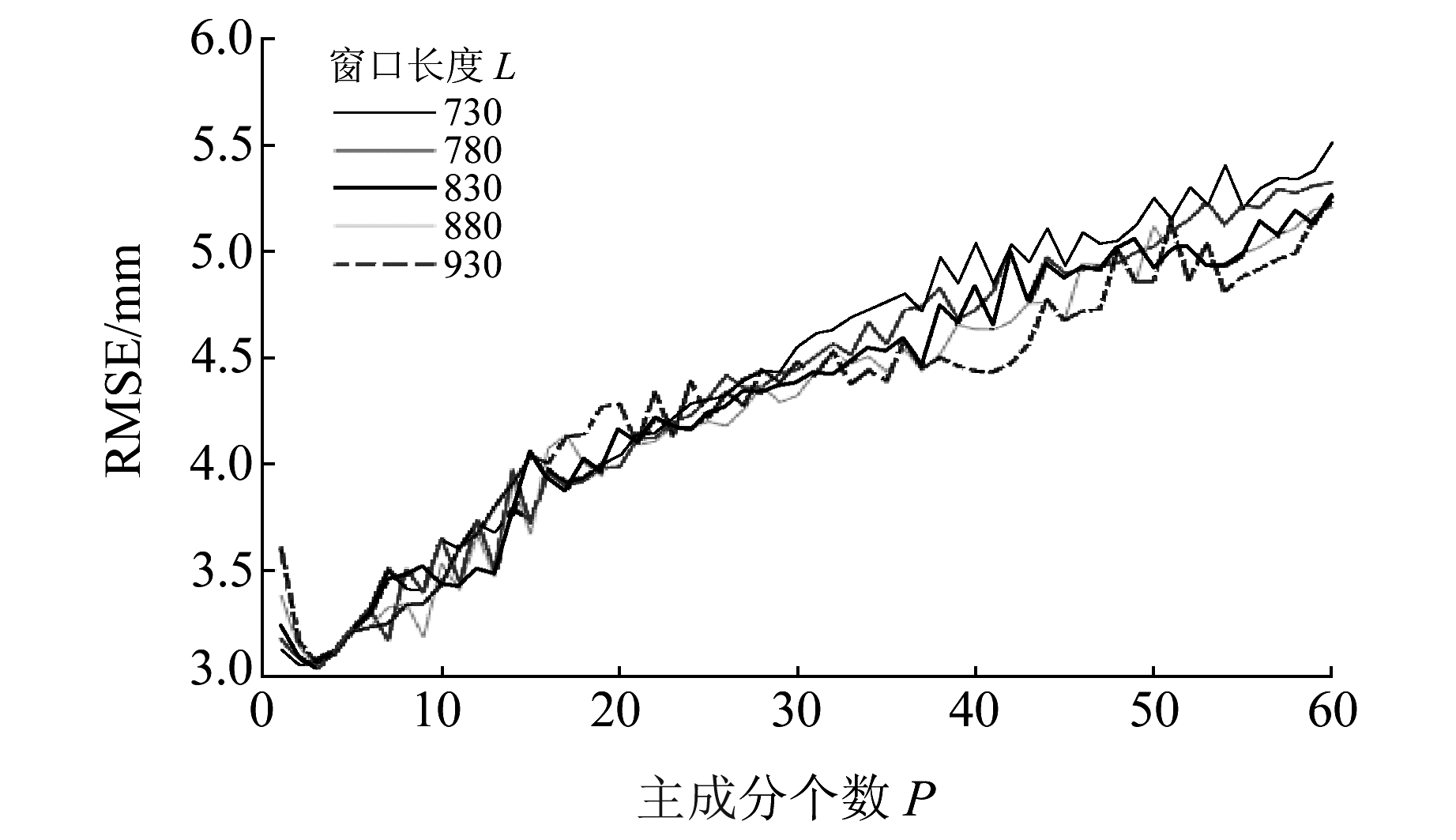
|
图 2 模拟数据的RMSE随窗口长度L与主成分个数P的变化情况 Fig. 2 The RMSE of the simulated data varies with the length of the window and the number of principal components |
由图 2可见,模拟数据的RMSE对主成分个数P的变化比对窗口长度L的变化更加敏感,在主成分个数0~10范围内每条曲线的RMSE都达到了最小值。经交叉验证后,选取最优窗口长度L为830、主成分个数P为3。
2.3 模拟数据结果分析将模拟时间序列
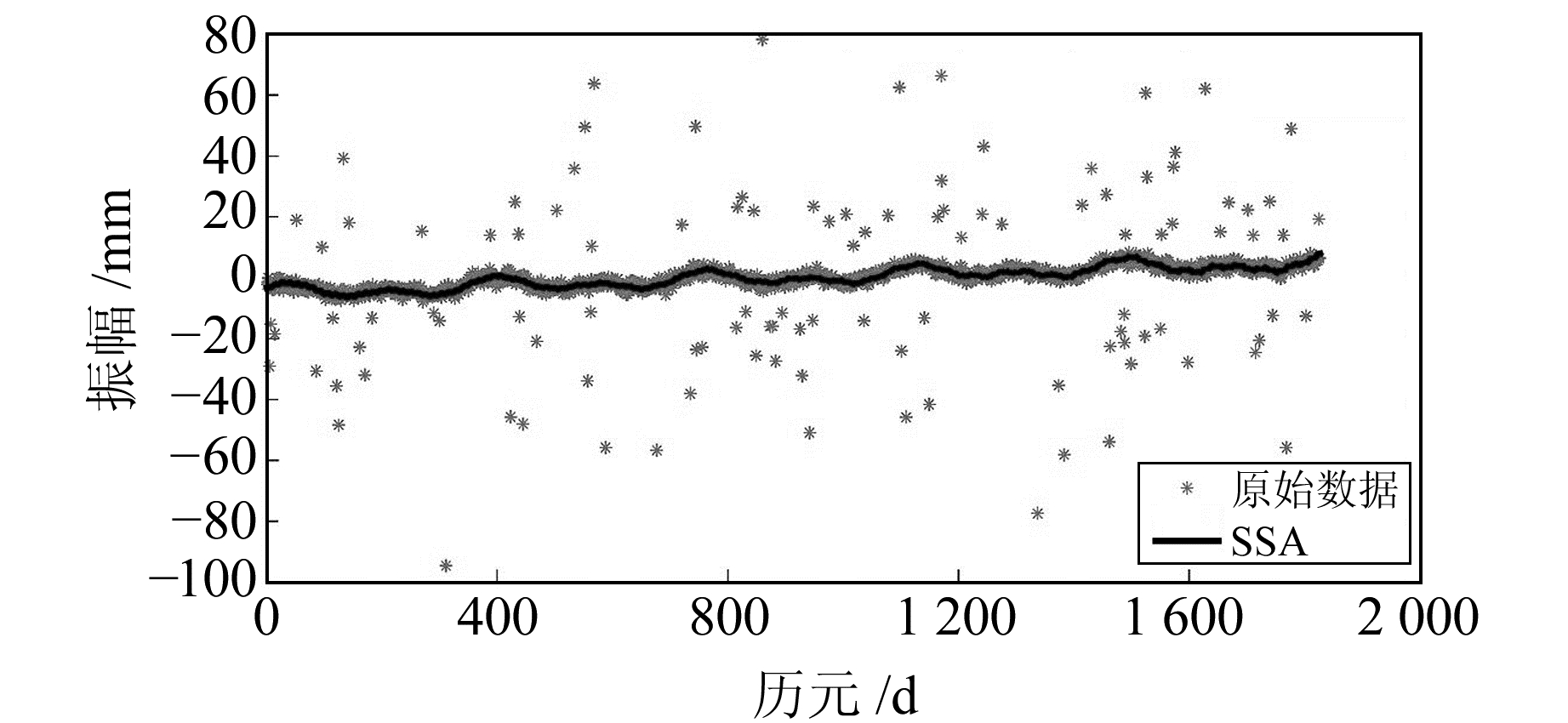
|
图 3 原始序列与重构序列 Fig. 3 Original sequence and reconstructed sequence |
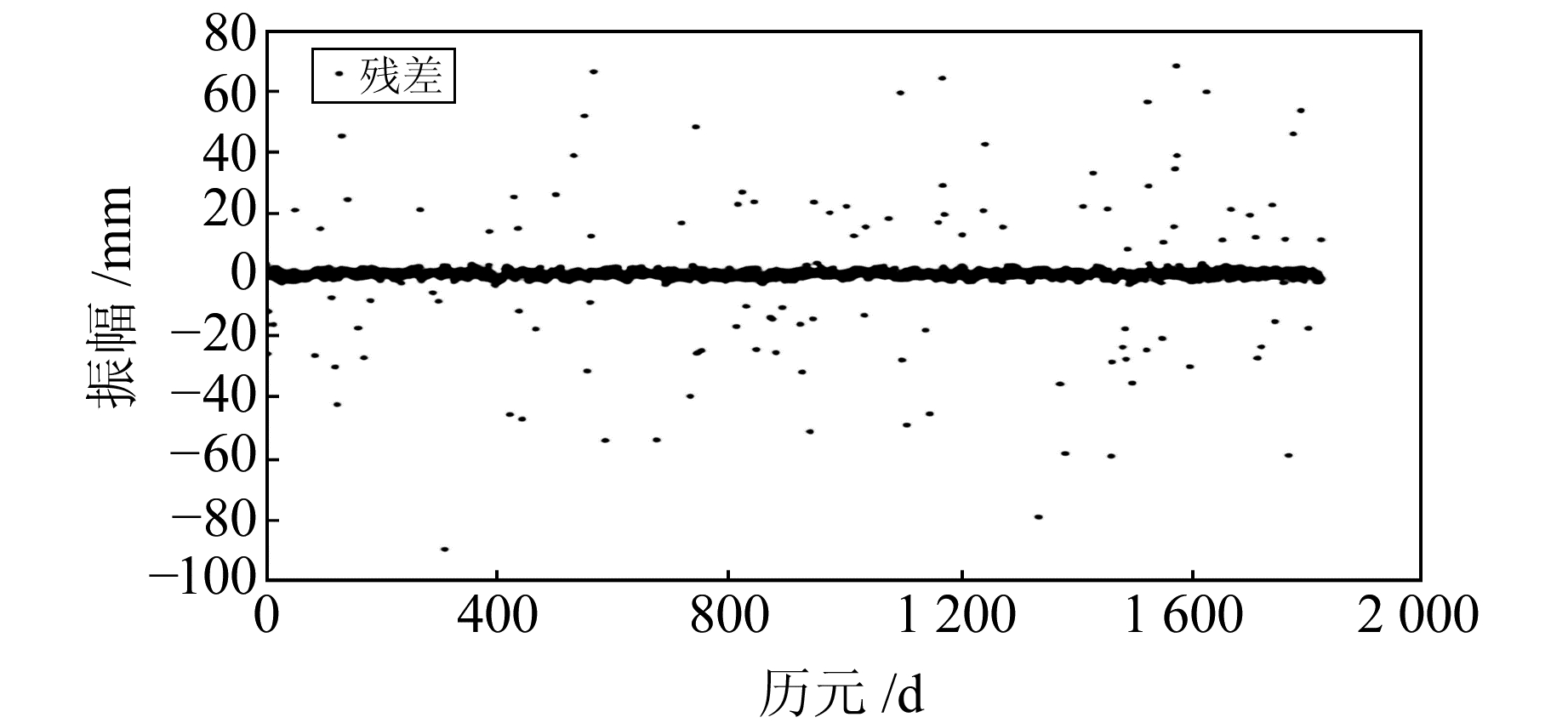
|
图 4 提取的残差序列 Fig. 4 The extracted residual sequence |
利用3σ法、MAD法和SSA-Sn法对模拟数据进行粗差探测(图 5)。由图可见,由于数据标准差σ会受到粗差的污染,不具有稳健性,因此3σ法只能探测出偏离较大的粗差,对偏离程度较小粗差的探测效果有限。相较于3σ法,MAD法具有50%的抗差稳健性,能够探测出绝大部分粗差。为进一步体现粗差探测的效果,进行3种方法的探测效果统计(表 2)。由表可知,3σ法的探测数为43、准确率为38.7%;MAD法的探测数为104、准确率为93.6%;SSA-Sn法的探测数为112,虽然该方法存在1个误判,但能够探测出所有的粗差点,其准确率相较于3σ法和MAD法分别提升61.3百分点和6.4百分点,因此SSA-Sn法对于偏离程度较大或较小的粗差都具有很好的探测效果。

|
图 5 3种方法的粗差探测结果 Fig. 5 Gross error detection results of three methods |
|
|
表 2 3种方法粗差探测对比 Tab. 2 Comparison of gross error detection of three methods |
Mao等[16]研究发现,白噪声+闪烁噪声+随机游走噪声为中国区域的最佳噪声模型。为验证SSA-Sn法对真实数据的探测准确率,将模拟数据
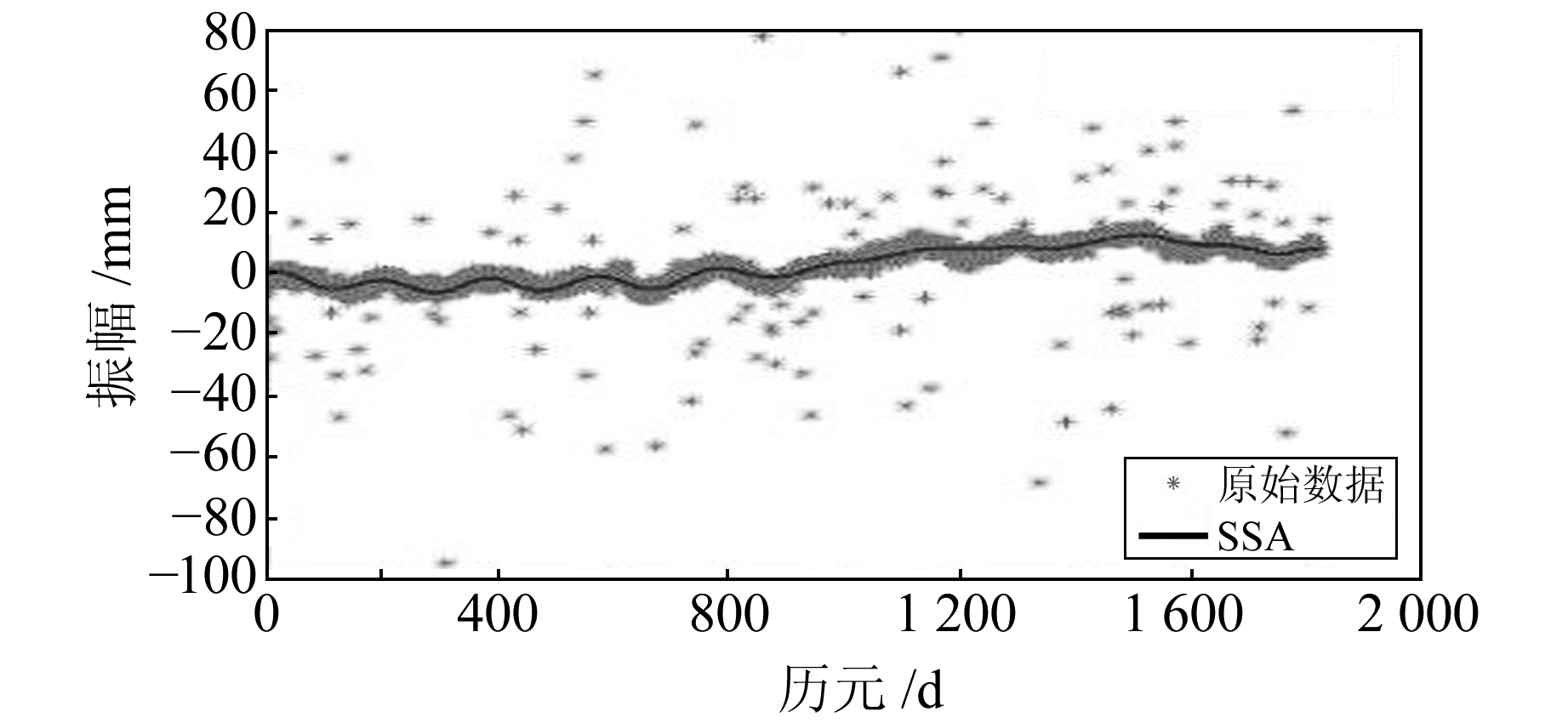
|
图 6 原始序列 |
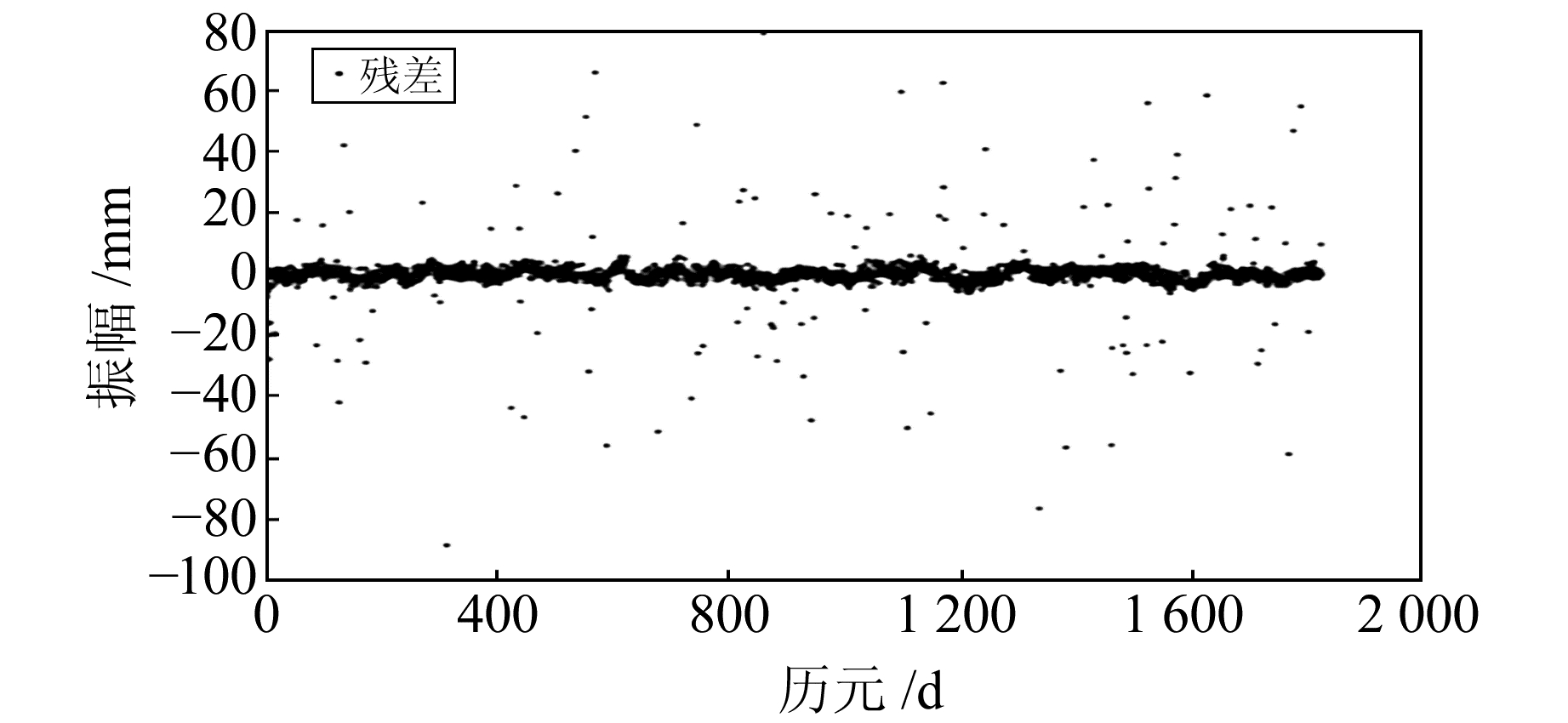
|
图 7 提取的残差序列 Fig. 7 The extracted residual sequence |
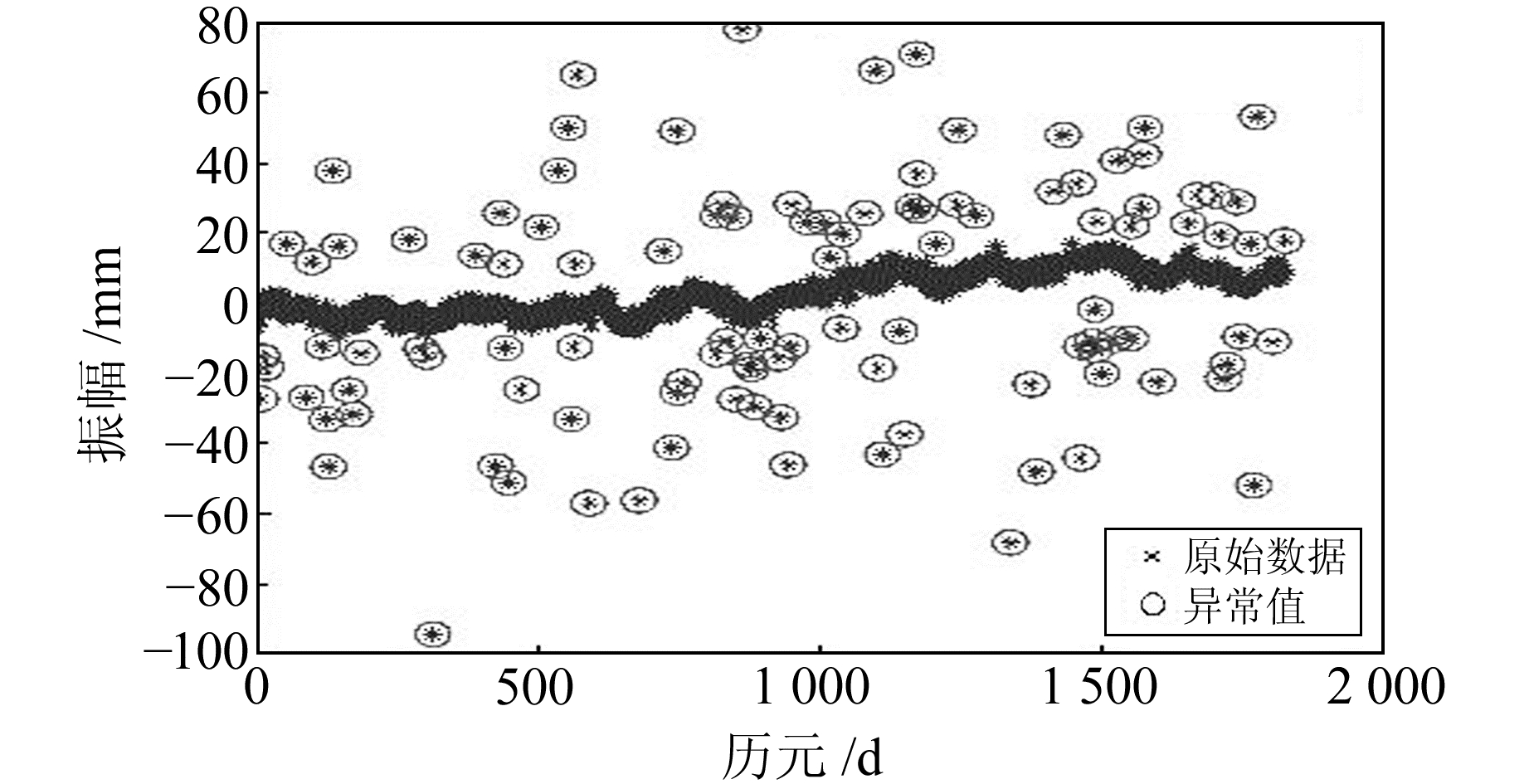
|
图 8 SSA-Sn法粗差探测结果 Fig. 8 SSA-Sn method gross error detection results |
为进一步验证SSA-Sn法探测粗差的有效性,使数据更加贴合实际,选用SOPAC GPS提供的原始时间序列数据,选取BJFS、SHAO、URUM三个测站高程U方向上2009~2015年共计6 a的实测数据进行处理,图 9为3个测站U方向的原始时间序列数据。由图 9(a)和图 9(b)可见,原始数据中粗差在时域和大小上分布范围较广。
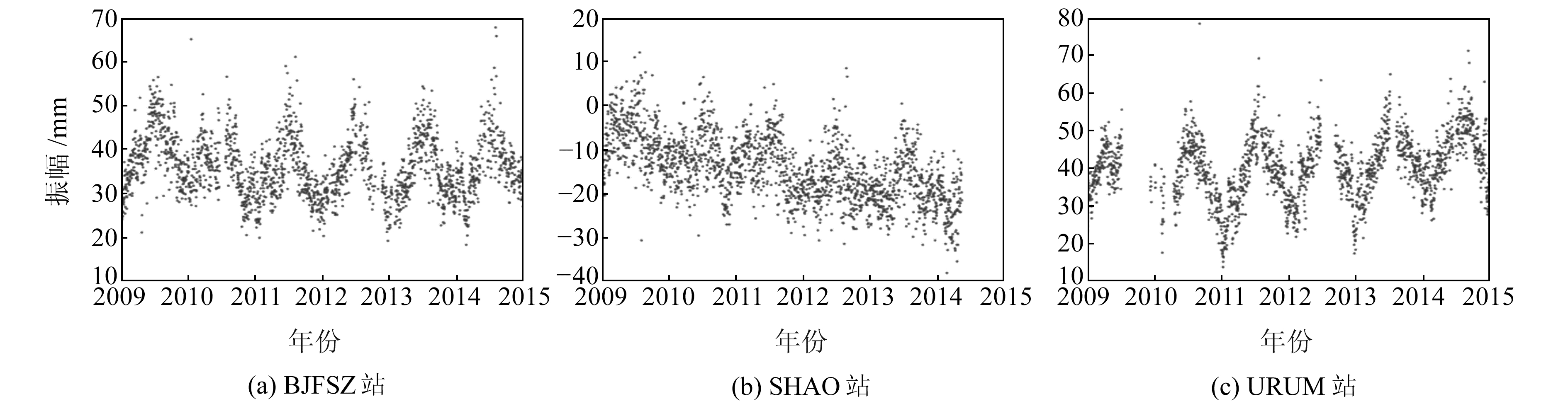
|
图 9 3个测站原始数据 Fig. 9 Raw data of three stations |
分别采用3σ法、MAD法和SSA-Sn法对3个测站的数据进行粗差探测(图 10)。由BJFS站结果可知,2009~2010年的5个数据与整体数据存在明显偏离,SSA-Sn法成功探测出2009~2010年处的粗差,但3σ法和MAD法未能全部探测出;由URUM站结果可知,3σ法和MAD法将2011年处的数据判定为粗差,但SSA-Sn法并未进行判定。结合图像分析后得知,URUM站2011年处的数据符合整体数据的周期趋势,不存在偏离,因此不属于粗差。综上所述,3σ法和MAD法均能准确探测出偏离程度较大的粗差,而SSA-Sn法对于偏离程度较小的粗差数据的探测效果更加优越。由于利用剔除粗差个数来评判粗差探测方法的优劣具有一定的局限性,本文采用SSA重构后的时间序列作为参照,以3种方法剔除粗差后的RMSE来评判粗差探测的效果(表 3)。由表可见,经SSA-Sn法剔除粗差后3个测站数据的RMSE分别为4.30 mm、4.03 mm和4.90 mm,均小于MAD法和3σ法处理后3个测站数据的RMSE。因此3种方法都能探测出一定数量的粗差,但SSA-Sn法的粗差探测效果最优。

|
图 10 3个测站3种方法的粗差探测结果 Fig. 10 Gross error detection results of three methods at three stations |
|
|
表 3 3种方法的粗差探测数量与剔除后的RMSE Tab. 3 Three methods of gross error detection quantity and RMSE after elimination |
1) 3σ法和MAD法的粗差探测率分别为38.7%和93.6%,而SSA-Sn法虽然存在1个误判,却能将模拟的粗差全部探测出来,并且对于噪声模型为白噪声+闪烁噪声+随机游走噪声这种贴合实际情况的模拟数据同样具有适用性。
2) 采用SOPAC GPS提供的BJFS、SHAO、URUM三个测站高程U方向的原始数据进行实验,从探测粗差个数以及剔除粗差后数据的RMSE两方面证明,SSA-Sn法的粗差探测效果优于3σ法和MAD法。
今后需要结合GNSS时间序列和奇异谱分析构建系统的奇异谱分析方法,从而达到更高效的粗差探测效果。
| [1] |
姚宜斌, 杨元喜, 孙和平, 等. 大地测量学科发展现状与趋势[J]. 测绘学报, 2020, 49(10): 1 243-1 251 (Yao Yibin, Yang Yuanxi, Sun Heping, et al. Geodesy Discipline: Progress and Perspective[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(10): 1 243-1 251)
(  0) 0) |
| [2] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [3] |
许国昌. GPS理论、算法与应用[M]. 北京: 清华大学出版社, 2007 (Xu Guochang. GPS Theory, Algorithms and Application[M]. Beijing: Tsinghua University Press, 2007)
(  0) 0) |
| [4] |
施闯. 大规模高精度GPS网平差与分析理论及其应用[M]. 北京: 测绘出版社, 2002 (Shi Chuang. The Adjustment and Analysis Theory of Large Scale High Precision GPS Network and Its Application[M]. Beijing: Surveying and Mapping Press, 2002)
(  0) 0) |
| [5] |
吴浩, 卢楠, 邹进贵, 等. GNSS变形监测时间序列的改进型3σ粗差探测方法[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1 282-1 288 (Wu Hao, Lu Nan, Zou Jingui, et al. An Improved 3σ Gross Error Detection Method for GNSS Deformation Monitoring Time Series[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1 282-1 288)
(  0) 0) |
| [6] |
王威, 许芬, 王宇谱. 一种基于小波分析的卫星钟差数据粗差处理方法[J]. 大地测量与地球动力学, 2021, 41(6): 623-627 (Wang Wei, Xu Fen, Wang Yupu. A Preprocess Method for Gross Error Detection Based on Wavelet Analysis[J]. Journal of Geodesy and Geodynamics, 2021, 41(6): 623-627)
(  0) 0) |
| [7] |
Hampel F R. The Influence Curve and Its Role in Robust Estimation[J]. Journal of the American Statistical Association, 1974, 69(346): 383-393 DOI:10.1080/01621459.1974.10482962
(  0) 0) |
| [8] |
明锋, 曾安敏, 景一帆. L1范数与IQR统计量组合的GNSS坐标序列粗差探测算法[J]. 测绘科学技术学报, 2016, 33(2): 127-132 (Ming Feng, Zeng Anmin, Jing Yifan. A New Method of Outlier Detection for GNSS Position Time Series Based on the Combination of L1-Norm and IQR Statistic[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 127-132)
(  0) 0) |
| [9] |
张恒璟, 程鹏飞. 基于GPS高程时间序列粗差的抗差探测与插补研究[J]. 大地测量与地球动力学, 2011, 31(4): 71-75 (Zhang Hengjing, Cheng Pengfei. Study on Robust Detection and Interpolation from Gross Errors of GPS Height Time Series[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 71-75)
(  0) 0) |
| [10] |
徐洪钟, 吴中如, 李雪红, 等. 基于小波分析的大坝变形观测数据的趋势分量提取[J]. 武汉大学学报: 工学版, 2003, 36(6): 5-8 (Xu Hongzhong, Wu Zhongru, Li Xuehong, et al. Abstracting Trend Component of Dam Observation Data Based on Wavelet Analysis[J]. Engineering Journal of Wuhan University, 2003, 36(6): 5-8)
(  0) 0) |
| [11] |
黄立人, 韩月萍, 高艳龙, 等. GNSS连续站坐标的高程分量时间序列在地壳垂直运动研究中应用的若干问题[J]. 大地测量与地球动力学, 2012, 32(4): 10-14 (Huang Liren, Han Yueping, Gao Yanlong, et al. Several Issues in Application of Elevation Component Time Series of GNSS CORS in Vertical Crustal Movement Studying[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 10-14)
(  0) 0) |
| [12] |
Rousseeuw P J, Croux C. Alternatives to the Median Absolute Deviation[J]. Journal of the American Statistical Association, 1993, 88(424): 1 273-1 283 DOI:10.1080/01621459.1993.10476408
(  0) 0) |
| [13] |
Klos A, Bogusz J, Figurski M, et al. On the Handling of Outliers in the GNSS Time Series by Means of the Noise and Probability Analysis[M]. Berlin, Heidelberg: Springer, 2015
(  0) 0) |
| [14] |
Wang X, Cheng Y, Wu S, et al. An Effective Toolkit for the Interpolation and Gross Error Detection of GPS Time Series[J]. Survey Review, 2016, 48(348): 202-211 DOI:10.1179/1752270615Y.0000000023
(  0) 0) |
| [15] |
蔡晓军, 杨建华. 基于多通道奇异谱的GNSS坐标序列粗差探测与数据插值[J]. 测绘工程, 2019, 28(5): 20-28 (Cai Xiaojun, Yang Jianhua. Gross Error Detection and Data Interpolation for GNSS Coordinates Time Series Based on Multichannel Singular Spectrum[J]. Engineering of Surveying and Mapping, 2019, 28(5): 20-28)
(  0) 0) |
| [16] |
Mao A L, Harrison C G A, Dixon T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research Atmospheres, 1999, 104(B2): 2 797-2 816
(  0) 0) |
2. School of Civil and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, 86 Hongqi Road, Ganzhou 341000, China;
3. Principal's Office, Nanchang Hangkong University, 696 South-Fenghe Road, Nanchang 330063, China
 2022, Vol. 42
2022, Vol. 42


