将GPS测得的大地高转换为我国工程实践中所需正常高的关键在于求取两者之间的差值,即高程异常值[1]。由于难以获得精确的重力数据,目前多采用拟合的方法来求取高程异常值,常用的拟合方法有数学模型法和神经网络法等[2]。其中,数学模型拟合法主要有平面拟合模型和曲面拟合模型2种。平面拟合模型的应用具有一定的局限性,主要适用于小范围的平坦地区;而曲面拟合模型则适用于覆盖面积较大、似大地水准面变化规律明显的区域。但这两种模型均存在一定的模型误差,且拟合的精度受地形因素的影响较大[3-4]。神经网络作为一种新兴的智能算法,能够极大地降低模型误差,现已在GPS高程异常拟合中得到广泛应用。普通的神经网络模型如BP神经网络等存在结构设计盲目性大、收敛速度慢等缺点[5]。小波神经网络(wavelet neural network, WNN)将小波理论和神经网络理论进行有机结合,不仅能避免网络结构设计的盲目性,还能有效提高神经网络的非线性拟合能力,在国内外学者中引起广泛关注[6-7]。但WNN也存在易陷入局部极小值和收敛速度慢等问题。为避免上述问题,本文提出一种改进的粒子群优化算法(improved particle swarm optimization, IPSO)对WNN模型进行优化。该算法采用非线性改变惯性权重和自适应学习因子相结合的方法对标准的粒子群优化算法(particle swarm optimization, PSO)进行改进,以避免PSO算法陷入局部极小值和发生振荡现象。同时以某矿区的实测GPS数据为例,对改进后WNN模型的实用性及有效性进行检验。
1 小波神经网络模型WNN是一种以小波基函数为隐含层节点、激励函数误差反向传播的神经网络[8],其结构如图 1所示。图中X为WNN的输入样本,Y为WNN的预测输出,ωij和ωjk分别为连接输入层与隐含层、隐含层与输出层的权值,ψ(x)为小波基函数。本文所采用的小波基函数为Morlet小波函数,其表达式为:
| $\psi \left( x \right) = \cos \left( {1.75x} \right){{\rm{e}}^{ - {x^2}/2}} $ | (1) |

|
图 1 WNN拓扑结构 Fig. 1 WNN topology |
输入序列xi(i=1, 2, 3, …, n)经过小波基函数处理后,可得到其在隐含层的输出值,即
| $u_{j}=\psi\left[\frac{\sum\limits_{i=1}^{n} \omega_{i j} x_{i}-b_{j}}{a_{j}}\right], j=1, 2, 3, \cdots, l $ | (2) |
式中,u为隐含层节点的输出值,a和b分别为小波基函数的伸缩因子和平移因子,n为输入层节点数,l为隐含层神经元个数。
输入信号经过隐含层处理后继续向前传播至输出层,由此得到WNN的输出,即
| $y_{k}=\sum\limits_{j=1}^{l} \omega_{j k} u_{j}, k=1, 2, 3, \cdots, m $ | (3) |
式中,yk为网络的实际输出,m为输出层节点数。
WNN的误差函数一般采用实际输出值与期望输出值的均方误差表示,即
| $E_{D}=\sum\limits_{k=1}^{m}\left(y_{k}-\hat{y}_{k}\right)^{2} $ | (4) |
式中,ED为网络的训练误差,
PSO算法是一种群体智能算法,在该算法中,每个粒子的特征均可用速度、位置和适应度值来表示[9]。在一个D维空间内,每个粒子均以一定的速度飞行,根据自身所积累的信息和群体中个体间信息的共享对速度进行更新,从而动态调整粒子在搜索空间中的位置。搜索过程持续进行,直到每个粒子均找到最佳位置或者达到迭代最大次数。
粒子群的速度和位置更新可表示为:
| $\begin{array}{c} v_{i+1}(t+1)=w_{i}(t)+c_{1} r_{1}\left(p_{i}-x_{i}\right)+ \\ c_{2} r_{2}\left(g_{i}-x_{i}\right) \end{array} $ | (5) |
| $x_{i}(t+1)=x_{i}(t)+v_{i}(t+1) $ | (6) |
式中,v为粒子速度;x为粒子位置;w为惯性权重,决定着粒子当前速度对下一位置速度的影响程度;c1和c2为学习因子;r1和r2为[0, 1]之间的随机数;p和g分别为粒子的个体极值和全局极值。
本文采用式(4),即小波神经网络的均方误差函数作为IPSO算法的适应度值函数。高程异常的拟合值与实际值越接近,网络的训练误差(粒子的适应度值)越小,粒子的适应度越高,当训练误差达到预期目标时,可认为当前粒子处于最优位置[10]。
2.2 改进的粒子群算法标准的PSO算法存在易陷入局部极小值、收敛速度慢等问题,且算法的收敛性能受惯性权重w的影响很大。当w值较大时,粒子的全局搜索能力较强,但容易跳过全局最优解,陷入局部极小值;当w值较小时,粒子的局部寻优能力较强,但搜索速度较慢。为了使PSO算法的全局搜索能力与局部搜索能力达到平衡,Shi等[11]提出一种惯性权重线性递减的粒子群优化策略(line particle swarm optimization, LPSO),即
| $w_{i}=w_{\max }-\frac{i\left(w_{\max }-w_{\min }\right)}{I_{\max }} $ | (7) |
式中,wmax和wmin分别为惯性权重的最大值和最小值,Imax为预设的最大迭代次数。
式(7)中,w仅与迭代次数i线性相关,但忽略了粒子群的进化速度和粒子的聚集程度,因此并不能满足PSO算法中复杂的非线性变换特性[12]。在此基础上,本文提出一种惯性权重的非线性递减策略,即
| $w_{i}=\left\{\begin{array}{l} w_{\max }, f \geqslant f_{\text {avg }} \\ w_{\min }+\frac{w_{\max }-w_{\min }}{1+e^{f_{\text {avg }}-f}}, f<f_{\text {avg }} \end{array}\right. $ | (8) |
式中,f为粒子当前的适应度值,favg为当前所有粒子的平均适应度值。
该方法的主要思想是根据当前粒子的适应度值与粒子群的平均适应度值的关系,对粒子的惯性权重进行动态调整。当粒子的适应度值大于或等于平均适应度值时,采用最大的惯性权重,以增大粒子群的搜索空间,加快算法的收敛速度;反之,则使惯性权重逐渐减小,以增强粒子寻找全局最优解的能力[13]。
学习因子c1和c2分别控制着粒子的自我寻优能力和粒子间的信息交互能力,在算法的迭代初期,c1值较大,c2值较小,有利于粒子快速找到大致的最优位置[14]。随着迭代过程的不断进行,粒子群中各粒子间的信息交互对寻找全局最优解的重要性不断增强,因此需要较小的c1值和较大的c2值,以增强粒子的局部寻优能力。而在标准的PSO算法中,c1和c2均为定值且相等,不利于算法的快速收敛和寻找全局最优解。本文在上述惯性权重非线性递减策略的基础上,对c1和c2进行如下优化:
| $c_{1}(t)=2-\mathrm{e}^{g_{t}-\frac{1}{N} \sum\limits_{i=1}^{N} p_{i}} $ | (9) |
| $c_{2}(t)=2-c_{1}(t) $ | (10) |
式中,N为粒子群中粒子总数,c1(t)和c2(t)分别为第t次迭代时c1和c2的取值,gt为当前粒子群的全局最优解,pi为第i个粒子的个体最优解。
从式(9)和式(10)可以看出,随着迭代的进行,c1值非线性递减,c2值非线性递增,这有利于算法的快速收敛,从而增强算法寻找全局最优解的能力。
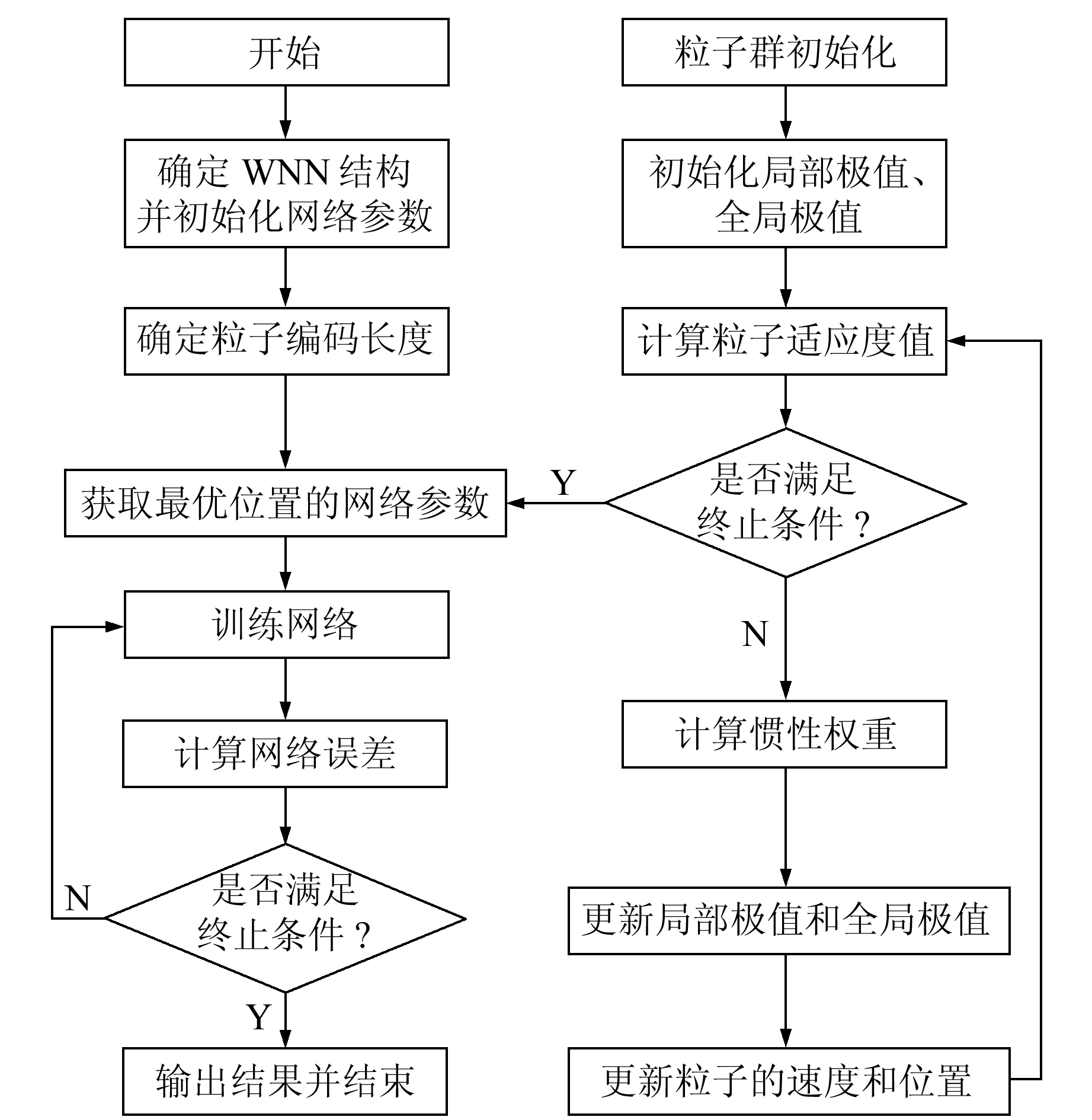
3 IPSO算法优化WNN参数为避免WNN算法出现振荡和陷入局部极小值等问题,本文采用上述改进后的PSO算法对WNN参数进行优化,基本步骤如下:
1) 确定WNN结构,本文中WNN结构是根据GPS高程异常拟合特点决定的。
2) 根据WNN结构确定改进粒子群算法的维度,即粒子长度。以WNN输入层与隐含层之间的权重wij、隐含层与输出层之间的权重wjk、伸缩因子a和平移因子b为元素,构建粒子的位置向量。
3) 初始化粒子群参数并确定适应度值函数。
4) 计算粒子的适应度值,并判断该值是否满足迭代终止的条件,若满足,则终止迭代并进入步骤8);若不满足,则进入步骤5)。
5) 根据式(5)、(6)、(8)、(9)、(10),更新粒子的速度和位置。
6) 根据粒子的适应度值对当前个体的极值和全局极值进行更新。
7) 返回步骤4),重新计算粒子的适应度值。
8) 输出迭代停止时相应的WNN参数。
IPSO-WNN算法的实现流程如图 2所示。
|
图 2 IPSO算法优化WNN流程 Fig. 2 Optimized WNN process by IPSO algorithm |
本文在上述IPSO-WNN算法的基础上,建立GPS高程拟合模型。在该模型中,WNN结构为2-4-1,其中输入层、输出层的节点个数由GPS高程拟合的特点决定,隐含层节点的个数由对比分析确定。由确定的WNN结构可求得IPSO算法的维度为20,算法中其他参数的设置如表 1所示。
|
|
表 1 IPSO算法参数 Tab. 1 IPSO algorithm parameters |
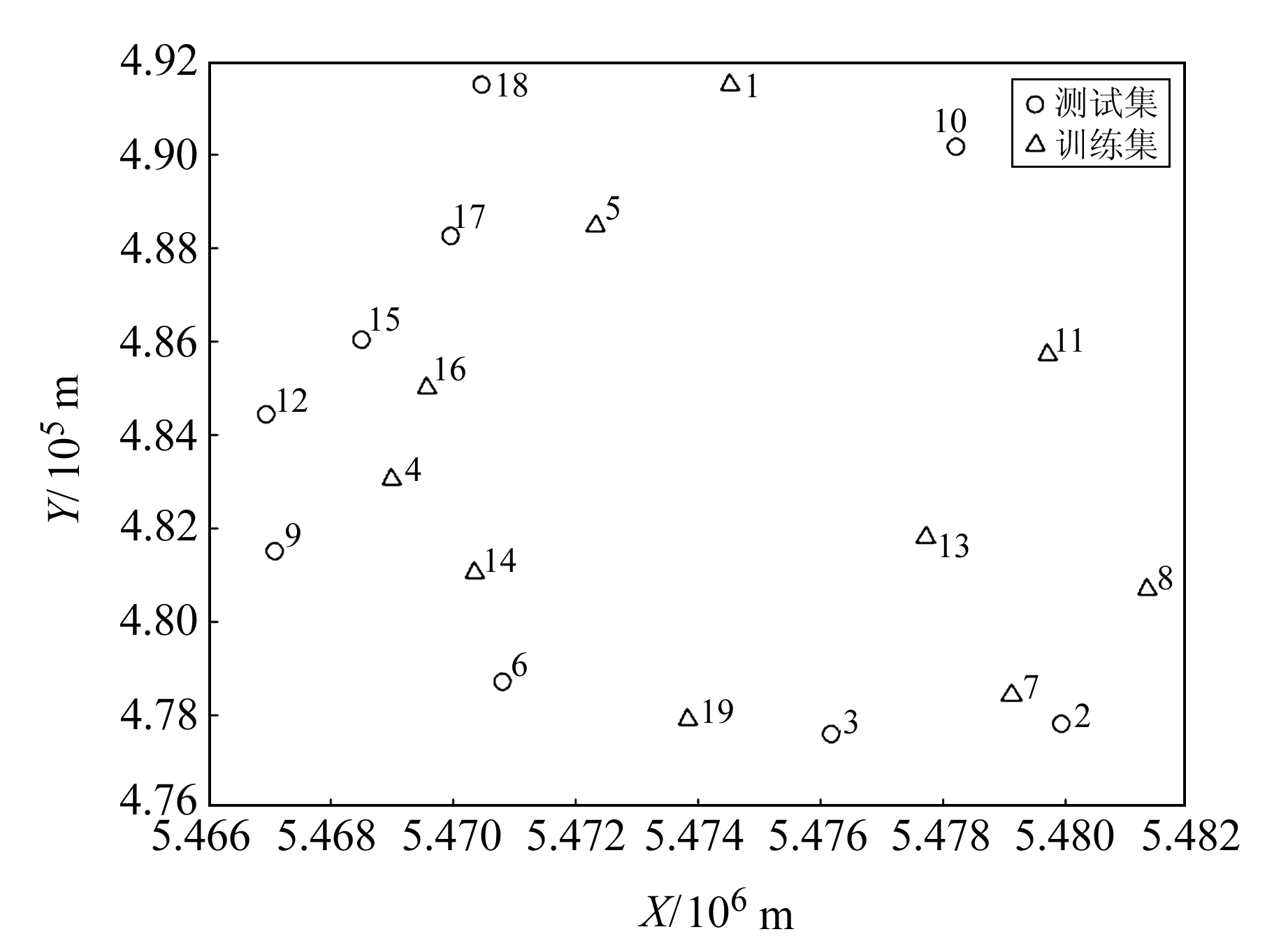
本文选取某矿区的实测GPS控制网数据,对提出的GPS高程拟合模型的拟合性能进行检验。测区内共有同精度的GPS水准点19个,覆盖面积为120 km2,各GPS点之间均已进行三等水准联测。测区位于我国北部高原地区,测区内地形起伏较大。为充分验证模型的有效性,在拟合过程中选取9个分布较为均匀的GPS点作为模型的训练集,其余10个GPS点作为模型的测试集。两组数据的分布情况如图 3所示。
|
图 3 GPS水准点分布 Fig. 3 Distribution of GPS leveling points |
由于本文所采用的实验测区范围较大,GPS水准点平面坐标间差值较大,为减小模型误差,对数据进行归一化处理[15]:
| $x_{i}^{\prime}=\frac{x_{i}-x_{\min }}{x_{\max }-x_{\min }} $ | (11) |
式中,x′为归一化后的输入序列,xi为原始输入序列,xmin和xmax分别为样本的最小值和最大值。
4.3 评价指标为验证IPOS-WNN模型进行GPS高程拟合的精度与稳定性,在上述数据的基础上,分别建立二次曲面模型、传统小波神经网络(WNN)、标准粒子群优化小波神经网络(PSO-WNN)、惯性权重线性递减的粒子群算法优化小波神经网络(LPSO-WNN)以及改进的粒子群算法优化小波神经网络(IPSO-WNN) 5种GPS高程拟合模型,并从以下两个方面进行对比:
1) 分别记录WNN、PSO-WNN、LPSO-WNN、IPSO-WNN 4种模型在迭代过程中的适应度值,比较4种模型的收敛速度与精度。
2) 为提高实验的可信度,分别将上述5种模型在测试集上进行10次独立实验,通过对比测试集中各点拟合残差的平均值以及数据均方误差的平均值,对模型的稳定性和外符合精度进行评价。其中,外符合精度的表达式为:
| $\delta=\pm \sqrt{\frac{\left[v_{i} v_{i}\right]}{n-1}} $ | (12) |
式中,n为测试集中点的个数,即i=1,2,3, …, n;vi为测试集中第i个点高程异常值的拟合值与实际值之差。
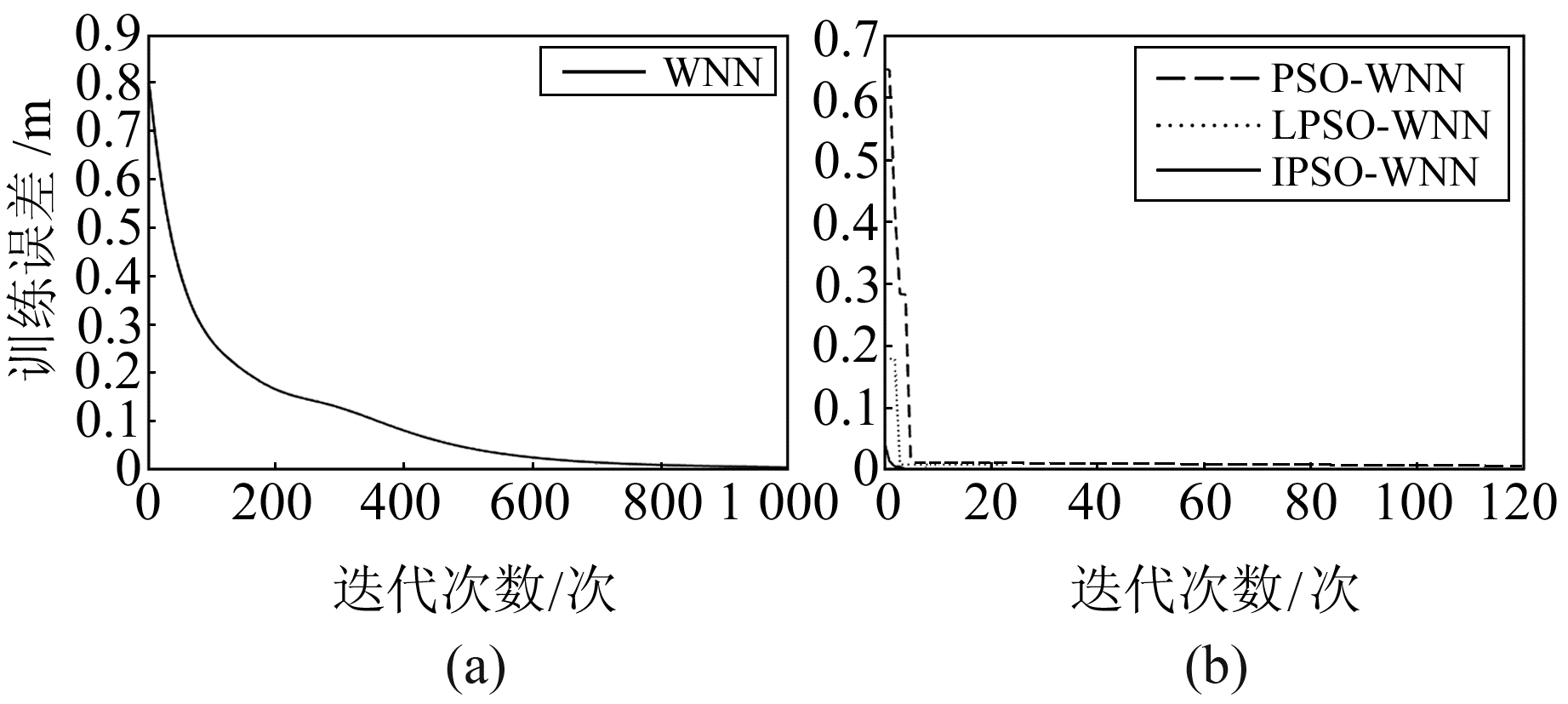
4.4 实验结果与分析图 4(a)为传统小波神经网络模型进行GPS高程拟合时网络训练误差随迭代次数的变化情况。分别采用标准PSO算法、LPSO算法、IPSO算法对WNN模型进行优化,优化后模型的训练误差随迭代次数的变化情况如图 4(b)所示。
|
图 4 模型训练误差 Fig. 4 Training error of models |
从图 4(a)可以看出,传统的WNN模型进行GPS高程拟合时算法收敛速度慢,当达到最大迭代次数时算法仍未收敛。从图 4(b)可以看出,PSO-WNN、LPSO-WNN、IPSO-WNN三种算法收敛时的迭代次数分别为114、23、14。由此可知,3种算法的收敛速度和精度均明显优于传统的WNN模型,其中IPSO-WNN模型的收敛精度最高、速度最快。表 2(单位cm)为各方案的平均拟合残差和外符合精度。由各模型的平均拟合残差绘制各检核点的残差变化图如图 5所示。
|
|
表 2 各模型拟合结果 Tab. 2 Fitting results of each model |
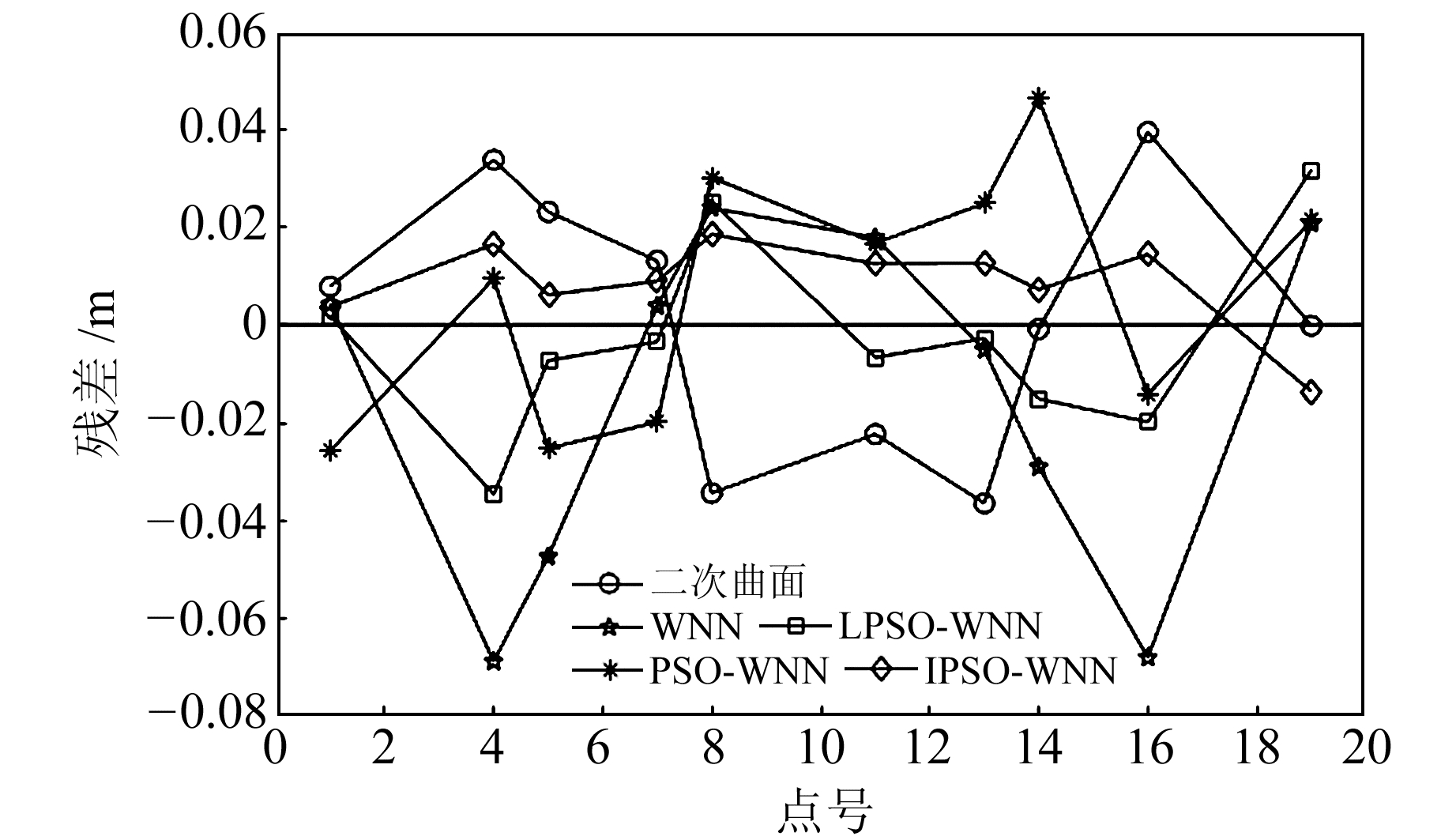
|
图 5 各模型拟合残差 Fig. 5 Fitting residual of each model |
从表 2可以看出,传统的WNN模型进行GPS高程拟合时拟合效果最差,最大拟合残差为-6.87 cm,外符合精度为3.91 cm,模型的拟合精度和稳定性均低于二次曲面模型。PSO-WNN、LPSO-WNN、IPSO-WNN模型的最大拟合残差分别为4.61 cm、-3.46 cm和1.85 cm,最小拟合残差分别为0.94 cm、0.19 cm和0.37 cm,外符合精度分别为2.66 cm、1.99 cm和1.29 cm,上述的拟合精度和稳定性均高于二次曲面模型。其中,IPSO-WNN模型的拟合精度最高、稳定性最好。从图 5可以看出,IPSO-WNN模型的残差曲线波动最小,与实际的高程异常值最为吻合,拟合效果最好。
5 结语本文采用IPSO-WNN模型进行GPS高程拟合,并通过实测数据与二次曲面模型、WNN、PSO-WNN、LPSO-WNN模型的拟合性能进行对比。结果表明,当测区内地形起伏较大时,传统的二次曲面模型和WNN模型的拟合精度较低,稳定性较差。采用粒子群优化后的小波神经网络模型的拟合性能较二次曲面模型和WNN模型均有所提高,其中,IPSO-WNN模型的拟合精度和稳定性明显高于PSO-WNN和LPSO-WNN模型,可有效避免传统小波神经网络易陷入局部极小值和收敛速度慢等问题。
| [1] |
唐丽娟. GPS高程转换方法研究及精度分析[J]. 全球定位系统, 2017, 42(6): 88-91 (Tang Lijuan. Research Analysis of GPS Elevation Fitting Method[J]. GNSS World of China, 2017, 42(6): 88-91)
(  0) 0) |
| [2] |
袁德宝, 张建, 赵传武, 等. 基于改进RBF神经网络的GNSS高程拟合[J]. 大地测量与地球动力学, 2020, 40(3): 221-224 (Yuan Debao, Zhang Jian, Zhao Chuanwu, et al. GNSS Height Fitting Based on Improved RBF Neural Network[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 221-224)
(  0) 0) |
| [3] |
谭江涛, 王章朋, 钟波, 等. 多面函数参数自适应选取方法在GPS高程拟合中的应用[J]. 大地测量与地球动力学, 2020, 40(8): 832-837 (Tan Jiangtao, Wang Zhangpeng, Zhong Bo, et al. Application of Self-Adaptive Parameter Selection for Multiquadric Function in GPS Elevation Fitting[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 832-837)
(  0) 0) |
| [4] |
谢洋洋, 付超, 解琨, 等. 灰色最小支持向量机模型在高程拟合中的应用[J]. 测绘科学, 2021, 46(3): 55-60 (Xie Yangyang, Fu Chao, Xie Kun, et al. Application of Grey Least Square Support Vector Machine Model in Height Fitting[J]. Science of Surveying and Mapping, 2021, 46(3): 55-60)
(  0) 0) |
| [5] |
王小辉, 王琪洁, 丁元兰, 等. 基于二次曲面和BP神经网络组合模型的GPS高程异常拟合[J]. 大地测量与地球动力学, 2012, 32(6): 103-105 (Wang Xiaohui, Wang Qijie, Ding Yuanlan, et al. Combined Model in Height Anomaly Fitting[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 103-105)
(  0) 0) |
| [6] |
杨帆, 于奇. 遗传小波神经网络的GPS高程拟合模型[J]. 导航定位学报, 2017, 5(2): 131-134 (Yang Fan, Yu Qi. GPS Elevation Fitting Based on Genetic Wavelet Neural Network Model[J]. Journal of Navigation and Positioning, 2017, 5(2): 131-134 DOI:10.3969/j.issn.2095-4999.2017.02.023)
(  0) 0) |
| [7] |
付建东, 吴良才. 基于小波神经网络GPS高程拟合的应用研究[J]. 北京测绘, 2015(3): 103-106 (Fu Jiandong, Wu Liangcai. Application of GPS Height Fitting Based on WNN[J]. Beijing Surveying and Mapping, 2015(3): 103-106 DOI:10.3969/j.issn.1007-3000.2015.03.027)
(  0) 0) |
| [8] |
杨迪威, 李少华, 沈远彤. 基于粒子群优化算法的小波神经网络[J]. 工程地球物理学报, 2007, 4(6): 529-532 (Yang Diwei, Li Shaohua, Shen Yuantong. Wavelet Neural Network Learning Algorithm Based on Particle Swarm Optimization[J]. Chinese Journal of Engineering Geophysics, 2007, 4(6): 529-532 DOI:10.3969/j.issn.1672-7940.2007.06.003)
(  0) 0) |
| [9] |
刘忠豹. 通过改进自适应PSO优化BP网络预测大坝变形[J]. 大地测量与地球动力学, 2019, 39(5): 528-532 (Liu Zhongbao. Prediction of Dam Deformation Based on the Improved BP Neural Network with Adaptive Particle Swarm Optimization[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 528-532)
(  0) 0) |
| [10] |
蒲伦, 唐诗华, 罗洁, 等. 利用粒子群算法优化的GPS高程拟合精度分析[J]. 测绘科学技术学报, 2018, 35(6): 563-568 (Pu Lun, Tang Shihua, Luo Jie, et al. Precision Analysis of GPS Height Fitting Optimized Based on Particle Swarm Optimization[J]. Journal of Geomatics Science and Technology, 2018, 35(6): 563-568)
(  0) 0) |
| [11] |
Shi Y H, Eberhart R C. Empirical Study of Particle Swarm Optimization[C]. 1999 Congress on Evolutionary Computation-CEC99, Washington, 1999
(  0) 0) |
| [12] |
杨尚波, 卢小平, 李珵, 等. 基于混沌粒子群优化神经网络的GPS高程拟合研究[J]. 测绘通报, 2013(9): 5-8 (Yang Shangbo, Lu Xiaoping, Li Cheng, et al. GPS Elevation Fitting by Neural Network Based on Chaotic PSO Algorithm[J]. Bulletin of Surveying and Mapping, 2013(9): 5-8)
(  0) 0) |
| [13] |
董红斌, 李冬锦, 张小平. 一种动态调整惯性权重的粒子群优化算法[J]. 计算机科学, 2018, 45(2): 98-102 (Dong Hongbin, Li Dongjin, Zhang Xiaoping. Particle Swarm Optimization Algorithm with Dynamically Adjusting Inertia Weight[J]. Computer Science, 2018, 45(2): 98-102)
(  0) 0) |
| [14] |
任超, 梁月吉, 蓝岚, 等. 不同组合方法对GPS高程拟合的影响[J]. 大地测量与地球动力学, 2015, 35(6): 1 036-1 040 (Ren Chao, Liang Yueji, Lan Lan, et al. Influence of Different Combination Methods of GPS Elevation Fitting[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 1 036-1 040)
(  0) 0) |
| [15] |
王昶, 王旭. GPS高程拟合分区方法研究[J]. 大地测量与地球动力学, 2016, 36(1): 26-29 (Wang Chang, Wang Xu. Research on GPS Height Fitting Partition Method[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 26-29)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

