2. 南昌航空大学校长办公室,南昌市丰和南大道696号,330063
大规模的地下矿产开采活动易引发地面塌陷、滑坡、泥石流等地质灾害,破坏地质结构,严重威胁矿区周边居民的生命和财产安全[1],因此对矿区地表进行长期的有效监测和精准预测尤为重要[2]。目前,已有学者对地表沉降预测进行研究,并取得一定的进展[3-4]。传统的灰色类预测模型虽然使用广泛,但适用性较差;而ARMA、ARIMA等经典模型的预测精度不稳定,需滚动预测才能保持预测精度;神经网络预测模型虽有较高的预测精度,但存在预测过程不稳定、参数设置复杂、自适应能力较差等问题。针对上述问题,本文提出将Prophet模型引入地表沉降预测研究。Prophet模型是一种自适应分解预测、拟合插值的新模型,对原始数据有较好的自适应性,使用灵活且无需对缺失项进行插值,也无需任何先验条件,拟合过程速度较快,有良好的预测精度[5]。本文在深入研究Prophet模型原理后,引入经验小波变换(EWT)方法,基于EWT和Prophet模型构建一种分解-预测的自适应预测新方法,以达到提升预测精度的目的[6]。
1 研究区概况及数据来源本文以德兴矿区为研究对象,研究区位于江西省上饶市德兴境内,属于江南丘陵地区,地势东南部偏高、西北部偏低,地貌整体起伏较大。实验数据选取覆盖德兴矿区的30景C波段升轨Sentinel-1A影像数据,时间跨度为2018-12-29~2019-12-24,时间间隔为12 d,具体参数见表 1。采用由美国航空航天局(NASA)提供的30 m分辨率SRTM1数据作为外部参考DEM,以消除地形误差对实验的影响。
|
|
表 1 Sentinel-1A数据参数 Tab. 1 Parameter of Sentinel-1A data |
SBAS-InSAR是以传统D-InSAR技术为基础,用来获取工作区地表形变时间序列的技术。该技术选取N+1幅SAR影像,通过设置合适的时间基线和空间基线,生成N个小基线集差分干涉对,去除地形相位后生成差分干涉图并进行相位解缠,将常规D-InSAR监测的观测结果用作单个观测值,采用奇异值分解(SVD)方法将每组小基线数据集进行连接,以解决在时域上采样过于稀疏的问题。同时结合稳定散射体的干涉相位信息,以获取更高的空间分辨率,最后根据最小二乘准则计算高精度的沉降形变时间序列。
2.2 Prophet模型原理Prophet预测模型[7]是一种高效分析时序信号的新模型,可以处理时序信号分析中产生的丢失值、异常值,对不同跨度样本的时序信号进行长短期预测,具备较好的预测精度、良好的自适应能力和一定的抗差性和鲁棒性。Prophet模型已经在GNSS高程信号预测[5]、电力需求预测[8]、空气指数预测[9]和TEC电离层预测[10]等领域得到广泛应用,并取得较好的预测效果,但几乎没有涉及地表沉降预测领域。Prophet模型的详细原理见文献[7]。
Prophet采用广义加法模型来进行拟合平滑和函数预测,将地表沉降时序数据自适应分解为:
| $y\left( t \right) = g\left( t \right) + s\left( t \right) + {\varepsilon _t} $ | (1) |
式中,y(t)为原始地表沉降时序数据;g(t)为沉降时序数据趋势项,表示时间序列非线性增长(非周期项)部分的变化函数;s(t)为高程方向的震荡周期项;εt为服从正态分布的残差项,可表示未预测到的随机噪声或趋势。SBAS-InSAR监测数据复杂,趋势项采用逻辑回归函数,表示为:
| $g\left( t \right) = \frac{c}{{1 + {{\rm{e}}^{[ - k(t - m)]}}}} $ | (2) |
式中,k为地表沉降趋势增长率;m为位移量参数;c为趋势上限值,随着时间t的增加,g(t)趋于c。在地壳板块运动中,s(t)主要包含季节性的周期震荡和微小的趋势变化,其拟合函数通过沉降时序数据的傅里叶级数进行构造:
| $s\left( t \right) = \sum\limits_{i = 1}^N {\left( {{a_n}\cos\left( {\frac{{2{\rm{ \mathsf{ π} }}nt}}{T}} \right) + {b_n}\sin \left( {\frac{{2\pi nt}}{T}} \right)} \right)} $ | (3) |
经验小波变换(EWT)是一种计算量小且具备较强鲁棒性的新变换方法,其核心思想是依据原始信号中的频谱特征,进行自适应分割后构建基于傅里叶变换的正交小波滤波器组,提取出具有紧支撑傅里叶频谱的不同AM-FM(调幅-调频)成分。具体过程为:
1) 对信号进行傅里叶变换,求得支撑区间(0,π)的傅里叶频谱F(ω);
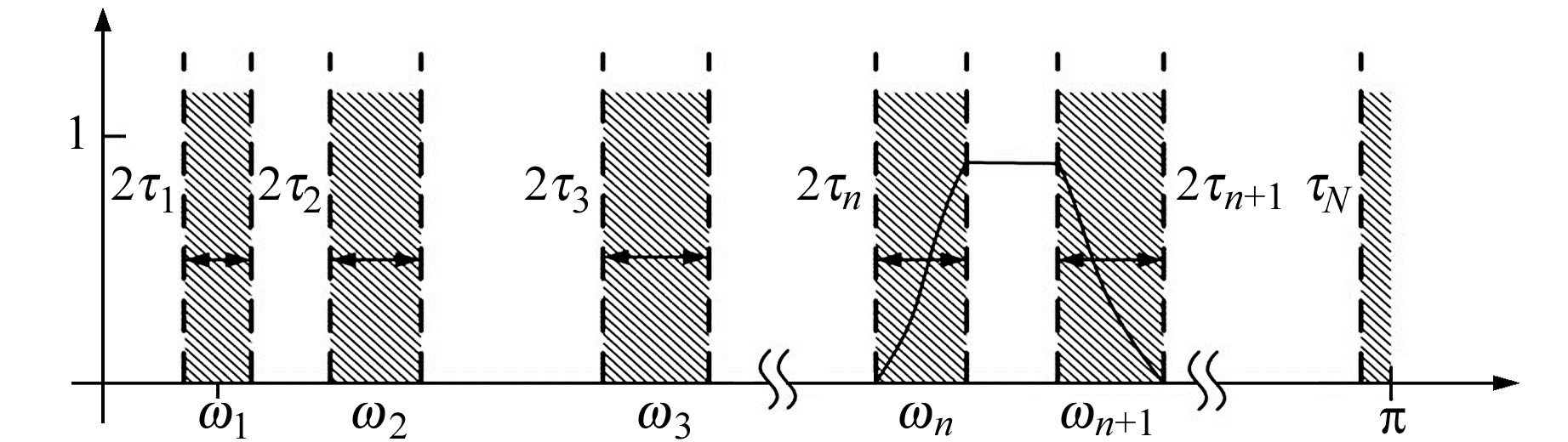
2) 对于自适应分割傅里叶频谱F(ω),依据香农定理将频谱分解为N个频带与N-1个分界频率,图 1为傅里叶频谱分割示意图;
|
图 1 傅里叶频谱分割 Fig. 1 Fourier spectrum segmentation |
3) 根据各分界频率构建经验小波φ(ω),确定经验尺度函数和经验小波函数;
4) 对F(ω)*φ(ω)反傅里叶变换,得到不同的模态分量。
首先假设将傅里叶支撑区间(0,π)分割成N个频带,则有N-1个分界频率,ωn为相邻频带的边界,ω0=0,ωN=π。各分割频带可表示为Λn=[ωn-1, ωn],则Un-1NΛn=[0, π],以ωN为中心,可以定义一个宽度为Tn=2τn的过渡带,如图 1中阴影部分所示。当确定好Λn后,经验小波被定义为在每个Λn上的带通滤波器,根据Meyer小波确定经验尺度函数和经验小波函数,从而构建经验小波[11]。f(t)重构信号表达式为:
| $\begin{array}{c} f\left( t \right) = W_f^\varepsilon \left( {0, t} \right)*{\varphi _1}\left( t \right) + \\ \sum\limits_{i = 1}^N {W_f^\varepsilon \left( {n, t} \right)*{\Psi _n}\left( t \right)} \end{array} $ | (4) |
式中,*为卷积运算符,Wfε(0, t)为傅里叶变换近似系数,Wfε(n, t)为傅里叶变换细节系数。
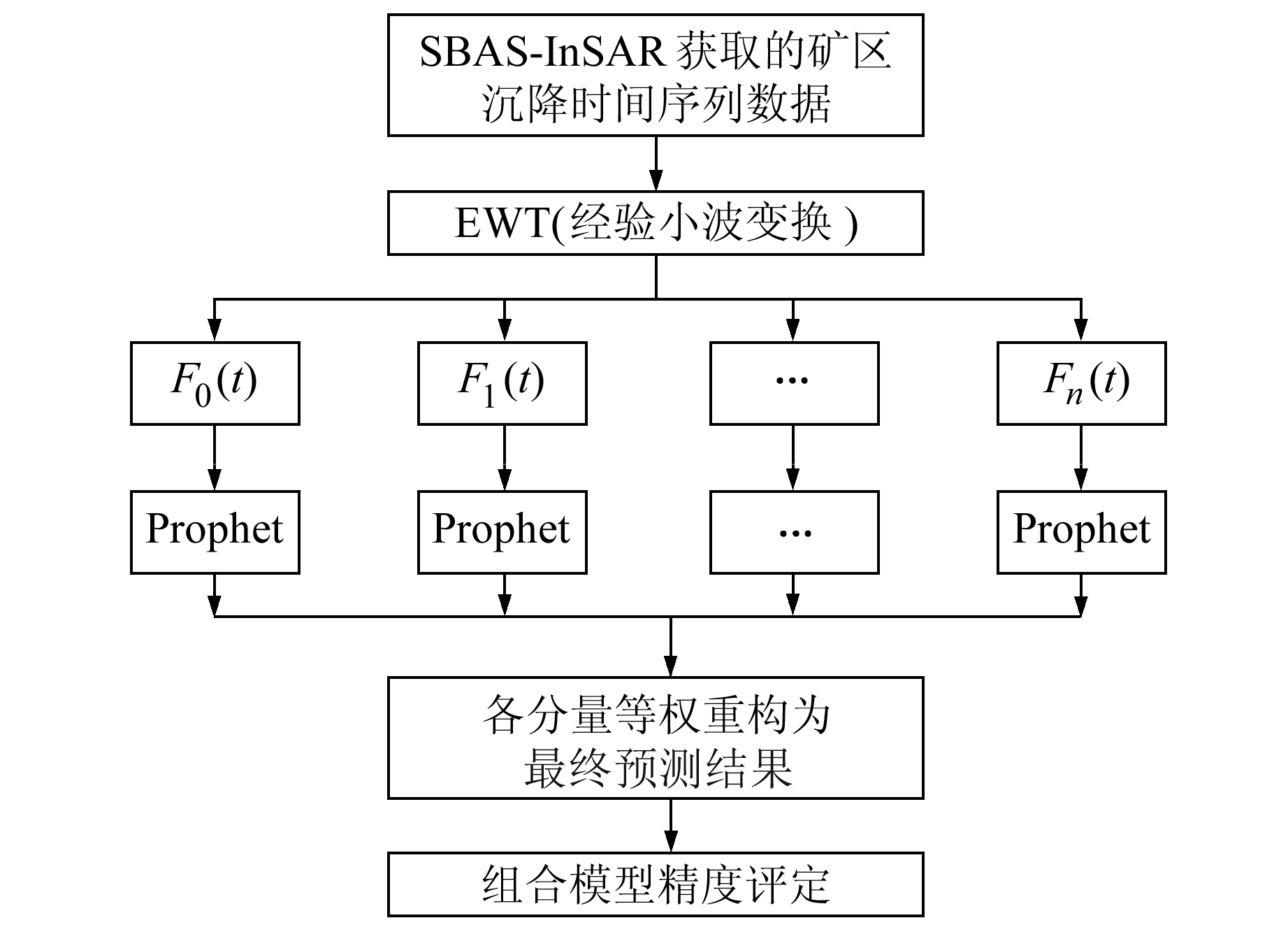
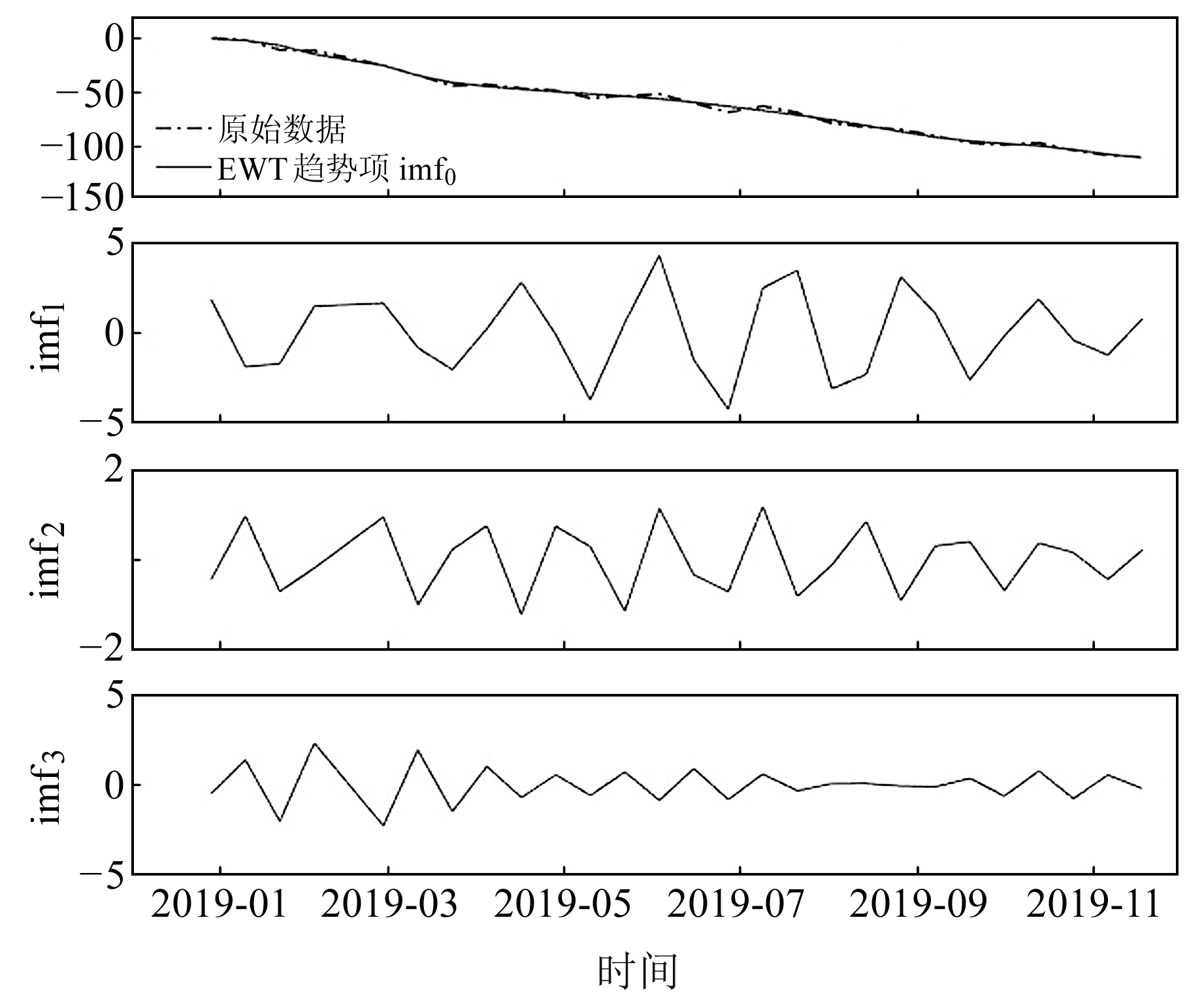
2.4 EWT-Prophet模型的沉降预测方法图 2为EWT-Prophet组合预测模型算法的流程,图 3为EWT分解示意图。可以看出,EWT将原始沉降数据自适应分解为1个趋势项信号和3个周期项信号,其中趋势项信号可有效反映原始沉降数据的趋势性,其余周期项信号可反映原始沉降数据的微小震荡变化。
|
图 2 EWT-Prophet流程 Fig. 2 Flow chart of EWT-Prophet |
|
图 3 EWT分解 Fig. 3 EWT decomposition |
本文组合模型先对沉降时序信号进行EWT分解,将原始时序信号分解为经验尺度分量F0和N个经验小波分量FN,再对各分量进行Prophet预测,将得到的所有预测分量叠加重构为最终的预测信号。该方法综合了EWT方法自适应能力强、理论性强和Prophet模型拟合预测效果好、预测速度快等特点。EWT-Prophet组合预测模型对地表沉降时序数据进行预测的主要步骤为:
1) 使用EWT对沉降数据进行分解:
| $f\left( t \right) = {f_0}\left( t \right) + \sum\limits_{k = 1}^n {{f_k}\left( t \right)} $ | (5) |
2) 对所有有效分量进行Prophet预测,将所有预测分量重构为最终的预测数据,并与单一的Prophet预测方法进行比较,验证组合模型的可靠性。
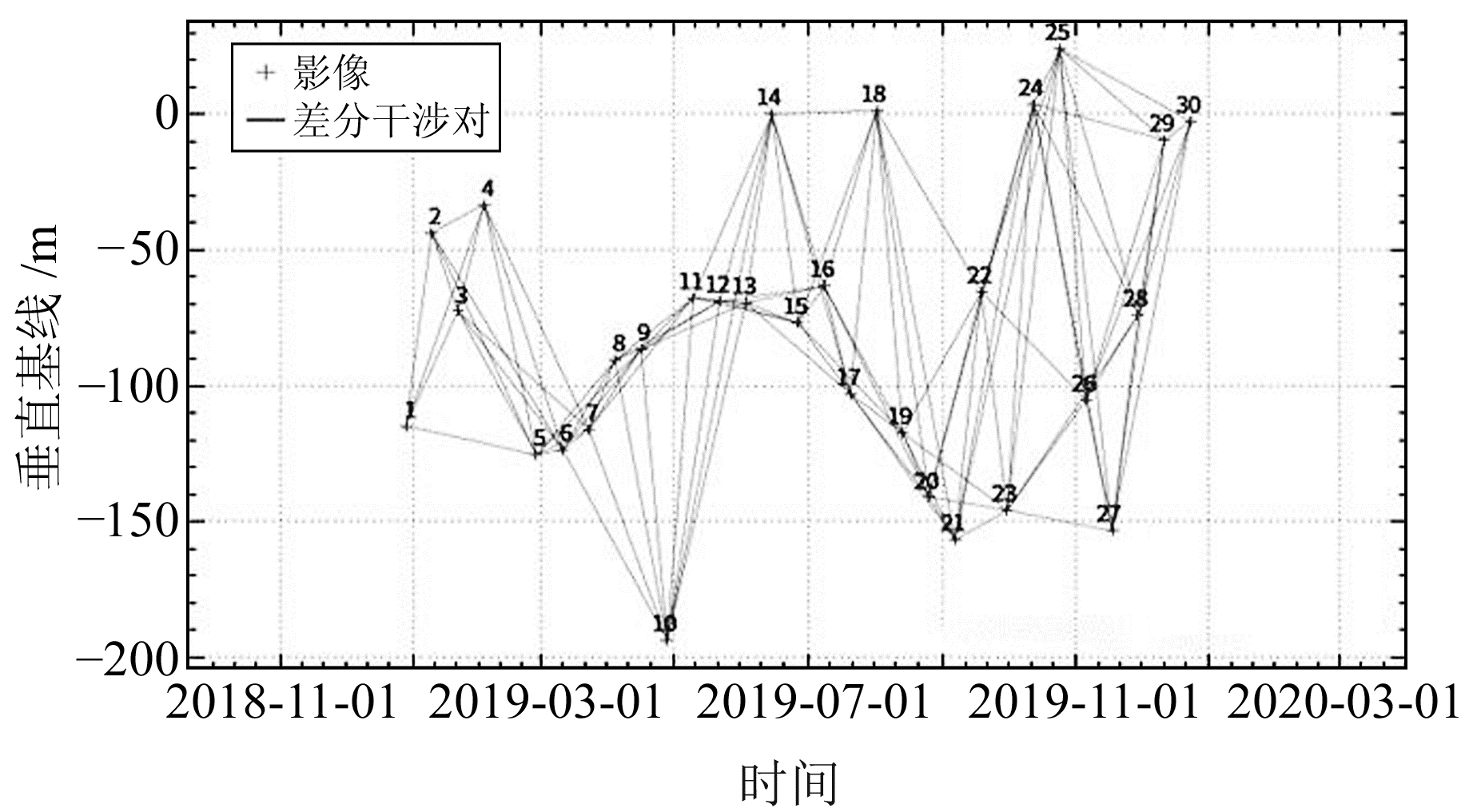
3 实验分析 3.1 矿区SBAS-InSAR监测及分析实验选取覆盖研究区的30景升轨Sentinel-1A数据,使用GAMMA软件进行SBAS-InSAR处理,选取2019-06-15的SAR影像作为公共主影像,再将辅影像配准到主影像上(配准精度达0.001像元),对干涉对进行多视处理(多视系数设置为4 ∶1)。实验的时间基线和空间基线阈值分别为60 d和200 m,最终构成112对干涉对用于时序分析,图 4为干涉对基线分布。根据干涉对时空基线分布图对影像进行干涉处理,利用外部DEM数据去除地形相位的影响,生成差分干涉图,并对其进行滤波增强处理,采用最小费用流方法进行相位解缠,得到研究区相位的真实值。通过查验每组产生的相干系数图、滤波后的干涉图和解缠图,移除干涉质量较差的干涉对,在具有高相干性的像素点上建立模型。通过奇异值分解方法反演估算形变速率并去除残余地形,计算相位残差并进行残差分离,最终得到研究区地表沉降速率及地表沉降分布情况。
|
图 4 干涉对时空基线分布 Fig. 4 Spatial-temporal baseline of interferometric pairs distribution |
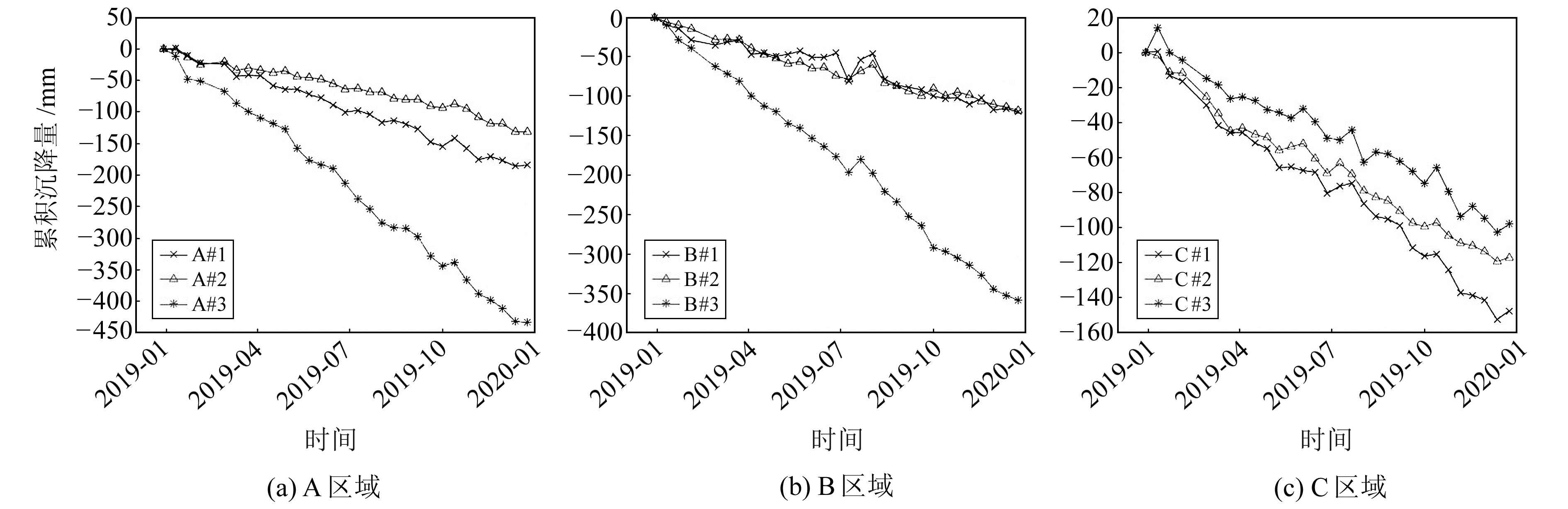
实验结果表明,研究区有3处明显沉降,本文将这3处沉降区域分别标记为A、B、C,并在每个区域中分别选取3个沉降特征点作为研究对象(分别标记为#1、#2、#3),各特征点位置如图 5所示。图 6为各区域中特征点的沉降时序,可以发现,A区域沉降最为严重,最大年平均沉降速率为490 mm/a,其中A#3位于沉降区中心,最大累积沉降量达440 mm,A#1和A#2在沉降区边缘,沉降量分别为184 mm和131 mm;B区域最大年平均沉降速率达390 mm/a,位于沉降中心的特征点B#3累积沉降量为358 mm,沉降区边缘的B#1和B#2累积沉降量分别为120 mm和118 mm;C区域最大年平均沉降速率可达233 mm/a,C#1、C#2和C#3的累积沉降量分别为148 mm、98 mm和117 mm。

|
图 5 A、B、C区域沉降速率 Fig. 5 Settlement rates in regions A, B and C |
|
图 6 A、B、C区域特征点时间序列形变 Fig. 6 Time series deformation of feature points in areas A, B and C |
马涛等[12]对采用SBAS-InSAR技术获取的时序沉降数据进行分析,并引入水准监测数据进行对比。结果表明,监测沉降数据的平均误差为1.62 mm,符合《地面沉降干涉雷达数据处理技术规范》中10 mm的精度要求,表明SBAS-InSAR技术监测沉降数据的精度具有可靠性。本文将监测数据作为真实观测数据进行回溯性预测研究。
3.2 地表沉降预测及结果分析以SBAS-InSAR技术获得的特征点沉降时序数据作为实际值,选取前27期(时间间隔为12 d)监测数据作为样本数据进行预测研究,预测后3期的沉降情况,并将预测结果与实际监测结果进行对比分析。为证明本文提出的组合预测模型在矿区沉降预测中的可行性,分别利用Prophet模型和EWT-Prophet组合模型进行实验,并对实验结果进行对比分析。
表 2和表 3为Prophet模型和EWT-Prophet组合模型的预测结果和相对误差统计。可以看出,组合模型的平均相对误差分别为1.55%、2.89%、1.57%,平均相对误差相较于单一模型分别提升48.68%、53.24%、68.21%。由此可见,引入单一Prophet模型进行对比不足以验证本文组合方法的有效性,因此引入经典ARMA预测模型进行对比分析。
|
|
表 2 Prophet模型预测值 Tab. 2 Predictive value of Prophet model |
|
|
表 3 EWT-Prophet组合模型预测值 Tab. 3 Predictive value of EWT-Prophet model |
表 4(单位mm)为不同方法预测结果的统计,表 5(单位mm)为预测结果残差绝对值统计。可以看出,在残差绝对值指标中,EWT-Prophet组合模型预测结果的残差绝对值最小,3期平均值分别为2.516 7 mm、5.065 6 mm、2.877 8 mm,表明本文方法优于单一Prophet模型和ARMA模型。
|
|
表 4 不同方法预测结果 Tab. 4 Prediction results of different methods |
|
|
表 5 预测结果残差绝对值 Tab. 5 Absolute values of residuals of prediction results |
为分析本文预测方法的有效性,利用均方根误差(RMSE)、平均百分比误差(MAPE)等指标对预测结果进行对比分析(表 6)。由表可知,EWT-Prophet组合模型的精度整体优于单一Prophet模型和ARMA模型,平均均方根误差和平均百分比误差分别为3.97 mm和2.00%,相较于Prophet模型和ARMA模型,RMSE分别提升51.53%、59.03%,MAPE分别提升57.81%、64.85%。实验结果表明,本文构建的组合模型具有更好的预测精度,且具有有效性和适用性。
|
|
表 6 预测精度比较 Tab. 6 Comparison of prediction accuracy |
本文以江西德兴矿区为研究区域,首先采用覆盖研究区的30景影像进行SBAS地表沉降监测,获取该地区30期时序沉降变化与累积沉降值。然后以SBAS监测值为研究时序数据样本,使用前27期监测值作为样本数据进行回溯性预测研究,利用EWT-Prophet组合模型与单一Prophet模型和ARMA模型进行预测研究。结果表明,组合模型结果整体优于单一模型,本文方法预测精度更佳,相较于Prophet模型和ARMA模型,RMSE分别提升了51.53%、59.03%,MAPE分别提升了57.81%、64.85%,说明组合模型具有适用性和有效性。
本文将EWT与Prophet预测模型相结合并引入SBAS-InSAR沉降研究,给类似的沉降时序信号数据分析提供了一种自适应强、预测效果好的组合方法,但此类分解-预测的组合方法也给预测过程带来额外的工作量。在研究过程中,矿区的沉降变化与诸多因素有关,如何建立一种高效、自适应强,并能及时反映突变情况的预测方法还有待进一步研究。
| [1] |
李秋元, 郑敏, 王永生. 我国矿产资源开发对环境的影响[J]. 中国矿业, 2002, 11(2): 47-51 (Li Qiuyuan, Zheng Min, Wang Yongsheng. Influences of Mineral Resource Exploitation on Environmental Quality in China[J]. China Mining Magazine, 2002, 11(2): 47-51 DOI:10.3969/j.issn.1004-4051.2002.02.015)
(  0) 0) |
| [2] |
梁涛. 利用短基线集InSAR技术监测矿区地表形变[J]. 测绘通报, 2014(增1): 82-84 (Liang Tao. Monitoring Surface Deformation in Mining Area by Short Baseline Set InSAR Technology[J]. Bulletin of Surveying and Mapping, 2014(S1): 82-84)
(  0) 0) |
| [3] |
宋海萍. 基于灰色系统模型的矿区地表沉降预测研究[J]. 矿山测量, 2020, 48(4): 35-37 (Song Haiping. Study on Mining Surface Subsidence Prediction Based on Grey System Model[J]. Mine Surveying, 2020, 48(4): 35-37 DOI:10.3969/j.issn.1001-358X.2020.04.009)
(  0) 0) |
| [4] |
周文韬, 张文君, 杨元继, 等. 矿区地表沉降监测的一种组合模型预测方法[J]. 大地测量与地球动力学, 2021, 41(3): 308-312 (Zhou Wentao, Zhang Wenjun, Yang Yuanji, et al. A Combined Model Prediction Method for Surface Subsidence Monitoring in Mining Areas[J]. Journal of Geodesy and Geodynamics, 2021, 41(3): 308-312)
(  0) 0) |
| [5] |
李威, 鲁铁定, 贺小星, 等. 基于Prophet-RF模型的GNSS高程坐标时间序列预测分析[J]. 大地测量与地球动力学, 2021, 41(2): 116-121 (Li Wei, Lu Tieding, He Xiaoxing, et al. Prediction and Analysis of GNSS Vertical Coordinate Time Series Based on Prophet-RF Model[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 116-121)
(  0) 0) |
| [6] |
鲁铁定, 黄佳伟, 鲁春阳, 等. 基于EWT- ARMA的短期电离层TEC预测模型[J]. 大地测量与地球动力学, 2021, 41(4): 331-335 (Lu Tieding, Huang Jiawei, Lu Chunyang, et al. Short-Term Ionospheric TEC Prediction Model Based on EWT-ARMA[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 331-335)
(  0) 0) |
| [7] |
Taylor S J, Letham B. Forecasting at Scale[J]. The American Statistician, 2018, 72(1): 37-45 DOI:10.1080/00031305.2017.1380080
(  0) 0) |
| [8] |
牛凯, 洪芳华, 费冬, 等. 基于Prophet算法的电力物资需求预测方法研究[J]. 科学技术创新, 2020(33): 163-164 (Niu Kai, Hong Fanghua, Fei Dong, et al. Research on Power Material Demand Forecasting Method Based on Prophet Algorithm[J]. Scientific and Technological Innovation, 2020(33): 163-164)
(  0) 0) |
| [9] |
常恬君, 过仲阳, 徐丽丽. 基于Prophet-随机森林优化模型的空气质量指数规模预测[J]. 环境污染与防治, 2019, 41(7): 758-761 (Chang Tianjun, Guo Zhongyang, Xu Lili. Scale Prediction of AQI Based on Prophet-Random Forest Optimization Model[J]. Environmental Pollution and Control, 2019, 41(7): 758-761)
(  0) 0) |
| [10] |
翟笃林, 张学民, 熊攀, 等. Prophet时序预测模型在电离层TEC异常探测中的应用[J]. 地震, 2019, 39(2): 46-62 (Zhai Dulin, Zhang Xuemin, Xiong Pan, et al. Detection of Ionospheric TEC Anomalies Based on Prophet Time-Series Forecasting Model[J]. Earthquake, 2019, 39(2): 46-62)
(  0) 0) |
| [11] |
Gilles J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3 999-4 010 DOI:10.1109/TSP.2013.2265222
(  0) 0) |
| [12] |
马涛, 赵彦军, 张伟. SBAS-InSAR技术在矿山开采区沉降监测中的应用[J]. 测绘与空间地理信息, 2020, 43(11): 210-212 (Ma Tao, Zhao Yanjun, Zhang Wei. Application of SBAS-InSAR Technology in Settlement Monitoring of Mining Area[J]. Geomatics and Spatial Information Technology, 2020, 43(11): 210-212 DOI:10.3969/j.issn.1672-5867.2020.11.058)
(  0) 0) |
2. Principal's Office, Nanchang Hangkong University, 696 South-Fenghe Road, Nanchang 330063, China
 2022, Vol. 42
2022, Vol. 42

