在地震前兆观测领域,体积式钻孔应变仪因具有灵敏度高、选点容易、占地面积小及日常维护方便等优点,被大量布设,并且按规范要求,其需安装在60 m以下的钻井底部,显著降低了地表人类活动及降雨等对其造成的干扰,有利于获得高质量的观测结果[1-4]。
要获得精确的应变数据,首先需要了解体积式钻孔应变仪准确的灵敏度,而灵敏度主要是通过对仪器进行标定得到的。现有的体积式钻孔应变仪在生产阶段都会计算出标定幅度,待仪器安装到钻孔并稳定运行后,可通过标定得到灵敏度。但由于受各种难以控制因素的影响,如探头尺寸误差、运输、下井安装及探头与井壁耦合等状况,致使传感器的工作状态发生变化,若直接使用原标定格值计算观测数据,得到的结果是不准确的。目前,许多学者对钻孔应变仪的标定问题进行了深入研究,得到一些成果[5-6]。本文以体积式钻孔应变仪为例,以体应变固体潮汐作为参考系,用潮汐因子对仪器观测资料进行校正,得到较好的结果。
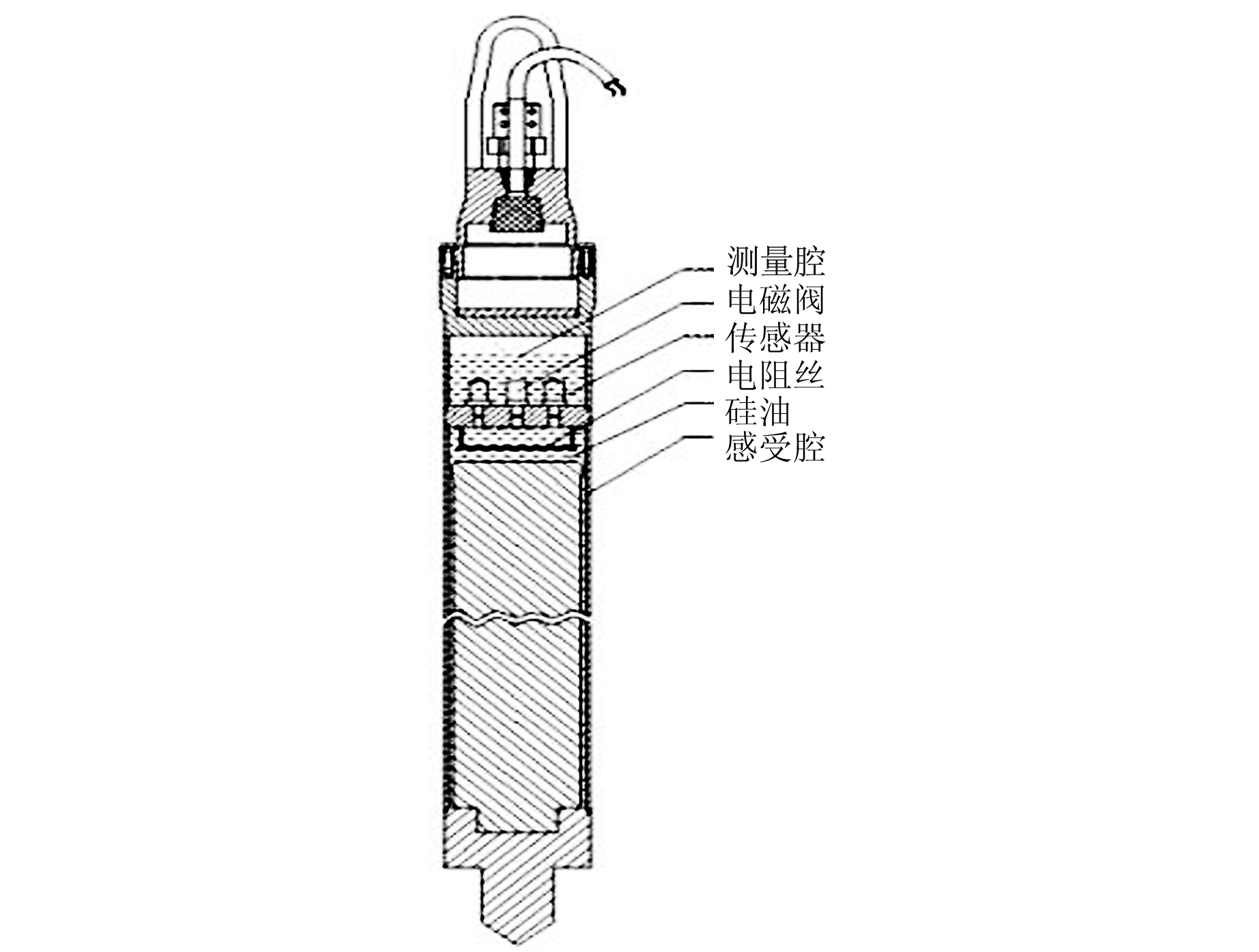
1 体应变仪的测量原理体积式钻孔应变仪的结构如图 1所示,其中探头分上腔(测量腔)和下腔(感受腔),下腔安装有标定电阻丝,并充满不可压缩的硅油;上腔安装有主压力传感器、备用压力传感器和电磁阀。探头一般埋设在60 m以下的钻井底部,用膨胀水泥将其与周围岩石耦合在一起。当探头接收到大地应力变化时,通过探头下腔的不锈钢筒传递给腔内的硅油,由于硅油不可压缩,外界应力变化被转换为压力变化并传递给测量腔的压力传感器。当压力变化达到临界值时,电磁阀开启,探头的上下腔压力平衡。
|
图 1 体应变探头示意图 Fig. 1 The map of volumetric strain probe |
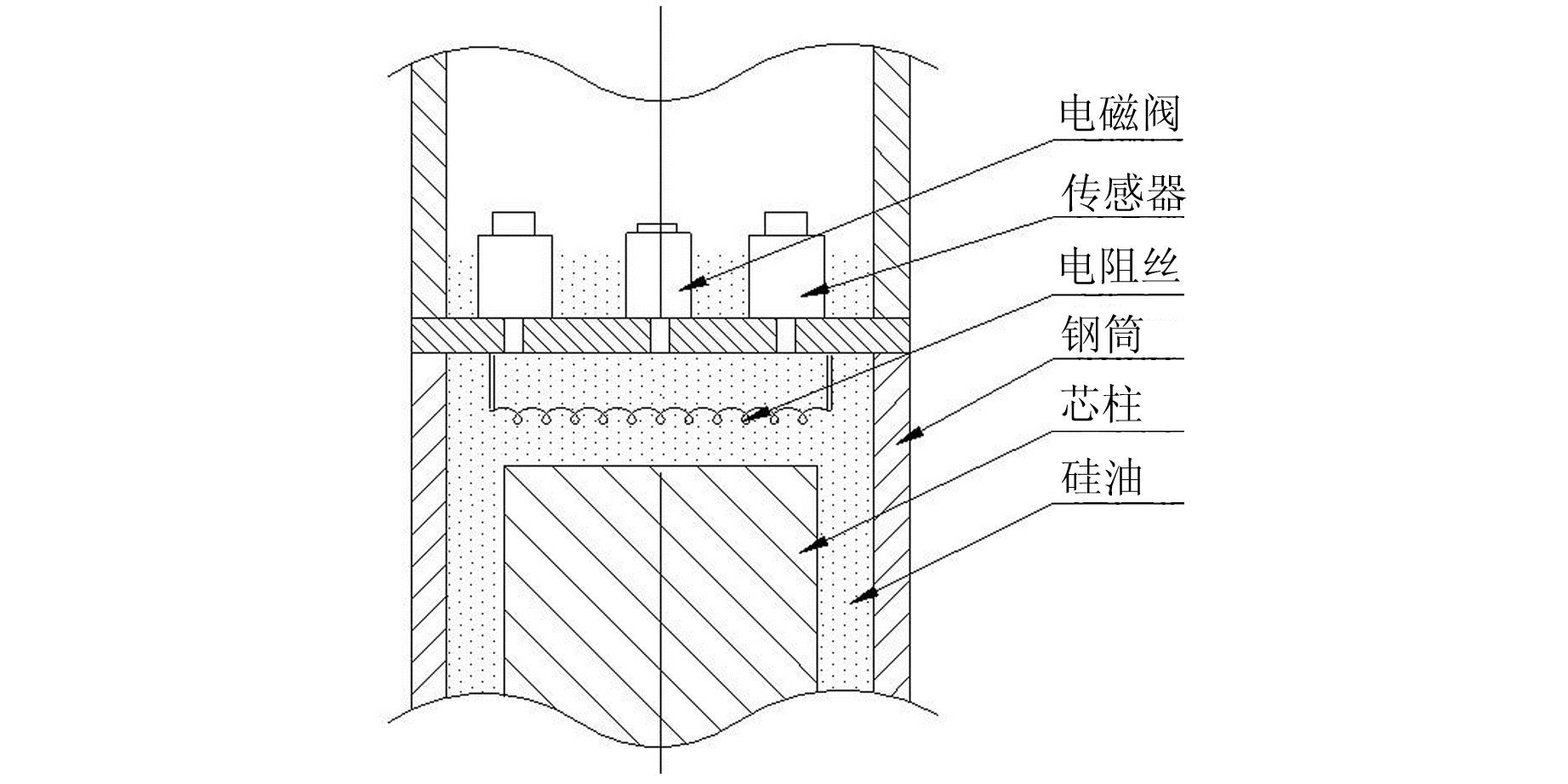
热标定能够检查体应变仪观测系统(由探头到电压输出口)是否灵敏、格值B(或灵敏系数A)是否有明显变化。体应变仪内有数个机械零件,仪器内部的压力传感器感受到的应力变化不是直接来自于外界,而是经过了层层传导,因此存在机械变形等损失。为给出体应变仪的格值B,仪器内置标定装置,即安装在下腔(感受腔)的内置热电阻丝,电阻丝周围充满硅油,通过给电阻丝通电将电能转换为热能(图 2),从而加热电阻丝周围的硅油使其产生热膨胀,压力传感器感受到硅油体积变化而产生压力变动。
|
图 2 体应变仪标定装置 Fig. 2 Calibration device of volumetric strain gauge |
热电阻丝产生的热能为:
| $ W=I^{2} R \Delta t $ | (1) |
硅油的热膨胀体积变化为:
| $ \Delta V=\frac{\eta W \alpha}{C \rho} $ | (2) |
式中,I为通电电流,取65 mA;R为热电阻丝电阻,取80 Ω;Δt为通电时间,取2 s;η为电能转化为热能的转化效率,按以往经验η=0.75;α为硅油的热膨胀系数,α=8.89×10-4/℃;C为硅油比热,C=1.42 J/g℃;ρ为硅油比重,ρ=0.95 g/cm3。
将式(1)代入式(2)得:
| $ \Delta V=\frac{\eta I^{2} R \Delta t \alpha}{C \rho} $ | (3) |
标定使硅油所产生的热膨胀体积变化为3.34×10-4 cm3。
对于TJ-2型体应变仪,硅油体积V=2 620 cm3,则标定幅度(ΔV/V)标=12.7×10-8,即标定1次产生的体应变量为12.7×10-8。
仪器标定1次的电压变化为Δu=u1-u0,其中u1为标定后仪器面板的电压读数,u0为标定前仪器面板的电压读数。仪器的灵敏度为:
| $ A=\frac{\Delta u}{(\Delta V / V)_{\text {标 }}}=\frac{u_{1}-u_{0}}{(\Delta V / V)_{\text {标 }}} $ | (4) |
仪器的格值为:
| $ B=\frac{1}{A}=\frac{(\Delta V / V)_{\text {标 }}}{u_{1}-u_{0}} $ | (5) |
假定标定电压差为Δu=13 mV,则仪器的格值B=0.98×10-9/0.1 mV。探头灌注硅油后可进行预标定,由标定数据可推算出探头安装后的格值或灵敏系数。
体应变仪在安装后需经过1个月左右的稳定期,之后就可进行现场标定。现场标定的电压输出幅度需大于室内标定的电压输出幅度,这是因为室内标定损耗了一部分ΔV,且探头的外壳(弹性筒)在室内是无约束的,硅油压力增加时容积略有膨胀,而安装在钻孔后探头四周受水泥包裹,容积不再膨胀,压力直接传递给传感器。
表 1为江苏六合地震台体积式钻孔应变仪2019-12-30标定数据,图 3为标定曲线。
|
|
表 1 六合地震台标定数据 Tab. 1 Calibration data of volumetric strain gauge at Liuhe seismic station |

|
图 3 六合体应变标定曲线 Fig. 3 Calibration curve of volumetric strain gauge at Liuhe seismic station |
按照观测规范,在每年01-01、07-01各校准1次仪器,更换或维修仪器之后也需进行校准,如出现应变固体潮曲线的幅度连续数日明显变得过小或过大等特殊情况,也可进行1次校准。各校准结果仅用于了解测量系统灵敏系数的不稳定性,并与以往校准结果平均值进行对比,只要未超过5%就无需更改出厂设置的格值。
从原理上讲,体应变仪通过热标定来计算仪器的灵敏度是没有问题的,但在实际计算中,有些取值是不准确的。例如通电时间Δt是通过用手按住标定按钮来实现的,2 s时间无法精确控制;电能转化为热能的转化效率η与电阻丝及体应变仪的保温都有关系,此处按经验取0.75是有误差的;热标定时的硅油膨胀体积变化也受硅油真空度的影响。
3 体应变仪的固体潮校正要利用体积式钻孔应变仪的观测值进行科学研究,就需要将观测值转化为实际应变值,而目前该过程都是通过仪器安装稳定后的实地热标定来完成的。为了得到体应变仪的精确数据,本文拟利用固体潮对仪器数据进行校正[7]。
3.1 固体潮数据的提取由于体应变仪会受零漂及其他干扰(如长期开采、注水等)的影响出现低频趋势变化,为消除这种变化,通常需要对观测数据进行别尔采夫滤波。
别尔采夫滤波的原理是将潮汐观测量分成由日、月引力作用形成的潮汐和由仪器零漂及其他干扰引起的低频趋势变化2个部分。别尔采夫滤波是一种18阶组合,可消除部分零漂,其滤出潮汐成分的功能优于日均值,广泛应用于时值序列的数据处理及短临异常提取[8]。
体应变数据的整点值Y(t)主要由两部分组成,即
| $ Y(t)=A(t)+B(t) $ | (6) |
其中,A(t)为体应变数据变化的趋势项,B(t)为体应变数据去掉趋势项的测值。用别尔采夫滤波消除趋势变化,计算t时刻应变数据的趋势变化值:
| $ A_{(t)}=\frac{Y_{(t)}+Y_{(t \pm 2)}+Y_{(t \pm 3)}+Y_{(t \pm 5)}+Y_{(t \pm 8)}+Y_{(t \pm 10)}+Y_{(t \pm 13)}+Y_{(t \pm 18)}}{15} $ | (7) |
校正后得到不含趋势项的测值序列Y′(t)=Y(t)-A(t),t=1, 2, 3, …, n, n=n′-36,其中n为需要计算的数据个数,n′为参加计算的数据个数。
用别尔采夫滤波对体应变整点数值进行处理,得到去掉低频趋势变化的潮汐部分数据,同时用固体潮公式计算得到理论的体应变固体潮数据。图 4分别给出泉州市局台2020-06、邹城台2020-12及黄坦台2020-12的计算和理论数据曲线,可以看出,2条曲线变化趋势大致相同。用线性回归法分析2条曲线的相关性,结果见表 2。

|
图 4 体应变观测值计算及理论潮汐数据 Fig. 4 Calculation and theoretical tidal data of volumetric strain observation |
|
|
表 2 台站体应变仪潮汐校正系数 Tab. 2 Tidal correction coefficient of volumetric strain gauge at seismic station |
地球应变固体潮可展开成振幅为常数、幅角为有关天文参数线性组合的484个谐波,其中99个为长周期潮,197个为日潮,150个为半日潮,14个为1/3日潮。由于地球液核动力学效应和气压场的扰动,在日波频段内,日波潮汐因子受到的干扰较大,观测精度低、可靠性差;而在半日波频段内,S2波等受气压影响较大,数据同样不可靠,只有M2波潮汐因子受到的干扰较小,精度最高、可靠性最好,因此选用M2波作为描述地壳弹性的参数[4, 6]。
体应变仪观测潮汐因子受安装钻井岩石的弹性参数影响,另外随着钻井水泥的固化,弹性模量会变大,观测到的潮汐因子数值也会变化。总之,体积式钻孔应变仪观测到的应变固体潮实际上是理论潮汐与各种环境因素的总和。
M2波潮汐因子为:
| $ R_{0}=\frac{H_{M_{2}}}{H_{M_{2}}^{0}} $ | (8) |
式中,HM2为理论M2波与各种环境因素合成的振幅,HM20为M2波的理论振幅。正常情况下要求R0近似等于1,但由于受环境因素影响,体应变仪安装后R0≠1,因此需要校正:
| $ \eta=\frac{1}{R_{0}} $ | (9) |
式中,η为潮汐校正系数。于是,
| $ \varepsilon=\eta \times B \times L $ | (10) |
式中,ε为应变量,与井下及地面的观测环境密切相关;B为热标定格值;L为仪器观测读数。
选取部分地震台站的数据进行对比。由表 2可以看出,5个台站计算和理论固体潮的相关系数都大于0.8,说明仪器自身数据质量完好,潮汐观测质量较高,体应变仪能够真实反映周围应力及应变场的变化。另外,泉州、黄坦、邹城、新安江4个地震台站的潮汐校正系数都在0.9~1.3之间,表明仪器理论M2波与各种环境因素合成的振幅与理论振幅偏差不大,热标定格值基本正确。而金坛地震台位于江苏省金坛市乌龙山景区内,钻孔深度为142 m,钻井岩性为石英砂岩,岩石较破碎,体应变仪前期受周围抽水影响较大,抽水停止后才能看到固体潮汐,且潮汐校正系数只有0.4,应该是受钻孔岩石破碎及各种环境因素影响较大。
4 结语体积式钻孔应变仪产出的应变数据是用仪器读数乘以格值来计算的,而格值是在仪器安装稳定后通过热标定值计算求得的,过程中既有标定时间的不准确性,又有计算公式中经验取值产生的误差,可能导致应变数据不准确。用应变固体潮潮汐因子对体应变仪观测数据进行校正,能够有效校正格值误差及钻井周围环境对仪器的影响,使观测应变值能精确反映周围应力及应变场的变化。
由于固体潮理论值是建立在假设地球模型上的,台站的空间点域与假设地球模型对应的空间点域的形状及质量分布不相同,且可能相差较大,导致理论固体潮与实际固体潮并不完全相符,直接用理论应变固体潮来确定潮汐校正系数是有误差的。但在目前阶段,还没有更好的对钻孔应变仪进行绝对标定的方法。
| [1] |
苏恺之, 李海亮, 张均, 等. 钻孔体应变观测新进展[M]. 北京: 地震出版社, 2003 (Su Kaizhi, Li Hailiang, Zhang Jun, et al. New Progress in Borehole Strain Observation[M]. Beijing: Seismological Press, 2003)
(  0) 0) |
| [2] |
马京杰, 李海亮. 小型化体积式钻孔应变仪的研制[J]. 大地测量与地球动力学, 2021, 41(2): 217-220 (Ma Jingjie, Li Hailiang. Development of Miniaturized Volume Borehole Strain Instrument[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 217-220)
(  0) 0) |
| [3] |
邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地绝对标定[J]. 地震, 2005, 25(3): 27-34 (Qiu Zehua, Shi Yaolin, Ouyang Zuxi. Absolute Calibration of 4-Component Borehole Strainmeters[J]. Earthquake, 2005, 25(3): 27-34)
(  0) 0) |
| [4] |
张凌空, 刘北顺, 高福旺, 等. 钻孔体应变观测潮汐因子计算模型[J]. 华北地震科学, 1998, 16(2): 10-14 (Zhang Lingkong, Liu Beishun, Gao Fuwang, et al. Calculation Model of Tidal Factor Observation by Borehole Body Strain[J]. North China Earthquake Sciences, 1998, 16(2): 10-14)
(  0) 0) |
| [5] |
何斌, 王恒知, 张岑, 等. 岩石弹性模量对钻孔体应变仪M2波视潮汐因子影响分析[J]. 大地测量与地球动力学, 2020, 40(8): 854-859 (He Bin, Wang Hengzhi, Zhang Cen, et al. Analysis of the Elastic Modulus of Borehole on M2 Apparent Tide Factors for Body Strainmeter[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 854-859)
(  0) 0) |
| [6] |
易志刚, 邱泽华, 宋茉. 钻孔体应变观测资料的实地校正[J]. 地震, 2007, 27(3): 117-123 (Yi Zhigang, Qiu Zehua, Song Mo. On the Spot Correction of Observational Data of Borehole Bulk Strain[J]. Earthquake, 2007, 27(3): 117-123)
(  0) 0) |
| [7] |
Hart R H G, Gladwin M T, Gwyther R L, et al. Tidal Calibration of Borehole Strain Meters: Removing the Effects of Small-Scale Inhomogeneity[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B11): 25 553-25 571 DOI:10.1029/96JB02273
(  0) 0) |
| [8] |
徐伟民, 陈石, 高孟潭, 等. 中国大陆重力场非潮汐时空变化特征的初步分析[J]. 地球物理学进展, 2012, 27(3): 861-871 (Xu Weimin, Chen Shi, Gao Mengtan, et al. The Preliminary Analysis to the Temporal Variation Characteristics of Non-Tidal Changes of Gravity in Mainland China[J]. Progress in Geophysics, 2012, 27(3): 861-871)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

