2. 中国地震局地震研究所,武汉市洪山侧路40号,430071;
3. 十堰市人民防空办公室,湖北省十堰市江汉南路76号,442000
地磁数据在观测中通常会受仪器故障、标定、雷击等因素的影响,导致记录缺数,如何尽可能不失真地重构补齐这些数据,并保证数据的连续性和可用性是一个亟需解决的问题[1]。目前国内对地磁秒数据补齐方法的研究较少[1-2],相关的补齐算法有均值替代法、最近邻域替代法、多重填补法及回归替代法[3]等。这些算法针对个别缺数情况有较好的优势,但无法应用于缺数在分钟以上的地磁秒数据中。
针对这一问题,本文通过研究湖北省所有地磁台站的秒数据文件发现,相邻台站数据的相关性高,且数据呈周期性,可依据相邻台站数据之间的相关性提取共同特性,再跟据数据自身个性补齐细节,从而尽可能不失真地补齐数据。
1 补数原理及实现为了不失真地补齐数据,需要做到以下几点:1)选取与所缺数据相关性高的数据,并确定移植的抽形图;2)对缺失的数据依据抽形图进行补数;3)对补好的抽形图进行细节修补;4)对修补完成的数据进行检测。
1.1 数据选取及傅里叶分解合成对于一组包含缺失值的地磁数据,可在数据库中找到一个与其最相似的对象。不同问题导致的缺数可选用不同标准进行相似性判定,最常见的是使用相关系数矩阵法,以选取与缺失数据关联性最强的数据作为抽形图。
抽形即拟合,选取何种拟合算法将直接决定修补数据的精度。本文选取傅里叶拟合法:首先将相似度高的地磁数据与所缺数据进行傅里叶分解,对分解后的正余弦波参数作对比分析,然后将调整后的波形合成便可得到所缺地磁数据的抽形图。
在实际工作中遇到的大多数非正弦周期函数都满足Dirichlet条件[4],其函数f(t)可表示为:
| $ f(t)=a_{0}+\sum\limits_{k=1}^{\infty}\left[a_{k} \cos (k w t)+b_{k} \sin (k w t)\right] $ | (1) |
式中,a0、ak、bk为傅里叶系数。由于地磁数据基本为秒采样序列,设为S(t):
| $ \begin{gathered} S(t)=a_{0}+\sum\limits_{k=1}^{m}\left[a_{k} \cos (k w t)+b_{k} \sin (k w t)\right], \\ m \leqslant[n / 2] \end{gathered} $ | (2) |
式(2)可写成矩阵的形式AX=S,其中,
| $ \boldsymbol{X}=\left[a_{0}, a_{1}, b_{1}, a_{2}, b_{2}, \cdots, a_{m}, b_{m}\right]^{\mathrm{T}} $ | (3) |
| $ \boldsymbol{S}=\left[S\left(t_{1}\right), S\left(t_{2}\right), \cdots, S\left(t_{n}\right)\right]^{\mathrm{T}} $ | (4) |
| $ \begin{gathered} \boldsymbol{A}= \\ {\left[\begin{array}{cccccc} 1 & \cos \left(w t_{1}\right) & \sin \left(w t_{1}\right) & \cos \left(2 w t_{1}\right) & \cdots & \cos \left(m w t_{1}\right) \\ 1 & \cos \left(w t_{2}\right) & \sin \left(w t_{2}\right) & \cos \left(2 w t_{2}\right) & \cdots & \cos \left(m w t_{2}\right) \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & \cos \left(w t_{n}\right) & \sin \left(w t_{n}\right) & \cos \left(2 w t_{n}\right) & \cdots & \cos \left(m w t_{n}\right) \end{array}\right]} \end{gathered} $ | (5) |
利用最小二乘法求得X=(ATA)-1ATS,即可求出傅里叶级数拟合中各项的傅里叶系数,根据2组数据之间波形的对比便可得到缺数数据的拟合图形。
1.2 基于ARMA预测模型的细节补齐算法地磁数据是按时间排列的序列,可作为时间序列进行分析,建立自回归滑动平均模型(ARMA模型)。ARMA模型能依据观测值进行预测,因此将完好的数据作为历史观测值,缺失数据作为预测值,利用ARMA模型进行预测,完好数据又可作为检验值对预测值进行检验。
时间序列zt的ARMA模型具有以下形式:
| $ \left\{\begin{array}{l} z_{t}-\varphi_{1} z_{t-1}-\cdots-\varphi_{p} z_{t-p}= \\ a_{t}-\theta_{1} a_{t-1}-\cdots-\theta_{q} a_{t-q} \\ E\left[a_{t}\right]=0, E\left[a_{t} a_{s}\right]= \\ \delta_{a}^{2} \delta_{t s}, \delta_{t t}=1, \delta_{t j}=0(t \neq j) \end{array}\right. $ | (6) |
式中,φi、θi为模型参数,p、q为模型的阶次。
利用ARMA模型进行预测的前提是输入的时间序列是平稳的,若为非平稳序列则需要通过差分方法转化为平稳序列后再进行ARMA模型拟合[5]。ARMA模型建模的预测流程见图 1。

|
图 1 ARMA模型建模流程 Fig. 1 Path of ARMA model |
选取2021-03-04恩施台FGM01地磁H分量数据。该测点当天受人为进洞线路改造影响,世界时09:23~10:01原始数据丢失,00:00~10:33数据突跳,噪声增加并产生台阶。为避免数据突跳对后期预测产生干扰,利用格拉布期准则对异常值进行剔除,并对实验数据作归一化处理,以消除量纲。
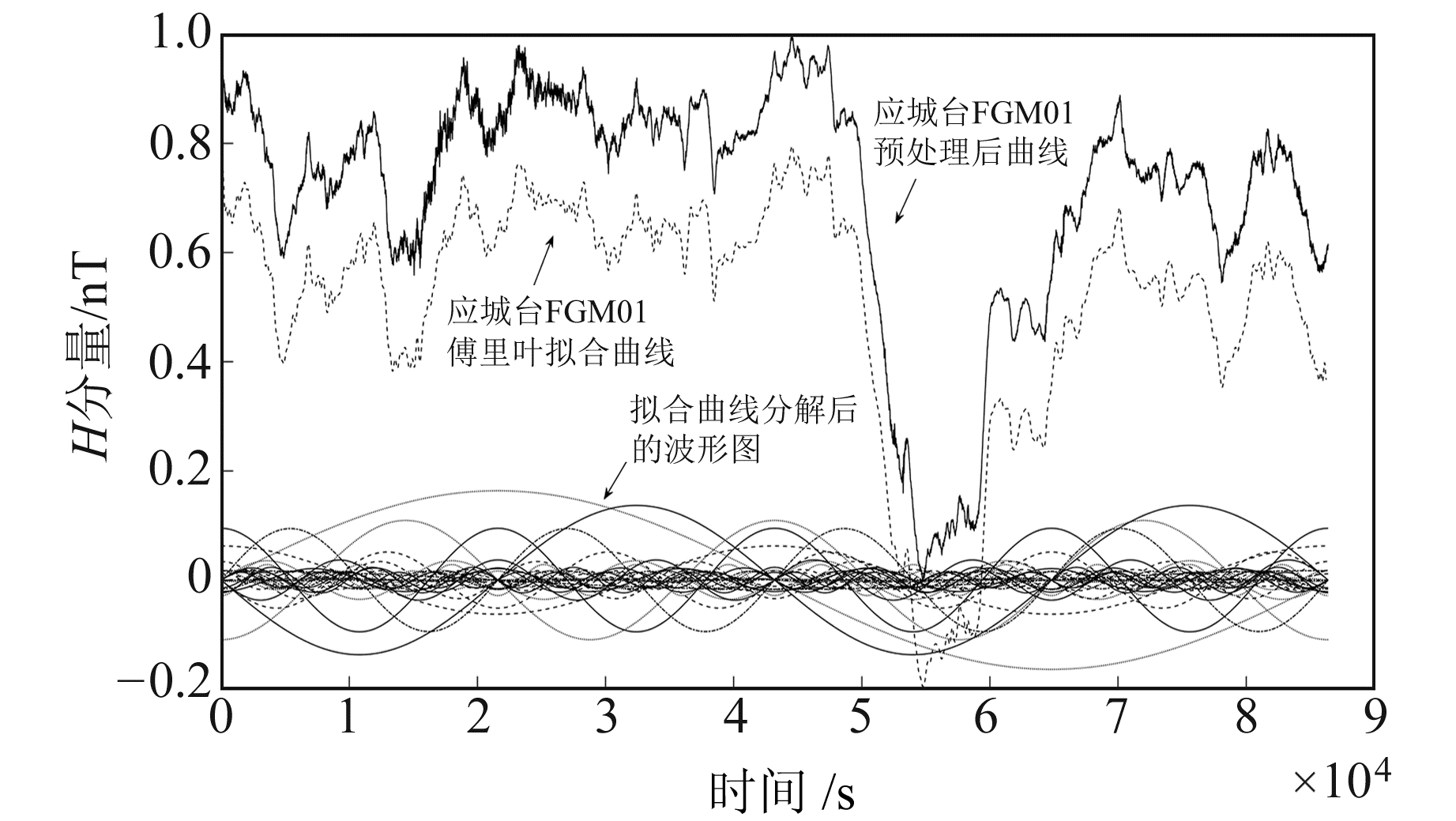
在数据库中寻找与恩施台FGM01地磁H分量预处理数据相似度高的数据。本文使用MATLAB中corrcoef函数筛选相关系数大于98%的数据,其中恩施台GM4地磁的相关系数为0.983 9,应城台GM4地磁、FGM01地磁及M15地磁的相关系数分别为0.993 6、0.994 3及0.994 2。因此,本文选择2021-03-04应城台FGM01地磁作为抽形图框架,对其作归一化处理后再进行傅里叶分解。为分辨拟合曲线,将同时段拟合曲线减去0.2 nT。从图 2可以看出,拟合曲线有截尾现象,但并不影响其整体形态。如果是尾部缺数,则可选取后1 d的部分数据作为验证数据,并不影响补数精度。
|
图 2 应城台FGM01地磁原始曲线、傅里叶拟合曲线及分解波形 Fig. 2 Original curve, Fourier fitting curve and decomposition waveform of FGM01 in Yingcheng station |
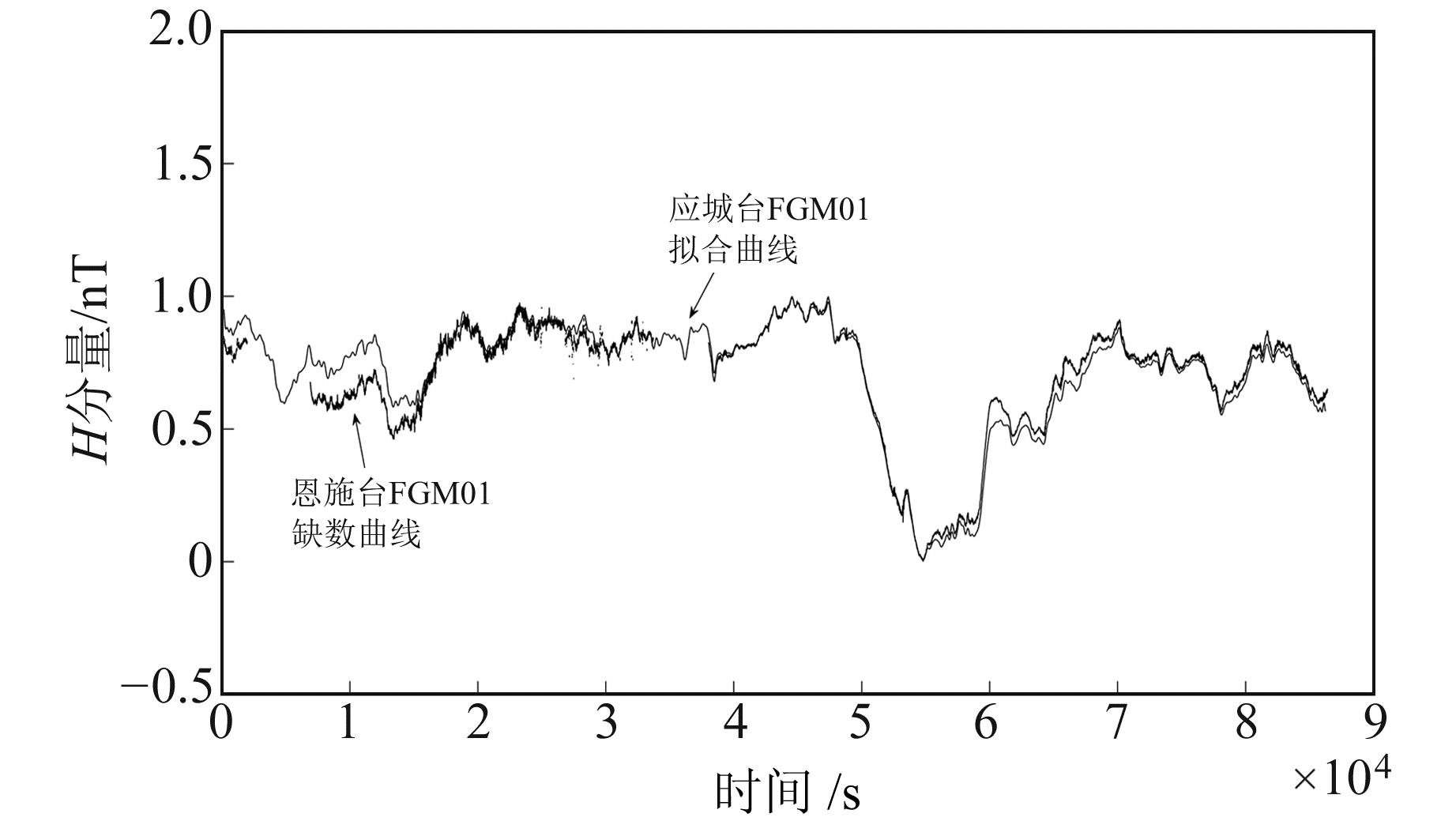
将应城台FGM01地磁抽形图移植到恩施台FGM01地磁(图 3)上发现,二者并不重合。取恩施台FGM01地磁后半段完整数据与同时段应城台FGM01地磁数据进行傅里叶分解,两者具有高度相似性,可认为部分与整体呈对应比例关系,即可得出缺失数据的波形参数。
|
图 3 应城台FGM01地磁拟合曲线与恩施台FGM01地磁缺数曲线对比 Fig. 3 Comparison of Yingcheng FGM01 fitting curve and Enshi FGM01 missing curve |
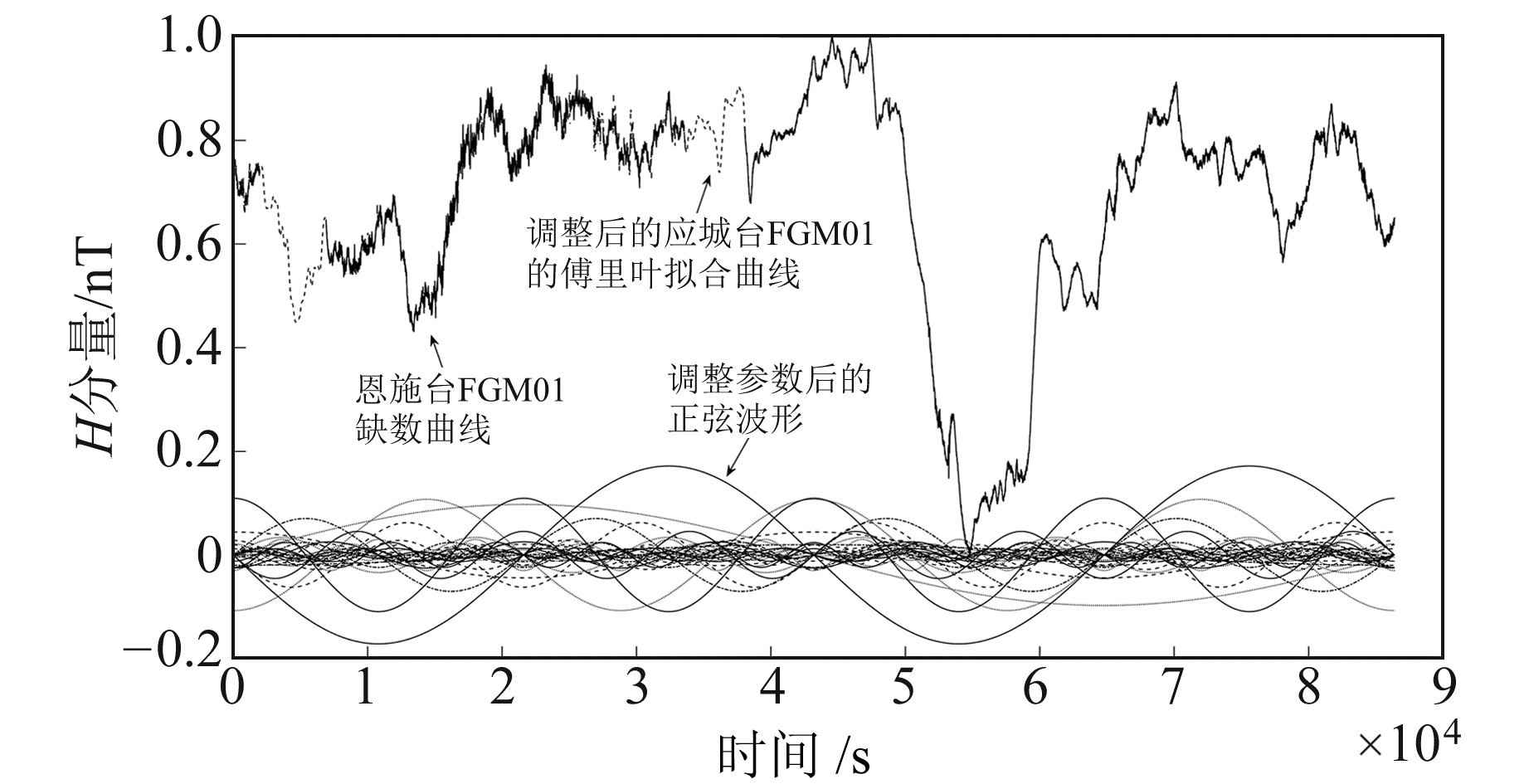
本文取波形个数为300个,对应波形参数如表 1所示,得到恩施台整体波形参数,合成后便可得到修改后的恩施台FGM01地磁抽形图(图 4)。
|
|
表 1 波形参数调整 Tab. 1 Waveform parameter adjustment |
|
图 4 调整后应城台FGM01地磁拟合曲线与恩施台FGM01地磁缺数曲线对比 Fig. 4 Comparison of Yingcheng FGM01 fitting curve and Enshi FGM01 missing curve after adjusting |
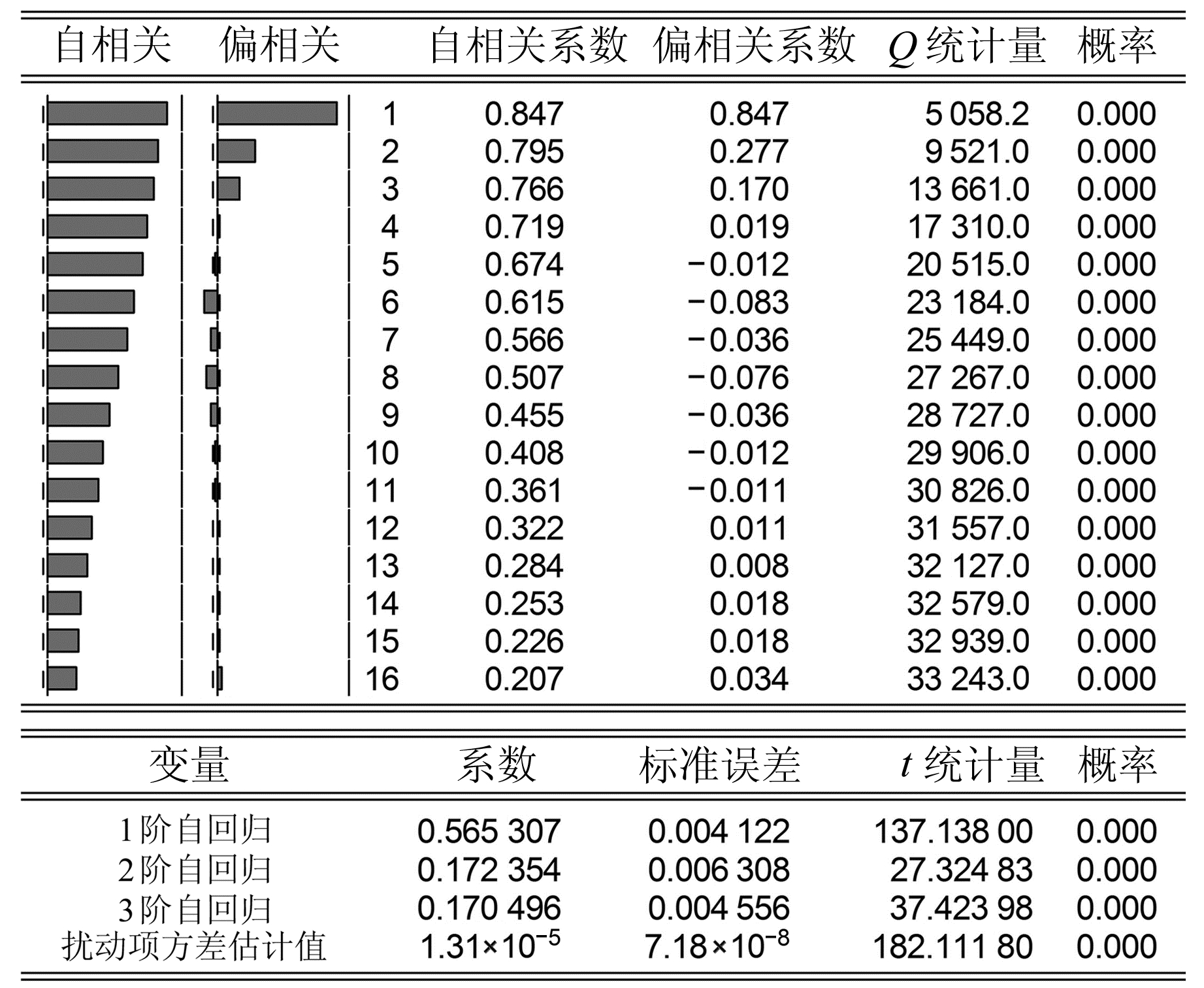
首先对结果进行平稳性与随机性检验。使用Eviews软件对数据进行单位根检验,结果显示,P值显著小于0.05,可以确认该数据为平稳数据。再利用Eviews软件作自相关和偏相关分析,结果如图 5所示,可以看出,该数据自相关系数拖尾,而偏相关系数3阶截尾。借助Eviews软件得到3阶自回归过程,对应的模型表达式[6]为:
| $ \begin{gathered} \Delta y_{t}=0.565307 \Delta y_{t-1}+0.172354 \Delta y_{t-2}+ \\ 0.170496 \Delta y_{t-3}+v_{t} \end{gathered} $ | (7) |
|
图 5 原始数据相关性及ARMA参数估计 Fig. 5 Correlation diagram of original data and estimation of ARMA parameters |
为了对比分析,将缺数数据减小0.05 nT,其补齐效果如图 6所示。
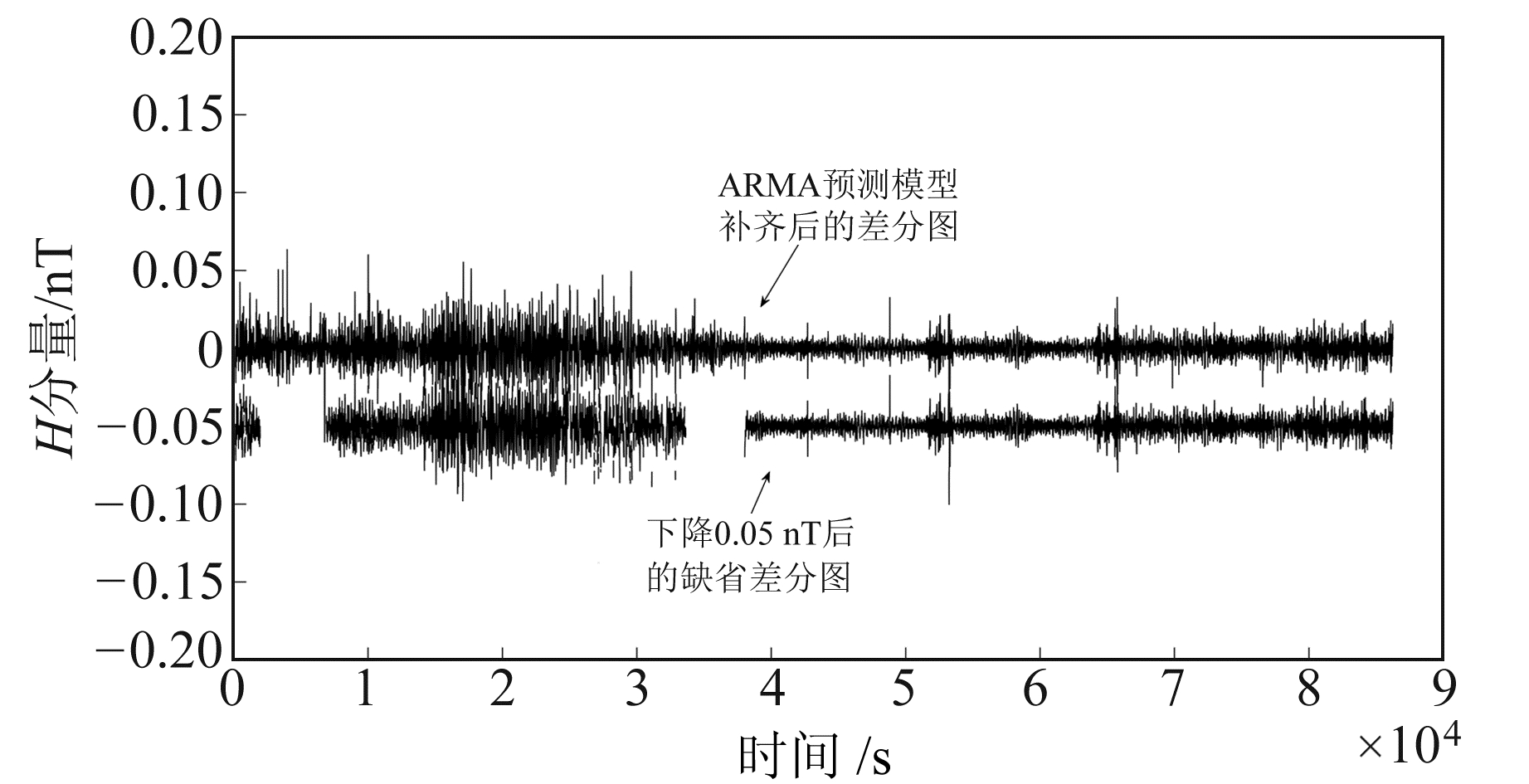
|
图 6 ARMA模型修补效果 Fig. 6 ARMA model supplement diagram |
将补齐后的差值与调整后的拟合结果叠加,便可得到完整曲线,如图 7所示,这样补齐的数据既能保证地磁数据的曲线形态,也能保留其自身特征,可认为是符合精度要求的。从图 7还可看出,修补数据的干扰较完整数据大,这是因为该时段本就受人为干扰,修补的数据是符合实际结果的。为方便对比,将修补的数据减小0.2 nT。
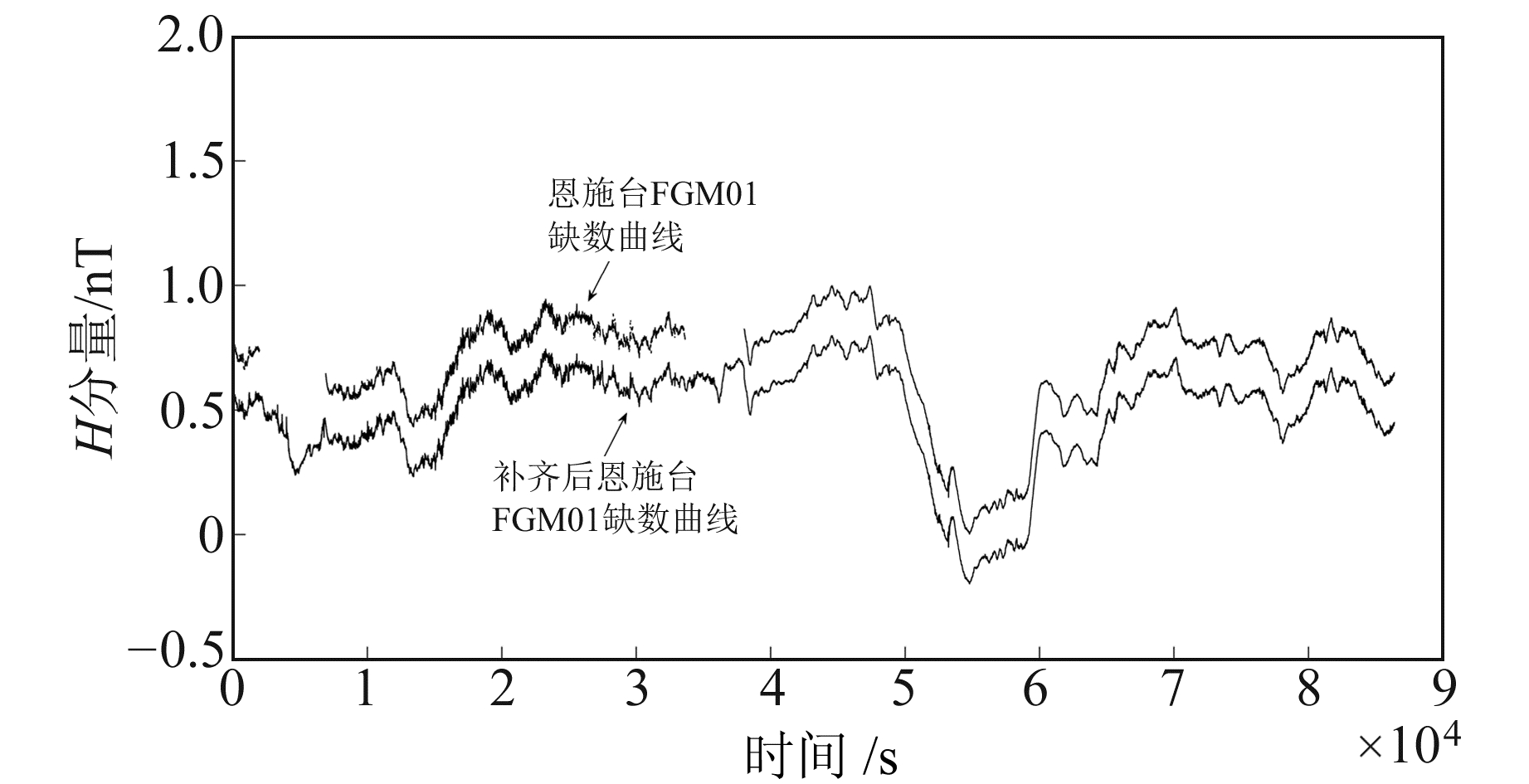
|
图 7 修补数据曲线与缺数曲线对比 Fig. 7 Comparison chart of complemented curve and missing curve |
从图 8可以看出,修补的数据既保证了原有数据的完整性,又保留了地磁数据的特性,验证了本文策略的可靠性。

|
图 8 修补后恩施台FGM01地磁数据与其他台站秒数据对比 Fig. 8 Comparison of Enshi FGM01 data and other second data of other stations after supplement |
为进一步验证本文策略的适用性与可靠性,选取2021-06-15恩施台FGM01地磁Z分量数据作为实验对象,将中间1 h数据人为去掉,其原始数据(减小2 nT)与修补数据(减小5 nT)的对比及残差如图 9所示。
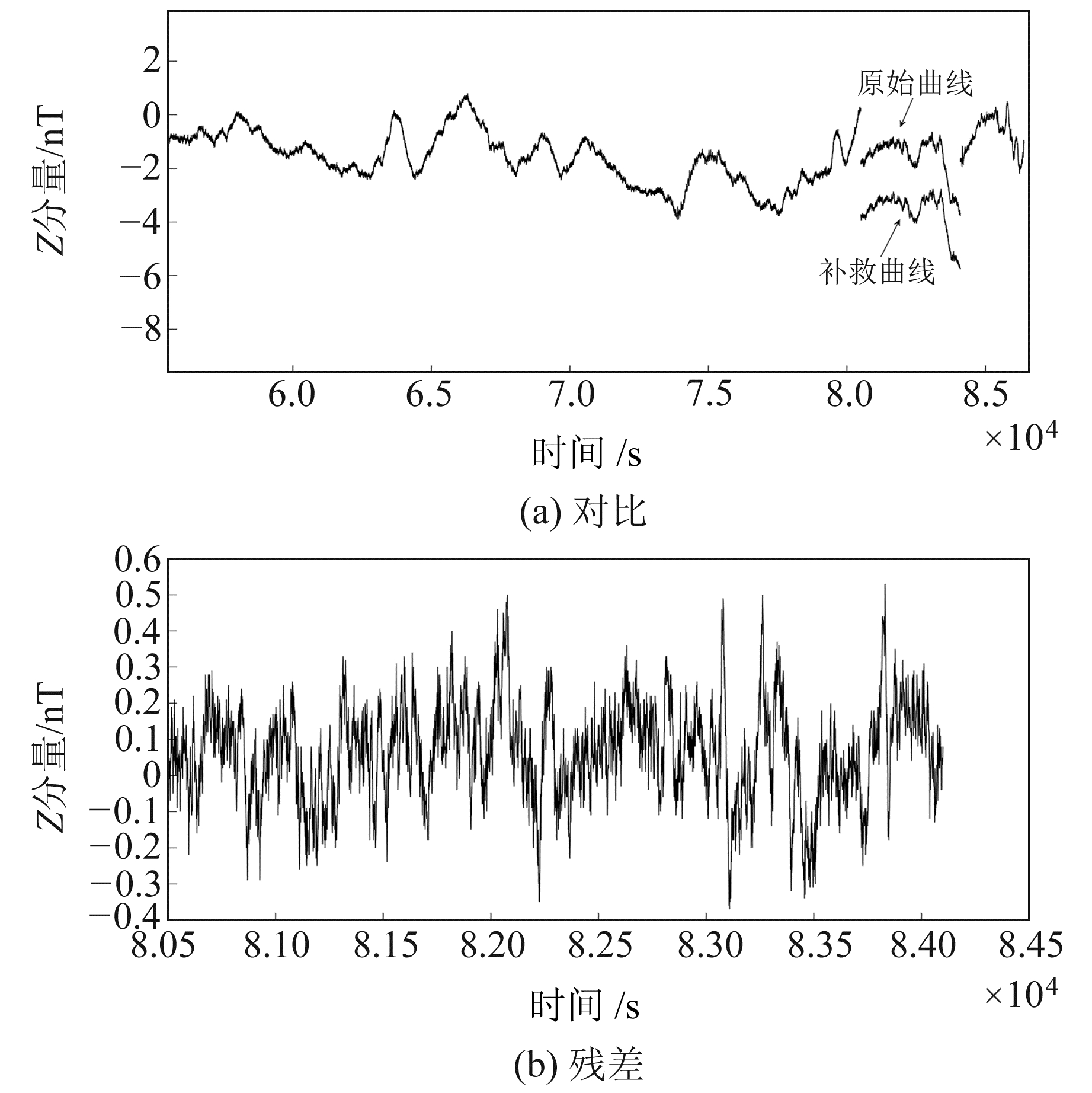
|
图 9 原始数据与修补数据曲线对比及对应残差 Fig. 9 Curve comparison and corresponding residuals between original data and patched data |
由图 9可以看出,修补数据与原始数据在形态与细节上几乎一致,与真实值之差基本在0.2 nT范围内,属于背景噪声,可认为是准确的。但随着时间的推移,修补数据与真实值之间的差异越来越大,说明该修补模型仅适用于对短期数据的修补,不适合大面积补数。
3 结语本文基于素描的思路,提出一种新的地磁秒数据修补策略,以相似度高的地磁数据作轮廓,结合ARMA模型进行细节填充,从而完成对地磁秒数据的修补。具体步骤如下:1)对地磁秒数据进行预处理,依据格拉布期准则剔除突跳点并进行归一化处理,以消除量纲;2)从数据库中寻找相似度高的地磁秒数据作为轮廓依托,抽取拟合曲线;3)对拟合曲线分解出的波形进行参数调整,利用调整后的曲线拟合缺省数据;4)将调整后的拟合曲线与缺数数据的差值平稳化,便于ARMA模型进行预测;5)用ARMA模型补齐缺失差值,然后叠加调整后的拟合数据,便可得到修补后的数据。
由于ARMA模型不具备长期预测精度,若地磁数据缺失1 d以上,预测得到的值将不准确,因此本文主要针对1 d内缺数作研究。实验结果显示,本文策略可获得较满意的修补效果,为地磁秒数据补齐策略提供了新的思路。
| [1] |
姚休义. 地磁台站观测异常识别与数据重构技术研究[D]. 北京: 中国地震局地球物理研究所, 2015 (Yao Xiuyi. Method of Artificial Electromagnetic Disturbances Identification and Data Reconstruction[D]. Beijing: Institute of Geophysics, CEA, 2015)
(  0) 0) |
| [2] |
孙海军. 地磁相对记录的两种补缺方法[J]. 内陆地震, 2004, 18(1): 84-89 (Sun Haijun. Two Supplement Methods of Relative Recording about Geomagnetism[J]. Inland Earthquake, 2004, 18(1): 84-89)
(  0) 0) |
| [3] |
夏立玲, 朱跃龙. 水环境数据缺失处理方法之优化研究[J]. 水电能源科学, 2018, 36(4): 158-161 (Xia Liling, Zhu Yuelong. Research on Approach Optimization of Missing Water-Quality Data[J]. Water Resources and Power, 2018, 36(4): 158-161)
(  0) 0) |
| [4] |
荣蓉, 赵丽妍, 韩曙光. 基于傅里叶级数拟合的女装图案流行趋势预测[J]. 浙江理工大学学报: 社会科学版, 2018, 40(2): 125-135 (Rong Rong, Zhao Liyan, Han Shuguang. Pattern Trend Forecast for Women's Wear Based on Fourier Series Fitting[J]. Journal of Zhejiang Sci-Tech University: Social Sciences Edition, 2018, 40(2): 125-135)
(  0) 0) |
| [5] |
黄激珊. ARMA预测模型和平滑ARMA预测模型的比较研究: 基于贵州省1950-2011年的年度CPI环比数据[J]. 现代经济信息, 2012(5): 324 (Huang Jishan. Comparative Study on ARMA Prediction Model and Smooth ARMA Prediction Model: Based on the Annual CPI Month on Month Data of Guizhou Province from 1950 to 2011[J]. Modern Economic Information, 2012(5): 324)
(  0) 0) |
| [6] |
邓自立, 王欣, 高媛. 建模与估计[M]. 北京: 科学出版社, 2007 (Deng Zili, Wang Xin, Gao Yuan. Modeing and Estimation[M]. Beijing: Science Press, 2007)
(  0) 0) |
2. Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China;
3. Shiyan Civil Air Defense Office, 76 South-Jianghan Road, Shiyan 442000, China
 2022, Vol. 42
2022, Vol. 42

