2. 中国地震局工程力学研究所,哈尔滨市学府路29号,150080
地壳内的介质具有不均匀性和各向异性[1],其波质点的概率密度呈椭球分布,被称为偏振椭球模型,并表现出核心密集、外层松散的特点。在三维空间,按时间序列绘制的位移记录散点动画就是波质点振动的轨迹[2],而位移记录的三维静态散点图物理意义十分明确,旨在反映波质点在空间的概率密度分布,不反映波质点出现的先后顺序。
在以偏振椭球模型和加速度记录三分量的协方差矩阵为桥梁计算震中方位角的研究中,美国与中国的学者习惯用地震记录的三分量数组计算震中方位角;而日本的学者则习惯用地震记录的水平两分量计算震中方位角或震中方位角的补角[3-4],再结合垂直分量进行校正。另外,对协方差矩阵求解震中方位角数理过程的研究较少,大多在输入地震记录后直接用协方差矩阵或径向能量法求解方位角,没有论证协方差矩阵的数理过程,本文对此进行补充。
1 计算原理与数据准备地震波在均匀的各向同性介质中传播时,根据胡克定律:
| $ F=-k \cdot \Delta x $ | (1) |
质点的加速度方向(受力方向)总是跟质点的位移方向相反。质点的加速度方向与位移方向有2种情况:1)当质点的运动方向背离平衡位置时,加速度方向与位移方向相同;2)当质点的运动方向指向平衡位置时,加速度方向与位移方向相反。
在这样的各向同性介质中,P波和S波都没有偏振现象,其质点呈线性往复运动[1],质点的轨迹痕迹是一条线段AB,即理想轨迹线,且P波质点在任意时刻的位移、速度、加速度矢量与P波的波射线必共线,表现出四线合一的特点,这是求解震中方位角的理论依据。
本文选用日本强震基岩观测网CHBH强震台的加速度数据,台站坐标为140.023 8°E、35.793 4°N,高程为-2 277 m,仪器采样率为100 Hz,记录持时187 s,震中距为150.494 1 km,震中方位角为70.983 7°,发震时间为2008-05-08 01:45:00,震中位于141.610°E、36.224°N,震级为7.0级,震源深度为51 km。以加速度三分量的时程数据为三维坐标系的三轴坐标,可以绘出以原点O为起点的加速度矢量端点密度分布图。与位移三分量时程数据的三维散点图不同,这类图不表示波质点的轨迹状态,而反映波质点的受力方向。由P波四线合一的性质可知,这些散点的线性回归方程对应的直线必然无限趋近于震中。
2 P波质点加速度矢量的端点概率密度研究认为,利用加速度地震记录在P波到达前0.6 s时求出的震中方位角误差最小[3-4];也有学者发现,利用加速度地震记录在P波到达前0.2 s时求出的震中方位角误差最小[5]。由于前2 s的采样点太少,本文取0.3~2.7 s的窗口绘制散点图,以研究P波的线性特征。
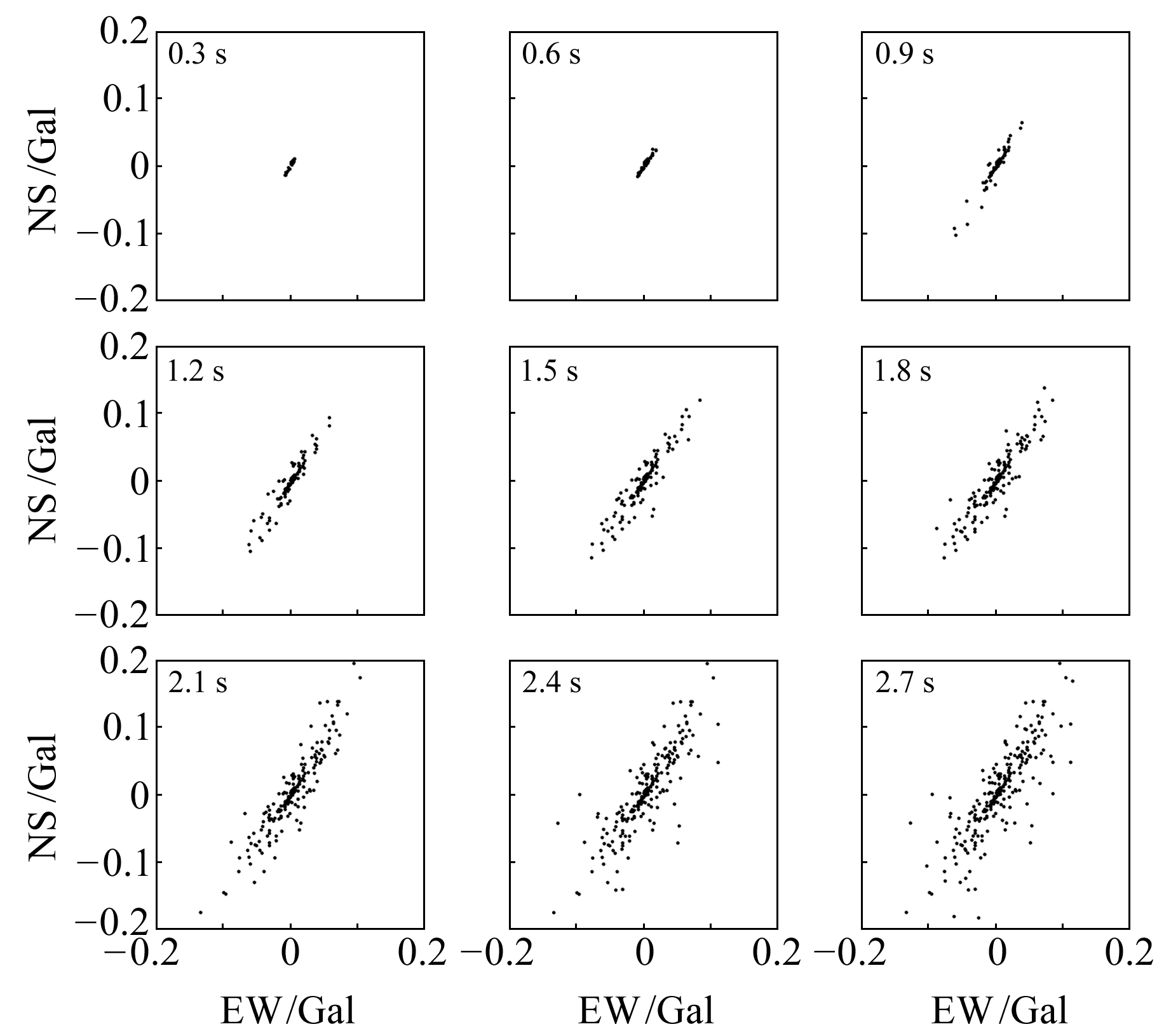
图 1采用CHBH台井下三分量地震记录加速度数据来表现以原点O为起点的P波质点加速度矢量的端点概率密度分布。结果表明,初至P波到达后的第0.6 s,窗口内波质点的受力矢量方向几乎共线;0.9~1.5 s窗口内质点的受力矢量出现法向分量,但概率密度呈椭球形展布;1.8~2.1 s窗口内质点受力矢量的法向分量开始向理想轨迹线AB的两端扩散;2.1~2.7 s窗口内质点受力矢量的法向分量不仅向理想轨迹线AB的两端扩散,而且矢量范数剧烈增加,范数值甚至达到径向分量的一半,使得概率密度分布的外轮廓呈椭圆形。
|
图 1 以原点O为起点的P波质点加速度矢量的端点概率密度分布 Fig. 1 Probability density distribution of the end point of the acceleration vector of the P-wave with the origin O as the starting point |
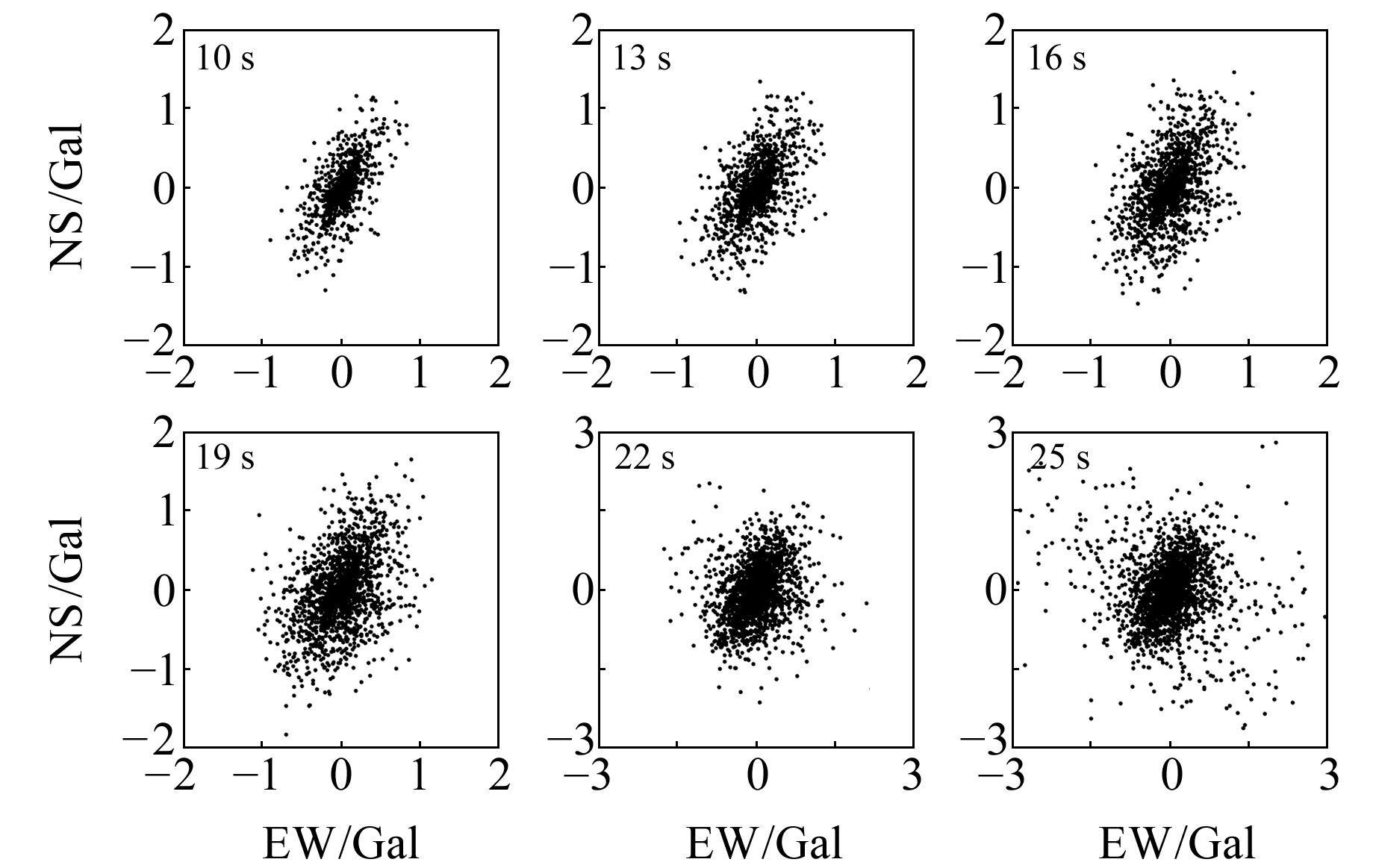
图 2也采用CHBH台井下三分量地震记录加速度数据,来表现以原点O为起点的P波到达后第10~25 s质点加速度矢量的端点概率密度分布。注意到图 2的坐标轴刻度范围扩大到图 1的10倍以上,表明在地震波到达后10~25 s内波质点所受的外力迅速增大,达到了图 1的10倍左右。由图 2可知,在地震波到达后10~16 s,窗口内波质点的受力矢量端点概率密度呈饱满的椭圆形分布;19 s后开始演变为圆形,并逐步失去线性特征;25 s后质点的受力矢量法向分量的范数超过径向分量,表明S波已经到达。
|
图 2 以原点O为起点的P波第10~25 s质点加速度矢量的端点概率密度分布 Fig. 2 Probability density distribution of the end point of the acceleration vector of the particle in the 10 to 25 s of the P-wave starting from the origin O |
将初至P波的时间窗口划分为5 s、10 s、15 s,再分别检验3个窗口内P波NS、EW及UD分量的概率密度分布,其中每个窗口有3个分量,共9组数据样本,每个样本的期望μ和方差σ如表 1所示。
|
|
表 1 加速度三分量记录的期望μ与标准差σ Tab. 1 Expectation of three component acceleration recording μ and standard deviation σ |
利用假设检验方法判断地磁低点时间是否服从高斯分布。设某一随机变量x(-3<x < 3)服从高斯分布,那么x落入[a, b]区间的概率为:
| $ \begin{gathered} p(a<x<b)=\frac{1}{\sqrt{2 \pi \sigma}} \int_{a}^{b} \mathrm{e}^{\frac{(x-\mu)^{2}}{2 \sigma^{2}}} \mathrm{~d} x, \\ a \geqslant-3, b \leqslant 3 \end{gathered} $ | (2) |
将表 1中各组样本的期望μ与标准差σ代入公式a=μ-σ、b=μ+σ中,求出a、b,再将a、b代入式(2)求出各组样本在(μ-σ,μ+σ)区间内的概率,即p(μ-σ<x<μ+σ)值。若这些值与0.682 69偏离较大,说明该数据一定不服从高斯分布;若偏离较小或相等,说明这组样本可能服从高斯分布。计算发现,表 1中各组样本的p值均约等于0.682 689 492 137 086…,这是加速度记录服从高斯分布的必要条件,但非充分条件[6],还需对样本的频率分布直方图进行考察。
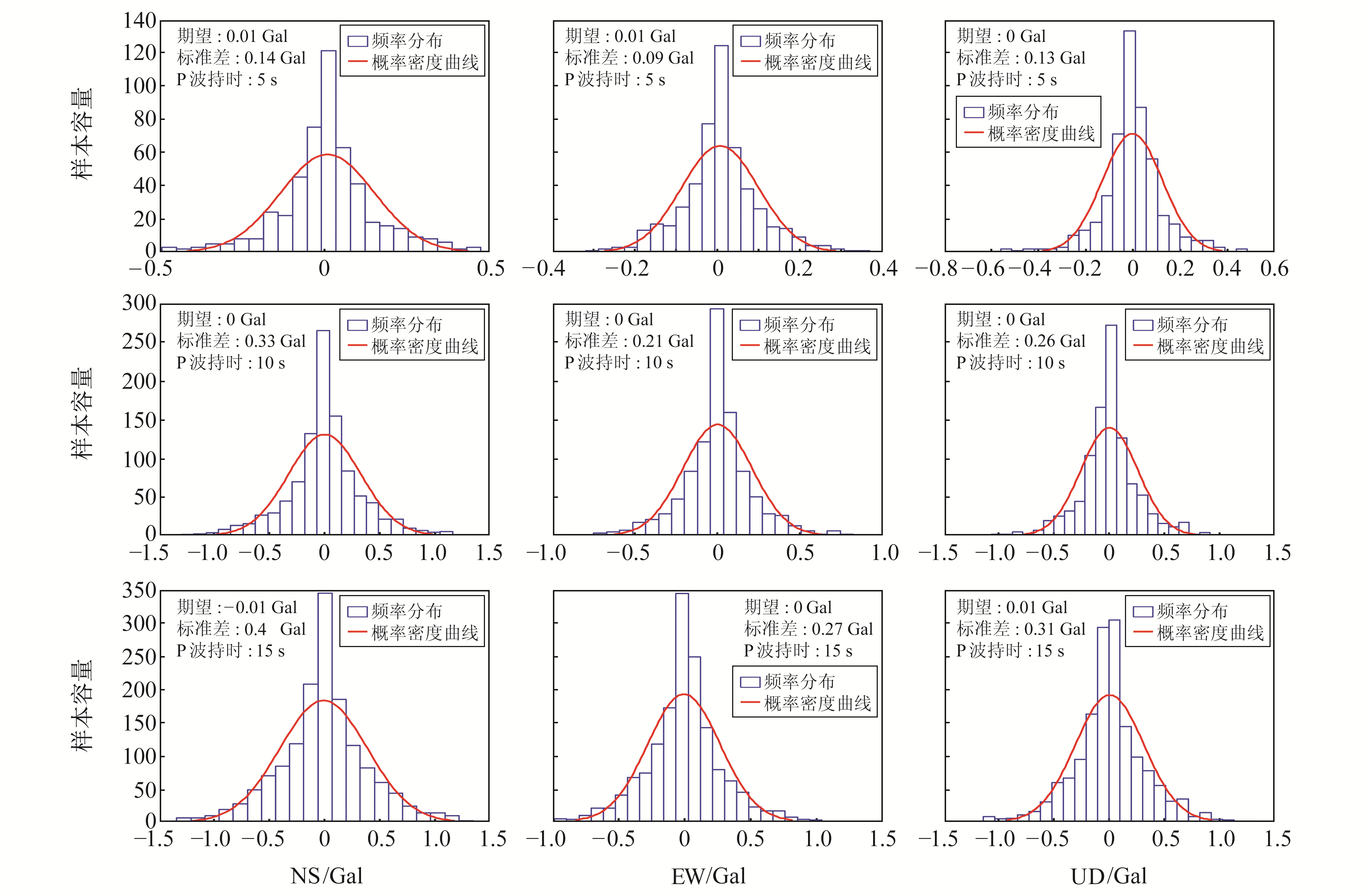
频率分布直方图能直观反映加速度记录的幅值落在任意区间的频次,其概率密度曲线能直观反映加速度幅值在连续区间上的频次变化趋势,对认识加速度记录的分布规律具有重要意义,同时也是判断加速度记录是否服从高斯分布的重要依据。从图 3可以看出,频率分布直方图呈钟形分布,其外轮廓与相同期望、方差的高斯密度曲线较为接近,这与加速度地震记录服从高斯分布的预期一致。图 3直观地反映出初至P波在持续时间不同的窗口中幅值的概率密度分布差异很大,窗口越短加速度记录幅值的标准差越小。
|
图 3 加速度三分量记录的频率分布直方图和与其相同期望、方差的高斯概率密度曲线 Fig. 3 Frequency distribution histogram of three component acceleration record and Gaussian probability density curve with the same expectation and variance |
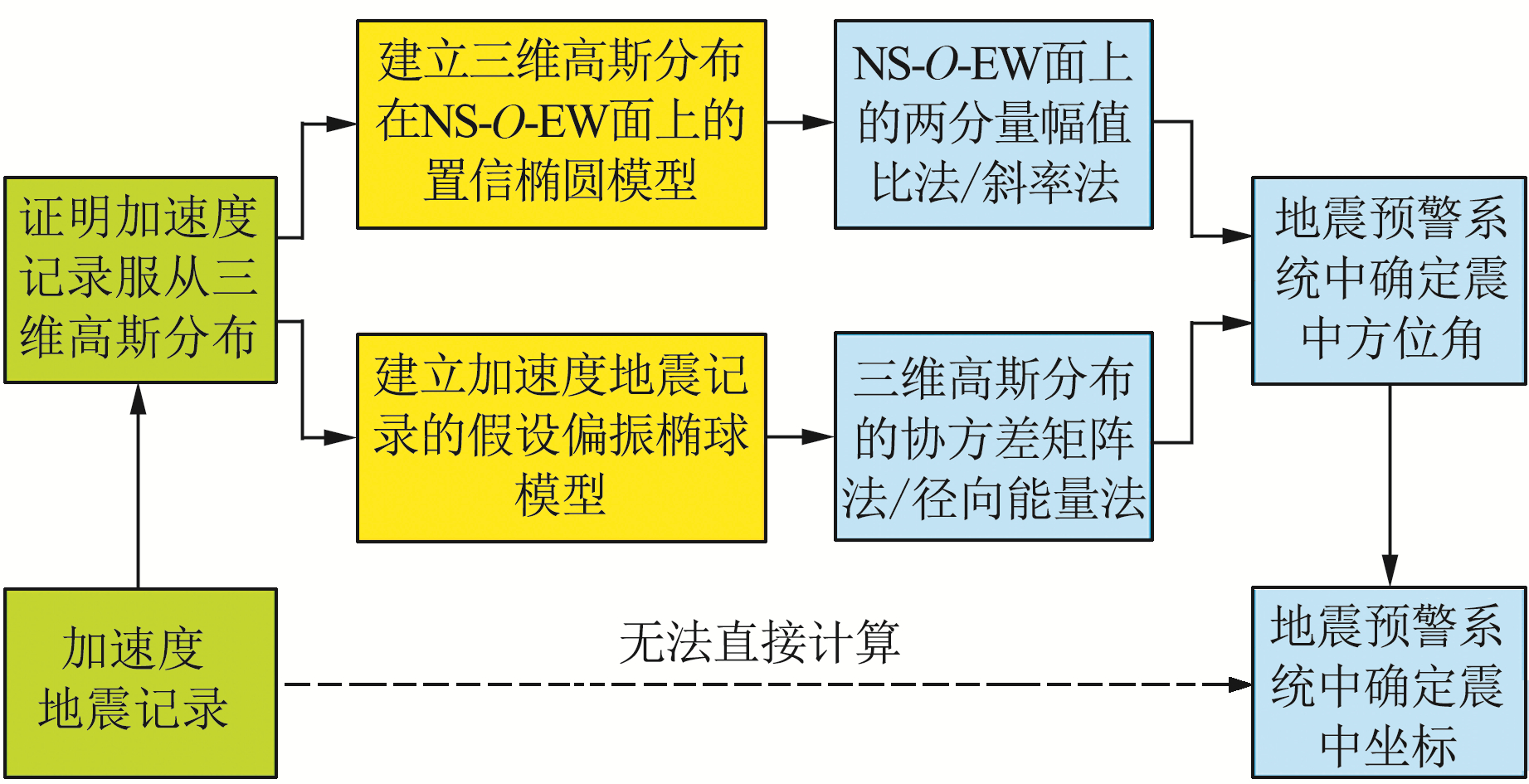
在已获得加速度记录但未获得位移记录的前提下,要求出偏振椭球模型的长轴、次长轴、短轴的矢量坐标,就必须先证明加速度记录的P波质点随机震动的受力矢量服从三维高斯分布。三维高斯分布在空间上的置信区域是一个概率密度椭球体Σ(类似于电子云模型),即离几何中心越近,P波质点的加速度矢量端点出现的几率越高(图 1和2)。根据三维高斯分布的定义,概率密度椭球体Σ三轴的长度、方向及椭球的旋转角度可通过分解加速度记录的协方差矩阵得到。根据P波四线合一的性质,偏振椭球长轴的延长线必经过震中,可通过求解偏振椭球的长轴参数求出震中方位角(图 4)。
|
图 4 三维高斯分布在快速计算震中方位角中的桥梁作用 Fig. 4 The role of 3D Gaussian distribution in fast calculation of epicenter azimuth |
加速度记录偏振椭球的长轴可看作是加速度矢量的主矢[3-4],次长轴和短轴可看作是加速度矢量法向偏差的主矢,那么加速度记录的偏振椭球就是质点受力矢量端点的集合。多数随机误差都服从高斯分布,不失一般性,P波质点在三维空间中的振动幅值变化服从三维高斯分布。如果P波和S波在地球的不均匀介质中传播,长周期地震记录的波质点运动也呈线性特征;而短周期地震记录的波质点运动在平面上呈现出更椭圆或无规律的轨迹;在更短周期的高频信号中,波质点运动显现出无规律的轨迹[1]。对同一地震记录作长周期滤波后,保留的短周期记录的线性会显著下降。
简言之,波质点运动有2个特点:1)波质点运动的线性规律会随着介质的不均匀性和各向异性的增强而下降;2)波质点运动的线性规律会随着地震信号频率的升高而下降,下降后呈现出更椭圆或无规律的轨迹,从而在平面内呈现出更椭圆、在空间内呈现出椭球状的偏振椭球。实际上,P波在不均匀介质中传播时速度记录也有对应的偏振椭球模型,但这种椭球模型不能反映出波质点的运动轨迹,仅能看作是以原点O为起点的速度矢量端点的概率密度分布。
5 结语对协方差矩阵进行分析能够计算出偏振椭球的几何参数,其原理是将波质点的运动看作结构随机的振动,将质点偏离线性运动轨迹线的距离看作随机误差,这种随机误差恰好服从三维高斯分布,从而用高斯分布的特性(置信椭圆)求出偏振椭球的几何参数。主要结论如下:
1) P波的先至性、纯净性、强线性使其能很好地满足地震预警快速反应的特点,初至P波拥有其他地震波不具备的四线合一性质。
2) 加速度记录不能像位移记录一样表现质点的运动轨迹,但由于P波的四线合一性质,使得加速度记录也可用来求取震中方位角。
3) 加速度记录的三分量各自独立地服从高斯分布,加速度记录整体服从三维高斯分布。
加速度记录服从三维高斯分布在快速地震定位中有着非常重要的应用。根据置信椭球的定义,当满足三维高斯分布条件时,利用地震记录三分量的协方差矩阵可计算出偏振椭球的长轴、次长轴和短轴矢量,从而求出震中方位角,该过程完美展示了三维高斯分布的置信椭球、地震记录的协方差矩阵与地震记录的偏振椭球之间的物理关系。
| [1] |
周银兴. 微震事件检测及震相自动识别研究[D]. 北京: 中国地震局地震预测研究所, 2009 (Zhou Yinxing. Research on the Micro-Earthquake Detection and Seismic Phase Automatic Identification[D]. Beijing: Institute of Earthquake Forecasting, CEA, 2009)
(  0) 0) |
| [2] |
黄中玉, 高林, 徐亦呜, 等. 三分量数据的偏振分析及其应用[J]. 石油物探, 1996, 35(2): 9-16 (Huang Zhongyu, Gao Lin, Xu Yiwu, et al. The Analysis of Polarization in Three Component Seismic Data and Its Application[J]. Geophysical Prospecting for Petrole, 1996, 35(2): 9-16)
(  0) 0) |
| [3] |
野田俊太, 山本俊六, 佐藤新二. 早期地震検知における地震諸元推定方法の精度および即時性向上[J]. 铁道公研报告, 2011, 25(7): 7-12 (Noda Shunta, Yamamoto Shunroku, Sato Shinji. Improvement of Earthquake-Parameter Estimation for Earthquake Early Warning[J]. RTRI Report, 2011, 25(7): 7-12)
(  0) 0) |
| [4] |
Noda S, Yamamoto S, Sato S. New Method for Estimating Earthquake Parameters for Earthquake Early Warning[J]. Quarterly Report of RTRI, 2012, 53(2): 102-106
(  0) 0) |
| [5] |
马亮. 用于地震预警的单台定位技术研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2013 (Ma Liang. Research on Earthquake Location Using Single Station for Earthquake Early Warning[D]. Harbin: Institute of Engineering Mechanics, CEA, 2013)
(  0) 0) |
| [6] |
卢建旗. 多道面波分析方法及其应用研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2013 (Lu Jianqi. Multi-Channel Analysis of Surface Wave and Its Utility[D]. Harbin: Institute of Engineering Mechanics, CEA, 2013)
(  0) 0) |
2. Institute of Engineering Mechanics, CEA, 29 Xuefu Road, Harbin 150080, China
 2022, Vol. 42
2022, Vol. 42

