在GNSS变形监测领域，由于卫星信号在传播过程中不可避免地受变形体或其周围环境干扰，会出现多路径效应。多路径效应无法通过双差方式消除，且会随监测站周围环境的变化而变化，严重影响GNSS监测的精度。另外，由于监测站与周围环境均相对稳定，多路径效应表现出明显的周期性特征^[1]，其与真实变形信号混杂在一起，严重干扰观测人员对变形体真实运动状态的判断。因此，如何有效提取多路径效应及削弱多路径效应的影响是GNSS变形监测领域需要解决的重点问题，许多学者在相关方面都进行过研究^[2-5]。最小二乘谐波估计最早由Amiri-Simkooei等^[6-7]于2007年提出，并将其应用于提取GNSS坐标时间序列中的周期项信号和海平面高程时间序列中的周期项信号。最小二乘谐波估计根据所用数据的不同可分为单元谐波估计和多元谐波估计，并且作为傅里叶变换的扩展，其既不要求数据均匀分布，对周期项信号的波长也没有整数周的要求，很适用于对变形监测GNSS坐标时间序列中多路径效应的提取。

本文主要研究最小二乘谐波估计在提取GNSS坐标时间序列中多路径效应方面的效果，并对比单元谐波估计和多元谐波估计的优劣。考虑到多路径效应常常与变形信号混杂，本文选取GNSS坐标时间序列仅受白噪声和多路径效应影响的稳定监测站数据，根据剔除多路径效应后GNSS坐标时间序列的稳定性，可直观地评价不同方法提取多路径效应的效果。

1 分析方法

假设存在以下线性观测方程：

$ E(\mathit{\boldsymbol{y}}) = \mathit{\boldsymbol{Ax}}, D(\mathit{\boldsymbol{y}}) = {\mathit{\boldsymbol{Q}}_y} $

(1)

式中，E(*)、D(*)分别代表期望与方差；y为维度为n×1的观测值向量，n为观测值的个数；x为维度为m×1的参数向量，m为参数的个数；A为参数向量的系数矩阵，维度为n×m；Q_y为观测值向量对应方差的协方差矩阵，维度为m×m。由于模型中存在未知的周期项信号，矩阵A是未知的。最小二乘谐波估计将周期项信号以谐波函数的形式考虑在数学模型中，并通过参数显著性检验来确定最优矩阵A。

1.1 单元谐波估计

根据傅里叶变换理论，对于任意给定的时间序列，可分解为一系列的正弦波a_kcosω_kt+b_ksinω_kt, k=1, …, q，因此式(1)可写为：

$ E(\mathit{\boldsymbol{y}}) = \mathit{\boldsymbol{Ax}} + \sum\limits_{k = 1}^q {{\mathit{\boldsymbol{A}}_k}} {\mathit{\boldsymbol{x}}_k}, D(\mathit{\boldsymbol{y}}) = {\mathit{\boldsymbol{Q}}_y} $

(2)

其中，

$ {\mathit{\boldsymbol{A}}_k} = \left[ {\begin{array}{*{20}{c}} {\cos {\omega _k}{t_1}}&{\sin {\omega _k}{t_1}}\\ \cdots & \cdots \\ {\cos {\omega _k}{t_n}}&{\sin {\omega _k}{t_n}} \end{array}} \right], {\mathit{\boldsymbol{x}}_k} = \left[ {\begin{array}{*{20}{l}} {{a_k}}\\ {{b_k}} \end{array}} \right], k = 1, \cdots , q $

确定每个ω_k及q大小的具体方法为：作原假设${H_0}:E(\mathit{\boldsymbol{y}}) = \mathit{\boldsymbol{Ax}} + \sum\limits_{k = 1}^{i - 1} {{\mathit{\boldsymbol{A}}_k}} {\mathit{\boldsymbol{x}}_k}$, 备选假设$E(\mathit{\boldsymbol{y}}) = \mathit{\boldsymbol{Ax}} + \sum\limits_{k = 1}^i {{\mathit{\boldsymbol{A}}_k}} {\mathit{\boldsymbol{x}}_k}$。

第1步，寻找可能满足条件的ω_i。寻找ω_i等价于确定谱密度$P\left( {{\omega _i}} \right) = \mathit{\boldsymbol{\widehat e}}_0^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}{\mathit{\boldsymbol{A}}_i}{\left( {\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}P_A^ \bot {\mathit{\boldsymbol{A}}_i}} \right)^{ - 1}}\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}{\mathit{\boldsymbol{\widehat e}}_0}, {\mathit{\boldsymbol{\widehat e}}_0} = P_A^ \bot \mathit{\boldsymbol{y}}, P_A^ \bot = \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}{\left( {\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}{\mathit{\boldsymbol{A}}_i}} \right)^{ - 1}}\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}$在何处取得最大值^[5]。借助于谱密度P(ω_i)的图像可以很好地求解该最大化问题^[6-7]：首先根据${\omega _k} = 2\pi /{t_k}, {t_{k + 1}} = {t_k}\left( {1 + \frac{{\alpha {t_k}}}{t}} \right), \alpha = 0.1, k = 1, 2, \cdots $生成所有可能的ω_i集合，其中t为时间序列的总时长，t₁对应该时间序列中的最大周期项信号；接着计算出集合中每个ω_i对应的P(ω_i)值，绘制P(ω_i)相对于ω_i的图像，如果图像中P(ω_i)最大值在ω_m处取得，说明ω_m就是此时满足条件的ω_i。

第2步，对寻找到的ω_i进行显著性检验。首先构造检验量${T_2} = \mathit{\boldsymbol{\widehat e}}_0^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}{\mathit{\boldsymbol{A}}_i}{\left( {\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}P_A^ \bot {\mathit{\boldsymbol{A}}_i}} \right)^{ - 1}}\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}{\mathit{\boldsymbol{\hat e}}_0}, {T_2} \sim {\chi ^2}(2, 0)$ ^[8-9]，如果T₂能够通过显著性检验，则拒绝原假设，接受备选假设，即认为备选假设中多出来的ω_i符合条件。将i加1后重复以上假设检验步骤，直至检验量T₂不能通过显著性检验，此时认为所有的周期项信号都被找到。

1.2 多元谐波估计

多元谐波估计作为单元谐波估计的扩展，认为多个时间序列中的周期项信号相同，且每个时间序列中的A也相同，则(2)式可改写为：

$ \begin{array}{*{20}{c}} {E({\mathop{\rm vec}\nolimits} (\mathit{\boldsymbol{Y}})) = \left( {{\mathit{\boldsymbol{I}}_r} \otimes \mathit{\boldsymbol{A}}} \right){\mathop{\rm vec}\nolimits} (\mathit{\boldsymbol{X}}) + }\\ {\sum\limits_{k = 1}^q {\left( {{\mathit{\boldsymbol{I}}_r} \otimes {\mathit{\boldsymbol{A}}_k}} \right)} {\mathop{\rm vec}\nolimits} \left( {{\mathit{\boldsymbol{X}}_k}} \right), D({\mathop{\rm vec}\nolimits} (\mathit{\boldsymbol{Y}})) = \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \otimes {\mathit{\boldsymbol{Q}}_y}} \end{array} $

(3)

式中，vec(·)为向量化算子，⊗代表克罗内克积，r为时间序列的个数，Y为维度为n×r的观测值向量，X为维度为m×r的参数向量，I_r为维度为r×r的单位矩阵，Σ的维度为r×r，其余变量含义同上。多元谐波估计中寻找周期项信号的方式与单元谐波估计相同，只是谱密度P(ω_i)具有不同的形式：${\rm{ }}P\left( {{\omega _i}} \right) = {\mathop{\rm tr}\nolimits} \left( {{{\mathit{\boldsymbol{\widehat E}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}_y^{ - 1}{\mathit{\boldsymbol{A}}_i}{{\left( {\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}P_A^ \bot {\mathit{\boldsymbol{A}}_i}} \right)}^{ - 1}}} \right.\left. {\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}\mathit{\boldsymbol{\widehat E}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{ - 1}}} \right), \mathit{\boldsymbol{\widehat E}} = P_A^ \bot \mathit{\boldsymbol{Y}}, P_A^ \bot = \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}{\left( {\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}{\mathit{\boldsymbol{A}}_i}} \right)^{ - 1}}\mathit{\boldsymbol{A}}_i^{\rm{T}}\mathit{\boldsymbol{Q}}_y^{ - 1}$。检验量T₂也有类似的改动，并且T₂~χ²(2r, 0)。需要强调的是，多元谐波估计要求各个时间序列对应的时间段完全一致。

2 算例分析 2.1 数据来源

本文数据来源于同济大学测绘学院楼顶4个监测点(TJ01、TJ02、TJ03、TJ04)2020-12-01~12-02的监测结果。由于监测点实际上并没有发生位移，因此GNSS坐标时间序列的波动均是由多路径效应和噪声引起的。另外，由于多路径效应受卫星入射角和周围环境共同作用，考虑到这些监测点的距离十分接近，对应于同一卫星的入射角几乎完全一样，因此可认为这些监测点的多路径效应具有相同的周期性特征。各监测点的GNSS坐标时间序列由同济大学自主研发的Ademos高精度监测软件实时解算得到，结果数据的采样间隔为1 min。

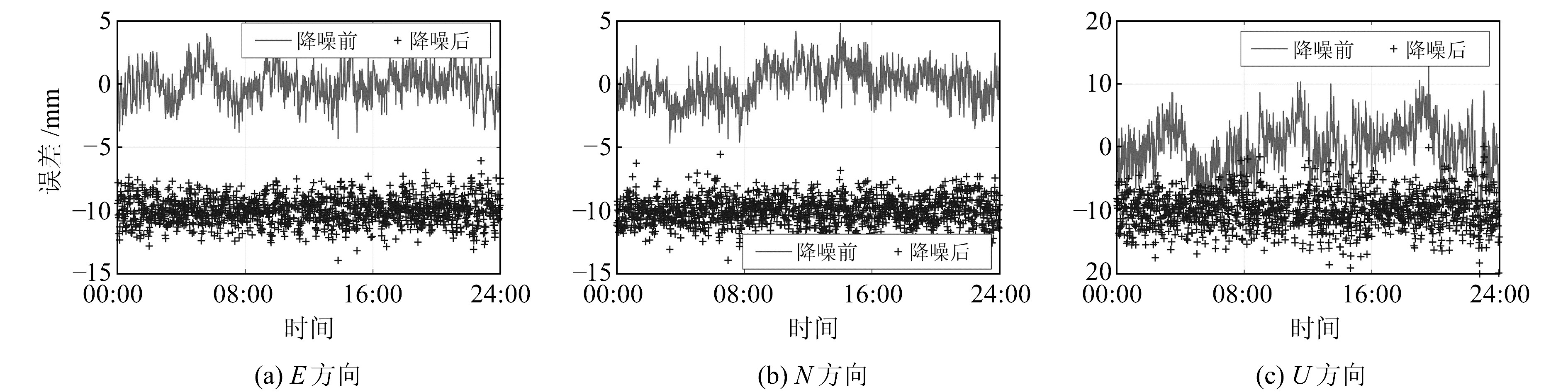
2.2 单元最小二乘谐波估计

以TJ01点为例进行单元最小二乘谐波估计分析，图 1展示了12-01 TJ01点去噪前后坐标时间序列的变化情况。本文利用12-02数据，特意在08:00和18:00附近各模拟了1 h的监测中断，用于进一步分析在数据发生中断的情况下多路径效应的提取效果，并在图 2展示了去噪前后坐标时间序列的变化情况。为便于查看，有意将去噪后的坐标时间序列向下偏移10 cm，图中线条表示去噪前的时间序列，十字点表示去噪后的时间序列。由于监测点实际没有发生位移，原始GNSS坐标时间序列中的不平稳信号均是由多路径效应引起的，利用单元谐波估计提取多路径效应后，GNSS坐标时间序列中明显不再存在不稳定信号，说明多路径效应得到了较好的剔除。将4个测点各自的信息进行统计后发现，经单元谐波估计去噪后4个测点E、N、U三方向的平均剔除率分别为23.85%、25.88%、27.23%(12-01)及23.97%、21.68%、26.73%(12-02)，降噪效果明显。由此可见，单元最小二乘谐波估计方法能有效提取GNSS坐标时间序列中的多路径效应。

2.3 多元最小二乘谐波估计

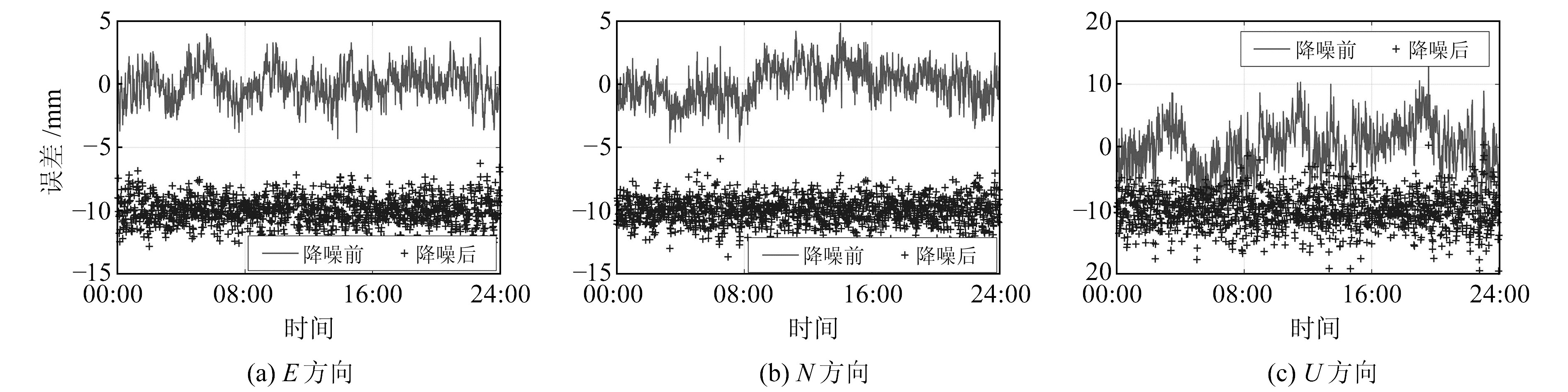
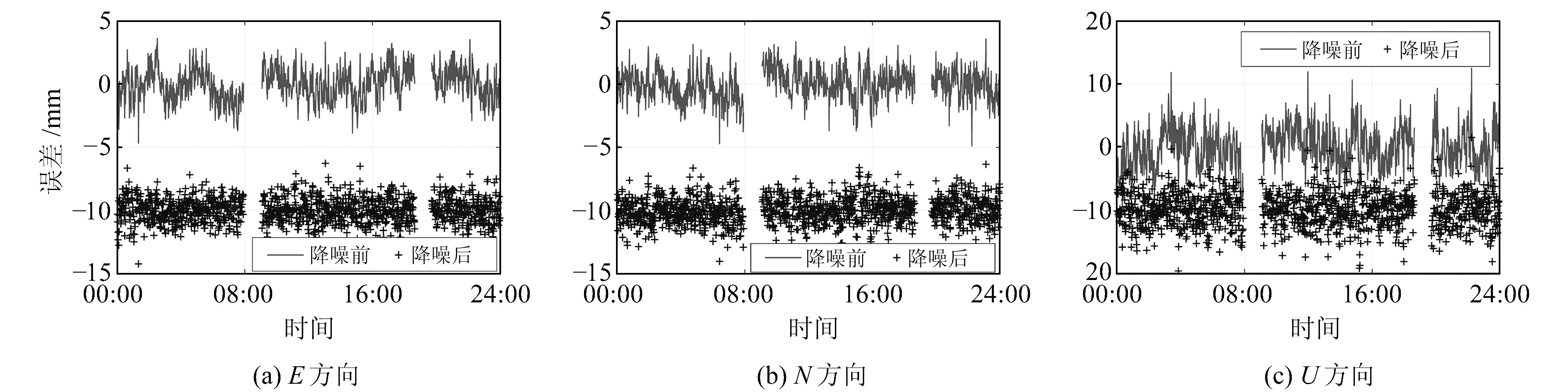
利用TJ01、TJ02、TJ03、TJ04监测点数据进行多元最小二乘谐波估计分析。与单元谐波估计类似，图 3和4分别展示了多元谐波估计12-01与12-02 TJ01点去噪前后的GNSS坐标时间序列，为便于查看，仍将去噪后的GNSS坐标时间序列向下偏移10 cm。原始GNSS坐标时间序列中的不平稳信号经多元谐波估计提取多路径效应后，不再存在不稳定信号，说明多路径效应得到了较好的剔除。将4个测点各自的信息进行统计后发现，经多元谐波估计去噪后4个测点E、N、U三方向的平均剔除率分别为26.52%、28.38%、31.73%(12-01)及21.55%、17.03%、26.68%(12-02)。在未发生数据中断的情况下，相比于单元谐波估计，多元谐波估计的去噪效果更明显，E、N、U三方向的平均剔除率分别有2.67%、2.50%、4.48%的提高。但在数据中断的情况下，单元谐波估计的去噪效果更好，相比于多元谐波估计，单元谐波估计在E、N、U三方向分别有2.42%、4.65%、0.05%的提高。

3 结语

本文首先介绍了2种最小二乘谐波估计方法的数学原理及实现步骤，并通过实验对比分析了单元谐波估计和多元谐波估计对GNSS坐标时间序列中多路径效应的提取能力。结果表明，单元谐波估计和多元谐波估计均可用于提取GNSS坐标时间序列中的多路径效应，不论监测数据是否发生中断，均能获得较好的去噪效果。在监测数据无长时间中断的情况下，多元谐波估计相比于单元谐波估计具有更强的多路径效应提取能力，能更好地提取GNSS坐标时间序列中的多路径效应；但若监测数据存在较长时间的中断，多元谐波估计并不能获得比单元谐波估计更优的提取效果。