区域GPS网因受到地壳运动、气候变化、海潮及大气潮负荷、解算策略等因素的影响,导致连续GPS坐标时间序列中存在时空相关误差,称为共模误差(common mode error, CME),准确提取CME对于研究噪声特征具有重要意义[1]。国内外学者对CME空间滤波方法进行了研究,先后提出带权均值法、主分量分析法(PCA)和Karhunen-Loeve展开法,通过比较这3种方法对GPS坐标时间序列的滤波处理效果发现,PCA提取共模误差的效果更优[2-3]。另外,明锋等[4]通过对比PCA和独立分量分析法(ICA)发现,ICA能够有效提取区域GPS观测网中的CME。
南极地壳运动特征是当今地球动力学研究的热点,南极地区GPS基准站的建设和连续运行可为研究坐标时间序列噪声特征提供数据保障。目前对于GPS坐标时间序列中CME和噪声特征的研究主要集中在南极半岛等区域,而对西南极区域的研究较少。本文利用POLENET计划和南极IGS站的GPS观测数据,对比分析PCA和ICA提取西南极区域GPS坐标时间序列中CME的效果,再采用极大似然估计法定量估计滤波前后各站坐标时间序列在不同组合噪声模型下的噪声含量,并确定最优噪声模型。
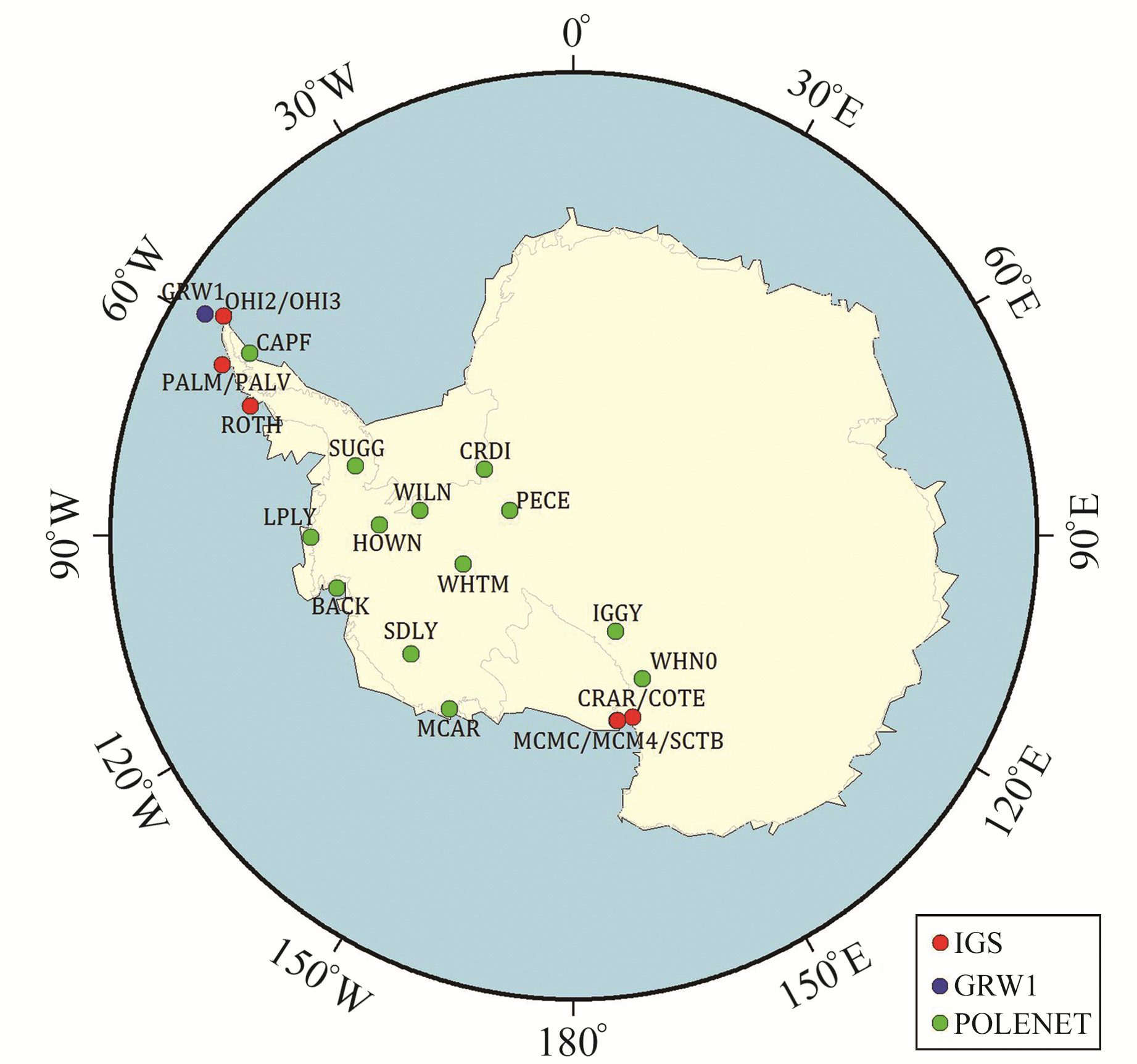
1 GPS站坐标残差时间序列获取 1.1 GPS数据及处理方法选取西南极区域24个GPS连续观测站,测站分布如图 1所示,包括10个IGS站、13个POLENET网站及中国南极长城站(GRW1),数据时间跨度为2010~2018年,测站最短时间跨度为6 a,最长时间跨度为9 a。
|
图 1 西南极24个GPS观测站分布 Fig. 1 Distribution of 24 GPS stations inwest Antarctica region |
采用Bernese 5.2软件双差定位程序对GPS数据进行处理,获得各测站单日解坐标。为将GPS基准站坐标精确统一到ITRF框架下,在解算过程中引入南极大陆其他5个IGS站(SYOG、MAW1、DAV1、CAS1和DUM1) 同时段的观测数据。在数据处理时,采用IGS欧洲定轨中心(CODE)提供的精密星历和地球定向参数等产品,整周模糊度采用无电离层组合模糊度固定(QIF)策略,基线组成方法采用OBS-MAX,卫星截止高度角为7°,采样间隔为30 s,对流层改正采用Saastamoinen模型,映射函数选用VMF3模型,潮汐改正选用FES2014b模型,采用ITRF2014框架。
1.2 残差时间序列预处理受仪器设备故障及外界环境因素影响,GPS坐标时间序列中不可避免地存在数据缺失和粗差,导致分析结果不准确,因此有必要对单日坐标时间序列进行粗差剔除和数据插值。首先采用多通道奇异谱分析和四分位距相结合的方法(MSSA-IQR)[5]进行异常值探测和剔除,然后从各站坐标时间序列中剔除线性趋势和周期项,得到残差时间序列,计算公式为:
| $ \begin{array}{l} {\upsilon _i} = y\left( {{t_i}} \right) - \left( {a + b{t_i} + c\sin \left( {2\pi {t_i}} \right) + d\cos \left( {2\pi {t_i}} \right) + } \right.\\ \left. {e\sin \left( {4\pi {t_i}} \right) + f\cos \left( {4\pi {t_i}} \right) + \sum\limits_{j = 1}^{{n_g}} {{g_i}} H\left( {{t_i} - {T_{gi}}} \right)} \right) \end{array} $ | (1) |
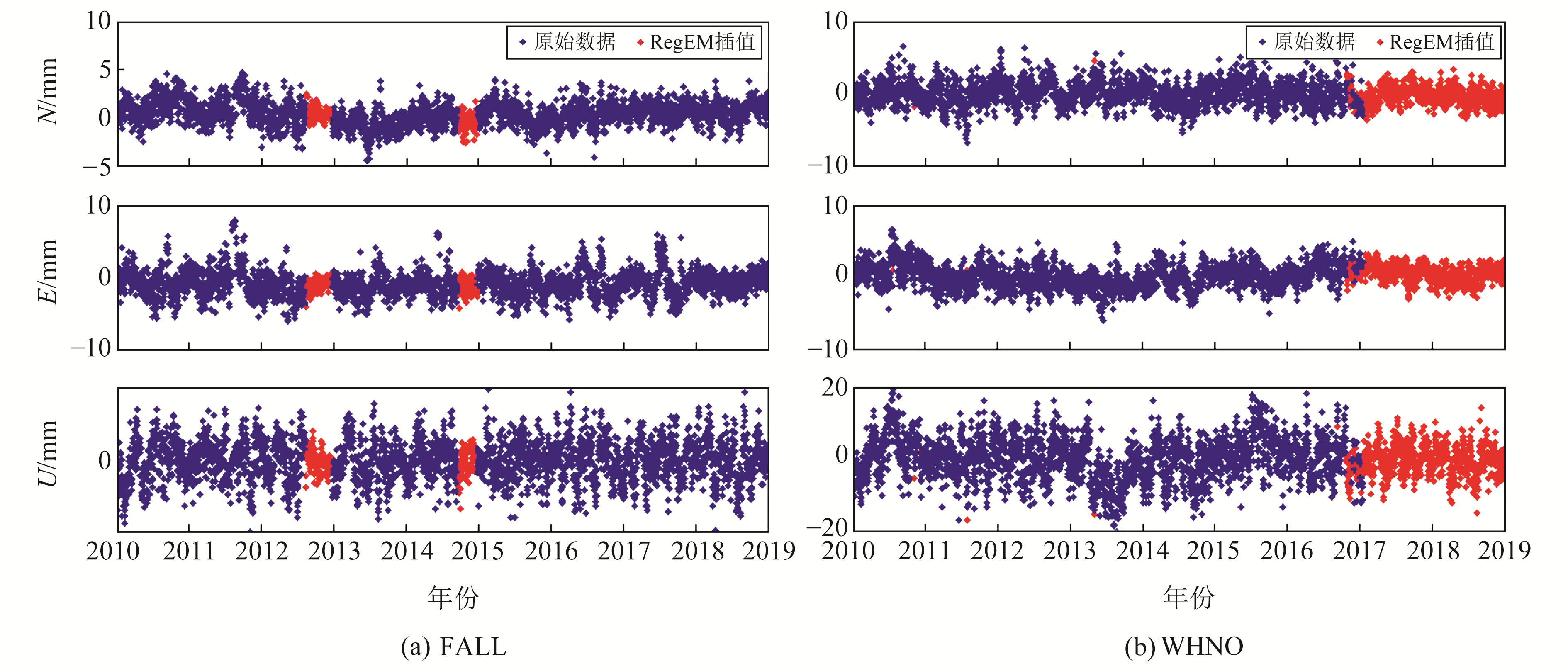
式中,υi为第i个历元的观测残差,y(ti)为测站坐标时间序列,ti为以a为单位的历元时间,a、b为测站坐标的初始历元和线性速度,c、d为时间序列的年周期系数,e、f为半年周期系数,g为历元Tg处的阶跃式偏移量,H为Heaviside阶梯函数。最后采用基于数据驱动的RegEM算法[6]进行残差时间序列插值,RegEM数据插值法可考虑站点坐标时间序列的物理背景,并顾及各站之间的相关性。图 2为RegEM算法插值后的FALL站和WHN0站残差时间序列,图中蓝色为原始数据,红色为RegEM插值结果。
|
图 2 FALL站和WHN0站RegEM插值结果 Fig. 2 The RegEM interpolation results of FALL and WHN0 station |
本文引入KMO检验[7]以验证各站坐标残差时间序列是否适用于PCA和ICA。KMO通过检验各站残差时间序列之间的简单相关系数和偏相关系数来确定数据是否适合进行因子分析,KMO值越接近1,说明变量间的相关性越强,数据越适合进行因子分析;KMO值接近0,则说明数据不适合进行因子分析。结果表明,各站坐标残差时间序列在N、E、U分量上的KMO值分别为0.804、0.824、0.888,通过Barttest检验显著性水平为0.05的结果,数据可用于主成分分析。
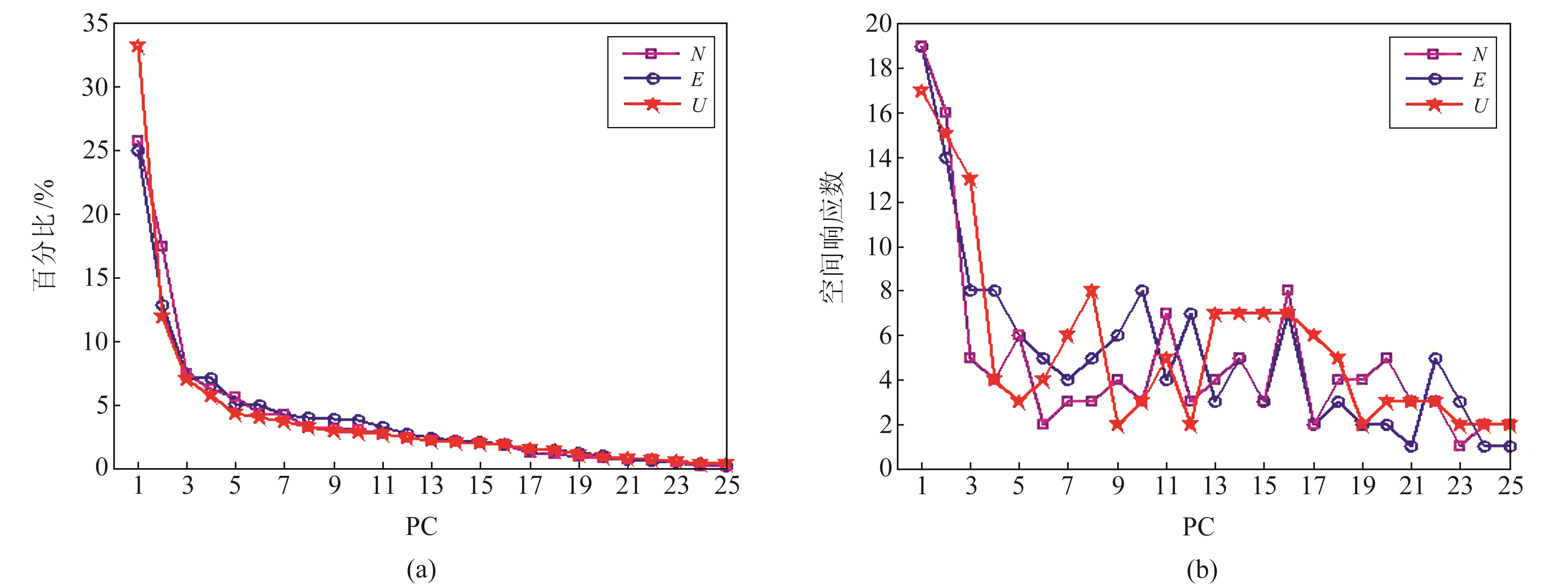
首先利用PCA方法对N、E、U分量的残差时间序列进行滤波处理,得到各主分量(PC)特征值占总特征值的百分比,结果如图 3(a)所示。从图中可以看出,N分量前3个PC的贡献率分别为25.75%、17.50%、7.37%,E分量前3个PC的贡献率分别为24.97%、12.85%、7.20%,U分量前3个PC的贡献率分别为33.24%、11.92%、6.99%。根据Dong等[8]对共模误差的定义,要求参与计算的主分量中至少有50%的测站标准化空间响应超过25%,且该分量的特征值超过所有特征值总和的1%,据此对各主分量的标准化空间响应进行显著性检验,统计各PC的标准化空间响应大于25%的测站数,结果如图 3(b)所示。从图中可以看出,N、E分量第1、2主分量的标准化空间响应大于25%的测站超过50%,即前2个PC可作为区域的CME进行计算,U分量前3个PC满足共模误差要求。
|
图 3 各PC特征值所占百分比和标准化空间响应超过25%的测站数 Fig. 3 The percentage of variance and number of stations with standardized spatial response exceeding 25% derived from PC |
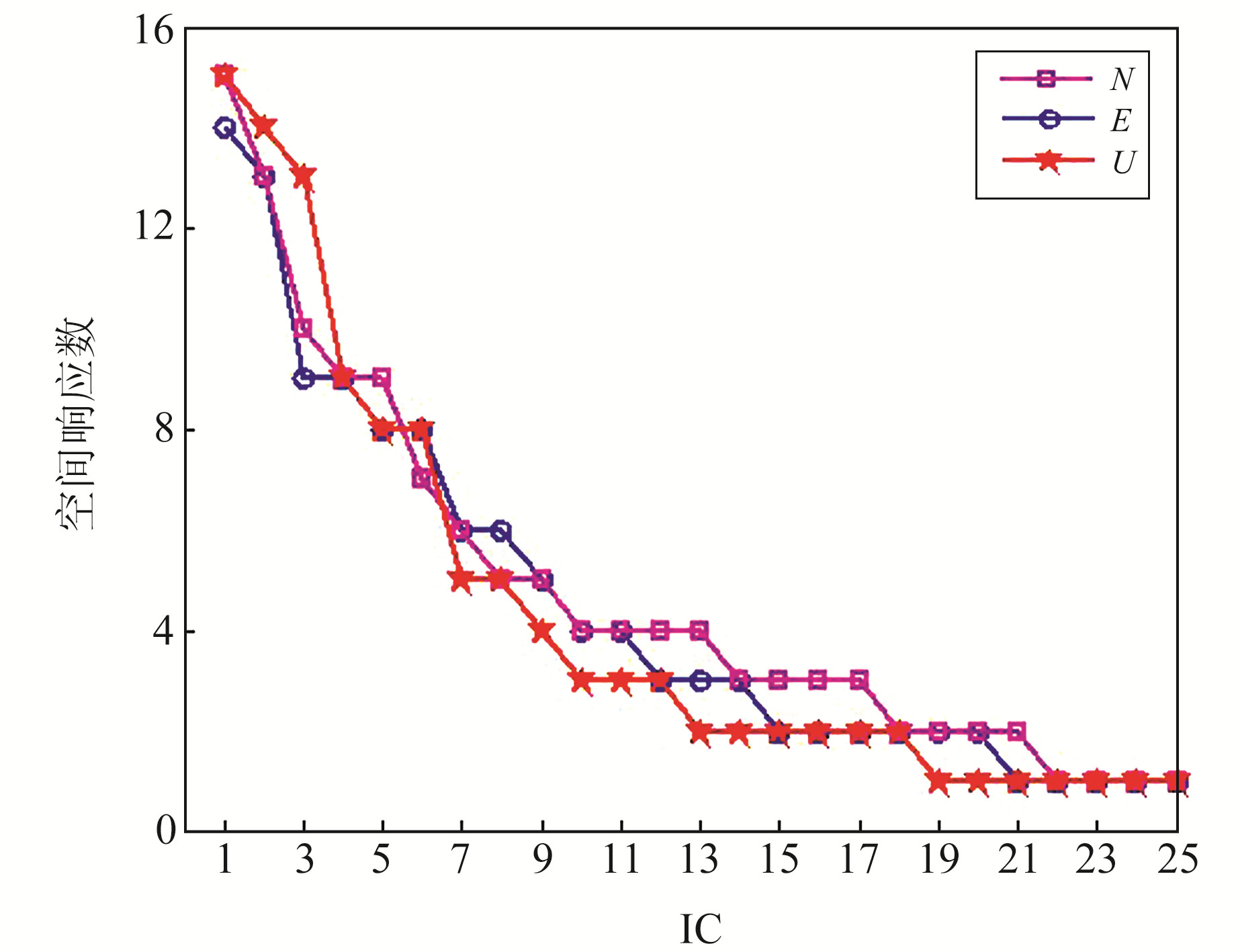
采用FastICA方法分别对N、E、U分量的残差时间序列进行ICA分解,得到各独立分量(IC)及其标准化空间响应。FastICA算法以各估计的信号源之间的互信息最小化为目标函数,采用基于牛顿迭代的固定点优化方案,其计算效率比传统的梯度法快10~100倍,且稳健性更好[8]。与PCA方法不同的是,ICA方法无法确定各IC之间的次序及各IC的特征值,因此本文分别统计N、E、U分量各IC的标准化空间响应大于25%的测站,并按照测站数大小对IC进行排列,结果如图 4所示。从图中可以看出,N、E分量前2个IC的标准化空间响应大于25%的测站数刚好超过50%,U分量前3个IC满足共模误差要求,因此水平分量选择前2个IC计算CME,U分量选择前3个IC计算CME。
|
图 4 各IC标准化空间响应超过25%的测站数 Fig. 4 Number of stations with standardized spatial response exceeding 25% derived from IC |
为比较PCA和ICA方法提取共模误差的效果,对剔除共模误差前后残差的绝对值进行求和,再除以测站数,得到单日L1范数离散度序列。图 5为2种方法剔除共模误差前后残差L1范数离散度,从图中可以看出,PCA方法滤波后残差的振幅略小于ICA方法,表明PCA方法对西南极区域GPS数据的适应性更好。此外,本文还统计了原始残差时间序列分别扣除PCA、ICA共模误差前后各测站残差时间序列的标准差RMS,表 1中括号内数值为RMS的降低率。从表 1可以看出,PCA滤波后各站残差RMS均值在N、E、U分量均比ICA方法小,尤其在U分量差异较大。综上可知,PCA和ICA空间滤波方法均能有效降低残差时间序列的标准差,提高GPS站坐标精度;PCA滤波法效果更优,是更适合在西南极区域提取共模误差的滤波方法。

|
图 5 PCA、ICA剔除共模误差后的L1范数离散度序列比较 Fig. 5 Comparison ofthe L1-norm dispersion series after CME elimination by PCA and ICA |
|
|
表 1 空间滤波前后测站残差时间序列的平均RMS Tab. 1 Root mean square of residual time series before and after spatial filtering |
GPS坐标时间序列噪声分析方法主要有极大似然估计法和功率谱分析法,分别从时间域和频率域对时间序列进行噪声分析,以确定噪声特征。其中,极大似然估计法不仅可同时估计噪声特征、测站速度场和周期性振幅等,还可避开频谱分析需要数据均匀采样的局限性。
本文采用Hector软件改进的极大似然估计法分析GPS坐标时间序列的噪声特征,该软件具有更高的数据处理速率,相比于CATS软件可选择更多的噪声模型。在数据处理过程中,顾及噪声模型参数对估计结果的影响,采用赤池信息量(Akaike information criteria, AIC)或贝叶斯信息量(Bayesian information criteria, BIC)最小的噪声模型估计准则,以获得更加稳健的噪声模型估计结果。使用AIC和BIC标准对不同噪声模型进行分析的公式为:
| $ \ln (L) = - \frac{1}{2}\left[ {N\ln (2\pi ) + \ln \det (\mathit{\boldsymbol{C}}) + {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}\mathit{\boldsymbol{r}}} \right] $ | (2) |
| $ {\rm{AIC}} = 2k + 2\ln (L) $ | (3) |
| $ {\rm{BIC}} = k\ln (N) + 2\ln (L) $ | (4) |
式中,k为待估参数的个数。
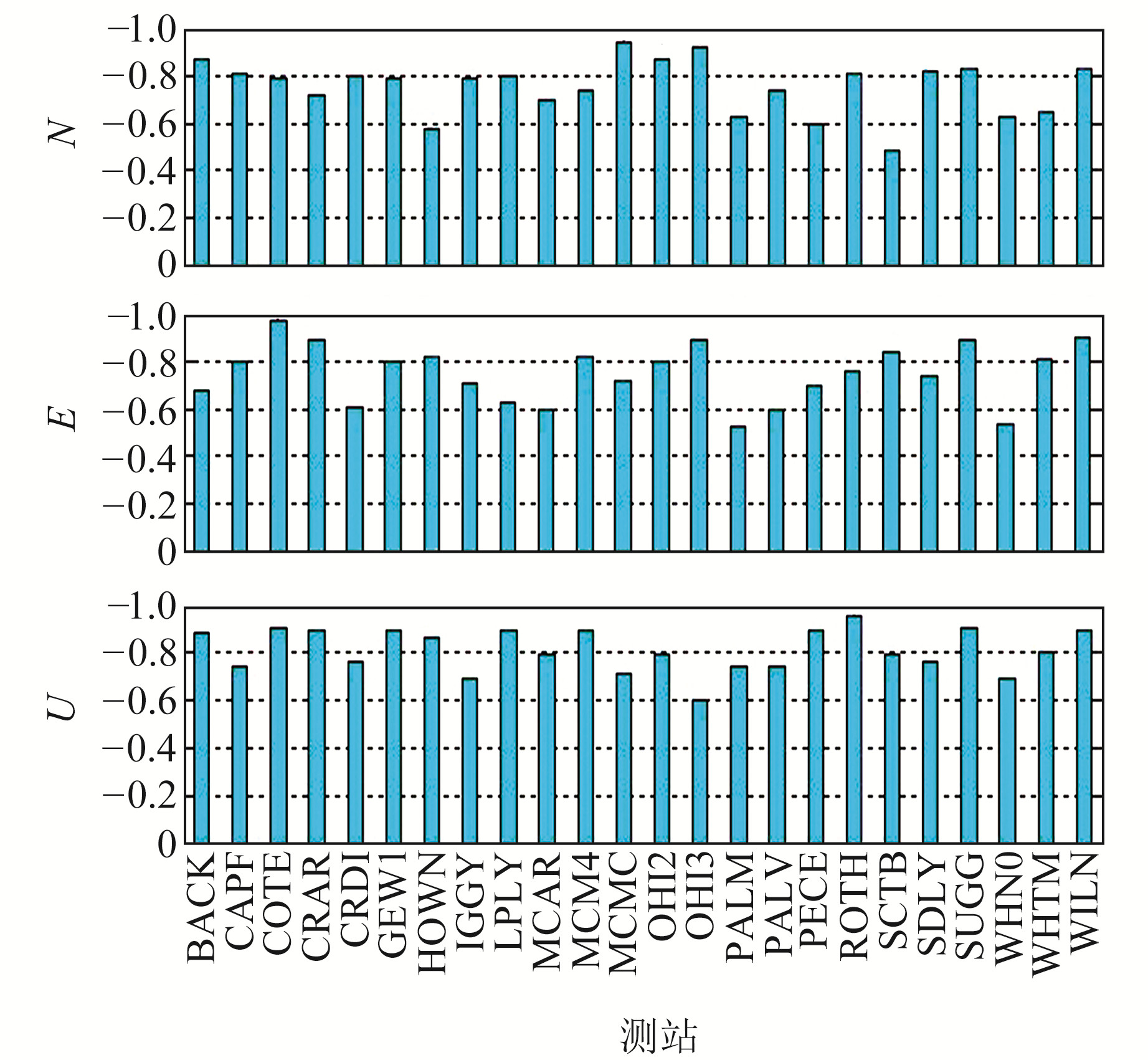
3.2 共模误差对测站噪声的影响利用PCA空间滤波法提取测站的共模误差,分析滤波前后时间序列的最优噪声模型,以确定共模误差对较长时间序列噪声的影响。时间序列中的噪声谱可用指数定律来描述,通过计算谱指数u可以判断噪声的大概类型。当u=0时对应白噪声,当u=-1时对应闪烁噪声,当u=-2时对应随机游走噪声[9]。图 6为滤波后的西南极GPS坐标时间序列谱指数,从图中可以看出,西南极24个GPS基准站各坐标分量的噪声谱指数均介于-1~-0.5之间,说明这些测站的噪声类型均不具有纯白噪声特征,而是白噪声与有色噪声的组合。
|
图 6 空间滤波后测站3个方向的谱指数 Fig. 6 Spectral index values in the three directions after spatial filtering |
为进一步分析各测站在空间滤波前后不同坐标分量的噪声特征,根据谱指数分析结果及有色噪声的确定性,假设坐标时间序列除包含WN外,还含有FN、RWN、PL、广义高斯-马尔可夫噪声(generalized Gauss Markov noise, GGM)及一阶自回归滑动平均模型噪声(auto-regressive moving average model noise(1, 1), ARMA(1)),选取WN、WN+FN、WN+RWN、WN+FN+RWN、WN+PL、WN+ARMA(1)、GGM+FN及GGM+RWN等8种噪声模型,根据极大似然估计法计算不同噪声模型下的AIC和BIC值。由于本文所选样本较小,选用BIC值作为判断模型可靠性的指标,即BIC值越小结果越可靠。
使用上述8种模型计算空间滤波前后24个GPS站N、E、U三分量的BIC值,然后确定每个测站不同坐标分量的最佳噪声模型,结果见表 2。从表中可以看出,西南极GPS站3个坐标分量时间序列的噪声特征并不完全相同,滤波后部分测站的噪声特征发生改变。空间滤波前,N分量的最优噪声模型比例最大的为WN+FN(45.83%),其次为WN+ARMA(1)(29.17%);E分量的最优噪声模型比例最大的为WN+FN(41.67%),其次为WN+ARMA(1)(33.33%);U分量的最优噪声模型比例最大的为WN+FN(48.00%),其次为GGM+FN(16.00%)和GGM+RWN(16.00%)。空间滤波后,E分量的最优噪声模型WN+FN和WN+ARMA(1)均占33.33%;N分量的最优噪声模型比例最大的为WN+ARMA(1)(41.76%),其次为WN+FN(25.00%);U分量的最优噪声模型比例最大的为WN+FN(45.83%),其次为WN+ARMA(1)(25.00%)和GGM+FN(16.67%)。通过对比滤波前后各测站时间序列的最优噪声模型可知,共模误差同时具有白噪声和有色噪声的特征。
|
|
表 2 空间滤波前后各站坐标最优噪声模型统计 Tab. 2 The optimal noise model statistics of each station coordinates before and after spatial filtering |
此外,CME会影响时间序列最优噪声模型的地域分布特征,空间滤波前GPS坐标时间序列最优噪声模型具有较强的区域分布一致性,空间滤波后区域分布特征不明显。以维多利亚地的MCMC、MCM4、SCTB、CRAR、COTE和WHN0站为例,空间滤波前6个测站三分量的最优噪声模型以WN+FN为主,滤波后各站不同分量的最优噪声模型按比例大小依次为WN+FN、GGM+RWN等,其原因为空间滤波会大幅降低GPS坐标时间序列的白噪声和闪烁噪声,当闪烁噪声占主导地位时,容易掩盖其他有色噪声。这同时也表明,对GPS坐标时间序列进行分析时,利用空间滤波扣除CME具有必要性。
3.3 共模误差对测站速度影响分析根据前文分析得到的空间滤波前后西南极24个测站各分量时间序列的最优噪声模型,采用极大似然估计法估计滤波前后各分量在ITRF2014框架下的速度及其不确定度,结果见表 3(单位mm/a)。从表中可以看出,经过PCA滤波后,87.50%(21个)测站的水平速度变化在±0.2 mm/a,79.17%(19个)测站的垂直速度变化在±0.3 mm/a,说明空间滤波对时间序列速度估计值的影响较小;N、E、U三分量的速度不确定度分别平均降低14.56%、20.66%和36.40%,说明垂直方向通过空间滤波扣除的共模误差量级大于水平方向,垂直方向不确定度的减小幅度更大。时间序列较短或非线性运动幅度较大的测站差异较大,因为这些测站的速度更易受系统误差的影响。
|
|
表 3 空间滤波前后最优噪声模型下各站速度及不确定度 Tab. 3 The velocity and uncertainty under the optimal noise model before and after spatial filtering |
通过分析不同空间滤波方法和滤波前后西南极区域24个GPS站的连续坐标时间序列,得到以下结论:
1) PCA和ICA空间滤波方法均能有效提取区域GPS坐标时间序列中的共模误差,但PCA方法的滤波效果略优于ICA方法,且在垂直方向的滤波效果优于水平方向。
2) 利用PCA滤波后的GPS站各坐标分量的噪声谱指数均介于-1~-0.5之间,表明这些测站的噪声是包括白噪声在内的多种噪声模型的组合。
3) GPS站各坐标分量时间序列的最优噪声模型以WN+FN、WN+ARMA(1)为主,其中多个测站的U分量还含有GGM。去除共模误差后,部分测站的最优噪声模型发生改变,但仍以WN+FN、WN+ARMA(1)为主,最优噪声的区域分布特征不明显。
4) 空间滤波前后GPS站各坐标分量的速度平均变化均小于0.1 mm/a,速度不确定度分别平均降低14.56%、20.66%和36.40%,说明共模误差对时间序列速度估计值的影响较小,但能有效降低白噪声和有色噪声的量级,从而大幅减小线性项的不确定性。
| [1] |
Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 057-18 070 DOI:10.1029/97JB01378
(  0) 0) |
| [2] |
Shen Y Z, Li W W, Xu G C, et al. Spatiotemporal Filtering of Regional GNSS Network's Position Time Series with Missing Data Using Principle Component Analysis[J]. Journal of Geodesy, 2014, 88(1): 1-12 DOI:10.1007/s00190-013-0663-y
(  0) 0) |
| [3] |
马超, 李斐, 张胜凯, 等. 顾及共性误差的南极半岛地区连续GPS站坐标时间序列分析[J]. 地球物理学报, 2016, 59(8): 2 783-2 795 (Ma Chao, Li Fei, Zhang Shengkai, et al. The Coordinate Time Series Analysis of Continuous GPS Stations in the Antarctic Peninsula with Consideration of Common Mode Error[J]. Chinese Journal of Geophysics, 2016, 59(8): 2 783-2 795)
(  0) 0) |
| [4] |
明锋, 杨元喜, 曾安敏. 共模误差PCA与ICA提取方法的比较[J]. 大地测量与地球动力学, 2017, 37(4): 385-389 (Ming Feng, Yang Yuanxi, Zeng Anmin. Analysis and Comparison of Common Mode Error Extraction Using Principal Component Analysis and Independent Component Analysis[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 385-389)
(  0) 0) |
| [5] |
Wang X, Cheng Y, Wu S, et al. An Effective Toolkit for the Interpolation and Gross Error Detection of GPS Time Series[J]. Survey Review, 2016, 48(348): 202-211 DOI:10.1179/1752270615Y.0000000023
(  0) 0) |
| [6] |
Schneider T. Analysis of Incomplete Climate Data: Estimation of Mean Values and Covariance Matrices and Imputation of Missing Values[J]. Journal of Climate, 2001, 14(5): 853-871 DOI:10.1175/1520-0442(2001)014<0853:AOICDE>2.0.CO;2
(  0) 0) |
| [7] |
Cerny B A, Kaiser H F. A Study of a Measure of Sampling Adequacy for Factor-Analytic Correlation Matrices[J]. Multivariate Behavioral Research, 1977, 12(1): 43-47 DOI:10.1207/s15327906mbr1201_3
(  0) 0) |
| [8] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3)
(  0) 0) |
| [9] |
Mandelbrot B B, Ness J W. Fractional Brownian Motions, Fractional Noises and Applications[J]. SIAM Review, 1968, 10(4): 422-437 DOI:10.1137/1010093
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

