传统二次多项式模型(QP模型)和BP神经网络模型在进行卫星钟差短期预报时存在精度不高的问题,而麻雀搜索算法(SSA)在单峰测试函数、多峰测试函数和固定维度测试函数中的收敛精度、速度及稳定性均优于其他群智能优化算法[1],这是由于SSA中麻雀不同的行为策略对全局搜索作出了重要贡献。基于此,本文提出SSA-BP神经网络模型,该模型是在BP神经网络的基础上采用麻雀搜索算法进行参数优化,通过迭代寻优确定BP神经网络的全局最优参数,从而进一步提高BP神经网络模型的短期钟差预报精度。
1 SSA原理SSA是一种新型群智能优化算法,主要是受麻雀觅食行为和反捕食行为的启发而提出的[2],具有较强的全局寻优能力,不依赖梯度信息,有良好的并行性和较快的收敛速度。
为了获得食物,麻雀通常可以采用发现者和加入者这2种行为策略进行觅食。种群中的个体会监视其他个体的行为,该种群中的加入者会与高摄取量的同伴争夺食物资源,以提高自己的捕食率[2]。此外,当麻雀种群意识到危险时会作出反捕食行为。
1) 在麻雀搜索算法中,发现者的位置更新如下:
| $ X_{i, j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {X_{i, j}^t\exp \left( { - \frac{i}{{\alpha {\rm{ite}}{{\rm{r}}_{\max }}}}} \right), {R_2} < {\rm{ST}}}\\ {X_{i, j}^t + Q\mathit{\boldsymbol{L}}, {R_2} \ge {\rm{ST}}} \end{array}} \right. $ | (1) |
式中,t为当前迭代数,j =1、2、3…、d代表维度,itermax为一个常数,表示最大迭代次数,Xi, j为第i个麻雀在第j维中的位置信息,α∈(0, 1)为一个随机数,R2∈(0, 1)和ST∈[0.5, 1]分别为预警值和安全值,Q为服从正态分布的随机数,L为一个1×d维的矩阵。
2) 对于加入者:
| $ \begin{array}{*{20}{c}} {X_{i, j}^{t + 1} = }\\ {\left\{ {\begin{array}{*{20}{l}} {Q\exp \left( { - \frac{{{X_{{\rm{worst }}}} - X_{i, j}^t}}{{{i^2}}}} \right), i > \frac{n}{2}}\\ {X_P^{t + 1} + \left| {X_{i, j}^t - X_P^{t + 1}} \right|{\mathit{\boldsymbol{A}}^ + }\mathit{\boldsymbol{L}}, i \le \frac{n}{2}} \end{array}} \right.} \end{array}{\rm{ }} $ | (2) |
式中,XP为目前发现者所占据的最优位置,Xworst为当前全局最差位置,A为一个1×d维的矩阵,每个元素随机赋值1或-1,并且A+=AT(AAT)-1。当i >n/2时,表明适应度值较低的第i个加入者没有获得食物,处于十分饥饿的状态,需要去往其他地方觅食。
3) 假设意识到危险的麻雀占麻雀总量的10%~20%,这些麻雀的初始位置在种群中随机产生,其数学表达式为:
| $ \begin{array}{*{20}{c}} {X_{i, j}^{t + 1} = }\\ {\left\{ {\begin{array}{*{20}{l}} {X_{{\rm{best }}}^t + \beta \left| {X_{i, j}^t - X_{{\rm{best }}}^t} \right|, {f_i} > {f_g}}\\ {X_{i, j}^t + K\left( {\frac{{\left| {X_{i, j}^t - X_{{\rm{worst }}}^t} \right|}}{{\left( {{f_i} - {f_w}} \right) + \varepsilon }}} \right), {f_i} = {f_g}} \end{array}} \right.} \end{array}{\rm{ }} $ | (3) |
式中,Xbest为当前全局最优位置,β为步长控制参数,服从均值为0、方差为1的正态分布随机数,K∈[-1, 1]为一个随机数,fi为当前麻雀个体的适应度值,fg和fw分别为当前全局最优和最差的适应度值,ε为常数,以避免分母出现0。
2 SSA-BP神经网络BP神经网络模型精度的提高是通过误差反向传播对神经网络的权值和阈值进行不断调整实现的,因此可使用SSA解决由权值、阈值随机初始化导致的陷入局部最优解的问题。SSA-BP神经网络计算流程的具体步骤为:
1) 数据预处理。将原始钟差数据归一化到[-1, 1]之间,目的是将预处理数据限定在一定范围内,解决因奇异样本数据不良导致的无法收敛或收敛过慢等问题。
2) 确定BP神经网络拓扑结构。本文实验根据滑动窗思想[3]确定输入层神经元个数n=5,因为只有一个输出变量,所以定义输出层神经元个数q=1,隐含层神经元个数p的确定根据经验公式:
| $ p = \sqrt {n + q} + \alpha $ | (4) |
式中,α的取值为1~10之间的常数。实验结果表明,p=9时该模型预报结果最优,因此网络拓扑结构设为5-9-1。
3) 参数初始化。确定SSA的最大迭代次数maxgen及种群规模sizepop,定义发现者producers所占种群比例为0.2,设置预警值R2和预警者数量。
4) 定义适应度函数并计算个体适应度值。用种群中的每个个体代表BP神经网络中的初始权值和阈值,根据输入层、隐含层和输出层的神经元数量可以得到初始编码长度dim=64。利用初始权值阈值进行神经网络训练,将预测输出值和实际输出值的误差绝对值求和作为适应度函数,适应度值越小表示误差越小。找到当前全局最优解并确定对应的位置。
5) 进行麻雀位置的更新。在迭代过程中,将适应度值较好的个体作为发现者,发现者会在搜索过程中优先获取食物,并为整个种群提供觅食方向[4]。根据预警值R2和安全值ST,使用式(1)更新发现者位置。加入者进行监视并与发现者竞争,使用式(2)更新位置。预警者占总量的10%~20%,这些麻雀的初始位置在种群中随机产生,fi为当前麻雀个体的适应度值,fg为当前全局最优适应度值。根据fi和fg的比较结果,使用式(3)更新预警者位置。
6) 查看位置更新之后的个体适应度值,并与当前最优适应度值进行比较,达到最大迭代次数之后选择全局最优解;否则,再次进行迭代。
7) 将输出的最优解作为神经网络的权值和阈值,通过之前确定的BP神经网络拓扑结构进行训练,利用误差反向传播微调参数,迭代训练直到达到预设的误差精度或迭代次数。
8) 使用SSA优化后的BP神经网络模型进行卫星钟差预报。
3 实验结果与分析 3.1 实验数据与模型评价指标为验证SSA-BP神经网络模型的有效性和稳定性,采用IGS提供的2020-06-20~06-29共2 880个历元的GPS卫星钟差数据进行实验,其中数据的采样间隔为5 min。以PRN05、PRN11、PRN25、PRN24等4种不同类型(Block Ⅱ R-M Rb、Block Ⅱ R Rb、Block Ⅱ F Rb、Block Ⅱ F Cs)的卫星作为实验对象,这样选择首先是因为这4颗卫星在当前时间段内钟差数据完整且不存在明显粗差,另外实验卫星包含了铷钟和铯钟,可检验模型对于不同类型卫星钟的预测效果。本文实验分为3个部分,使用上述数据对QP模型[6]、BP神经网络模型[7-9]、PSO-BP神经网络模型[10]和SSA-BP神经网络模型进行实验对比。
对卫星钟差数据进行尺度变化,归一化数据以提高模型收敛速度,减少运算量[5]:
| $ {\bar X_i} = \frac{{{X_i} - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}} $ | (5) |
式中,Xi为归一化后的数据,Xi为归一化前的数据,Xmax和Xmin分别为卫星钟差数据范围内的最大值和最小值。
采用标准差(SD)和均方根误差(RMSE)作为评价各种模型预报稳定性与精确度的依据,计算公式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{SD}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{E_i} - u} \right)}^2}} } }\\ {{\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{X_i} - X_i^\prime } \right)}^2}} } } \end{array}} \right. $ | (6) |
式中,n为预测钟差数据的历元个数,Ei为预报误差值,u为预报误差的平均值,为钟差数据实际值,X′ i为钟差数据的模型预测值。
3.2 实验1采用2020-06-20前12 h共144个历元数据预测未来24、72、144个历元的钟差数据,对比实验采用2020-06-20全天24 h共288个历元数据预测未来24、72、144个历元的钟差数据。为验证QP模型、BP神经网络模型、PSO-BP神经网络模型、SSA-BP神经网络模型在钟差预报过程中的精度和稳定性及不同历史数据对于钟差预报精度和稳定性的影响,计算4颗卫星在4种模型下的RMSE和SD,结果见表 1和2。
|
|
表 1 12 h历史数据下4种模型预报结果统计 Tab. 1 Statistics of prediction results of four models under 12 h historical data |
|
|
表 2 24 h历史数据下4种模型预报结果统计 Tab. 2 Statistics of prediction results of four models under 24 h historical data |
由表 1在3个时间段的预报结果可知,随着预报时长的增加,4种模型的预报误差均有所上升,但SSA-BP神经网络模型预报误差的变化较小,具有更好的抗干扰能力,且精度高于其他3种模型。4颗卫星在2 h预报过程中,PSO-BP和SSA-BP神经网络模型精度均能保持在亚ns级,4颗卫星的SSA-BP神经网络模型12 h预报误差平均为4.91 ns左右。由表 2可知,随着历史数据的增加,在相同预报时长下,4种模型的预报精度均有所上升,在2 h预报过程中,4种模型均处于亚ns级,其中PRN25号卫星SSA-BP神经网络模型的预报误差保持在0.1 ns以内。随着预报时长的增加,各模型的预报误差都有所上升,但4颗卫星SSA-BP神经网络模型12 h预报误差平均仍保持在1.90 ns左右,说明经SSA优化后的神经网络模型提升了最终预报结果的精度。
限于篇幅,下面仅给出PRN05号卫星在不同历史数据下4种模型预报12 h共144个历元的误差,结果见图 1。通过对12 h和24 h历史数据进行对比可以看出,SSA-BP神经网络模型在不同历史数据下的预报效果均优于其他3种模型,说明使用SSA对BP神经网络的初始权值和阈值进行优化后,可得到更优、更稳定的结果。

|
图 1 不同历史数据预报未来12 h误差对比 Fig. 1 Comparison of 12 h prediction errors with different historical data |
为更直观地对比模型的提升效果,当历史数据为24 h时,给出4颗卫星预报12 h的RMSE和SD的柱状统计,结果见图 2。

|
图 2 24 h历史数据预报未来12h钟差 Fig. 2 Using 24 h historical data to predict the next 12 h clock bias |
整体来看,经过优化后的BP神经网络模型在预报精度和稳定性方面更优,其中SSA-BP神经网络模型的性能更好。以PRN05号卫星铷钟为例,利用24 h历史数据预报12 h钟差,SSA-BP神经网络模型相比另外3种模型在精度方面分别提升58.2%、85.3%、50.6%,在稳定性方面分别提升29.0%、84.5%、46.7%。以PRN24号卫星铯钟为例,SSA-BP神经网络模型相比另外3种模型在精度方面分别提升23.3%、50.3%、18.8%,在稳定性方面分别提升37.2%、46.0%、17.8%。这可能是由铷钟存在显著频漂,与铯钟的钟差序列有差异导致的。
3.3 实验2为验证历史数据时长对预报精度的影响,利用2020-06-20~06-29共2 880个历元的IGS精密卫星钟差数据,使用SSA-BP神经网络模型,以PRN05、PRN11、PRN24、PRN25号卫星为例,分别选取时长为144、288、576、864、1 152、1 440、1 728、2 016、2 304、2 592和2 880个历元的历史数据进行12 h(144个历元)的短期钟差预报,以确定一个或多个合适的历史数据时长。
使用SSA-BP神经网络模型绘制4颗卫星不同历史数据时长下的预报误差变化趋势,结果见图 3。可以看出,随着时长的增加,预报误差有逐渐减小的趋势,在时长为864个历元时,4颗卫星的预报误差达到局部最小值,之后出现明显的波动,并且在时长为2 016个历元时达到另一个最小值,之后4颗卫星的误差开始波动上升。由此可以确定,在当前实验条件下,864个历元(3 d)和2 016个历元(7 d)为较好的历史数据时长,但要确定最佳时长还需要对这2个历元进行进一步的实验。
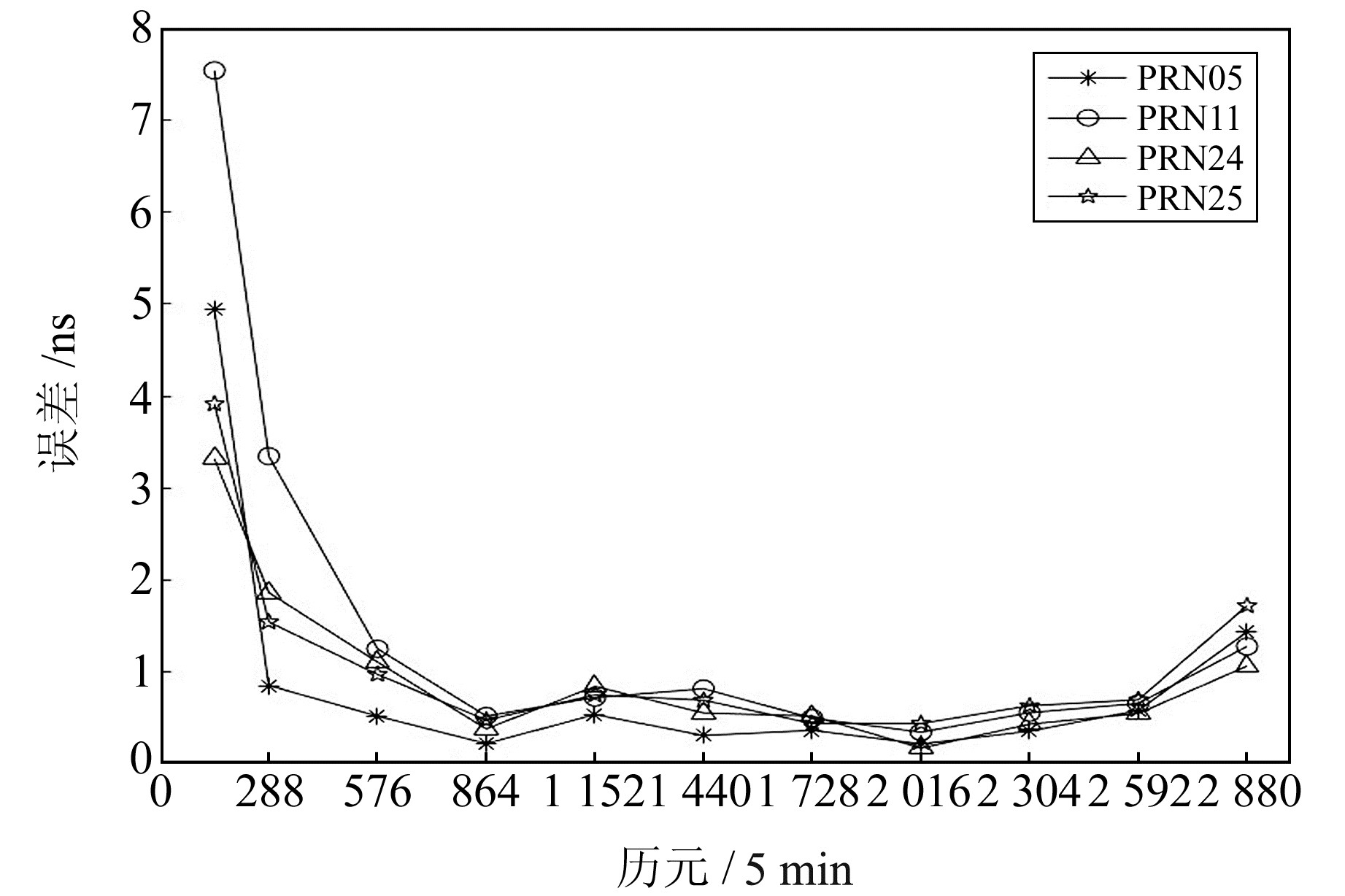
|
图 3 不同时长预报未来12 h误差 Fig. 3 Prediction errors in the next 12 h with different durations |
采用2020-06-20~06-22共864个历元的历史数据预测72、144、288个历元的钟差数据,对比实验采用2020-06-20~06-26共2 016个历元数据预测未来72、144、288个历元的钟差数据。为验证实验2中2个历元的最佳时长及4种模型在最佳时长下的预报精度和稳定性,计算4颗卫星在4种模型下的RMSE和SD,结果见表 3和4。
|
|
表 3 3 d历史数据下4种模型预报结果统计 Tab. 3 Statistics of the prediction results of the four models under 3 d historical data |
|
|
表 4 7 d历史数据下4种模型预报结果统计 Tab. 4 Statistics of the prediction results of the four models under 7 d historical data |
由表 3和4可知,历史数据时长为7 d时预报精度达到最优,4种模型对于4颗卫星6 h的预报精度均保持在亚ns级;在12 h预报中,2种优化后的BP神经网络模型精度也保持在1 ns以内,其中SSA-BP神经网络模型的结果更优。通过对比2次实验中SSA-BP神经网络模型24 h预报结果可知,PRN05号卫星在精度和稳定性方面分别提升7.2%、19.9%,PRN11号卫星分别提升67.4%、65.9%,PRN25号卫星提升76.4%、77.9%,PRN24号卫星提升60.2%、54.8%。
图 4为PRN05号卫星在不同历史数据时长下4种模型预报24 h共288个历元的误差结果。其中,SSA-BP神经网络模型在3 d和7 d的历史数据下,预测24 h的结果误差均在0附近波动,总体起伏不大,体现出良好的稳定性,说明经过SSA优化后的BP神经网络模型并没有陷入局部最优解,也在一定程度上说明了本文神经网络结构的可行性。
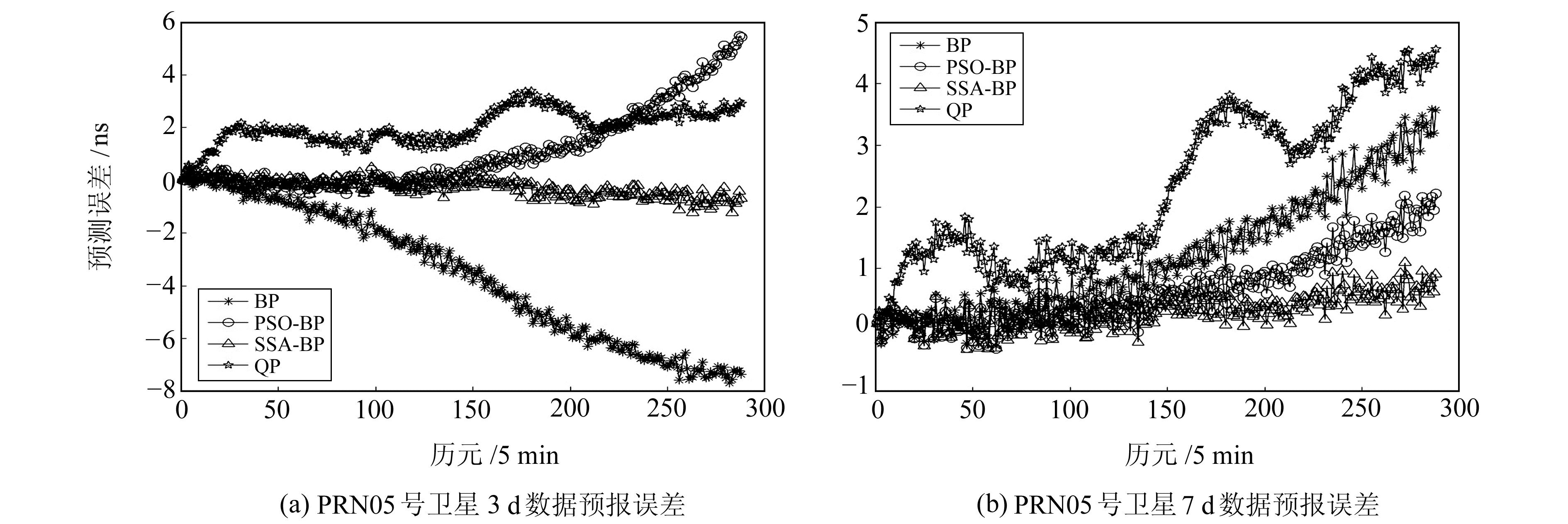
|
图 4 不同历史数据预报未来24 h误差对比 Fig. 4 Comparison of future 24 h prediction errors with different historical data |
实验结果表明,在7 d的历史数据拟合下,模型拥有更好的预报精度和稳定性,故给出历史数据时长为7 d时,4颗卫星预报未来24 h钟差的RMSE和SD,结果见图 5。
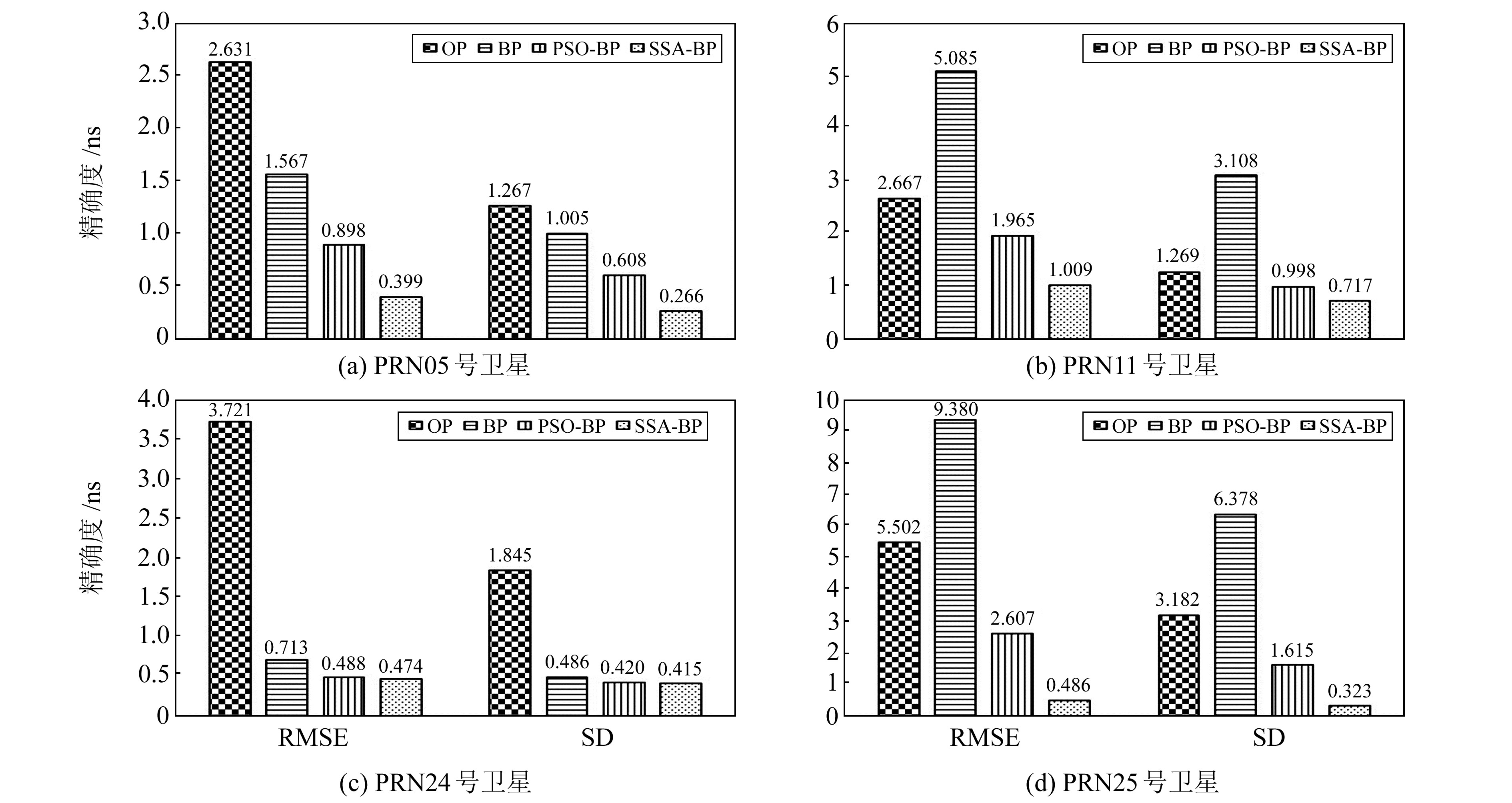
|
图 5 7 d历史数据预报未来24h钟差 Fig. 5 Using 7 d historical data to predict the next 24 h clock bias |
整体来看,相对于其他3种模型,SSA-BP神经网络模型的预报精度更优,稳定性也更高。4颗卫星SSA-BP神经网络模型24 h预报的平均误差为0.592 ns,以PRN11号卫星铷钟为例,SSA-BP神经网络模型精度比QP模型、BP神经网络模型、PSO-BP神经网络模型分别提升62.2%、80.2%、48.7%,稳定性分别提升43.5%、76.9%、27.4%。以PRN24号卫星铯钟为例,SSA-BP神经网络模型精度比其他3种模型分别提升87.3%、33.5%、2.9%,稳定性分别提升77.5%、14.6%、1.2%。进一步证明了SSA-BP神经网络模型对于不同类型的卫星在钟差预报方面具有优越性。
4 结语本文结合SSA和BP神经网络提出一种新的卫星钟差预报模型——SSA-BP神经网络模型。基于IGS提供的卫星钟差数据,使用SSA-BP神经网络模型、PSO-BP神经网络模型、传统BP神经网络模型和QP模型进行钟差预报实验,结果表明,SSA-BP神经网络模型的预报效果最优,在相同历史数据下,随着预报时长的增加,结果的精度变化不大,误差曲线保持在一定范围内波动。
本文实验仅针对卫星钟差的短期预报,对于中长期预报及其他影响卫星钟差预报精度的因素还需作进一步研究。
| [1] |
薛建凯. 一种新型的群智能优化技术的研究与应用——麻雀搜索算法[D]. 上海: 东华大学, 2020 (Xue Jiankai. Research and Application of a Novel Swarm Intelligence Optimization Technique——Sparrow Search Algorithm[D]. Shanghai: Donghua University, 2020)
(  0) 0) |
| [2] |
Xue J K, Shen B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm[J]. Systems Science and Control Engineering, 2020, 8(1): 22-34 DOI:10.1080/21642583.2019.1708830
(  0) 0) |
| [3] |
郭承军, 滕云龙. 神经网络在卫星钟差短期预报中的应用研究[J]. 测绘科学, 2011, 36(4): 198-200 (Guo Chengjun, Teng Yunlong. Application of Neural Network in Satellite Clock Bias Short-Term Prediction[J]. Science of Surveying and Mapping, 2011, 36(4): 198-200)
(  0) 0) |
| [4] |
Li H M, Zhang Y. Study of Transformer Fault Diagnosis Based on Sparrow Optimization Algorithm[C]. International Conference on Control, Robotics and Intelligent System, Xiamen, 2020
(  0) 0) |
| [5] |
郭秋, 李培. 基于人工神经网络的导航卫星钟差预报方法[J]. 实验室研究与探索, 2017, 36(12): 65-68 (Guo Qiu, Li Pei. Research on Prediction of Satellite Clock Bia Based on Improved Neural Network[J]. Research and Exploration in Laboratory, 2017, 36(12): 65-68 DOI:10.3969/j.issn.1006-7167.2017.12.017)
(  0) 0) |
| [6] |
吕栋, 欧吉坤, 于胜文. 基于MEA-BP神经网络的卫星钟差预报[J]. 测绘学报, 2020, 49(8): 993-1 003 (Do ng, Ou Jikun, Yu Shenwen. Prediction of the Satellite Clock Bias Based on MEA-BP Neural Network[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 993-1 003)
(  0) 0) |
| [7] |
雷雨, 赵丹宁. 极限学习机在卫星钟差预报中的应用[J]. 大地测量与地球动力学, 2013, 33(5): 53-57 (Lei Yu, Zhao Danning. Application of Extreme Learning Machine in Satellite Clock Error Prediction[J]. Journal of Geodesy and Geodynamics, 2013, 33(5): 53-57)
(  0) 0) |
| [8] |
郭振华, 韩保民, 赵金生. 基于灰色BP网络的卫星钟差预报[J]. 山东理工大学学报: 自然科学版, 2012, 26(4): 39-42 (Guo Zhenhua, Han Baomin, Zhao Jinsheng. Satellites Clock Bias Forecast Based on Gray System and BP Neural Network[J]. Journal of Shandong University of Technology: Natural Science Edition, 2012, 26(4): 39-42)
(  0) 0) |
| [9] |
孙娓娓. BP神经网络的算法改进及应用研究[D]. 重庆: 重庆大学, 2009 (Sun Weiwei. Study on Improved Algorithm and Application of BP Neural Network[D]. Chongqing: Chongqing University, 2009)
(  0) 0) |
| [10] |
陈希鸣, 黄张裕, 秦洁, 等. 粒子群算法优化的神经网络短期钟差预报[J]. 测绘科学, 2019, 44(9): 7-12 (Chen Ximing, Huang Zhangyu, Qin Jie, et al. Prediction of the Short-Term Satellite Clock Error Based on Particle Swarm Optimization Neural Network[J]. Science of Surveying and Mapping, 2019, 44(9): 7-12)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


