高程基准的统一是大地测量的长期目标[1],对工业、经济及大型工程建设都具有重要的支撑作用。随着GNSS技术的广泛应用及我国北斗系统的全面建成,构建高精度高程基准成为高程测量实时化建设需要突破的关键技术。发达国家近几十年不断精化本国大地水准面,美国最新大地水准面模型Geoid18[2]的分辨率优于2 km,内符合精度优于2 cm;澳大利亚发布的AUSGeoid2020内符合精度达到亚cm级[3];加拿大同美国正合作构建Geoid2022,届时可全面覆盖加拿大区域[4]。我国的大地水准面研究技术不论是在理论还是工程应用方面均已走在世界前列[5-6],李建成[1]在2020-10中国测绘学会年会上指出,中国似大地水准面的拟合精度已达2~3 cm,但构建高精度(似)大地水准面仍有提升空间,还需开展更多研究分析。本文研究构建市级区域似大地水准面的虚拟球谐方法,并以南昌市为例进行计算分析。
1 位模型计算大地水准面地球外部引力位的球谐表达式[7]为:
| $ \begin{gathered} V_{(r, \theta, \lambda)}=\frac{G M}{r}\left\{1+\sum\limits_{n=2}^{\infty} \sum\limits_{m=2}^{n}\left(\frac{a}{r}\right)^{n} \bar{P}_{n m}(\theta) \times\right. \\ \left.\left[\bar{C}_{n m} \cos (m \lambda)+\bar{S}_{n m} \sin (m \lambda)\right]\right\} \end{gathered} $ | (1) |
式中,GM为地心引力常数,r为地心距,θ和λ分别为地心余纬和地心经度,a为椭球长半轴,
| $ U_{(r, \theta, \lambda)}=\frac{G M}{r}\left(1-\sum\limits_{n=1}^{\infty} J_{2 n}\left(\frac{a}{r}\right)^{2 n} P_{2 n}(\theta)\right) $ | (2) |
式中,J2n为系数值,当J2已知时,其他数值可以计算得出;P2n(θ)为勒让德函数。将式(1)减去式(2)可得扰动位重力异常位T:
| $ T_{(r, \theta, \lambda)}=V_{(r, \theta, \lambda)}-U_{(r, \theta, \lambda)} $ | (3) |
| $ \begin{gathered} T_{(r, \theta, \lambda)}=\frac{G M}{r} \sum\limits_{n=2}^{\infty} \sum\limits_{m=2}^{n}\left(\frac{a}{r}\right)^{n} \bar{P}_{nm }(\cos \theta) \times \\ {\left[\bar{C}_{n m}^{*} \cos (m \lambda)+\bar{S}_{n m} \sin (m \lambda)\right]} \end{gathered} $ | (4) |
| $ \bar{C}_{2 n m}^{*}=\bar{C}_{2 n m}+J_{2 n} / \sqrt{2 n+1} $ | (5) |
式中,球谐系数
| $ N=\frac{T}{\gamma} $ | (6) |
式中,γ为正常重力值,可通过公式直接计算获取。
利用式(6)计算出的大地水准面有2个误差源,分别为位系数误差和截断到Nmax阶所引起的误差,后者被称为模型截断误差,可采用重力异常进行估算。大地水准面上的重力异常表达式为:
| $ \Delta g=\sum\limits_{n=2}^{N_{\max }} \Delta g_{n} $ | (7) |
| $ \begin{gathered} \Delta g_{n}=\frac{G M}{R^{2}}(n-1) \times \\ \sum\limits_{m=0}^{n}\left[\bar{C}_{n m}^{*} \cos m \lambda+\bar{S}_{n m} \sin m \lambda\right] \bar{P}_{n m}(\theta) \end{gathered} $ | (8) |
由此可得:
| $ \begin{gathered} \frac{\Delta g_{n}}{n-1}\left(\frac{R}{r}\right)^{2}= \\ \frac{G M}{r^{2}} \sum\limits_{m=o}^{n}\left[\bar{C}_{n m}^{*} \cos m \lambda+\bar{S}_{nm } \sin m \lambda\right] \bar{P}_{n m}(\theta) \end{gathered} $ | (9) |
将式(9)代入式(6)可得:
| $ N=\frac{r}{\bar\gamma} \sum\limits_{n=2}^{N_{\max }}\left(\frac{R}{r}\right)^{n+2} \frac{\Delta g_{n}}{n-1} $ | (10) |
扰动引力分量的截断误差表达式为:
| $ \sigma_{N}=\frac{r}{\bar\gamma} \sqrt{\sum\limits_{n=N+1}^{+\infty}\left(\frac{1}{n-1}\right)^{2}\left(\frac{R}{r}\right)^{2 n+4} C_{n}} $ | (11) |
式中,R为地球平均半径;Cn可利用Moritz两分量模型和Lapp参数进行计算:
| $ \begin{gathered} C_{n}=3.405 \frac{n-1}{n+1} 0.998\ 06^{n+2} \times \\ 140.03 \frac{n-1}{(n-2)(n+2)} 0.914\ 232^{n+2} \end{gathered} $ | (12) |
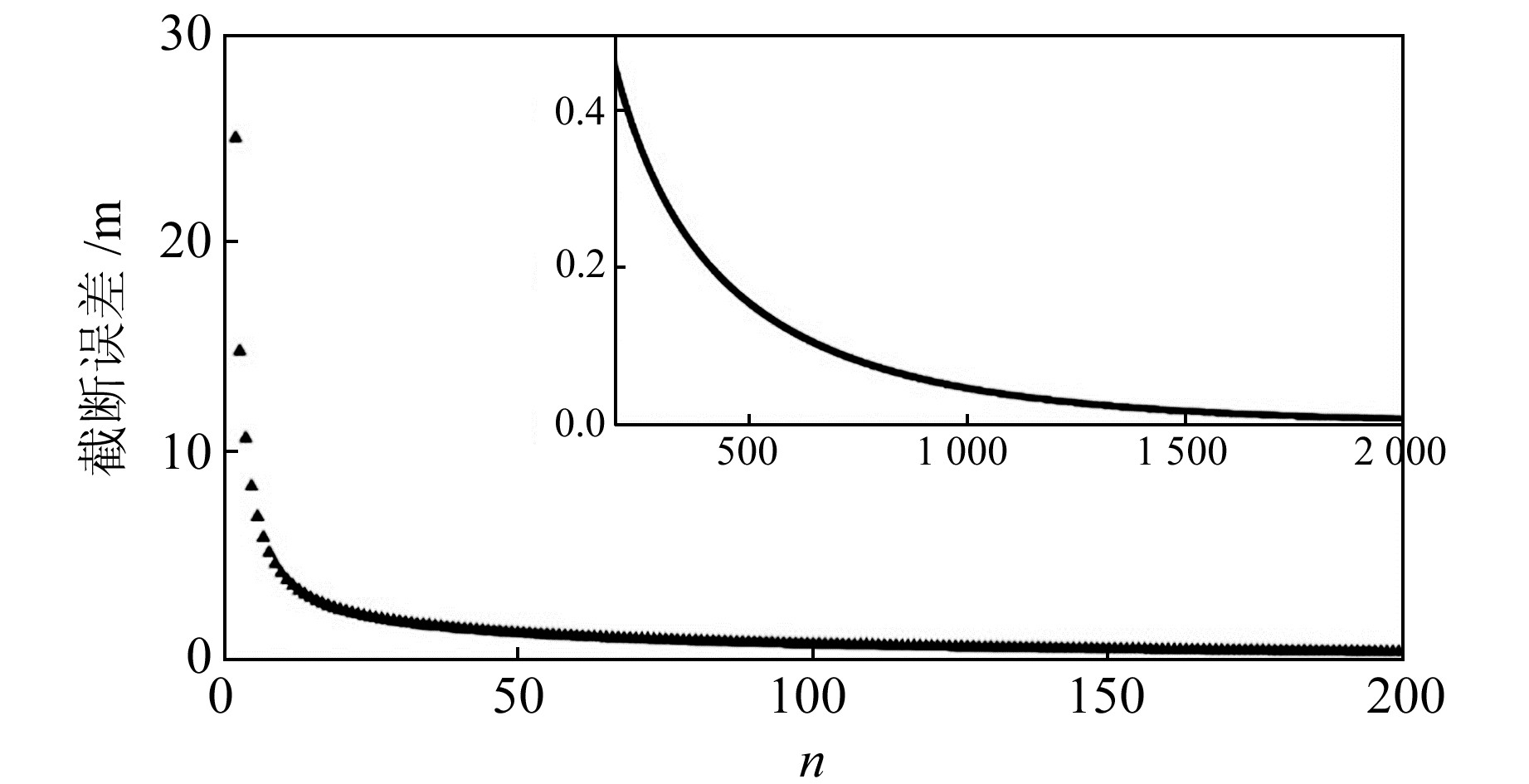
其中,C2=7.5 mGal2,计算阶次的上限为100 000,R=6 371 km,结果如图 1所示。由图可知,要达到cm级精度的大地水准面,截断阶次要达到2 000以上。
|
图 1 大地水准面模型截断误差 Fig. 1 Geoid model truncation error |
球冠谐模型是构建区域大地水准面模型的典型方法[8]。在球冠坐标系下,球冠半径为θ0,任一点的坐标为(r, θ, λ),θ为余纬,λ为经度。在球冠谐分析中,地球外部重力场位满足Laplace方程,同样可用分离变量法获得方程的解[9]。由于球冠谐分析中,余纬的边界条件[9]为:
| $ T\left(r, \theta_{0}, \lambda\right)=f(r, \lambda) $ | (13) |
| $ \left.\frac{\partial T(r, \theta, \lambda)}{\partial \theta}\right|_{\theta=\theta_{0}}=g(r, \lambda) $ | (14) |
可以看出,两式等号右端的函数均与θ无关,而在球谐分析中,仅有缔合勒让德函数与θ有关。式(13)和式(14)的基函数可以通过以下2个方程分别满足:
| $ p_{n}^{m}(\theta)=0 $ | (15) |
| $ \left.\frac{\partial p_{n}^{m}(\theta)}{\partial \theta}\right|_{\theta=\theta_{0}}=0 $ | (16) |
由于其经度范围和球谐分析中的经度范围相同,因此对应的本征值m为整数变量。当给定式(15)和式(16)的θ0时,可单独确定一组对应m的n值序列,此时的n为非整数,非整阶缔合勒让德函数的特征值可通过Muller方法计算得到[10]。通过球冠来确定非整阶勒让德函数序列[11]时, 需要2个正交基数,令k为n值序列的下标,并定义k-m为奇数时,采用式(15)获取的本征值序列;k-m为偶数时采用式(16)获取的本征值序列。可以看出,球冠谐函数描述的地球重力场是局部区域的,与全球区域的球谐函数存在差异:在求解关于余纬的偏微分方程时,球谐分析中方程的本征值是整数,而球冠谐分析中的本征值是非整数。扰动位球冠谐展开式为:
| $ \begin{gathered} T=\frac{G M}{r} \sum\limits_{k=2}^{N} \sum\limits_{m=0}^{k}\left(\frac{a}{r}\right)^{n} \times \\ {\left[C_{k}^{m} \cos m \lambda+S_{k}^{m} \sin m \lambda\right] P_{n}^{m}(\theta)} \end{gathered} $ | (17) |
式中,n为勒让德函数的阶数,为非整数。规格化非整阶缔合勒让德函数Pnm(θ)的值可通过超几何函数计算得到[12]。
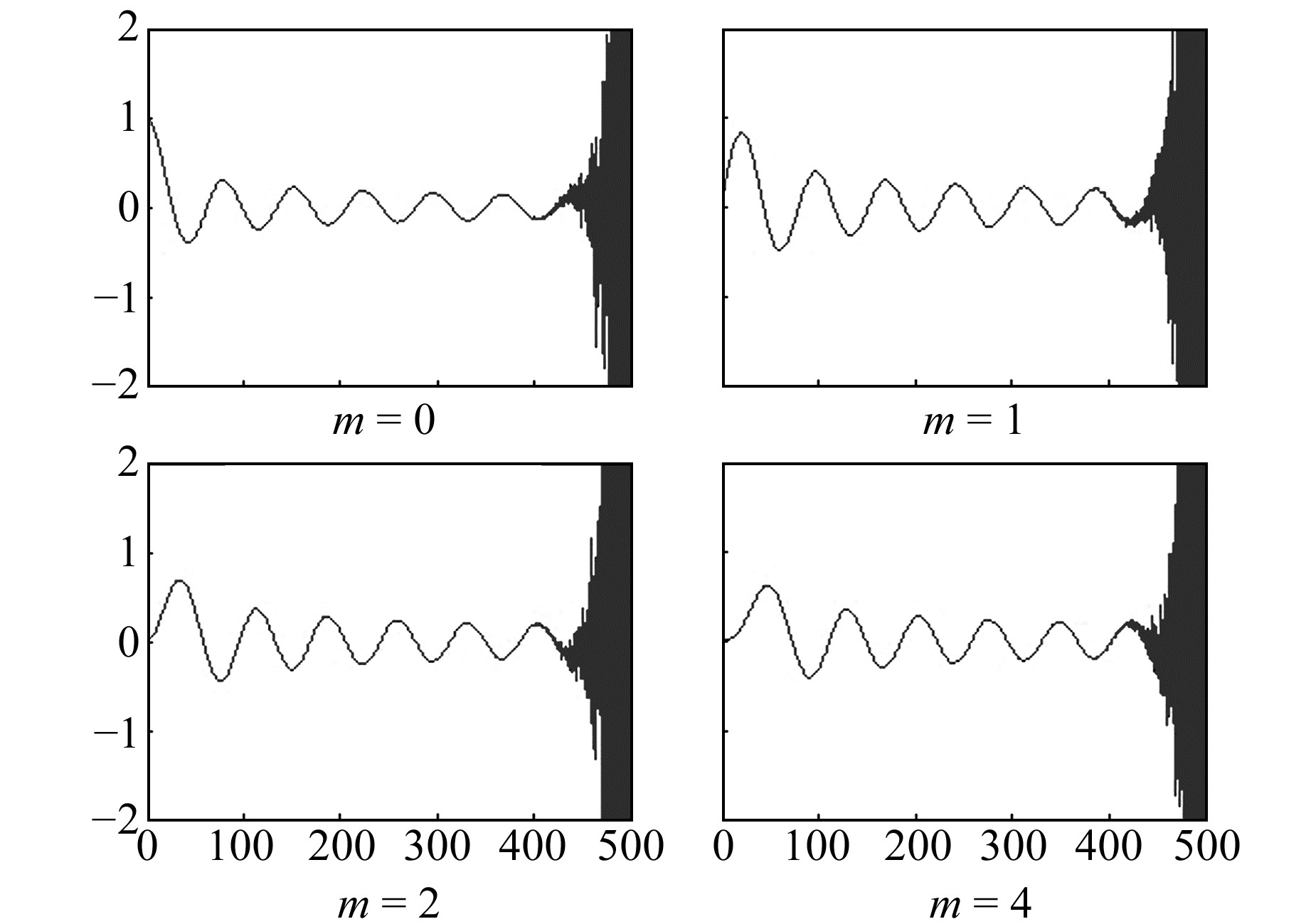
由于受非整阶缔合勒让德函数的限制,球冠谐模型很难达到高分辨率,球冠半径较小(如5°以下)的函数变化更为迅速。图 2为球冠半径为5°,m=0、1、2、4时的函数值,可以看出,能计算出的零根值数量在10个左右。Haines[13]利用逼近方法改进算法,但仍有较大误差。利用球冠谐模型逼近区域大地水准面可达到cm级的逼近精度,但随着区域的扩大及地形的复杂化,球冠谐模型仍受阶次扩展的限制。为克服这一限制,借用球冠谐映射方法,将球冠坐标系变换后采用整阶次缔合勒让德函数进行计算[14]。
|
图 2 缔合勒让德函数值 Fig. 2 Legendre values |
确定逼近区域后,根据球冠谐理论设计球冠半径和球冠中心,在保持相当精度的前提下,将球冠谐函数改进为虚拟球谐函数。将余纬θ的定义域(0,θ0)映射到(0,π)上,用整阶次缔合勒让德函数代替非整阶缔合勒让德函数。虚拟球谐方法需要将原坐标系转换到新坐标系中:
| $ \left\{\begin{array}{l} r^{\prime}=r \\ \lambda^{\prime}=\lambda \\ \theta^{\prime}=s \theta \end{array}\right. $ | (18) |
式中,
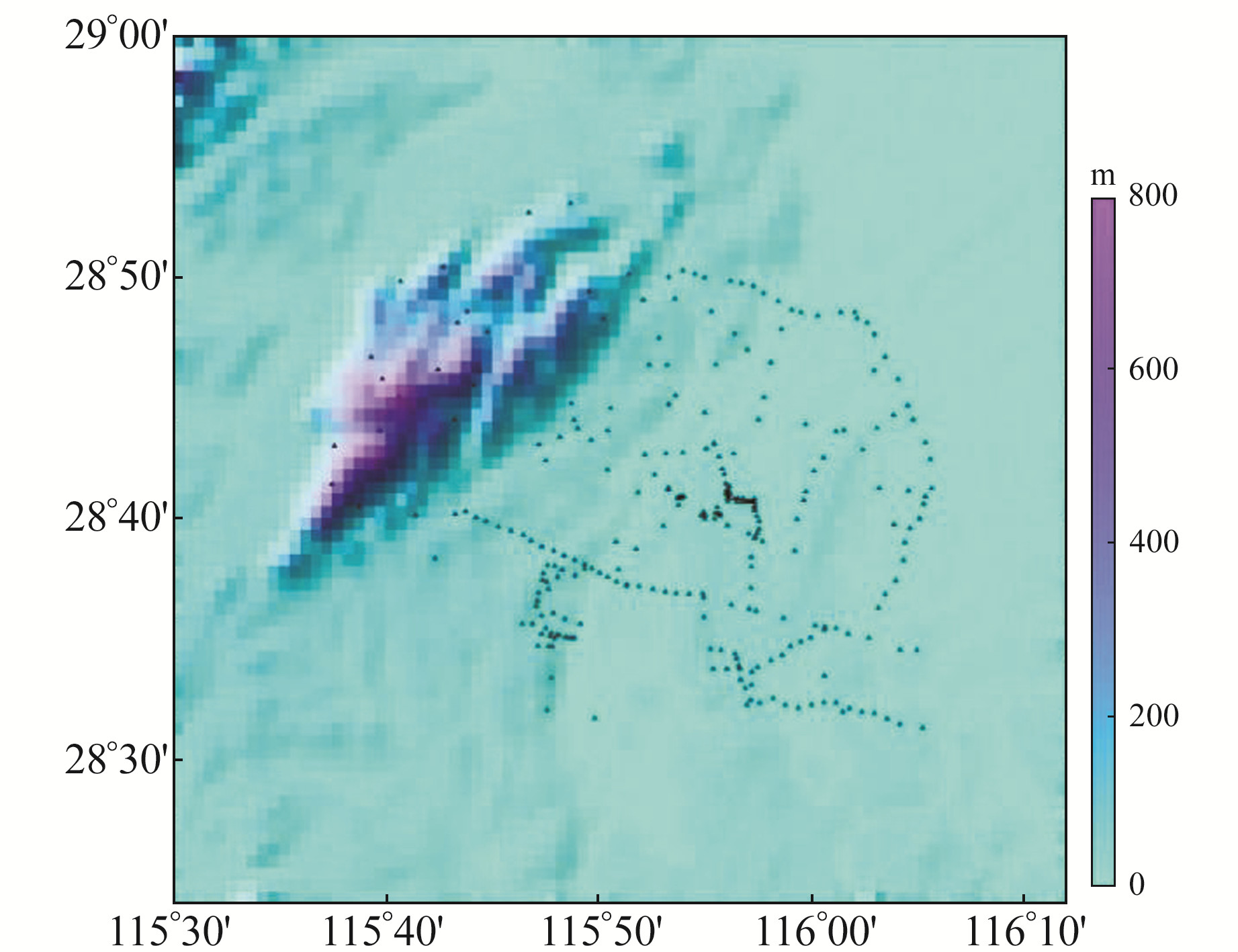
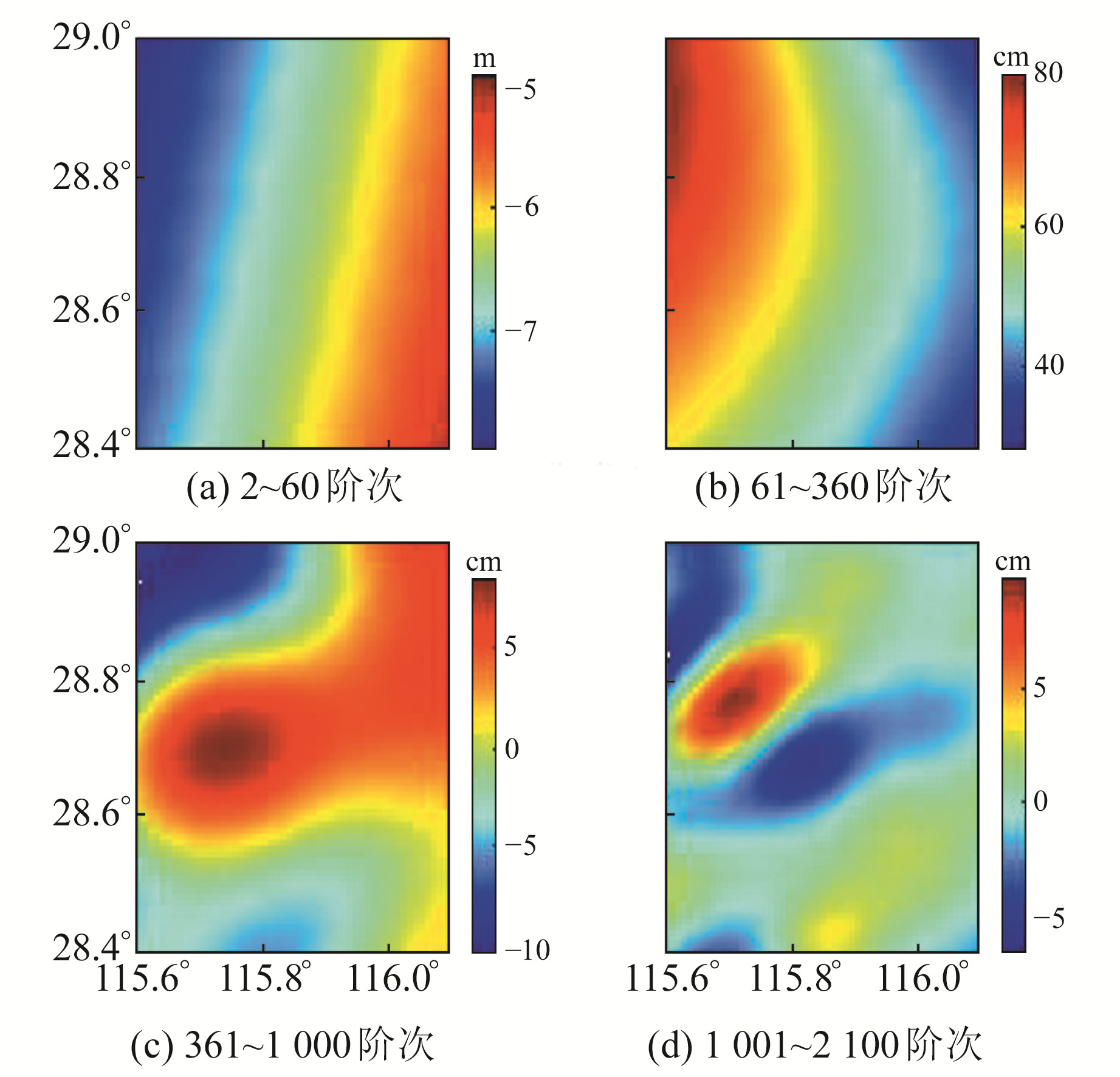
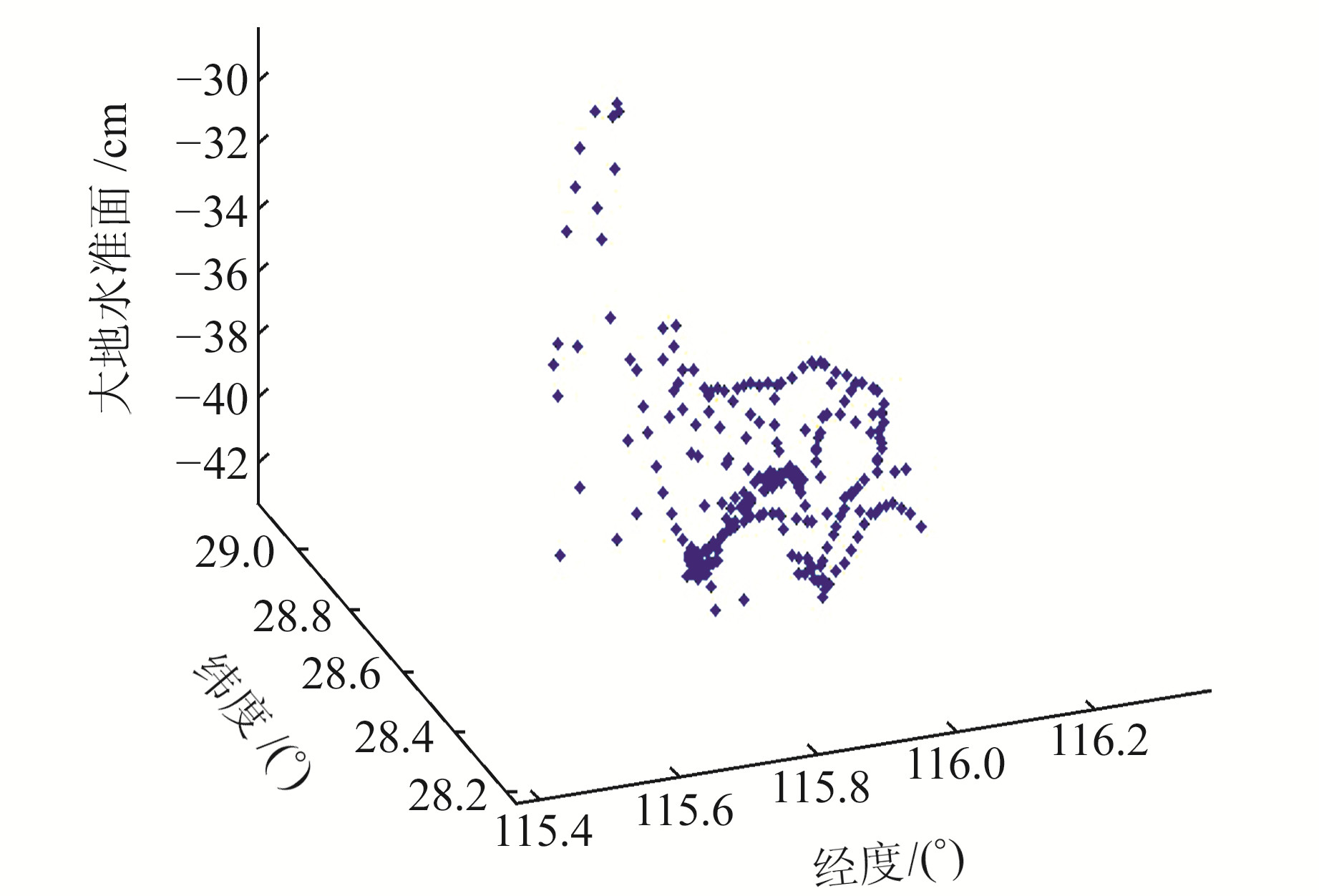
以南昌市为例进行实验(图 3),数据点由主要交通路线随机采样获得。通过EGM2008模型计算该区域内阶次分别为2~60、61~360、361~1 000、1 001~2 100的大地水准面,计算结果如图 4所示。可以看出,60阶次内的重力场模型计算的大地水准面起伏范围达到2 m,61~360阶次范围内的大地水准面起伏范围达到40 cm,360阶次以上的大地水准面起伏范围大约为20 cm,此时的起伏范围已经较小。对图 3中的采样点进行数值计算,得到剩余大地水准面数据范围为-42~-30 cm,具体见图 5。在此基础上,增加1 cm的白噪声误差。
|
图 3 数据采集范围 Fig. 3 Data collection range |
|
图 4 不同阶次大地水准面起伏情况 Fig. 4 The geoid undulates in different orders |
|
图 5 去除360阶次重力场模型后的大地水准面数据 Fig. 5 The geoid after removing the 360-order gravitational field model |
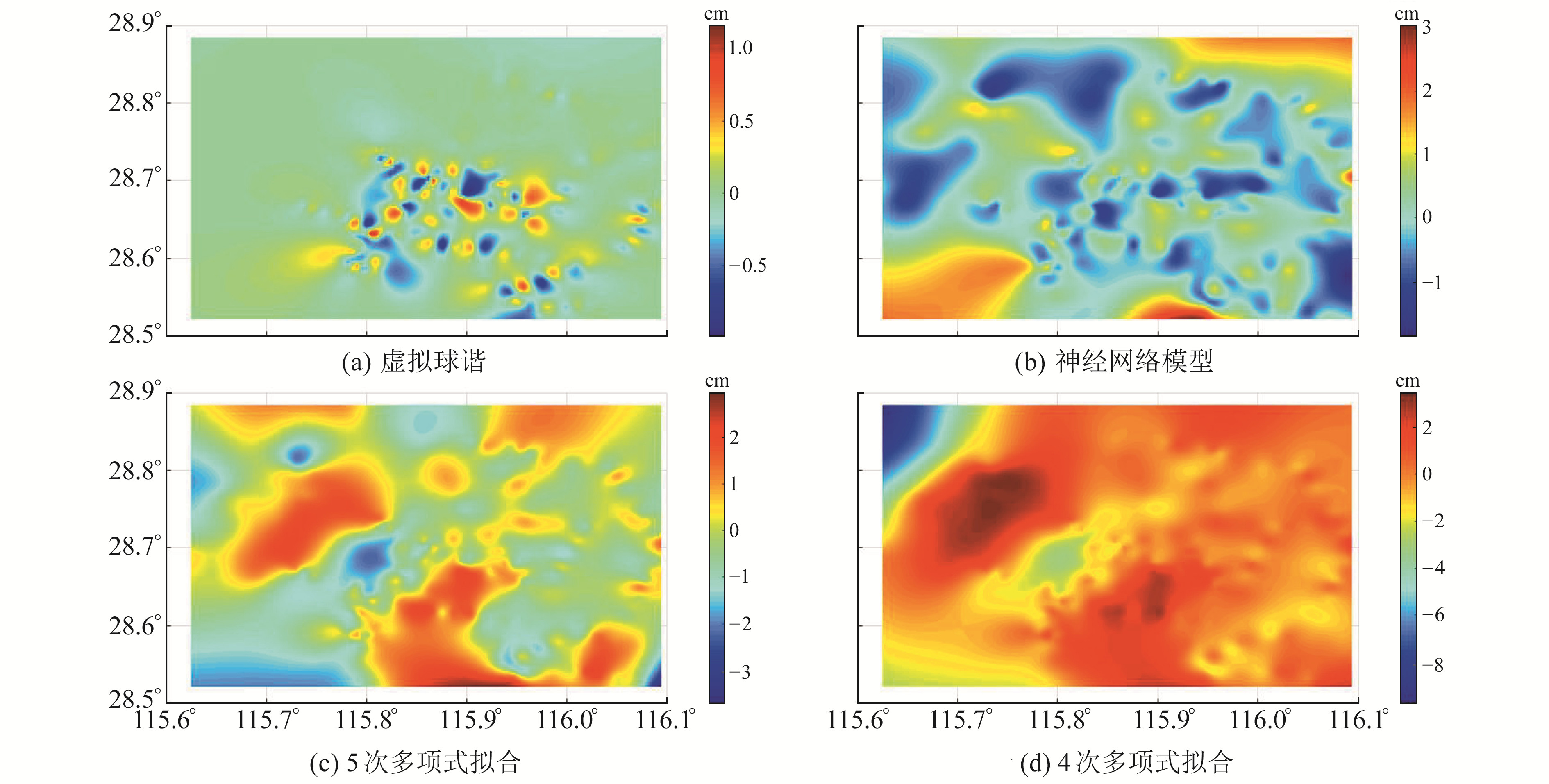
通过重力场模型滤波后得到新的观测值,然后将地理坐标转换为球冠坐标。实验数据范围大约在1°左右,其中半径为0.5°,添加0.5°的过渡带。根据虚拟球谐理论设置虚拟半径[15]为1°,模型阶次设定为13,利用式(18)将球冠坐标转换为新的虚拟坐标,并在新坐标系下利用球谐函数构建模型。为突出虚拟球谐理论的优越性,加入多项式拟合和神经网络模型进行对比,结果如图 6所示。
|
图 6 误差分布 Fig. 6 Error distribution |
实验结果表明,虚拟球谐方法的拟合精度最高,达到1 cm,RMS值和STD值是4种方法中最小的,都只有0.308 cm;其次是神经网络模型,拟合精度基本优于2 cm;4次多项式的拟合误差较大,接近5 cm。具体实验结果如表 1所示。
|
|
表 1 精度表 Tab. 1 Precision table |
本文研究构建市级大地水准面的虚拟球谐理论及方法,并以南昌市为例,对比分析了虚拟球谐方法、多项式拟合方法及神经网络模型。从实验结果可以看出,虚拟球谐方法的RMS值只有0.308 cm,低于多项式拟合和神经网络模型,表明虚拟球谐方法偏差更小、效果更好。本文仅采用重力场位模型数据对观测值进行简单的移去和恢复操作,没有综合利用重力数据和地形数据,因此未来仍需作进一步探索研究。
| [1] |
李建成. 智能时代测绘学科发展战略[C]. 中国测绘学会2020学术年会, 郑州, 2020 (Li Jiancheng. Surveying and Mapping Discipline Development Strategy in Intelligent Age[C]. Chinese Society for Geodesy Photogrammetry and Cartography 2020 Annual Meeting, Zhengzhou, 2020)
(  0) 0) |
| [2] |
National Geodetic Survey. The NGS Geoid Page[EB/OL].https://www.ngs.noaa.gov/GEOID, 2021
(  0) 0) |
| [3] |
Geoscience Australia. AUSGeoid2020[EB/OL]. http://www.ga.gov.au/ausgeoid, 2021
(  0) 0) |
| [4] |
Government of Canada. Height Reference System[EB/OL]. https://www.nrcan.gc.ca/height-reference-system-modernization/9054#_Toc3729015, 2021
(  0) 0) |
| [5] |
冯进凯, 王庆宾, 黄炎, 等. 一种基于自适应点质量的区域(似)大地水准面拟合方法[J]. 武汉大学学报: 信息科学版, 2019, 44(6): 837-843 (Feng Jinkai, Wang Qingbin, Huang Yan, et al. Quasigeoid/Geoid Determination with Adaptive Position Point Mass[J]. Geomatics and Information Science of Wuhan University, 2019, 44(6): 837-843)
(  0) 0) |
| [6] |
董明旭, 李建成, 华亮春, 等. 湖南省似大地水准面2017模型及精度分析[J]. 大地测量与地球动力学, 2019, 39(1): 66-71 (Dong Mingxu, Li Jiancheng, Hua Liangchun, et al. Hunan 2017 GNSS Gravity Quasi-Geoid Model and Its Precision Analysis[J]. Journal of Geodesy and Geodynamics, 2019, 39(1): 66-71)
(  0) 0) |
| [7] |
Heiskanen W A, Moritz H. Physical Geodesy[M]. San Francisco: Freeman and Company, 1967
(  0) 0) |
| [8] |
Li J C, Chao D B, Ning J S. Spherical Cap Harmonic Expansion for Local Gravity Field Representation[J]. Manuscripta Geodaetica, 1995, 20(4): 265-277
(  0) 0) |
| [9] |
Haines G V. Spherical Cap Harmonic Analysis[J]. Journal of Geophysical Research: Solid Earth, 1985, 90(B3): 2 583-2 591 DOI:10.1029/JB090iB03p02583
(  0) 0) |
| [10] |
彭富清, 于锦海. 球冠谐分析中非整阶Legendre函数的性质及其计算[J]. 测绘学报, 2000, 29(3): 204-208 (Peng Fuqing, Yu Jinhai. The Characters and Computation of Legendre Function with Non-Integral Degree in SCHA[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 204-208)
(  0) 0) |
| [11] |
吴招才, 刘天佑, 高金耀. 局部重力场球冠谐分析中的导数计算及应用[J]. 海洋与湖沼, 2006, 37(6): 488-492 (Wu Zhaocai, Liu Tianyou, Gao Jinyao. Derivative Calculation and Application in Spherical Cap Harmonic Analysis of Local Gravity Field[J]. Oceanologia et Limnologia Sinica, 2006, 37(6): 488-492)
(  0) 0) |
| [12] |
Lebedev N N. Special Functionsn and Their Application[M]. Englewood: Prentice-Hall, 1965
(  0) 0) |
| [13] |
Haines G V. Computer Programs for Spherical Cap Harmonic Analysis of Potential and General Fields[J]. Computers & Geosciences, 1988, 14(4): 413-447
(  0) 0) |
| [14] |
王建强, 赵国强, 朱广彬. 常用超高阶次缔合勒让德函数计算方法对比分析[J]. 大地测量与地球动力学, 2009, 29(2): 126-130 (Wang Jianqiang, Zhao Guoqiang, Zhu Guangbin. Contrastive Analysis of Common Computing Methods of Ultra-High Degree and Order Fully Normalized Associated Legendre Function[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 126-130)
(  0) 0) |
| [15] |
王建强, 储王宁, 戴必旭, 等. 大地水准面数值计算及结构分析[J]. 测绘科学, 2017, 42(4): 129-132 (Wang Jianqiang, Chu Wangning, Dai Bixu, et al. Geoid Numerical Calculation and Structural Analysis[J]. Science of Surveying and Mapping, 2017, 42(4): 129-132)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

