研究地球重力场需要计算fnALFs数值及其各阶导数和定积分数值,使用的递推公式目前主要有标准向前按列或行递推公式[1-2]、贝尔科夫递推公式[3]及跨阶次递推公式[4]等。随着卫星重力学研究的发展,需要计算超高阶的fnALFs数值,目前主要通过选择合适的计算方法和修正语言编程2种途径来提高计算速度和扩展递推阶次,如傅里叶级数展开法[5-7]和多项式逼近法[8]等。
标准向前按列递推公式的应用很广泛[9-12],但这些研究都是通过对算法进行改进来扩展递推阶次。本文不讨论算法,只是在Paul[1]理论研究的基础上完善扇谐项和准扇谐项推导的严谨性,基于fnALFs的2个导数公式给出推导fnALFs定积分递推公式的新方法,且本文给出的递推公式可从第2阶开始递推。
1 关于fnALFs及其积分的按列递推公式首先给出完善后的fnALFs标准按列递推公式:
| $ \begin{gathered} \overline{\boldsymbol{P}}{}_{n}^{m}(\cos \theta)= \\ \left\{\begin{array}{l} A_{1} \cos \theta \overline{\boldsymbol{P}}{}_{n-1}^{m}(\cos \theta)-A_{2} \overline{\boldsymbol{P}}{}_{n-2}^{m}(\cos \theta), \\ \ \ \ \ 0 \leqslant m \leqslant(n-2) \\ A_{3} \cos \theta \overline{\boldsymbol{P}}{}_{n-1}^{n-1}(\cos \theta), m=n-1 \\ A_{4} \sin \theta \overline{\boldsymbol{P}}{}_{n-1}^{n-1}(\cos \theta), m=n \end{array}\right. \end{gathered} $ | (1) |
式中,θ∈[0, π]。其中,
| $ \left\{ {\begin{array}{*{20}{l}} {{A_1} = \sqrt {\frac{{(2n - 1)(2n + 1)}}{{(n - m)(n + m)}}} }\\ {{A_2} = \sqrt {\frac{{(2n + 1)(n - m - 1)(n + m - 1)}}{{(2n - 3)(n - m)(n + m)}}} }\\ {{A_3} = \sqrt {2n + 1} }\\ {{A_4} = \sqrt {\frac{{2n + 1}}{{2n}}} } \end{array}} \right. $ |
fnALFs定积分的标准按列递推公式为:
| $ \begin{gathered} \overline{\boldsymbol{I}}{}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)= \\ \left\{\begin{array}{l} B_{1} \overline{\boldsymbol{I}}{}_{n-2}^{m}\left(\theta_{1}, \theta_{2}\right)+B_{2} \overline{\boldsymbol{Z}}{}_{n-1}^{m}\left(\theta_{1}, \theta_{2}\right), \\ \ \ \ \ 0 \leqslant m \leqslant(n-2) \\ B_{3} \overline{\boldsymbol{Z}}{}_{n-1}^{n-1}\left(\theta_{1}, \theta_{2}\right), m=n-1 \\ B_{4} \overline{\boldsymbol{I}}{}_{n-2}^{n-2}\left(\theta_{1}, \theta_{2}\right)-B_{5} \overline{\boldsymbol{Z}}{}_{n-1}^{n-2}\left(\theta_{1}, \theta_{2}\right), m=n \end{array}\right. \end{gathered} $ | (2) |
式中,
| $ \left\{\begin{array}{l} B_{1}=\frac{(n-2)}{(n+1)} \times \\ \ \ \ \ \ \ \ \ \sqrt{\frac{(2 n+1)(n-m-1)(n+m-1)}{(2 n-3)(n-m)(n+m)}} \\ B_{2}=\frac{1}{(n+1)} \sqrt{\frac{(2 n-1)(2 n+1)}{(n-m)(n+m)}} \\ B_{3}=\frac{1}{(n+1)} \sqrt{(2 n+1)} \\ B_{4}=\frac{n}{2(n+1)} \sqrt{\frac{\left(2-\delta_{0}^{n}\right)(2 n-1)(2 n+1)}{\left(2-\delta_{0}^{n-2}\right)(n-1) n}} \\ B_{5}=\frac{1}{2(n+1)} \sqrt{\frac{\left(2-\delta_{0}^{n}\right)(2 n+1)}{\left(2-\delta_{0}^{n-2}\right)(n-1) n}} \end{array}\right. $ |
当积分区间很小时,可采用式(3):
| $ \begin{array}{c} \overline{\boldsymbol{I}}{}_{n}^{n}\left(\theta_{1}, \theta_{2}\right)=\sqrt{\frac{2(2 n+1) !}{\left(2^{n} n !\right)^{2}}}(\sin \theta)^{n+2} \times\\ \left.\sum\limits_{j=0}^{\infty} \frac{(2 j) !(\sin \theta)^{2 j}}{\left(2^{j} j !\right)^{2}(n+2 j+2)}\right|_{\theta_{1}} ^{\theta_{2}} \end{array} $ | (3) |
以上公式的精度评定见文献[1]。
2 关于式(1)的证明| $ \begin{gathered} \boldsymbol{P}_{n}(\cos \theta)=\frac{1}{2^{n} n !} \frac{\mathrm{d}^{n}\left(\cos ^{2} \theta-1\right)^{n}}{\mathrm{~d}(\cos \theta)^{n}}= \\ \sum\limits_{k=0}^{\text {int}\left[\frac{n}{2}\right]} \frac{(-1)^{k}}{2^{n}(n-k) ! k !} \frac{(2 n-2 k) !}{(n-2 k) !}(\cos \theta)^{n-2 k} \end{gathered} $ | (4) |
式中,int[·]表示取整数,n=0, 1, 2, …。
| $ \begin{gathered} \boldsymbol{P}_{n}^{m}(\cos \theta)=\sin ^{m} \theta \frac{\mathrm{d}^{m} \boldsymbol{P}_{n}(\cos \theta)}{\mathrm{d}(\cos \theta)^{m}}= \\ \sum\limits_{k=0}^{\text {int}\left[\frac{(n-m)}{2}\right]} \frac{(-1)^{k}(2 n-2 k) ! \sin ^{m} \theta(\cos \theta)^{n-m-2 k}}{2^{n}(n-k) ! k !(n-m-2 k) !} \end{gathered} $ | (5) |
显然,当m=0时,式(5)等同于式(4)。关于fnALFs的定义[13-15]为:
| $ \begin{gathered} \overline{\boldsymbol{P}}{}_{n}^{m}(\cos \theta)=N_{n}^{m} \boldsymbol{P}_{n}^{m}(\cos \theta)= \\ \sqrt{\frac{\left(2-\delta_{0}^{m}\right)(2 n+1)(n-m) !}{(n+m) !}} \boldsymbol{P}_{n}^{m}(\cos \theta) \end{gathered} $ | (6) |
规格化的目的是使不同阶次的
| $ \begin{gathered} (n-m) \boldsymbol{P}_{n}^{m}(\cos \theta)=(2 n-1) \cos \theta \boldsymbol{P}_{n-1}^{m}(\cos \theta)- \\ (n+m-1) \boldsymbol{P}_{n-2}^{m}(\cos \theta) \end{gathered} $ | (7) |
式(7)被称为标准按列(次)递推公式。利用式(6)将式(7)规格化,直接得到式(1)中的第1种情况。关于
根据式(5)可得:
| $ \left\{\begin{array}{l} \boldsymbol{P}_{n}^{n-1}(\cos \theta)=\sin ^{n-1} \theta \frac{(2 n) !}{2^{n} n !} \cos \theta \\ \boldsymbol{P}_{n}^{n}(\cos \theta)=\sin ^{n} \theta \frac{(2 n) !}{2^{n} n !} \end{array}\right. $ | (8) |
根据式(8)可直接得到:
| $ \left\{\begin{array}{l} \boldsymbol{P}_{n}^{n-1}(\cos \theta)=(2 n-1) \cos \theta \boldsymbol{P}_{n-1}^{n-1}(\cos \theta) \\ \boldsymbol{P}_{n}^{n}(\cos \theta)=(2 n-1) \sin \theta \boldsymbol{P}_{n-1}^{n-1}(\cos \theta) \end{array}\right. $ | (9) |
将式(9)规格化,就可得到式(1)中第2种和第3种情况。
3 关于式(2)的证明定义ALFs的3个定积分公式:
| $ \left\{\begin{array}{l} \boldsymbol{I}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\int_{\theta_{1}}^{\theta_{2}} \boldsymbol{P}_{n}^{m}(\cos \theta) \sin \theta \mathrm{d} \theta \\ \boldsymbol{J}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\int_{\theta_{1}}^{\theta_{2}} \cos \theta \boldsymbol{P}_{n}^{m}(\cos \theta) \sin \theta \mathrm{d} \theta \\ \boldsymbol{K}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\int_{\theta_{1}}^{\theta_{2}} \sin \theta \boldsymbol{P}_{n}^{m}(\cos \theta) \sin \theta \mathrm{d} \theta \end{array}\right. $ | (10) |
| $ \boldsymbol{Z}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\left.\sin ^{2} \theta \boldsymbol{P}_{n}^{m}(\cos \theta)\right|_{\theta_{1}} ^{\theta_{2}} $ | (11) |
将式(10)和式(11)中的Pnm(cosθ)变换为
ALFs的一个导数公式[15]为:
| $ \begin{gathered} (2 n+1) \sin ^{2} \theta \frac{\mathrm{d} \boldsymbol{P}_{n}^{m}(\cos \theta)}{\mathrm{d}(\cos \theta)}=(n+1)(n+m) \times \\ \boldsymbol{P}_{n-1}^{m}(\cos \theta)-n(n-m+1) \boldsymbol{P}_{n+1}^{m}(\cos \theta) \end{gathered} $ | (12) |
另一个导数公式[15]为:
| $ \begin{gathered} \sin ^{2} \theta \frac{\mathrm{d} \boldsymbol{P}_{n}^{m}(\cos \theta)}{\mathrm{d}(\cos \theta)}= \\ \sin \theta \boldsymbol{P}_{n}^{m+1}(\cos \theta)-m \cos \theta \boldsymbol{P}_{n}^{m}(\cos \theta) \end{gathered} $ | (13) |
式(13)可根据式(5)直接得到。设有:
| $ \boldsymbol{H}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\int_{\theta_{1}}^{\theta_{2}} \sin ^{2} \theta \frac{\mathrm{d} \boldsymbol{P}_{n}^{m}(\cos \theta)}{\mathrm{d}(\cos \theta)} \sin \theta \mathrm{d} \theta $ | (14) |
对式(14)采用分部积分法,并考虑式(10)和式(11)可得:
| $ \boldsymbol{H}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=-\boldsymbol{Z}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)+2 \boldsymbol{J}_{n}^{m}\left(\theta_{1}, \theta_{2}\right) $ | (15) |
同理,根据式(12)和式(13)可得:
| $ \begin{gathered} \boldsymbol{H}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\frac{(n+1)(n+m)}{(2 n+1)} \boldsymbol{I}_{n-1}^{m}\left(\theta_{1}, \theta_{2}\right)- \\ \frac{n(n-m+1)}{(2 n+1)} \boldsymbol{I}_{n+1}^{m}\left(\theta_{1}, \theta_{2}\right) \end{gathered} $ | (16) |
| $ \boldsymbol{H}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\boldsymbol{K}_{n}^{m+1}\left(\theta_{1}, \theta_{2}\right)-m \boldsymbol{J}_{n}^{m}\left(\theta_{1}, \theta_{2}\right) $ | (17) |
根据式(7)可得:
| $ \begin{gathered} (2 n+1) \boldsymbol{J}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=(n-m+1) \boldsymbol{I}_{n+1}^{m}\left(\theta_{1}, \theta_{2}\right)+ \\ (n+m) \boldsymbol{I}_{n-1}^{m}\left(\theta_{1}, \theta_{2}\right) \end{gathered} $ | (18) |
根据式(15)~式(18)可得:
| $ \begin{array}{c} \boldsymbol{I}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\frac{(n-2)(n+m-1)}{(n+1)(n-m)} \boldsymbol{I}_{n-2}^{m}\left(\theta_{1}, \theta_{2}\right)+ \\ \frac{(2 n-1)}{(n+1)(n-m)} \boldsymbol{Z}_{n-1}^{m}\left(\theta_{1}, \theta_{2}\right) \end{array} $ | (19) |
式(19)只适用于0≤m≤(n-2)的情况。
下面推导m=n-1时n的情况。根据式(8)中Pnn-1(cosθ)的表达式可得:
| $ \begin{gathered} \boldsymbol{I}_{n}^{n-1}\left(\theta_{1}, \theta_{2}\right)=\frac{(2 n) !}{2^{n} n !} \int_{\theta_{1}}^{\theta_{2}} \sin ^{n} \theta \mathrm{d}(\sin \theta)= \\ \left.\frac{(2 n) !}{2^{n}(n+1) !} \sin ^{n+1} \theta\right|_{\theta_{1}} ^{\theta_{2}}=\frac{(2 n-1)}{(n+1)} \boldsymbol{Z}_{n-1}^{n-1}\left(\theta_{1}, \theta_{2}\right) \end{gathered} $ | (20) |
在式(19)中,令m=n-1且不考虑等号右端第1项,就等价于式(20)。将式(19)和式(20)规格化,就可得到式(2)中第1种和第2种情况。
根据式(8)中Pnn(cosθ)的表达式,经过理论推导可得:
| $ \begin{gathered} \boldsymbol{I}_{n}^{n}\left(\theta_{1}, \theta_{2}\right)=\frac{(2 n) !}{2^{n} n !} \int_{\theta_{1}}^{\theta_{2}} \sin ^{n+1} \theta \mathrm{d} \theta=\frac{(2 n) !}{2^{n} n !} \times \\ \left\{-\left.\frac{\sin ^{n} \theta \cos \theta}{(n+1)}\right|_{\theta_{1}} ^{\theta_{2}}+\frac{n}{(n+1)} \int_{\theta_{1}}^{\theta_{2}} \sin ^{n-1} \theta \mathrm{d} \theta\right\}= \\ \frac{n(2 n-3)(2 n-1)}{(n+1)} \boldsymbol{I}_{n-2}^{n-2}\left(\theta_{1}, \theta_{2}\right)- \\ \frac{(2 n-1)}{(n+1)} \boldsymbol{Z}_{n-1}^{n-2}\left(\theta_{1}, \theta_{2}\right) \end{gathered} $ | (21) |
在两极附近y=sinθ值很小,依据式(21)的递推会产生较大误差。根据
| $ \begin{gathered} \frac{1}{\sqrt{1-y^{2}}}=1+\frac{1}{2} y^{2}+\frac{1 \cdot 3}{2 \cdot 4} y^{4}+ \\ \frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6} y^{6}+\cdots=\sum\limits_{j=0}^{\infty} \frac{(2 j) !}{\left(2^{j} j !\right)^{2}} y^{2 j} \end{gathered} $ |
可得:
| $ \begin{gathered} \boldsymbol{I}_{n}^{n}\left(\theta_{1}, \theta_{2}\right)=\frac{(2 n) !}{2^{n} n !} \int_{\theta_{1}}^{\theta_{2}} \sin ^{n+1} \theta \mathrm{d} \theta= \\ \frac{(2 n) !}{2^{n} n !} \int_{y_{1}}^{y_{2}} \frac{y^{n+1}}{\sqrt{1-y^{2}}} \mathrm{~d} y= \\ \frac{(2 n) !}{2^{n} n !} \sum\limits_{j=0}^{\infty} \int_{y_{1}}^{y_{2}} \frac{(2 j) !}{\left(2^{j} j !\right)^{2}} y^{n+2 j+1} \mathrm{~d} y= \\ \left.\frac{(2 n) !}{2^{n} n !} y^{n+2} \sum\limits_{j=0}^{\infty} \frac{(2 j) ! y^{2 j}}{\left(2^{j} j !\right)^{2}(n+2 j+2)}\right|_{y_{1}} ^{y_{2}} \end{gathered} $ | (22) |
将式(21)和式(22)规格化,可得式(2)中第3种情况和式(3)。关于式(2)中第3种情况,文献[1]给出的系数为:
| $ \left\{\begin{array}{l} B_{4}=\frac{n}{2(n+1)} \sqrt{\frac{(2 n-1)(2 n+1)}{(n-1) n}} \\ B_{5}=\frac{1}{2(n+1)} \sqrt{\frac{(2 n+1)}{(n-1) n}} \end{array}\right. $ | (23) |
这显然与本文结果不一致。由此可见,文献[1]中的公式只能从第3阶开始递推,而不能从第2阶开始递推。
4 数值计算与分析第n阶fnALFs数值计算结果的精度检验公式[1]为:
| $ \boldsymbol{T}(n)=\frac{1}{(2 n+1)}\left|(2 n+1)-\sum\limits_{m=0}^{n}\left[\overline{\boldsymbol{P}}_{n}^{m}(\cos \theta)\right]^{2}\right| $ | (24) |
关于fnALFs数值积分最简单的精度检验公式[1]为:
| $ \boldsymbol{H}_{n}^{m}=\left|\frac{\left[\overline{\boldsymbol{I}}{}_{n}^{m}\left(\theta_{1}, \theta_{m}\right)+\overline{\boldsymbol{I}}{}_{n}^{m}\left(\theta_{m}, \theta_{2}\right)\right]-\overline{\boldsymbol{I}}{}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)}{\left[\overline{\boldsymbol{I}}{}_{n}^{m}\left(\theta_{1}, \theta_{m}\right)+\overline{\boldsymbol{I}}{}_{n}^{m}\left(\theta_{m}, \theta_{2}\right)\right]}\right| $ | (25) |
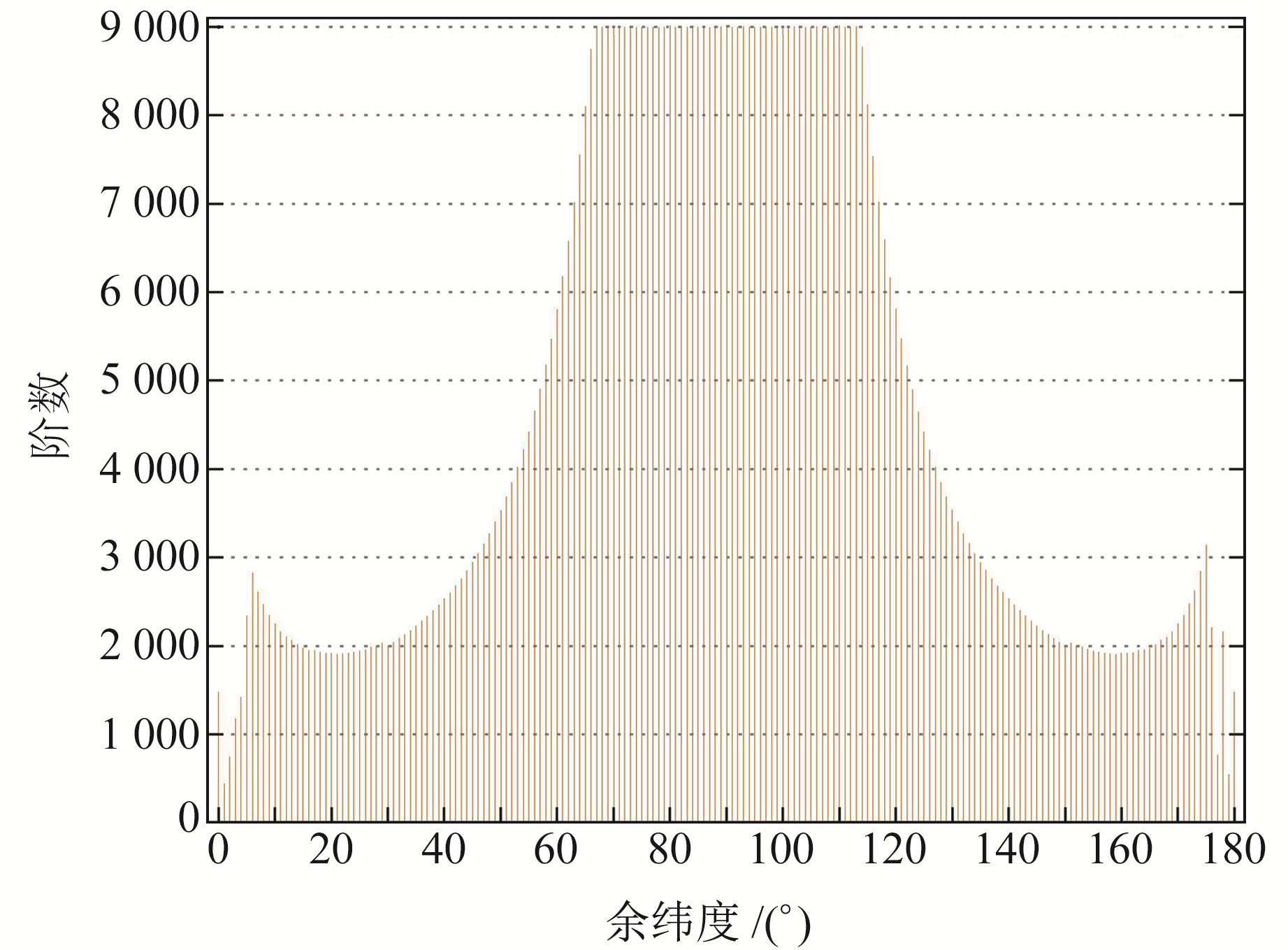
式中,θ1<θm<θ2。理论上T(n)和Hnm应该等于0,但由于计算机的存储和计算误差,使得其计算结果不为0。只有当其小于某个实数(如10-12)时,表明其在第n阶上是适用的,否则不适用。图 1给出了递推公式(1)的适用性。
|
图 1 公式(1)的适用性(T(n)<10-12) Fig. 1 Applicabilty to equation (1) |
图 1表明,在±23°纬度范围内,式(1)可将fnALFs递推至9 000阶;在±44°、±62°和±86°纬度范围内,可分别将fnALFs递推至3 000阶、2 000阶和1 000阶。在两极区域(纬度绝对值大于86°范围内),递推公式效果较差。
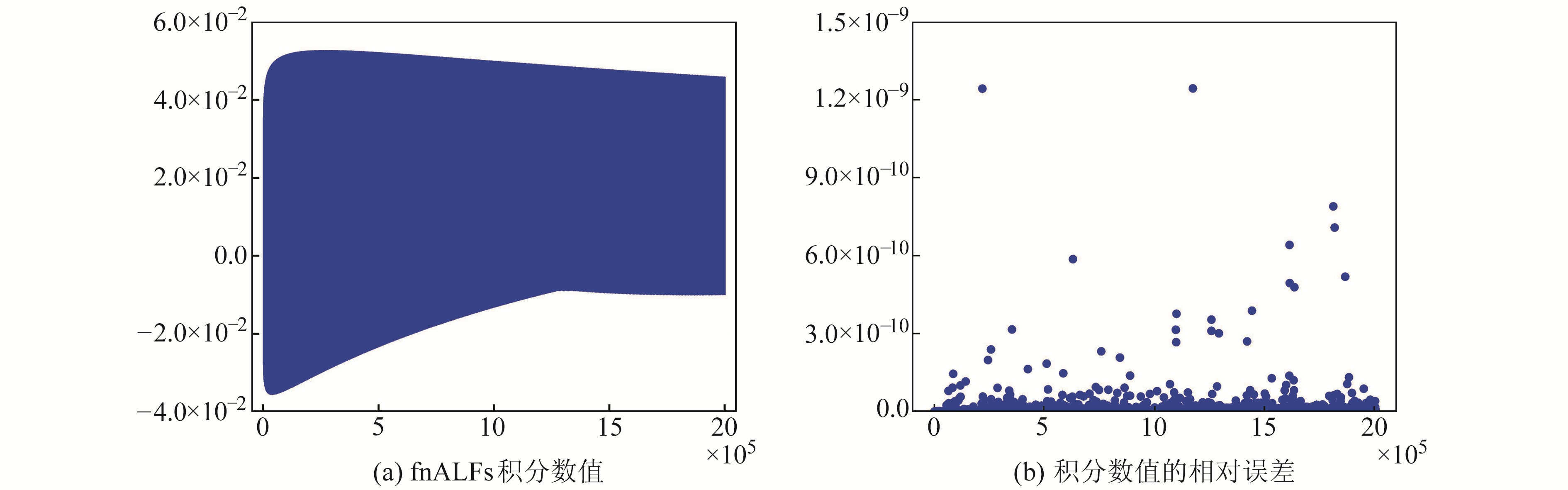
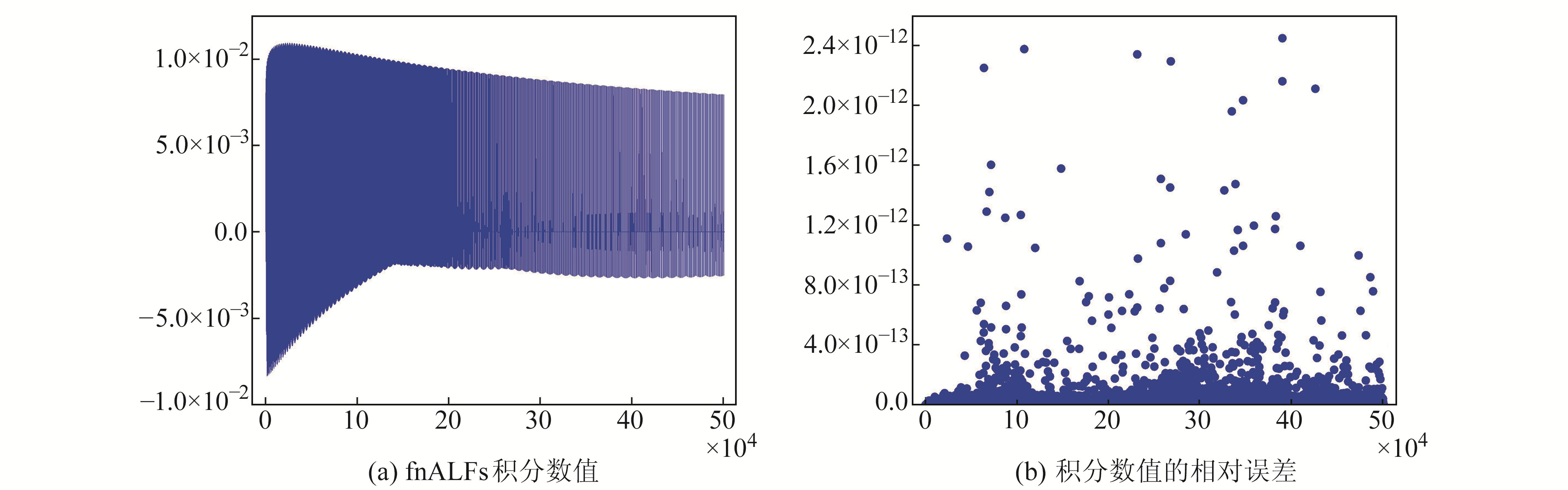
利用式(2)和式(3)计算fnALFs积分数值,当θ1=45°、θ2=46°时,
|
图 2 θ1=45°、θ2=46°且n=2 000阶时积分数值结果 Fig. 2 Integral numerical results when θ1=45°, θ2=46°, n=2 000 |
|
图 3 θ1=5°、θ2=6°且n=1 000阶时积分数值结果 Fig. 3 Integral numerical results when θ1=5°, θ2=6°, n=1 000 |
实际上,ALFs的带谐项(次为零)、扇谐项(次等于阶)、准带谐项(次等于1)及准扇谐项(次为阶减1)很特殊,统称为边界项,在其他形式递推公式的推导过程中表现尤为明显,甚至要扩展边界项范围,边界项的递推必须单独讨论。
ALFs导数公式的应用广泛,由其推导ALFs定积分公式的过程显得很简单。递推公式应明确指出最低可从第几阶开始,不然在应用中难免会出错。根据式(15)~式(18)还可得到如下2个形式的积分公式:
| $ \begin{gathered} \boldsymbol{J}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=\frac{(n+m)}{(n+2)} \boldsymbol{I}_{n-1}^{m}\left(\theta_{1}, \theta_{2}\right)+ \\ \frac{1}{(n+2)} \boldsymbol{Z}_{n}^{m}\left(\theta_{1}, \theta_{2}\right) \end{gathered} $ | (26) |
| $ \begin{aligned} \boldsymbol{K}_{n}^{m}\left(\theta_{1}, \theta_{2}\right)=& \frac{(n+m-1)(m+1)}{(n+2)} \boldsymbol{I}_{n-1}^{m-1}\left(\theta_{1}, \theta_{2}\right)-\\ & \frac{(n-m+1)}{(n+2)} \boldsymbol{Z}_{n}^{m-1}\left(\theta_{1}, \theta_{2}\right) \end{aligned} $ | (27) |
式(26)和式(27)只是一个计算式,当然也可得到其递推公式。
本文完善了ALFs扇谐项和准扇谐项的递推公式,利用ALFs的2个导数公式给出了定积分的标准向前按列递推公式,使推导过程更简明,可为ALFs的理论研究提供一定的参考。
| [1] |
Paul M K. Recurrence Relations for Integrals of Associated Legendre Functions[J]. Bulletin Géodésique, 1978, 52(3): 177-190
(  0) 0) |
| [2] |
Gleason D M. Partial Sums of Legendre Series via Clenshaw Summation[J]. Manuscripta Geodaetica, 1985, 10: 115-130
(  0) 0) |
| [3] |
Belikov M V. Spherical Harmonic Analysis and Synthesis with the Use of Column-Wise Recurrence Relations[J]. Manuscripta Geodaetica, 1991, 16(6): 384-410
(  0) 0) |
| [4] |
Swarztrauber P N. The Vector Harmonic Transform Method for Solving Partial Differential Equations in Spherical Geometry[J]. Monthly Weather Review, 1993, 121(12): 3415-3437 DOI:10.1175/1520-0493(1993)121<3415:TVHTMF>2.0.CO;2
(  0) 0) |
| [5] |
Földváry L. Sine Series Expansion of Associated Legendre Functions[J]. Acta Geodaetica et Geophysica, 2015, 50(2): 243-259 DOI:10.1007/s40328-014-0092-2
(  0) 0) |
| [6] |
Gruber C, Abrykosov O. On Computation and Use of Fourier Coefficients for Associated Legendre Functions[J]. Journal of Geodesy, 2016, 90(6): 525-535 DOI:10.1007/s00190-016-0891-z
(  0) 0) |
| [7] |
Fukushima T. Fast Computation of Sine/Cosine Series Coefficients of Associated Legendre Function of Arbitrary High Degree and Order[J]. Journal of Geodetic Science, 2018, 8(1): 162-173 DOI:10.1515/jogs-2018-0017
(  0) 0) |
| [8] |
Seif M R, Sharifi M A, Eshagh M. Polynomial Approximation for Fast Generation of Associated Legendre Functions[J]. Acta Geodaetica et Geophysica, 2018, 53(2): 275-293 DOI:10.1007/s40328-018-0216-1
(  0) 0) |
| [9] |
Fukushima T. Numerical Computation of Spherical Harmonics of Arbitrary Degree and Order by Extending Exponent of Floating Point Numbers[J]. Journal of Geodesy, 2012, 86(4): 271-285 DOI:10.1007/s00190-011-0519-2
(  0) 0) |
| [10] |
Fukushima T. Numerical Computation of Spherical Harmonics of Arbitrary Degree and Order by Extending Exponent of Floating Point Numbers: Ⅱ First-, Second-, and Third-Order Derivatives[J]. Journal of Geodesy, 2012, 86(11): 1019-1028 DOI:10.1007/s00190-012-0561-8
(  0) 0) |
| [11] |
Fukushima T. Numerical Computation of Spherical Harmonics of Arbitrary Degree and Order by Extending Exponent of Floating Point Numbers: Ⅲ Integral[J]. Computers and Geosciences, 2014, 63: 17-21 DOI:10.1016/j.cageo.2013.10.010
(  0) 0) |
| [12] |
Xing Z B, Li S S, Tian M, et al. Numerical Experiments on Column-Wise Recurrence Formula to Compute Fully Normalized Associated Legendre Functions of Ultra-High Degree and Order[J]. Journal of Geodesy, 2019, 94(1): 1-16
(  0) 0) |
| [13] |
Hobson E W. The Theory of Spherical and Ellipsoidal Harmonics[M]. UK: Cambridge University Press, 1955
(  0) 0) |
| [14] |
Heiskanen W A, Moritz H. Physical Geodesy[M]. San Francisco: W H Freeman and Co, 1967
(  0) 0) |
| [15] |
陆仲连. 球谐函数[M]. 北京: 解放军出版社, 1988 (Lu Zhonglian. Spherical Harmonic Functions[M]. Beijing: PLA Publishing House, 1988)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

