2. 中国测绘科学研究院,北京市莲花池西路28号,100036
带有齿轮系统及量测螺旋系统的LCR-G型和Burris型相对重力仪由于其特殊的结构,会存在周期误差,该误差主要由齿轮偏心、齿轮齿距分度误差、量测螺杆螺纹距误差等机制产生[1]。短周期项对重力基准网解算精度的影响平均约在3 μGal以下,而中长周期项的影响最大超过20 μGal[2-3]。因此,重力基准网的解算必须考虑周期项的影响。目前,重力基准网对周期项的解算主要是利用其周期项的展开式。一般情况下需考虑7个周期项,但是当7个周期项全部考虑时,由于参数过多会发生过拟合现象,且7个周期项全部解算精度要达到2 μGal以上大约需要200多个观测值[3-4],但在实际观测中很难保证每台仪器均获得200个以上的观测量。因此,相对重力仪周期项的选取是重力基准网解算的一个难题。
目前相对重力仪周期项的选取主要采用以下2种方法:1)根据误差传播定律,得出周期项的取舍标准[5],然后对周期项进行筛选;2)采用逐步回归分析法[6],利用多元回归方程中各变量方差的贡献进行显著性检验,根据检验结果对周期项进行保留或剔除。但这2种方法在筛选过程中均需要大量的观测量来支撑。在机器学习领域,有学者使用正则化方法[7-8]对多项式回归方程的冗余项进行剔除,结果表现良好,能有效防止过拟合现象。因此,本文基于2000国家重力基本网及2020最新国家重力基准网的观测数据,使用正则化方法,以LCR-G型相对重力仪为例,研究国家重力基准网中相对重力仪周期项参数的确定方法。
1 周期误差标定的原理 1.1 周期误差数学模型相对重力仪周期项的函数模型[9]为:
| $ Z(R)=\sum\limits_{n=1}^{P} A_{n} \cos \left(\frac{2 \pi R}{T_{n}}+\varphi_{n}\right) $ | (1) |
式中,An为各周期项的振幅,φn为各周期项的初相,R为仪器读数,Tn为相对重力仪的传动周期,一般情况下,n≤7。
由于该函数模型的形式不适合平差过程中的误差方程组建,因此,对其进行推导变换。令Xn=Ancosφn、Yn=-Ansinφn,将Xn和Yn作为误差参数代入式(1)得:
| $ Z(R)=\sum\limits_{n=1}^{P}\left(X_{n} \cos \frac{2 \pi R}{T_{n}}+Y_{n} \sin \frac{2 \pi R}{T_{n}}\right) $ | (2) |
式中,
在重力基准网平差解算过程中,相对重力仪的参数结果分为以下几种情况:
1) 如果Xn=0、Yn=0,则振幅An为0,该周期项可以忽略;
2) 如果Xn≠0、Yn=0,则振幅An=Xn,初相φn=0,周期项函数为纯余弦函数
3) 如果Xn=0、Yn≠0,则振幅An=Yn,初相φn=π/2,周期项函数为纯正弦函数
4) 如果Xn≠0、Yn≠0,则振幅An=
重力基准网平差采用间接平差模型,将经过固体潮改正、海潮改正、气压改正、仪器高改正、零漂改正后测段起、止点的最后观测值和仪器读数作为观测量,其误差方程为[4]:
| $ \begin{aligned} V_{i j}=& g_{j}-g_{i}+\sum\limits_{K=1}^{M}\left(g_{R Z_{i}}^{K}-g_{R Z_{j}}^{K}\right) \cdot C_{K}+\\ & \sum\limits_{n=1}^{P} X_{n}\left(\cos \frac{2 \pi R_{i}}{T_{n}}-\cos \frac{2 \pi R_{j}}{T_{n}}\right)+\\ & \sum\limits_{n=1}^{P} Y_{n}\left(\sin \frac{2 \pi R_{i}}{T_{n}}-\sin \frac{2 \pi R_{j}}{T_{n}}\right) \end{aligned} $ | (3) |
式中,gi、gj分别为测站i、j点平差后的重力值,gRZi、gRZj分别为测站i、j点经过5项改正的相对联测最后观测值,Ri、Rj分别为仪器在测站i、j点的观测读数,CK为重力仪的M次多项式格值函数的K次格值改正因子,Xn、Yn为重力仪周期误差参数,Tn为周期误差的周期,其周期值大小见表 1,1个计数单位(1格)相当于mGal。
|
|
表 1 LCR-G型重力仪传动周期 Tab. 1 The drived period of LCR-G gravity meters |
| $ \begin{gathered} \boldsymbol{R}_{\lambda}(\boldsymbol{\beta})= \\ \min _{\left(\boldsymbol{\beta}_{0}, \boldsymbol{\beta} \in R\right)}\left[\frac{1}{2 N} \sum\limits_{i=1}^{N}\left(\boldsymbol{y}_{i}-\boldsymbol{\beta}_{0}-\boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{\beta}\right)^{2}+\lambda \boldsymbol{P}_{\alpha}(\boldsymbol{\beta})\right] \end{gathered} $ | (4) |
式中,N为观测量的个数,β为待求量,xi和yi为观测量,λ为惩罚因子,α为正则化参数,Pα(β)为惩罚项,其表示形式如下:
| $ \begin{gathered} \boldsymbol{P}_{\alpha}(\boldsymbol{\beta})=\frac{1-\alpha}{2}\left(\|\boldsymbol{\beta}\|_{\mathrm{L} .2}^{2}\right)+\alpha\left(\|\boldsymbol{\beta}\|_{\mathrm{L} .1}\right)= \\ \sum\limits_{j=1}^{p}\left[\frac{1}{2}(1-\alpha) \boldsymbol{\beta}_{j}^{2}+\alpha\left|\boldsymbol{\beta}_{j}\right|\right] \end{gathered} $ | (5) |
式中,p为待求参数的个数。α=1时,式(5)为Lasso算法模型;α=0时,式(5)为Ridge算法模型;α∈(0, 1)时,式(5)为ElasticNet算法模型。
通过调整惩罚因子λ和正则化参数α,确定出剔除周期项的最优参数值并对无效的周期项进行剔除;然后再利用周期项取舍标准,剔除误差超限的周期项,从而完成对周期项参数的筛选;最后通过平差对周期项进行精确解算,计算出仪器周期项的振幅及初相,并对其结果进行分析。
2.2 周期项取舍标准| $ \sqrt{M_{\varphi_{n}}^{2}+M_{A_{n}}^{2} / A_{n}^{2}}<0.7 $ | (6) |
式中,An为周期项的振幅,MA和Mφ分别为周期项的振幅中误差和相位中误差[4]:
| $ \left\{\begin{array}{l} M_{A}=\pm \frac{1}{A} \sqrt{X^{2} M_{X}^{2}+Y^{2} M_{Y}^{2}} \\ M_{\varphi}=\pm \frac{1}{A^{2}} \sqrt{X^{2} M_{Y}^{2}+Y^{2} M_{X}^{2}} \end{array}\right. $ | (7) |
式中,MX、MY分别为周期项的点位中误差,A为对应周期的振幅。
当初相φ的求定误差大于29°或者振幅误差比小于2时,考虑剔除相应的周期项。
3 实验分析 3.1 数据介绍本文以2000国家重力基本网和2020最新国家重力基准网中G796、G922两台LCR-G型相对重力仪观测数据为例,对其周期项进行参数解算,相应的观测量统计信息见表 2。由表 2可以看出,两台仪器的观测量个数均比待求量个数多,保证了足够的多余观测量来解算相对重力仪的周期参数;最大段差、最小段差、平均段差分别在同一量级,可以保证所选观测数据具有同一性。
|
|
表 2 重力仪观测量统计 Tab. 2 Statistics of gravity meters observation |
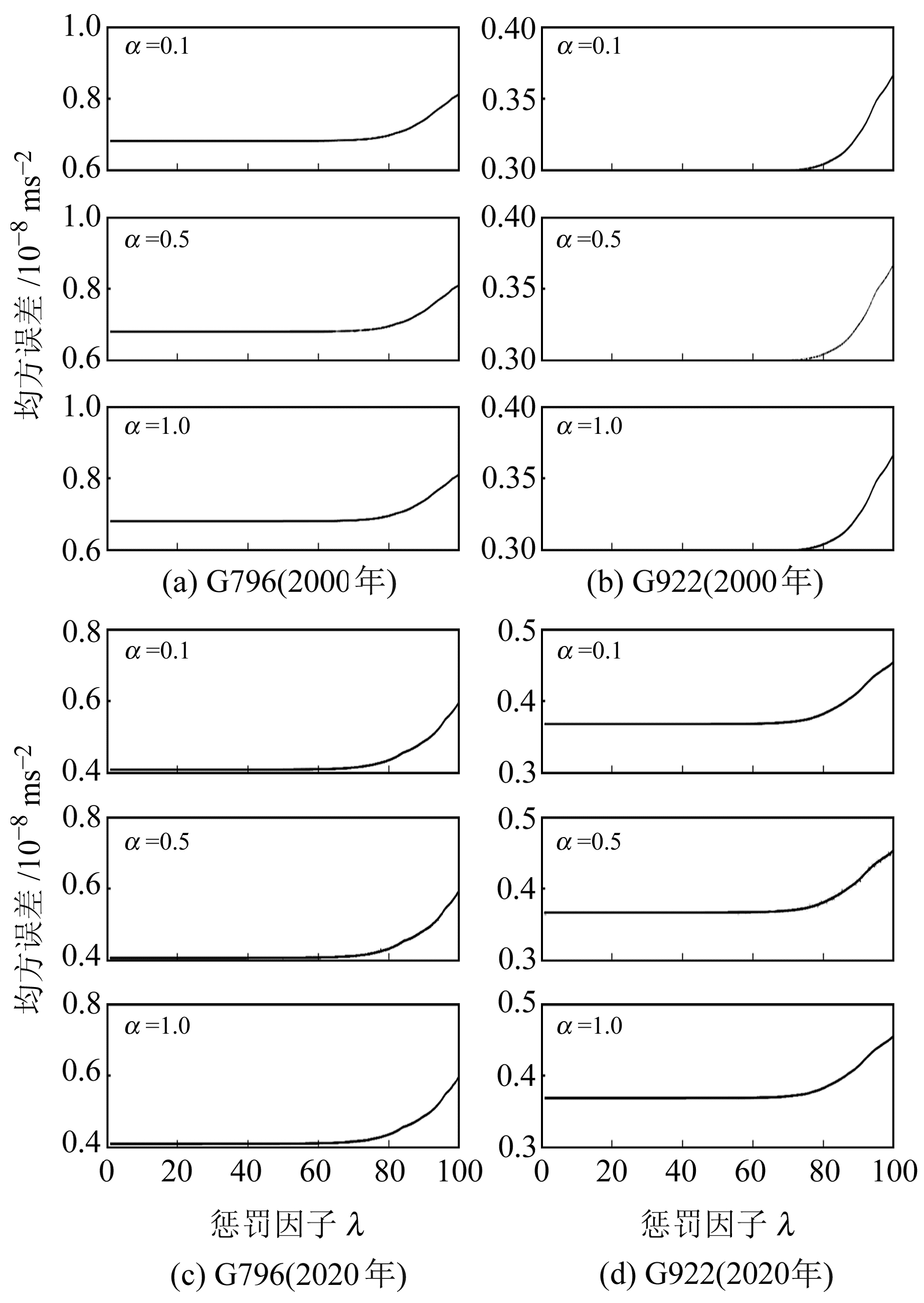
首先,不考虑周期项对重力基准网进行平差,将得到的各个重力点上的重力值及所有仪器的格值一次项作为输入数据,组建由G796、G922两台仪器周期项构成的多元线性方程组,并采用正则化算法进行解算,正则化参数α分别取0.1、0.5、1.0,惩罚因子λ取0~100,由解算结果计算的均方误差如图 1所示。从图 1可以看出,当惩罚因子λ大于80时,均方误差均开始增大;正则化参数α的取值对周期项的均方误差几乎没有影响。由此得出,在解算仪器周期项时,惩罚因子λ取80,正则化参数α的值可以任意选取。
|
图 1 重力仪周期项均方误差 Fig. 1 The mean square error of periodic terms of gravity meters |
采用正则化方法,惩罚因子λ取80,正则化参数α分别取0.1、0.5、1.0,解算的G796、G922仪器周期参数结果见图 2。可以看出,正则化方法对周期项的剔除效果明显,正则化参数α的选取对周期项的筛选几乎不产生影响。

|
图 2 重力仪周期项振幅 Fig. 2 The amplitude values of periodic terms of gravity meters |
采用式(6)对由正则化方法解算的周期项再次进行判定,去掉误差超限的周期项,最终的筛选结果见表 3。
|
|
表 3 重力仪周期项参数筛选结果 Tab. 3 The select results of periodic terms of gravity meters |
由于固定线性项和不固定线性项的标定结果基本一致[10],因此,采用不固定线性项的方式来求解标定参数。将表 3中筛选出的有效周期项确定的参数代入国家重力基准网的误差方程,重新进行平差得到周期项的振幅和相位,结果见表 4。由表 4可知,通过正则化方法确定的周期项,振幅中误差优于4.2 μGal,相位中误差优于27.7,解算结果精度均在周期项取舍标准要求以内。2000国家重力基本网G796重力仪周期项振幅最大可达12 μGal,G922重力仪周期项振幅最大可达8.0 μGal;2020最新国家重力基准网G796重力仪周期项振幅最大可达10.7 μGal,G922重力仪周期项振幅最大可达7.5 μGal。两台仪器的振幅在近20 a内均有所下降,可能是由于仪器出厂时间较长、部件老化引起的;相同仪器在近20 a内所确定的周期并不相同,分析认为是相对重力仪解算的周期项的振幅和相位大小与采用的观测数据及仪器观测时所处的环境有关。
|
|
表 4 重力仪周期项计算结果 Tab. 4 The results of periodic terms of gravity meters |
考虑周期项前后重力基准网平差重力值的变化见表 5。可以看出,考虑周期项后,对2000国家重力基本网的平差重力值最大影响可达6.22 μGal,对2020最新国家重力基准网的影响可达4.73 μGal。由此可见,周期项对重力基准网影响的数量级达到μGal,不可忽视。
|
|
表 5 考虑周期项前后重力值变化的统计 Tab. 5 The statistics of gravity value differences before and after considering the periodic terms |
本文基于国家重力基准网观测数据,采用正则化方法及周期项取舍标准对G796、G922两台相对重力仪的周期项进行筛选,并通过平差对周期项进行精确解算,得出结论如下:1)使用正则化方法结合周期项取舍标准,可以有效筛选出带有齿轮系统及量测螺旋系统的相对重力仪的周期项,并且通过实验确定,正则化方法惩罚因子λ取80最优,正则化参数α的选取对周期项几乎没有影响;2)周期误差对2000国家重力基本网和2020最新国家重力基准网的重力值平差结果影响最大分别可达6.22 μGal和4.73 μGal,由此可见,周期项对重力基准网影响的数量级达到μGal;3)相对重力仪的周期会随着观测环境或者时间变化,最终解算结果不一致,这是由于周期函数模型与实际周期变化有差异,模型只能近似而不能真正模拟周期的变化。
| [1] |
Valliant H D. Gravity Meter Calibration at Lacoste and Romberg[J]. Geophysics, 1991, 56(5): 705-711 DOI:10.1190/1.1443089
(  0) 0) |
| [2] |
晁定波, Baker E M. Lacoste-Romberg"G"型重力仪周期误差检定的优化问题[J]. 武汉测绘科技大学学报, 1986, 11(1): 32-44 (Chao Dingbo, Baker E M. The Optimization Problem of Calibrating the Periodic Errors of Lacoste and Romberg Model "G" Gravity Meter[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1986, 11(1): 32-44)
(  0) 0) |
| [3] |
刘乃苓, 江志恒. 拉科斯特重力仪中长周期格值标定因子的选择[J]. 地壳形变与地震, 1991, 11(1): 65-74 (Liu Nailing, Jiang Zhiheng. On the Choice of the Scale Function Factors of LCR Gravimeter[J]. Crustal Deformation and Earthquake, 1991, 11(1): 65-74)
(  0) 0) |
| [4] |
Jiang Z H, Zuo C H, Qiu Q X, et al. China Gravity Basic Net 1985[J]. Scientia Sinica: Series B, 1988, 31(9): 1143-1152
(  0) 0) |
| [5] |
党亚民, 丘其宪, 徐善. LCR-G型重力仪周期误差的研究[J]. 武汉测绘科技大学学报, 1996, 21(2): 120-123 (Dang Yamin, Qiu Qixian, Xu Shan. Study on Periodic Errors of Lacoste and Romberg G Gravity Meters[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1996, 21(2): 120-123)
(  0) 0) |
| [6] |
王庆宾. 重力基本网数据处理研究[D]. 郑州: 信息工程大学, 2001 (Wang Qingbin. Study on Data Processing of Gravity Basic Systern[D]. Zhengzhou: Information Engineering University, 2001)
(  0) 0) |
| [7] |
Tibshirani R. Regression Shrinkage and Selection via the Lasso[J]. Journal of the Royal Statistical Society: Series B(Methodological), 1996, 58(1): 267-288 DOI:10.1111/j.2517-6161.1996.tb02080.x
(  0) 0) |
| [8] |
Zou H, Hastie T. Regularization and Variable Selection via the Elastic Net[J]. Journal of the Royal Statistical Society: Series B(Statistical Methodology), 2005, 67(2): 301-320 DOI:10.1111/j.1467-9868.2005.00503.x
(  0) 0) |
| [9] |
管泽霖, 宁津生. 地球形状及外部重力场[M]. 北京: 测绘出版社, 1981 (Guan Zelin, Ning Jinsheng. Earth Shape and External Gravity Field[M]. Beijing: Surveying and Mapping Press, 1981)
(  0) 0) |
| [10] |
党亚民. 关于拉科斯特G型重力仪标定的讨论[J]. 测绘科技动态, 1995(1): 9-13 (Dang Yamin. Discussion on the Calibration of Lacoste G Gravimeter[J]. Developments in Surveying and Mapping, 1995(1): 9-13)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing100036, China
 2022, Vol. 42
2022, Vol. 42


