作为正反演计算中较为简单常用的模型构建单元，有限圆柱体模型被广泛应用于地球物理学领域的正反演模拟计算、数据处理与解释之中^[1]。对于有限圆柱体模型，从重力位到重力二阶梯度张量，其正演计算解析公式问题已经基本被学者解决^[2-6]，而对于有限圆柱体模型的重力位三阶梯度张量正演解析公式，还未见国内外学者进行报道或发表。鉴于重力曲率张量在未来多个领域的广泛应用前景，本文首先根据引力位计算公式推导得到有限圆柱体模型重力曲率张量的正演解析公式，而后通过理论分析与模型实验对比来分析验证所推公式的正确性。

1 公式推导

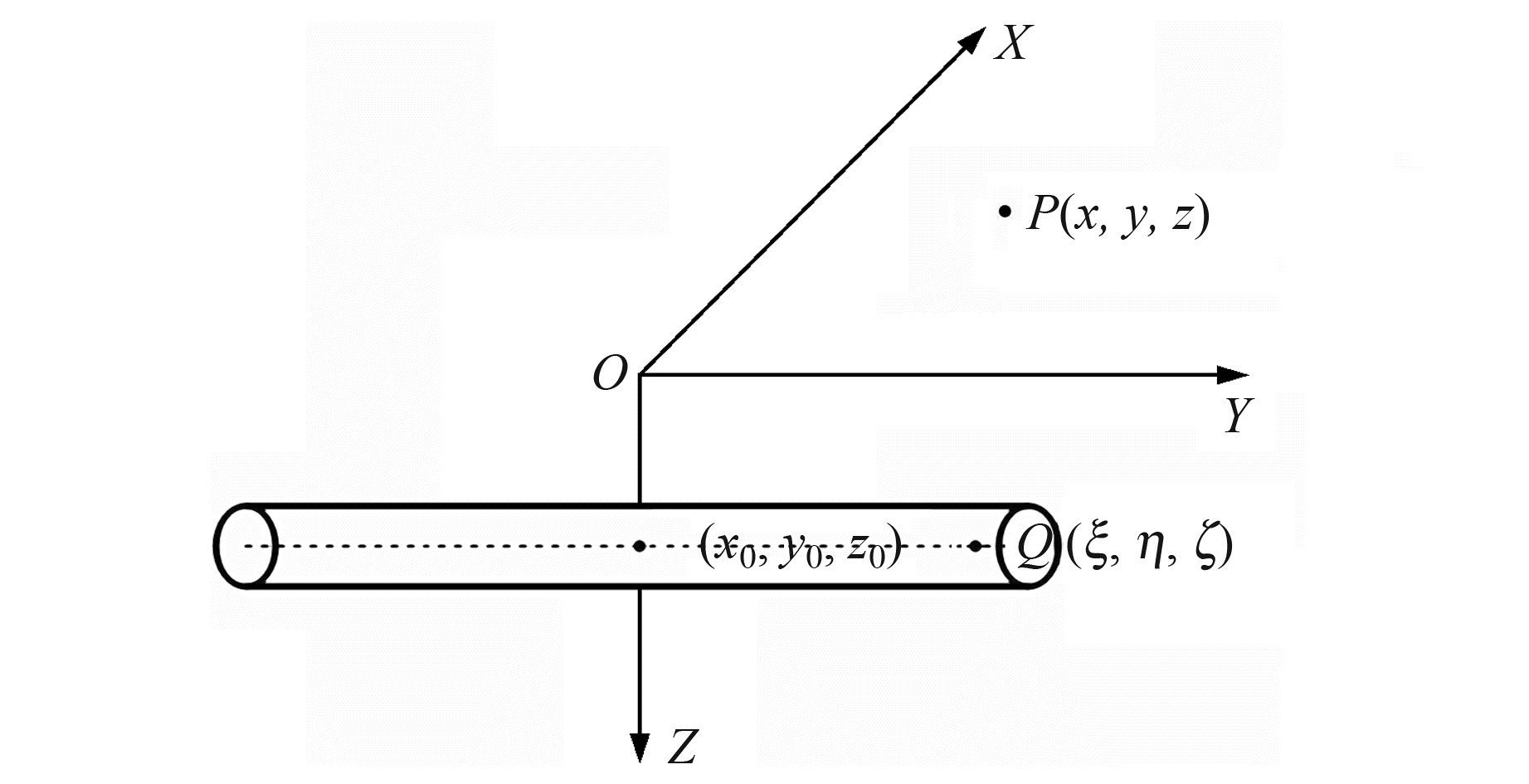
设有一长为2L的剩余密度均匀的水平圆柱体，圆柱体的中心坐标为(x₀, y₀, z₀)，其截面积为S，剩余密度为ρ，坐标系与水平圆柱体的关系如图 1所示，Y轴平行于水平圆柱体的走向，X轴垂直于柱轴。将其看作质量集中于轴线Q(ξ, η, ζ)上的有限长水平物质线，故水平圆柱体任一体积元dv=dξdηdζ=S·dη。设空间中任一观测点坐标为P(x, y, z)，则根据牛顿万有引力定律可得有限长水平圆柱体在P点产生的重力位为^[7]：

$ U=G\rho \iiint\limits_{V}{\frac{1}{r}\text{d}\xi }\text{d}\eta \text{d}\zeta =G\rho S\int_{{{y}_{0}}-L}^{{{y}_{0}}+L}{\frac{1}{r}}\text{d}\eta $

(1)

式中，ρ为密度，G=6.672×10^-11 m³/kg·s²为万有引力常数，r=[(ξ-x)² +(η-y)²+(ζ-z)²]^1/2为观测点与体积元dξdηdζ之间的距离。

对式(1)积分要用到的积分公式为：

$ \left\{ \begin{align} & \int{\frac{\text{d}u}{\sqrt{{{u}^{2}}+{{A}^{2}}}}}=\ln (u+\sqrt{{{u}^{2}}+{{A}^{2}}})+C \\ & \int{\frac{\text{d}u}{{{({{u}^{2}}+{{A}^{2}})}^{\frac{3}{2}}}}}=\frac{u}{{{A}^{2}}\sqrt{{{u}^{2}}+{{A}^{2}}}}+C \\ & \int{\frac{u\text{d}u}{{{({{u}^{2}}+{{A}^{2}})}^{\frac{3}{2}}}}}=-\frac{1}{\sqrt{{{u}^{2}}+{{A}^{2}}}}+C \\ \end{align} \right. $

(2)

令ξ-x=a，η-y=b，ζ-z=c。

重力二阶梯度是重力位各方向上的二阶导数，其张量形式为：

$ \left[ \begin{matrix} {{U}_{xx}} & {{U}_{xy}} & {{U}_{xz}} \\ {{U}_{yx}} & {{U}_{yy}} & {{U}_{yz}} \\ {{U}_{zx}} & {{U}_{zy}} & {{U}_{zz}} \\ \end{matrix} \right]=\left[ \begin{matrix} \frac{{{\partial }^{2}}U}{\partial {{x}^{2}}} & \frac{{{\partial }^{2}}U}{\partial x\partial y} & \frac{{{\partial }^{2}}U}{\partial x\partial z} \\ \frac{{{\partial }^{2}}U}{\partial y\partial x} & \frac{{{\partial }^{2}}U}{\partial {{y}^{2}}} & \frac{{{\partial }^{2}}U}{\partial y\partial z} \\ \frac{{{\partial }^{2}}U}{\partial z\partial x} & \frac{{{\partial }^{2}}U}{\partial z\partial y} & \frac{{{\partial }^{2}}U}{\partial {{z}^{2}}} \\ \end{matrix} \right] $

(3)

根据众多学者对重力梯度张量正演模拟和反演解释的研究^[2-6]可得，有限圆柱体的重力位梯度张量解析公式为：

$ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ {{U}_{xx}}=G\rho S\cdot \\ & \frac{b[{{a}^{2}}({{a}^{2}}+{{c}^{2}})+{{r}^{2}}({{a}^{2}}-{{c}^{2}})]}{{{r}^{3}}{{({{a}^{2}}+{{c}^{2}})}^{2}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. \\ \end{align} $

(4a)

$ {{U}_{xy}}=-G\rho S\frac{a}{{{r}^{3}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(4b)

$ {{U}_{xz}}=G\rho S\frac{abc(3{{r}^{2}}-{{b}^{2}})}{{{r}^{3}}{{[{{a}^{2}}+{{c}^{2}}]}^{2}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(4c)

$ {{U}_{yy}}=\frac{\partial {{V}_{y}}}{\partial y}=-G\rho S\frac{b}{{{r}^{3}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(4d)

$ {{U}_{yz}}=\frac{\partial {{V}_{y}}}{\partial z}=-G\rho S\frac{c}{{{r}^{3}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(4e)

$ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ {{U}_{zz}}=G\rho S\cdot \\ & \frac{b[{{c}^{2}}({{c}^{2}}+{{a}^{2}})+{{r}^{2}}({{c}^{2}}-{{a}^{2}})]}{{{r}^{3}}{{({{a}^{2}}+{{c}^{2}})}^{2}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. \\ \end{align} $

(4f)

重力曲率张量是重力位在各个方向上的三阶导数，根据张量的对称性可知，U_ijk=U_jki=U_kij, i、j、k∈{x, y, z}。重力曲率张量的正演解析公式可由重力位梯度张量求导得到，也可通过对重力位进行3次求偏导得到。

由式(2)可得：

$ \frac{\partial r}{\partial x}=-\frac{\xi-x}{r}, \frac{\partial r}{\partial y}=-\frac{\eta-y}{r}, \frac{\partial r}{\partial z}=-\frac{\zeta-z}{r} $

(5)

并且$ \frac{\partial }{\partial x}\left( \frac{1}{r} \right)=-\frac{\xi -x}{{{r}^{3}}}、\frac{\partial }{\partial y}\left( \frac{1}{r} \right)=-\frac{\eta -y}{{{r}^{3}}}、\frac{\partial }{\partial z}\left( \frac{1}{r} \right)=-\frac{\zeta -z}{{{r}^{3}}}$、故可得：

$ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{U}_{xxx}}=\frac{\partial {{U}_{xx}}}{\partial x} \\ & =G\rho S\cdot ab\frac{[{{a}^{2}}({{a}^{2}}+{{c}^{2}})+{{r}^{2}}({{a}^{2}}-{{c}^{2}})][3({{a}^{2}}+{{c}^{2}})+4{{r}^{2}}]-{{r}^{2}}(6{{a}^{2}}+2{{r}^{2}})({{a}^{2}}+{{c}^{2}})}{{{r}^{5}}{{({{a}^{2}}+{{c}^{2}})}^{3}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. \\ \end{align} $

(6a)

$ {{U}_{xxy}}=\frac{\partial {{U}_{xx}}}{\partial y}=G\rho S\frac{{{r}^{2}}-3{{a}^{2}}}{{{r}^{5}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6b)

$ {{U}_{xxz}}=\frac{\partial {{U}_{xx}}}{\partial z}=G\rho S\cdot bc\frac{(-3{{r}^{2}}+{{b}^{2}}-6{{a}^{2}}){{r}^{2}}({{a}^{2}}+{{c}^{2}})+{{a}^{2}}(3{{r}^{2}}-{{b}^{2}})[3({{a}^{2}}+{{c}^{2}})+4{{r}^{2}}]}{{{r}^{5}}{{[{{a}^{2}}+{{c}^{2}}]}^{3}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6c)

$ {{U}_{xyy}}=\frac{\partial {{U}_{xy}}}{\partial y}=-G\rho S\frac{3ab}{{{r}^{5}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6d)

$ {{U}_{xyz}}=\frac{\partial {{U}_{xy}}}{\partial z}=-G\rho S\frac{3ac}{{{r}^{5}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6e)

$ {{U}_{xzz}}=\frac{\partial {{U}_{xz}}}{\partial z}=G\rho S\cdot ab\frac{(-3{{r}^{2}}+{{b}^{2}}-6{{c}^{2}}){{r}^{2}}({{a}^{2}}+{{c}^{2}})+{{c}^{2}}(3{{r}^{2}}-{{b}^{2}})[3({{a}^{2}}+{{c}^{2}})+4{{r}^{2}}]}{{{r}^{5}}{{[{{a}^{2}}+{{c}^{2}}]}^{3}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6f)

$ {{U}_{yyy}}=\frac{\partial {{U}_{yy}}}{\partial y}=G\rho S\frac{{{r}^{2}}-3{{b}^{2}}}{{{r}^{5}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6g)

$ {{U}_{yyz}}=\frac{\partial {{U}_{yy}}}{\partial z}=-G\rho S\frac{3bc}{{{r}^{5}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6h)

$ {{U}_{yzz}}=\frac{\partial {{U}_{yz}}}{\partial z}=G\rho S\frac{{{r}^{2}}-3{{c}^{2}}}{{{r}^{5}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. $

(6i)

$ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{U}_{zzz}}=\frac{\partial {{U}_{zz}}}{\partial z}= \\ & G\rho S\cdot bc\frac{[{{c}^{2}}({{a}^{2}}+{{c}^{2}})+{{r}^{2}}({{c}^{2}}-{{a}^{2}})][3({{a}^{2}}+{{c}^{2}})+4{{r}^{2}}]-{{r}^{2}}(6{{c}^{2}}+2{{r}^{2}})({{a}^{2}}+{{c}^{2}})}{{{r}^{5}}{{({{a}^{2}}+{{c}^{2}})}^{3}}}\left| \begin{matrix} {{y}_{0}}+L \\ {{y}_{0}}-L \\ \end{matrix} \right. \\ \end{align} $

(6j)

2 正演计算公式的正确性检验

为了检验本文所推导公式的正确性，通过对理论模型重力位二阶梯度张量异常结果进行中心差分计算，得到所用模型的重力位三阶梯度张量结果，而后与本文解析公式计算结果进行对比。

2.1 理论模型的重力三阶梯度张量分布

首先给出模型参数：圆柱体的横截面半径R=4 m，圆柱体长2L=40 m，剩余密度为2.67 g/cm³，其中心坐标为(0, 0, 40 m)，X、Y坐标范围均为-100~100 m。地面测网大小为200 m×200 m，网格间距为1 m×1 m。利用式(6)计算得到该有限圆柱体模型的重力三阶梯度张量分布，如图 2所示。

2.2 解析解的正确性检验

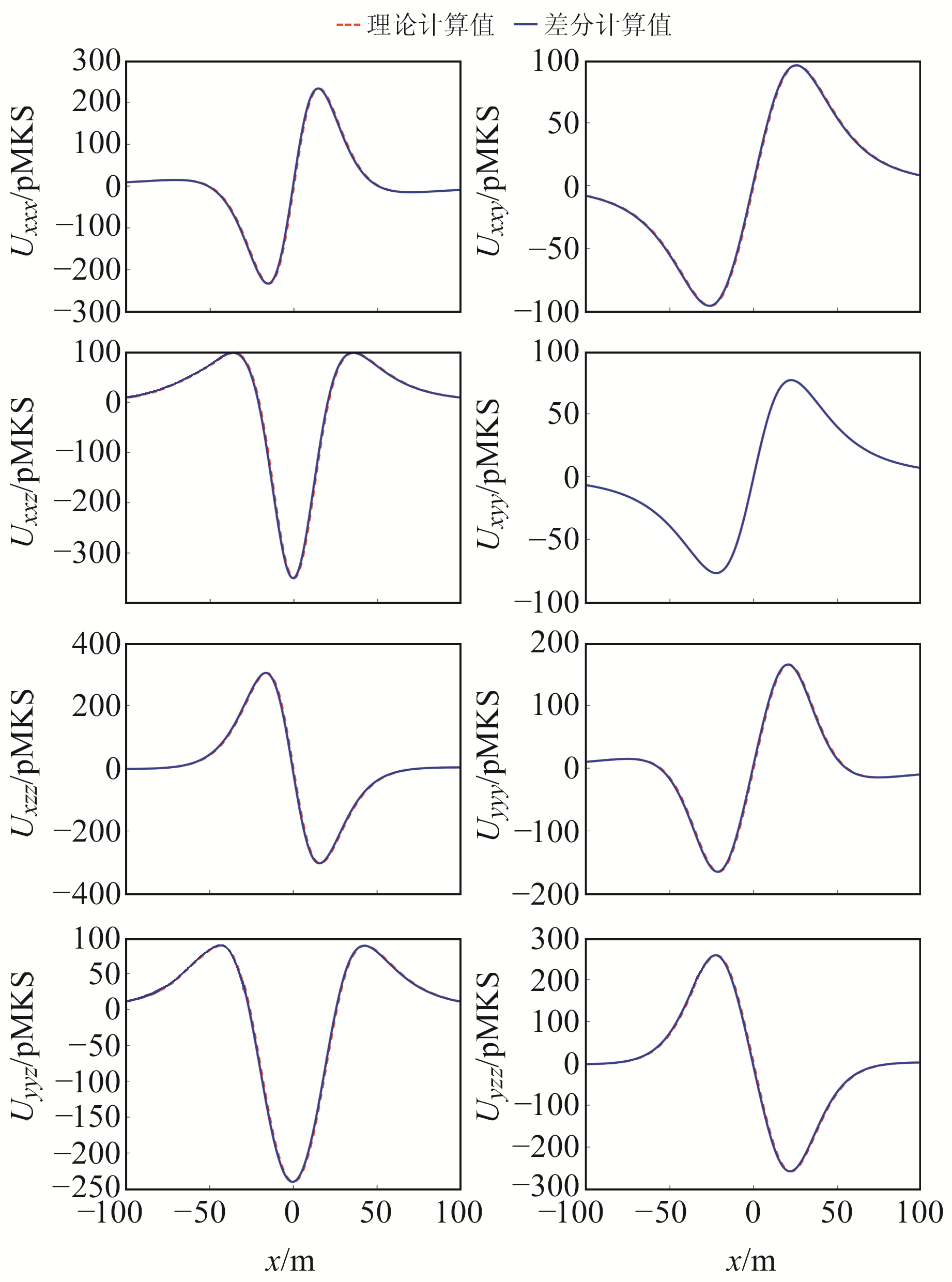
由导数的定义可知，重力三阶梯度张量可由其二阶梯度张量通过中心差分得到，故可通过与二阶梯度张量差分计算结果进行对比，以检验本文三阶张量正演计算公式的正确性。图 3为图 2所示剖面的重力三阶梯度张量曲线的差分结果，差分点距设置为1 m。由图可知，本文所计算的差分结果都逼近于重力三阶梯度张量计算结果。图 4为所计算的差分结果与理论结果之间的误差曲线。由图可知，整体误差都较小，并且误差在峰值处达到最大，证明了本文推导公式的正确性。

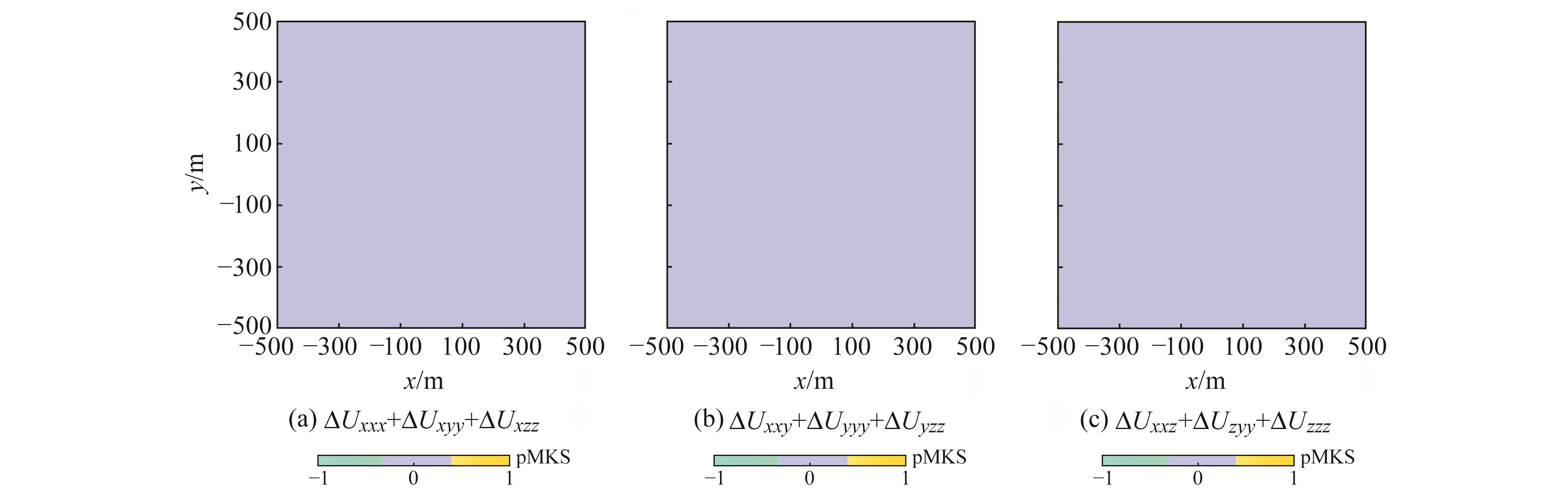
根据扰动重力位在场源外部空间应当满足拉普拉斯方程，重力位三阶梯度张量的部分分量应当满足U_xxx+U_xyy+U_xzz=0、U_xxy+U_yyy+U_yzz=0、U_xxz+U_yyz+U_zzz=0^[8]。基于该原理检验所推公式的正确性，计算结果如图 5所示。可以看出，计算结果满足上述3个方程，误差均为0，这从另外一个方面证明了本文推导公式的正确性。

3 结语

鉴于有限圆柱体模型在地球物理学领域的正反演模拟与计算、数据处理与解释中的重要性，本文根据引力位解析公式，经过推导得到有限圆柱体重力曲率张量的正演解析公式，并基于理论模型实验，从对所推解析公式的正演结果与重力位梯度张量中心差分的计算结果进行对比以及检验正演计算结果是否满足拉普拉斯方程2个方面验证了所推导公式的正确性。本文研究成果可为今后重力位三阶梯度张量的仿真模拟、实测数据的处理与转换计算以及反演解释提供理论基础。