近年来,胶东半岛及附近海域地区震群多发,表现出明显的小震时空丛集现象。尤其是2013年乳山震群和2017年长岛震群,丛集特征异常突出,前者记录到13 000多次地震,且现在仍有零星活动;后者在1 a时间内发生近3 000次地震,其中ML3.0以上多达47次。2021-01-06在长岛西侧的渤海海域再次发生蓬莱4.3级震群。
显著震群活动被认为是强震前兆现象之一[1],如1976年唐山7.8级地震前,胶东半岛北侧的砣矶岛和黑山岛分别出现爆发式震群活动[2-3]。中小地震的时空丛集,是区域应力场调整的表现形式之一。Dieterich[4]研究发现,小震丛集现象受地震区附近特征弹性应力变化所驱使,且可能与大地震的成核过程有关。华北地区6级以上地震长期平静,接近有完整记录以来的最长时间间隔;山东地区自1995年苍山5.2级地震后,5级以上地震平静期超过25 a。因此,对胶东半岛地震丛集现象进行深入研究,对分析该区域当前震情趋势和判定未来强震危险性具有一定参考意义。在前期工作基础上[5-6],本文基于最邻近事件距离(nearest neighbor distance)算法对胶东半岛近年来地震活动的丛集特征进行分析。
1 理论与方法 1.1 最邻近事件距离方法地震活动在某个范围内可视为背景地震与丛集地震的组合叠加[5, 7-8]。由于丛集地震是自激发点过程,主要受前期地震影响,而背景地震是时空随机点过程,两者在物理性质和产生机理上存在区别,因此在大多数情况下需要将丛集地震和背景地震活动进行区分[5]。已有诸多方法对地震时空丛集程度进行量化分析,或进一步从地震活动中区分背景地震和丛集地震[6, 9-10]。
最邻近事件距离方法是近年来发展的有明确统计物理意义的丛集地震分析方法之一[5, 11-13],应用结果显示其能够很好地区分丛集地震和背景地震[14-15]。最邻近事件距离算法步骤如下:
对确定的地震目录{ti, θi, φi, hi, mi}, i=1…N,其中t、θ、φ、h和m分别为发震时刻、震中经度、震中纬度、震源深度和震级,在忽略深度影响的前提下,定义任意两个地震事件在时空能量域的距离为[5, 16]:
| $ {n_{ij}} = \left\{ \begin{array}{l} c{\tau _{ij}}r_{ij}^d{10^{ - b({m_i} - {m_0})}}, {\tau _{ij}} \ge 0\\ \infty , {\tau _{ij}} < 0 \end{array} \right. $ | (1) |
式中,τij=tj-ti,rij为地表距离,m0为参考震级,c为常量系数,d为震中分布的分形维数,b为G-R关系中的b值。进一步定义震级归一化的最邻近事件距离η*以及η*的时间和空间分量{T, R}[5, 16]:
| $ \eta _j^* = {\min _i}{n_{ij}} $ | (2) |
| $ {T_{ij}} = {\tau _{ij}}{10^{ - b{m_i}/2}}, {R_{ij}} = r_{ij}^d{10^{ - b{m_i}/2}} $ | (3) |
在以往分析地震活动的统计方法中,往往未将时间、空间和能量域进行统一考量。最邻近事件距离方法可综合考虑地震在时空和能量域的分布,给出归一化度量,可有效地对N维复杂问题进行简化,因而能够很方便地识别和区分丛集地震。
1.2 混合概率密度分解以往基于最邻近事件距离方法的分析,多是基于其时空分量的二维分布进行简单统计,或直观进行区分,未进一步开展更深层次分析。裴韬等[8]假设背景地震和丛集地震分别满足不同参数的二维泊松过程,参考N阶距离的概念,将二维泊松过程转化为一维混合概率密度函数,基于对距离阶数的不同选择,采用遗传算法进行混合密度分解,从而实现提取地震丛集模式的目的。基于此,本文在计算最邻近事件距离基础上,定义混合密度分布函数为:
| $ {\rm{PDF}} = \omega \cdot {\rm{pd}}{{\rm{f}}_1} + \left( {1 - \omega } \right){\rm{pd}}{{\rm{f}}_2} $ | (4) |
式中,pdf1和pdf2分别为丛集地震和背景地震的概率密度函数,2个函数均取为正态分布,ω为比例系数。计算完成一组地震的最邻近事件距离η*后,基于式(4)对其概率分布进行最佳拟合,由此根据2个函数的相对权重来量化区分背景地震和丛集地震。
2 数据资料和研究区域胶东半岛地区现代地震活动特点为小震丛集现象较突出,震群或小序列活动占有相当大的比例[17-18]。从历史资料来看,胶东半岛陆地区域地震活动水平较低,历史地震目录中仅有2次M5中强地震,却发现有较多震群记录[19]。在现代地震记录中,显著震群活动也时有发生(图 1)。采用前文分析方法对胶东半岛地区近年来的地震活动丛集情况进行分析。
|
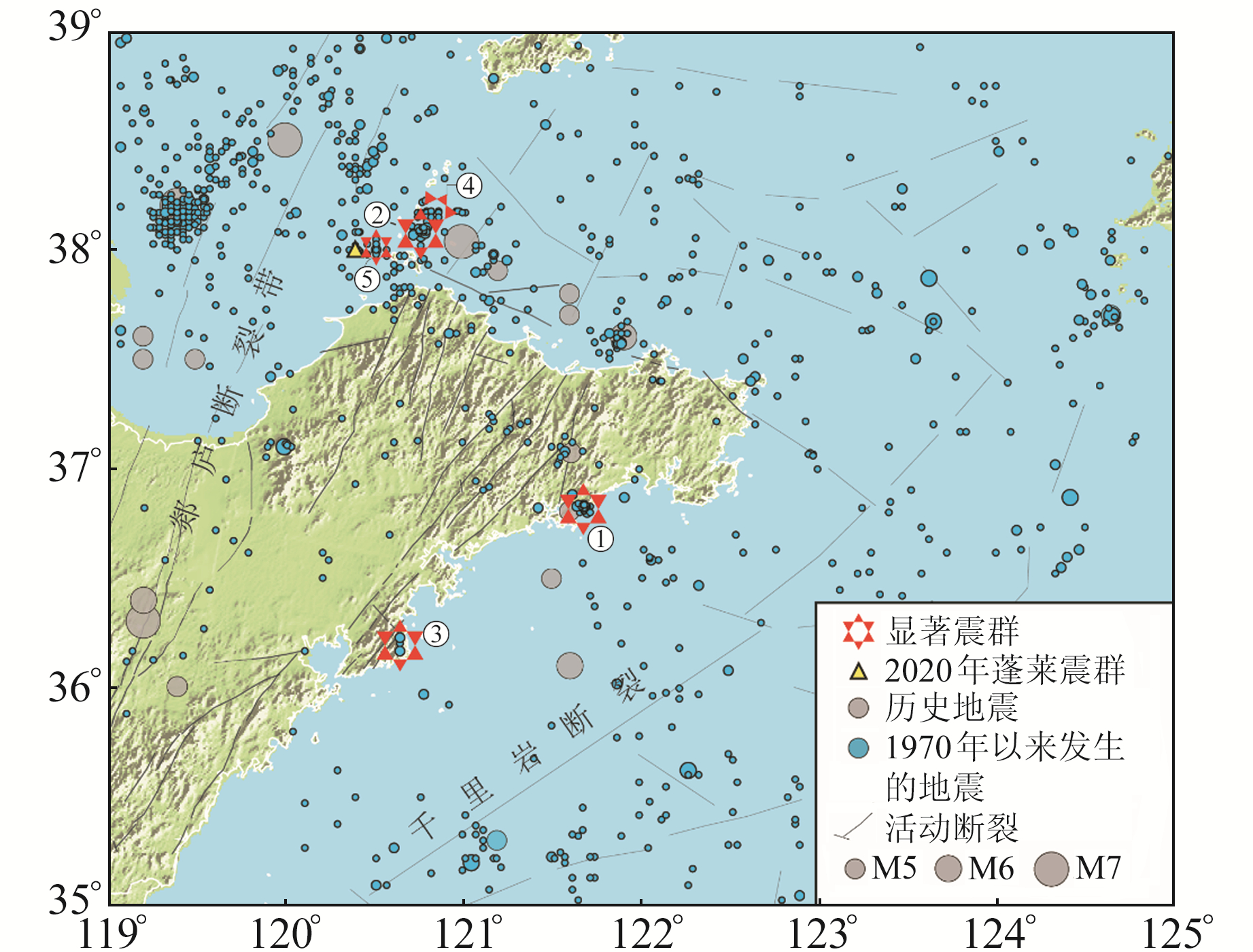
①2013年乳山震群;②2017年大竹山岛震群;③2003年崂山震群;④1976年砣矶岛震群;⑤1976黑山岛震群 图 1 胶东半岛地区现代地震震中分布 Fig. 1 Epicenter distribution of Jiaodong peninsula area since 1970 |
根据研究区范围内地震目录的G-R关系,确定该区域内最小完整性震级为ML=1.5,因此地震目录选取ML≥1.5地震进行研究。选择一定时间范围的地震目录,利用最小二乘法计算b值,根据地震目录中的经纬度计算空间分形维数d,将其作为该时空范围内计算任意2次事件时空距离的参数,以目录中第1个地震事件为参考震级m0,计算每2个事件之间的时空距离nij,常量系数c取为1,进而计算每次地震事件的最邻近事件距离η*。
3.1 乳山震群前半岛地区小震丛集特征乳山震群为研究区最显著的丛集活动,震群开始于2013-10-01。为避免乳山震群的影响,本文选择1996~2013年乳山震群前的地震记录,使用上述方法进行计算,结果如图 2所示。
|
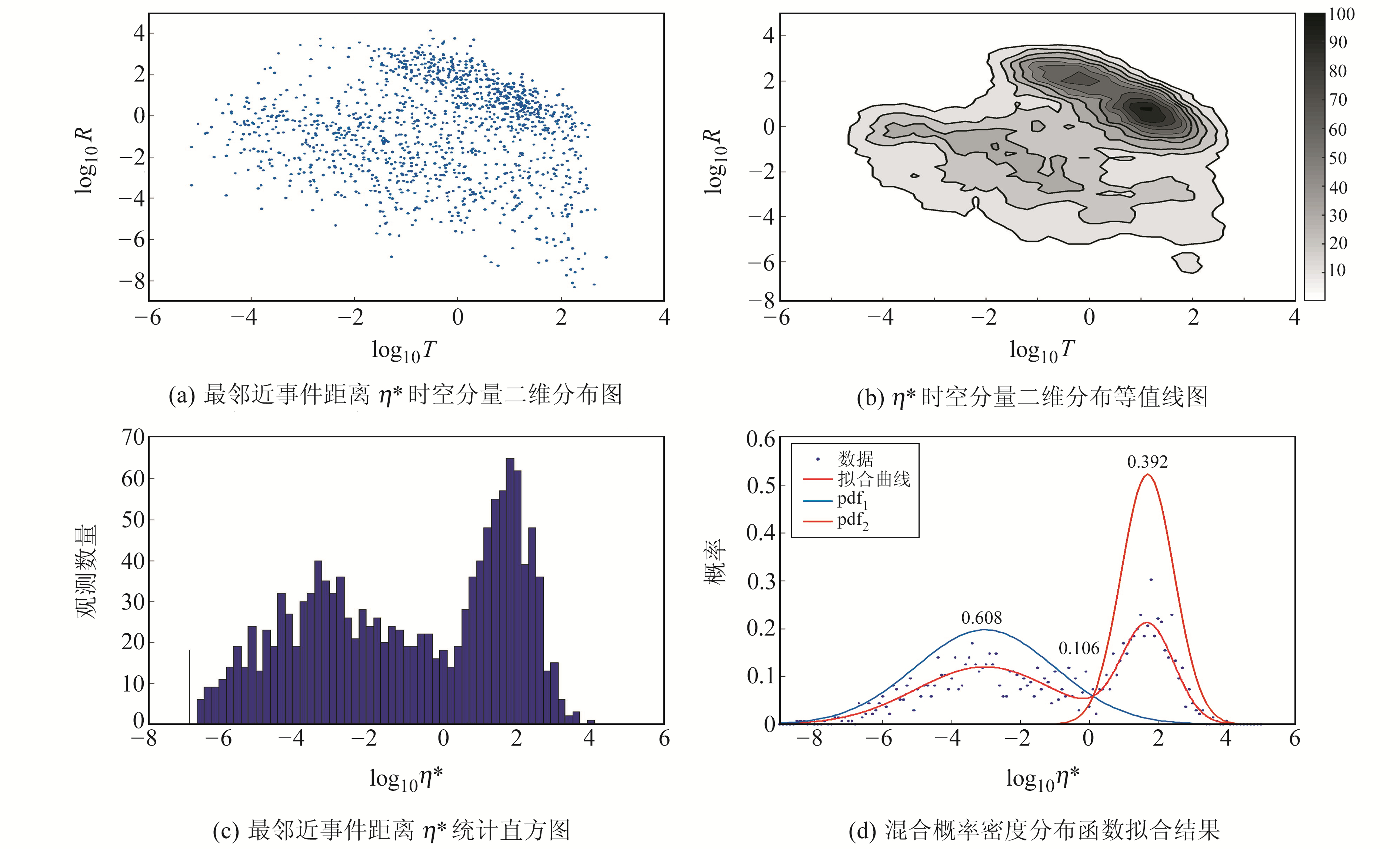
图 2 胶东半岛1996~2013年地震活动η*分析结果 Fig. 2 Analysis results of earthquake activity η* in Jiaodong peninsula area from 1996 to 2013 |
图 2(a)为最邻近事件距离η*时空分量{T, R}的二维分布,整体上在两处集中,该现象在密度分布等值线图上更加明显(图 2(b))。基于前人研究[2],本文认为已区分出丛集地震和背景地震。图 2(c)为最邻近事件距离η*统计直方图,在此基础上,利用式(4)对其混合概率密度分布函数进行拟合,结果如图 2(d)所示。可以看出,丛集地震权重ω为0.608,表明胶东半岛地区在1996~2013年的地震活动中,约60.8%的事件为丛集地震,而背景地震的发生率则为39.2%。
3.2 近10 a半岛地区小震丛集特征考虑到胶东半岛地区近10 a小震活动频发,依次发生2013年乳山震群、2017年长岛震群和2021年蓬莱震群,选择胶东半岛及附近地区(36°~39°N, 119°~123°E)作为研究区,选取2010~2020年ML≥1.5地震目录,使用前文GMM方法进行计算,结果如图 1所示。
从最邻近事件距离η*统计结果(图 3)来看,该区以丛集地震活动为主,代表丛集地震的概率密度函数的权重为0.75;受构造应力变化引发的背景地震仅有25%。根据前文对胶东半岛地区1996~2013年地震活动的分析,该时间段丛集地震发生率为60.8%。

|
图 3 胶东半岛2010~2020年地震活动η*分析结果 Fig. 3 Analysis results of earthquake activity η* in Jiaodong peninsula area from 2010 to 2020 |
由图 2(a)、2(b)和图 3(a)、3(b)可以看出,最邻近事件距离η*的统计特征可很好地区分丛集地震和背景地震,且从图 3(b)可以看出,近10 a来该区域以丛集地震活动为主。对比图 2(c)和图 3(c)可以明显看出,乳山地震前,该区域虽然存在丛集地震,但仍以背景地震活动为主;近10 a来该区域丛集增强,活动以丛集地震为主。对比图 2(d)和图 3(d)可以直观看出,胶东半岛地区的地震丛集率从乳山震群前的60.8%增加至近10 a的75%,丛集率显著提高,与地震活动的实际情况一致,更直观地反映出胶东半岛地区地震活动的变化情况。
3.4 小震丛集特征的时间变化对前文选取的胶东半岛地区的地震进行逐月滑动计算年地震丛集率,结果如图 4所示。η*计算过程中需要用到G-R关系中的b值和震中分布的分形维数d,鉴于两者与应力水平和断层面的不均匀性有关[2],因此图 4给出这2个中间参数随时间的变化情况。
|
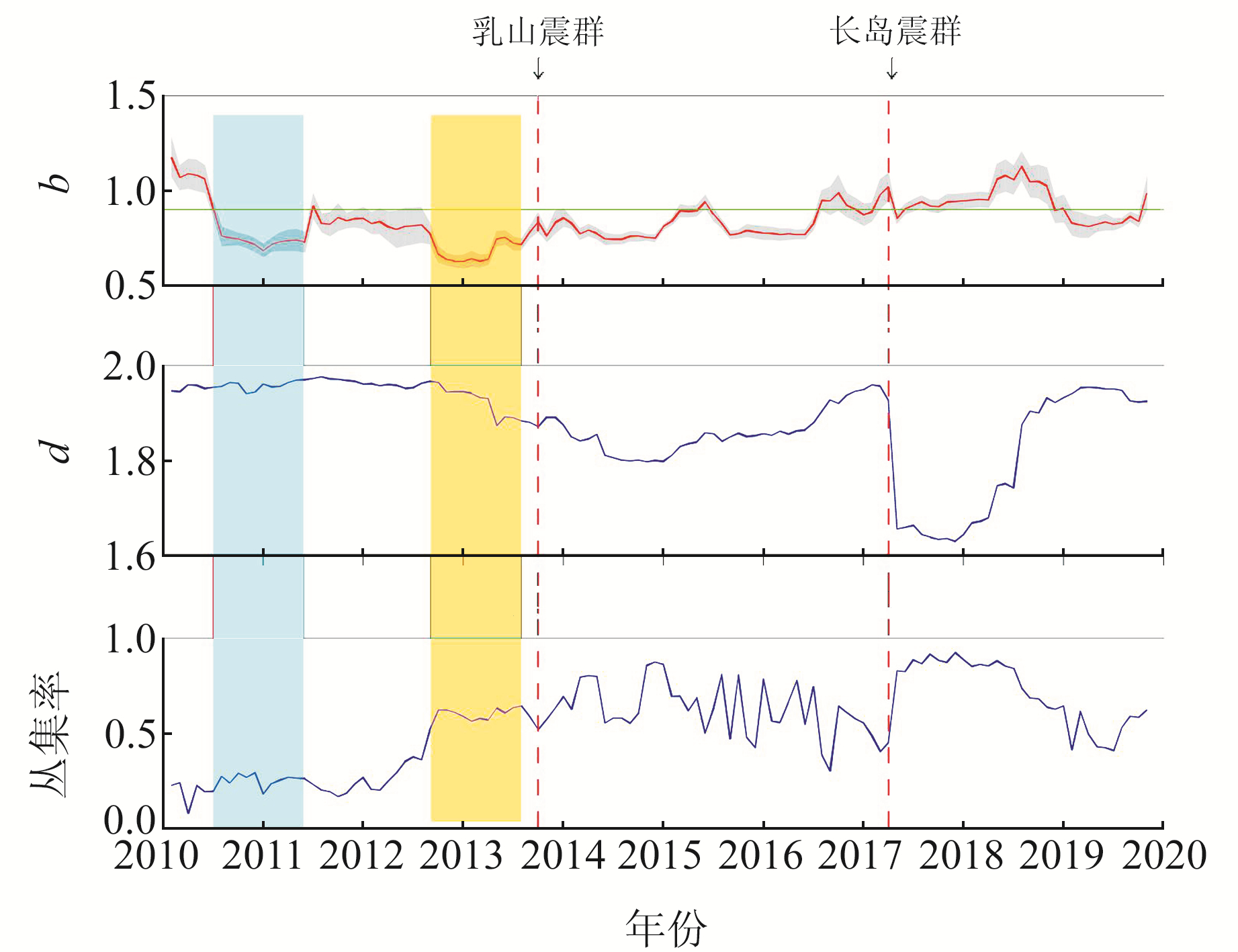
淡蓝色矩形区为低b值、低丛集率时段;黄色矩形区为低b值.高丛集率时段 图 4 胶东半岛地区地震b值、分形维数、丛集率随时间变化 Fig. 4 Variation of b value, fractal dimension and clustering rate of earthquakes in Jiaodong peninsula area |
从图 4可以看出,2013年乳山和2017年长岛2次显著震群的发生,使得本区分形维数和丛集率均出现明显的降低和升高变化。值得注意的是,在2013-10-01乳山震群和2013-11-23莱州M4.6地震前约1 a多时间,地震丛集率已出现升高变化,且同时出现低b值特征,可能表明在这2次较强地震活动前,区域范围内已出现应力水平的增强。
在2010年下半年至2011年上半年期间,虽然b值曲线出现同样的低值过程,但地震丛集率却无较大变化;该时段内丛集水平较低,说明地震活动主要为背景地震,背景地震的低b值则反映区域应力水平的增强;山东地区在该时间段内无显著地震事件发生,反而是整个华北地区,在经历汶川地震后长期平静的基础上,从2009年陕西河津M4.8地震开始,连续发生10多次M4地震,使得中等地震活动显著增强,这与胶东半岛地区的低b值变化一致。
上述分析表明,应力水平增强不一定触发较强的地震活动,低b值异常配合高丛集率可能是该区域地震活动较好的预测指标。
4 结语基于最邻近事件距离算法,对其统计分布进行2个正态分布的混合概率密度函数拟合,2个分布分别对应背景地震和丛集地震,根据其相对权重来量化一定时空区间内的地震丛集程度。相比以往的分析方法,该方法具有以下优点:
1) 已综合考虑地震在时空能量域的分布,相比其他参数,能更全面地体现地震的时空丛集情况。
2) 可以一维统计直方图和二维时空分布图来展示背景地震和丛集地震,并通过混合概率函数拟合统计结果,从而具有统计物理意义。
利用该方法对胶东半岛地区近年来的地震活动进行分析,结果表明:
1) 该区域地震存在明显的小震成丛活动,近年来丛集率显著提高,与乳山、长岛等显著震群活动一致。
2) 2013年乳山震群和莱州地震前,本区存在小震低b值和丛集率升高现象,可能反映区域应力水平的增强,且与这2次(组)显著事件的孕育有关。
3) 2011年前后的低b值应当也可反映区域应力水平,但本区并未出现小震丛集现象,因此低b值异常配合高丛集率可能是该区域地震活动较好的预测指标。
| [1] |
梅世蓉, 薛艳, 尹京苑. 唐山、邢台地震序列特征与三维速度结构的关系——兼论强震群型地震的预测问题[J]. 地震学报, 1999, 21(2): 159-165 (Mei Shirong, Xue Yan, Yin Jingyuan. Relationship between the Earthquake Sequences of Tangshan and Xingtai and the Three-Dimensional Velocity Structure: Discussing on Predicting Strong Earthquakes of Swarm Type[J]. Acta Seismologica Sinica, 1999, 21(2): 159-165 DOI:10.3321/j.issn:0253-3782.1999.02.006)
(  0) 0) |
| [2] |
魏光兴, 李秉锋. 1976年春季山东庙岛群岛两次小震群[J]. 地震学报, 1980, 2(3): 258-267 (Wei Guangxing, Li Bingfeng. Two Small Earthquake Swarms at Miaodao Archipelago, Shandong Province, in Spring 1976[J]. Acta Seismologica Sinica, 1980, 2(3): 258-267)
(  0) 0) |
| [3] |
朱传镇, 傅昌洪, 罗胜利. 震群与大地震关系的研究(华北地区)[J]. 地震学报, 1981, 3(2): 105-117 (Zhu Chuanzhen, Fu Changhong, Luo Shengli. Study of Earthquake Swarms in Relation to Large Earthquakes(North China Area)[J]. Acta Seismologica Sinica, 1981, 3(2): 105-117)
(  0) 0) |
| [4] |
Dieterich J. A Constitutive Law for Rate of Earthquake Production and Its Application to Earthquake Clustering[J]. Journal of Geophysical Research: Solid Earth, 1994, 99(B2): 2601-2618 DOI:10.1029/93JB02581
(  0) 0) |
| [5] |
郑建常, 李东梅, 王鹏, 等. 基于最邻近事件距离算法的丛集地震识别方法及应用[J]. 地震, 2014, 34(4): 100-109 (Zheng Jianchang, Li Dongmei, Wang Peng, et al. Method and Application of Clustering Seismicity Identification Based on Nearest-Neighbor Distance[J]. Earthquake, 2014, 34(4): 100-109)
(  0) 0) |
| [6] |
王鹏, 郑建常, 李晓红, 等. 基于最邻近事件距离算法的华北地区地震丛集特征研究[J]. 大地测量与地球动力学, 2017, 37(12): 1229-1233 (Wang Peng, Zheng Jianchang, Li Xiaohong, et al. Study on the Characteristics of Earthquake Clustering in North China Based on the Nearest-Neighbor Distance[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1229-1233)
(  0) 0) |
| [7] |
Zhuang J C, Chang C P, Ogata Y, et al. A Study on the Background and Clustering Seismicity in the Taiwan Region by Using Point Process Models[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B5)
(  0) 0) |
| [8] |
裴韬, 周成虎, 杨明, 等. 混合二维泊松过程的分解算法及其在提取地震丛集模式中的应用[J]. 地震学报, 2004, 26(1): 53-61 (Pei Tao, Zhou Chenghu, Yang Ming, et al. The Algorithm of Decomposing Superimposed 2-D Poisson Processes and Its Application to the Extracting Earthquake Clustering Pattern[J]. Acta Seismologica Sinica, 2004, 26(1): 53-61 DOI:10.3321/j.issn:0253-3782.2004.01.007)
(  0) 0) |
| [9] |
王炜. 华北几次大震前的地震空间集中度C值的异常变化[J]. 地震研究, 1986, 9(2): 147-158 (Wang Wei. Anomalous Variation of C Values for Seismic-Spatial Concentrative Degree before Several Large Earthquakes in North China[J]. Journal of Seismological Research, 1986, 9(2): 147-158)
(  0) 0) |
| [10] |
Zhuang J C, Ogata Y, Vere-Jones D. Stochastic Declustering of Space-Time Earthquake Occurrences[J]. Journal of the American Statistical Association, 2002, 97(458): 369-380 DOI:10.1198/016214502760046925
(  0) 0) |
| [11] |
Zaliapin I, Ben-Zion Y. Asymmetric Distribution of Aftershocks on Large Faults in California[J]. Geophysical Journal International, 2011, 185(3): 1288-1304 DOI:10.1111/j.1365-246X.2011.04995.x
(  0) 0) |
| [12] |
Zaliapin I, Ben-Zion Y. Earthquake Clusters in Southern California I: Identification and Stability[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(6): 2847-2864 DOI:10.1002/jgrb.50179
(  0) 0) |
| [13] |
Zaliapin I, Ben-Zion Y. Earthquake Clusters in Southern California II: Classification and Relation to Physical Properties of the Crust[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(6): 2865-2877 DOI:10.1002/jgrb.50178
(  0) 0) |
| [14] |
Zaliapin I, Ben-Zion Y. A Global Classification and Characterization of Earthquake Clusters[J]. Geophysical Journal International, 2016, 207(1): 608-634 DOI:10.1093/gji/ggw300
(  0) 0) |
| [15] |
Zaliapin I, Ben-Zion Y. Discriminating Characteristics of Tectonic and Human-Induced Seismicity[J]. Bulletin of the Seismological Society of America, 2016, 106(3)
(  0) 0) |
| [16] |
Zaliapin I, Gabrielov A, Keilis-Borok V, et al. Clustering Analysis of Seismicity and Aftershock Identification[J]. Physical Review Letters, 2008, 101(1)
(  0) 0) |
| [17] |
刘西林, 刘涛涛, 郑建常, 等. 山东及其近海小震群活动特征研究[J]. 防灾减灾工程学报, 2007, 27(4): 457-464 (Liu Xilin, Liu Taotao, Zheng Jianchang, et al. Study on the Characteristics of the Small Seismic Swarms Occurring in Shandong Province and Its Nearby Ocean Floor[J]. Journal of Disaster Prevention and Mitigation Engineering, 2007, 27(4): 457-464)
(  0) 0) |
| [18] |
李冬梅, 周翠英, 董翔, 等. 山东地区震群活动与周围地区中强地震的关系[J]. 华北地震科学, 2011, 29(4): 21-26 (Li Dongmei, Zhou Cuiying, Dong Xiang, et al. Relationship between Earthquake Swarms in Shandong Area and Mid-Strong Earthquakes in Its Surrounding Area[J]. North China Earthquake Sciences, 2011, 29(4): 21-26)
(  0) 0) |
| [19] |
山东省地震史料编辑室. 山东省地震史料汇编[M]. 北京: 地震出版社, 1983 (Editorial Office of Seismic Historical Data of Shandong Province. Seismic Historical Data Compilation of Shandong Province[M]. Beijing: Seismological Press, 1983)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


