全球导航卫星系统(GNSS)反演的水汽具有全天候、近实时/实时、低成本以及高精度等优点,近年来在GNSS气象学研究中得到快速发展,在干旱、暴雨、台风和强对流等极端天气的分析与临阵预报等方面被广泛应用。大气加权平均温度(Tm)是水汽转换系数K的主要影响参数,因此Tm在GNSS水汽反演过程中作为关键参量[1-2],其计算精度直接影响GNSS水汽反演结果的精度[3]。目前,大气加权平均温度的计算模型分为两类:第一类是基于实测的气象参数,采用统计回归等方法拟合的经验模型;第二类是基于局部或全球多年的Tm数据拟合的不需要气象参数的经验模型[4-5]。本文在Bevis公式基础上进行改进,使所求Tm值达到最优效果且具有良好的实时性,属于第一类需要地表气象参数的经验模型研究。
在诸多学者的研究中,Bevis等[6-7]分析认为,北美地区Tm与地表温度(Ts)具有较强的相关性,由此建立著名的Bevis线性回归模型(Tm=70.2+0.72Ts)。由于该模型方程的系数具有显著的季节性和局地性,若要在其他地区使用,需要根据当地的探空资料对Bevis公式的系数重新估计。随着GNSS水汽探测技术的不断发展,Bevis模型的局地精化和基于实测气象参数的Tm模型构建得到极大的发展。李建国等[8]研究适合于中国东部地区和不同季节的关于Tm和Ts的线性回归方程(Tm=44.05+0.81Ts);陈永奇等[9]利用香港探空站的多年探空资料构建精度优于Bevis公式的Tm和Ts的线性模型,并将其用于香港地区的GPS水汽估计;于胜杰等[10]分析Bevis公式与高度的关系,在此基础上建立可适用于中国大陆不同地区、不同海拔范围的Tm公式;李黎等[11]基于湖南地区3个探空站资料,构建该地区Tm与Ts的本地化线性模型,取得良好的效果;莫智翔等[12]建立顾及多因子的中国西部地区精化模型,使其精度得到改善。
由于中国南部地区南北跨度大、地形地貌复杂多变,且呈现西高东低的趋势,又有明显的季节性差异,在该地区进行GNSS水汽反演时,目前Tm模型所提供的Tm值的精度不能达到最优效果,为提高计算结果的精度,需要对Bevis模型进行优化改进。本文分析中国南部地区Tm与Ts等气象因子的相关性发现,Tm与Ts有较强的正相关性,与海拔高度和纬度有明显的负相关性。本文利用中国南部地区19个探空站共3 a的实测数据,对Bevis模型进行改进,建立顾及地面温度、季节变化、纬度和测站高程的多因子Tm模型,并进行精度评定。
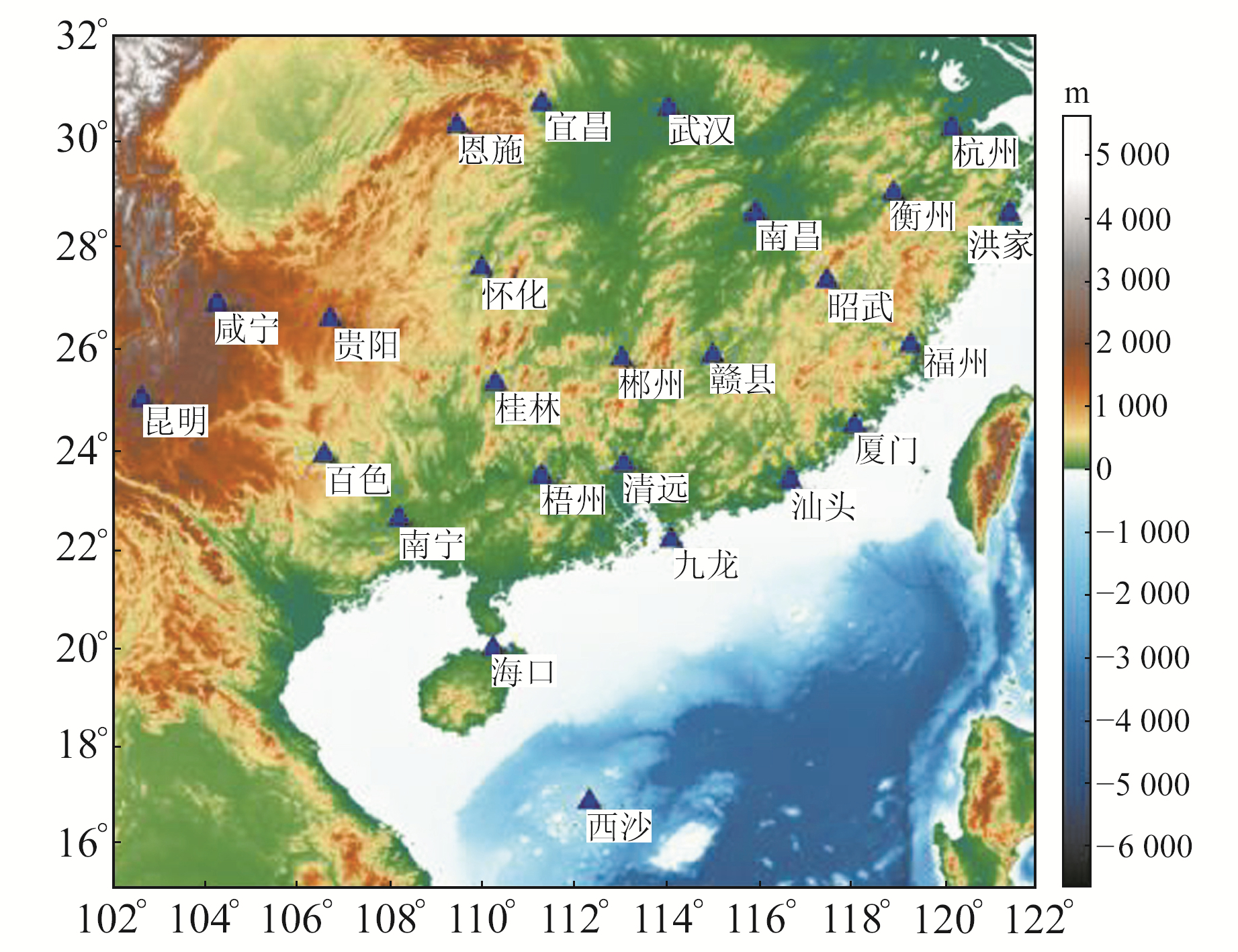
1 研究区域及大气加权平均温度计算原理 1.1 研究区域本文选取中国南部地区25个探空站作为研究对象,其中19个探空站用来建模,6个探空站用来进行精度验证。本文采用2015~2018年共4 a的探空站实测数据(数据采样间隔为12 h),该数据可以通过http//weather.uwyo.edu/upperair/sounding.html免费下载,其中2015~2017年的实测数据作为建模数据,2018年的实测数据作为参考数据,用于精度验证。站点的地理分布如图 1所示。
|
图 1 中国南部地区25个探空站的地理分布 Fig. 1 Geographical distribution of 25 radiosonde stations in southern China |
大气加权平均温度Tm可以通过数值积分法求得,该方法精度高、易实现,已经成为诸多学者精确求得大气加权平均温度的方法。Tm计算公式为:
| $ {T_m} = \frac{{\int_{{h_z}}^\infty {\left( {e/T} \right){\rm{d}}z} }}{{\int_{{h_z}}^\infty {(e/{T^2}){\rm{d}}z)} }}{\rm{ }} $ | (1) |
式中,e为水汽压,T为气温,hz为高程。
由式(1)可知,大气加权平均温度需要利用水汽压和气温数据由数值积分法求得。由于探空站的分布并不均匀,导致很多地区缺乏探空资料,因此有些地区Tm很难精确计算,通常是根据区域探空数据采用统计回归方法(最小二乘原理)拟合出Tm与地面温度Ts等气象要素的关系[12]。其中较为广泛使用的是Bevis等[6-7]提出的Tm-Ts线性回归公式。Landskron等[13]提出的GPT3模型是目前全球范围内最为先进的经验对流层格网模型,可提供包括Tm在内的多种对流层参数。GPT3模型改良映射函数系数,从而克服低截止高度角引起的映射函数误差,是精度最高的GPT系列模型。GPT3模型仅需输入测站位置信息和相应日期就可以得到测站点处的Tm值,用作精度评定的对照模型,具有很高的研究意义。
2 中国南部地区Tm精化模型的建立 2.1 Tm与Ts等气象因子相关性分析中国南部地区纬度跨度大,地势多变。有研究表明,Tm与高程[3]、Ts[6]和纬度[14]具有一定相关性。为探究中国南部地区Tm与Ts、高程和纬度之间的关系,本文选用2017年中国南部地区19个探空站数据,利用数值积分法计算出2017年的Tm与Ts、高程和纬度的相关性(图 2)。

|
图 2 Tm与Ts等气象因子的相关性分析 Fig. 2 Correlation analysis of meteorological factors such as Tm and Ts |
由图 2(a)可见,Tm与Ts呈现出正相关的关系,并且表现出较强的相关性,所以在建立Tm模型时,需考虑地面温度这个重要因素。由图 2(b)、(c)可见,Tm与高程和纬度呈现出负相关的关系,因此在建立Tm模型时需考虑高程和纬度的变化并对其进行改正。
2.2 模型建立根据Bevis公式,利用2015~2017年的探空资料,运用最小二乘原理拟合出只考虑Ts因素的Tm-SC1模型公式:
| $ {T_m} = a + b\cdot{T_s} $ | (2) |
式中,Ts为测站温度,a、b为模型系数(表 1)。
|
|
表 1 使用中国南部2015~2017年探空数据计算的Tm-SC1模型系数 Tab. 1 Model coefficients of Tm-SC1 model calculated using sounding data from 2015 to 2017 over southern China |
Yao等[15]的研究表明,利用经验模型计算的Tm值与数值积分法获取的Tm值所得到的残差序列存在明显的周期性,对原有模型计算的Tm进行补偿可以改善计算结果的精确度。因此采用具有1 a周期和0.5 a周期的三角函数来拟合残差(季节和地理变化反映在残差中)。参考Yao等[15]的建模思路,将三角函数的计算值进行季节性修正后添加到Tm建模过程中。通过以上分析可知,Tm不仅与Ts表现出较强的线性正相关,而且与海拔高度和纬度表现出明显的负相关,与季节变化也有密切关系。所以在构建模型过程中,加入地面温度、海拔、季节变化和纬度因素,避免计算模型系数的不确定性,使新模型更加完整和符合实际情况,建立一种新的模型关系式:
| $ \begin{array}{l} {T_m} = {a_1} + {a_2}{T_s} + {a_3}{\rm{cos}}\left( {\frac{{2{\rm{ \mathsf{ π} }}\cdot{\rm{doy}}}}{{365.25}}} \right) + \\ {a_4}{\rm{sin}}\left( {\frac{{2{\rm{ \mathsf{ π} }}\cdot{\rm{doy}}}}{{365.25}}} \right) + {a_5}{\rm{cos}}\left( {\frac{{4{\rm{ \mathsf{ π} }}\cdot{\rm{doy}}}}{{365.25}}} \right) + \\ {a_6}{\rm{sin}}\left( {\frac{{4{\rm{ \mathsf{ π} }}\cdot{\rm{doy}}}}{{365.25}}} \right) + {a_7} \times h + {a_8} \times {\rm{lati}} \end{array} $ | (3) |
式中,h为测站高度,lati为纬度,doy为年积日,a1、a2、a3、a4、a5、a6、a7和a8均为模型系数。
利用中国南部地区19个探空站2015~2017年各个站点的大气加权平均温度、地面温度、测站高程和纬度来确立新模型的系数。首先利用数值积分法计算出中国南部地区每一个探空站点的Tm值,然后代入相应的Tm、Ts、测站高程和纬度数据,利用公式拟合计算得到中国南部区域的Tm-SC2模型系数值[12](表 2)。
|
|
表 2 使用中国南部2015~2017年探空数据计算的Tm-SC2模型系数 Tab. 2 Model coefficients of Tm-SC2 model calculated using sounding data from 2015 to 2017 over southern China |
将2018年探空数据获得的Tm作为参考值,来验证新Tm模型在中国南部地区的计算精度。选用偏差(bias)和均方根误差(RMS)进行精度评定,其表达式为:
| $ {\rm{bias}} = \frac{1}{N}{\rm{ }}\sum\limits_{i = 1}^N {} (X_m^{{M_i}}{\rm{ - }}X_m^{{R_i}}) $ | (4) |
| $ {\rm{RMS}} = \frac{1}{N}\sum\limits_{i = 1}^N {} {(X_m^{{M_i}}{\rm{ - }}X_m^{{R_i}})^2} $ | (5) |
式中,N为数据的样本数,XmMi表示第i个模型计算值,XmRi表示第i个模型参考值。
3.1 中国南部地区Tm模型精度评估以中国南部地区19个探空站2018年的探空资料为数据源,将数值积分法获得的Tm作为参考值,对新建立的Tm模型进行精度评估。分别用Bevis模型和GPT3模型对2018年19个探空站数据进行处理,与数值积分法求得的Tm参考值作比较并统计出偏差和RMS,以验证新建立的Tm模型在中国南部地区是否有更好的精度(表 3)。
|
|
表 3 2018年中国南部地区19个探空站4种模型的精度统计 Tab. 3 Accuracy statistics of 4 models of 19 radiosonde stations in southern China in 2018 |
由表 3可知,在中国南部地区Bevis模型、GPT3模型和Tm-SC1模型均表现出明显的正偏差,其年均值分别为1.68 K、0.38 K和0.76 K,从偏差值可以看出,GPT3模型优于Bevis模型和Tm-SC1模型。中国南部地区的Tm-SC2模型表现出明显的负偏差,其年均值为-0.10 K,说明新建立的Tm-SC2模型比Bevis和GPT3模型的偏差更小、考虑因子更多、精度更高。Bevis模型和GPT3模型的RMS误差平均值分别为2.98 K和2.63 K,说明GPT3模型的精度优于Bevis模型。从RMS误差来看,Tm-SC1模型的平均RMS为2.57 K,精度相比Bevis模型提高约0.41 K(13.8%),与GPT3模型相比提高约0.06 K (2.2%);Tm-SC2模型的平均RMS为1.64 K,精度相比Bevis模型提高约1.34 K(44.9%),与GPT3模型相比提高约0.99 K (37.6%),与Tm-SC1模型相比提高约0.93 K(36.2%),说明Tm-SC2模型在中国南部地区比其他3个模型有更高的精度,且模型更稳定。为更好地验证模型的精度及不同模型在一年四季中的适用性,本文对日均值的偏差和RMS进行统计分析,其结果如图 3、图 4所示。

|
图 3 利用2018年探空资料评估中国南部地区不同模型的日均bias分布散点图 Fig. 3 Scatter plot of daily average bias distribution of different models in southern China using radiosonde data in 2018 |
|
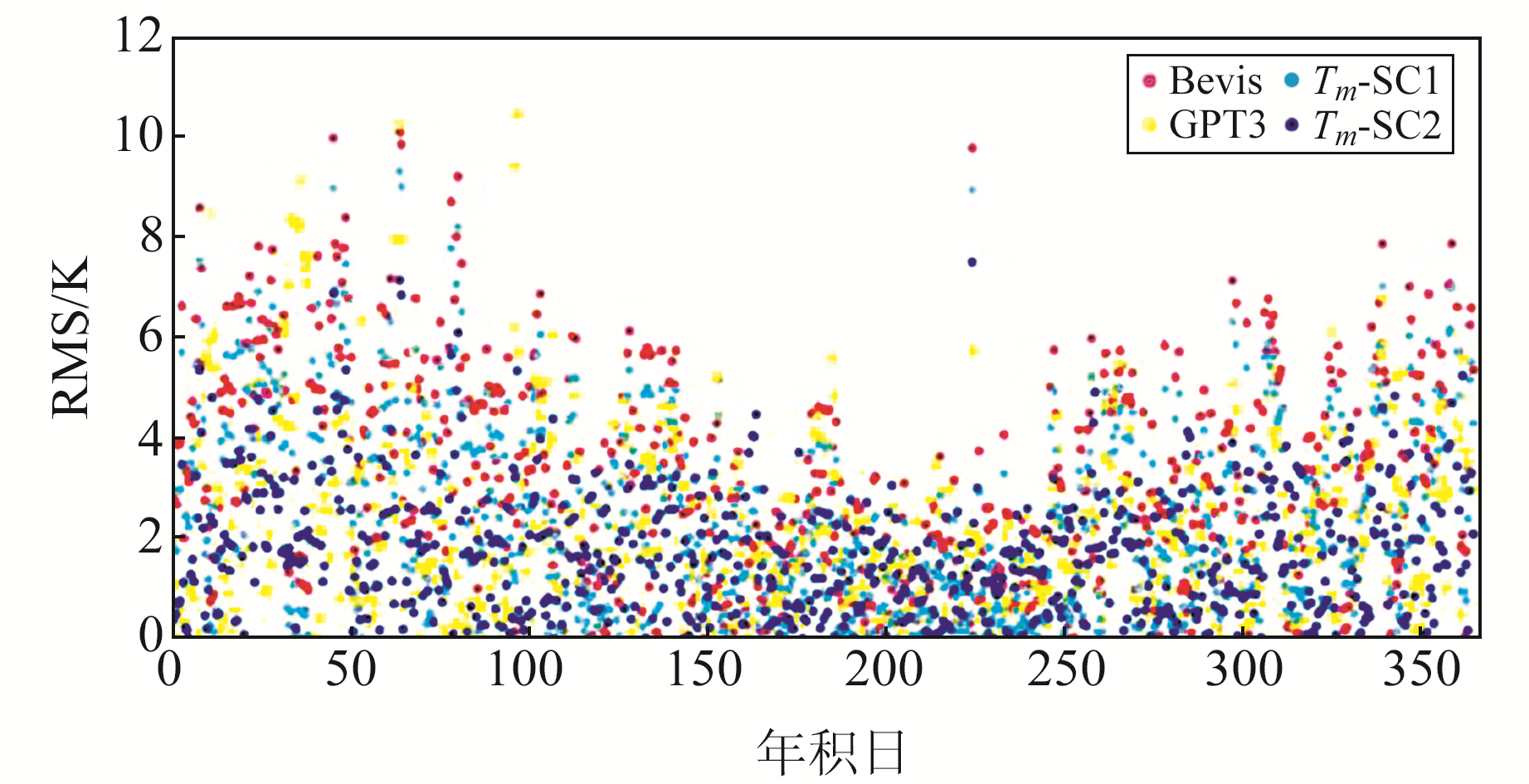
图 4 利用2018年探空资料评估中国南部地区不同模型的日均RMS分布散点图 Fig. 4 Scatter plot of daily average RMS distribution of different models in southern China using radiosonde data in 2018 |
从图 3可见,新建立的Tm-SC1和Tm-SC2模型都比Bevis模型和GPT3模型的精度高,并且Tm-SC2模型受季节的影响要明显小于Tm-SC1模型和Bevis模型,在全年期间均较为平稳。Tm-SC1模型和Bevis模型受季节影响较大,有很明显的坡度曲线,在夏季误差较小,在春、冬季节出现明显的波峰,误差较大。对于GPT3模型,在全年期间表现出明显的负偏差且误差范围较大,在春季和冬季期误差达到较大值,GPT3模型考虑了Tm的年周期和半年周期的变化,出现这种结果是由于受到系统误差的影响。通过上述分析,进一步说明了在相同条件下,考虑了季节变化的Tm-SC2模型的精度明显要高于其他3种模型,显示出较小的偏差,没有明显的季节性变化,特别是在春、冬两季对比更为明显。
从图 4可见,Tm-SC2模型的RMS值在全年期间较为平稳,精度最高,但所有模型均显示出明显的坡度曲线,在春、冬两季的RMS值较大,夏季的RMS值较小,均表现出了明显的季节性变化。出现这种情况的原因是,所选取的探空站位于中纬度地区,四季变化较为明显,Tm值在夏季变化较为平稳,在冬季变化较大。Tm-SC2模型与其他模型的RMS值相比误差更小、变化更稳定,能够明显提高Tm的计算精度。为检验各个模型在不同探空站的计算精度,对不同模型在同一探空站的年均偏差和RMS进行统计,研究不同模型在相同高程和纬度条件下的表现,同时对各个探空站的年均偏差和RMS进行精度分析,检验不同模型在考虑高程和纬度的条件下在中国南部地区的适用性(图 5)。

|
图 5 2018年中国南部地区19个探空站4种模型的精度对比 Fig. 5 Precision comparison of four models of 19 radiosonde stations in southern China in 2018 |
由图 5可见,Tm-SC2模型在九龙、郴州、福州、清远、汕头、南宁、海口等15个探空站相对于Tm-SC1模型、Bevis模型和GPT3模型都有更好的适用性,其他几个探空站虽然精度差别不大,但也有所提高。从柱状图可以明显看出,精度得到很好改善的探空站,均处在低纬度沿海地区和海拔较高地区,由此说明,在考虑海拔和纬度的条件下,新建立的Tm-SC2模型对Tm的计算精度有很大改善。进一步分析整个研究区域的精度可知,Tm-SC1模型、Bevis模型和GPT3模型表现出明显的正偏差,而Tm-SC2模型表现出明显的负偏差,年均偏差为-0.10 K,且精度有所提高;Tm-SC1模型相比于Bevis模型和GPT3模型其精度(RMS值)分别提高13.8%和2.2%,Tm-SC2相比于Bevis模型和GPT3模型其精度(RMS值)分别提高44.9%和37.6%。综上所述,Tm-SC2模型可作为新的高精度区域精化模型应用于中国南部地区的GNSS气象学研究中。为更好地进行精度分析,本文对各个探空站的年均偏差和RMS作统计分析,结果如图 6、图 7所示。

|
图 6 2018年中国南部地区19个探空站4种模型的年均bias分布 Fig. 6 Distribution of average annual bias for 4 models of 19 radiosonde stations in southern China in 2018 |

|
图 7 2018年中国南部地区19个探空站4种模型的年均RMS分布 Fig. 7 Distribution of average annual RMS for 4 models of 19 radiosonde stations in southern China in 2018 |
由图 6可见,Tm-SC2模型在中国南部地区表现出明显的负偏差,Tm-SC1模型、Bevis模型和GPT3模型在南部地区表现出明显的正偏差。由数据对比可知,在低纬度和海拔较高的地区,Tm-SC2模型相较于其他3种模型偏差更稳定,偏差绝对值小于1.5 K,这是由于Tm-SC2模型考虑了海拔和纬度这两个重要因素,并对其进行了修正。综上所述,Tm-SC2模型在中国南部地区精度最高且更稳定。
由图 7可见,在中国南部地区,Tm-SC2模型相较于其他3种模型表现出较小的RMS值,这是由于Tm-SC2模型在计算Tm时顾及了高程、纬度和日偏差等诸多气象因子并对其进行了改正,因此Tm-SC2模型在中国南部地区计算Tm时精度最高。Tm-SC2模型在中国南部地区的RMS小于1.7 K,对比其他3种模型,其年均RMS精度更高。为研究新建立的Tm模型在空间域上的有效性和适用性,除去用于建模的19个探空站外,在研究区域南北各选取包括西沙站(59981)、宜昌站(57461)以及海拔较高的威宁站(56691)在内的6个站进行精度验证,统计各站的年均偏差和RMS,结果如表 4所示。
|
|
表 4 2018年探空站资料检验中国南部地区Tm-SC模型在研究区域外有效性的精度统计 Tab. 4 Accuracy statistics for testing the effectiveness of the Tm-SC model in southern China outside the studied area using radiosonde data in 2018 |
由表 4可知,在研究区域外选取的探空站中,Tm-SC2模型的精度明显优于其他3种模型。从年均偏差来看,无论是海拔较高的探空站还是高纬度地区,Tm-SC2模型的精度都有明显提升,海拔较高的威宁站和研究区域以南的西沙站精度提升明显。从年均RMS来看,Tm-SC2模型相较于其他3种模型误差更小更稳定、精度更高,这是由于Tm-SC2模型顾及多个影响因子并且对残差序列进行了补偿。综上所述,本文建立的Tm-SC2模型在空间域上有更好的稳定性和实用性,可为中国南部地区GNSS反演PWV提供更高精度的Tm值。
3.2 不同模型反演PWV的精度分析在GNSS反演PWV的过程中,Tm是关键参数,Tm值的计算精度直接影响GNSS反演PWV的计算精度,本文研究目的是提高中国南部地区计算Tm的精度,进而为中国南部地区计算GNSS-PWV服务。由于GNSS基准站与探空站在大多数情况下不在同一位置,并且GNSS基准站在一般情况下是为大地测量服务,未安装气象传感器,无法获取气象数据,这十分不利于研究Tm对GNSS-PWV计算的影响。因此,本文采用Huang等[17]提出的计算Tm对GNSS-PWV影响的方法,并对计算结果进行分析。
| $ \begin{array}{l} \frac{{{\rm{RM}}{{\rm{S}}_{{\rm{pwv}}}}}}{{{\rm{PWV}}}} = \frac{{{\rm{RM}}{{\rm{S}}_K}}}{K} = {\rm{ }}\frac{{{k_3}\cdot{\rm{RM}}{{\rm{S}}_{{T_m}}}}}{{\left( {k{\prime _2} + {\rm{ }}\frac{{{k_3}}}{{{T_m}}}} \right)T_m^2}} = \\ \;\;\;\;\;\;\;\;\;\frac{{{k_3}}}{{\left( {k{\prime _2} + {\rm{ }}\frac{{{k_3}}}{{{T_m}}}} \right){T_m}}}\cdot\frac{{{\rm{RM}}{{\rm{S}}_{{T_m}}}}}{{{T_m}}} \end{array} $ | (6) |
式中,RMSpwv、RMSK、RMSTm分别为PWV、转换系数K和Tm的RMS误差,RMSpwv/PWV为PWV的相对误差,其中Tm和PWV是2018年中国南部地区探空资料的年均值。RMSpwv和RMSpwv/PWV用于评估由模型计算的Tm的误差对计算GNSS-PWV的影响。各模型计算结果如表 5所示。
|
|
表 5 2018年中国南部地区4种模型计算PWV的理论RMS误差和相对误差的精度统计 Tab. 5 Accuracy statistics of RMSPWV and RMSPWV/PWV of PWV calculated by 4 models in southern China in 2018 |
从表 5可知,Bevis模型和GPT3模型均表现出较大的RMSpwv和RMSpwv/PWV值,Tm-SC1模型和Tm-SC2模型相较于前两者精度都有所提高,且Tm-SC2模型的整体RMSpwv值小于0.21 mm,平均RMSpwv值为0.16 mm。通过RMSpwv/PWV值对比分析可知,Tm-SC2模型的RMSpwv/PWV更小、更稳定,平均值为0.43%,范围为0.38%~0.56%。从数据结果来看,Tm-SC1和Tm-SC2模型相较于Bevis和GPT3模型波动范围更小、更稳定,提供的Tm值更加精确。综上所述,Tm-SC2模型计算出的Tm值在计算GNSS-PWV时,相比其他模型精度更高、更稳定。
4 结语1) 本文利用最小二乘原理和回归分析方法,采用2015~2017年19个探空站数据,建立适用于中国南部地区的Tm-SC1模型和Tm-SC2模型。以2018年探空站获取的Tm作为参考值,计算出Tm-SC1模型平均偏差和平均RMS分别为0.76 K和2.57 K,Tm-SC2模型平均偏差和平均RMS分别为-0.10 K和1.64 K。
2) 将Tm-SC2模型与Tm-SC1模型、Bevis模型和GPT3模型的日均和年均误差相比较可知,考虑海拔高度、季节变化以及纬度等因素的Tm-SC2模型在中国南部地区表现出更好的稳定性,相较于其他3种模型的平均偏差和RMS精度更高。
3) 计算各模型反演PWV值时的RMSpwv和RMSpwv/PWV误差,得到Tm-SC2模型的PWV的RMS和相对误差的平均值分别为0.16 mm和0.43%,比其他3种模型表现出更好的适用性。
综上可知,考虑多个因子的Tm-SC2模型可以得到更精确的Tm值,同时在中国南部地区表现出良好的精度和稳定性,可以进一步改善中国南部地区GNSS大气水汽反演的精度。
| [1] |
黄良珂, 吴丕团, 王浩宇, 等. 中国西南地区GPS大气水汽转换系数模型精化研究[J]. 大地测量与地球动力学, 2019, 39(3): 256-261 (Huang Liangke, Wu Pituan, Wang Haoyu, et al. Refining the GPS Atmospheric Water Vapor Conversion Factor Model over Southwest China[J]. Journal of Geodesy and Geodynamics, 2019, 39(3): 256-261)
(  0) 0) |
| [2] |
刘立龙, 万庆同, 周威, 等. 基于傅里叶级数的中国沿海地区Tm模型精化研究[J]. 大地测量与地球动力学, 2019, 39(11): 1 137-1 141 (Liu Lilong, Wan Qingtong, Zhou Wei, et al. Research on Refinement of Tm Model in China's Coastal Area Based on Fourier Series[J]. Journal of Geodesy and Geodynamics, 2019, 39(11): 1 137-1 141)
(  0) 0) |
| [3] |
Huang L K, Liu L L, Chen H, et al. An Improved Atmospheric Weighted Mean Temperature Model and Its Impact on GNSS Precipitable Water Vapor Estimates for China[J]. GPS Solutions, 2019, 23(2): 1-16
(  0) 0) |
| [4] |
Yao Y B, Xu C Q, Zhang B, et al. GTM-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal International, 2014, 197(1): 202-212 DOI:10.1093/gji/ggu008
(  0) 0) |
| [5] |
黄良珂, 彭华, 刘立龙, 等. 顾及垂直递减率函数的中国区域大气加权平均温度模型[J]. 测绘学报, 2020, 49(4): 432-442 (Huang Liangke, Peng Hua, Liu Lilong, et al. An Empirical Atmospheric Weighted Mean Temperature Model Considering the Lapse Rate Function for China[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4): 432-442)
(  0) 0) |
| [6] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15 787-15 810 DOI:10.1029/92JD01517
(  0) 0) |
| [7] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [8] |
李建国, 毛节泰, 李成才. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J]. 气象学报, 1999, 57(3): 283-292 (Li Jianguo, Mao Jietai, Li Chengcai. The Approach to Remote Sensing of Water Vapor Based on GPS Linear Regression Tm in Eastern Region of China[J]. Acta Meteorologica Sinica, 1999, 57(3): 283-292 DOI:10.3969/j.issn.1001-7313.1999.03.004)
(  0) 0) |
| [9] |
陈永奇, 刘焱雄, 王晓亚, 等. 香港实时GPS水汽监测系统的若干关键技术[J]. 测绘学报, 2007, 36(1): 9-12 (Chen Yongqi, Liu Yanxiong, Wang Xiaoya, et al. GPS Real-Time Estimation of Precipitable Water Vapor-Hong Kong Experiences[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 9-12 DOI:10.3321/j.issn:1001-1595.2007.01.002)
(  0) 0) |
| [10] |
于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 741-744 (Yu Shengjie, Liu Lintao. Validation and Analysis of the Water-Vapor-Weighted Mean Temperature from Tm-Ts Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741-744)
(  0) 0) |
| [11] |
李黎, 宋越, 易金花, 等. 湖南三地加权平均温度分区分时模型研究[J]. 测绘科学, 2018, 43(1): 54-58 (Li Li, Song Yue, Yi Jinhua, et al. Research on Subregional and Seasonal Modeling of Weighted Average Temperature in Three Region of Hunan[J]. Science of Surveying and Mapping, 2018, 43(1): 54-58)
(  0) 0) |
| [12] |
莫智翔, 黎杏, 黄良珂, 等. 顾及多因子影响的中国西部地区大气加权平均温度模型精化研究[J]. 大地测量与地球动力学, 2021, 41(2): 145-151 (Mo Zhixiang, Li Xing, Huang Liangke, et al. Refinement of Atmospheric Weighted Mean Temperature Model Considering the Effects of Multiple Factors for Western China[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 145-151)
(  0) 0) |
| [13] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [14] |
Emardson T R, Derks H J P. On the Relation between the Wet Delay and the Integrated Precipitable Water Vapour in the European Atmosphere[J]. Meteorological Applications, 2000, 7(1): 61-68 DOI:10.1017/S1350482700001377
(  0) 0) |
| [15] |
Yao Y B, Zhang B, Xu C Q, et al. Improved One/Multi-Parameter Models that Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperature in Ground-Based GPS Meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282 DOI:10.1007/s00190-013-0684-6
(  0) 0) |
| [16] |
姚宜斌, 孙章宇, 许超钤. Bevis公式在不同高度面的适用性以及基于近地大气温度的全球加权平均温度模型[J]. 测绘学报, 2019, 48(3): 276-285 (Yao Yibin, Sun Zhangyu, Xu Chaoqian. Applicability of Bevis Formula at Different Height Level and Global Weighted Mean Temperature Model Based on Near-Earth Atmospheric Temperature[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(3): 276-285)
(  0) 0) |
| [17] |
Huang L K, Jiang W P, Liu LL, et al. A New Global Grid Model for the Determination of Atmospheric Weighted Mean Temperature in GPS Precipitable Water Vapor[J]. Journal of Geodesy, 2019, 93(2): 159-176 DOI:10.1007/s00190-018-1148-9
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


