2. 东南大学交通学院,南京市东南大学路2号,218889
全球导航卫星系统(GNSS)能够增加可观测卫星的数量和多样性[1],极大推动了卫星导航定位技术的发展。GNSS信号穿过大气时,会受到电离层和对流层折射的影响而产生延迟,是GNSS的一个主要误差源。电离层属于弥散性介质,其延迟效应可以通过频率间差分消除,而对流层属于中性大气,信号传播速度与频率无关,无法采用类似方法消除延迟效应[2]。对流层天顶延迟(zenith total delay,ZTD)一般能达到2.3 m左右[3],可分为静力学延迟(zenith hydrostatic delay,ZHD)和湿延迟(zenith wet delay,ZWD)两个部分。静力学延迟较为稳定,但湿延迟极易受天气效应影响,随机性极强,难以用模型估计[4],所以对流层延迟的精确估计是提高GNSS实时导航定位精度的关键技术之一。
目前国内外常用的对流层模型可分为气象和无气象参数模型两大类。经典的气象模型有Hopfield模型[5]、Saastamoinen模型[6]和Black模型[7]等,这些模型能够对干延迟进行高精度估计,但对湿延迟的估计效果并不理想[8]。此类模型的应用依赖于地表气象参数,这极大限制了模型的应用范围。无气象参数模型或是对地表气象参数进行经验建模,再代入第一类模型中计算,或是直接对ZTD进行时空分析,这两种方法都能摆脱对气象参数的依赖,应用范围更广泛。无气象参数模型常用的有EGNOS模型[9]、GPT系列模型[10-11]和CTrop模型[12]等,这些模型仅需输入测站的概略坐标和年积日即可获取经验ZTD延迟。由于对流层延迟变化复杂,难以通过一个固定的数学模型进行表达,人工神经网络技术可为解决这一问题提供途径[13],其强大的自适应学习能力和非线性逼近能力可以避免参数化建模的缺点,从而通过权值的自动调整达到最佳的逼近效果。
中国大陆构造环境监测网(Crustal Movement Observation Network of China,CMONOC)提供260多个连续监测站,用于监测中国区域地壳运动、重力场变化以及电离层与对流层参数。CMONOC提供逐小时由GAMIT/GLOBK软件解算的高精度ZTD产品(下文简称ZTDC),可以进行对流层延迟的建模[14]。陈俊平等[3]通过分析ZTDC的时空变化规律,构建2.5°×2.0°分辨率的SHAtrop模型。该模型考虑到高程改正,仅需要输入经纬度与时间即可满足中国区域GNSS用户实时导航ZTD改正的需求,优于常见的EGONS模型、UNB3模型和GPT2模型。采用CMONOC提供的对流层延迟产品,基于BP神经网络技术,建立多个弱神经网络非线性映射,集成构造BP-Adaboost模型。用户仅需输入测站的概略坐标、年积日和时间,即可获得高精度的ZTD估计值。将新模型与GPT3模型、CTrop模型和SHAtrop模型进行比较,可证明建模方法的有效性。
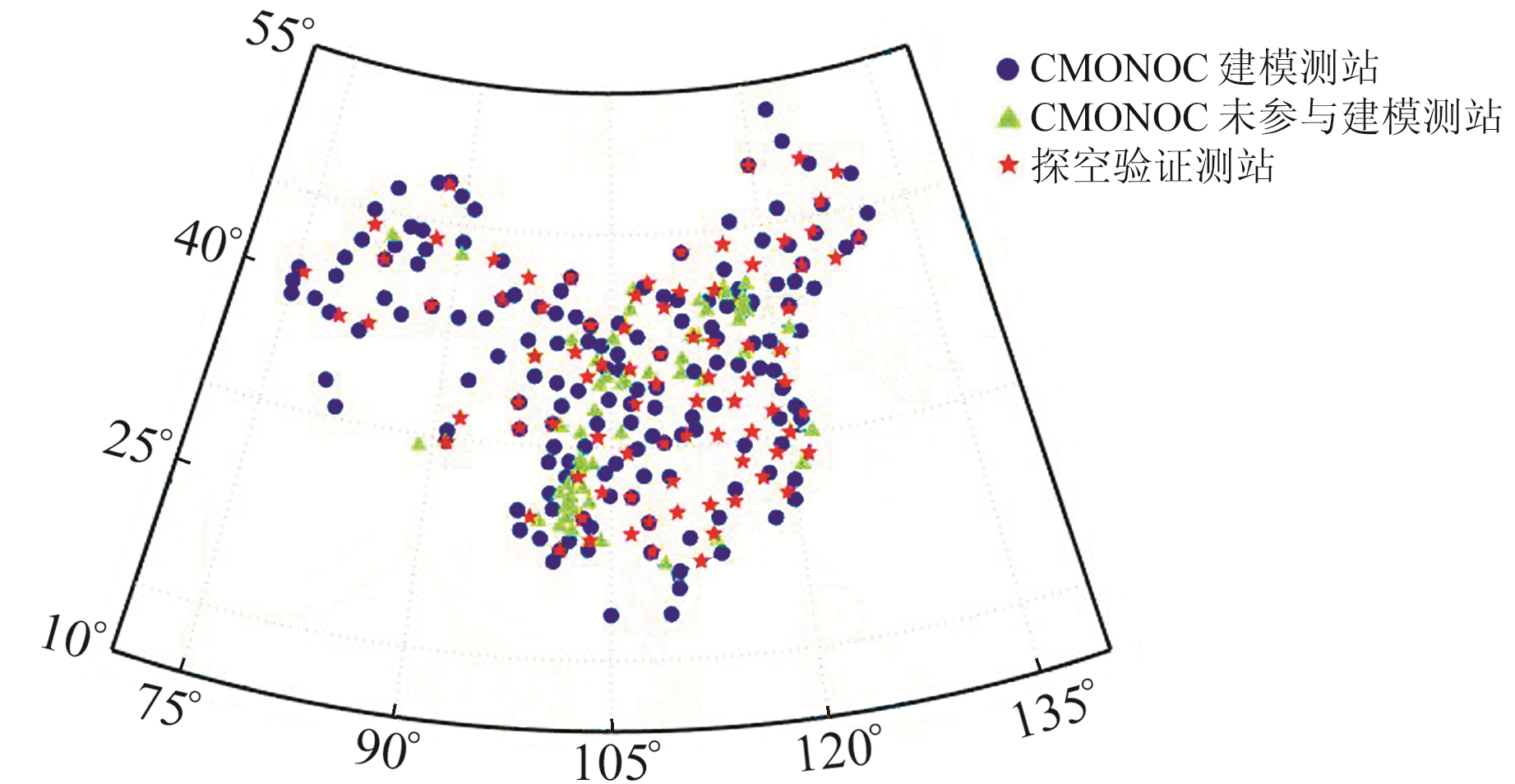
1 建模数据与验证数据选取2014~2019年具有连续观测数据的CMONOC测站,剔除其中误差大于5 mm的ZTD值,共得到测站217个。均匀选取其中155个测站2014~2018年的数据进行建模,利用剩余62个测站2019年的数据进行验证,得到训练样本1 883 076个、检验样本136 958个。为进一步验证模型的适用性,同时选取由IGRA(integrated global radiosonde archive)提供的中国区域内86个探空站的数据,剔除探空数据中观测层数少于12或顶层水汽压大于0.015 hPa的数据,得到检验样本48 910个,计算各个探空站的ZTD精确值(下文简称ZTDR)。建模测站和验证测站的分布如图 1所示。
|
图 1 CMONOC与探空测站分布 Fig. 1 Distribution of CMONOC and radiosonde stations |
由于探空数据仅给出各个等压面的气温、水汽压、位势高度等参数,可以利用Saastamoinen公式计算干延迟、利用积分方法计算湿延迟,并相加得到测站最终的ZTD值[8]:
| $ \left\{ \begin{array}{l} {\rm{ZHD}} = 0.002\;276{\rm{ }}8 \times \\ \;\;\;\;\frac{P}{{1 - 0.002\;6{\rm{cos}}\left( {2\varphi } \right) - 0.000\;000\;28h}}\\ {\rm{ZWD}} = {10^{ - 6}}\sum\limits_i^{} {} \left[ {\frac{{({h_i}{\rm{ - }}{h_{i + 1}})({N_{{{\rm{w}}_{i + 1}}}}{\rm{ - }}{N_{{{\rm{w}}_i}}})}}{{({\rm{ln}}{N_{{{\rm{w}}_i}}}{\rm{ - ln}}{N_{{{\rm{w}}_{i + 1}}}})}}} \right] \end{array} \right. $ | (1) |
式中,P为大气压(单位hPa);φ为纬度;h为大地高;Nwi为探空数据第i层大气折射率指数的湿分量,可由公式(2)计算得到:
| $ {N_{\rm{w}}} = {\rm{ }}\left( {{k_2}{\rm{ - }}{k_1}\frac{{{R_{\rm{d}}}}}{{{R_{\rm{w}}}}}} \right)\cdot{\rm{ }}\frac{e}{T} + {k_3}\frac{e}{{{T^2}}} $ | (2) |
式中,Rd和Rw为干空气和湿空气常数,k1、k2和k3为折射率常数,e为水汽压(单位hPa),T为热力学温度[15-16]。探空数据使用的位势高由位势除以重力常数(gn=9.806 65 m/s2)得到,并不严格等于几何高度。因此为统一探空站与CMONOC测站的高程系统,联合公式(3)和公式(4)将位势高转换成几何高度并最终转换为大地高[2]:
| $ {h_{\rm{d}}} = {\rm{ }}\frac{C}{{{g_n}}}{\rm{ }} = {\rm{ }}\frac{1}{{{g_n}}}\int_0^h {} g\left( {\varphi , h} \right)\cdot{\rm{d}}h $ | (3) |
| $ \begin{array}{l} g\left( {\varphi , h} \right) = {g_n}(1 - 0.002\;637\;3{\rm{cos}}\left( {2\varphi } \right) + \\ 5.9 \times {10^{ - 6}}{\rm{co}}{{\rm{s}}^2}\left( {2\varphi } \right))\cdot(1 - 3.14 \times {10^{ - 7}}h) \end{array} $ | (4) |
式中,hd为位势高(单位m),C为位势,h为正高(单位m)。采用平均偏差(bias)和均方根误差(RMS)作为评定标准。平均偏差表示准确度,即模型与真值的偏离程度;均方根误差表示精度,用于衡量模型的可靠性和稳定性[17],其计算公式为:
| $ \left\{ \begin{array}{l} {\rm{bias}} = \frac{1}{n}\sum\limits_{i = 1}^n {} ({\rm{ZT}}{{\rm{D}}_i}{\rm{ - ZTD}}_i^0)\\ {\rm{RMS}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {} {{({\rm{ZT}}{{\rm{D}}_i}{\rm{ - ZTD}}_i^0)}^2}} \end{array} \right. $ | (5) |
式中,n表示样本总数,ZTDi为模型的对流层延迟,ZTDi0为对流层延迟的精确值。
2 BP-Adaboost模型的建立BP-Adaboost算法的思想是合并多个“弱”神经网络的输出,进而得到更加精确的估计值[18-19]。其算法步骤如下:
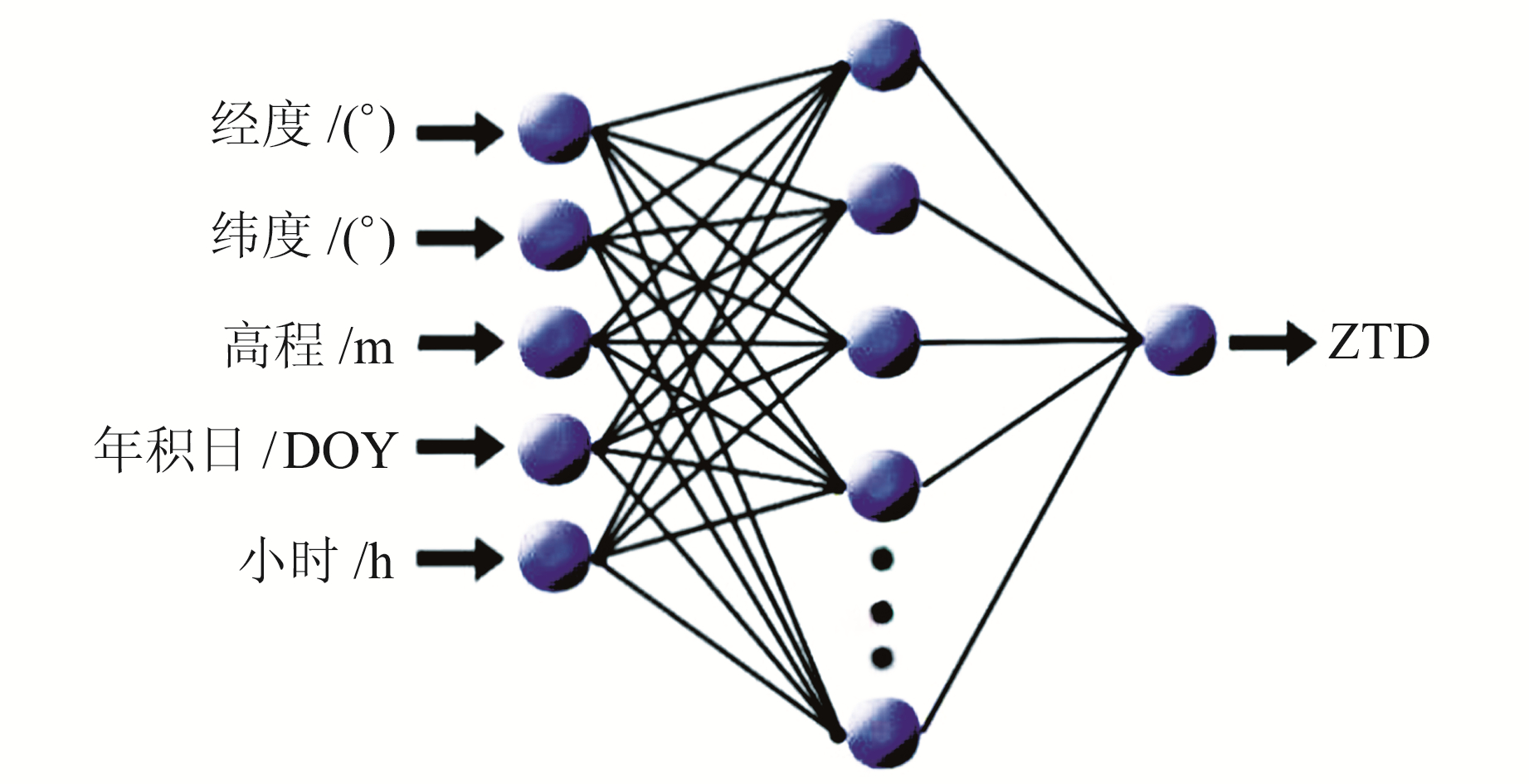
1) 神经网络初始化及训练。弱预测器选取前馈神经网络(feedforward neural network,FNN)。FNN网络由输入层、隐含层、输出层以及模型参数组成,模型的学习误差ε取0.1 mm。FNN网络输入层节点数为5,分别代表测站经度、纬度、高程、年积日(day of year,DOY)和小时;输出层节点数为1,代表ZTD(单位mm)。隐含层节点的选取无规律可循,一般通过试算确定。节点数过多可能导致学习时间过长且结果不稳定,节点数过少会导致网络不收敛。单个FNN网络基本结构如图 2所示。
|
图 2 FNN结构 Fig. 2 Feed forward neural network structure |
激活函数选取Tan-Sigmoid,其表达式为:
| $ f\left( x \right) = {\rm{ }}\frac{2}{{1 + {{\rm{e}}^{{\rm{ - }}2x}}}}{\rm{ }}{\rm{ - }}1 $ | (6) |
FNN训练采用最速下降法,调用MATLAB的toolbox。
2) 累积误差计算。共选取20个FNN网络,将其合并成BP-Adaboost强预测器,用于精确计算ZTD。将n个训练样本的分布权值初始化为D0(i)=1/n, i=1, 2, 3, …, n,每个网络的累积误差初始化为Error(t)=0, t=1, 2, 3, …, 20。若第t个FNN(FNNt)得到的第i个样本的预测误差大于50 mm,则认为该样本是需要加强学习的样本,需要按照公式(7)更新该网络的累积误差Error(t)及样本的分布误差Dt,否则FNNt对应的累积误差及样本的分布权值不变:
| $ \begin{array}{l} \left\{ \begin{array}{l} {\rm{Error}}\left( t \right) = {\rm{Error}}\left( t \right) + {D_t}\left( i \right)\\ {D_t}\left( i \right) = {D_{t{\rm{ - }}1}}\left( i \right)\cdot1.1 \end{array} \right.\\ \;\;\;\;\;\;\;\;\;\;t = 1, 2, 3, \ldots , 20 \end{array} $ | (7) |
具体的累积误差计算流程如图 3所示。

|
图 3 累积误差计算流程 Fig. 3 Cumulative error calculation flow chart |
3) 各弱预测器权重计算。第t个FNN网络的权重Pt可由公式(8)计算并归一化得到:
| $ \begin{array}{l} \left\{ \begin{array}{l} {p_t} = {\rm{ }}\frac{{0.5}}{{{\rm{exp}}\{ |{\rm{Error}}\left( t \right)|\} }}\\ {p_t} = {\rm{ }}\frac{{{p_t}}}{{\sum\limits_{t = 1}^{20} {} {p_t}}} \end{array} \right.\\ \;\;\;\;\;t = 1, 2, 3, \cdots , 20 \end{array} $ | (8) |
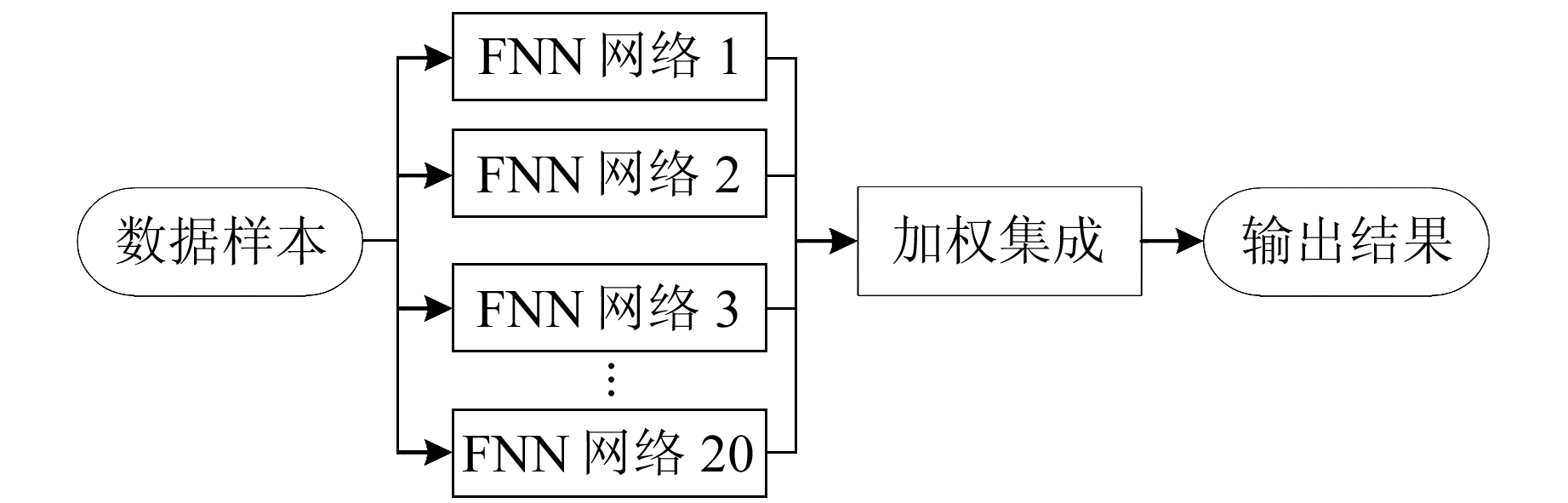
最后利用BP-Adaboost计算ZTD时,取这20个FNN网络预测结果的加权平均值作为最终的ZTD输出。算法流程如图 4所示。
|
图 4 BP-Adaboost算法流程 Fig. 4 The steps of BP-Adaboost algorithm |
为确定第1步中各FNN网络隐含层节点的个数,试算隐含层节点数为7~36共30种BP-Adaboost模型,由CMONOC验证站2019年ZTDC进行检验,得到其bias和RMS(图 5)。

|
图 5 不同隐含层节点数结构的bias和RMS Fig. 5 Bias and RMS with different hidden layer node number structure |
由图 5可见,当隐含层节点数少于27时,其bias绝对值和RMS均呈现出下降趋势;当节点数超过27时,bias与RMS趋于平缓,精度提升有限。所以隐含层节点数确定为27,选取的FNN网络结构为5×27×1。
3 精度验证为讨论BP-Adaboost模型的适用性,利用2019年CMONOC的141个参与建模测站(CMONOC建模站)、62个未参与建模测站(CMONOC验证站)和86个探空站的ZTD精确值分别比较CTrop模型、GPT3模型以及SHAtrop模型在中国区域的精度,结果见表 1(单位mm)。
|
|
表 1 4种模型的bias与RMS Tab. 1 Bias and RMS of the four models |
由表 1可见,BP-Adaboost模型的精度最优。当用CMONOC建模站和验证站进行数据评定时,BP-Adaboost的bias仅为0.62 mm和-1.16 mm,表明该模型没有明显的系统误差,体现出和GNSS数据相当程度的自洽性。其RMS比CTrop模型、GPT3模型和SHAtrop模型分别减小9.6%、2.8%和3.3%。当用探空站进行数据验证时,新模型bias为-12.32 mm,其绝对值为4种模型中最小,其RMS与GPT3模型相当,但比其他2种模型分别提高3.9%和2.5%。
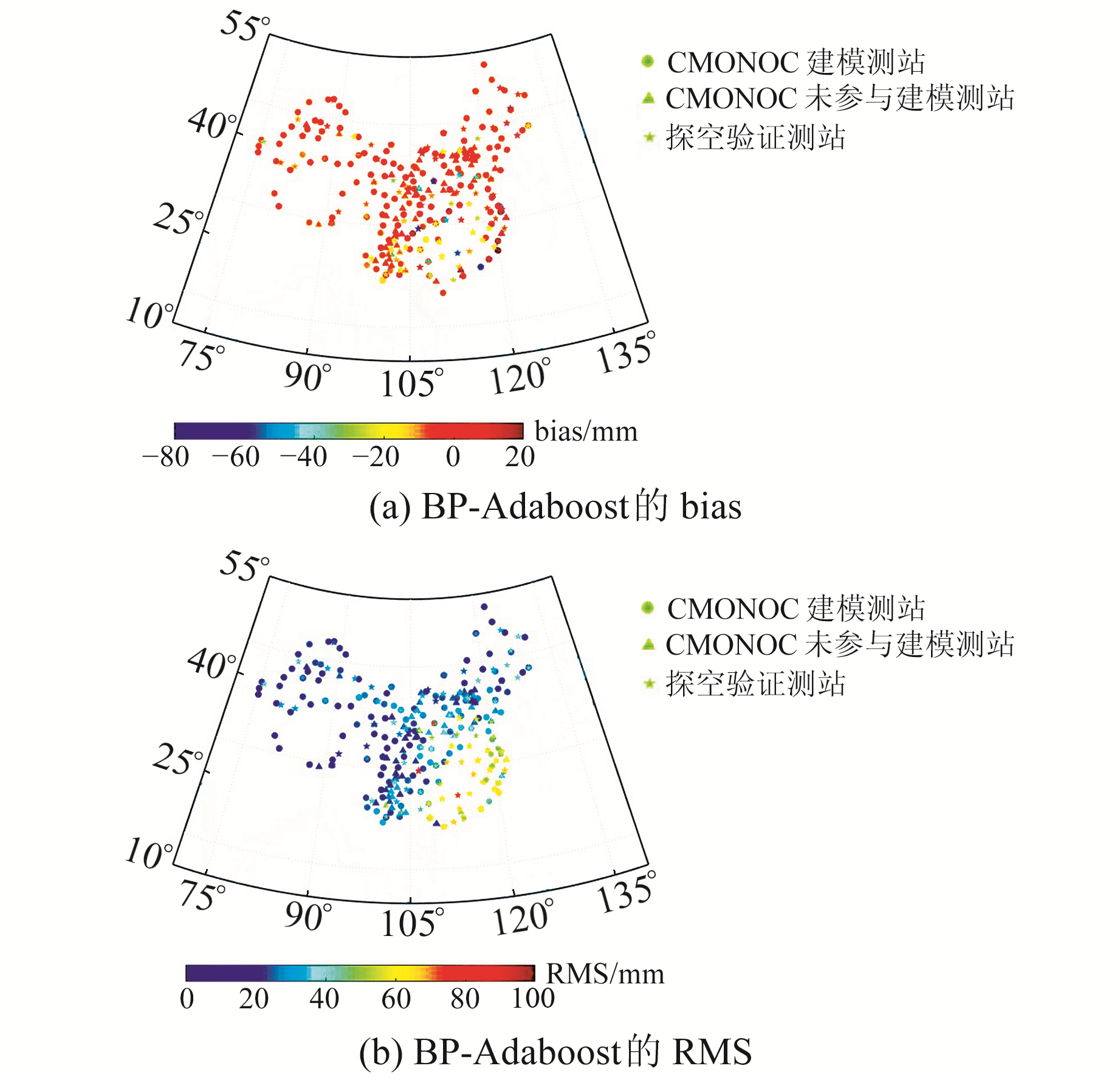
3.1 模型精度的空间分析为进一步分析BP-Adaboost模型的空间适用性,绘制出各个CMONOC站与探空站的bias与RMS分布(图 6)。
|
图 6 BP-Adaboost模型各测站的bias与RMS分布 Fig. 6 Bias and RMS distribution of each station in BP-Adaboost model |
由图 6可见,BP-Adaboost模型的RMS在整体上呈现出东南区域精度低于西北区域的分布规律,这可能是因为中国的东南区域水汽变化较活跃,难以建模。进一步定量讨论模型精度的水平分布,将中国区域按纬度划分为41°~50° N、31°~40° N和21°~30° N三个区间段,在3个纬度内的bias和RMS如表 2(单位mm)所示。
|
|
表 2 不同纬度区间4种模型的bias与RMS Tab. 2 Bias and RMS of four models in different latitude intervals |
由表 2可见,4种模型均在31°~40° N内取得最高精度。在高纬度地区,BP-Adaboost模型均取得最优精度,3类验证数据表明,在41°~50° N区间段内其RMS分别优于GPT3模型3.8%、4.7%和1.7%;而在31°~40° N内BP-Adaboost模型精度分别优于GPT3模型2.1%、1.5%和3.2%,充分说明BP-Adaboost模型在不同纬度的适用性。新模型在低纬度精度较差的原因可能是低纬度的CMONOC测站较少、建模数据有限。
为进一步分析这4种模型在不同海拔高度的适用性,按照测站高程,将各个测站按照0~2 km、2~4 km以及大于4 km这3个区间分别统计,如表 3(单位mm)所示。
|
|
表 3 3个高程区间的bias和RMS Tab. 3 Bias and RMS of three altitude sections |
由表 3可见,各个模型精度均随海拔高程升高而增加。在高程0~2 km区间内,两组CMONOC测站数据验证结果中BP-Adaboost模型都表现出最优的精度,在探空数据验证结果中BP-Adaboost与GPT3模型相当,均优于其他2种模型;在2~4 km区间内,两组CMONOC测站数据验证中BP-Adaboost模型均取得最优精度,但探空数据的结果显示,SHAtrop模型精度最高,BP-Adaboost模型精度略低;在大于4 km的区间内没有CMONOC验证站,其余2组数据的结果表明,BP-Adaboost模型精度仍然优于其他3种模型。以上结论充分说明了BP-Adaboost模型在不同高度区间的适用性。
3.2 模型精度的季节性分析为分析模型在不同时间段的适用精度,计算这4种模型在每个季度的RMS(图 7)。

|
图 7 4种模型的季节性RMS Fig. 7 Seasonal RMS of four models |
由图 7可见,4种模型在冬季精度高而在夏季精度较低,在春秋两季精度相当,原因可能是夏季水汽活动较为剧烈。除夏季和秋季的探空数据验证结果外,BP-Adaboost模型都取得最优的精度。CMONOC建模测站验证的春季和夏季结果表明,BP-Adaboost模型精度比GPT3模型在2个季节分别提高5.2%和3.8%,表现出更佳的适用性和与GNSS观测数据的自洽性。
4 结语本文利用CMONOC提供的155个测站2014~2018年的ZTDC产品,采用BP-Adaboost算法将多个弱神经网络集成为强预测器,从而建立无气象参数的ZTD模型,并对模型进行精度评定,得出以下结论:
1) 利用2019年CMONOC参与建模的155个测站以及未参与建模的62个测站数据进行验证,BP-Adaboost模型在中国区域内的总体bias为0.62 mm和-1.16 mm,优于常用的CTrop模型、GPT3模型和SHAtrop模型,表明该模型没有明显的系统误差;其RMS为25.30 mm和26.72 mm,比上述3种模型精度分别提高9.6%、2.8%和3.3%。
2) 利用IGRA提供的中国区域内86个无线电探空站的ZTDR进行验证,BP-Adaboost模型的bias为-12.32 mm,RMS为46.29 mm;其RMS略高于GPT3模型,但明显优于其他2种常用模型。该数据的验证结果中4种模型均出现一定的负偏差。
3) BP-Adaboost模型的精度分布呈现出内陆高、东南沿海低的特性,在高纬度地区BP-Adaboost模型的优势更明显,这是因为CMONOC在内陆地区的测站更为密集、建模数据更加丰富,证明BP-Adaboost算法建模的有效性,即如果融合更丰富的数据,该算法能进一步提高建模精度。BP-Adaboost在高海拔地区也优于其他3种模型。
4) 4种模型的精度都呈现出夏季低而冬季高的特性。CMONOC两组数据验证结果表明,BP-Adaboost的精度均优于其他3种模型,其精度在春季和夏季比GPT3模型高5%左右。除秋季外,其余3个季节探空数据的验证结果中4种模型精度相当。
本文初步论证集成神经网络在对流层应用中的有效性,新模型相比于已有的模型,精度有较为显著的提高,可以进一步用于GNSS导航及GNSS气象学等相关领域的应用研究。
| [1] |
Hofmann-Wellenhof B, Lichtenegger H, Wasle E. GNSS-Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More[M]. New York: Springer Science and Business Media, 2007
(  0) 0) |
| [2] |
Nilsson T, Böhm J, Wijaya D D, et al. Path Delays in the Neutral Atmosphere[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013
(  0) 0) |
| [3] |
陈俊平, 王君刚, 王解先, 等. SHAtrop: 基于陆态网GNSS数据的中国大陆区域ZTD模型[J]. 武汉大学学报: 信息科学版, 2019, 44(11): 1 588-1 595 (Chen Junping, Wang Jungang, Wang Jiexian, et al. SHAtrop: Empirical ZTD Model Based on CMONOC GNSS Network[J]. Geomatics and Information Science of Wuhan University, 2019, 44(11): 1 588-1 595)
(  0) 0) |
| [4] |
Baltink H K, van der Marel H, van der Hoeven A G A. Integrated Atmospheric Water Vapor Estimates from a Regional GPS Network[J]. Journal of Geophysical Research: Atmospheres, 2002, 107(D3)
(  0) 0) |
| [5] |
Hopfield H S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research: Atmospheres, 1969, 74(18): 4 487-4 499 DOI:10.1029/JC074i018p04487
(  0) 0) |
| [6] |
Saastamoinen J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[J]. Geophys, 1972(15): 247-251
(  0) 0) |
| [7] |
Black H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research: Solid Earth, 1978, 83(B4): 1 825-1 828 DOI:10.1029/JB083iB04p01825
(  0) 0) |
| [8] |
Chen B Y, Liu Z Z. A Comprehensive Evaluation and Analysis of the Performance of Multiple Tropospheric Models in China Region[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 54(2): 663-678
(  0) 0) |
| [9] |
Penna N, Dodson A, Chen W. Assessment of EGNOS Tropospheric Correction Model[J]. Journal of Navigation, 2001, 54(1): 37-55 DOI:10.1017/S0373463300001107
(  0) 0) |
| [10] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [11] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [12] |
Sun Z Y, Zhang B, Yao Y B. An ERA5-Based Model for Estimating Tropospheric Delay and Weighted Mean Temperature Over China With Improved Spatiotemporal Resolutions[J]. Earth and Space Science, 2019, 6(10): 1 926-1 941 DOI:10.1029/2019EA000701
(  0) 0) |
| [13] |
Zheng D Y, Hu W S, Wang J, et al. Research on Regional Zenith Tropospheric Delay Based on Neural Network Technology[J]. Survey Review, 2015, 47(343): 286-295 DOI:10.1179/1752270614Y.0000000130
(  0) 0) |
| [14] |
Jiang P, Ye S R, Chen D Z, et al. Retrieving Precipitable Water Vapor Data Using GPS Zenith Delays and Global Reanalysis Data in China[J]. Remote Sensing, 2016, 8(5): 1-21
(  0) 0) |
| [15] |
Mendes V B. Modeling the Neutral-Atmospheric Propagation Delay in Radiometric Space Techniques[J]. Brunswick University of New Brunswick, 1999
(  0) 0) |
| [16] |
Smith E K, Weintraub S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies[J]. Proceedings of the IRE, 1953, 50(8): 1 035-1 037
(  0) 0) |
| [17] |
姚宜斌, 曹娜, 许超钤, 等. GPT2模型的精度检验与分析[J]. 测绘学报, 2015, 44(7): 726-733 (Yao Yibin, Cao Na, Xu Chaoqian, et al. Accuracy Assessment and Analysis for GPT2[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 726-733)
(  0) 0) |
| [18] |
Freund Y, Schapire R, Abe N. A Short Introduction to Boosting[J]. Journal of Japanese Society for Artificial Intelligence, 1999, 14(5): 771-780
(  0) 0) |
| [19] |
Islam M M, Yao X, Murase K. A Constructive Algorithm for Training Cooperative Neural Network Ensembles[J]. IEEE Transactions on Neural Networks, 2003, 14(4): 820-834 DOI:10.1109/TNN.2003.813832
(  0) 0) |
2. School of Transportation, Southeast University, 2 Dongnandaxue Road, Nanjing 218889, China
 2022, Vol. 42
2022, Vol. 42


