InSAR的精度会受到电离层效应的影响,需要进行电离层校正。目前常用的校正方法为距离向频谱分割法RSS[1],该方法基于电离层的色散特性区分电离层延迟相位和其他非色散相位,具有清晰的物理机制,已成功应用于GNSS双频观测电离层校正中[2]。然而RSS精度受相位噪声影响较大,在实际处理中需要通过多视和低通滤波(下文统称为平滑处理)去除高频噪声、提高电离层估算精度。但不同平滑参数下获取的RSS电离层相位差异较大,且RSS方法计算的电离层相位是主、从影像成像时刻电离层状态的差值,难以通过相位条纹形态判断其可靠性,需要处理人员依据经验进行判断,缺乏客观依据。
针对上述问题,本文拟选用国际参考电离层IRI模型计算的电离层分布为参考,辅助确定RSS方法估算电离层相位的平滑处理参数。重点探讨无明显地表形变区和缓慢形变区RSS方法校正电离层时平滑处理参数的选取策略,以期推广到因地震或其他原因引发的强烈形变区RSS方法校正电离层时的平滑处理中。
1 方法与原理 1.1 RSS估算电离层相位对于重轨InSAR,在不考虑相位噪声的情况下,其干涉相位成分可以表示为:
| $ \Delta {\varphi _{{\rm{InSAR}}}} = (\Delta {\varphi _{{\rm{disp}}}} + \Delta {\varphi _{{\rm{geo}}}} + \Delta {\varphi _{{\rm{tropo}}}}) + \Delta {\varphi _{{\rm{iono}}}} $ | (1) |
式中,Δφdisp为地表形变相位,Δφgeo为包含平地和地形的几何相位,Δφtropo为对流层延迟相位,上述相位统称为非色散相位;Δφiono为色散的电离层延迟相位。RSS方法根据电离层的色散特性估算得到电离层相位[1]:
| $ \Delta {\hat \varphi _{{\rm{iono}}}} = {\rm{ }}\frac{{{f_{\rm{L}}}{f_{\rm{H}}}}}{{{f_0}(f_{\rm{H}}^2{\rm{ - }}f_{\rm{L}}^2)}}{\rm{ }}(\Delta {\varphi _{\rm{L}}}{f_{\rm{H}}}{\rm{ - }}\Delta {\varphi _{\rm{H}}}{f_{\rm{L}}}) $ | (2) |
式中,fH和fL分别为被分割的高、低频谱子频带影像的中心频率,f0为全频带影像的中心频率,ΔφH和ΔφL分别为高、低频率的子频带干涉相位。最后,将电离层从全频带InSAR相位中减去,即可得到电离层校正后的InSAR相位:
| $ \Delta \hat \varphi {_{{\rm{InSAR}}}} = \Delta {\varphi _{{\rm{InSAR}}}}{\rm{ - }}\Delta \hat \varphi {_{{\rm{iono}}}} $ | (3) |
由于现有的在轨卫星带宽较窄,频谱分割后生成的子频带干涉图中含有较多噪声,因此通过多视和低通滤波去除相位噪声对RSS估算精度的提升有重要作用[3]。然而多视视数和滤波窗口的增加会导致较小空间尺度的电离层变化无法被反演,获取更高估算精度和保留更多电离层细节之间的矛盾导致平滑参数的选取困难且主观。
1.2 IRI模型计算差分电离层相位IRI模型是由国际空间研究委员会(Committee on Space Research,COSPAR)与国际无线电科学联合会(International Union of Radio Science,URSI)联合提出的经验型电离层预报模型,采用最新的IRI 2016开源软件可计算得到指定时间、地点的天顶方向电子总含量(certical total electron content, VTEC)[4]。由于SAR为侧视成像,根据式(4)可将VTEC转化为SAR影像中某一位置处的电离层延迟相位[1]:
| $ {\varphi _{{\rm{iono}}}}\left( f \right) = {\rm{ - }}\frac{{4{\rm{ \mathsf{ π} }}K}}{{cf}}\frac{{{\rm{VTEC}}}}{{{\rm{cos}}\theta }} $ | (4) |
式中,f为载波频率,c为光速,K为常数40.28 m3/s2,θ为SAR侧视角。IRI模型程序只能计算单点的电离层VTEC,全景SAR影像范围内的电离层延迟相位可通过循环迭代得到。
IRI模型时空分辨率不高,但能客观反映一般情况下区域内大尺度电离层空间的变化趋势和数量级。由于高频空间噪声会干扰对InSAR反演的电离层整体分布特征的判断,因此IRI模型可为InSAR提供客观参考,便于相互印证。
2 实验区选择与结果分析SAR干涉数据选用L波段ALOS-2 PALSAR的条带模式数据。实验区优先选择电离层环境相对简单的中、低纬度区域以及无形变或缓慢形变区。有研究表明,地震[6]、地下核爆[7]等强烈地表形变会对电离层产生异常扰动,而IRI模式主要反映的是平静电离层的平均状态,对瞬时电离层扰动反映不足[8]。在不考虑对流层延迟及地形等其他相位时认为,无地表形变区InSAR相位变化主要是由电离层引起的,故通过研究电离层校正前后InSAR相位标准差变化可评价校正效果。为尽量减少干扰电离层和其他InSAR相位因素的影响,将实验区选择在低纬度无显著形变的巴西阿克里州(Acre),以及中纬度有缓慢形变的中国甘肃省定西市。综合考虑多视对低相干噪声的抑制效果与高相干区域的保留效果后,选择方位向(az)和距离向(rng)多视视数为16×8和32×16(下文均表示为az×rng);采用高斯滤波的方法,选择方位向和距离向尺寸均为200、400、600、800像素的滤波窗口,获得相对平滑的电离层条纹。
2.1 无明显形变研究区实验区为巴西阿克里州东南角,位于世界上地震活动最少的稳定大陆区之一的南美洲中部板块内部[9]。主从影像成像时间为2014-08-13和2014-08-27,时间基线为14 d,研究时间段内无地震报道,因此该区域地表形变可忽略不计。数据模式为High sensitive,数据带宽42 mHz。
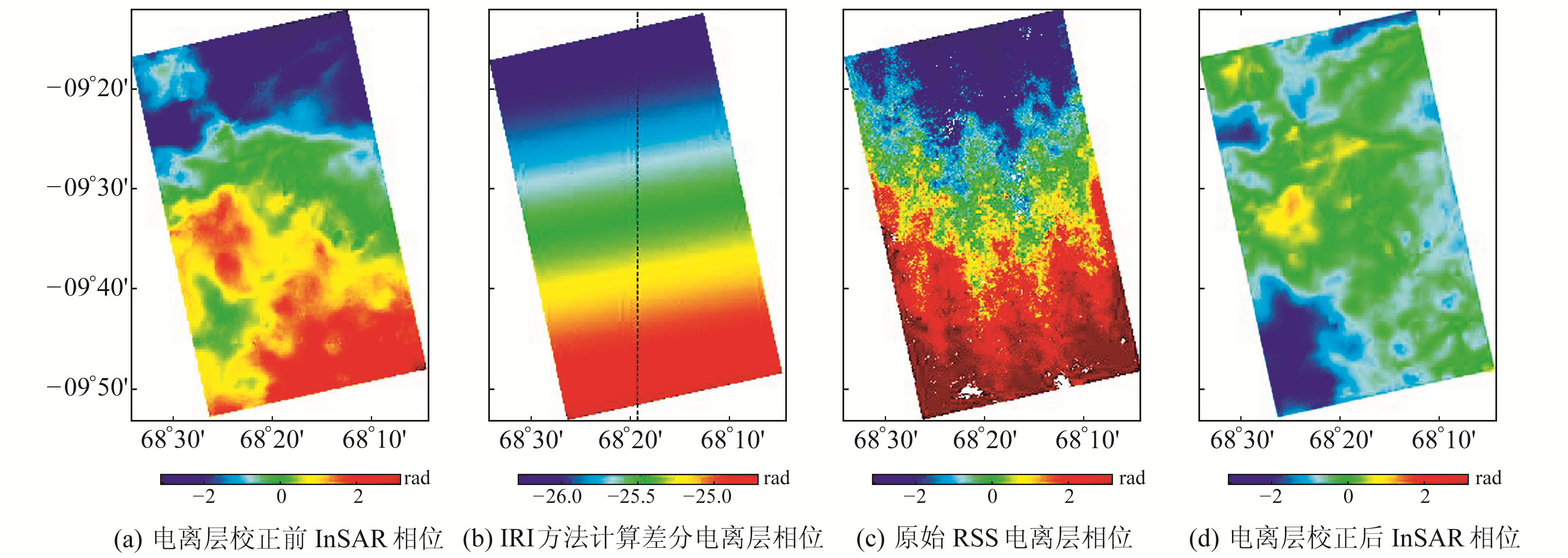
该实验区主要处理结果如图 1所示。图 1(a)为全频带InSAR相位图,其相位主要由电离层延迟、对流层延迟和残余地形相位等组成。图 1(c)为32×16多视下RSS方法反演出的原始相位分布,可以看出,与图 1(b)IRI计算的相位分布相差甚远,存在较多的空间高频信号,不能明显反映电离层的变化趋势,需要对其进行平滑处理。
|
图 1 阿克里州地区处理结果 Fig. 1 The processing results of Acre |
不同多视视数和滤波窗口处理后的RSS电离层相位分布如图 2所示。RSS与IRI电离层相位在形态上较为相似,但不同平滑参数的RSS电离层相位在细节上有所不同。当多视视数及滤波窗口较小时,RSS电离层存在较多细小结构,而随着多视视数和窗口尺寸的增加,RSS电离层条纹更加平直,与IRI电离层形态更加接近。多视和滤波共同起到了平滑电离层的作用,但二者对电离层条纹延伸趋势的影响各有不同。对于多视16×8(az×rng)的RSS电离层相位,即使选用较大滤波窗口,仍无法获得相对平滑的电离层条纹。因此,在平滑参数的选择中,足够数量的多视视数是获取理想结果的必要条件。从目视效果上看,当多视视数为32×16、滤波窗口达到400像素及以上时,RSS电离层条纹和IRI电离层条纹基本一致,即对于没有更多电离层扰动的无明显形变区域,上述参数能取得较好的平滑效果。

|
图 2 阿克里州地区不同平滑参数下RSS法估算电离层相位 Fig. 2 Ionospheric phase estimated by RSS with different smoothing parameters in Acre |
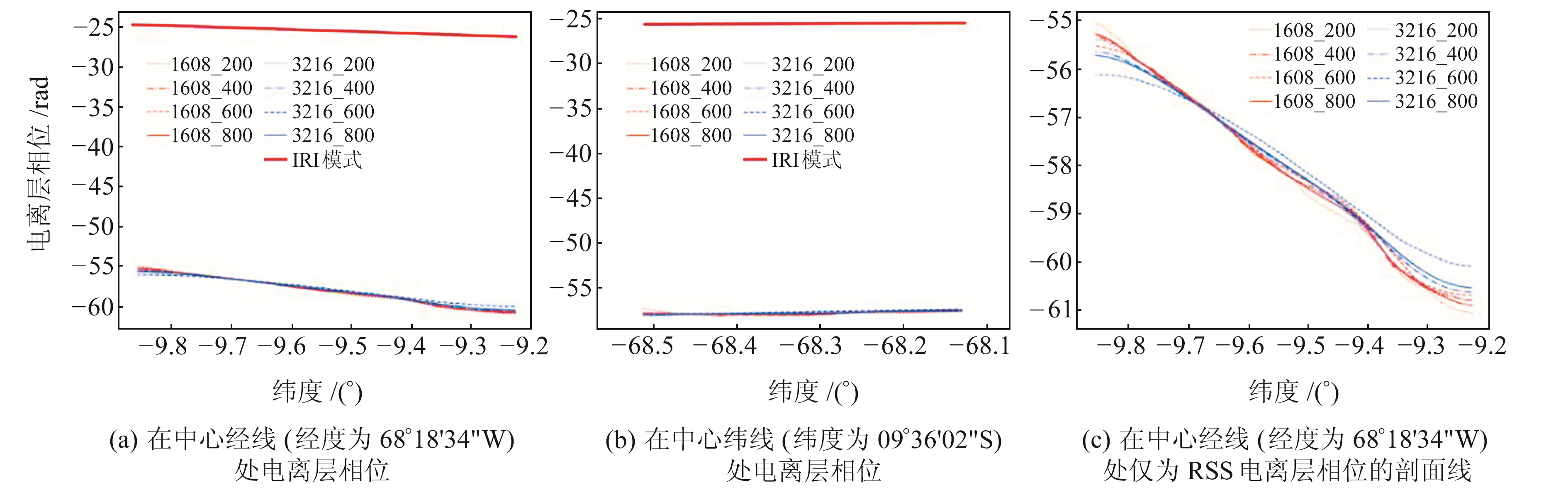
由图 2可见,电离层在空间分布上主要随纬度变化,因此分别在IRI和RSS电离层相位中心经线和中心纬线处绘制剖面线进行分析。不同平滑参数下阿克里州RSS及IRI电离层相位剖面线如图 3所示(图例中数字格式为“方位向视数与距离向视数_滤波窗口”)。由图 3(a)和(b)可见,整体上所有RSS电离层相位(蓝色和橘色线)都表现出与IRI电离层相位(红色粗线)较高的相似性,但IRI与RSS存在一个整体偏差,可能是因为IRI差分电离层相位为绝对值而RSS电离层相位为相对值。因此比较IRI与RSS电离层相位差异的重点是其分布形态而非具体数值。数值变化范围上,RSS沿经线方向变化大,在研究范围(约0.7°)内约6 rad;沿纬线方向变化小,不足1 rad,因此后续主要沿经线方向进行讨论。图 3(c)展示了放大后不同平滑参数下RSS电离层相位剖面线,整体来看,不同平滑参数RSS电离层相位较为接近。当多视视数及滤波窗口较小(如3216_200)时,曲线仍有明显波动,但值域范围较小。
|
图 3 不同平滑参数下阿克里州RSS及IRI电离层相位剖面线 Fig. 3 RSS and IRI ionospheric phase profile lines with different smoothing parameters in Acre |
为定量比较不同参数RSS电离层与IRI的相似程度,计算电离层相位变化范围较大的中心经线上IRI与RSS差值的均方根偏差RMSD。选取中心经线上相干系数最高时(上标h表示)RSS与IRI电离层相位的差Δφconst为参考值,以减少该参考点自身误差及解缠错误的影响:
| $ \Delta {\varphi _{{\rm{const}}}} = \Delta \varphi _{{\rm{RSS}}}^{\rm{h}} - \Delta \varphi _{{\rm{IRI}}}^{\rm{h}} $ | (5) |
RMSD表示为:
| $ {\rm{RMSD}} = \sqrt {\frac{{\sum\limits_i^n {} {{[(\Delta \varphi _{{\rm{RSS}}}^i{\rm{ - }}\Delta \varphi _{{\rm{IRI}}}^i) - \Delta {\varphi _{{\rm{const}}}}]}^2}}}{n}} $ | (6) |
式中,n为中心经线上RSS或IRI电离层相位的总像素数,ΔφRSSi和ΔφIRIi分别为中心经线上纵坐标为i处的RSS和IRI电离层相位。由表 1可见,相同的滤波窗口下,RMSD随着多视视数的增加而减小;相同的多视视数下,RMSD总体上也随着滤波窗口的增加而减小,但在滤波窗口达到600像素后减小程度不足10-2rad,此时再增加平滑窗口对提高RSS与IRI电离层相似性效果较小,RSS反映电离层空间细节的能力进一步减弱。
|
|
表 1 阿克里州中心经线处RSS与IRI电离层差值的均方根偏差及电离层校正前后InSAR相位标准差 Tab. 1 RMSD of the difference between IRI and RSS at the central meridian in Acre, and standard deviation of InSAR phase before and after ionospheric correction |
综合考虑目视效果、RMSD统计结果和保留小尺度电离层空间结构的需求,最终选择多视视数为32×16、滤波窗口为600像素的RSS电离层,电离层校正后的InSAR相位如图 1(d)所示。由图 1(d)可见,电离层校正后影像中仍存在部分小区域残存相位,由于此处未完成对流层延迟校正,其结果仍存在对流层延迟相位或残留地形误差的影响,但原始InSAR相位中电离层基本得到去除,从而在一定程度上说明了RSS电离层校正的有效性。
由表 1可见,随着多视视数和滤波窗口的增加,电离层校正后InSAR相位标准差逐渐减小,由校正前的1.499 rad减小至0.637 rad,并在多视视数为32×16、滤波窗口为600像素时达到最小,这与基于IRI选取的RSS参数结果一致,初步验证了上述方法选取平滑参数的可行性。
2.2 缓慢形变研究区实验区位于甘肃省东南部的定西市北部安定区,主从影像成像时间为2018-05-22和2018-07-17。由于受到青藏高原东北部东昆仑断裂的挤压和西秦岭北缘断裂走滑等动力因素的影响,该区域地震频发[10]。主从影像成像时间段内,距离影像西南部边缘约50 km处的甘肃甘南州卓尼县于2018-06-30发生3.1级地震,但该地震对研究区影响不大,因此可认为该研究区为缓慢地表形变区。
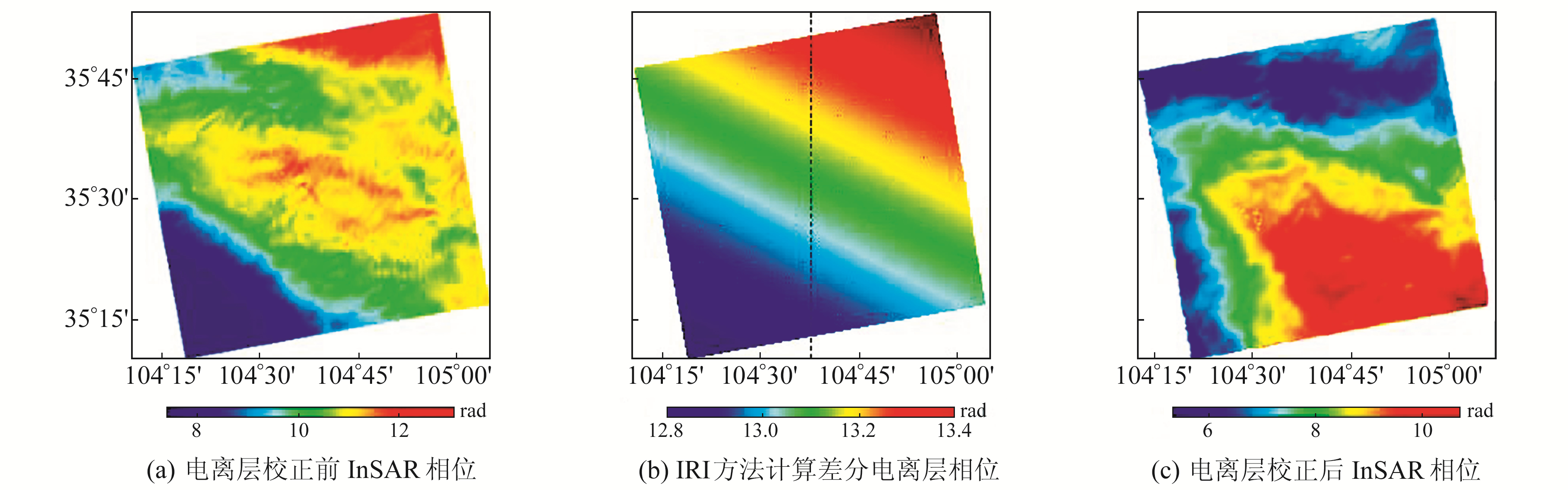
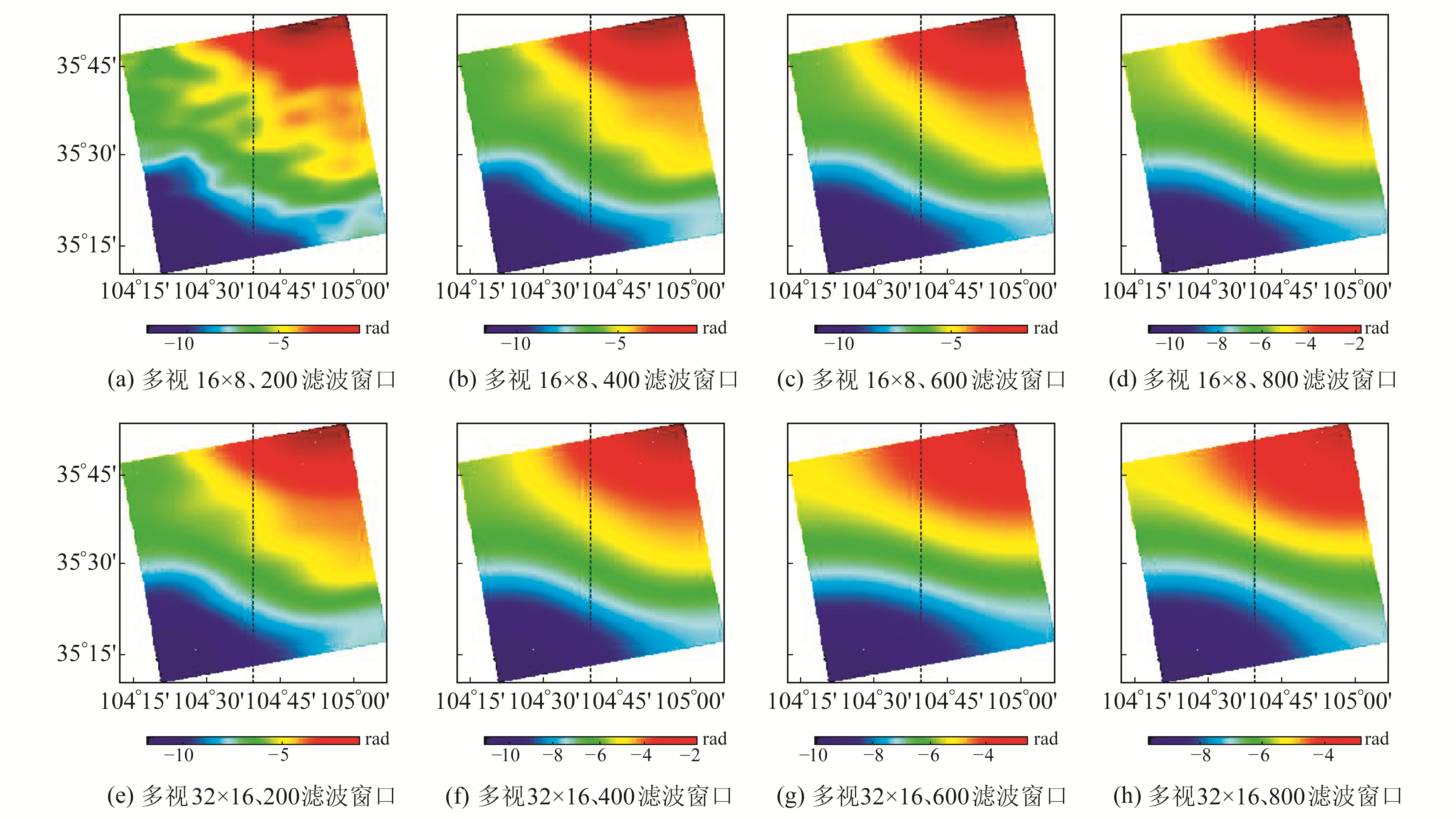
采用与巴西阿克里州相同的实验流程及参数,得到结果如图 4和图 5所示。对比图 4(b)和图 5可见,RSS电离层条纹相比于IRI电离层条纹较为弯曲,但二者在整体趋势上仍具有一定的相似性。由此推断,缓慢地表形变区的电离层虽然受到一定扰动因素的影响,但仍能将IRI模型作为参照。当多视视数为16×8、滤波窗口达600像素及以上,以及多视视数为32×16、滤波窗口达400像素及以上时,增大滤波窗口对电离层条纹的改变不再明显,因此需要在上述范围中进一步选择平滑参数。
|
图 4 定西研究区处理结果 Fig. 4 The processing results of Dingxi city |
|
图 5 定西研究区不同平滑参数下RSS法估算的电离层相位 Fig. 5 Ionospheric phase estimated by RSS with different smoothing parameters in Dingxi city |
定西研究区中心经线上RSS与IRI差值的RMSD计算结果如表 2所示,总体上看,RMSD随多视视数和滤波窗口的增加而减小。当多视视数为16×8时,RMSD随滤波窗口的增加缓慢减小;当多视视数为32×16时,RMSD随滤波窗口的增大迅速减小,但平滑参数选取过大时,小于滤波窗口的电离层结构被平滑掉。为获得较小的RMSD同时保留更多电离层空间结构细节,在定西实验区仍选用32×16的多视视数和600像素尺寸的滤波窗口。
|
|
表 2 定西地区中心经线处RSS与IRI电离层差值的均方根偏差 Tab. 2 RMSD of the difference between IRI and RSS at the central meridian in Dingxi city |
由电离层校正后的InSAR结果(图 4(c))可以看出,在电离层校正后干涉相位中仍存在较为复杂的变化。不同于阿克里州实验区,定西地区在图 4(a)的InSAR相位条纹中表现出一些地形特征,因此在电离层校正后同样残存了对流层延迟和地形相位残差,且存在一定的地表形变,这些因素导致校正后的InSAR相位仍存在一定的空间变化。
3 结语本文研究在InSAR电离层校正中以IRI电离层相位为参考选取合适的RSS平滑参数。通过目视对比可知,在无显著地表形变的巴西阿克里州实验区和存在缓慢形变的中国甘肃省定西市实验区,IRI和RSS电离层相位在空间模式上均具有良好的相似性,从而进一步验证了RSS方法的可行性。选用ALOS-2 PALSAR条带模式数据计算RSS与IRI电离层相位偏差,确定一组多视视数为32×16(az×rng)、滤波窗口尺寸为600像素的平滑处理参数。根据此参数估算的电离层相位在两个实验区均取得较好的校正结果,从而证明参考IRI模型选取RSS平滑参数在无形变区域和缓慢形变区的可行性。
RSS方法平滑参数的选取主要与数据带宽和相干性有关,当使用ALOS-2 PALSAR条带模式数据在类似区域选取平滑参数时,可以简化处理环节、提高效率、取得更为可靠的结果,对于其他有显著地表形变区域的RSS电离层平滑处理也具有一定的参考意义。
致谢: 感谢日本宇航探测研究机构JAXA提供PALSAR-2数据(PI No. 3321)及北京大学高性能计算校级公共平台提供计算环境。
| [1] |
Gomba G, Parizzi A, Zan F D, et al. Toward Operational Compensation of Ionospheric Effects in SAR Interferograms: The Split-Spectrum Method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1-16 DOI:10.1109/TGRS.2016.2527798
(  0) 0) |
| [2] |
Jakowski N, Mayer C, Hoque M M, et al. Total Electron Content Models and Their Use in Ionosphere Monitoring[J]. Radio Science, 2011, 46(6): 1-11
(  0) 0) |
| [3] |
Fattahi H, Simons M, Agram P. InSAR Time-Series Estimation of the Ionospheric Phase Delay: An Extension of the Split Range-Spectrum Technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5 984-5 996 DOI:10.1109/TGRS.2017.2718566
(  0) 0) |
| [4] |
Bilitza D, Altadill D, Truhlik V, et al. International Reference Ionosphere 2016: From Ionospheric Climate to Real-Time Weather Predictions[J]. Space Weather, 2017, 15(2): 418-429 DOI:10.1002/2016SW001593
(  0) 0) |
| [5] |
Bilitza D, Altadill D, Zhang Y L, et al. The International Reference Ionosphere 2012-a Model of International Collaboration[J]. Journal of Space Weather and Space Climate, 2014(4): 689-721
(  0) 0) |
| [6] |
王泽民, 孙伟, 安家春. 2015-04-25尼泊尔MS8.1地震前后电离层VTEC异常变化分析[J]. 大地测量与地球动力学, 2016, 36(2): 133-137 (Wang Zemin, Sun Wei, An Jiachun. Anomaly Variation Analysis of the Ionospheric VTEC before and after the 25 April 2015 MS8.1 Nepal Earthquake[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 133-137)
(  0) 0) |
| [7] |
刘祎, 周晨, 张雪芹, 等. 基于GNSS数据的朝鲜核爆电离层效应观测研究[J]. 地球物理学报, 2020, 63(4): 1 308-1 317 (Liu Yi, Zhou Chen, Zhang Xueqin, et al. GNSS Observations of Ionospheric Disturbances in Response to the Underground Nuclear Explosion in North Korea[J]. Chinese Journal of Geophysics, 2020, 63(4): 1 308-1 317)
(  0) 0) |
| [8] |
Alizadeh M M, Wijaya D D, Hobiger T, et al. Ionospheric Effects on Microwave Signals[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013
(  0) 0) |
| [9] |
Assumpção M, Ferreira J, Barros L, et al. Intraplate Earthquakes: Intraplate Seismicity in Brazil[M]. Cambridge: Cambridge University Press, 2014
(  0) 0) |
| [10] |
郑文俊, 袁道阳, 何文贵, 等. 甘肃东南地区构造活动与2013年岷县-漳县MS6.6级地震孕震机制[J]. 地球物理学报, 2013, 56(12): 4 058-4 071 (Zheng Wenjun, Yuan Daoyang, He Wengui, et al. Geometric Pattern and Active Tectonics in Southeastern Gansu Province: Discussion on Seismogenic Mechanism of the Minxian-Zhangxian MS6.6 Earthquake on July 22, 2013[J]. Chinese Journal of Geophysics, 2013, 56(12): 4 058-4 071)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


