2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
基于多路径效应的全球导航卫星系统多路径反射测量(GNSS multipath reflectometry,GNSS-MR)技术具有时间分辨率高、全天候、实时自动化、覆盖面积广等优点,在积雪深度探测方面具有较大潜力。张双成等[1]利用实测GPS数据对基于信噪比(signal-to-noise, SNR)的GNSS-MR探测雪深的算法进行了初步验证。Ozeki等[2]提出无几何距离的线性组L4观测值反演积雪深度,与SNR观测量探测的结果较为一致。但上述研究均采用二次多项式拟合方法获取残差序列,无法准确拟合SNR信号趋势,同时由于卫星高度角的增加,使天线接收的反射信号来自不同地表和位置,干扰有效反射信号,导致反演结果极易出现跳变现象。本文利用自适应噪声的完全集合经验模态分解[3](complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)代替二次多项式获取残差序列,并以美国科罗拉多州NWOT测站数据为例进行雪深反演,验证本文方法的有效性。
1 GNSS-MR反演雪深原理GNSS天线接收机可以同时接收卫星发射的直射信号Ad和经地表面反射的反射信号Ar。图 1是基于信噪比观测值的GNSS-MR雪深探测示意图。

|
图 1 GNSS-MR雪深探测示意图 Fig. 1 Diagram of GNSS-MR for snow depth |
直射信号与反射信号的振幅存在如下关系:
| $ {A_{\rm{d}}} \gg {A_{\rm{r}}} $ | (1) |
记Ac为合成信号的振幅, φ为直射信号与经地表积雪面反射的信号的夹角,其关系为[4]:
| $ {\rm{SN}}{{\rm{R}}^2} = A_{\rm{c}}^2 = A_{\rm{d}}^2 + A_{\rm{r}}^2 + 2{A_{\rm{d}}}{A_{\rm{r}}}{\rm{cos}}\varphi $ | (2) |
由于Ad≫Ar,通常采用低阶多项式拟合方法来去除趋势项,获得低卫星高度角下SNR残差序列[1]。多路径效应下的反射信号振幅可表示为:
| $ {A_{\rm{r}}} = {A_{\rm{d}}}{\rm{cos}}\left( {\frac{{4{\rm{ \mathsf{ π} }}h}}{\lambda }{\rm{sin}}\theta + \varphi } \right) $ | (3) |
式中,λ为载波波长,θ为卫星高度角,h为垂直反射距离。取f=2h/λ,对SNR残差序列进行Lomb-Scargle频谱分析,可得到GPS多路径反射信号的频率f,从而得到h;再结合图 1,可获取积雪厚度。
2 CEEMDANCEEMDAN是对经验模态分解(empirical mode decomposition, EMD)改进后得到的一种变换形式[5], 其每个本征模态函数(intrinsic mode function, IMF)对应一个频率,具有各自的物理意义。因此,可通过CEEMDAN将原始SNR信号分解成各阶IMF并重构,从而获取高质量的残差序列。
设原始SNR信号为x(t),Ej(·) 是对信号进行EMD分解后的第j阶IMF分量,ωi(t) 为第i次添加的高斯白噪声(i=1,2,…,I),εk为幅值(其中k=0,1,…,K,K是模态总体数量)。CEEMDAN分解步骤如下:
1) 与EEMD[6]算法相同,在x(t) 中加入白噪声εkωi(t),对其进行EMD分解得到多个IMF分量并求集合平均值。第1阶最终分量IMF1(t)为:
| $ {\rm{IM}}{{\rm{F}}_1}\left( t \right) = \frac{1}{I}\sum\limits_{i = 1}^I {{E_1}\left[ {x\left( t \right) + {\varepsilon _0}{\omega _i}\left( t \right)} \right]} $ | (4) |
2) 当k=1时,计算1阶残差r1(t):
| $ {r_1}\left( t \right) = x\left( t \right) - {\rm{IM}}{{\rm{F}}_1}\left( t \right) $ | (5) |
3) 对1阶残差r1(t) 添加经EMD分解后的噪声分量,得到一个新信号,即r1(t)+ε1E1[ωi(t)],再对其分解,得到的集合平均值为该阶的IMF最终分量:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{\rm{IM}}{{\rm{F}}_2}\left( t \right) = \\ \frac{{\rm{1}}}{I}\sum\limits_{i = 1}^I {} {E_1}\left[ {{r_1}\left( t \right) + {\varepsilon _1}{E_1}\left[ {{\omega _i}\left( t \right)} \right]} \right] \end{array} $ | (6) |
4) 当k=2,…,K时, 计算第k阶残差rk(t):
| $ {r_k}\left( t \right) = {r_{k - 1}}\left( t \right){\rm{ - IM}}{{\rm{F}}_k}\left( t \right) $ | (7) |
5) 对k阶残差rk(t) 添加噪声分量εkEk[ωi(t)],获得一个新信号,计算集合平均值,得第k+1阶的最终IMF为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;{\rm{IM}}{{\rm{F}}_{k + 1}}\left( t \right) = \\ \frac{1}{I}\sum\limits_{i = 1}^I {} {E_1}\left[ {{r_k}\left( t \right) + {\varepsilon _k}{E_k}\left[ {{\omega _i}\left( t \right)} \right]} \right] \end{array} $ | (8) |
6) 重复第4步,直到获得的残差不可再被分解。残差最后满足:
| $ R\left( t \right) = x\left( t \right) - \sum\limits_{k = 1}^K {} {\rm{IM}}{{\rm{F}}_k}\left( t \right) $ | (9) |
x(t) 最终被分解为K个IMF分量和1个残余分量:
| $ x\left( t \right) = \sum\limits_{k = 1}^K {} {\rm{IM}}{{\rm{F}}_k}\left( t \right) + R\left( t \right) $ | (10) |
本文观测数据来自美国科罗拉多州NWOT观测站(https://www.unavco.org),地理坐标为(40°03′19.4″N, 105°35′25.8″W),接收机类型为大地测量型Trimble NetRS,天线类型为TRM41249,测站高3 m,数据采集间隔为5 s。实测数据来自U-C气象站(40°01′48″N, 105°34′48″W),其距NWOT测站2.2 km,由美国国家气候中心提供(https://gis.ncdc.noaa.gov/maps/ncei/summaries/daily)。
本实验收集了NWOT测站2016-11~2017-03连续125 d的GPS观测原始数据。为对比CEEMDAN算法和二次多项式拟合算法反演雪深的精度差异,以平均误差(ME)、均方根误差(RMSE)和相关系数(R)作为精度评价指标:
| $ \left\{ \begin{array}{l} {\rm{ME}} = \frac{{\sum\limits_{i = 1}^n {} \left( {{X_1}\left( i \right) - {X_2}\left( i \right)} \right)}}{n}\\ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {} {\rm{ }}{{({X_1}\left( i \right) - {X_2}\left( i \right))}^2}}}{n}} \\ R = \\ \frac{{\sum\limits_{i = 1}^n {} {\rm{ }}({X_1}\left( i \right) - \bar X{_1}\left( i \right))({X_2}\left( i \right) - {{\bar X}_2}\left( i \right))}}{{\sum\limits_{i = 1}^n {} {{({X_1}\left( i \right) - \bar X{_1}\left( i \right))}^2}\sum\limits_{i = 1}^n {} {{({X_2}\left( i \right) - \bar X{_2}\left( i \right))}^2}}} \end{array} \right. $ | (11) |
式中,n为数据总数,i为数据序号,X1(i)、X2(i)分别为实测和反演雪深值,X指平均值。
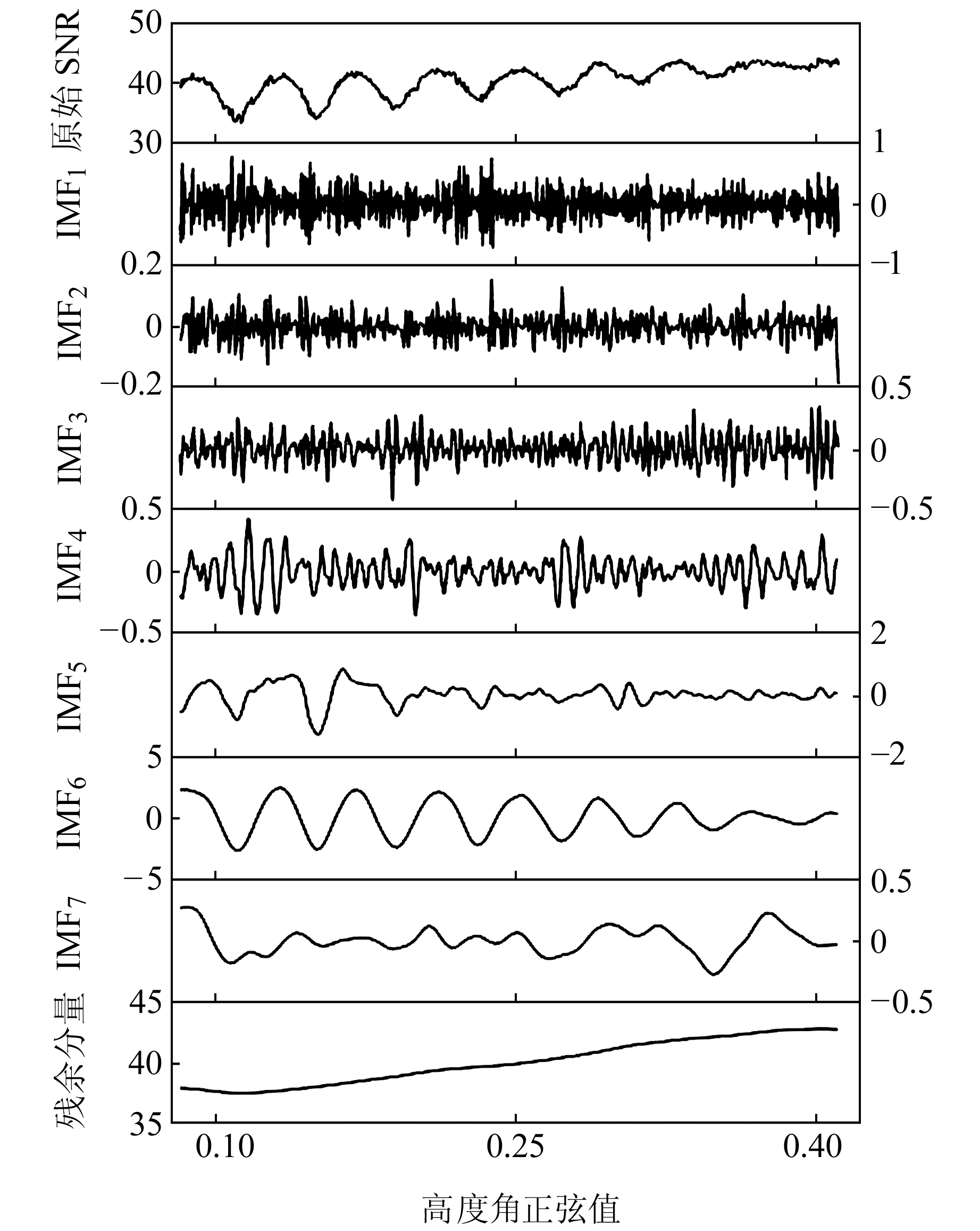
限于篇幅,仅以2016-12-16 GPS 32号卫星原始信噪比序列为例说明,截取高度角为5°~25°,波段为L2,利用CEEMDAN对其分解,结果如图 2所示。分解获得的残余分量就是SNR信号的趋势项,作为自适应结果,克服了二次多项式拟合带来的振幅异常情况。
|
图 2 CEEMDAN分解SNR序列 Fig. 2 Decomposition of SNR sequence by CEEMDAN |
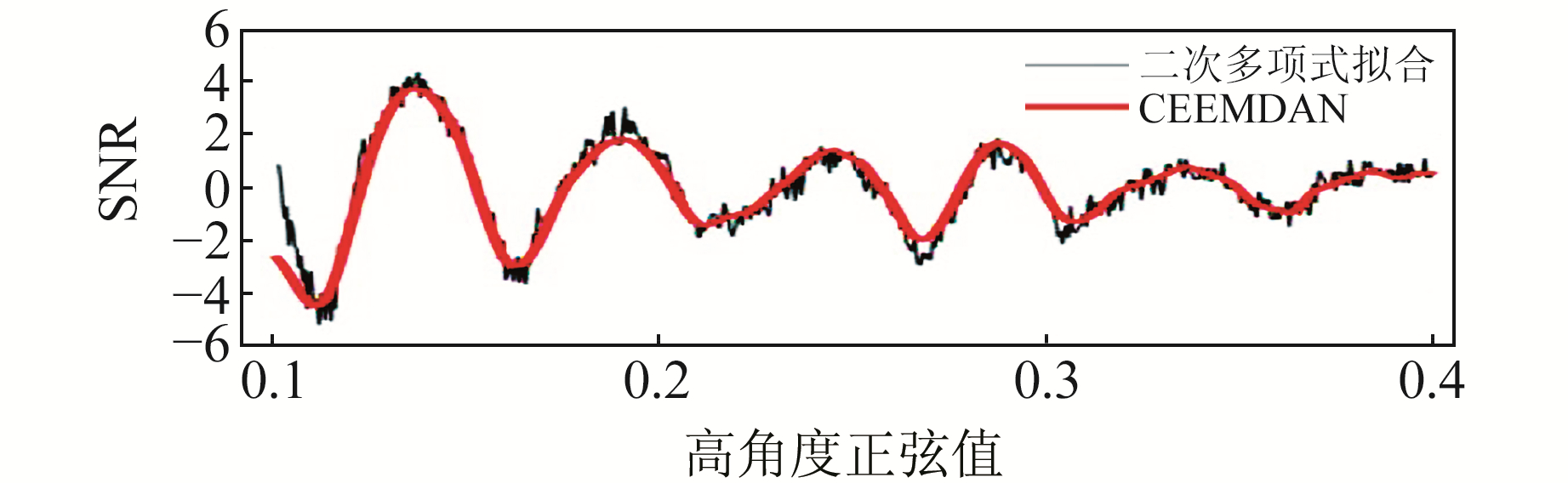
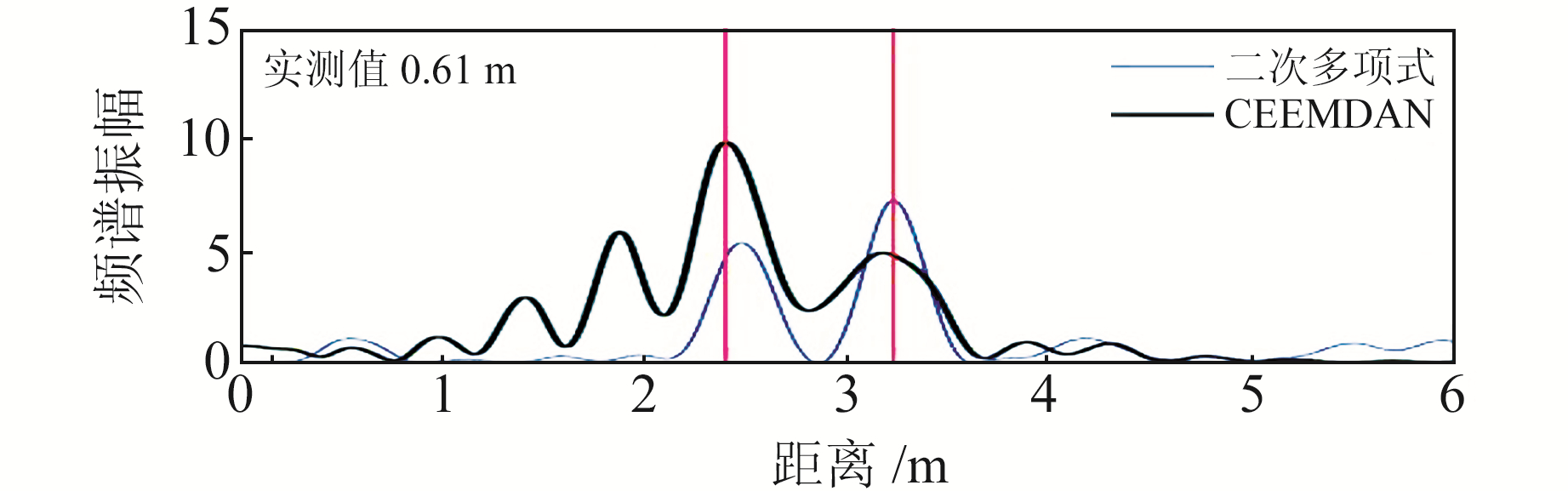
考虑到IMF分量与原信噪比序列的相关性[7]和振幅变化趋势,表 1列出了部分IMF分量与原始信号的相关系数。可以看出,对于不同年积日和不同卫星,对应的IMF个数及与原始信号的相关性也不同。经过对比,在2016-12-16将IMF6和IMF7组合作为有效残差序列,随后对其组合进行Lomb-Scargle谱分析得到频率f。图 3是在2016-12-16用2种方法获取的残差序列,可以看出,二次多项式拟合方法在高度角正弦值为0.17~0.19之间出现高频振荡时没能准确地拟合出SNR变化趋势;而CEEMDAN方法提取的残差序列更为光滑,无高频振荡部分。另外,该方法避免了模态混叠现象,能有效防止其他信号的干扰。图 4表示2种方法获取信噪比残差序列的Lomb-Scargle谱分析图,横轴表示天线相位中心到积雪表面的距离,纵轴表示SNR反射信号频谱振幅,位于振幅最高峰值对应的距离就是垂直反射距离。由图可见,采用二次多项式方法时,最高峰值低于准确峰值,使得反演结果出现负值;雪深实测值为0.61 m,本文方法反演值为0.597 m,更接近实测雪深值。
|
|
表 1 不同IMF分量与原始信号的相关系数 Tab. 1 Correlation coefficients between different IMF components and the original signal |
|
图 3 2种方法获得的残差序列 Fig. 3 Residual sequences obtained by two methods |
|
图 4 SNR残差序列Lomb-Scargle谱分析图 Fig. 4 Lomb-Scargle spectrum analysis diagram of SNR residual sequence |
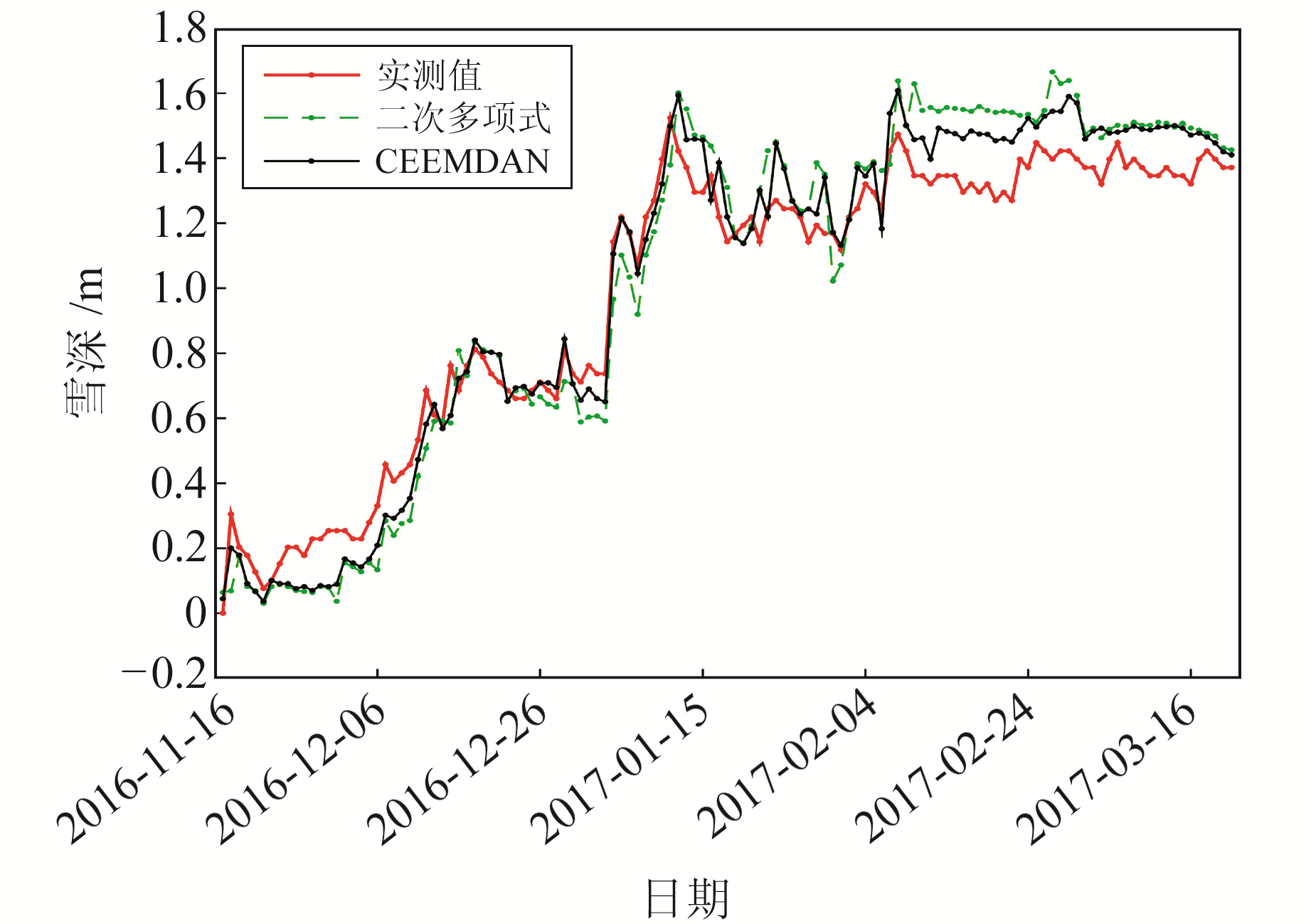
统计3颗GPS卫星在2016-11-16~2017-03-21的观测数据,卫星运行周期为11 h 58 min,1 d内至少有2次经过同一测站上空,因此会出现多个SNR数据,以均值作为当天有效雪深值,2种方法的雪深反演结果如图 5所示。由图 5(a)看出,PRN28卫星在2016-12-06、2016-12-13~14和2016-12-24~27雪深值均为负值,尤其在12-06雪深探测值为-0.18 m,与其他反演值相差太大,且在其他卫星也出现该异常现象,应剔除该异常值,将其余雪深值作为有效雪深探测值。相比之下,图 5(b)反演结果更佳,有效避免了异常跳变的情况。图 6表示2种方法在多星融合下反演的雪深变化,可以看出,利用CEEMDAN进行GNSS-MR雪深反演的雪深值与实测雪深有较高的吻合度。结合表 2,相比二次多项式拟合方法,CEEMDAN均方根误差降低了30.7%,与实测值相关系数为0.965,该结果进一步说明本文方法用于雪深探测具有良好的精度。

|
图 5 2种方法多卫星反演雪深与实测雪深的对比 Fig. 5 Comparison between actual snow depth and multi-satellite inversion of snow depth based on two methods |
|
图 6 2种方法多卫星融合反演雪深与实测雪深 Fig. 6 Comparison between actual snow depth and multi-satellite fusion inversion results of snow depth based on two methods |
|
|
表 2 2种方法反演雪深与实际雪深的平均误差与均方根误差 Tab. 2 ME and RMSE between the retrieved snow depth and the actual snow depth based on two methods |
1) CEEMDAN分解得到的残余分量可准确体现原始SNR信号的趋势,由实验数据分析可知,该方法可有效改善二次多项式拟合方法出现的异常跳变现象。
2) 本文方法可精确地提取SNR反射信号与直射信号的干涉信号,反演结果与实测数据的相关系数大于0.96,RMSE比使用传统二次多项式法降低30.7%,ME优于3 cm,验证了该方法用于GNSS-MR雪深反演的优越性。
| [1] |
张双成, 戴凯阳, 南阳, 等. GNSS-MR技术用于雪深探测的初步研究[J]. 武汉大学学报: 信息科学版, 2018, 43(2): 234-240 (Zhang Shuangcheng, Dai Kaiyang, Nan Yang, et al. Preliminary Research on GNSS-MR for Snow Depth[J]. Geomatics and Information Science of Wuhan University, 2018, 43(2): 234-240)
(  0) 0) |
| [2] |
Ozeki M, Heki K. GPS Snow Depth Meter with Geometry-Free Linear Combinations of Carrier Phases[J]. Journal of Geodesy, 2012, 86(3): 209-219 DOI:10.1007/s00190-011-0511-x
(  0) 0) |
| [3] |
Torres M E, Colominas M A, Schlotthauer G, et al. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C]. International Conference on Acoustics, Speech and Signal Processing, Prague, 2011
(  0) 0) |
| [4] |
Bilich A, Larson K M. Mapping the GPS Multipath Environment Using the Signal-to-Noise Ratio(SNR)[J]. Radio Science, 2007, 42(6)
(  0) 0) |
| [5] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995
(  0) 0) |
| [6] |
周先春, 嵇亚婷. 基于EEMD算法在信号去噪中的应用[J]. 电子设计工程, 2014, 22(8): 12-14 (Zhou Xianchun, Ji Yating. Methods Based on EEMD in Signal De-Noising[J]. Electronic Design Engineering, 2014, 22(8): 12-14 DOI:10.3969/j.issn.1674-6236.2014.08.004)
(  0) 0) |
| [7] |
林丽, 余轮. 基于相关系数的EMD改进算法[J]. 计算机与数字工程, 2008, 36(12): 28-29 (Lin Li, Yu Lun. Improvement on Empirical Mocomposition Based on Correlation Coefficient[J]. Computer and Digital Engineering, 2008, 36(12): 28-29)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2022, Vol. 42
2022, Vol. 42


