2. 山东科技大学测绘与空间信息学院,青岛市前湾港路579号,266590;
3. 山东黄金矿业(玲珑)有限公司,山东省招远市黄水路999号,265400
随着北斗三代卫星导航系统组建完成,GNSS及其应用已发展到新阶段,PNT(positioning navigation timing)服务在日常生活中发挥着重要作用。然而卫星导航系统自主性差、数据输出率低,城市环境下车辆导航的卫星信号极易受到多重因素影响,使得导航结果难以满足需求。惯性导航系统(INS, inertial navigation system)不依赖外界信息自主导航,依靠陀螺仪输出的角速度与加速度计测量的加速度输出位置信息,具有短时精度高、抗干扰性强的优点,但同时也容易累积误差[1]。实际应用中将GNSS与INS应用卡尔曼滤波(Kalman filter, KF)进行组合,可实现优势互补。GNSS可抑制误差累积,INS可辅助接收机信号跟踪[2]。组合方法不仅可以提高导航精度,而且可以提高系统整体的抗干扰性。GNSS/INS组合模式可分为松组合、紧组合与深组合。隋心等[3]提出一种紧组合的BDS/GPS系统间双差模型,实验结果表明,复杂环境下紧组合的精度优于松组合。姚卓等[4]对GNSS/INS松、紧组合模型进行分析,并针对卫星信号长时间失锁的复杂环境,提出一种附加约束条件的组合导航模型,可增强组合导航系统的可靠性。Chai等[5]提出一种自回归模型对INS数据进行检测,可在出现数据缺口时预测INS数据,提高导航精度。沈凯等[6]针对城市复杂环境提出一种自适应鲁棒滤波算法,可在GNSS短时失锁的情况下达到m级定位精度。邵梦杨等[7]对城市复杂环境中GNSS接收机的多路径效应进行分析。
目前针对城市复杂环境下车辆导航的研究较少,本文通过处理GNSS/INS实测数据,对城市高楼群、树木密集区等特殊场景进行车辆导航实验分析,提出一种自适应卡尔曼滤波(adaptive Kalman filter, AKF)算法,该算法基于新息与量测构造自适应因子来调整卡尔曼增益。实验结果表明,该算法计算简单、易于实现,且较常规的卡尔曼滤波具有更高的导航精度和稳定性。
1 GNSS/INS松组合模型 1.1 经典卡尔曼滤波GNSS/INS通过卡尔曼滤波器进行整合。离散化的经典卡尔曼滤波方程可表示为[2]:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}}{_k} = {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{_{k/k - 1}}\mathit{\boldsymbol{X}}{_{k - 1}} + {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{_{k - 1}}\mathit{\boldsymbol{W}}{_{k - 1}}\\ \mathit{\boldsymbol{Z}}{_k} = {\rm{ }}\mathit{\boldsymbol{H}}{_k}\mathit{\boldsymbol{X}}{_k} + {\rm{ }}\mathit{\boldsymbol{V}}{_k} \end{array} \right. $ | (1) |
式中,Xk、Xk-1分别为k时刻与k-1时刻的系统状态矩阵,Φk/k-1为k-1时刻到k时刻的系统状态一步转移矩阵,Γk-1为系统噪声驱动矩阵,Wk-1为k-1时刻的系统噪声矢量,Zk为k时刻的量测向量,Hk为量测矩阵,Vk为量测噪声。其中Wk-1、Vk均满足均值为0的正态分布且两者协方差为0,E(WkWkT)=Qk、E(VkVkT)=Rk。则卡尔曼滤波计算的步骤为:
1) 状态一步预测:
| $ {\mathit{\boldsymbol{\hat X}}_{k/k - 1}} = {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{_{k/k - 1}}\mathit{\boldsymbol{\hat X}}{_{k - 1}} $ | (2) |
2) 状态一步预测均方误差:
| $ \mathit{\boldsymbol{P}}{_{k/k - 1}} = {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{_{k/k - 1}}\mathit{\boldsymbol{P}}{_{k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k/k - 1}^{\rm{T}} + {\rm{ }}\mathit{\boldsymbol{Q}}{_{k - 1}} $ | (3) |
3) 滤波增益:
| $ \mathit{\boldsymbol{K}}{_k} = {\rm{ }}\mathit{\boldsymbol{P}}{_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}{({\rm{ }}\mathit{\boldsymbol{H}}{_k}\mathit{\boldsymbol{P}}{_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\rm{ }}\mathit{\boldsymbol{R}}{\rm{ }})^{ - 1}} $ | (4) |
4) 状态估计:
| $ {\mathit{\boldsymbol{\hat X}}_k} = \mathit{\boldsymbol{\hat X}}{_{k/k - 1}} + {\rm{ }}\mathit{\boldsymbol{K}}{_k}({\rm{ }}\mathit{\boldsymbol{Z}}{_k} - {\rm{ }}\mathit{\boldsymbol{H\hat X}}{_{k/k - 1}}) $ | (5) |
5) 状态估计均方误差:
| $ \mathit{\boldsymbol{P}}{_k} = ({\rm{ }}\mathit{\boldsymbol{I}}{\rm{ }} - {\rm{ }}\mathit{\boldsymbol{K}}{_k}\mathit{\boldsymbol{H}}{_k}){\rm{ }}\mathit{\boldsymbol{P}}{_{k/k - 1}} $ | (6) |
以GNSS接收机相位中心为站心的导航坐标系选取平台的失准角、三维速度误差、三维位置误差、陀螺零偏与加速度计偏差作为松组合的15维状态矩阵,其形式为:
| $ \begin{array}{l} \mathit{\boldsymbol{X}}{\rm{ }} = [\phi _E^n\;\;\phi _N^n\;\;\phi _U^n\;\;\delta v_E^n\;\;\delta v_N^n\;\;\delta v_U^n\;\;\delta \varphi \\ \delta \lambda \;\;\delta h\;\;{\varepsilon _e}\;\;{\varepsilon _n}\;\;{\varepsilon _u}\;\;{\nabla _e}\;\;{\nabla _n}\;\;{\nabla _u}{]^{\rm{T}}} \end{array} $ |
量测方程由GNSS的导航位置、速度分别与惯导机械编排的位置、速度作差得到。转移矩阵的形式由姿态误差方程、速度误差方程、位置误差方程得到,此处不再论述。图 1为松组合基本流程图。

|
图 1 松组合基本流程 Fig. 1 Basic flow chart of loosely coupled |
经典卡尔曼滤波模型需要准确可靠的函数模型与随机模型以获得状态参数的最优估计[8-9]。然而在使用经典卡尔曼滤波时,系统噪声与量测噪声的统计特性难以准确获得,无法实时反映当前时刻的真实噪声状态,导致滤波器的性能无法满足导航需要[10]。为此国内外学者建立一种动态导航定位的自适应抗差滤波理论,应用抗差估计原理来控制观测异常,引进自适应因子控制动力学模型误差的影响[11]。本文使用一种基于新息的自适应滤波,可检测观测质量。利用量测新息
| $ {{\mathit{\boldsymbol{\tilde Z}}}_{k/k - 1}} = {\rm{ }}\mathit{\boldsymbol{Z}}{_k} - {\rm{ }}\mathit{\boldsymbol{H\hat X}}{}{_{k/k - 1}} $ | (7) |
| $ \mathit{\boldsymbol{C}}{_k} = {\rm{ }}\mathit{\boldsymbol{H}}{_k}\mathit{\boldsymbol{P}}{_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\rm{ }}\mathit{\boldsymbol{R}}{_k} $ | (8) |
然后构造判别统计量:
| $ \beta = {\rm{ }}\sqrt {\frac{{\mathit{\boldsymbol{Z}}_k^{\rm{T}}\mathit{\boldsymbol{Z}}{_k}}}{{{\rm{tr}}({\rm{ }}\mathit{\boldsymbol{C}}{_k})}}} {\rm{}} $ | (9) |
再计算自适应因子α:
| $ \alpha = \left\{ \begin{array}{l} {\rm{ }}1, \;\;\left| \beta \right| \le c\\ c/\left| \beta \right|, \;\;\left| \beta \right| > c \end{array} \right. $ | (10) |
最后利用α调整卡尔曼增益:
| $ \mathit{\boldsymbol{K}}{_k} = \left( {1/\alpha } \right){\rm{ }}\mathit{\boldsymbol{P}}{_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}{({\rm{ }}\mathit{\boldsymbol{H}}{_k}\mathit{\boldsymbol{P}}{_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\rm{ }}\mathit{\boldsymbol{R}}{_k})^{ - 1}} $ | (11) |
式中,c为常数,一般设置为0.9~1,此处设置为0.9。
2 数据采集本文实验数据采集于山东科技大学(青岛校区)周围区域,实验环境包括开阔场景和易产生多路径效应或遮挡卫星信号的高楼、树木、高大门廊等城市典型特殊场景。图 2为车辆行驶轨迹,其中A区域为山东科技大学J1教学楼前,B区域为高大树木密集区域,C区域为高大门廊区域。

|
图 2 车辆行驶轨迹 Fig. 2 Vehicle trajectory |
数据采集时间为2020-03,实验设备为SPAN-LCI惯导和基准站双频GNSS接收机,移动站为四系统接收机,其中接收机采样间隔为0.2 s,IMU的主要性能指标见表 1。
|
|
表 1 惯导仪器性能指标 Tab. 1 Performance index of inertial navigation instrument |
使用Inertial Explorer 8.7软件处理事后差分GNSS,采用自编软件对原始观测值进行处理,分析整个实验线路的定位结果和数据质量。图 3为GNSS定位误差、PDOP值和可见卫星数。
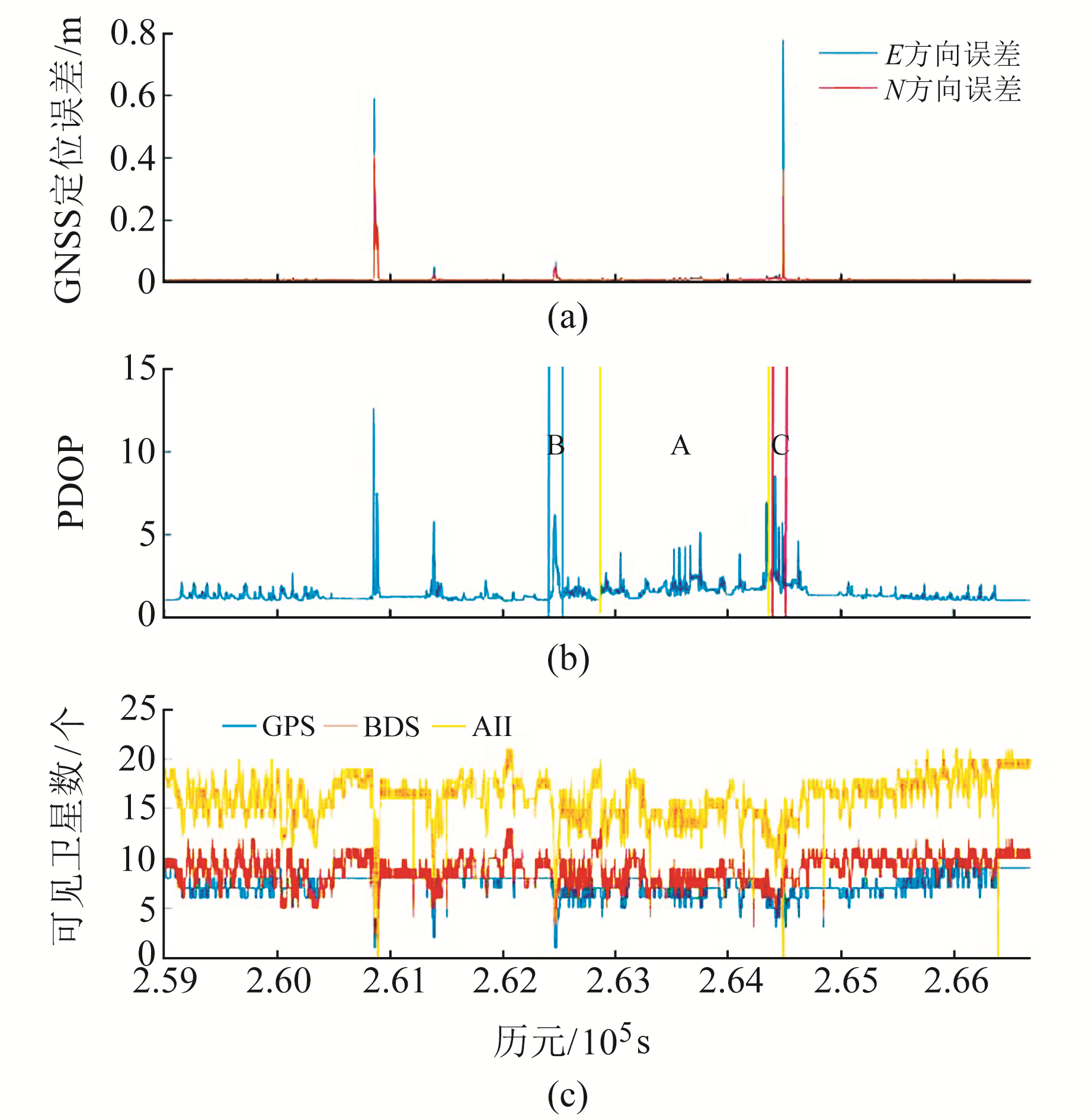
|
图 3 GNSS定位误差、PDOP和可见卫星数 Fig. 3 GNSS positioning error, PDOP and number of visible satellites |
图 3中历元区间262 800~264 450为A区域,262 455~262 478为B区域,264 488~264 497为C区域。由图可见,整个线路的差分定位精度为cm级。对比个别定位误差出现波动区间的PDOP值可知,这些区域受到高大门廊、高大树木遮挡导致卫星信号变差,从而使解算的PDOP值较大。其中高大门廊区域的最大PDOP值为5.79,树木密集区平均PDOP值为5.43。从整个线路的可见卫星数可以看出,测区B、C部分时段的可见卫星数小于4,因此无法进行卫星定位。由于GNSS解算使用RTK模式,因此可见卫星仅显示有基准站与移动站的共视卫星。
3.2 组合导航算例 3.2.1 模拟卫星信号失锁实验以高精度后处理软件IE8.7的紧组合结果作为参考真值,处理整个线路的组合导航数据,并选取GNSS观测条件良好的线路,人为中断GNSS来测试IMU单独导航的性能。在GNSS观测条件良好的直线路段,几乎可以忽略多路径效应对卫星信号的影响。该路段GNSS定位结果与紧组合相比平面误差小于1 cm,平均高程误差为1.25 cm。从第2 s开始人为中断GNSS观测20 s,GNSS定位结果、GNSS/INS组合导航结果与模拟GNSS中断的导航结果,如图 4所示。
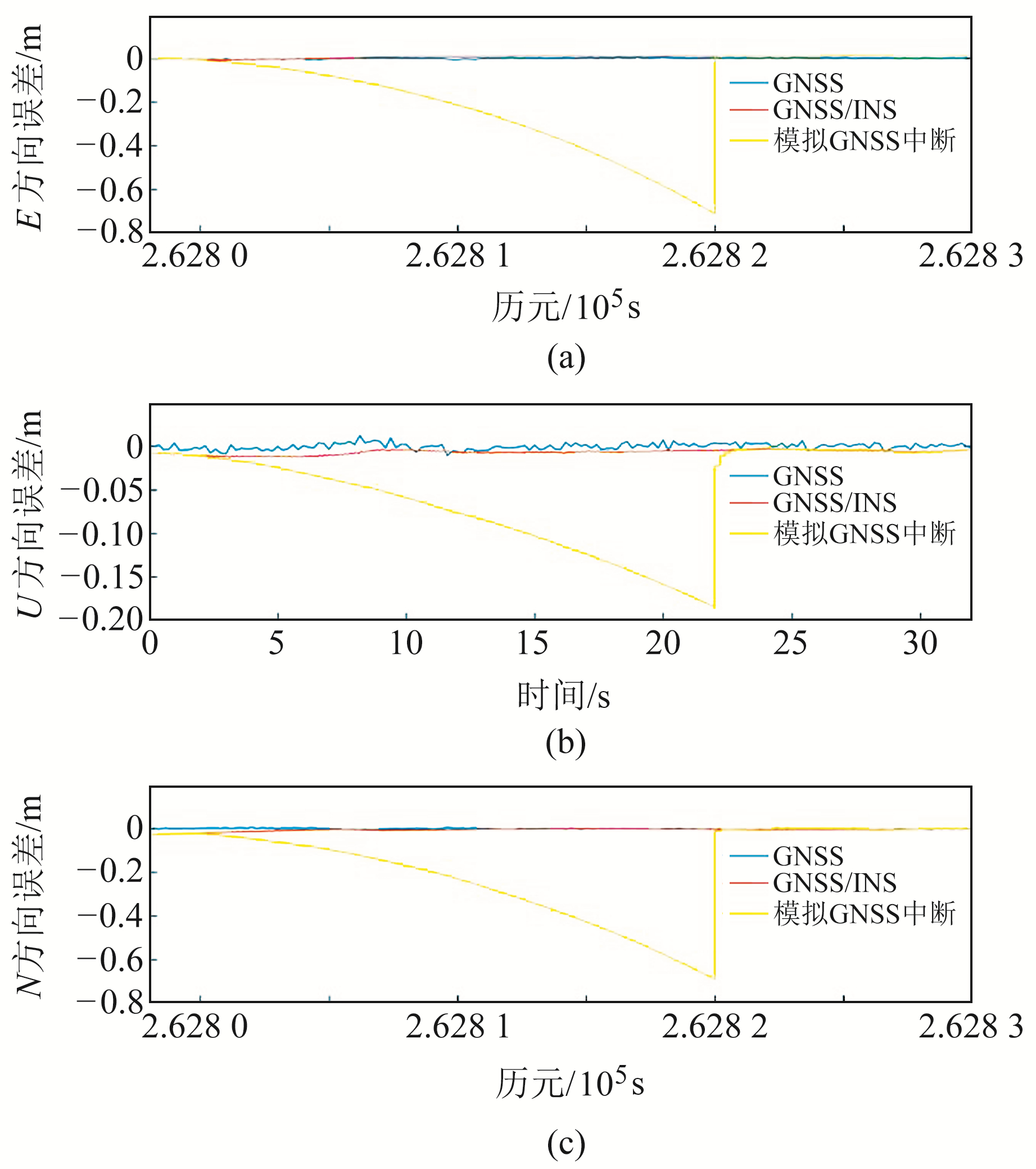
|
图 4 模拟GNSS中断的组合导航 Fig. 4 Integrated navigation simulating GNSS interruption |
由图可见,GNSS导航结果与组合导航结果精度一致。当人为中断卫星信号时,组合导航退化为单系统导航,卫星信号中断5 s以内,INS导航结果在E、N方向的累积误差均小于0.1 m,U方向累积误差为0.04 m;卫星信号中断10 s时,E、N方向累积误差约为0.4 m,U方向累积误差为0.075 m;当卫星信号中断20 s时,E、N方向累积误差达到0.7 m,U方向累积误差为0.18 m。当重新接收到卫星信号时,组合导航系统生效,GNSS导航结果对INS累积误差产生抑制作用,导航结果在2个历元内恢复到cm级定位精度。由此可见,组合导航结果相对于GNSS导航更为稳定,且组合导航系统在缺失卫星导航的短时间内仍能够提供较高精度的导航结果。
3.2.2 卫星信号遮挡下的组合导航图 5为图 2中B、C区域的GNSS定位结果,由图可见,2个区域均有部分路段无法实现GNSS定位。图 6和图 7为单GNSS导航结果与GNSS/INS组合导航对比(黄色区域为GNSS信号失锁时间段)。

|
图 5 GNSS定位结果 Fig. 5 GNSS positioning results |

|
图 6 树木密集区域GNSS导航与组合导航结果 Fig. 6 Results of GNSS navigation and integrated navigation in tree intensive area |
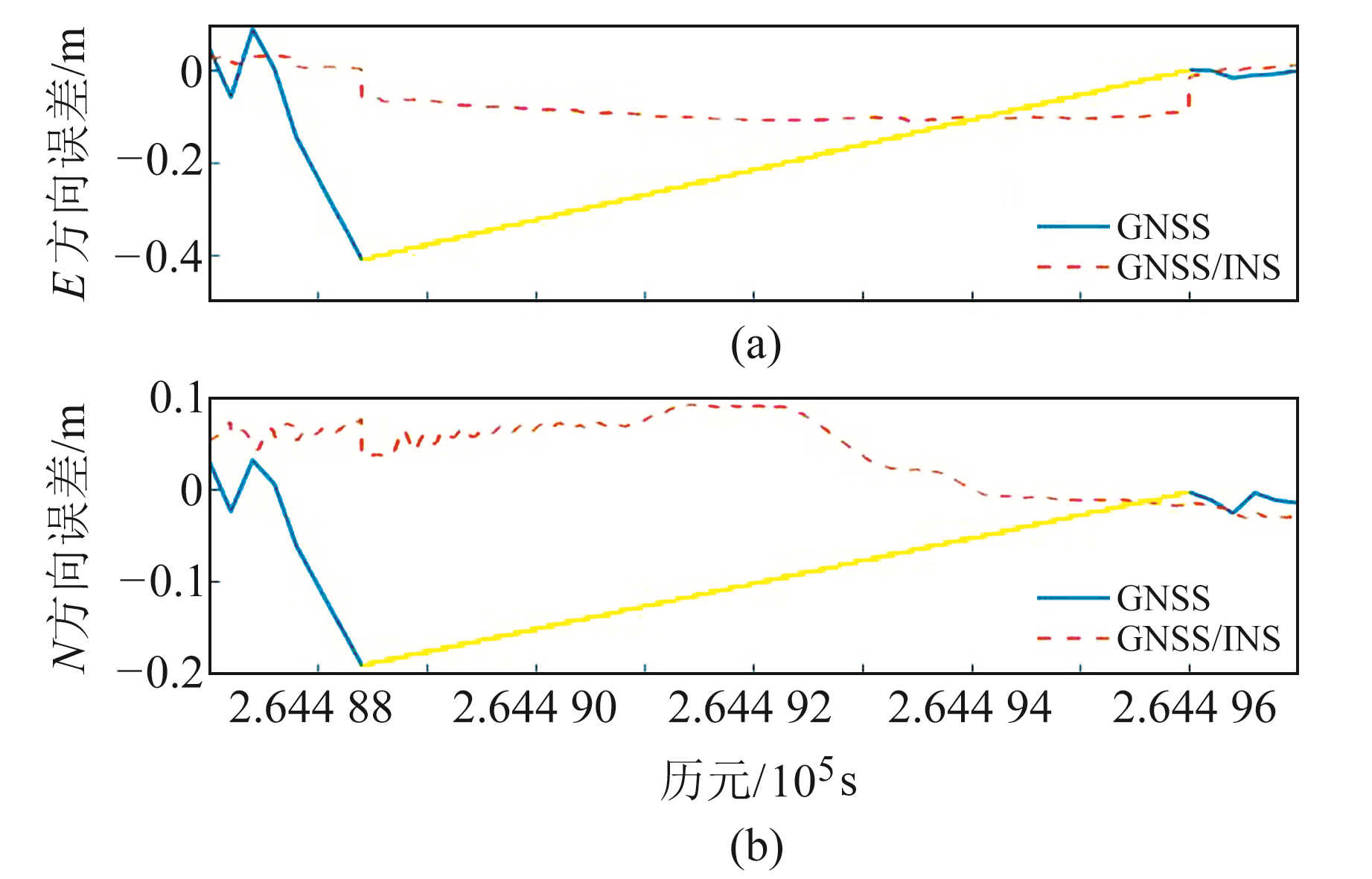
|
图 7 高大门廊区域GNSS导航与组合导航结果 Fig. 7 Results of GNSS navigation and integrated navigation in high porch area |
从图 6可以看出,由于GNSS无法对B区域部分路段进行定位,而GNSS/INS组合导航系统定位误差开始累积,当重新接收到卫星信号时,定位误差迅速减小。结合图 5可以看出,第1个历元区间的起始方位角近似90°,因此E方向误差累积较快,8 s累积误差达1.037 m,N方向误差累积较慢,8 s累积误差为0.255 m;第2个历元区间起始方位角近似0°,因此N方向误差累积较快,6 s累积误差为0.465 m,E方向误差累积较慢,6 s累积误差为0.236 m。
从图 7可以看出,C区域受到高大门廊遮挡,组合导航系统在N方向误差产生波动,由于车辆通过门廊区域会减速,此时单INS系统导航结果更稳定,因此E、N方向累积误差均较小,可提供亚m级精度的导航结果。
3.2.3 自适应卡尔曼滤波算法A区域定位误差较小,但由于受到高楼、树木以及水面影响,其PDOP值仍然较大,部分时间段大于3,少数历元甚至大于4。由于接收机与其存在一定距离,卫星信号不至于被遮挡,但会导致较严重的多路径效应,使得信号受到一定影响。并且由于树木遮挡,使得只有高度角较高的卫星可见,卫星的空间几何构型和定位环境较差,导致定位误差波动较大[12]。图 8为该区域GNSS定位误差。
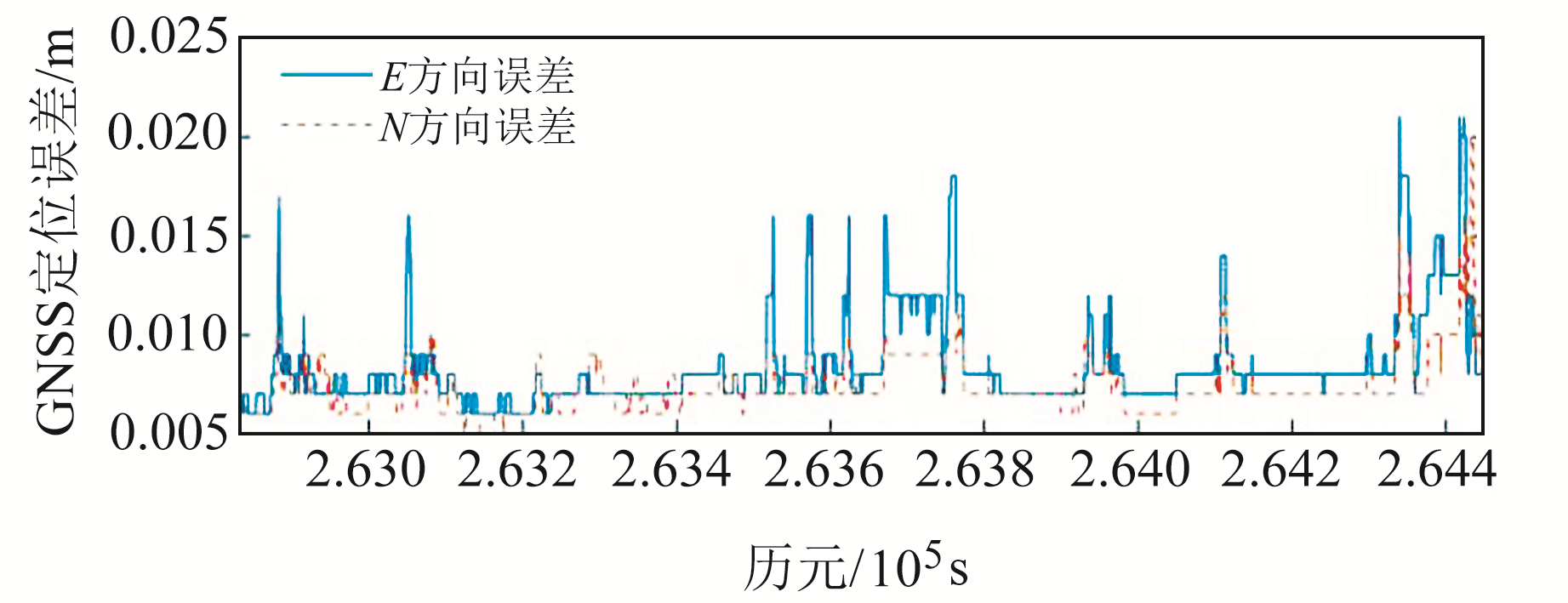
|
图 8 A区域GNSS定位误差 Fig. 8 GNSS positioning errors in area A |
常规卡尔曼滤波无法检测该区域的数据质量,因此使用自适应卡尔曼滤波进行处理,图 9和图 10为该区域KF和AKF在位置、速度误差方面的对比。

|
图 9 KF、AKF位置误差 Fig. 9 KF, AKF position errors |

|
图 10 KF、AKF速度误差 Fig. 10 KF, AKF velocity errors |
从图 9可以看出,AKF算法较KF算法解算的导航误差波动更小,结果更加准确,在历元区间263 450~263 650更为明显。整个区间内KF算法E方向最大误差为0.258 m,而AKF算法最大误差为0.177 m;KF算法N方向最大误差为0.276 m,AKF算法为0.208 m。
由图 10可知,AKF算法较常规KF算法解算的导航速度精度更高。表 2(单位m)和表 3(单位m/s)为该区域常规卡尔曼滤波与自适应滤波位置、速度的结果对比。
|
|
表 2 卡尔曼滤波算法位置结果对比 Tab. 2 Comparison of location results of Kalman filtering algorithm |
|
|
表 3 卡尔曼滤波算法速度结果对比 Tab. 3 Comparison of velocity results of Kalman filtering algorithm |
由表 2和表 3可知,自适应滤波相比于常规卡尔曼滤波在位置精度方面提升约30%,在速度精度方面也有所提升,可有效解决观测数据质量检测的问题,该算法较KF算法具有更高的导航精度和稳定性。
4 结语利用常规卡尔曼滤波处理卫星信号失锁区域数据,然后利用提出的基于新息的自适应卡尔曼滤波进行实验验证。结果表明:
1) GNSS/INS松组合可在卫星信号失锁的短时间内提供较高精度的导航结果,组合导航系统方向累积误差的大小与卫星信号失锁时行驶方向的方位角有关,且车辆加减速时组合系统的可观测性得到提升。
2) 本文提出的自适应卡尔曼滤波算法可在卫星信号受多路径效应严重影响时显著提高GNSS/INS组合导航结果的稳定性和定位精度,相比于常规滤波算法精度可提高约30%。
| [1] |
严恭敏. 捷联惯导算法及车载组合导航系统研究[D]. 西安: 西北工业大学, 2004 (Yan Gongmin. Research on SINS and Vehicle-Borne Integrated Navigation System[D]. Xi'an: Northwestern Polytechnical University, 2004) http://cdmd.cnki.com.cn/article/cdmd-10699-2004062822.htm
(  0) 0) |
| [2] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2012 (Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Kalman Filter and Integrated Navigation Principle[M]. Xi'an: Northwestern Polytechnical University Press, 2012)
(  0) 0) |
| [3] |
隋心, 李玉星, 沈佳琦, 等. 复杂环境下BDS/GPS紧组合高精度定位方法[J]. 导航定位学报, 2019, 7(1): 83-87 (Sui Xin, Li Yuxing, Shen Jiaqi, et al. High-Accurate Positioning Method of BDS/GPS Tight Combination under Complicated Environment[J]. Journal of Navigation and Positioning, 2019, 7(1): 83-87)
(  0) 0) |
| [4] |
姚卓, 章红平. 里程计辅助车载GNSS/INS组合导航性能分析[J]. 大地测量与地球动力学, 2018, 38(2): 206-210 (Yao Zhuo, Zhang Hongping. Performance Analysis on Vehicle GNSS/INS Integrated Navigation System Aided by Odometer[J]. Journal of Geodesy and Geodynamics, 2018, 38(2): 206-210)
(  0) 0) |
| [5] |
Chai D S, Chen G L, Wang S L, et al. Loosely Coupled GNSS/INS Integration Based on an Auto Regressive Model in a Data Gap Environment[J]. Acta Geodaetica et Geophysica, 2018, 53(4): 691-715 DOI:10.1007/s40328-018-0238-8
(  0) 0) |
| [6] |
沈凯, 刘庭欣, 左思琪, 等. 复杂城市环境下GNSS/INS组合导航可观测度分析及鲁棒滤波方法[J]. 仪器仪表学报, 2020, 41(9): 252-261 (Shen Kai, Liu Tingxin, Zuo Siqi, et al. Observability Analysis and Robust Fusion Algorithms of GNSS/INS Integrated Navigation in Complex Urban Environment[J]. Chinese Journal of Scientific Instrument, 2020, 41(9): 252-261)
(  0) 0) |
| [7] |
邵梦杨, 郭磊, 王甫红. 城市典型环境下单频导航型GNSS接收机多路径误差特性分析[J]. 测绘通报, 2018(9): 1-7 (Shao Mengyang, Guo Lei, Wang Fuhong. Multipath Error Analysis of Single Frequency Navigation GNSS Receiver in Typical Urban Environment[J]. Bulletin of Surveying and Mapping, 2018(9): 1-7)
(  0) 0) |
| [8] |
Gao X L, Luo H Y, Ning B K, et al. RL-AKF: An Adaptive Kalman Filter Navigation Algorithm Based on Reinforcement Learning for Ground Vehicles[J]. Remote Sensing, 2020, 12(11): 1 704 DOI:10.3390/rs12111704
(  0) 0) |
| [9] |
Ryan J G, Bevly D M. On the Observability of Loosely Coupled Global Positioning System/Inertial Navigation System Integrations with Five Degree of Freedom and Four Degree of Freedom Inertial Measurement Units[J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(2): 021023 DOI:10.1115/1.4025985
(  0) 0) |
| [10] |
杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报, 2001, 30(4): 293-298 (Yang Yuanxi, He Haibo, Xu Tianhe. Adaptive Robust Filtering for Kinematic GPS Positioning[J]. Acta Geodaetica et Cartographic Sinica, 2001, 30(4): 293-298)
(  0) 0) |
| [11] |
徐天河, 杨元喜. 改进的Sage自适应滤波方法[J]. 测绘科学, 2000, 25(3): 22-24 (Xu Tianhe, Yang Yuanxi. The Improved Method of Sage Adaptive Filtering[J]. Developments in Surveying and Mapping, 2000, 25(3): 22-24)
(  0) 0) |
| [12] |
柴大帅. 多星座GNSS/INS组合导航理论与方法研究[D]. 徐州: 中国矿业大学, 2020 (Chai Dashuai. Study on the Theory and Method in Integrated Navigation of Multi-Constellation GNSS/INS[D]. Xuzhou: China University of Mining and Technology, 2020) http://cdmd.cnki.com.cn/Article/CDMD-10290-1020962693.htm
(  0) 0) |
2. College of Geodesy and Geomatics, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266590, China;
3. Shandong Gold Mining (Linglong) Co Ltd, 999 Huangshui Road, Zhaoyuan 265400, China
 2022, Vol. 42
2022, Vol. 42


