2. 中国科学院上海天文台,上海市南丹路80号,200030;
3. 上海大学通信与信息工程学院,上海市上大路99号,200444
由于BDS发展时间较短,其精密定轨使用的光压模型一般是基于GPS卫星建立的ECOM经验模型。但GPS卫星采用的姿态控制模式为动偏(yaw steering,YS)+连续动偏(continuous yaw steering,CYS),而早期BDS-2 IGSO与MEO卫星采用动偏+零偏(orbit normal,ON)控制模式,BDS-2 GEO则始终采用零偏控制模式。若直接将ECOM模型应用于BDS-2卫星定轨,将不可避免地出现不适应的问题,如零偏期间轨道精度严重下降[1]。针对此问题,国内学者提出一系列解决方案[2-4],在一定程度上改善了卫星零偏期间轨道精度下降的问题,但仍然明显低于动偏期间的精度。
2016年起,BDS-2中部分卫星陆续将地影期的姿态控制模式由零偏转为连续动偏,同时BDS-3 IGSO与MEO也采用连续动偏的控制模式。即使卫星采用与GPS相同的姿态控制模式,但由于GPS卫星本体为正方体,将ECOM 5参数模型应用于本体为长方体的卫星,如BDS、Galileo与QZSS等,也会产生与太阳高度角相关的系统误差。为减少系统误差的影响,Yan等[5]将可校正Box-Wing模型作为ECOM 5参数模型的先验模型,与单独使用ECOM 5参数模型相比,卫星激光测距残差由14 cm减少到5 cm;王晨[6]研究发现,BDS-3 MEO卫星使用拓展版ECOM模型可有效减少ECOM 5参数模型的系统误差;Li等[7]利用BDS-3卫星表面光学参数建立Box-Wing模型,并将其作为ECOM 5参数模型的先验模型,与拓展版ECOM模型相比,可提高BDS-3 MEO卫星的轨道重叠精度与卫星激光测距检核精度。
以上光压模型适用性的研究对象多为BDS-2卫星与BDS-3 MEO卫星,并未对北斗中其他类型卫星加以分析,也没有区分地影期与非地影期。因此本文研究北斗卫星分别处于地影期与非地影期时ECOM 5参数模型、Box-Wing+ECOM 5参数模型与拓展版ECOM模型的适用性。
1 北斗卫星姿态控制模式卫星姿态通常用偏航角ψ表示:
| $ \psi = {\rm{arctan}}({\rm{ - tan}}\beta /{\rm{sin}}\mu ) $ | (1) |
式中,β为太阳高度角,μ为卫星轨道角。将式(1)对时间求导,可得偏航角变化速率:
| $ \dot \psi = \frac{{\dot \mu {\rm{tan}}\beta {\rm{cos}}\mu }}{{{\rm{si}}{{\rm{n}}^2}\mu + {\rm{ta}}{{\rm{n}}^2}\beta }} $ | (2) |
式中,
在太阳高度角较高,即卫星处于非地影期时,卫星能够按照式(1)维持卫星姿态,称为动偏控制模式。当太阳高度角较低,即卫星处于地影期且运行到近日点(μ=180°)与远日点(μ=0°)时,由式(2)可知,偏航角变化速率会达到最大值,该值可能会超过卫星的可调节范围。因此为了保证卫星的正常运行,需要在地影期采取特殊的姿态控制模式。不同卫星采取的策略不同,其中GPS与GLONASS采用连续动偏的控制模式,在近日点与远日点分别进行“正午机动”与“午夜机动”来维持卫星姿态[8],而BDS-2采用一种相对简单的控制模式,在太阳高度角小于一定范围时采用零偏的控制模式,即ψ=0°。郭靖[2]使用RKPPP(reverse kinematic precise point positioning)方法估计BDS-2卫星的偏航角发现,BDS-2 IGSO与MEO卫星在|β|≤4°且μ=90°时卫星姿态会由动偏转为零偏;当|β|>4°且μ=90°时卫星姿态由零偏转为动偏。由于零偏期间轨道精度较差,因此BDS-2部分IGSO、MEO卫星与BDS-3 IGSO、MEO卫星在地影期采用连续动偏的控制模式。据Wang等[9]的研究,采取新姿态控制模式的北斗卫星在|β|≤3°时由动偏转为连续动偏,当|β|>3°时由连续动偏转为动偏。
2 太阳光压模型 2.1 ECOM光压模型1994年Beutler等[10]借鉴Colombo模型建立了ECOM 9参数光压模型,其将太阳光压摄动力与其他未模型化的摄动力分解到DYB坐标系下D、Y、B方向,其中D为卫星指向太阳的方向,Y为卫星指向地心的方向,B为卫星太阳帆板轴向。1999年Springer等[11]删减D向与Y向周期项参数,提出一种更简洁、精确的ECOM 5参数光压模型,下文简称为ECOM1。该模型目前被各大IGS研究机构所使用。
2015年Arnorld等[12]发现,使用ECOM1模型估计地心与地球自转参数时会出现周期性误差,这与ECOM1模型忽略D方向偶数阶的周期项与B方向奇数阶的周期项有关,因此其在ECOM1基础上提出了拓展版ECOM光压模型,下文简称为ECOM2。
ECOM2有多种形式,其中D4B1组合(将D方向的傅里叶级数展开至4阶、B方向展开至1阶)和D2B1组合(将D方向的傅里叶级数展开至2阶、B方向展开至1阶)的定轨效果较好,本文选用前者进行计算。
2.2 Box-Wing光压模型Box-Wing光压模型不同于ECOM经验模型,经验模型将光压参数作为待求参数代入观测方程中进行求解,而Box-Wing模型中太阳光压是通过提前预设的卫星相关参数直接获取,不需要观测数据参与。因此,Box-Wing模型的合理性很大程度上取决于所输入卫星参数的准确度。但由于卫星在轨运行过程中存在老化的问题,难以获取其表面光学参数的准确信息,因此在实际的卫星定轨中,Box-Wing模型不会被单独使用,而仅作为经验模型的先验模型提供太阳光压的先验值,剩余的光压摄动力通过经验模型来吸收。本文所使用的北斗卫星表面光学系数取自CSNO(China Satellite Navigation Office)2019年公布的数据。
3 光压模型适用性分析实验 3.1 实验数据与定轨策略选取2020年年积日(doy)200~360的MGEX观测网数据,在全球均匀选取60个可同时观测到BDS-2与BDS-3的测站。利用武汉大学精密定轨软件PANDA,联合BDS-2与BDS-3进行轨道解算,对比ECOM1、Box-Wing+ECOM1(以下简称BW+ECOM1)与ECOM2三种光压模型分别在地影期与非地影期下对北斗MEO与IGSO卫星(BDS-2中7颗IGSO与3颗MEO,BDS-3中3颗IGSO与24颗MEO)的适用性,具体定轨策略见表 1。轨道解算结果使用卫星激光测距外符合检核、轨道重叠弧段内符合检核和与MGEX精密轨道产品比较3种手段进行精度评估。
|
|
表 1 定轨策略信息 Tab. 1 Information of orbit determination strategy |
卫星激光测距(satellite laser ranging,SLR)技术由于具有mm级测量精度而常用于评价卫星轨道的外符合精度,其主要反映卫星轨道的径向精度。目前ILRS(International Laser Ranging Service)仅提供8颗北斗IGSO与MEO卫星的激光数据:C08、C10与C11卫星在地影期采用零偏的控制模式;C13卫星在地影期采用连续动偏的控制模式;BDS-3中CAST(China Academy of Space Technology)制造的C20、C21卫星与SECM(Shanghai Engineering Center for Microsatellites)制造的C29与C30卫星在地影期采用连续动偏的控制模式。将SLR残差绝对值大于0.5 m的检核点作为粗差进行剔除,约剔除0.5%的数据。图 1给出部分北斗卫星的SLR残差,其中虚线范围内为地影期(BDS-2:|β|≤4°;BDS-3:|β|≤3°),表 2为SLR残差统计结果。

|
图 1 北斗卫星在不同光压模型下的SLR残差 Fig. 1 SLR residuals of different solar radiation pressure models for Beidou satellites |
|
|
表 2 北斗卫星在不同光压模型下的SLR残差统计 Tab. 2 SLR residuals statistics of different solar radiation pressure models for Beidou satellites |
由图 1可见,在地影期采用零偏控制模式的C10卫星的SLR残差与非地影期相比明显增加,而采用连续动偏控制模式的C13、C20与C29卫星在地影期的SLR残差却未明显增加。采用ECOM1模型时,C10卫星在姿态由动偏转零偏的过程中残差RMS值由7.5 cm增加到13.3 cm,而C13卫星由动偏转为连续动偏时残差RMS值仅由6.9 cm增加到7.8 cm。造成这种差异主要是因为ECOM模型是基于名义姿态,在卫星本体仅有+X面、+Z面与-Z面受照,-X面作为散热板不受照的情况下建立的;而采用零偏控制模式的卫星,-X面与+X面会轮流受照。由于两者光学属性差异较大,导致零偏时期卫星轨道精度下降[13]。而采用连续动偏控制模式的卫星仅在近日点与远日点进行“正午机动”或“午夜机动”,持续时间约40 min,其余时间仍然采用动偏的控制模型,因此连续动偏时期的卫星轨道精度与动偏时期相比并没有明显下降,体现了地影期卫星采用连续动偏控制模式的优越性。
研究表明,ECOM2可改善GPS与GLONASS轨道精度[12]。但由表 2可知,无论BDS-2卫星是否处于地影期,ECOM1的SLR残差RMS值始终最小。以C13卫星为例,非地影期使用ECOM1的SLR残差RMS值与BW+ECOM1相比减少20.7%,与ECOM2相比减少33.7%;地影期使用ECOM1的SLR残差RMS值与BW+ECOM1相比减少37.1%,与ECOM2相比减少46.2%。表明BDS-2卫星不同于GPS卫星,使用ECOM1时轨道径向精度最优。
通过表 2还可以发现,BDS-3 MEO卫星使用BW+ECOM1与ECOM2的SLR残差RMS值要低于ECOM1。当卫星处于非地影期时,CAST制造的C20、C21卫星使用BW+ECOM1与ECOM2的SLR残差RMS值与ECOM1相比分别减少26.7%与11.7%,对于SECM制造的C29、C30卫星则分别减少29.5%与14.8%。当卫星处于地影期时,C20、C21卫星使用BW+ECOM1与ECOM2的SLR残差RMS值与ECOM1相比分别减少23.8%与12.7%,对于C29、C30卫星则分别减少了16.9%与11.2%。此外,当BDS-3 MEO卫星使用BW+ECOM1与ECOM2时,SLR残差均值同ECOM1相比明显减少。以上分析表明,对于BDS-3 MEO卫星使用BW+ECOM1与ECOM2可以减少ECOM1模型的系统误差,提高径向精度。
3.3 轨道重叠弧段检核本文的定轨弧段长度为3 d,连续2个观测弧段有2 d的重叠轨道,实验数据可组成160个长度为2 d的重叠弧段,通过重叠轨道的互差研究轨道内符合精度。图 2为北斗卫星采用不同光压模型时在轨道坐标系下3个方向的RMS值及一维方向RMS值的均值,图中虚线左边为非地影期,虚线右边为地影期,同时X轴将北斗中IGSO与MEO卫星分为7类,其中BDS-2 IGSO(ON)表示在地影期采用ON模式的BDS-2 IGSO卫星,BDS-2 MEO(CYS)表示在地影期采用CYS模式的BDS-2 MEO卫星。

|
图 2 重叠轨道各个方向的RMS值 Fig. 2 RMS values in all directions of the overlapping orbitals |
当卫星处于非地影期时,由图 2可知,当BDS-2卫星使用ECOM1时,各个方向内符合精度要略高于另外2种光压模型,这与SLR检核中BDS-2使用ECOM1时残差最小的结论一致。对于BDS-3 MEO卫星,虽然BW+ECOM1与ECOM2内符合精度略优于ECOM1,但3类光压模型在一维方向的RMS均值差异均小于1 cm,表明虽然ECOM1存在缺陷,但仍具有较好的内符合精度。对于BDS-3 IGSO卫星,因目前MGEX测站中可观测到该类卫星的测站较少,导致观测数不足,而内符合精度容易受到观测数的影响,所以BDS-3 IGSO卫星相较于其他卫星的内符合精度偏低。虽然BDS-3 IGSO整体内符合精度较低,但ECOM1的表现要略优于另外2种光压模型。
当卫星处于地影期时,卫星姿态控制模式由动偏转为连续动偏或零偏,相较于非地影期,卫星内符合精度明显降低。对比BDS-2中采用连续动偏与零偏的MEO与IGSO卫星可以发现,零偏时段的内符合精度明显低于连续动偏时段,再次体现了连续动偏控制模式的优越性。对比地影期3种光压模型内符合精度的表现可以发现,ECOM2明显优于ECOM1与BW+ECOM1,主要体现在切向与法向内符合精度的提升,提升量约为20%~70%。但径向内符合精度略有下降,在SLR检核中BDS-2卫星也有类似情况,这可能与ECOM2过度参数化有关。虽然径向内符合精度略有下降,但ECOM2在一维方向RMS均值相较于ECOM1与BW+ECOM2有13%~74%的提升,表明ECOM2更适用于地影期的北斗卫星定轨。
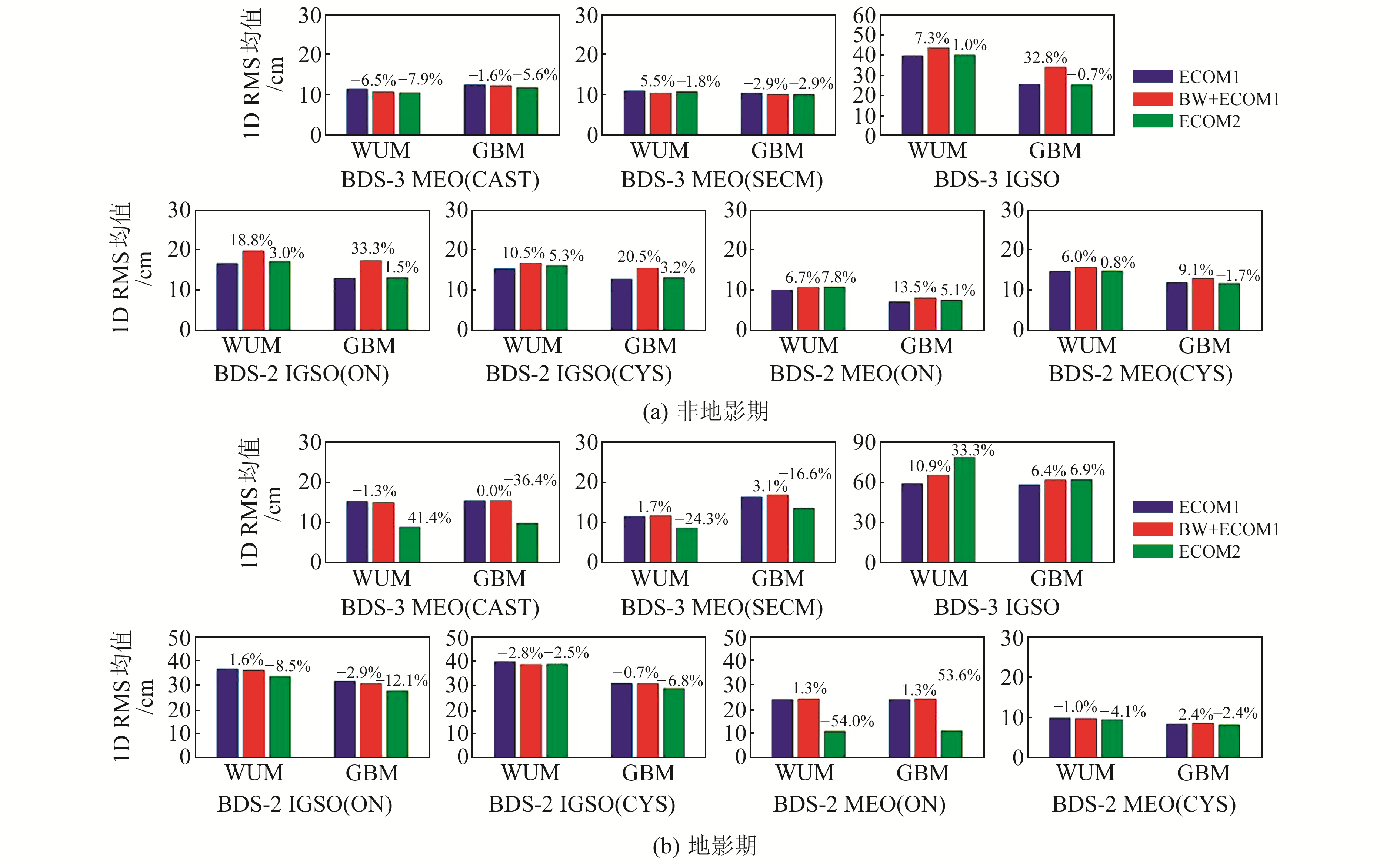
3.4 与MGEX轨道产品比较目前提供BDS-3卫星精密轨道产品的研究机构主要有德国地学研究中心(GFZ)与武汉大学(WHU)。本节将3种光压模型的轨道分别与GFZ的GBM、WHU的WUM在2020年年积日300~360期间的轨道产品进行比较,统计北斗各类卫星在轨道坐标系下一维方向RMS的均值,同时计算BW+ECOM1与ECOM2的RMS均值相对于ECOM1变化的百分比,结果见图 3。
|
图 3 3种光压模型的轨道与精密轨道产品对比 Fig. 3 Comparison between tracks of three solar radiation pressure models and precision track products |
由图 3可知,在非地影期,除BDS-3 IGSO卫星轨道与WUM、GBM差异较大外,其余北斗卫星轨道与精密轨道产品的差异小于20 cm,表明3种光压模型在卫星处于动偏时均能获得较好的结果。对于非地影期的BDS-2卫星,除个别卫星外,其余卫星使用BW+ECOM1的RMS均值要比ECOM1高约15%,使用ECOM2的RMS均值比ECOM1高约3%。对于BDS-3 MEO卫星,使用BW+ECOM1与ECOM2的RMS均值要比ECOM1低约4%。其结果仍然表明,ECOM1适用于BDS-2卫星,BW+ECOM1与ECOM2适用于BDS-3 MEO。
在地影期,除BDS-3 IGSO卫星外,其余卫星使用ECOM2的RMS均值要明显低于另外2种光压模型,表明地影期时北斗卫星使用ECOM2时的外符合精度最优。对于BDS-3 IGSO,无论其是否处于地影期,3种光压模型的轨道与精密轨道产品相比均有较大误差,但ECOM1要略优于另外2种光压模型。
4 结语本文分别使用ECOM1、BW+ECOM1、ECOM2三种光压模型进行BDS-2+BDS-3联合定轨,通过SLR外符合检核、轨道重叠弧段内符合检核和与MGEX轨道产品比较,分析北斗IGSO与MEO卫星在地影期与非地影期采用不同光压模型时的轨道精度,获得以下结论:
1) 当卫星处于非地影期时,BDS-2 IGSO与MEO卫星采用ECOM1时轨道精度最优,SLR检核的RMS值与BW+ECOM1、ECOM2相比减少约20%~30%;BDS-3 MEO采用3种光压模型的轨道精度基本一致,内符合精度差异小于1 cm,但BW+ECOM1与ECOM2的内、外符合精度要略优于ECOM1。
2) 当卫星处于地影期时,除BDS-3 IGSO卫星外,其余北斗卫星使用ECOM2时轨道精度要高于另外2种光压模型,虽然SLR检核与轨道重叠弧段检核表明轨道径向精度略有下降,但重叠弧段的切向与法向的内符合精度却有20%~70%的提升,因此当BDS-2 IGSO、MEO与BDS-3 MEO处于地影期时,推荐使用ECOM2。
3) BDS-3 IGSO卫星由于观测数较少,导致其无论是否处于地影期,内、外符合精度都要远低于其他北斗卫星,但综合来看,ECOM1的表现要略优于另外2种光压模型。
| [1] |
Guo J, Xu X L, Zhao Q L, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143-159 DOI:10.1007/s00190-015-0862-9
(  0) 0) |
| [2] |
郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014 (Guo Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan: Wuhan University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm
(  0) 0) |
| [3] |
毛悦, 宋小勇, 王维, 等. IGSO姿态控制模式切换期间定轨策略研究[J]. 武汉大学学报: 信息科学版, 2014, 39(11): 1 352-1 356 (Mao Yue, Song Xiaoyong, Wang Wei, et al. IGSO Satellite Orbit Determining Strategy Analysis with the Yaw-Steering and Orbit-Normal Attitude Control Mode Switching[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1 352-1 356)
(  0) 0) |
| [4] |
毛悦, 宋小勇, 贾小林, 等. 北斗卫星ECOM光压模型参数选择策略分析[J]. 测绘学报, 2017, 46(11): 1 812-1 821 (Mao Yue, Song Xiaoyong, Jia Xiaolin, et al. Analysis about Parameters Selection Strategy of ECOM Solar Radiation Pressure Model for Beidou Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1 812-1 821)
(  0) 0) |
| [5] |
Yan X Y, Liu C C, Huang G W, et al. A Priori Solar Radiation Pressure Model for Beidou-3 MEO Satellites[J]. Remote Sensing, 2019, 11(13): 1 605 DOI:10.3390/rs11131605
(  0) 0) |
| [6] |
王晨. 北斗导航卫星光压模型构建与精化研究[D]. 武汉: 武汉大学, 2019 (Wang Chen. Solar Radiation Pressure Modelling for Beidou Navigation Satellites[D]. Wuhan: Wuhan University, 2019) http://cdmd.cnki.com.cn/Article/CDMD-10486-1020604180.htm
(  0) 0) |
| [7] |
Li X X, Yuan Y Q, Zhu Y T, et al. Improving BDS-3 Precise Orbit Determination for Medium Earth Orbit Satellites[J]. GPS Solutions, 2020, 24(2): 1-13 DOI:10.1007/s10291-020-0967-3?utm_source=xmol
(  0) 0) |
| [8] |
Kouba J. A Simplified Yaw-Attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1): 1-12 DOI:10.1007/s10291-008-0092-1
(  0) 0) |
| [9] |
Wang C, Guo J, Zhao Q L, et al. Yaw Attitude Modeling for Beidou I06 and Beidou-3 Satellites[J]. GPS Solutions, 2018, 22(4): 1-10
(  0) 0) |
| [10] |
Beutler G, Brockmann E, Gurtner W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics(IGS): Theory and Initial Results[J]. Manuscr Geod, 1994, 19(6): 367-386
(  0) 0) |
| [11] |
Springer T A, Beutler G, Rothacher M. A New Solar Radiation Pressure Model for GPS Satellites[J]. GPS Solutions, 1999, 2(3): 50-62 DOI:10.1007/PL00012757
(  0) 0) |
| [12] |
Arnold D, Meindl M, Beutler G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8): 775-791 DOI:10.1007/s00190-015-0814-4
(  0) 0) |
| [13] |
李晓杰, 刘晓萍, 祖安然, 等. 基本导航模式下BDS-3卫星地影期间的定轨精度分析[J]. 武汉大学学报: 信息科学版, 2020, 45(6): 854-861 (Li Xiaojie, Liu Xiaoping, Zu Anran, et al. Orbit Accuracy for BDS-3 Satellites during the Earth Eclipsing Period in Basic Navigation Model[J]. Geomatics and Information Science of Wuhan University, 2020, 45(6): 854-861)
(  0) 0) |
2. Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China;
3. School of Communication and Information Engineering, Shanghai University, 99 Shangda Road, Shanghai 200444, China
 2022, Vol. 42
2022, Vol. 42


