实时动态定位(real-timekinematic,RTK)是实现BDS高精度定位不可替代的技术之一。RTK的实质是通过双差组合消除或削弱观测误差的影响,进而恢复整周模糊度的整数特性[1]。由于大气延迟误差和测站距离具有强相关性,随着测站间距离的增加,将残余的大气延迟误差和整周模糊度进行分离较为困难。研究者对BDS三频整周模糊度固定进行了大量研究。范建军等[2]利用虚拟观测值的统计特性搜索确定宽巷整周模糊度;Feng[3]提出一种基于综合噪声最小的弱电离层组合三频几何模糊度解算策略;李博峰等[4]、谢建涛等[5]利用无几何和无电离层线性组合实现中长基线三频整周模糊度解算;Li等[6]提出一种长基线可控失败率的整周模糊度解算方法;刘炎炎等[7]研究了一种基于几何模型的三频逐级整周模糊度解算方法;何俊等[8]利用无几何模式和几何模式实现了单历元三频整周模糊度固定;Chen等[9]提出一种无几何、无电离层和多路径抑制联合约束的三频整周模糊度解算方法;高扬骏等[10]通过构造最优组合观测量并使用自适应抗差滤波求解窄巷模糊度。
针对BDS中长基线条件下整周模糊度受大气延迟误差影响固定率不高的问题,本文利用三频线性组合观测值所受电离层延迟误差之间的关系,提出一种BDS中长基线三频整周模糊度确定方法,在超宽巷整周模糊度易于固定的基础上,根据超宽巷与宽巷组合观测值之间所受电离层延迟误差较接近的特点解算宽巷整周模糊度,然后利用无电离层组合观测值解算窄巷整周模糊度并实现RTK定位。
1 BDS中长基线三频整周模糊度确定 1.1 双差超宽巷与宽巷整周模糊度解算为了消除双差组合后残余误差对整周模糊度的影响,本文利用BDS超宽巷整周模糊度波长较长的特性和MW组合解算B2-B3双差超宽巷整周模糊度:
| $\begin{array}{l} \Delta \nabla N_{uv, (0, - 1, 1)}^{pq} = \left( {\frac{{\Delta \nabla \mathit{\Phi }_{uv, 3}^{pq}}}{{{\lambda _3}}} - \frac{{\left. {\Delta \nabla \mathit{\Phi }_{uv, 2}^{pq}} \right)}}{{{\lambda _2}}}} \right) - \\ \;\;\;\;\;\frac{{{f_3} - {f_2}}}{{{f_3} + {f_2}}} \cdot \left( {\frac{{\Delta \nabla P_{uv, 3}^{pq}}}{{{\lambda _3}}} + \frac{{\Delta \nabla P_{uv, 2}^{pq}}}{{{\lambda _2}}}} \right) \end{array}$ | (1) |
式中,P为测码伪距,Φ为载波相位,Δ∇为双差标志,上标p和q为卫星的PRN,下标u和v为参考站接收机,下标(0,-1,1)为频率组合系数,λ为波长,f为频率,N为整周模糊度。
可以将连续观测弧段的Δ∇Nuv, (0, -1, 1)pq取平均值,削弱伪距观测值噪声的影响:
| $\Delta \nabla \bar N_{uv, (0, - 1, 1)}^{pq} = \frac{{\sum\limits_{{\rm{epoch = 1}}}^n {\Delta \nabla N_{uv, (0, - 1, 1)}^{pq, e}} }}{n}$ | (2) |
式中,下标epoch为观测历元,Δ∇Nuv, (0, -1, 1)pq为n个历元Δ∇Nuv, (0, -1, 1)pq的平均值。
BDS的B2-B3超宽巷组合和B1-B3宽巷组合双差载波相位观测方程为:
| $\begin{array}{l} \Delta \nabla \mathit{\Phi }_{uv, (0, - 1, 1)}^{pq} = \Delta \nabla \rho _{uv}^{pq} + \Delta \nabla T_{uv}^{pq} - {\mu _{(0, - 1, 1)}} \cdot \\ \frac{{\Delta \nabla \kappa }}{{f_1^2}} - {\lambda _{(0, - 1, 1)}} \cdot \Delta \nabla \mathit{N}_{uv, (0, - 1, 1)}^{pq} + \Delta \nabla {\varepsilon _{\mathit{\Phi , }(0, - 1, 1)}} \end{array}$ | (3) |
| $\begin{array}{l} \Delta \nabla \mathit{\Phi }_{uv, (0, - 1, 1)}^{pq} = \Delta \nabla \rho _{uv}^{pq} + \Delta \nabla T_{uv}^{pq} - {\mu _{(1, 0, - 1)}} \cdot \\ \frac{{\Delta \nabla \kappa }}{{f_1^2}} - {\lambda _{(1, 0, - 1)}} \cdot \Delta \nabla \mathit{N}_{uv, (1, 0, - 1)}^{pq} + \Delta \nabla {\varepsilon _{\mathit{\Phi , }(1, 0, - 1)}} \end{array}$ | (4) |
式中,ρ为卫星至接收机的几何距离,
式(3)和式(4)作差后可得B1-B3双差宽巷整周模糊度:
| $\begin{array}{l} \Delta \nabla \hat N_{uv, (1, 0, - 1)}^{pq} = \frac{{\Delta \nabla \mathit{\Phi }_{uv, (0, - 1, 1)}^{pq} - \Delta \nabla \mathit{\Phi }_{uw, (1, 0, - 1)}^{pq}}}{{{\lambda _{(1, 0, - 1)}}}} + \\ \;\;\frac{{{\lambda _{(0, - 1, 1)}}}}{{{\lambda _{(1, 0, - 1)}}}} \cdot \Delta \nabla N_{uv, (0, - 1, 1)}^{pq} + \frac{{{\mu _{(0, - 1, 1)}} - {\mu _{(1, 0, - 1)}}}}{{{\lambda _{(1, 0, - 1)}}}} \cdot \\ \;\;\;\;\;\;\;\;\frac{{\Delta \nabla \kappa }}{{f_1^2}} - \frac{{\Delta \nabla {\varepsilon _{\mathit{\Phi }, (0, - 1, 1)}} - \Delta \nabla {\varepsilon _{\mathit{\Phi }, (1, 0, - 1)}}}}{{{\lambda _{(1, 0, - 1)}}}} \approx \\ \;\;\;\;\;\;\;\frac{{\Delta \nabla \mathit{\Phi }_{uv, (0, - 1, 1)}^{pq} - \Delta \nabla \mathit{\Phi }_{uv, (1, 0, - 1)}^{pq}}}{{{\lambda _{(1, 0, - 1)}}}} + \frac{{{\lambda _{(0, - 1, 1)}}}}{{{\lambda _{(1, 0, - 1)}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta \nabla N_{wv, (0, - 1, 1)}^{pq} \end{array}$ | (5) |
式中,Δ∇Nuv, (0, -1, 1)pq表示已固定的B2-B3双差超宽巷整周模糊度;
BDS的B1-B2和B1-B3无电离层组合双差伪距和载波相位观测方程为:
| $\begin{array}{l} \Delta \nabla P_{uv, {\rm{I}}{{\rm{F}}_{12}}}^{pq} = \Delta \nabla \rho _{uv}^{pq} + \Delta \nabla T_{{\rm{dry }}, uv}^{pq} + {\rm{MF}}_u^{pq} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;{\rm{RZT}}{{\rm{D}}_{{\rm{wet }}, uv}} + \Delta \nabla {\varepsilon _{P, {\rm{I}}{{\rm{F}}_{12}}}} \end{array}$ | (6) |
| $\begin{array}{l} \;\;\;\;\;\;\;\;\Delta \nabla \mathit{\Phi }_{uv,{\rm{I}}{{\rm{F}}_{12}}}^{pq} = \Delta \nabla \rho _{uv}^{pq} + \Delta \nabla T_{{\rm{dry}},uv}^{pq} + {\rm{MF}}_u^{pq} \cdot\\ {\rm{RZT}}{{\rm{D}}_{{\rm{wet }}, uv}} - {\lambda _{(2.487\;2, - 1.487\;2, 0)}} \cdot \Delta \nabla N_{uv, 1}^{pq} - \frac{{{f_2}}}{{{f_1} + {f_2}}} \cdot \\ \;\;\;\;\;\;\;\;{\lambda _{(1, - 1, 0)}} \cdot \Delta \nabla N_{uv, (1, - 1, 0)}^{pq} + \Delta \nabla {\varepsilon _{\mathit{\Phi }, {\rm{I}}{{\rm{F}}_{12}}}} \end{array}$ | (7) |
| $\begin{array}{l} \;\;\;\;\;\;\Delta \nabla \mathit{\Phi }_{uv,{\rm{I}}{{\rm{F}}_{13}}}^{pq} = \Delta \nabla \rho _{uv}^{pq} + \Delta \nabla T_{{\rm{dry}},uv}^{pq} + {\rm{MF}}_u^{pq} \cdot\\ \left. {{\rm{RZT}}{{\rm{D}}_{{\rm{wet }}, uv}} - {\lambda _{(2, 943\;7, 0, - 1, 943\;7}}} \right) \cdot \Delta \nabla N_{uv, 1}^{pq} - \frac{{{f_3}}}{{{f_1} + {f_3}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{(1, 0, - 1)}} \cdot \Delta \nabla N_{uv, (1, 0, - 1)}^{pq} + \Delta \nabla {\varepsilon _{\mathit{\Phi }, I{{\rm{F}}_{13}}}} \end{array}$ | (8) |
式中,下标IF12和IF13分别为B1-B2和B1-B3无电离层组合,Δ∇Tdry, uvpq为对流层的干分量延迟误差,MFupq为测站u上卫星p、q的星间投影函数之差,RZTDwet, uv为测站u、v间的相对天顶对流层的湿分量延迟误差。
假定历元i测站u、v同步观测到s+1颗卫星,由式(6)、式(7)和式(8)可得B1-B2和B1-B3无电离层组合双差伪距和载波相位观测方程:
| $\mathit{\boldsymbol{L}}\left( i \right) = \mathit{\boldsymbol{A}}\left( i \right)\mathit{\boldsymbol{B}}\left( i \right)$ | (9) |
其中,
| $ \mathit{\boldsymbol{A}}(i) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}(i)}&{{\bf{MF}}(i)}&{{{\bf{0}}_s}}&{}\\ {\mathit{\boldsymbol{C}}(i)}&{{\bf{MF}}(i)}&{{\lambda _{(2.487\;2, - 1.487\;2, 0)}} \cdot {\mathit{\boldsymbol{I}}_s}}&{}\\ {\mathit{\boldsymbol{C}}(i)}&{{\bf{MF}}(i)}&{{\lambda _{(2, 943\;7, 0, - 1, 943\;7)}} \cdot {\mathit{\boldsymbol{I}}_s}}&{} \end{array}} \right] $ |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{B}}(i) = }\\ {{{\left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{X}}&{{\rm{RZT}}{{\rm{D}}_{{\rm{wet }}, uw}}}&{\Delta \nabla N_{uv, 1}^1}&{\Delta \nabla N_{uv, 1}^2}& \cdots &{\Delta \nabla N_{uv, 1}^s} \end{array}} \right)}^{\rm{T}}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = {{\left( {\begin{array}{*{20}{l}} x&y&z \end{array}} \right)}^{\rm{T}}}}\\ {\mathit{\boldsymbol{L}}(i) = {{\left( {\begin{array}{*{20}{l}} {l_1^1}& \cdots &{l_1^s}&{l_2^1}& \cdots &{l_2^s}&{l_3^1}& \cdots &{l_3^s} \end{array}} \right)}^{\rm{T}}}} \end{array} $ |
| $ {\bf{MF}}(i) = {\left( {\begin{array}{*{20}{l}} {{\rm{MF}}_u^1}&{{\rm{MF}}_u^2}& \cdots &{{\rm{MF}}_u^s} \end{array}} \right)^{\rm{T}}} $ |
| $ \begin{array}{l} \;\;l_1^s = \Delta \nabla P_{uw, {\rm{I}}{{\rm{F}}_{12}}}^s - \Delta \nabla \rho _{uv}^s - \Delta \nabla T_{{\rm{dry}}, uv}^{pq}\\ l_2^s = \Delta \nabla \mathit{\Phi }_{uv, {\rm{I}}{{\rm{F}}_{12}}}^s - \Delta \nabla \rho _{uv}^s - \Delta \nabla T_{{\rm{dry}}, uv}^s + \\ \;\;\;\;\;\frac{{{f_2}}}{{{f_1} + {f_2}}} \cdot {\lambda _{(1, - 1, 0)}} \cdot \Delta \nabla N_{uv, (1, - 1, 0)}^s\\ l_3^s = \Delta \nabla \mathit{\Phi }_{uv, {\rm{I}}{{\rm{F}}_{13}}}^s - \Delta \nabla \rho _{uv}^s - \Delta \nabla T_{{\rm{dry}}, uv}^s + \\ \;\;\;\;\;\;\frac{{{f_3}}}{{{f_1} + {f_3}}} \cdot {\lambda _{(1, 0, - 1)}} \cdot \Delta \nabla N_{uv, (1, 0, - 1)}^s \end{array} $ |
式中,上标为省略基准的卫星编号,Is和0s分别为s维单位矩阵和s维零矩阵,A(i) 为观测方程的系数矩阵,B(i) 为观测方程的待估系数向量,L(i) 为观测方程的常数项向量,C(i) 为方向余弦系数矩阵,MF(i) 为双差卫星的星间投影函数之差向量,X为待估的位置参数。根据最小二乘参数估计方法,可估计位置参数、相对天顶对流层的湿分量延迟误差及双差窄巷整周模糊度,利用LAMBDA算法搜索并确定双差窄巷整周模糊度。
2 算例与分析利用河北省采集的2条BDS实测中长基线进行算法检验。观测时间为2017-10-14,观测时长约为2 h,观测数据的采样间隔为1 s,卫星截止高度角设置为15°。基线数据具体信息如表 1所示。
|
|
表 1 基线数据信息 Tab. 1 Data information of baseline |
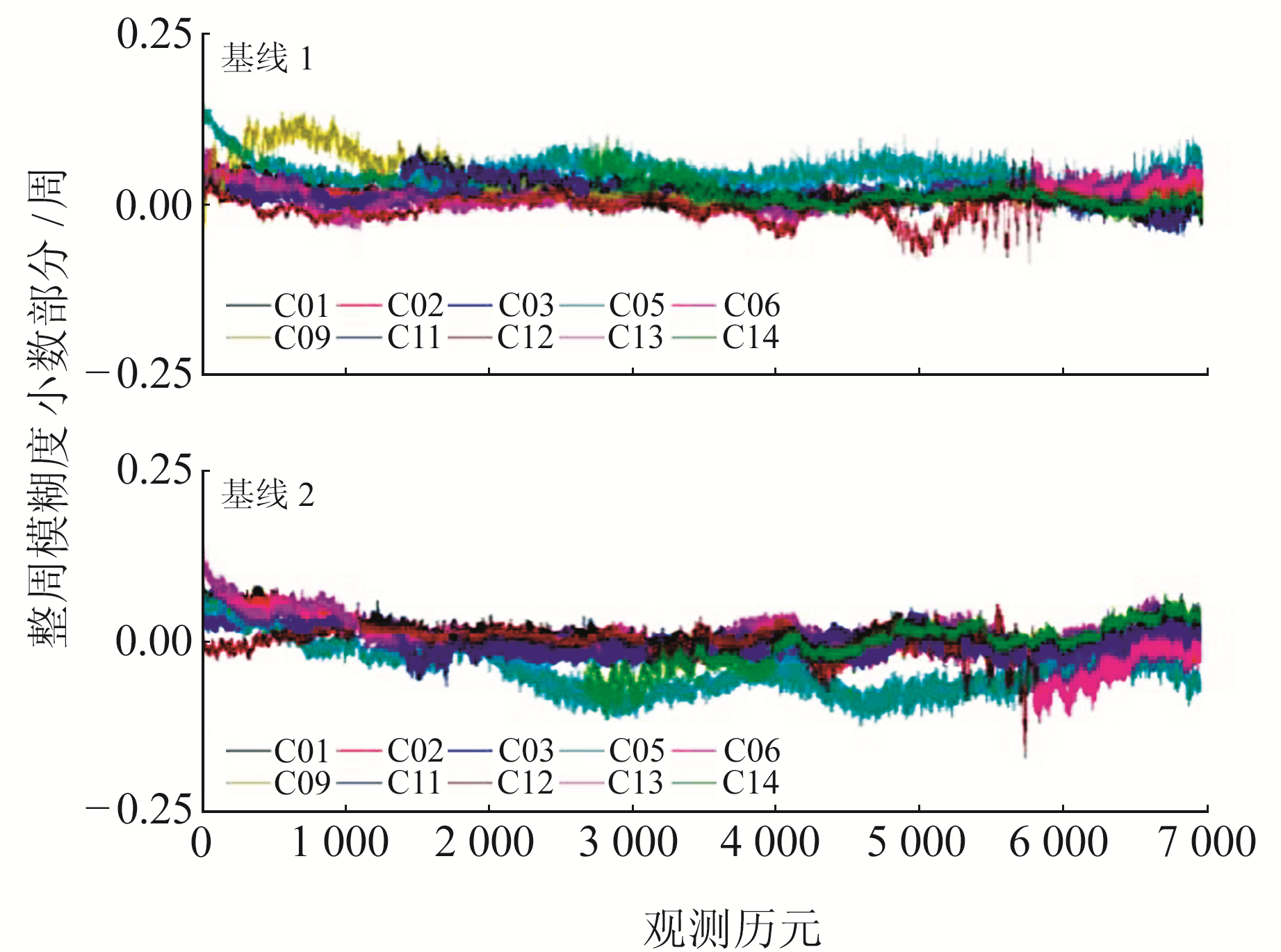
图 1为观测时段内卫星对应的B2-B3双差超宽巷整周模糊度小数部分,可以看出,2条基线中B2-B3双差超宽巷整周模糊度小数部分均在0.25周以内。由于B2-B3双差超宽巷整周模糊度对应的波长较长,约为4.9 m,取平均值可以削弱噪声、快速准确地得到正确的双差整周模糊度。
|
图 1 B2-B3双差超宽巷整周模糊度小数部分 Fig. 1 Fractional part of double differenced extra-wide-lane integer ambiguity for B2-B3 |
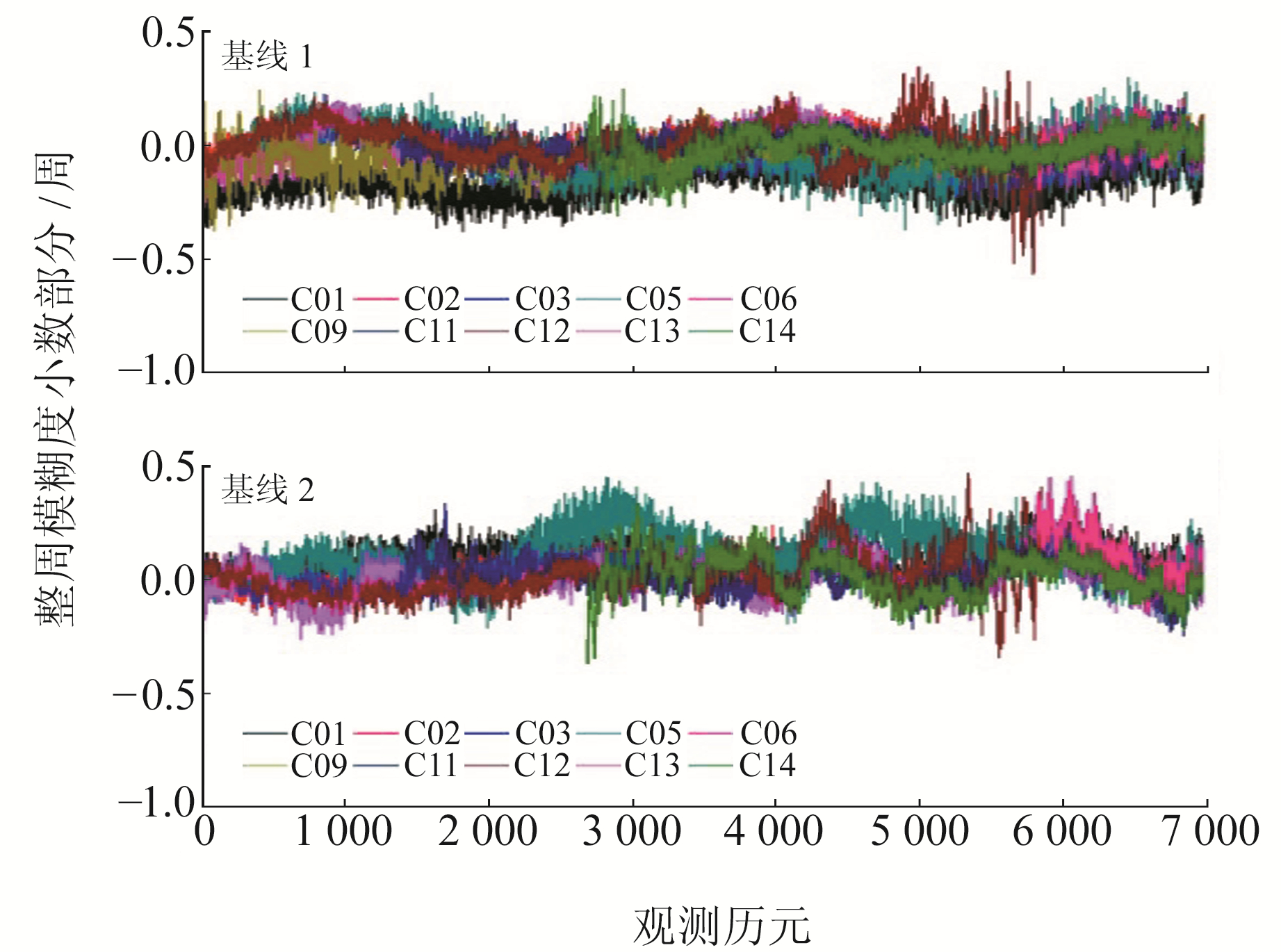
B2-B3双差超宽巷整周模糊度准确固定后,利用B2-B3超宽巷组合观测值和B1-B3宽巷组合观测值所受电离层延迟误差较接近的特点解算B1-B3宽巷整周模糊度。图 2为观测时段内卫星对应的B1-B3双差宽巷整周模糊度小数部分,可以看出,基线1和基线2的B1-B3双差宽巷整周模糊度小数部分绝大多数在0.5周以内。取平均值可以削弱残余电离层延迟误差对整周模糊度的影响,从而较为准确地固定B1-B3双差宽巷整周模糊度。
|
图 2 B1-B3双差宽巷整周模糊度小数部分 Fig. 2 Fractional part of double differenced wide-lane integer ambiguity for B1-B3 |
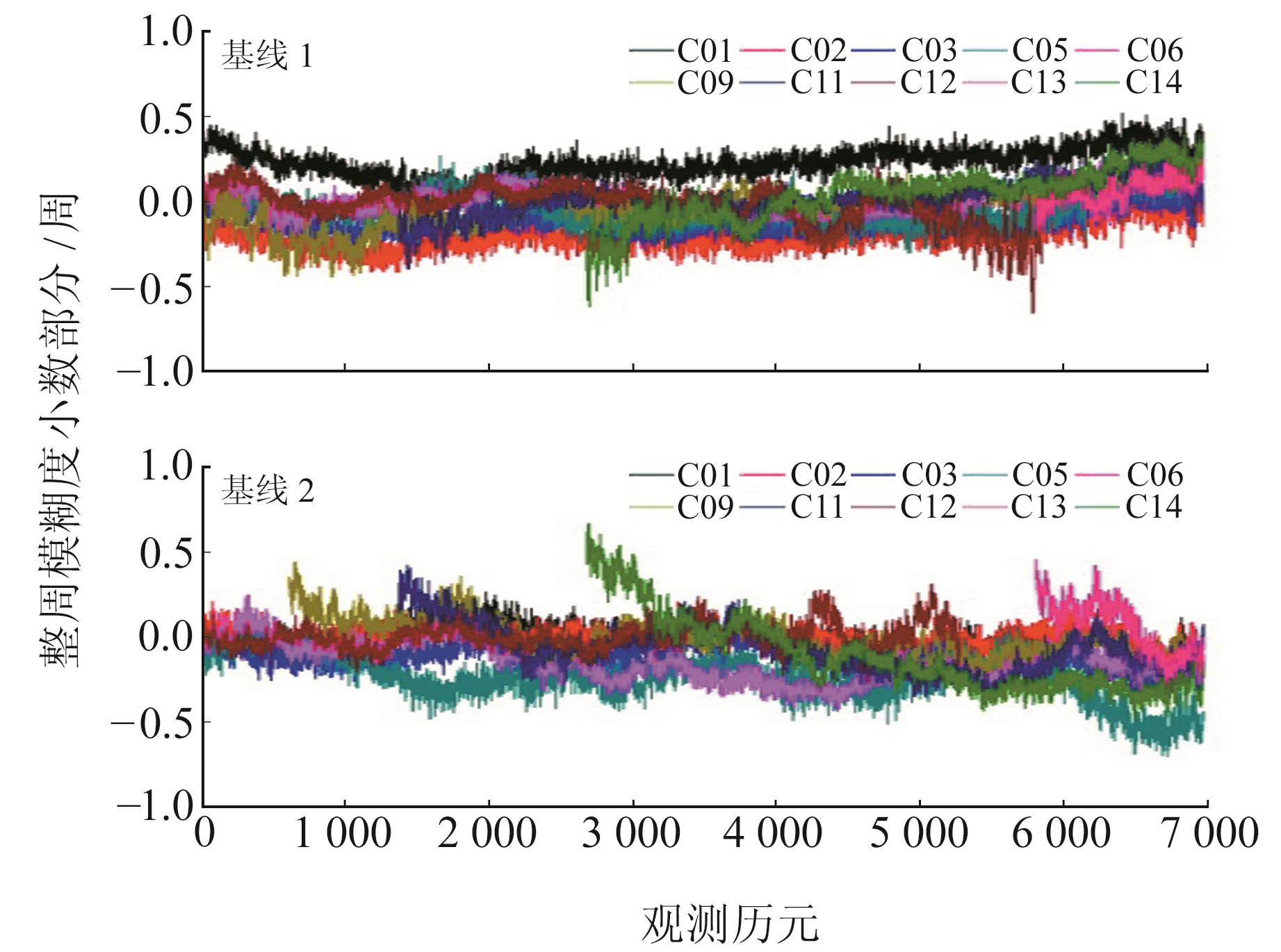
利用B1-B3和B1-B2无电离层组合观测值及对应的整周模糊度可分解的特点解算双差窄巷整周模糊度。图 3为观测时段内卫星对应的双差窄巷整周模糊度小数部分。由于无电离层组合消除了电离层延迟误差对整周模糊度的影响,图 3中基线1和基线2的双差窄巷整周模糊度小数部分绝大多数控制在0.5周以内,根据LAMBDA算法可以准确固定双差窄巷整周模糊度。
|
图 3 双差窄巷整周模糊度小数部分 Fig. 3 Fractional part of double differenced narrow-lane integer ambiguity |
表 2为观测时段内卫星对应的B2-B3双差超宽巷整周模糊度(EWL)、B1-B3双差宽巷整周模糊度(WL)和双差窄巷整周模糊度(NL)的固定率。从表 2可以看出,由于B2-B3双差超宽巷整周模糊度对应的波长较长,2条基线的B2-B3双差超宽巷整周模糊度固定率均为100%;利用已固定的B2-B3双差超宽巷整周模糊度辅助解算B1-B3双差宽巷整周模糊度的固定率超过99%;在双差超宽巷与宽巷整周模糊度固定的情况下,双差窄巷整周模糊度的固定率也较高,超过97%。
|
|
表 2 整周模糊度固定率 Tab. 2 Fixed rate of ambiguity |
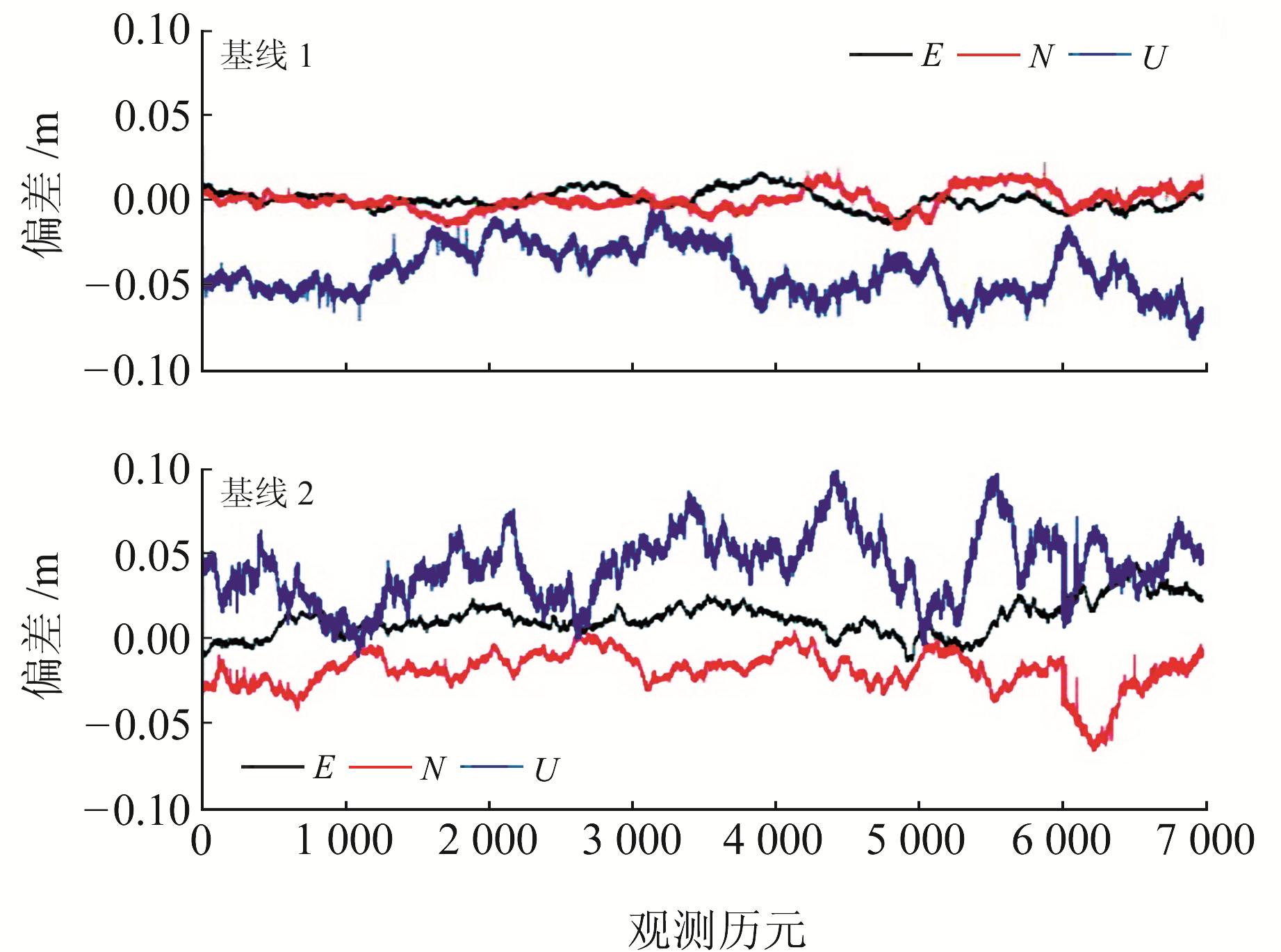
图 4为RTK定位结果与准确值之差在东(E)、北(N)、天(U)3个方向的时间序列。可以看出,流动站在E、N、U三个方向的定位精度为cm级,基线1在E方向和N方向的偏差不超过2 cm,在U方向的偏差不超过8 cm。由于第二条基线较长,基线2在E方向和N方向的偏差绝大多数在5 cm以内,在U方向的偏差不超过10 cm。
|
图 4 RTK定位误差 Fig. 4 RTK positioning error |
表 3为2条基线在E、N、U三个方向的偏差均方根(RMS)。由表 3可知,2条基线在E方向的RMS最小,其次为N方向,U方向的RMS最大,RTK在3个方向的定位精度均为cm级。RTK在E、N、U三个方向的定位结果与准确值之差的时间序列和统计信息进一步验证了双差整周模糊度的准确性和可靠性。
|
|
表 3 定位结果的RMS Tab. 3 RMS of positioning results |
提出一种BDS中长基线三频整周模糊度确定方法。首先利用超宽巷整周模糊度波长较长的特点确定B2-B3超宽巷整周模糊度,再根据超宽巷与宽巷组合观测值所受电离层延迟误差较接近的特点固定B1-B3宽巷整周模糊度,最后利用无电离层组合观测值搜索确定窄巷整周模糊度并实现高精度定位。实验表明,中长基线下双差超宽巷与宽巷整周模糊度具有较高的固定正确率,窄巷整周模糊度固定正确率超过97%,该方法可正确有效地固定中长基线三频载波相位整周模糊度,同时获得cm级的定位精度。
| [1] |
高星伟, 过静珺, 程鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743-748 (Gao Xingwei, Guo Jingjun, Cheng Pengfei, et al. Fusion Positioning of Beidou/GPS Based on Spatio Temporal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 743-748)
(  0) 0) |
| [2] |
范建军, 王飞雪. 一种短基线GNSS的三频模糊度解算(TCAR)方法[J]. 测绘学报, 2007, 36(1): 43-49 (Fan Jianjun, Wang Feixue. A Method for GNSS Three Frequency Ambiguity Resolution Based on Short Baselines[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 43-49)
(  0) 0) |
| [3] |
Feng Y M. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-Reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862 DOI:10.1007/s00190-008-0209-x
(  0) 0) |
| [4] |
李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 296-301 (Li Bofeng, Shen Yunzhong, Zhou Zebo. A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 296-301 DOI:10.3321/j.issn:1001-1595.2009.04.003)
(  0) 0) |
| [5] |
谢建涛, 郝金明, 刘伟平, 等. 中长基线的BDS三频线性组合观测量优化[J]. 武汉大学学报: 信息科学版, 2017, 42(12): 1 779-1 784 (Xie Jiantao, Hao Jinming, Liu Weiping, et al. BDS Triple Frequency Linear Combination Observation Optimization for Medium-Long Baseline[J]. Geomatics and Information Science of Wuhan University, 2017, 42(12): 1 779-1 784)
(  0) 0) |
| [6] |
Li B F, Shen Y Z, Feng Y M, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy, 2014, 88(2): 99-112 DOI:10.1007/s00190-013-0670-z
(  0) 0) |
| [7] |
刘炎炎, 叶世榕, 江鹏, 等. 基于北斗三频的短基线单历元模糊度固定[J]. 武汉大学学报: 信息科学版, 2015, 40(2): 209-213 (Liu Yanyan, Ye Shirong, Jiang Peng, et al. Instantaneous Ambiguity Resolution of Short Baselines Using Beidou Triple Frequency Observations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 209-213)
(  0) 0) |
| [8] |
何俊, 刘万科, 张小红. 北斗短基线三频实测数据单历元模糊度固定[J]. 武汉大学学报: 信息科学版, 2015, 40(3): 361-365 (He Jun, Liu Wanke, Zhang Xiaohong. Single Epoch Ambiguity Resolution of BDS Triple Frequency Measured Data under Short Baseline[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 361-365)
(  0) 0) |
| [9] |
Chen D Z, Ye S R, Xia J C, et al. A Geometry-Free and Ionosphere-Free Multipath Mitigation Method for BDS Three-Frequency Ambiguity Resolution[J]. Journal of Geodesy, 2016, 90(8): 703-714 DOI:10.1007/s00190-016-0903-z
(  0) 0) |
| [10] |
高扬骏, 吕志伟, 周朋进, 等. 北斗中长基线三频模糊度解算的自适应抗差滤波算法[J]. 测绘学报, 2019, 48(3): 295-302 (Gao Yangjun, Lü Zhiwei, Zhou Pengjin, et al. Adaptive Robust Filtering Algorithm for BDS Medium and Long Baseline Three Carrier Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(3): 295-302)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

