随着高层、超高层建筑及造型复杂的桥梁等大型结构的不断涌现,结构物的安全性被提升到重要层面。GNSS技术与传统监测方法相比具有许多独特的优势,其全天候、低频敏感的特性可准确地获得结构在环境荷载作用下的准静态响应和动态位移,对于长周期监测具有可靠性[1],但受精度和采样率的限制,其对高频振动信息不敏感。加速度计具有高精度、不受环境干扰等优点,采样频率高达1 000 Hz[2],能够弥补GNSS监测技术的不足,实现高频、高精度的结构振动监测[3]。
本文基于EMD,结合GNSS与加速度计,提出一种动态位移重构算法,并通过模拟数据进行频谱分析,验证该算法的可行性。
1 EMD经验模态分解(empirical mode decomposition,EMD)是一种适用于非线性、非平稳信号分析的自适应信号时频处理方法[4]。与傅里叶、小波分解等传统时域和频域分析方法相比具有自适应性、局部特性等优势。该方法根据数据本身的时间尺度特征对原始信号进行多次筛选,得到有限个频率由高到低排序的特征模态函数(intrinsic mode function,IMF)。
经验模态分解的主要步骤为:
1) 找到信号x(t)的极大值和极小值,通过三次样条拟合得到上、下包络线,计算其均值得m1(t)。
2) 得到第1个分量h1(t)=x(t)-m1(t),检查其是否满足模态分量的条件:
① h1(t)的极大值点和过零点数目最多相差1个;
② h1(t)的上、下包络线平均值为0。若不满足,则重复步骤1)和步骤2),直至得到满足模态函数(IMF)条件的模态分量c1(t)。
3) 原始信号减去第1个模态分量,得到信号r1(t),将r1(t)作为新的原始信号,重复以上操作,直至筛选条件小于预设值,经验模态分解结束。
| $ {\rm{SD = }}\frac{{\sum\limits_{t = 0}^T {{{\left| {{h_{k - 1}}\left( t \right) - {h_k}\left( t \right)} \right|}^2}} }}{{\sum\limits_{t = 0}^T {h_{k - 1}^2\left( t \right)} }} $ | (1) |
最终原始信号分成若干个经验模态分量和1个残余信号:
| $ x\left( t \right) = \sum\limits_{i = 0}^n {{c_i} + {r_n}\left( t \right)} $ | (2) |
GNSS在进行高精度变形测量时,能够监测到结构的绝对变形,但受多路径误差、残余大气延迟误差等非建模系统误差的影响,动态测量精度难以保证。GNSS动态位移可表示为[5]:
| $ y\left( n \right) = M\left( n \right) + D\left( n \right) + N\left( n \right) $ | (3) |
式中,M(n)为观测中的多路径误差、电离层误差等低频噪声,D(n)为结构的真实动态响应,N(n)为随机噪声。
2.1.2 GNSS低频动态位移提取GNSS信号中主要包括结构实际振动信息、多路径误差和随机噪声3个部分,其中多路径噪声呈低频特性,主要分布在0~0.2 Hz频段。切比雪夫滤波是在通带或阻带上频率响应幅度等波纹波动的滤波器,能够用于削弱GNSS数据的多路径误差[6]。本文将其截止频率设置为0.4 Hz,适用于0.4~5 Hz范围内的各种动态运动,包括地震事件下大多数工程结构的振动[7]。
利用EMD与切比雪夫滤波相结合处理GNSS信号的流程如图 1所示,可分为2个重要步骤:

|
图 1 混合滤波器处理流程 Fig. 1 Hybrid filter processing flow |
1) 利用切比雪夫高通滤波器来削弱GNSS信号中的多路径误差,根据实验设定的具体振动频率、幅值设计滤波器参数。
2) 对去除多路径误差的信号进行EMD,得到n个特征模态函数(IMF)和1个残余分量,对每个分量与加速度积分位移进行相关性分析,判断其是否为高频位移分量;重构相关系数较大的IMF分量,得到结构高频动态位移,剩余的分量用于提取结构低频动态位移。
2.2 加速度动态位移重构加速度计采样频率高,能够获取高频信息,得到结构的振动响应。通过对去噪后的加速度数据进行二次积分可获取动态位移,但由于初始速度与位移未知,会造成结果漂移,且位移结果不包括静态与准静态位移。本文利用加速度计获取高频动态位移,利用GNSS提取低频动态位移和准静态位移,然后将两者结合重构整体位移。
2.2.1 加速度计重构位移首先使用带通滤波器去除加速度数据中的噪声,然后应用双积分方程计算位移:
| $ s\left( t \right) = {s_0} + {\upsilon _0} \times t + \int {_0^t\left( {\int {_0^ta\left( t \right){\rm{d}}t} } \right)}{\rm{d}}t $ | (4) |
式中,s(t)为时间t的位移,a(t)为时间t的加速度,s0为初始位置,υ0为初始速度。初始位置s0和初始速度υ0不能使用加速计进行测量,只能通过单独的方法进行计算,可利用加速度计获得动态位移,然后将某个值作为初始位置来计算相对位移,并根据GNSS测量的静态或准静态位移进行调整[8]。
2.2.2 加速度计重构位移模拟实验通过模拟实验得到5组不同振动频率下的加速度积分位移与真值的比较,具体如图 2所示,其中频率分别为0.5 Hz、1 Hz、1.5 Hz、2 Hz与2.5 Hz,幅值为10 mm。可以看出,5组模拟实验加速度积分所得振幅整体上与真实值较为一致,频率较低时前3组的积分结果较后2组更为准确。该结果表明,加速度计积分算法在不同振动频率下均能保持较高的可靠性。

|
图 2 不同频率下频域积分结果与真值比较 Fig. 2 Comparison of frequency domain integration results and true values at different frequencies |
整体动态位移的重构流程[9]如图 3所示,具体为:1)加速度数据经过EMD重构,去除高频噪声;2)经过去噪处理后的加速度数据通过带通滤波处理,得到特定频率范围内的序列,频域二次积分后去除线性趋势,得到高频动态位移;3)采用上述混合滤波器提取GNSS高频动态位移后,对剩余低频分量提取低频动态位移,然后进行插值与加速度积分重构的高频动态位移信号采样率保持一致;4)加速度重构的高频动态位移和GNSS提取的低频动态位移结合,重构结构整体变形。采用快速傅里叶变换(fast Fourier transformation,FFT)[10]峰值拾取法对结构进行振动分析,提取频率得到结构的动力响应。
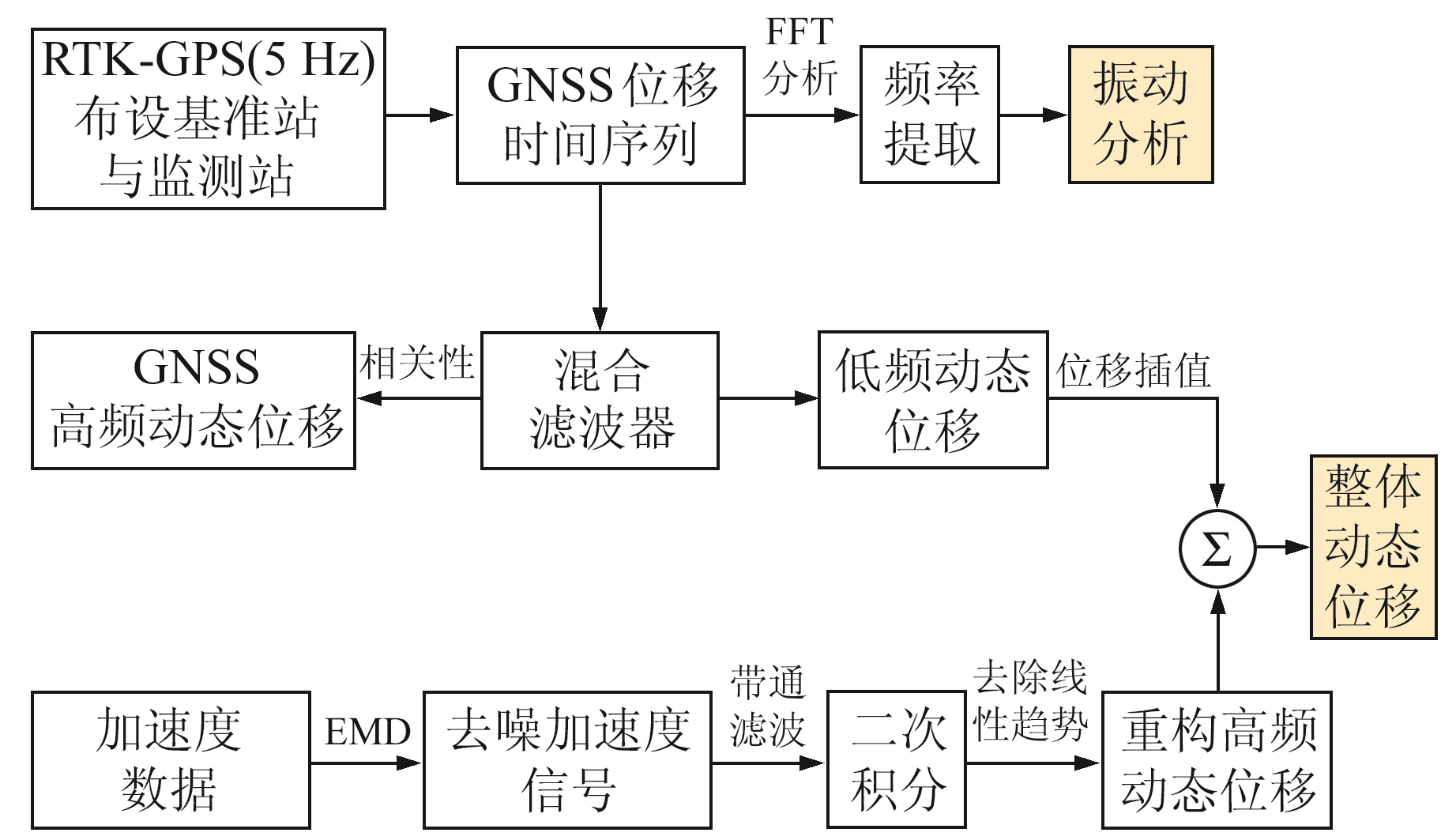
|
图 3 整体动态位移重构流程 Fig. 3 Flow chart of overall dynamic displacements reconstruction |
利用振动模拟仿真平台设计一系列实验,通过控制终端设置不同振动频率及幅值,振动台能够沿着平面X、Y轴方向运动以模拟变形,如图 4所示。采用GNSS RTK模式部署基站与监测站,考虑到随着基线长度的增加,RTK定位误差会增大,将基站设立在北京建筑大学测绘学院楼顶,监测站布设于学校南门口,将GNSS天线放置于振动台上。利用采样频率为5 Hz的GNSS接收机和采样频率为100 Hz的惯导加速度计模块收集平台振动响应,振动平台X轴指向正北方向,同时保持惯导与系统方向一致且时间同步,便于2种传感器进行数据融合。

|
图 4 振动仿真模拟平台 Fig. 4 Vibration simulation platform |
采用自主研发的GNSS高精度变形监测系统,该系统能够实现监测数据的实时传输、解算与展示,主要由5个部分组成,包括GNSS天线、GNSS接收机终端、4G网络传输系统、云端服务器和供电系统,如图 5所示。采样频率为5 Hz的GNSS高精度变形监测终端接收经过天线放大处理的卫星信号,将卫星信号通过4G网络传输至云端服务器。服务器对卫星原始数据进行在线解算,通过在线数据处理平台实时显示变形序列,了解卫星状况与解算状态,便于相关人员及时发现异常情况,并采取必要措施,实现mm级实时位移形变监测与预警。供电系统为整个变形监测系统提供电源。
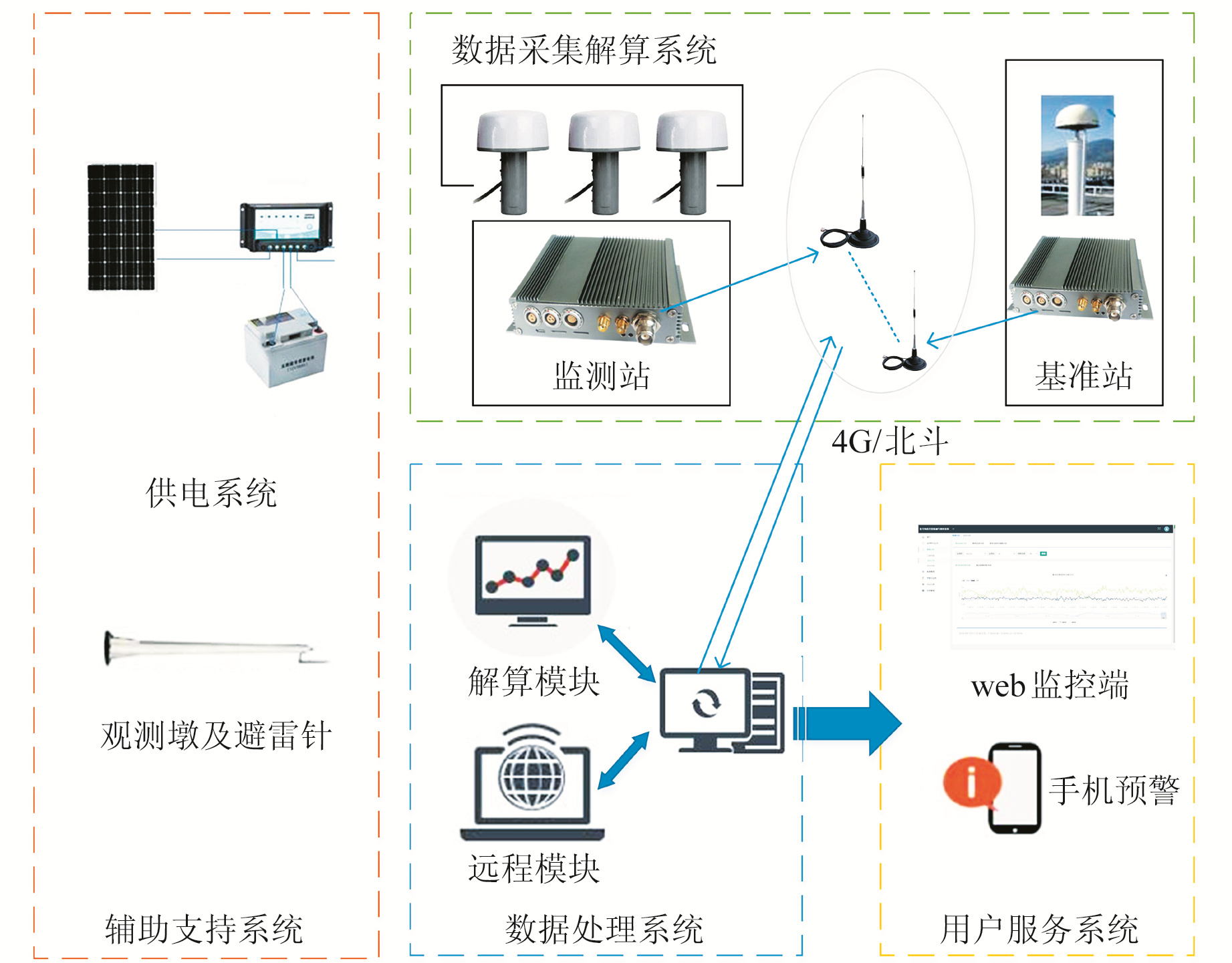
|
图 5 GNSS高精度变形监测系统 Fig. 5 GNSS high precision deformation monitoring system |
进行14组模拟实验,具体数据如表 1所示。对于振动频率较低的GNSS信号,利用FFT分析可较为准确地识别,但随着频率设置越来越高,GNSS信号用于频谱分析出现弊端。从X、Y轴加速度原始数据(图 6)可明显看出,系统准确探测出了瞬时增大的加速度及时刻,与实验人工记录的信息相符。
|
|
表 1 不同频率、振幅振动台模拟实验 Tab. 1 Vibration platform simulation experiment with different frequencies and amplitudes |
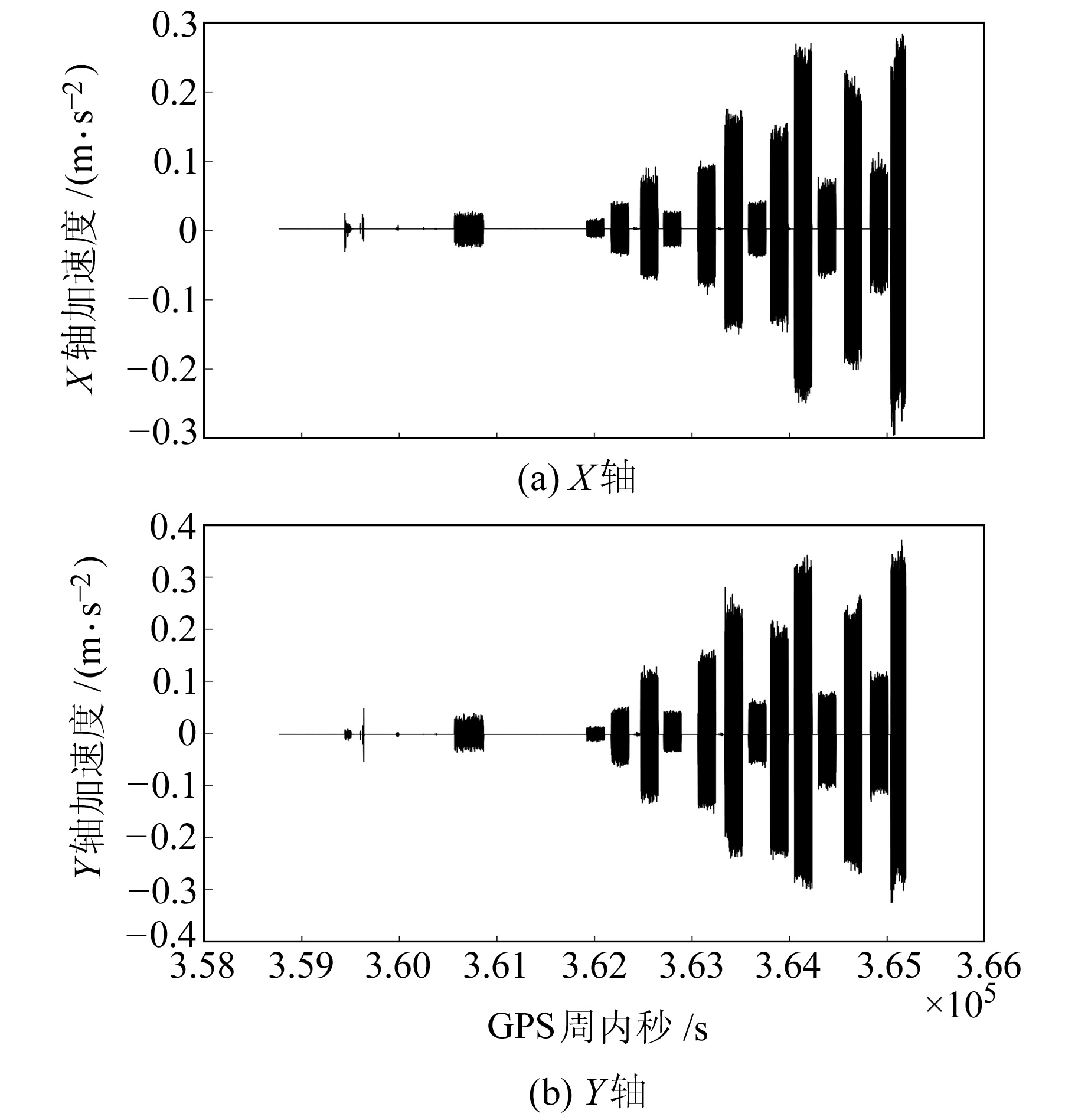
|
图 6 加速度时间序列原始数据 Fig. 6 Original acceleration time series data |
当模拟实验振动参数设置为0.2 Hz、50 mm时,从GNSS频率谱中得到振动频率为0.234 4 Hz,但受多路径噪声影响,在0值附近仍然有较大幅值(图 7(a))。加速度计采样频率较高,受高频噪声影响,频谱分析较为杂乱,出现多组主要幅值且呈现高频特性(图 7(b))。

|
图 7 北向GNSS、加速度原始序列与频谱分析 Fig. 7 North direction of GNSS, acceleration original sequence and spectrum analysis |
当振动参数设置频率为1.5 Hz、振幅为50 mm时,GNSS时间序列经过FFT分析后得到的频谱如图 8(a)所示。可以看到,在1.5 Hz附近幅值较大,但并没有主要幅值,而将加速度数据频谱局部放大(图 8(b))后可以清晰地看到,在1.5 Hz处存在主要幅值,说明加速度计可识别较高振动频率,但需要对数据进行滤波处理。

|
图 8 振动频率1.5 Hz的GNSS、加速度计频谱分析 Fig. 8 Spectrum analysis of GNSS and accelerometer with vibration frequency of 1.5 Hz |
总体而言,通过14组振动模拟实验发现:
1) GNSS可以较为准确地识别1 Hz及以下的振动频率,此时存在主要幅值,而难以识别1.5 Hz及以上的频率;2)加速度计可识别高频振动,对于2.5 Hz频率也可准确识别,但是由于采样频率较高,噪声影响较大,需要对数据进行滤波处理;3)实验过程中受环境影响,存在GNSS接收信号问题,此时加速度计可以有效弥补数据缺失问题,有利于进一步开展研究。
3.2.2 位移重构及频谱分析以振动频率1.5 Hz、振幅50 mm为例对本文位移重构算法进行验证。加速度数据利用1~1.6 Hz带通滤波处理,然后进行二次积分;去除线性趋势后,将最终得到的积分位移结果与GNSS原始位移序列进行对比,如图 9所示。可以看出,两者基本吻合,但GNSS监测数据受到随机噪声的影响,数值上比加速度计积分位移稍大。
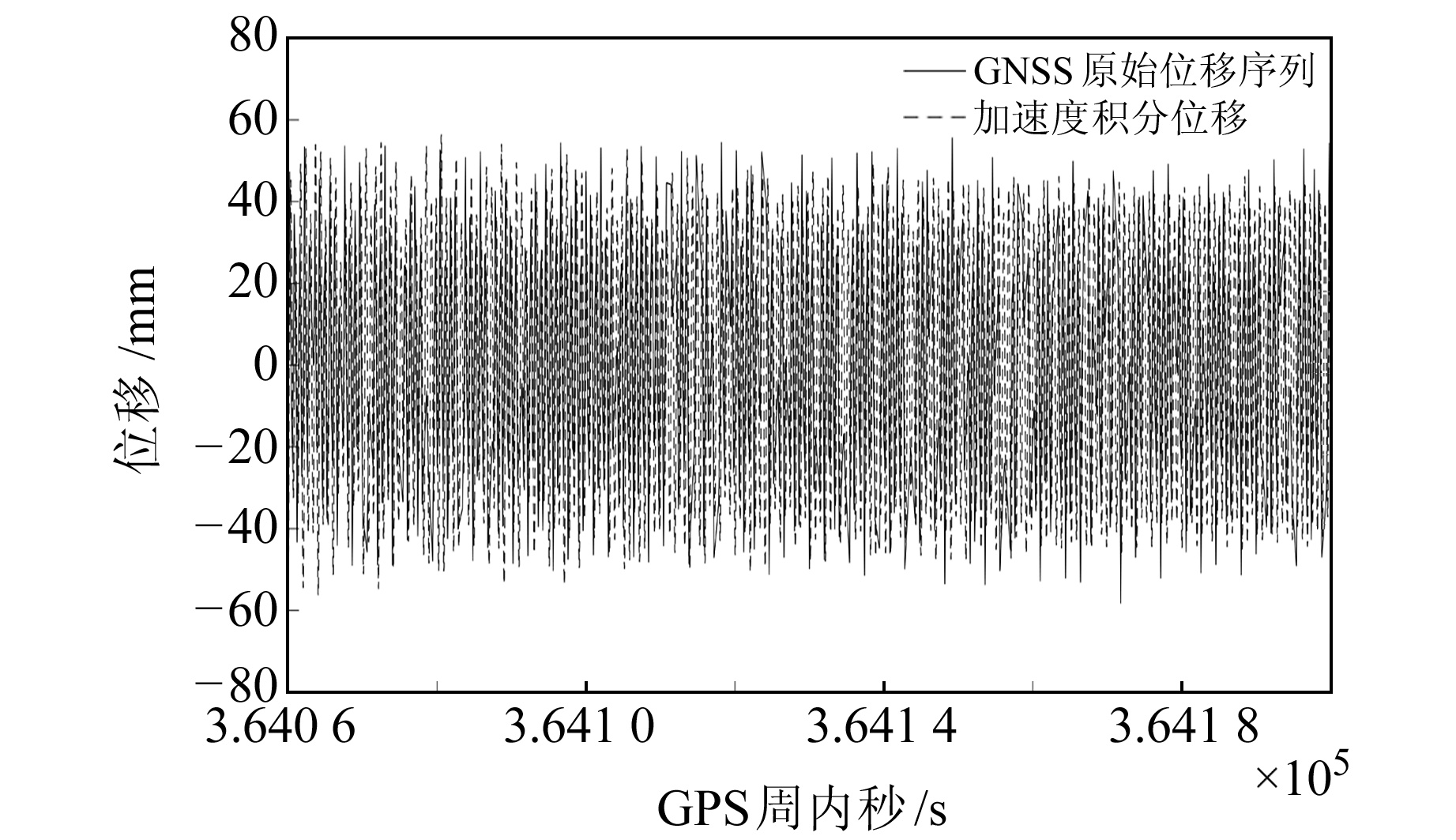
|
图 9 加速度积分位移与GNSS原始位移对比 Fig. 9 Comparison of acceleration integral displacements nd GNSS original displacements |
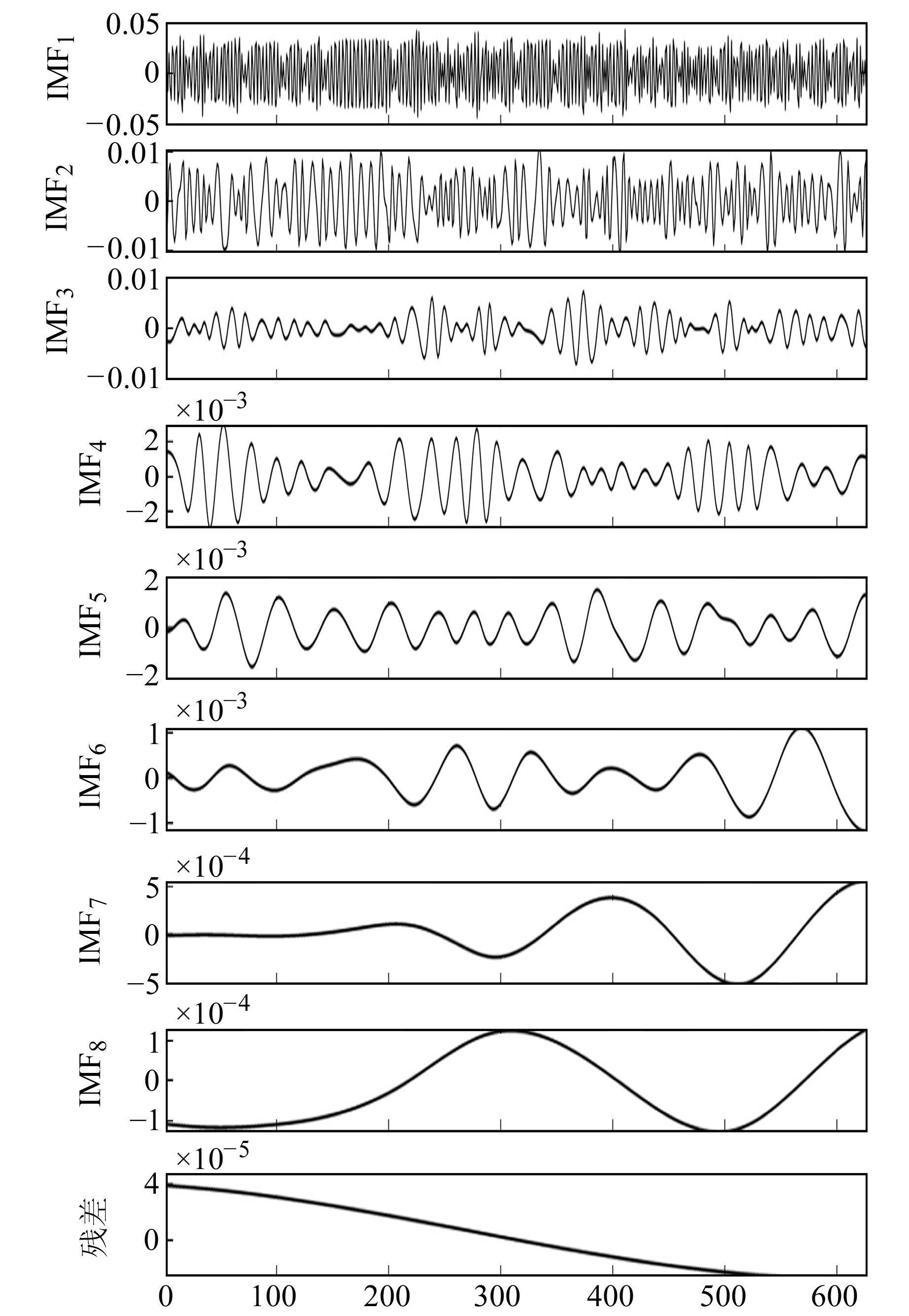
利用一阶切比雪夫高通滤波处理后的GNSS序列如图 10所示,滤波后的GNSS位移序列经多尺度分解后得到8个IMF分量与1个趋势项。从图 11中可以看出,高频振动信息主要分布在IMF1中,与加速度积分的高频动态位移相关性较高,从IMF2开始相关系数基本为0。低频动态位移主要分布在后7项IMF,重构得到低频动态位移,如图 12所示。

|
图 10 滤波前后GNSS原始北向位移时间序列 Fig. 10 Time series of north direction of GNSS original displacements before and after filtering |
|
图 11 滤波后GNSS位移序列EMD分解 Fig. 11 EMD decomposition of GNSS displacement sequences after filtering |

|
图 12 GNSS提取的低频位移 Fig. 12 Low frequency displacements extracted by GNSS |
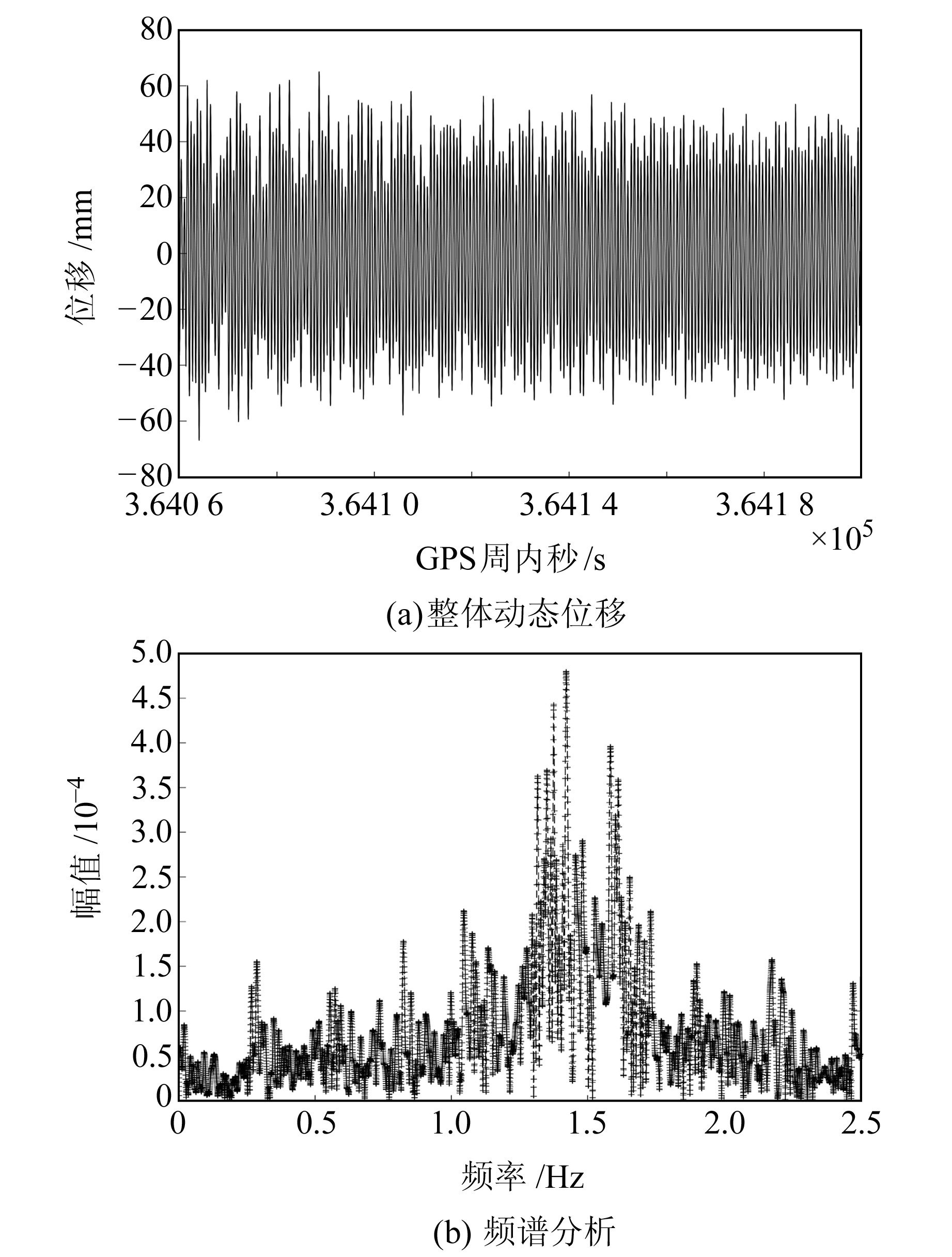
整体动态位移重构结果如图 13(a)所示。可以看出,实际位移相比设置振幅较大,但整体范围相符。从FFT频谱分析(图 13(b))可以看出,利用本文位移重构算法得到的结构整体动态位移中既包含高频振动频率,也有低频信息,其中低频信息是由周围环境造成的,可用于研究环境荷载对振动的影响规律。
|
图 13 整体动态位移及频谱分析 Fig. 13 Overall dynamic displacements and spectrum analysis |
综上,GNSS接收信号受环境影响出现问题时,加速度计可有效弥补数据的缺失,并对结构振动进行分析,两者结合可用于监测结构动态变形,且能够同时识别低频及高频振动信息。
4 结语为识别结构的真实动态响应,本文采用GNSS与加速度计相结合的方式,提出一种基于EMD与切比雪夫滤波相结合的混合型滤波器,并对GNSS采集到的数据进行滤波处理,得到结构的低频动态位移,利用位移重构算法得到结构整体动态位移,能够同时识别低频及高频振动信息。另外,本文通过设计一系列振动台模拟实验,验证了混合滤波与位移重构算法的可行性,认为GNSS/加速度计监测技术在结构振动位移监测方面具有一定的适用性。
| [1] |
Casciati F, Fuggini C. Engineering Vibration Monitoring by GPS: Long Duration Records[J]. Earthquake Engineering and Engineering Vibration, 2009, 8(3): 459-467 DOI:10.1007/s11803-009-9058-8
(  0) 0) |
| [2] |
Roberts G W, Meng X L, Dodson A H. Integrating a Global Positioning System and Accelerometers to Monitor the Deflection of Bridges[J]. Journal of Surveying Engineering, 2004, 130(2): 65-72 DOI:10.1061/(ASCE)0733-9453(2004)130:2(65)
(  0) 0) |
| [3] |
于先文, 薛红琳. 基于GPS/加速度计组合的桥梁振动监测方法[J]. 东南大学学报: 自然科学版, 2013, 43(增2): 329-333 (Yu Xianwen, Xue Honglin. Method of Bridge Vibration Monitoring Based on GPS and Accelerometer[J]. Journal of Southeast University: Natural Science Edition, 2013, 43(S2): 329-333)
(  0) 0) |
| [4] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [5] |
Wang J, Meng X L, Qin C B, et al. Vibration Frequencies Extraction of the Forth Road Bridge Using High Sampling GPS Data[EB/OL]. https://core.ac.uk/download/pdf/42494439.pdf, 2016
(  0) 0) |
| [6] |
熊春宝, 路华丽, 朱劲松, 等. 基于GPS-RTK和加速度计的桥梁动态变形监测试验[J]. 振动与冲击, 2019, 38(12): 69-73 (Xiong Chunbao, Lu Huali, Zhu Jinsong, et al. Dynamic Deformation Monitoring of Bridge Structures Based on GPS-RTK and Accelerometers[J]. Journal of Vibration and Shock, 2019, 38(12): 69-73)
(  0) 0) |
| [7] |
Vazquez B G E, Gaxiola-Camacho J R, Bennett R, et al. Structural Evaluation of Dynamic and Semi-Static Displacements of the Juarez Bridge Using GPS Technology[J]. Measurement, 2017, 110: 146-153 DOI:10.1016/j.measurement.2017.06.026
(  0) 0) |
| [8] |
Yu J Y, Meng X L, Shao X D, et al. Identification of Dynamic Displacements and Modal Frequencies of a Medium-Span Suspension Bridge Using Multimode GNSS Processing[J]. Engineering Structures, 2014, 81: 432-443 DOI:10.1016/j.engstruct.2014.10.010
(  0) 0) |
| [9] |
韩厚增, 王坚, 孟晓林. GPS与加速度计融合桥梁变形信息提取模型研究[J]. 中国矿业大学学报, 2015, 44(3): 549-556 (Han Houzeng, Wang Jian, Meng Xiaolin. Reconstruction of Bridge Dynamics Using Integrated GPS and Accelerometer[J]. Journal of China University of Mining and Technology, 2015, 44(3): 549-556)
(  0) 0) |
| [10] |
Imrich L, Alojz K, Ján E, et al. Dynamic Deformation Monitoring of Bridge Structure[J]. Selected Scientific Papers-Journal of Civil Engineering, 2013, 8(2): 13-20 DOI:10.2478/sspjce-2013-0014
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


