2. 湖北省地震局,武汉市洪山侧路48号,430071;
3. 武汉地震工程研究院有限公司, 武汉市洪山侧路40号,430071;
4. 中国地质大学(武汉)海洋地质资源湖北省重点实验室,武汉市鲁磨路388号,430074
井间地震是将震源与检波器放置在相邻的两口井中,在一口井中激发地震,在另一井中接收信号。与常规单分量相比,井间三分量检波器可采集到包含丰富运动学和动力学信息的矢量波场[1]。但在标准正交坐标系中,各分量极性和幅值会随检波器放置状态(包括方位角和倾角)的变化而变化。由于井下检波器摆放状态完全随机,地震响应水平分量随机分布在X、Y分量各地震道上,因井斜程度不同和介质各向异性,Z分量各地震道上的响应幅值也会存在不同程度的损失,这对后期利用三分量资料开展岩性研究造成一定干扰[2]。因此,在预处理中需要对三分量检波器进行方向校正,在VSP中称之为检波器重定向,是井间地震数据处理的关键[3]。
目前设计的全数字三分量检波器利用倾斜度和重力测试可实现垂直分量倾斜校正,利用姿态检测技术可自动进行水平分量数据校正[4],但在实际生产中还未大规模应用。现阶段国内外主要利用直达P波偏振特征来估算检波器的方位角与入射倾角[5-6]。三分量地震记录的偏振分析一般是在时间域实现,常被应用于随机噪声压制、波场识别与分离、介质属性分析等方面[7]。具体分析方法有两大类:一是基于最大能量准则分析法,在时窗内计算不同分量中波场的振幅或能量,使之达到最大时的角度即为偏振角[8];二是基于主成分分析(PCA)法,在时窗内构造协方差矩阵,对该矩阵的特征值和特征向量进行求解,从而获得相应的偏振信息。相比较而言,后者原理简单,实现方便,所求偏振角精度较高[9]。
目前,在跨孔井间弹性波波速测试中,关于波形识别的研究较少,如果能将三分量地震偏振分析应用到初至波形起跳的识别中,可以大幅提升在复杂地层中采集的原始资料的质量。本文基于PCA方法进行偏振分析,构建层状介质模型进行理论试算,分析利用协方差矩阵求取偏振角的有效性,并将该方法应用于跨孔井间弹性波波速测试,通过偏振旋转可使P波和S波能量得到不同程度的加强,使初至起跳的拾取更加高效和准确。
1 三分量地震偏振分析 1.1 PCA方法求解偏振角某一波场延续时间T内,质点振动的3个分量X、Y、Z可用矩阵来描述[10]:
| $ \mathit{\boldsymbol{C}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} Z\\ X\\ \mathit{Y} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{z_1}}\\ {{x_1}}\\ {{y_1}} \end{array}\begin{array}{*{20}{c}} {{z_2}}\\ {{x_2}}\\ {{y_2}} \end{array}\begin{array}{*{20}{c}} \cdots \\ \cdots \\ \cdots \end{array}\begin{array}{*{20}{c}} {{z_N}}\\ {{x_N}}\\ {{y_N}} \end{array}} \right] $ | (1) |
式中,N=T/Δt+1为时窗内采样点数,C为3×N矩阵,规定其中各分量在延续时间内的均值为0,则协方差矩阵可通过式(2)计算:
| $ {S_{ij}} = \frac{{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{C}}^{\rm{T}}}}}{N} = \left[ {\frac{1}{N}\sum\limits_{k = 1}^N {{c_{ij}}{c_{jk}}} } \right] $ | (2) |
协方差矩阵S为3×3实对称矩阵,矩阵中元素为三分量振动的自相关和互相关数值,即各分量之间的协方差。矩阵S存在3个非负实特征值λ1、λ2、λ3,且满足λ1≥λ2≥λ3,令特征向量为u1、u2、u3,则存在如下关系式:
| $ \left( {\mathit{\boldsymbol{S}}{\rm{ - }}{\lambda ^2}\mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{u}}{\rm{ = }}{\bf{0}} $ | (3) |
式中,I为3×3单位矩阵,0为元素值均为0的列向量。
椭球极化参数由特征向量u和特征值λ来表示,特征向量表示3个互相垂直的极化方向,而特征值为地震相平均能量的度量。如果信号为线性偏振(如体波),在理想情况下协方差矩阵仅有一个非零特征值,此时存在λ1>>λ2、λ3,λ1对应的特征向量代表极化方向;在波场互相干扰或存在噪声的情况下,可得到3个特征值,此时为椭球偏振,对应的3个特征向量可确定3个轴的取向,其中最大特征值对应的特征向量代表主偏振方向[11]。
主特征向量u1归一化后的3个标量元素(u11, u21, u31)分别为在直角坐标系Z、X、Y方向的位移标量,因此可求解水平方向方位角θ和垂直方向倾角α,表达式分别为[12]:
| $ \left\{ {\begin{array}{*{20}{l}} {\theta = {{\tan }^{ - 1}}\left( {\frac{{{u_{31}}}}{{{u_{21}}}}} \right)}\\ {\alpha = {{\tan }^{ - 1}}\left( {\frac{{{u_{11}}}}{{\sqrt {u_{21}^2 + u_{31}^2} }}} \right){\rm{sign}}\left( {{u_{11}}{u_{21}}} \right)} \end{array}} \right. $ | (4) |
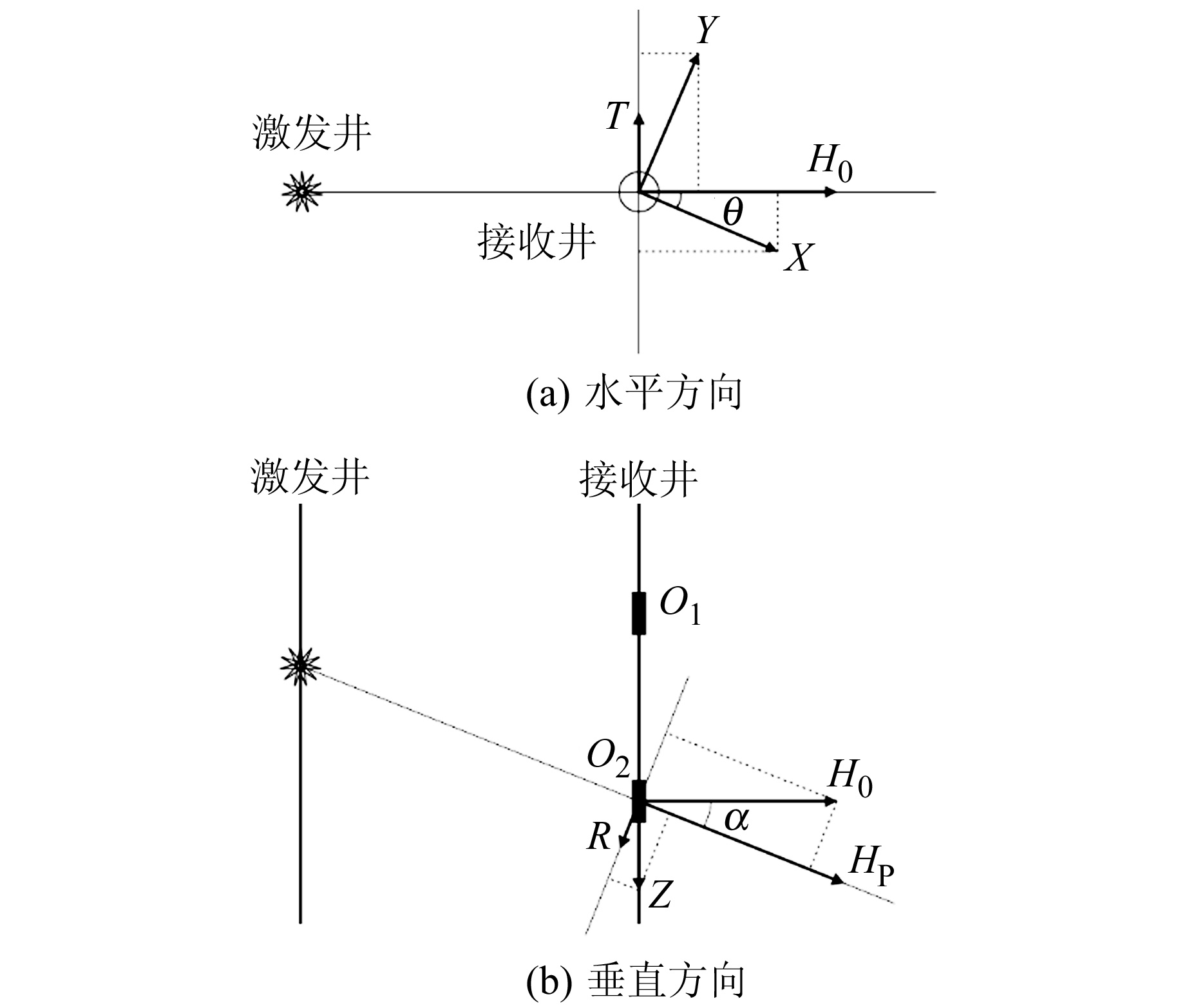
在求得水平方向和垂直方向旋转角后,对采集到的原始三分量记录进行坐标旋转。首先在水平面内进行旋转,如图 1(a)所示,水平分量H0与X分量正向的夹角为θ,根据几何关系可知,变换公式为:
| $ \begin{array}{l} {H_0} = X\cos \theta + Y\sin \theta \\ T = Y\cos \theta - X\sin \theta \end{array} $ | (5) |
旋转后P波和SV波的水平分量主要存在于H0分量中,而T分量中主要为SH波能量。图 1(b)为垂直方向旋转,变换公式为:
|
图 1 坐标旋转示意图 Fig. 1 Schematic diagram of coordinate rotation |
| $ \begin{array}{l} {H_{\rm{p}}} = {H_0}\cos \alpha + Z\sin \alpha \\ R = Z\cos \alpha - {H_0}\sin \alpha \end{array} $ | (6) |
通过坐标旋转后,P波能量主要集中在HP分量中,SV波和SH波能量分别集中在R分量和T分量中,有利于后期资料处理。
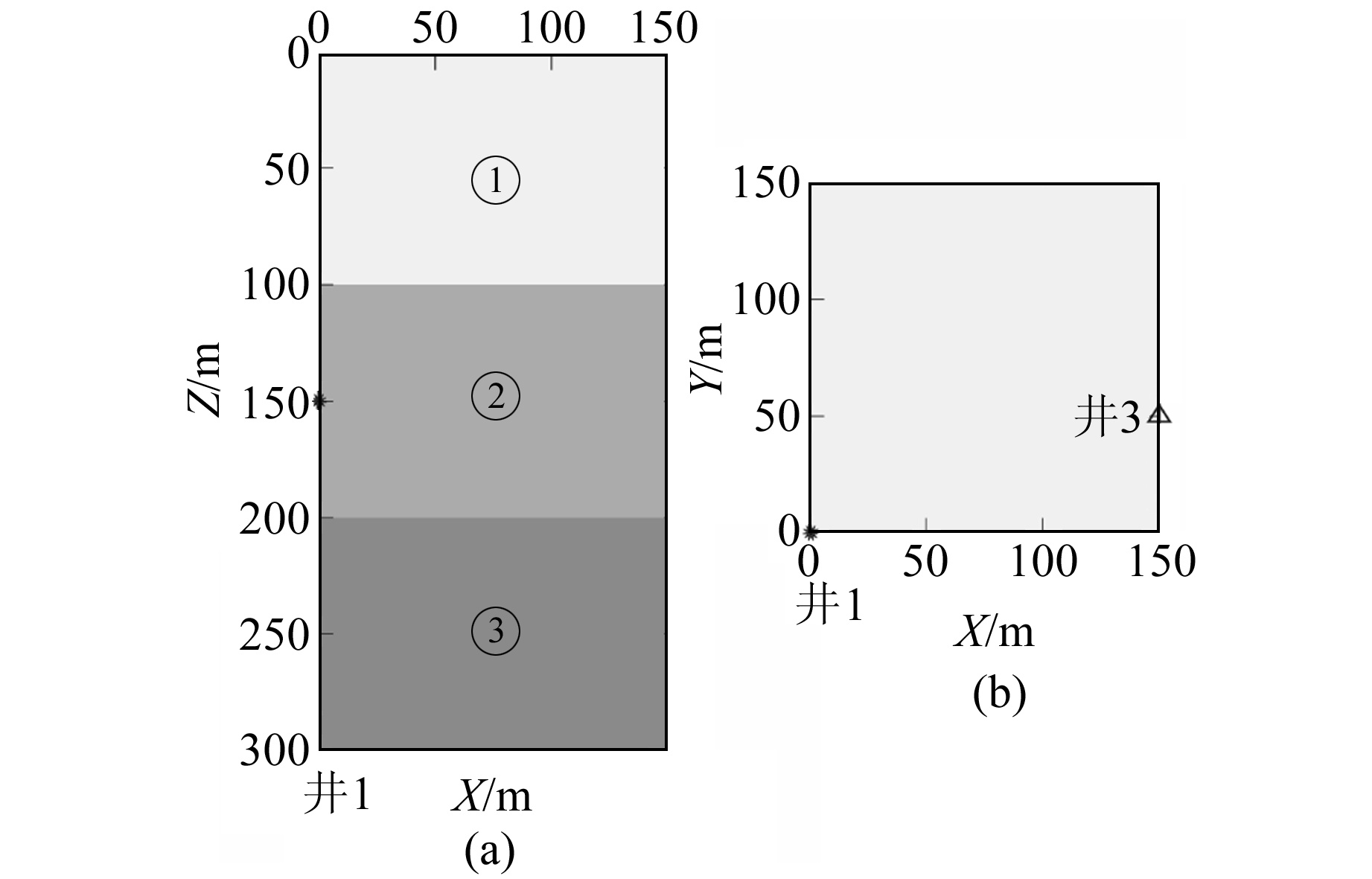
2 理论模型试算 2.1 正演模拟为说明利用协方差矩阵求取偏振角的有效性,构建三维均匀层状介质模型进行理论试算。模型大小为150 m×150 m×300 m,网格间距为1.0 m,物性参数见表 1。图 2(a)为模型XOZ平面示意图,井位分布见图 2(b),激发点设置在井1,深度在150 m处,接收井设置在井3,全井接收。
|
|
表 1 层状理论模型物性参数 Tab. 1 The parameters of theoretical layered model |
|
图 2 激发和接收井位分布 Fig. 2 Distribution of shooting and receiving wells |
采用弹性介质交错网格有限差分法进行数值模拟,选择时间2阶、空间6阶精度。具体参数为:时间采样间隔为0.1 ms,道间距为1.0 m,记录长度为300 ms,雷克子波主频为120 Hz,震源类型为胀缩力震源。
通过三维数值模拟得到理论三分量地震记录(图 3)。在均匀层状介质模型中,除初至纵波(P)、透射纵波(Tp)和上下界面反射纵波(Rp)外,还存在上下界面处的转换横波(Rps、Tps)。X分量上P波能量较强,特别是在震源深度附近幅值最大,也有S波分布;Y分量上P波和S波能量均较弱;Z分量上有S波分布。在界面所在深度100 m和200 m附近存在多种波形相互叠加。

|
图 3 层状模型理论三分量记录 Fig. 3 Three-component records of theoretical layered model |
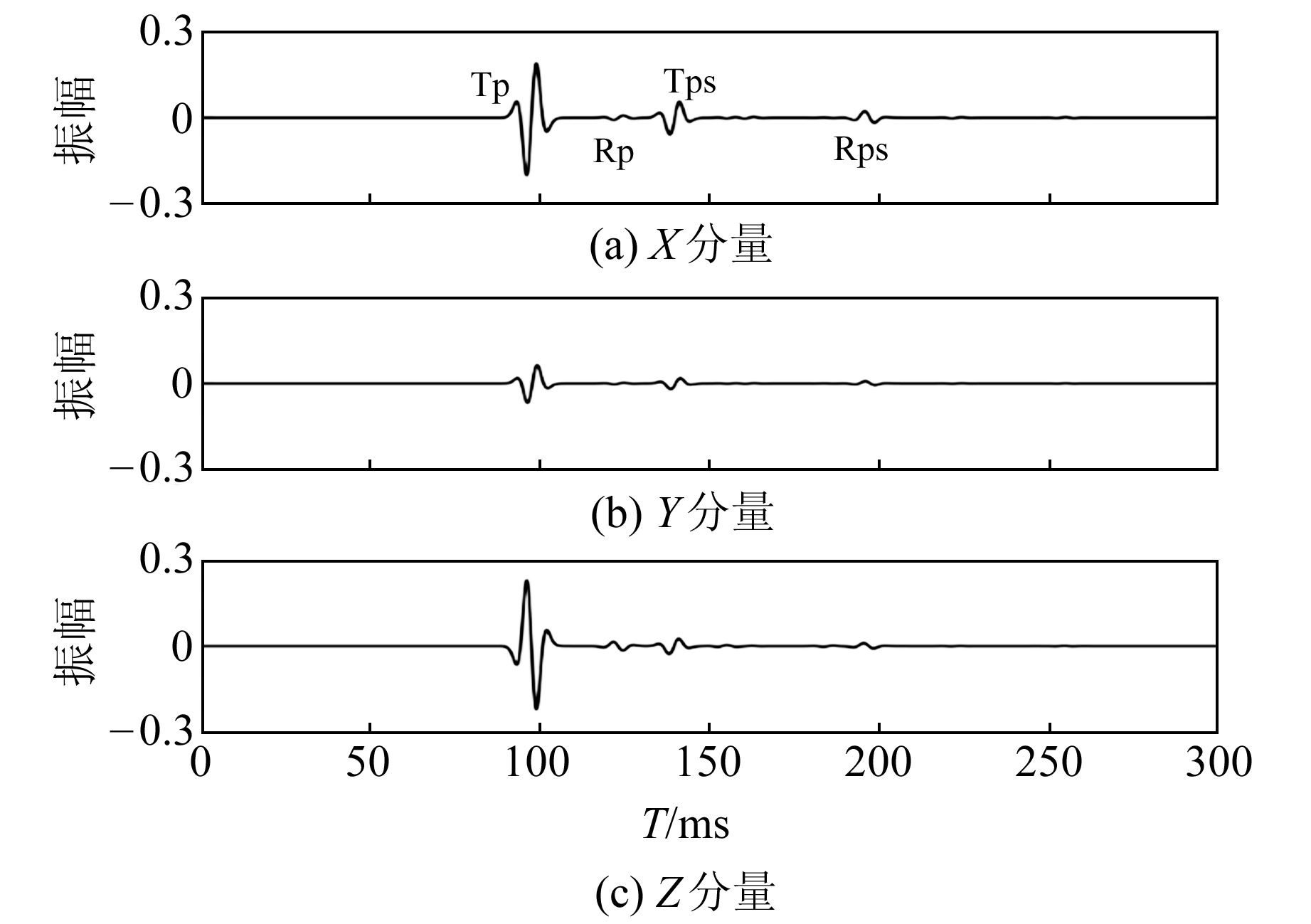
选取第4道进行偏振分析,三分量波形见图 4。由激发点与接收点的相对位置和Snell定律可知,水平方向方位角θ =18.434 9°,垂直方向倾角α=-47.922 2°。
|
图 4 井3接收第4道三分量波形 Fig. 4 Three-component waveform of channel 4 of well-3 |
通过PCA方法计算得到θ =18.369 6°,α=-47.681 0°,与理论值偏差分别为0.065 3°和0.241 2°。如果考虑到原始记录因网格化数值模拟存在的系统误差,计算得到的θ和α精度较高。
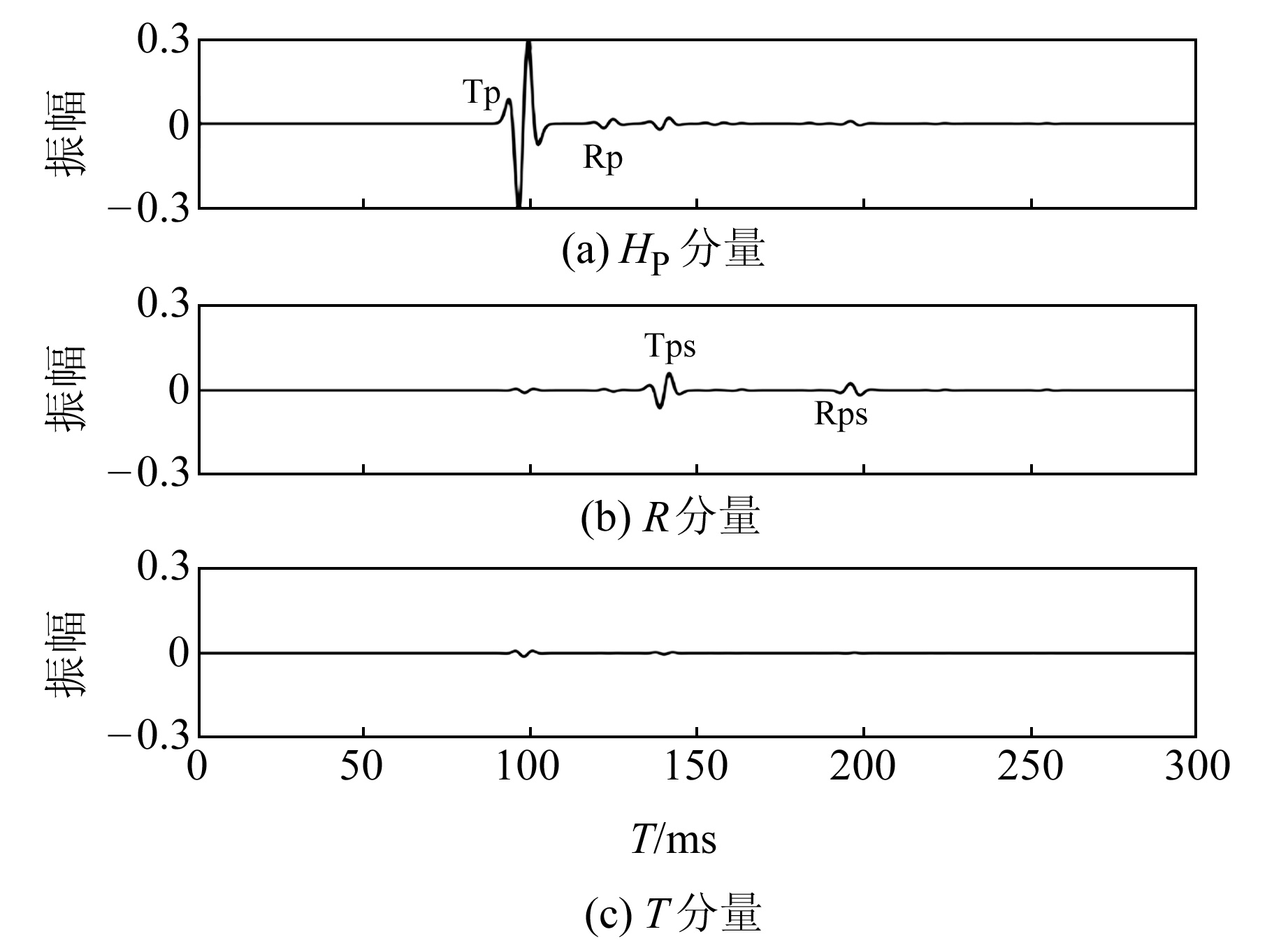
利用式(5)和式(6)进行坐标旋转,得到HP分量、R分量和T分量波形图见图 5。与图 4原始三分量波形相比,坐标旋转后各波形运动学特征无改变,R分量中主要包含S波成分,P波能量较弱;HP分量中P波成分得到加强,S波能量被压制;T分量中能量几乎为0,由于该分量方向与射线平面垂直,理论上无SV波存在,试算结果与理论一致。
|
图 5 井3接收第4道旋转后三分量波形 Fig. 5 Three-component waveform after rotation of channel 4 of well-3 |
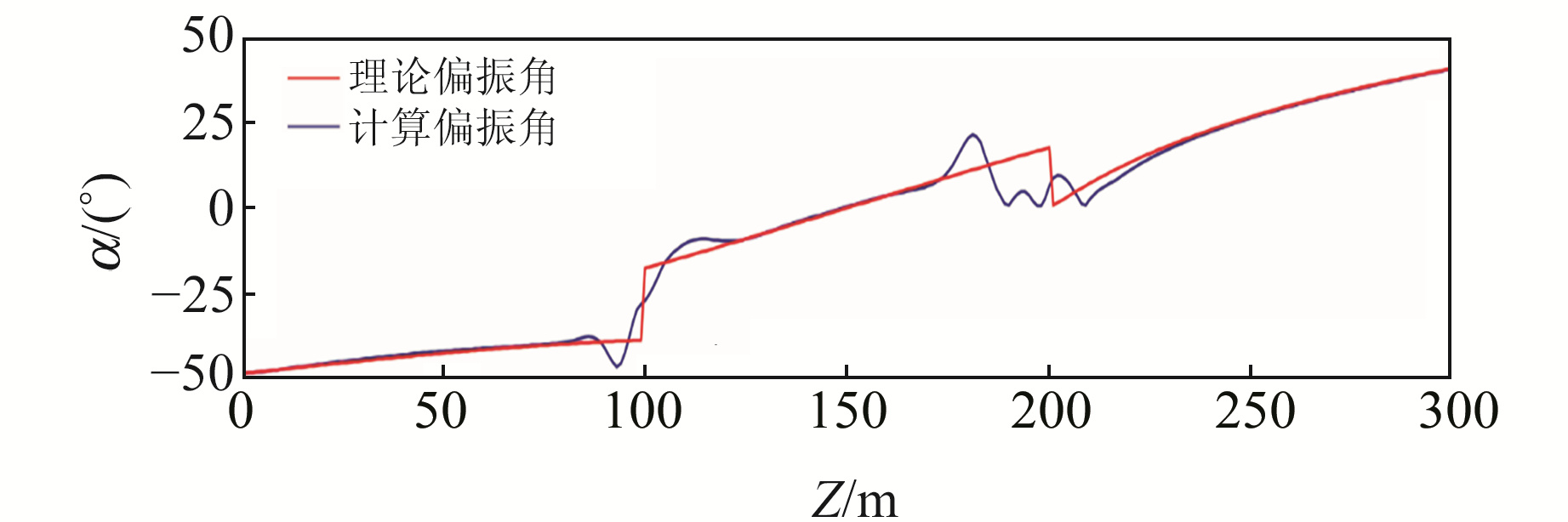
将图 3整个三分量记录进行偏振分析,通过PCA方法计算得到垂直方向倾角(图 6)。图中蓝色实线为计算结果,红色实线为Snell定律计算的理论结果。通过对比可知,对于无波形叠加的记录道,计算的偏振角与理论值吻合较好;在界面分层深度附近,因多种波形叠加在直达P波上,影响了P波偏振椭圆的极化特征,导致偏振角计算出现误差,但与理论值相差较小。
|
图 6 层状模型垂直方向偏振曲线 Fig. 6 Vertical polarization curve of layered model |
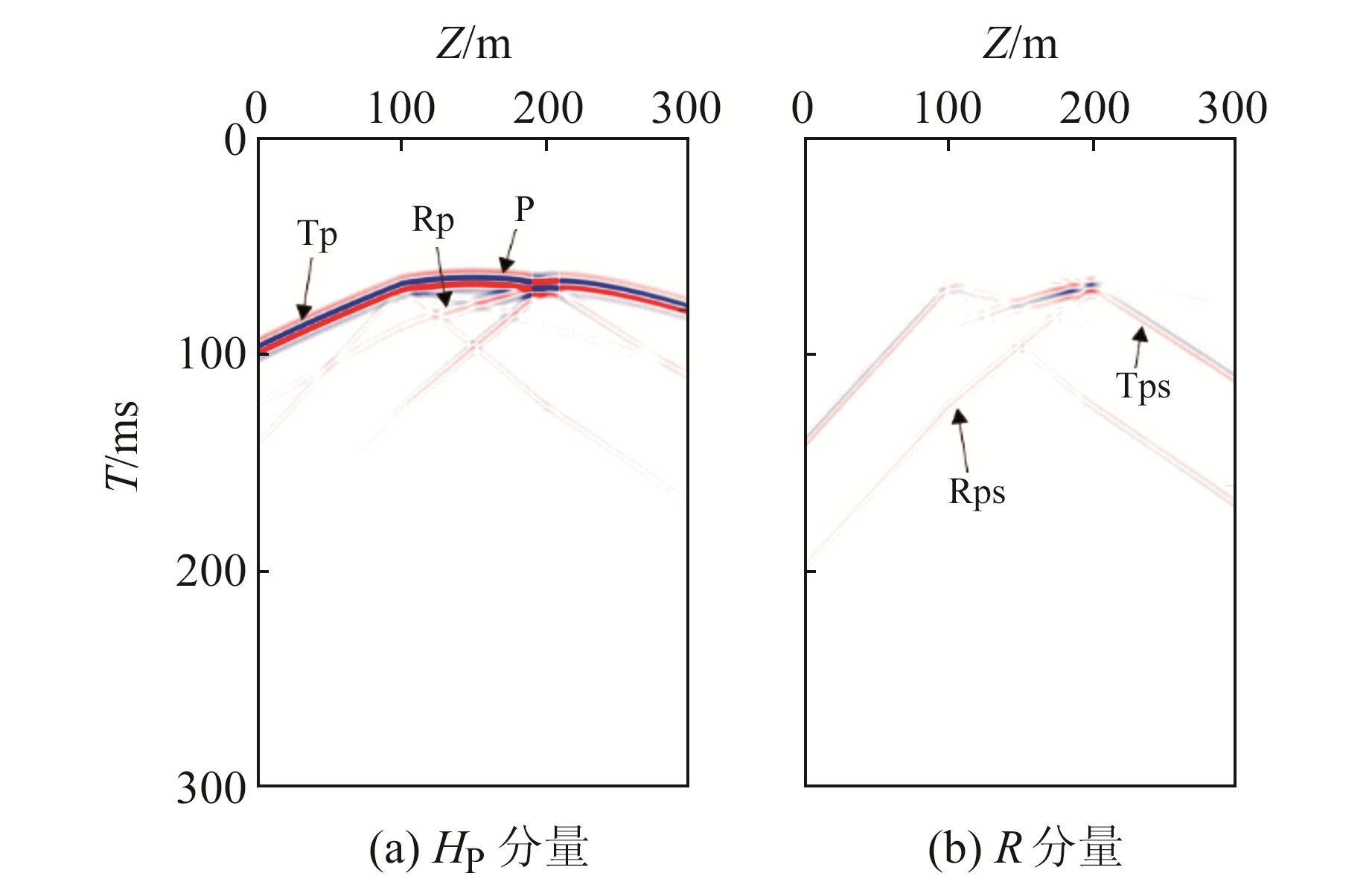
利用式(5)和式(6)进行坐标旋转得到HP分量和R分量记录(图 7)。可以看出,HP分量中P波能量得到加强,S波能量被压制;R分量中主要为S波成分,几乎无法看到直达P波,仅在100~200 m深度范围内存在部分界面反射P波能量,这是由于反射P波偏振方向与该深度处S波偏振方向之间夹角较小,垂直方向坐标旋转会将部分反射P波能量旋转到R分量上。
|
图 7 井3偏振后三分量记录 Fig. 7 Three-component records after rotation of well-3 |
跨孔井间弹性波波速测试一般采用单孔激发、单孔或两孔接收的方式,孔中由三分量传感器接收信号。该方法是一种快速、准确的原位测试技术,能提供高分辨率的P波和S波波速曲线,并可根据波速计算动弹性模量、动剪切模量、动泊松比等动力学参数,为岩土工程设计提供依据。
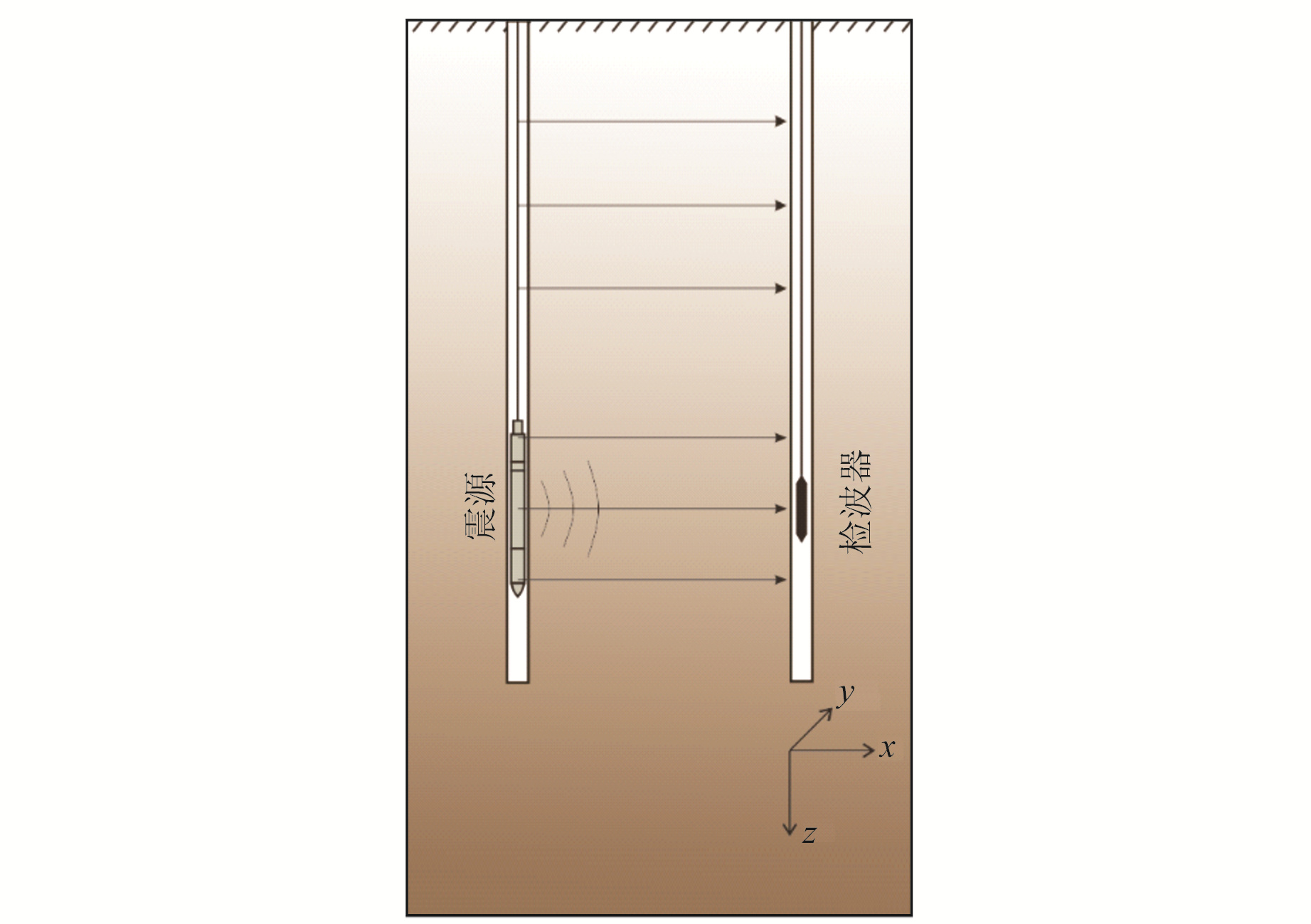
本次野外数据采集采用IPG5000脉冲发生器和BIS-SH震源探头,接收采用BGK3信号检波器。图 8为实际工作示意图,将震源下放至钻孔中预定深度,使用充气气囊机制与井壁耦合,震源方向可通过地面刚性抗扭管进行调节,将三分量检波器下放至另一钻孔中相同深度并紧贴孔壁,激发震源,记录相应波形图;检查无误后将震源旋转180°,反向激发并再次记录相应波形。从上至下(或从下至上)依次按上述步骤进行采集,即可完成整个钻孔波速测试。
|
图 8 跨孔波速测试工作示意图 Fig. 8 Schematic diagram of cross-hole wave velocity test |
通过改变震源的极性方向,结合正向激发和反向激发的三分量记录,从中选取振幅能量较大、初至较明显的分量,分别读取P波初至与S波初至,根据孔距即可得到地下岩土层P波和S波速度,波速计算公式为:
| $ V = \frac{L}{t} $ | (7) |
由式(7)可知,影响波速计算的2个参数分别为距离L和初至走时t。考虑各钻孔因各种外界因素可能会存在偏差和倾斜,导致其不严格与地面垂直或互相平行,因此需要同时进行井斜测试,以便对激发点和接收点之间的距离L进行校正。参数t的拾取与原始记录质量密切相关。
由于测试采用水平同步方式进行,理论上激发点与接收点位于同一水平面,Z分量与旋转后R分量一致,垂直方向倾角为0°,S波主要分布在Z分量上。但在实际操作中,震源与接收探头下放深度往往存在人为误差、接收探头紧贴孔壁时存在偏差、孔壁可能存在倾斜等因素,导致采集的三分量波形中P波和S波能量会根据钻孔倾斜程度在3个分量上重新分布,不利于初至波拾取。
本文以某港口地层跨孔弹性波波速测试为例,选取其中一对钻孔采集的实测资料,图 9为其三分量记录,图中(a)~(c)为正向激发,(d)~(f)为反向激发。可以看出,P波初至起跳较为明显,而S波由于地层岩性不同,能量衰减程度存在差异。此时如果钻孔倾斜或激发点和接收点不在同一水平面,会导致S波能量分散投影到3个分量上,从而影响初至S波的拾取。

|
图 9 实测资料三分量记录 Fig. 9 Three-component records of measured data |
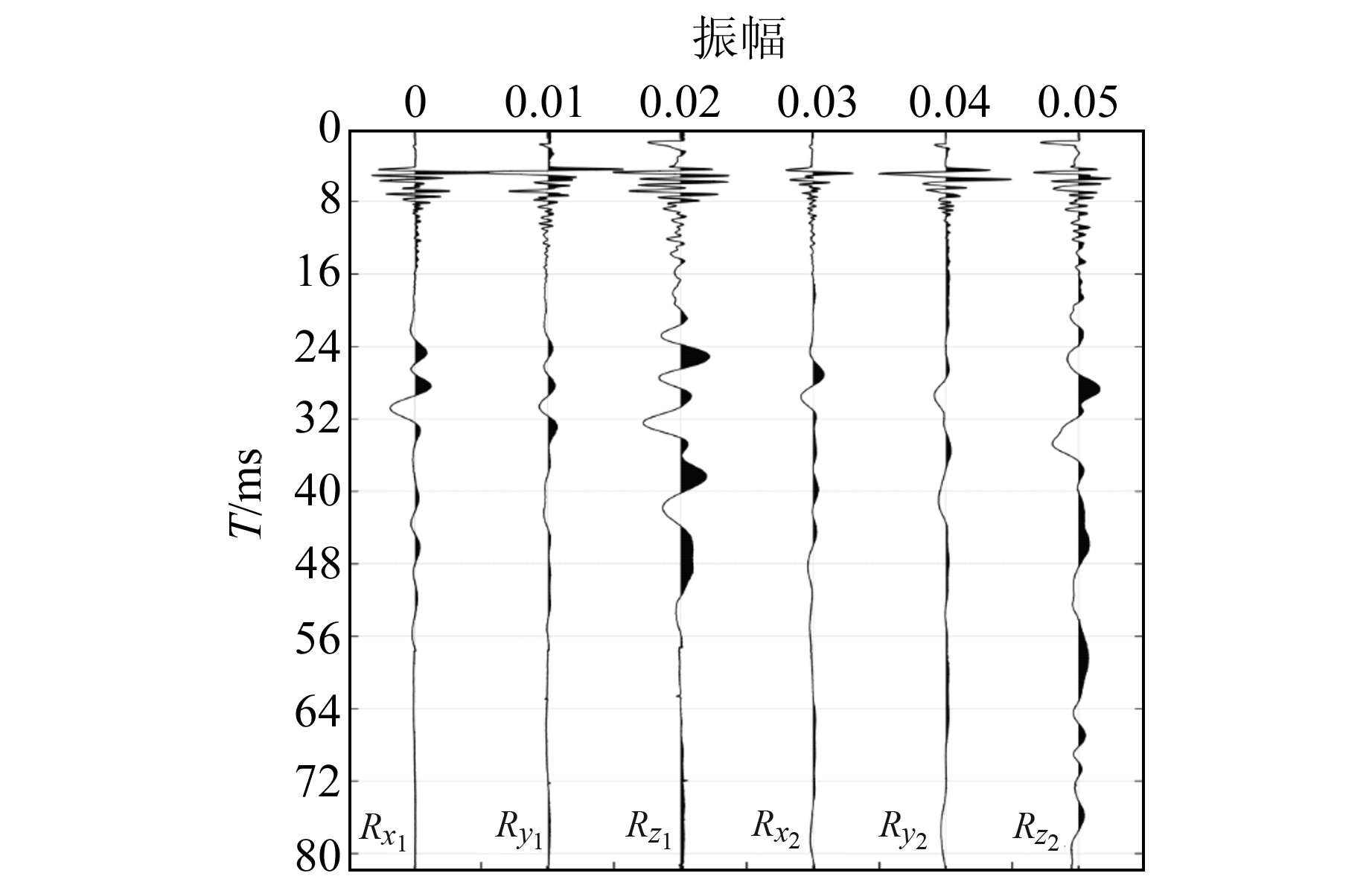
图 10为第12道三分量波形图,其中Rx1、Ry1、Rz1分别为正向激发X、Y、Z分量,Rx2、Ry2、Rz2分别为反向激发X、Y、Z分量。
|
图 10 实测资料第12道三分量波形 Fig. 10 Three-component waveform of measured data of channel 12 |
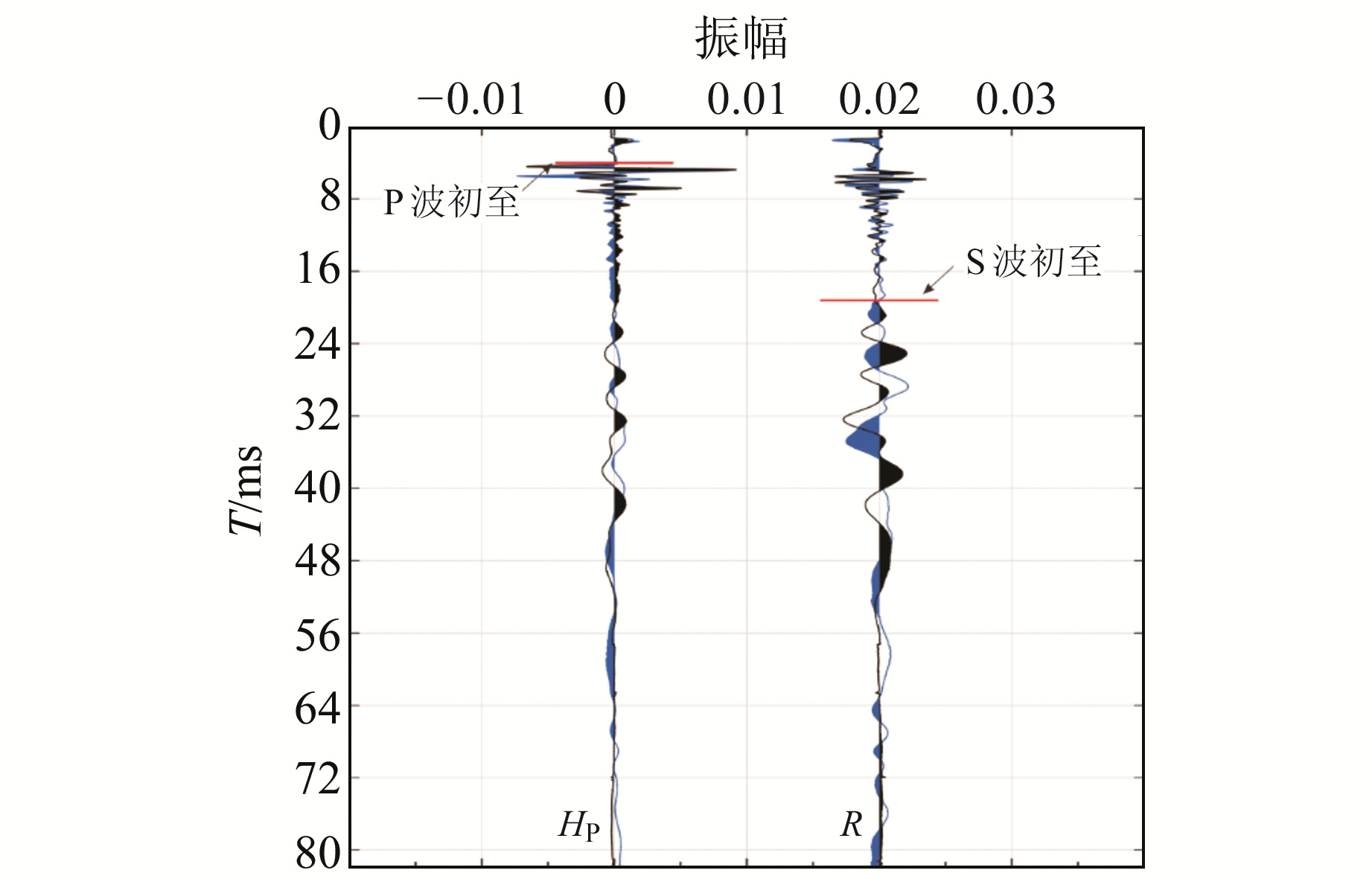
利用初至P波构建协方差矩阵,求取三分量波形的水平方位角和垂直倾角,通过式(5)和式(6)进行坐标旋转,得到HP分量和R分量(图 11,图中黑色实线为正向分量,蓝色实线为反向分量)。通过与图 10对比可知,HP分量中P波能量得到加强,振幅增大到原始记录的2倍左右;S波能量主要集中在R分量中,与原始记录S波振幅相比,同样存在小幅度增加。通过偏振旋转可将正向分量与反向分量进行重叠,S波初至更加明显,从而容易识别和读取,得到的横波速度也更加精确。
|
图 11 实测资料第12道旋转后三分量波形 Fig. 11 Three-component waveform after rotation of measured data of channel 12 |
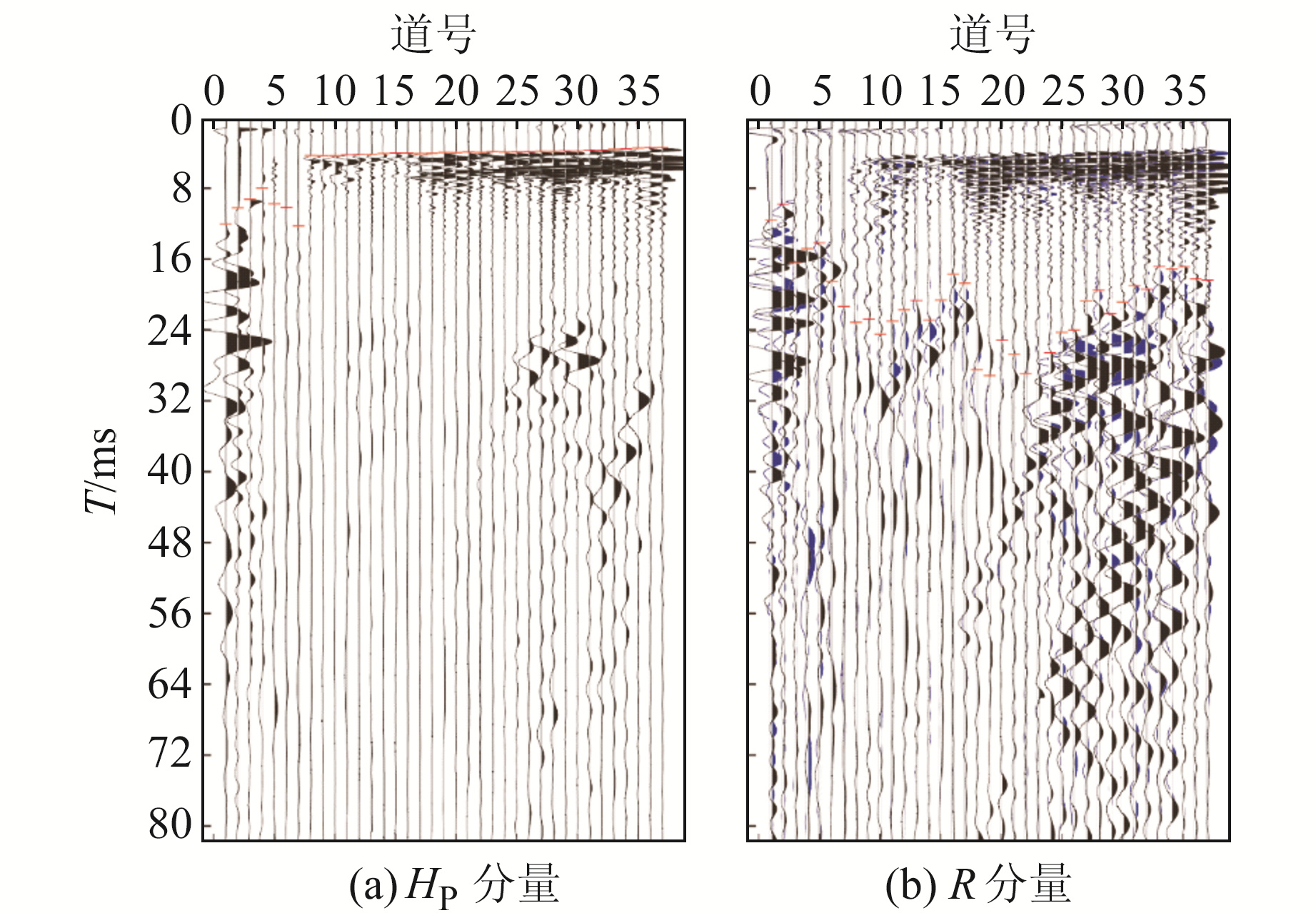
对每一道三分量记录重复上述步骤,得到经偏振旋转后的HP分量和R分量记录(图 12),P波初至在HP分量中读取,S波初至在R分量中读取。相比原始三分量记录而言,可减少筛选具有较明显初至分量的步骤,而且P波和S波能量均存在不同程度的加强,对初至拾取更加有利。从图中可以明显看出,深度10 m附近和18~26 m处存在明显的横波低速带。
|
图 12 实测资料旋转后三分量记录 Fig. 12 Three-component records after rotation of measured data |
本文介绍了一种基于PCA方法的井间地震三分量记录偏振分析方法,通过构建理论层状介质模型,详细论证了该方法在偏振分析中的有效性,并将该方法应用于跨孔井间波速测试。通过实测资料计算,获得以下结论:
1) 利用PCA方法求取三分量记录中直达P波的偏振状态方便、有效,在无其他波形混叠的情况下,得到的偏振旋转角精度较高;但在界面深度处存在波形叠加时,会影响初至P波偏振椭圆的极化特征,从而导致偏振旋转角计算出现误差,不过该误差较小。
2) 跨孔井间波速测试采集的三分量资料经偏振旋转后,在HP分量中读取P波初至,在R分量中读取S波初至,与原始三分量记录相比,可减少筛选具有较明显初至分量的步骤,且P波和S波能量均存在不同程度的加强,可在复杂地层中更加准确地拾取初至起跳,为岩土工程设计提供更加精确的动力学参数。
3) 该方法对初至P波的信噪比依赖较高,在实际应用中如果未能获取信号质量较好的初至P波,可能无法得到理想的偏振旋转角,后续工作将在该方法的抗噪能力上作进一步研究。
| [1] |
刘守伟, 王华忠, 陈生昌, 等. VSP上下行反射波联合成像方法研究[J]. 地球物理学报, 2012, 55(9): 3126-3133 (Liu Shouwei, Wang Huazhong, Chen Shengchang, et al. Joint Imaging Method of VSP Upgoing and Downgoing Reflection Wave[J]. Chinese Journal of Geophysics, 2012, 55(9): 3126-3133)
(  0) 0) |
| [2] |
陈志德, 王桂水, 关昕, 等. 喇嘛甸3D3C地震数据重新定位及定向分析[J]. 石油地球物理勘探, 2011, 46(4): 561-569 (Chen Zhide, Wang Guishui, Guan Xin, et al. Re-Location and Re-Orientation Techniques for 3D3C Seismic Data of Lamadian Survey[J]. Oil Geophysical Prospecting, 2011, 46(4): 561-569)
(  0) 0) |
| [3] |
Takahashi T, Ohta K, Ohtomo H. A Processing Technique for Three Component Seismic Data: Use of Polarisation Characteristics[J]. Exploration Geophysics, 1988, 19(1-2): 362-364 DOI:10.1071/EG988362
(  0) 0) |
| [4] |
李怀良, 庹先国, 刘勇, 等. 一种数字三分量地震微测井仪器设计[J]. 地球物理学报, 2017, 60(11): 4241-4252 (Li Huailiang, Tuo Xianguo, Liu Yong, et al. Design of a Digital 3C Mciro-VSP Uphole Instrument[J]. Chinese Journal of Geophysics, 2017, 60(11): 4241-4252 DOI:10.6038/cjg20171112)
(  0) 0) |
| [5] |
Capizzi P, Luca L D, Vitale M. Polarization Analysis on Three-Component Seismic Data[J]. Bollettino Di Geofisica Teorica Ed Applicata, 2003, 44(3-4): 329-335
(  0) 0) |
| [6] |
刘建华, 刘福田, 胥頤. 三分量地震资料的偏振分析[J]. 地球物理学进展, 2006, 21(1): 6-10 (Liu Jianhua, Liu Futian, Xu Yi. Polarization Analysis of Three-Component Seismic Data[J]. Progress in Geophysics, 2006, 21(1): 6-10 DOI:10.3969/j.issn.1004-2903.2006.01.002)
(  0) 0) |
| [7] |
陈赟, 高乐, 赵烽帆. 一种基于频率域偏振分析提高三分量地震资料信噪比的方法[J]. 地球物理学进展, 2007, 22(1): 255-261 (Chen Yun, Gao Le, Zhao Fengfan. A Method to Enhance the Signal/Noise Ratio of Three-Component Seismic Data Based on the Polarization Analysis in Frequency Domain[J]. Progress in Geophysics, 2007, 22(1): 255-261 DOI:10.3969/j.issn.1004-2903.2007.01.037)
(  0) 0) |
| [8] |
傅旦丹, 刘一峰, 温书亮, 等. 海上多分量地震勘探水平分量方位校正[J]. 石油物探, 2003, 42(4): 460-463 (Fu Dandan, Liu Yifeng, Wen Shuliang, et al. Orientation Correction for Horizontal Components in Marine Multi-Component Seismic Exploration[J]. Geophysical Prospecting for Petrole, 2003, 42(4): 460-463 DOI:10.3969/j.issn.1000-1441.2003.04.007)
(  0) 0) |
| [9] |
陈赟, 张中杰, 田小波. 基于加窗Hilbert变换的复偏振分析方法及其应用[J]. 地球物理学报, 2005, 48(4): 889-895 (Chen Yun, Zhang Zhongjie, Tian Xiaobo. Complex Polarization Analysis Based on Windowed Hilbert Transform and Its Application[J]. Chinese Journal of Geophysics, 2005, 48(4): 889-895 DOI:10.3321/j.issn:0001-5733.2005.04.022)
(  0) 0) |
| [10] |
王权海, 苗放. 提高地震数据信噪比的PCA方法[J]. 地球物理学进展, 2011, 26(3): 1039-1044 (Wang Quanhai, Miao Fang. Enhancement of Singal to Noise Ratio of Seismic Date Based on the PCA Method[J]. Progress in Geophysics, 2011, 26(3): 1039-1044 DOI:10.3969/j.issn.1004-2903.2011.03.032)
(  0) 0) |
| [11] |
李英康, 崔作舟. 分离纵波和横波的偏振旋转法[J]. 地球物理学报, 1994, 37(增2): 372-382 (Li Yingkang, Cui Zuozhou. P and S-Waves Separated by Polarization Revolving Method[J]. Chinese Journal of Geophysics, 1994, 37(S2): 372-382)
(  0) 0) |
| [12] |
Meersman K, Baan M, Kendall J M. Signal Extraction and Automated Polarization Analysis of Multicomponent Array Data[J]. Bulletin of the Seismological Society of America, 2006, 96(6): 2415-2430 DOI:10.1785/0120050235
(  0) 0) |
2. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China;
3. Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Road, Wuhan 430071, China;
4. Hubei Key Laboratory of Marine Geological Resources, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
 2021, Vol. 41
2021, Vol. 41


