准确获取重力异常变化是开展地震分析预报和相关科研工作的前提,尤其是我国东部地震活动背景弱,重力变化量级小[1],对流动重力观测数据的处理更应谨慎。重力仪一次项格值系数在重力观测数据处理中发挥着重要作用,会影响数据精度、异常提取与地震趋势判定的准确度。研究表明,一次项格值系数会随时间与空间发生变化,从而对观测数据的处理结果及其研究成果产生系统误差[2-5]。我国地震重力测量数据处理通常将重力仪零漂率作为常数进行整体解算[6],一次项格值系数则采用基线场标定结果,但标定周期通常为3~5 a,因此数据处理结果中可能会存在由于重力仪零漂率变化和格值系数变化带来的误差。为削弱甚至消除格值系数误差的影响,学者们提出多种改正方法,如区域适定法[7-8]、标定结果内插法[9]、绝对段差标定法[5]、重力差值法[10]等。
本文以海南岛2016~2020年10期流动重力复测资料为例,研究一次项格值系数对提取重力变化的影响,总结适用于海南地区的流动重力数据处理方法,为东部同类(弱地震背景)地区的流动重力数据处理提供参考。
1 海南岛流动重力测量2016年以来,海南流动重力测网基本稳定在67个测点和73个测段,其中仅琼中测点为绝对点,观测所用仪器均为CG-5重力仪,图 1为流动重力测网。2016~2020年海南岛共完成10期流动重力测量工作,每年2期。因只有1个绝对点,且绝对观测周期较长,仅2019-06由中国地震局地震研究所进行过1次绝对观测,使得利用绝对重力点实测值标定仪器一次项格值系数存在困难。因此,在对海南流动重力观测资料进行平差处理时,一般采用仪器共用单位标定的一次项格值系数。
|
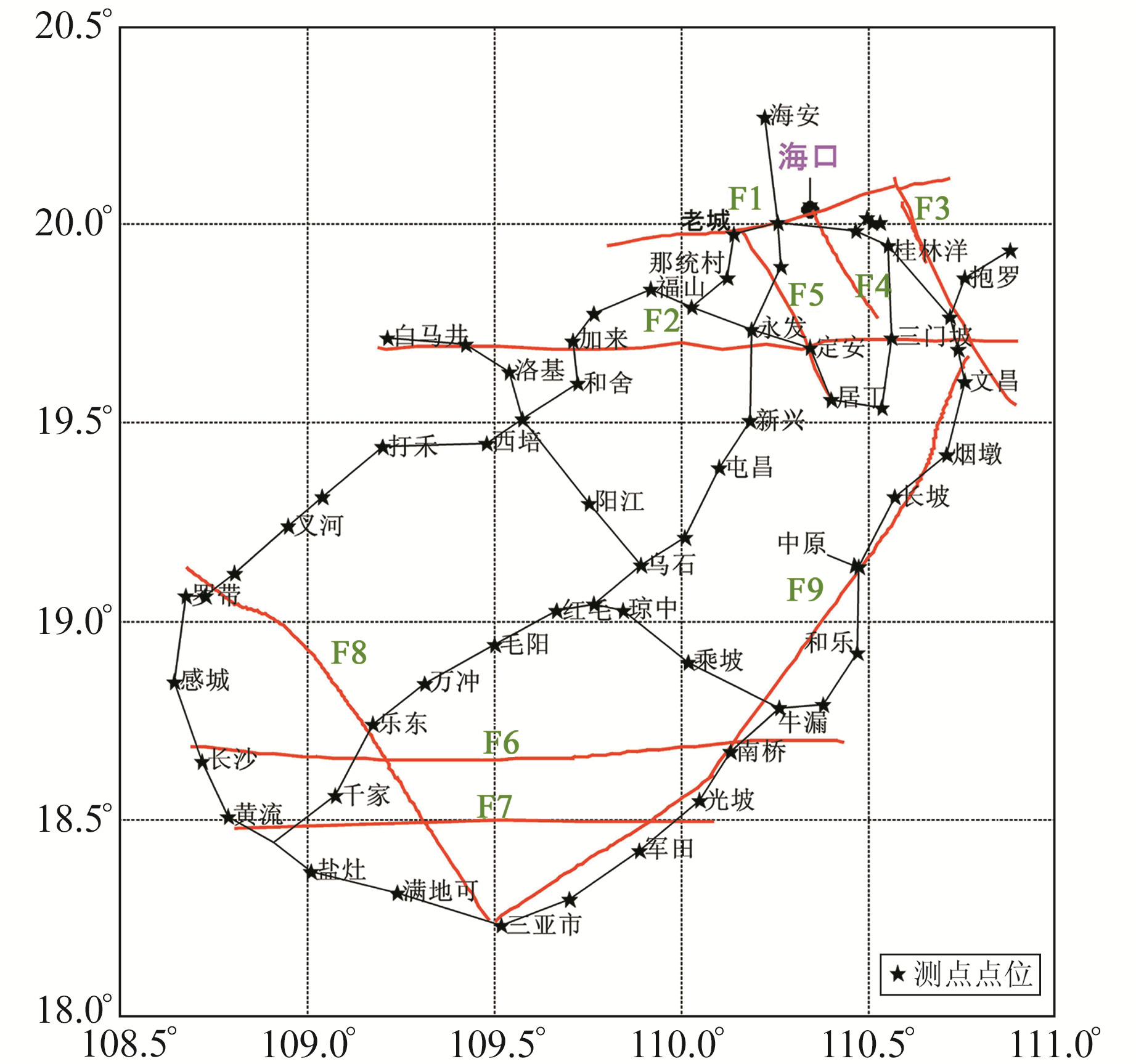
F1 : 马袅-铺前断裂; F2: 王五-文教断裂; F3 : 铺前-清澜断裂; F4: 海口-云龙断裂; F5 : 长流-仙沟断裂; F6 : 尖峰-吊罗断裂; F7: 九所-陵水断裂; F8: 昌城-乐东-田独断裂; F9 : 文昌-琼海- 三亚断裂 图 1 海南流动重力测网 Fig. 1 Mobile gravity network in Hainan |
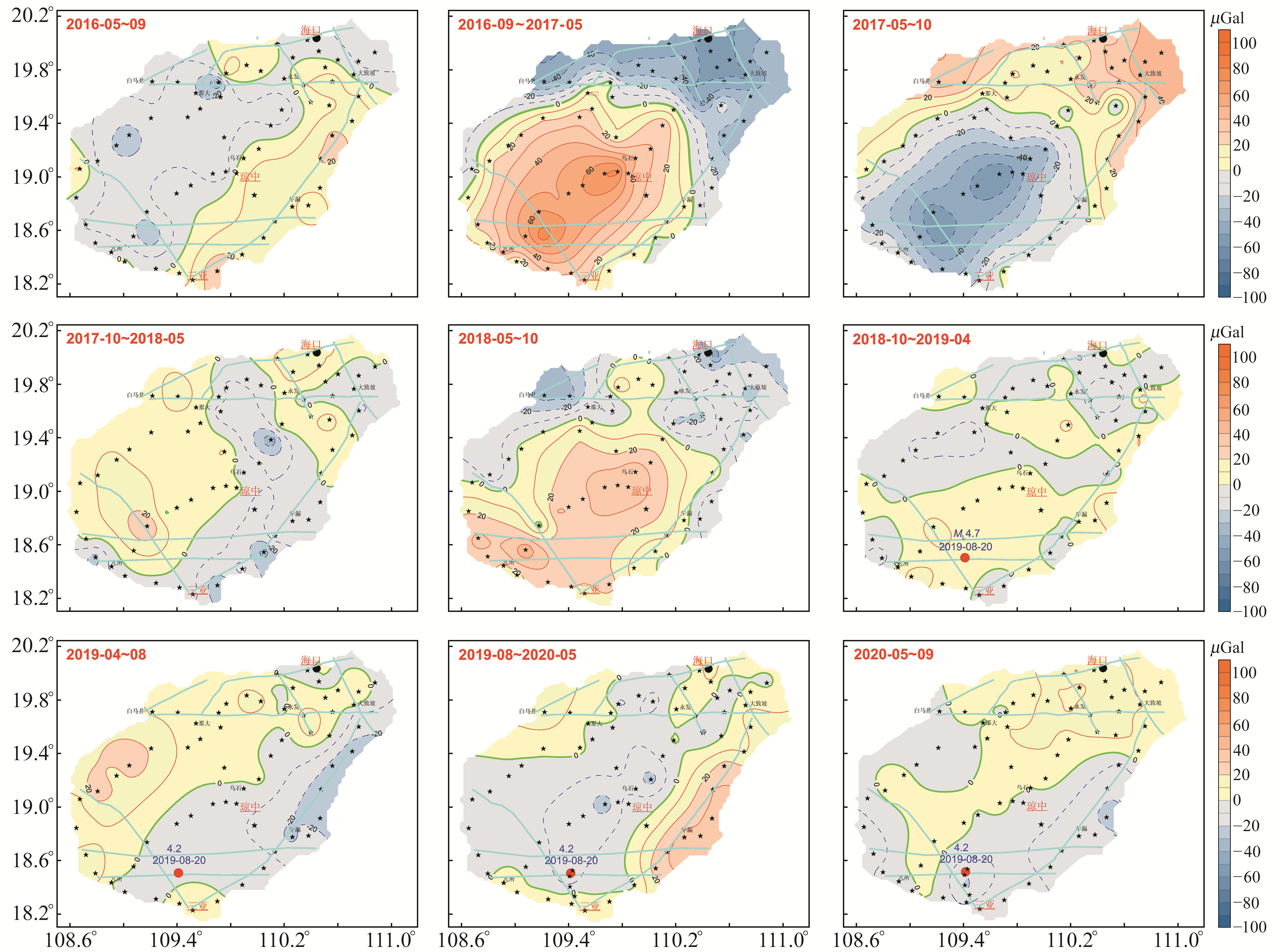
表 1为2016年以来海南测网流动重力测量的观测时间、仪器编号、采用的一次项格值系数以及拟稳平差后的平差精度。从表中可以看出,各期平差精度均在10 μGal以内。2017年第1期、2018年第2期和2020年第1期的观测仪器发生变更。在平差过程中,2016年第1期至2018年第1期的一次项格值系数采用广东省地震局的标定结果,2018年第2期到2019年第2期采用江苏省地震局的标定结果,2020年第1、2期采用广东省地震局的标定结果。2016年以来海南重力场差分动态变化见图 2。由图 2可知,2016-09~2017-05、2017-05~10、2018-05~10期间海南重力场变化异常明显,其中2016-09~2017-05期间出现NE向重力场正负差异达100 μGal,2017-05~10期间出现NE向重力场正负差异达90 μGal,2018-05~10期间琼西南地区出现40 μGal的重力场变化。异常明显的差分动态变化均发生于相邻两期仪器发生变更期间,如2016第2期的测量仪器为C232和C369,而2017年第1期的测量仪器为C509和C524。
|
|
表 1 流动重力观测时间、仪器型号、一次项格值系数和点值精度 Tab. 1 The mobile gravity observation time, instrument types, primary term scale coefficient and point values accuracy |
|
图 2 海南重力场差分动态变化 Fig. 2 The differential dynamic changes of gravity field in Hainan |
在目前常用的几种一次项格值系数改正方法中,区域适定法需要利用测区积累的多期资料;标定结果内插法需要利用多期基线场标定结果,时效性较差。因此,本文根据所用实测数据,选用重力差值法对一次项格值系数进行改正。
在平差计算仅采用2个测点进行基准约束时,一次项格值系数误差对重力点值的影响为:
| $ \Delta X = \Delta E\left( {{X_i} - G} \right) $ |
式中,ΔE为一次项格值系数误差;G为起算点基准值或拟稳点的重心基准值;Xi为第i个测点的重力值。为增加数据样本,将任意i、j两点的重力值相减组成重力段差DXij:
| $ {D_{{X_{ij}}}} = {X_j} - {X_i} $ |
则ΔE对DXij的影响为ΔDXij=ΔE(Xj-Xi),即格值系数误差对重力段差的影响与重力段差呈线性关系[2, 10]。相邻两期检测和改正一次项格值系数的基础是假设真实的重力场变化在短期内不会出现重力段差变化与重力差呈线性关系。2016年以来,海南流动重力测量仪器多次发生变更,本文以2016年第1期的一次项格值系数为基准,以每一期2台仪器观测数据的整体平差所得的重力值与2016年第1期的重力值计算重力差变化,以求取一次项系数改变量ΔE。
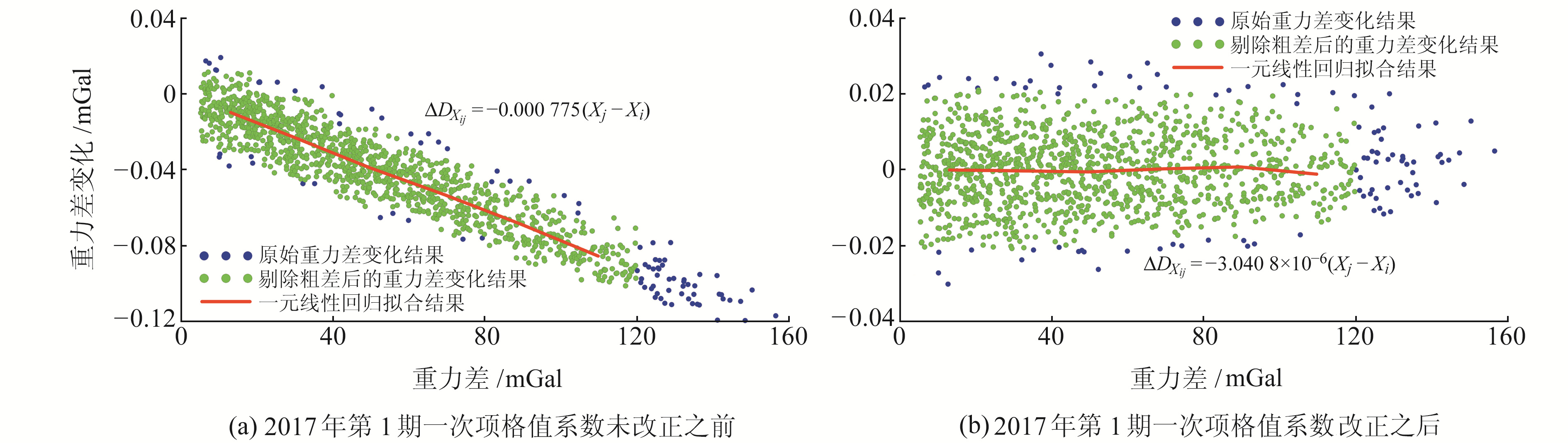
利用重力差值法对2016年第1期以后各期重力仪的一次项格值系数进行重新改正。以2016年第1期和2017年第1期为例,对重力段差值(DXij)与重力段差值变化(ΔDXij)的关系进行说明。图 3(a)中2017年第1期数据平差的仪器格值系数采用表 1中数值,在计算2016年第1期和2017年第1期重力段差值与重力段差值变化的关系过程中,对DXij和ΔDXij进行预处理来剔除粗差[6],以减弱随机误差对回归分析结果的影响。由图 3(a)可知,重力段差值与重力段差值变化具有明显的线性关系,对两者进行一元线性回归分析可得ΔDXij=-0.000 775(Xj-Xi),即一次项系数改变量ΔE为-0.000 775。因此,对2017年第1期2台仪器的格值系数均改正-0.000 775,以消除线性关系,然后重新进行平差,并比较一次项格值系数改正后两期平差结果的重力段差值与重力段差值变化的关系(图 3(b))。同时对两者关系进行一元线性回归分析可得ΔDXij=-3.040 8×10-6(Xj-Xi),一次项格值系数的改正量3.040 8×10-6远小于0.000 775,即改正后重力段差值变化几乎不受重力差值的影响,从而达到了消除两者线性关系的效果。
|
图 3 海南2016年第1期和2017年第1期重力段差值与重力段差值变化的关系 Fig. 3 The relationship between the gravity differences and the changes of gravity differences of the first period of 2016 and 2017 in Hainan |
对各期观测数据重新进行拟稳平差处理,得到一次项格值系数改正量、改正后的一次项格值系数和改正一次项格值系数后的平差精度(表 2)。由表 2可知,各期平差精度均小于10 μGal;2017年第1期一次项格值系数改正量最大,为0.000 775,其次为2019年第1期,为0.000 256 41,有7期观测仪器的一次项格值系数改正量超过0.000 1。
|
|
表 2 流动重力观测时间、仪器型号、改正后的一次项格值系数和点值精度 Tab. 2 The mobile gravity observation time, instrument types, corrected primary term scale coefficient and point values accuracy |
图 4为改正一次项格值系数后,2016年以来海南差分重力场动态变化。由图 4可知,2016年以来海南差分重力场变化较平稳,重力场变化基本在30 μGal以内。比较图 2和图 4可知,图 2中2016-09~2017-05、2017-05~10、2018-05~10的显著重力场异常在图 4中不存在。2019年第2期的观测仪器为C834和C845,而2020年第1期的观测仪器变更为C369和C526,仪器一次项格值系数的改正量为0.000 082 70(低于0.000 1)。图 2和图 4中2019-09~2020-03海南重力场变化存在差异,相对而言,图 4中琼东南地区的重力场变化高值区缩小,琼南地区的重力场变化正值区明显扩大。其他相邻两期的差分重力场动态变化与一次项格值系数未改正前的差分重力场动态变化也有所区别,但均无明显异常。

|
图 4 一次项格值系数改正后海南重力场差分动态变化 Fig. 4 The differential dynamic changes of gravity field after correcting the primary term scale coefficient in Hainan |
若未进行一次项格值系数改正,根据地震重力异常与地震孕育发生的关系可知[11],海南岛在2016-09~2017-05、2017-05~10、2018-05~10期间的显著重力场变化异常预示海南地区可能发生5级以上地震。但2016年以来,海南岛及近海仅发生2次MS3.0以上地震,分别为2019-08-20三亚MS3.5和MS4.2地震,且这些地震均位于海南南部,与图 2中揭示的3个重力场变化异常无明显对应关系,即上述重力场变化异常为虚假异常的可能性较大。
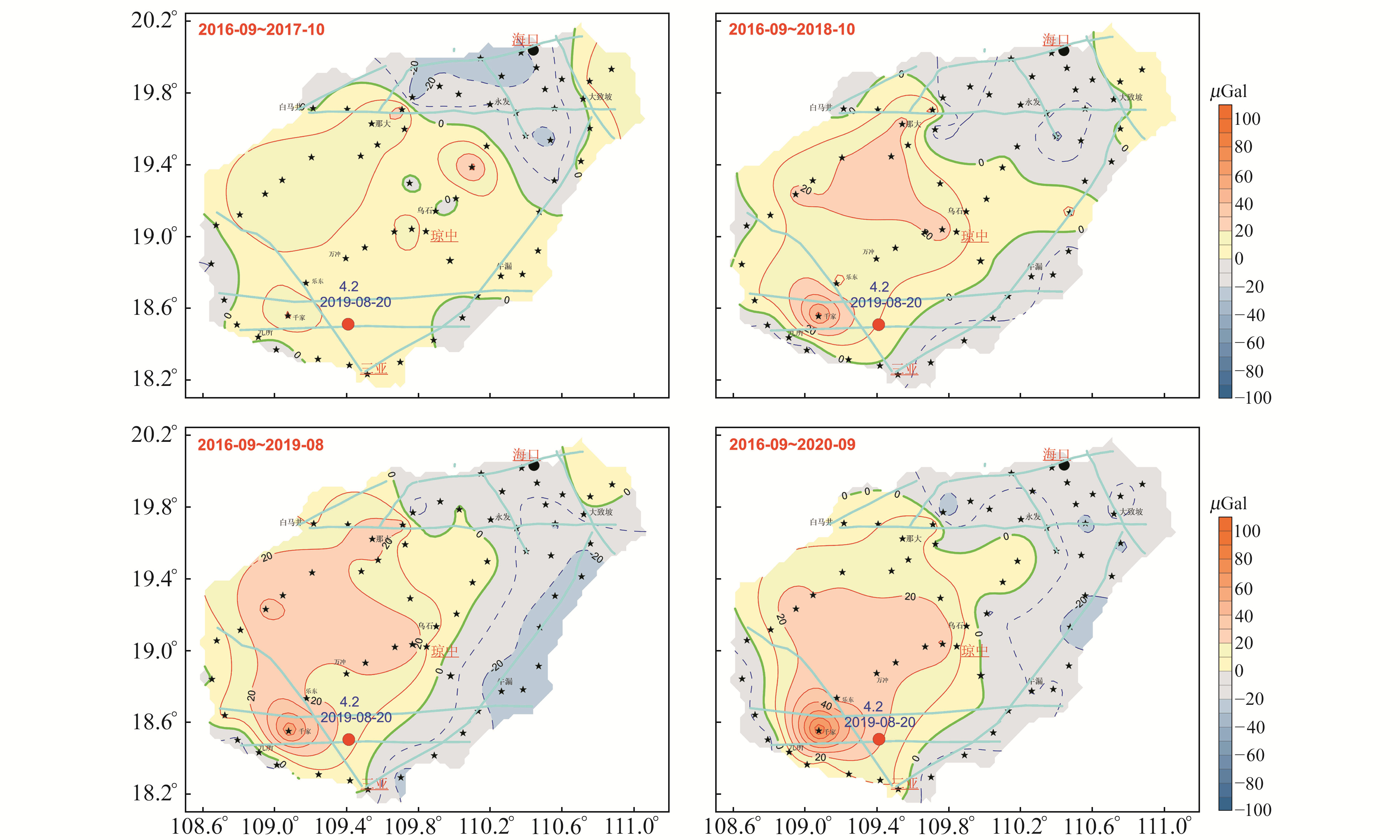
4 一次项格值系数改正后海南重力场累积动态变化与地震的关系从一次项格值系数改正后海南重力场累积动态变化来看(图 5),2017-10以来海南西南地区逐渐形成一个北西向的正负重力场变化异常梯度带,总体表现为自西北向东南由正转负的特征,其正负变化差异幅度也随着时间变化逐渐增大,至2019-08异常梯度带重力正负变化差异达50 μGal,范围约60 km。三亚MS3.5和MS4.2地震震中位于2016-09~2019-08累积重力变化异常梯度带上。胡敏章等[1]研究地震分析预报的重力异常指标认为,5级地震对应的重力异常变化范围约为140 km,而三亚地震震级小于5级,其异常范围也小于140 km。因此认为,虽然三亚4.2级地震前震中附近地区出现重力场异常变化,但这些异常特征尚未达到发生5级地震的条件。
|
图 5 海南重力场累积动态变化 Fig. 5 The accumulative dynamic changes of gravity field in Hainan |
1) CG-5重力仪一次项格值系数具有随时间变化的特征,在海南流动重力测网无法利用绝对重力值标定仪器一次项格值系数的情况下,采用重力差值法改正一次项格值系数,可有效降低因一次项格值系数误差产生的重力场变化误差,提高重力场变化特征分析的可靠性和科学性,进一步提高地震预测和震后趋势判定的准确性。尤其是2016年以来海南流动重力测量所使用的CG-5重力仪多次发生变更,相邻两期观测仪器一次项格值系数出现明显不匹配的现象,若不改正仪器一次项格值系数,基于海南重力测点重力值差最大约为160 mGal的情况,若一次项格值系数相差0.000 1,即可产生最大约为16 μGal的重力场变化误差,远大于平差精度,这会严重影响利用重力场变化预测区域地震趋势的准确性和客观性。
2) 利用改正后的一次项格值系数,重新采用拟稳平差法对海南2016年以来的流动重力观测资料进行处理,分析海南重力场变化特征。结果表明,2016年以来海南重力场差分动态变化较平稳,无显著异常。
3) 一次项格值系数改正后,海南累积重力场动态变化表明,2019-08-20三亚MS4.2地震前,2016-09~2018-10和2016-09~2019-08期间,震中附近地区出现重力场累积变化异常梯度带,但该区域无明显的活动断层分布,震前重力变化梯度带范围也小于100 km,重力场变化最大约为50 μGal。综合分析认为,该异常为三亚MS4.2地震的前兆异常。
致谢: 感谢中国地震局地震研究所郝洪涛博士提供重力差值法改正一次项格值系数软件。
| [1] |
胡敏章, 郝洪涛, 李辉, 等. 地震分析预报的重力变化异常指标分析[J]. 中国地震, 2019, 35(3): 417-430 (Hu Minzhang, Hao Hongtao, Li Hui, et al. Quantitative Analysis of Gravity Changes for Earthquake Prediction[J]. Earthquake Research in China, 2019, 35(3): 417-430 DOI:10.3969/j.issn.1001-4683.2019.03.001)
(  0) 0) |
| [2] |
郝洪涛, 李辉, 刘子维, 等. 基于重力差方法检测重力仪一次项格值系数变化[J]. 大地测量与地球动力学, 2011, 31(1): 87-90 (Hao Hongtao, Li Hui, Liu Ziwei, et al. Study on Change of Scale Parameters in Linear Term of Gravimeter with Gravity Difference Method[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 87-90)
(  0) 0) |
| [3] |
梁伟锋, 刘芳, 祝意青, 等. 重力仪一次项系数对重力场动态变化的影响研究[J]. 大地测量与地球动力学, 2015, 35(5): 882-886 (Liang Weifeng, Liu Fang, Zhu Yiqing, et al. Research on the Effect of One Degree Term of Chromatic Polynomial of Gravimeter on Gravity Dynamic Change[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 882-886)
(  0) 0) |
| [4] |
冯建林, 檀玉娟, 秦建增, 等. CG-5重力仪一次项格值系数对宁夏重力场变化的影响[J]. 大地测量与地球动力学, 2017, 37(3): 319-322 (Feng Jianlin, Tan Yujuan, Qin Jianzeng, et al. The Effect of One Degree Term of Chromatic Polynomial of CG-5 Gravimeter on Gravity Change in Ningxia Area[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 319-322)
(  0) 0) |
| [5] |
隗寿春, 祝意青, 赵云峰, 等. CG-5重力仪格值系数对重力数据处理的影响[J]. 大地测量与地球动力学, 2019, 39(2): 210-214 (Wei Shouchun, Zhu Yiqing, Zhao Yunfeng, et al. Impact on Gravity Data Process of Scale Factor Coefficient of CG-5 Gravimeter[J]. Journal of Geodesy and Geodynamics, 2019, 39(2): 210-214)
(  0) 0) |
| [6] |
刘绍府, 刘冬至, 李辉. 高精度重力测量平差及其软件[J]. 地震, 1991, 11(4): 57-66 (Liu Shaofu, Liu Dongzhi, Li Hui. Adjustment of High Precision Gravity Measurements and Its Software[J]. Earthquake, 1991, 11(4): 57-66)
(  0) 0) |
| [7] |
贾民育, 邢灿飞, 孙少安. 滇西实验场重力资料的最佳解[J]. 地震学报, 1994, 16(增1): 100-108 (Jia Minyu, Xing Canfei, Sun Shao'an. Optimum Solution of the Gravity Data in the Western Yunnan Experimental Field[J]. Acta Seismological Sinica, 1994, 16(S1): 100-108)
(  0) 0) |
| [8] |
孙少安, 项爱民, 吴维日. LCR-G型重力仪仪器参数的时变特征[J]. 大地测量与地球动力学, 2002, 22(2): 101-105 (Sun Shao'an, Xiang Aimin, Wu Weiri. Time-Varying Characteristics of LCR-G Gravimeter Parameters[J]. Journal of Geodesy and Geodynamics, 2002, 22(2): 101-105)
(  0) 0) |
| [9] |
Ukawa M, Nozaki K, Ueda H, et al. Calibration Shifts in Scintrex CG-3M Gravimeters with an Application to Detection of Microgravity Changes at Iwo-Tou Caldera, Japan[J]. Geophysical Prospecting, 2010, 58(6): 1123-1132
(  0) 0) |
| [10] |
郝洪涛, 李辉, 孙和平, 等. CG-5重力仪零漂改正及格值系数检测应用研究[J]. 武汉大学学报: 信息科学版, 2016, 41(9): 1265-1271 (Hao Hongtao, Li Hui, Sun Heping, et al. Application of Zero Drift Correct and Detection of Scale Parameters of CG-5 Gravimeter[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1265-1271)
(  0) 0) |
| [11] |
祝意青, 申重阳, 张国庆, 等. 我国流动重力监测预报发展之再思考[J]. 大地测量与地球动力学, 2018, 38(5): 441-446 (Zhu Yiqing, Shen Chongyang, Zhang Guoqing, et al. Rethinking the Development of Earthquake Monitoring and Prediction in Mobile Gravity[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 441-446)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

