当观测模型的系数阵呈良态时,最小二乘法能获得最优无偏的参数估值。然而,当模型的系数阵呈病态时,微小的观测误差会导致解的巨大波动,使常规最小二乘估计的解不可靠[1]。为此,学者们提出多种估计方法,如Tikhonov正则化、岭估计、截断奇异值分解(truncated singular value decomposition,TSVD)和Liu估计等[2-9]。目前关于病态模型的有偏性研究大都集中于Tikhonov正则化或TSVD正则化[10-12],鲜有涉及Liu估计的相关研究。不同于Tikhonov正则化,Liu估计除含有正则化参数外,还额外引入了一个修正因子,因此可更加灵活地处理病态问题[7-9]。但由于引入了正则化参数和修正因子,Liu估计是有偏的。事实上,Liu估计正是通过牺牲参数估值的无偏性来换取其有效性。
基于以上研究,本文首先分析了由于引进正则化参数和修正因子而导致的Liu估计解及其残差的偏差;然后将偏差从残差中扣除,并利用偏差改正后的残差导出Liu估计的单位权方差估计公式;最后用数值算例和病态测边网算例验证公式的有效性。
1 病态模型及其Liu估计解法测量上常用的Gauss-Markov模型为:
| $ \boldsymbol{y}=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{e} $ | (1) |
式中,y为m维观测向量,A为m×n的系数矩阵,x为n维未知参数,e为误差向量且满足E(e)=0, D(e)=σ02 P -1,其中,E(·)和D(·)分别为求数学期望和方差,σ02和P分别为先验单位权方差和观测值的权阵。考虑到不等权模型可变化为等权模型,为便于推导,此处设权阵为单位阵。式(1)的最小二乘估值为:
| $ \hat{\boldsymbol{x}}_{L}=\boldsymbol{N}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{y} $ | (2) |
式中,N = A T A。当系数矩阵病态时,最小二乘解变得极不可靠。Liu[7]采用Liu估计解算病态模型参数,其在最小二乘准则的基础上额外增加了一个约束项,即
| $ \boldsymbol{e}^{\mathrm{T}} \boldsymbol{e}+\boldsymbol{f}^{\mathrm{T}} \boldsymbol{f}=\min $ | (3) |
式中,f =
| $ \hat{\boldsymbol{x}}_{\mathrm{Liu}}=\boldsymbol{Q}_{\kappa}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{y}-d \hat{\boldsymbol{x}}\right) $ | (4) |
式中,Q κ=(A T A +κ I n)-1,κ>0为正则化参数,d为修正因子,
当式(4)中
| $ \hat{\boldsymbol{x}}_{\mathrm{Liu}}=\left(\boldsymbol{Q}_{\kappa}-d \boldsymbol{Q}_{\kappa}^{2}\right) \boldsymbol{A}^{\mathrm{T}} \boldsymbol{y} $ | (5) |
将式(5)代入式(1)中可得残差:
| $ \hat{\boldsymbol{e}}=\left(\boldsymbol{I}_{m}-\boldsymbol{A}\left(\boldsymbol{Q}_{k}-d \boldsymbol{Q}_{k}^{2}\right) \boldsymbol{A}^{\mathrm{T}}\right) \boldsymbol{y} $ | (6) |
对式(6)两边取期望,得:
| $ E(\hat{\boldsymbol{e}})=\boldsymbol{A}\left((\kappa+d) \boldsymbol{Q}_{\kappa}-\kappa d \boldsymbol{Q}_{\kappa}^{2}\right) \boldsymbol{x} $ | (7) |
显然,由于Liu估计引入了κ和d,导致E(
当式(4)中
| $ \hat{\boldsymbol{x}}_{\mathrm{Liu}}=\left(\boldsymbol{Q}_{k} \boldsymbol{A}^{\mathrm{T}}-d \boldsymbol{Q}_{\kappa} \boldsymbol{N}^{-1} \boldsymbol{A}^{\mathrm{T}}\right) \boldsymbol{y} $ | (8) |
将式(8)代入式(1),可得残差为:
| $ \hat{\boldsymbol{e}}=\left(\boldsymbol{I}_{m}-\boldsymbol{A} \boldsymbol{Q}_{\kappa}\left(\boldsymbol{I}_{n}-d \boldsymbol{N}^{-1}\right) \boldsymbol{A}^{\mathrm{T}}\right) \boldsymbol{y} $ | (9) |
对式(9)取期望可得残差的偏差:
| $ E(\hat{\boldsymbol{e}})=(\alpha+d) \boldsymbol{A} \boldsymbol{Q}_{\kappa} \boldsymbol{x} $ | (10) |
传统基于残差计算单位权方差的公式为:
| $ \hat{\sigma}_{0}^{2}=\frac{\hat{\boldsymbol{e}}^{\mathrm{T}} \hat{\boldsymbol{e}}}{m-n} $ | (11) |
但Liu估计的残差是有偏的,因此采用式(11)计算的单位权方差显然也是有偏的。为能够应用残差估计单位权方差,须对残差中的偏差进行改正。当
| $ \begin{gathered} \overline{\boldsymbol{e}}=\hat{\boldsymbol{e}}-E(\hat{\boldsymbol{e}})= \\ \left(\boldsymbol{I}_{m}-\boldsymbol{A}\left(\boldsymbol{Q}_{\kappa}+\kappa \boldsymbol{Q}_{\kappa}^{2}-\kappa d \boldsymbol{Q}_{\kappa}^{3}\right) \boldsymbol{A}^{\mathrm{T}}\right) \boldsymbol{y} \end{gathered} $ | (12) |
式中,
| $ \begin{aligned} D(\overline{\boldsymbol{e}})=& \sigma_{0}^{2}\left(\boldsymbol{I}_{m}-\boldsymbol{A}\left(\boldsymbol{Q}_{\kappa}+\kappa \boldsymbol{Q}_{\kappa}^{2}-\kappa d \boldsymbol{Q}_{\kappa}^{3}\right) \boldsymbol{A}^{\mathrm{T}}\right)\cdot \\ &\left(\boldsymbol{I}_{m}-\boldsymbol{A}\left(\boldsymbol{Q}_{\kappa}+\kappa \boldsymbol{Q}_{\kappa}^{2}-\kappa d \boldsymbol{Q}_{\kappa}^{3}\right) \boldsymbol{A}^{\mathrm{T}}\right) \end{aligned} $ | (13) |
令H =(Q κ+κ Q κ2-κd Q κ3) N,推导可得:
| $ \begin{gathered} \operatorname{tr}(\boldsymbol{H})=n-\kappa(\kappa+d) \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{2}\right)+\kappa^{2} d \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{3}\right) ,\\ \operatorname{tr}\left(\boldsymbol{H}^{2}\right)=n-2 \kappa(\kappa+d) \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{2}\right)+ \\ 2 \kappa^{2} d \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{3}\right)+\kappa^{2}(\kappa+d)^{2} \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{4}\right)- \\ 2 \kappa^{3} d(\kappa+d) \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{5}\right)+\kappa^{4} d^{2} \operatorname{tr}\left(\boldsymbol{Q}_{k}^{6}\right) \end{gathered} $ | (14) |
则方差阵的迹为:
| $ \begin{gathered} \operatorname{tr}(D(\overline{\boldsymbol{e}}))=\sigma_{0}^{2}\left(m-2 \operatorname{tr}(\boldsymbol{H})+\operatorname{tr}\left(\boldsymbol{H}^{2}\right)\right)= \\ \sigma_{0}^{2}\left(m-n+\kappa^{2}(\kappa+d)^{2} \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{4}\right)-\right. \\ \left.2 \kappa^{3} d(\kappa+d) \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{5}\right)+\kappa^{4} d^{2} \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{6}\right)\right) \end{gathered} $ | (15) |
由二次型的数学期望公式有:
| $ E\left(\overline{\boldsymbol{e}}^{\mathrm{T}} \overline{\boldsymbol{e}}\right)=\operatorname{tr}(D(\overline{\boldsymbol{e}}))+E(\overline{\boldsymbol{e}})^{\mathrm{T}} E(\overline{\boldsymbol{e}}) $ | (16) |
经过偏差改正后,
| $ \hat{\sigma}_{0}^{2}=\frac{\overline{\boldsymbol{e}}^{\mathrm{T}} \overline{\boldsymbol{e}}}{\left(m-n+\kappa^{2}(\kappa+d)^{2} \operatorname{tr}\left(\boldsymbol{Q}_{k}^{4}\right)-2 \kappa^{3} d(\kappa+d) \operatorname{tr}\left(\boldsymbol{Q}_{k}^{5}\right)+\kappa^{4} d^{2} \operatorname{tr}\left(\boldsymbol{Q}_{k}^{6}\right)\right)} $ | (17) |
当
| $ \begin{gathered} \overline{\boldsymbol{e}}=\hat{\boldsymbol{e}}-E(\hat{\boldsymbol{e}})= \\ \left(\boldsymbol{I}_{m}-\boldsymbol{A}\left(\boldsymbol{Q}_{\kappa}-d \boldsymbol{Q}_{\kappa} \boldsymbol{N}-1+(\kappa+d) \boldsymbol{Q}_{\kappa}^{2}\right) \boldsymbol{A}^{\mathrm{T}}\right) \boldsymbol{y} \end{gathered} $ | (18) |
其方差为:
| $ D(\overline{\boldsymbol{e}})=\sigma_{0}^{2}\left(\boldsymbol{I}_{m}-\boldsymbol{K}-\boldsymbol{K}^{\mathrm{T}}-\boldsymbol{K} \boldsymbol{K}^{\mathrm{T}}\right) $ | (19) |
式中,K = A (Q κ-d Q κ N -1+(κ+d) Q κ2) A T。推导可得:
| $ \begin{aligned} &\operatorname{tr}(\boldsymbol{K})=\operatorname{tr}\left(\boldsymbol{K}^{\mathrm{T}}\right)=n-\kappa(\kappa+d) \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{2}\right), \\ &\operatorname{tr}\left(\boldsymbol{K} \boldsymbol{K}^{\mathrm{T}}\right)=n-2 \kappa(\kappa+d) \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{2}\right)+ \\ &\ \ \ \ \sum\limits_{i=1}^{4} h_{i} \operatorname{tr}\left(\boldsymbol{M}_{i}\right)+g_{i} \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{i}\right) \end{aligned} $ | (20) |
式中,
| $ \begin{aligned} &h_{1}=\kappa d, h_{2}=\kappa d(\kappa+d), \\ &h_{3}=-\kappa^{2} d(\kappa+d), h_{4}=-d, \\ &g_{1}=d, g_{2}=0, g_{3}=-\kappa d(\kappa+d) ,\\ &g_{4}=\kappa^{2}(\kappa+d)^{2}, \\ &\boldsymbol{M}_{1}=\boldsymbol{N}^{-1} \boldsymbol{Q}_{\kappa}, \boldsymbol{M}_{2}=\boldsymbol{N}^{-1} \boldsymbol{Q}_{\kappa}^{2} ,\\ &\boldsymbol{M}_{3}=\boldsymbol{N}^{-1} \boldsymbol{Q}_{\kappa}^{3}, \boldsymbol{M}_{4}=\boldsymbol{N}^{-1} \end{aligned} $ | (21) |
则D(
| $ \begin{gathered} \operatorname{tr}(D(\hat{\boldsymbol{e}}))= \\ \sigma_{0}^{2}\left(m-n+\sum\limits_{i=1}^{4} h_{i} \operatorname{tr}\left(\boldsymbol{M}_{i}\right)+g_{i} \operatorname{tr}\left(\boldsymbol{Q}_{k}^{i}\right)\right) \end{gathered} $ | (22) |
顾及式(16)可得单位权方差:
| $ \sigma_{0}^{2}=\frac{\overline{\boldsymbol{e}}^{\mathrm{T}} \overline{\boldsymbol{e}}}{m-n+\sum\limits_{i=1}^{4} h_{i} \operatorname{tr}\left(\boldsymbol{M}_{i}\right)+g_{i} \operatorname{tr}\left(\boldsymbol{Q}_{\kappa}^{i}\right)} $ | (23) |
Hilbert矩阵是一类典型的病态矩阵,假设A ∈ R m×n为某一Hilbert矩阵,其元素构成为:
| $ a_{i j}=\frac{1}{i+j-1}, 1 \leqslant i \leqslant m, 1 \leqslant j \leqslant n $ | (24) |
本文取m=11、n=9。假设未知参数的真值均为1,则不含误差的常数项为y =[2.83 1.93 1.52 1.27 1.10 0.97 0.87 0.79 0.72 0.67 0.62]T。本算例中,法矩阵的条件数为3.43×1017,严重病态。按照式(1)分别往常数项中添加不同量级的误差(σ0=0.1、0.01、0.001),分别采用最小二乘法和Liu估计法估计未知参数,比较其估值
|
|
表 1 σ0=0.1时不同算法解算的参数估值 Tab. 1 Parameter estimates derived by different approaches when σ0=0.1 |
|
|
表 2 σ0=0.01时不同算法解算的参数估值 Tab. 2 Parameter estimates derived by different approaches when σ0=0.01 |
|
|
表 3 σ0=0.001时不同算法解算的参数估值 Tab. 3 Parameter estimates derived by different approaches when σ0=0.001 |
|
|
表 4 本文公式和传统公式估计的单位权方差 Tab. 4 The unit weight variance estimated by traditional formula and formula in this paper |
可以看出,使用最小二乘法时,估值与真值的差值范数分别为3.67×106(σ0=0.1)、1.47×106(σ0=0.01)和9.13×104(σ0=0.001)。在添加了不同量级的误差后,Liu估计能够有效地抵御模型的病态性影响,参数估值的精度较最小二乘解有大幅提升。当
模拟500次实验,每次实验均按上述策略随机添加误差,分别采用传统公式与本文公式估计单位权方差,结果如图 1所示。由于Liu估计的偏差性,传统公式估计的单位权方差与模拟真值的偏差较大,当消除了残差中的偏差之后,本文公式估计的单位权方差与真值更为接近。当
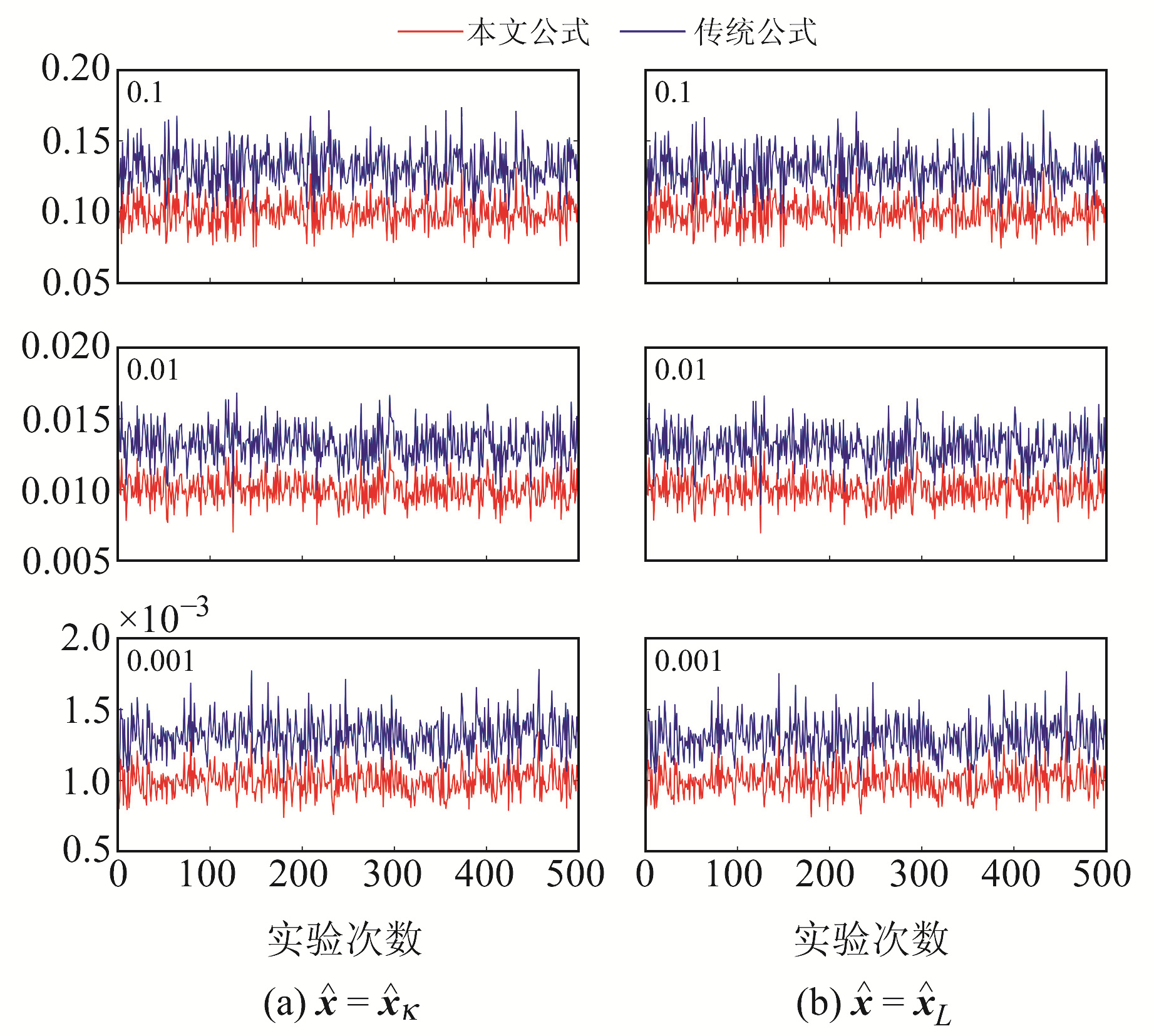
|
图 1 500次实验2种方法估计的单位权方差 Fig. 1 The unit weight variance estimated by two approaches for 500 experiments |
为进一步验证本文公式的有效性,模拟一个病态测边网。图 2为网的点位平面分布,其中共有11个点位,包括9个已知点P1~P9和2个未知点P10、P11,P10和P11的真实坐标分别为(0, 0, 0)和(7, 10, -5)。表 5为P10、P11坐标及其到已知点的距离观测值,各观测值的精度均为5 mm。现要求利用这些距离观测值求解未知点的坐标。本算例中,由于测边网的几何构型较差,其观测方程的法矩阵条件数为4.585 1×103,存在病态。
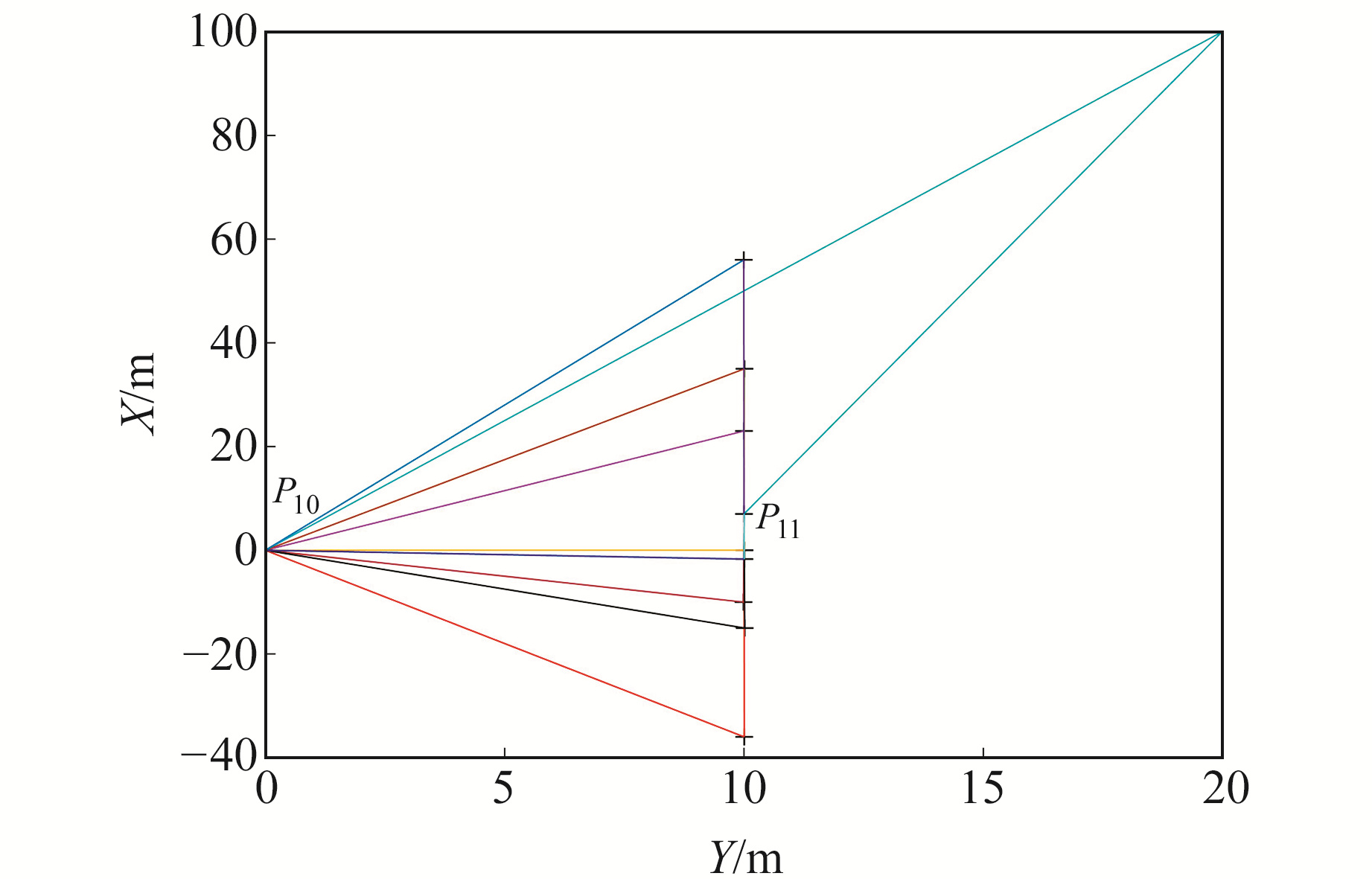
|
图 2 空间测边网的点位平面分布 Fig. 2 The distribution of the points of the space net in XY plane |
|
|
表 5 控制点的坐标及距离观测值 Tab. 5 The coordinates and distance observations of control points |
分别采用最小二乘法和Liu估计法求解坐标,结果如表 6所示。与数值算例类似,最小二乘解与真实坐标存在较大偏差,与真值的差值范数为2.659 4;而Liu估计则与真实坐标较为接近,与真值的差值范数仅为为0.277 0(
|
|
表 6 不同算法解算的参数估值及与真值的差值范数 Tab. 6 Parameter estimates derived by different approaches and norms of their differences with true values |
模拟500实验,每次实验均按相同策略向观测值中添加随机误差,分别采用传统公式和本文公式估计单位权方差,结果如图 3所示。由图可知,本文公式估计的单位权方差小于传统公式,当
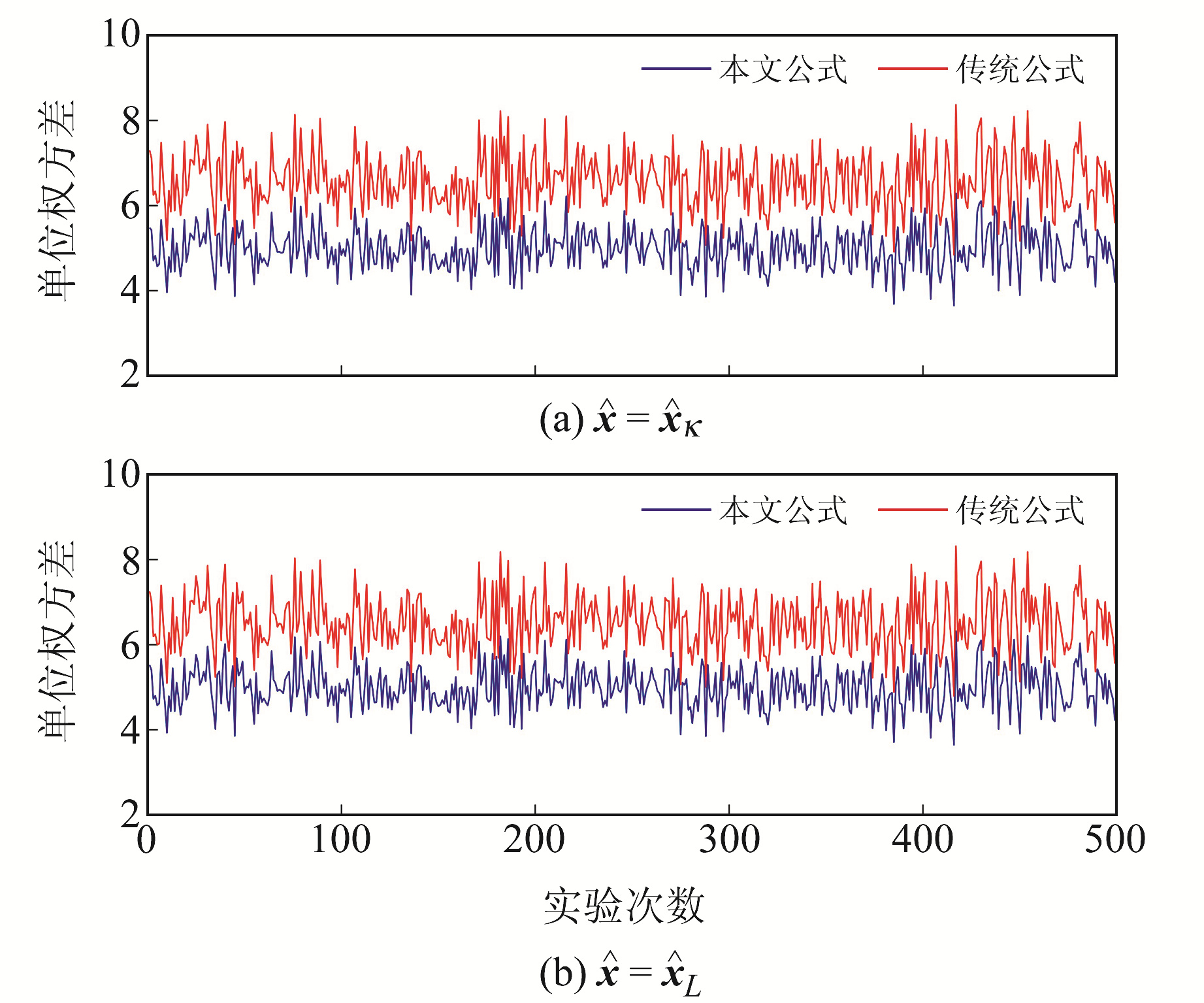
|
图 3 500次实验2种方法估计的单位权方差 Fig. 3 The unit weight variance estimated by two approaches for 500 experiments |
Liu估计是病态模型的常用解法之一,其通过引入正则化参数和修正因子有效地削弱了系数阵小奇异值对参数估值及其方差的放大,但同时也引进了偏差,进一步导致其残差也是有偏的。本文首先计算了Liu估计残差的偏差,并将其从残差中剔除,得到偏差改正后的残差;然后基于向量二次型的数学期望公式,利用改正后的残差导出Liu估计的单位权方差估计公式;最后设计2个算例对本文公式进行验证。结果表明,残差中的偏差会严重影响单位权方差的估计,在将偏差从残差中扣除后,利用改正后的残差估计的单位权方差更符合实际情形。
| [1] |
Johansen T A. On Tikhonov Regularization, Bias and Variance in Nonlinear System Identification[J]. Automatica, 1997, 33(3): 441-446 DOI:10.1016/S0005-1098(96)00168-9
(  0) 0) |
| [2] |
Tikhonov A N. Regularization of Ill-Posed Problems[J]. Doklady Akademii Nauk SSSR, 1963, 151(1): 49-52
(  0) 0) |
| [3] |
Xu P L. Truncated SVD Methods for Discrete Linear Ill-Posed Problems[J]. Geophysical Journal International, 1998, 135(2): 505-514 DOI:10.1046/j.1365-246X.1998.00652.x
(  0) 0) |
| [4] |
Hansen P C. Truncated Singular Value Decomposition Solutions to Discrete Ill-Posed Problems with Ill-Determined Numerical Rank[J]. SIAM Journal on Scientific and Statistical Computing, 1990, 11(3): 503-518 DOI:10.1137/0911028
(  0) 0) |
| [5] |
Xu P L. Iterative Generalized Cross-Validation for Fusing Heteroscedastic Data of Inverse Ill-Posed Problems[J]. Geophysical Journal International, 2009, 179(1): 182-200 DOI:10.1111/j.1365-246X.2009.04280.x
(  0) 0) |
| [6] |
Fierro R D, Hansen P C. Accuracy of TSVD Solutions Computed from Rank-Revealing Decompositions[J]. Numerische Mathematik, 1995, 70(4): 453-471 DOI:10.1007/s002110050128
(  0) 0) |
| [7] |
Liu K J. Using Liu-Type Estimator to Combat Collinearity[J]. Communications in Statistics-Theory and Methods, 2003, 32(5): 1009-1020 DOI:10.1081/STA-120019959
(  0) 0) |
| [8] |
Liu X Q. Improved Liu Estimator in a Linear Regression Model[J]. Journal of Statistical Planning and Inference, 2011, 141(1): 189-196 DOI:10.1016/j.jspi.2010.05.030
(  0) 0) |
| [9] |
Li Y L, Yang H. A New Liu-Type Estimator in Linear Regression Model[J]. Statistical Papers, 2012, 53(2): 427-437 DOI:10.1007/s00362-010-0349-y
(  0) 0) |
| [10] |
Xu P L, Shen Y Z, Fukuda Y, et al. Variance Component Estimation in Linear Inverse Ill-Posed Models[J]. Journal of Geodesy, 2006, 80(2): 69-81 DOI:10.1007/s00190-006-0032-1
(  0) 0) |
| [11] |
沈云中, 刘大杰. 正则化解的单位权方差无偏估计公式[J]. 武汉大学学报: 信息科学版, 2002, 27(6): 604-606 (Shen Yunzhong, Liu Dajie. Unbiased Estimation Formula of Unit Weight Mean Square Error in Regularization Solution[J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 604-606)
(  0) 0) |
| [12] |
嵇昆浦, 沈云中. TSVD正则化解法的单位权方差无偏估计[J]. 武汉大学学报: 信息科学版, 2020, 45(4): 626-632 (Ji Kunpu, Shen Yunzhong. Unbiased Estimation of Unit Weight Variance by TSVD Regularization[J]. Geomatics and Information Science of Wuhan University, 2020, 45(4): 626-632)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

