地球自转参数(earth rotation parameters, ERP)包括反映地球自转轴相对于地壳运动的极移运动参数XP和YP、反映地球自转角不规则特征的UT1-UTC和反映地球自转速率变化的日长变化参数LOD[1]。这些参数对于建立和维持天球参考框架与地球参考框架以及实现两者之间的相互转化极为重要,同时也影响协调世界时与世界时等系统间的相互计算[2]。
甚长基线干涉测量(very long baseline interferometry, VLBI)是可以高精度解算所有地球定向参数的大地测量技术[3],其在诸多地球自转参数解算方法中具有一定优势。本文基于2020年VLBI观测资料进行地球自转参数序列解算和精度分析,同时选取其中某一时段的解算结果与同时段利用GPS技术解算的结果进行比较,以分析2种技术的解算差异。考虑到国际VLBI服务组织(IVS)发布的CONT17连续加密观测资料稳定性强、观测精度高,而目前利用其XA、XB两种频率通道分别解算地球自转参数并对两者解算性能进行比较的研究较少,因此本文将同时对该方面进行研究。
1 精度评价VLBI解算地球自转参数的原理可参考文献[4-5],本文不再赘述。
将由VLBI观测资料解算的地球自转参数序列(记为ERPVLBI)与IERS发布的EOP14 C04序列(记为ERPIERS)作差,差值均方根可作为一种外符合精度并以此来评定解算精度[6]。设序列长度为n,则外符合精度计算公式可表示为:
| $ {\rm{RMS = }}\sqrt {\left( {\sum\limits_1^n {{{\left( {{\rm{ER}}{{\rm{P}}_{{\rm{VLBI}}}} - {\rm{ER}}{{\rm{P}}_{{\rm{IERS}}}}} \right)}^2}} } \right)/n} $ | (1) |
本文实验数据来自IVS发布的观测资料(https://ivscc.gsfc.nasa.gov/sessions/2020/),时间段为2020-01-01~11-19(简化儒略日为58 849~59 172),且优先选用观测精度较高的XA、XE频率通道数据[4]。在解算策略上,岁差/章动模型为IAU2006/2000A,解算基准为国际地球参考框架ITRF2014和国际天球参考框架ICRF3,对流层映射函数选取VMF3模型,电离层延迟等信息由观测文件读取,射电源位置的先验值取自IVS发布的结果,台站位置改正顾及固体潮汐、海洋潮汐、大气负载等因素的影响。LOD序列实际上可通过UT1-UTC序列转换得到,因此本文仅解算极移序列与UT1-UTC序列。
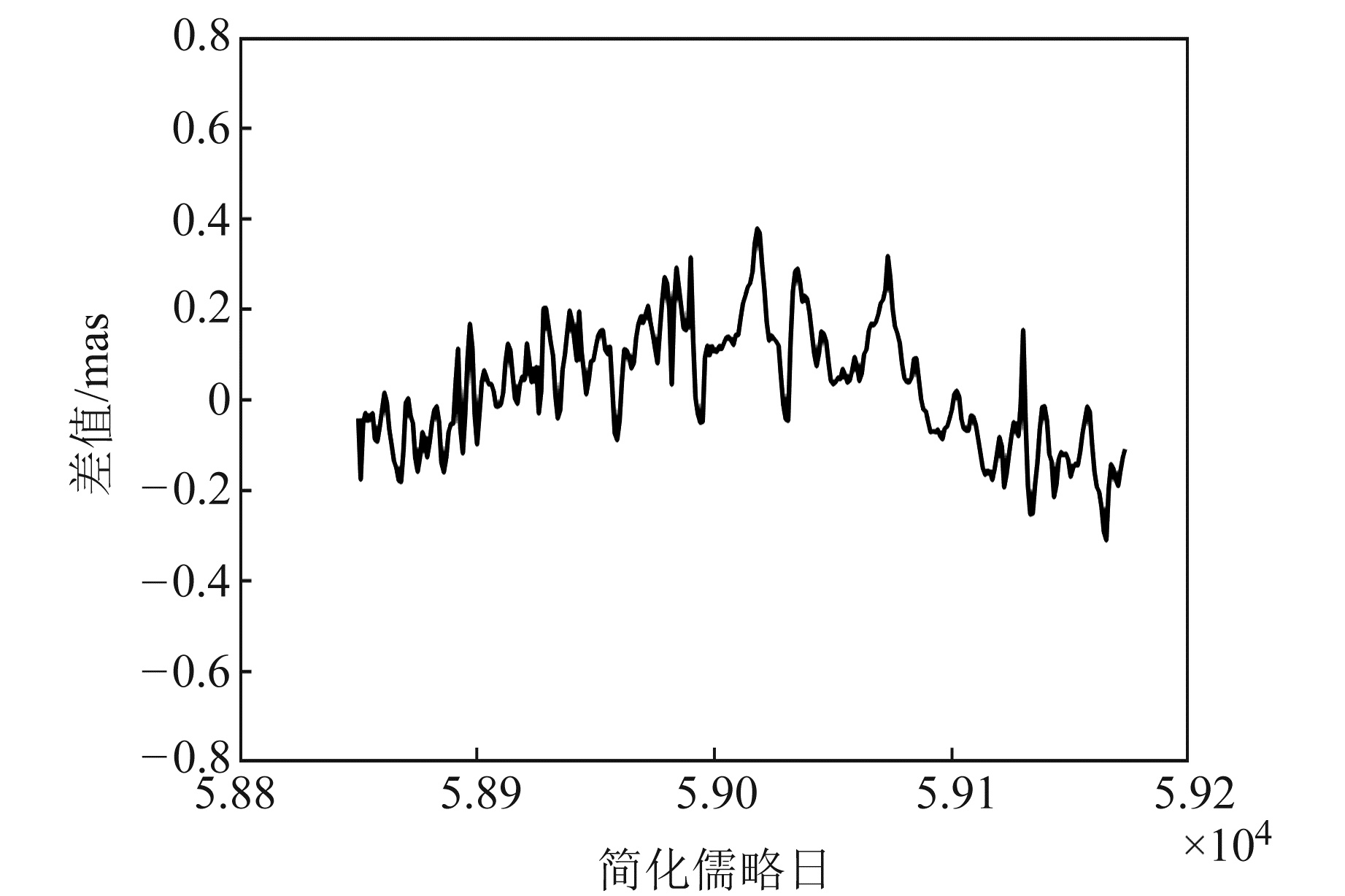
VLBI观测不连续,所选时段内的观测文件数目仅为130,因此在解算完成后通过三次样条插值得到整个时间段的参数序列。IERS发布的EOP14 C04序列参数值为每日0时的计算结果,而VLBI观测文件却并不严格以0时作为起始观测时刻,因此需要将VLBI解算结果转化为与EOP14 C04序列对应时刻的参数序列。图 1~3分别为VLBI解算结果插值得到的各参数序列(XP、YP、UT1-UTC)与EOP14 C04序列之差。
|
图 1 极移X方向差值 Fig. 1 Polar motion differences in X direction |

|
图 2 极移Y方向差值 Fig. 2 Polar motion differences in Y direction |
|
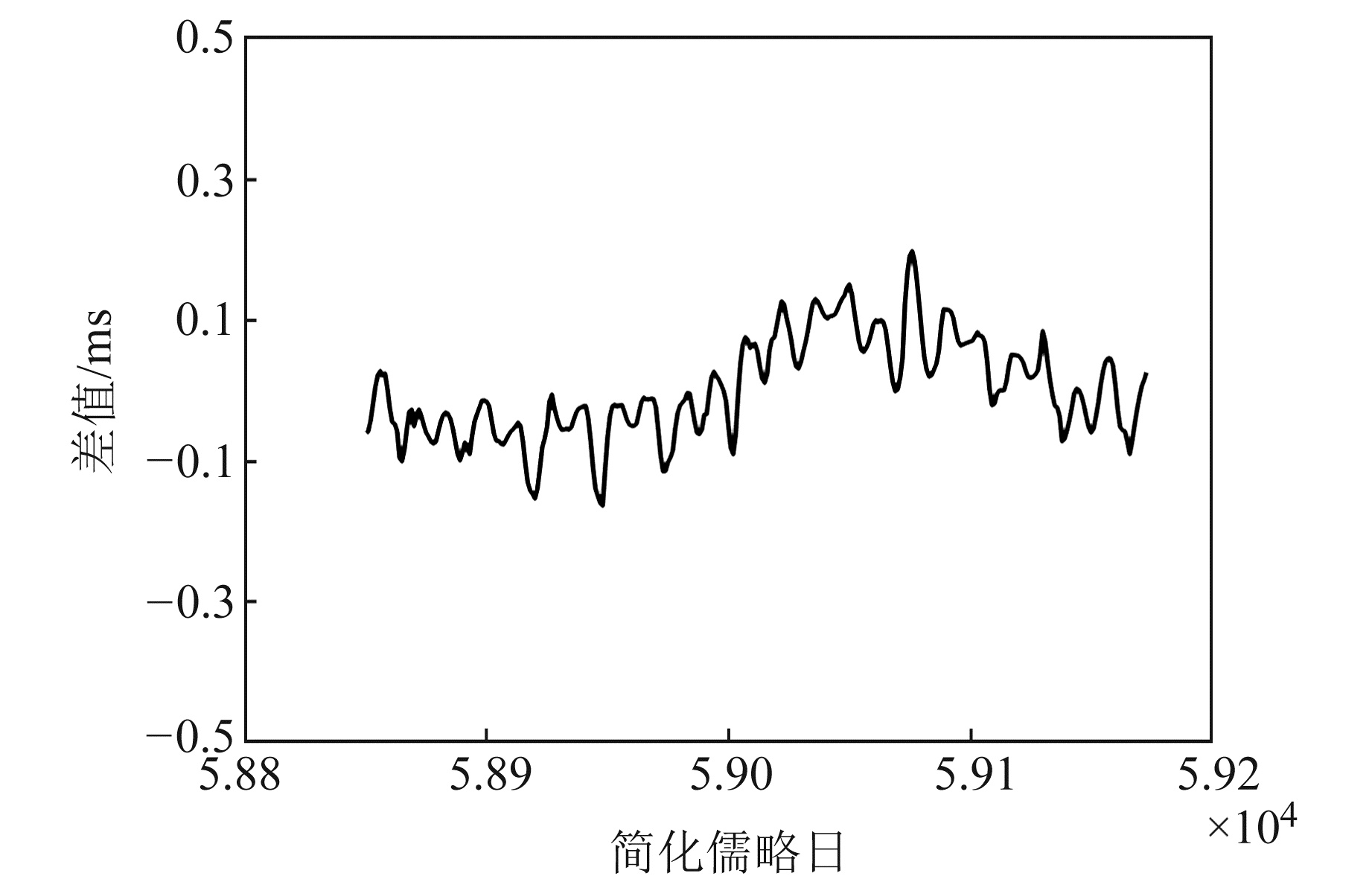
图 3 UT1-UTC差值 Fig. 3 Differences of UT1-UTC |
从图 1~3可以看出,3种参数的残差序列均未表现出明显的系统误差,XP与YP残差序列主要集中在-0.2~0.2 mas之间,UT1-UTC残差序列主要集中在-0.1~0.1 ms之间。表明VLBI解算结果与IERS发布的真值序列基本一致。3种残差序列在部分时段出现离群值,这可能是由该时段参与解算的观测台站过少或插值过程引起的。总体来说,残差序列均存在一定波动,说明目前VLBI技术的观测稳定性还有待提升。表 1为3种差值序列信息统计,包括各差值序列的绝对值最大值、序列均值以及根据式(1)计算得到的均方根值。解算结果与前人研究成果[4, 7-8]基本处于同一精度水平,表明本文结果具有可靠性和高精度。
|
|
表 1 差值序列信息 Tab. 1 Information of difference sequences |
为进一步比较VLBI的解算精度,从解算结果中选取2020-10-01~15的参数序列,与同时段利用GAMIT 10.7软件解算的GPS数据得到的参数序列进行比较。所选用的IGS站点在全球分布均匀,图 4为VLBI和GPS站点分布情况。GAMIT解算策略中,大部分选项保持默认,参数模型与VLBI解算过程保持一致。GPS数据无法直接求解UT1-UTC序列,因此给予其强约束(本文设为10 μs)来实现间接求解[8]。分别计算2种技术解算结果的外符合精度,结果见表 2。

|
图 4 VLBI及GPS站分布 Fig. 4 Distribution of VLBI and GPS stations |
|
|
表 2 VLBI与GPS解算结果的外符合精度统计 Tab. 2 Statistics of external coincidence accuracy of VLBI and GPS solution |
从表 2可以看出,GPS解算的3个参数序列的精度均略优于VLBI,但基本可认为两者处于同一水平。考虑到GPS技术在该时段内可保持数据连续、数据量充足且所选测站在全球均匀分布的相对优势,同时VLBI和GPS台站分布不一致、所选实验时段随机也会产生一定影响,故认为这种差距并不影响VLBI解算结果的高精度特点。
2.2 利用CONT17连续加密观测资料解算ERPIVS每次连续加密观测持续时间约为15 d,可提供连续、丰富的高精度原始观测资料,也是当前VLBI观测的最高精度,对于实现地球自转参数的连续高精度解算具有重要作用[9]。IVS最近一次连续加密观测为CONT17,观测时间为2017-11-28~12-12[10],观测资料全部为观测精度较高的X波段,且分别采用XA、XB频率通道。本次实验将分别利用这2种频道数据解算地球自转参数序列,同时以EOP14 C04序列作为外部参考序列计算其外符合精度,以比较分析2种频道数据的解算结果。实验数据处理策略与§2.1保持一致。图 5~7为解算完成后的XP、YP、UT1-UTC序列与EOP14 C04相应参数序列的差值结果。

|
图 5 2种频道解算的极移X方向外符合差值 Fig. 5 The external coincidence differences of polar motion in X direction solved by two frequencies |

|
图 6 2种频道解算的极移Y方向外符合差值 Fig. 6 The external coincidence differences of polar motion in Y direction solved by two frequencies |
|
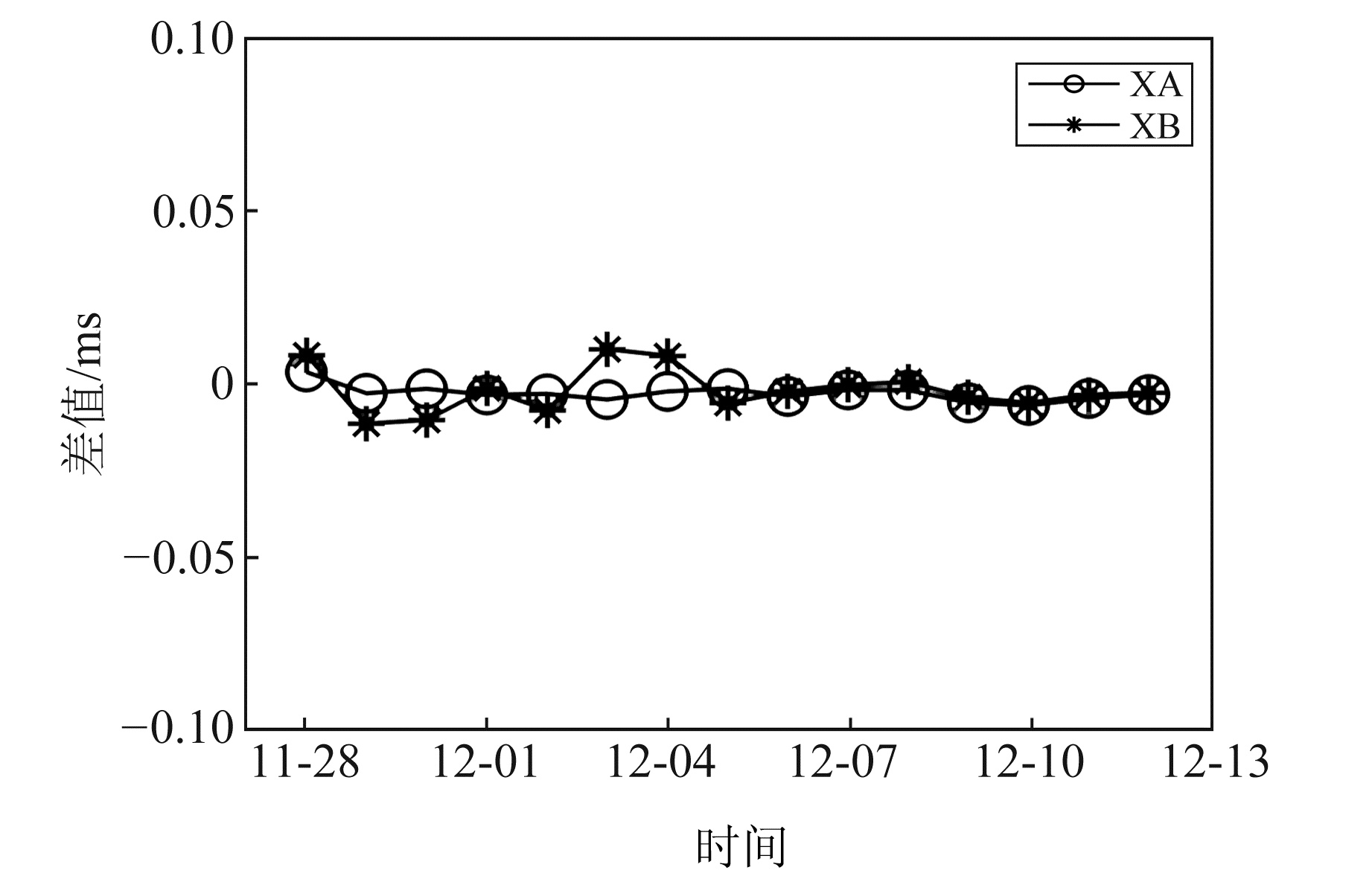
图 7 2种频道解算的UT1-UTC外符合差值 Fig. 7 The external coincidence differences of UT1-UTC solved by two frequencies |
从图 5~7可以看出,利用2种频道数据进行解算,XP、YP差值序列均位于-0.1~0.1 mas之间,UT1-UTC差值序列位于-0.02~0.01 ms之间。若不考虑时段影响,该结果远好于§2.1的差值结果。这是由于CONT17观测资料在实验时段内保持连续,在解算完成后无需进行大量缺失数据的插值工作,不会受到插值方法的影响,因此可保障其解算结果的高精度。XA频道的差值序列均相对平缓,而XB频道的差值序列则表现出一定的波动性,且这种波动在极移分量序列中表现更为明显,表明在解算地球自转参数时,利用XA频道数据解算得到的结果更稳定。
表 3为分别利用2种频道数据解算各参数序列的外符合精度。可以看出,XA频道与XB频道在解算2个极移分量参数序列时差距微小,可认为处于同一精度水平;而在解算UT1-UTC序列时,相比于XB频道,XA频道解算的外符合精度具有明显提升,提升效果可达50%。综上可知,利用2种频道数据解算的结果均处于高精度水平,而考虑到解算结果的稳定性及UT1-UTC序列外符合精度的差异,利用XA频道数据解算地球自转参数序列更具有优势。
|
|
表 3 2种频道解算结果的外符合精度统计 Tab. 3 Statistics of external coincidence accuracy solved by two frequencies |
本文利用2020年VLBI观测资料解算地球自转参数序列,并以EOP14 C04序列作为外部参考序列计算外符合精度。结果表明,利用VLBI技术解算地球自转参数的结果满足高精度要求。将本文计算结果与同时段GPS观测数据解算的地球自转参数结果进行对比。结果表明,VLBI技术的解算精度与GPS技术差距很小,这种差距很可能与实验所选取的时段、GPS测站在全球均匀分布且观测数据连续有关。同时,本文首次根据CONT17连续加密观测资料的XA、XB频率通道数据分别解算地球自转参数并比较其解算性能。结果表明,2种频道数据解算的地球自转参数序列均具有高精度,但在解算结果的稳定性及UT1-UTC序列的解算精度方面,XA频道数据优势更大。
| [1] |
王新静, 袁运斌, 潭冰峰, 等. 用GPS观测资料解算地球自转参数的方法及影响因素分析[J]. 大地测量与地球动力学, 2016, 36(10): 902-906 (Wang Xinjing, Yuan Yunbin, Tan Bingfeng, et al. Estimation of the ERPs Based on GPS Data and the Analysis of the Impact Factor[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 902-906)
(  0) 0) |
| [2] |
Wei E H, Yan W, Jin S G, et al. Improvement of Earth Orientation Parameters Estimate with Chang'E-1 ΔVLBI Observations[J]. Journal of Geodynamics, 2013, 72: 46-52 DOI:10.1016/j.jog.2013.04.001
(  0) 0) |
| [3] |
张志斌, 王广利, 刘祥, 等. 中国VLBI网观测地球定向参数能力分析[J]. 武汉大学学报: 信息科学版, 2013, 38(8): 911-915 (Zhang Zhibin, Wang Guangli, Liu Xiang, et al. Analysis of EOP Determination via Chinese VLBI Network[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 911-915)
(  0) 0) |
| [4] |
魏二虎, 刘文杰, Wei J N, 等. VLBI和GPS观测联合解算地球自转参数和日长变化[J]. 武汉大学学报: 信息科学版, 2016, 41(1): 66-71 (Wei Erhu, Liu Wenjie, Wei J N, et al. Estimation of Earth Rotation Parameters and ΔLOD with Combining VLBI and GPS Observations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 66-71)
(  0) 0) |
| [5] |
郑勇. VLBI单基线解算地球自转参数的秩亏性证明[J]. 解放军测绘学院学报, 1993(2): 1-4 (Zheng Yong. The Demonstration of Rank Deficiency for One VLBI Baseline Estimation Earth Orientation Parameters[J]. Journal of the PLA Institute of Surveying and Mapping, 1993(2): 1-4)
(  0) 0) |
| [6] |
Hellmers H, Thaller D, Bloßfeld M, et al. Combination of VLBI Intensive Sessions with GNSS for Generating Low Latency Earth Rotation Parameters[J]. Advances in Geosciences, 2019, 50: 49-56 DOI:10.5194/adgeo-50-49-2019
(  0) 0) |
| [7] |
刘聪, 孟鹏飞, 刘鑫. 基于VLBI与BDS联合解算ERP的算法研究[J]. 全球定位系统, 2018, 43(3): 26-31 (Liu Cong, Meng Pengfei, Liu Xin. Algorithm Study on the Earth Rotation Parameters with the Combination of VLBI and BDS[J]. GNSS World of China, 2018, 43(3): 26-31)
(  0) 0) |
| [8] |
徐天河, 王潜心, 于素梅, 等. 利用区域网GPS/BDS数据确定地球自转参数[J]. 导航定位学报, 2015, 3(3): 13-17 (Xu Tianhe, Wang Qianxin, Yu Sumei, et al. Earth Rotation Parameters Determination Using Local GPS/BDS Network Data[J]. Journal of Navigation and Positioning, 2015, 3(3): 13-17)
(  0) 0) |
| [9] |
Karbon M, Soja B, Nilsson T, et al. Earth Orientation Parameters from VLBI Determined with a Kalman Filter[J]. Geodesy and Geodynamics, 2017, 8(6): 396-407 DOI:10.1016/j.geog.2017.05.006
(  0) 0) |
| [10] |
Behrend D, Thomas C, Gipson J, et al. On the Organization of CONT17[J]. Journal of Geodesy, 2020, 94(10): 100 DOI:10.1007/s00190-020-01436-x
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

