2. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001;
3. 南宁师范大学自然资源与测绘学院,南宁市明秀东路175号,530001
精密单点定位(PPP)技术具有单机作业、操作简便、高精度等优点,被广泛应用于广域精密定位、低轨卫星定轨、水汽反演与电离层监测、地震与海啸监测和预警等领域[1-4]。但在实际应用中,用户不仅需要高精度的位置信息,而且更注重位置信息的可靠性,因此对PPP结果进行质量检核具有重要意义。
不同于陆地测量,海上测量定位模式大多为动态,测量不具备复现性,缺乏类似IGS长期观测站的高精度坐标作为外部质量检核信息,同时GNSS观测数据受到多路径、外部观测环境等因素影响易包含粗差,从而导致PPP质量可能不可靠。目前针对海上PPP质量检核的研究较少,而PPP的精度和可靠性对海洋定位领域的应用具有重要意义,因此有必要对其开展更深入的研究。
系统间交叉验证质量检核方法就是将任意2个或多个系统组合的PPP结果进行对比,如果定位结果的差值在阈值范围内,则证明定位结果的质量可被采纳;如果定位结果的差值在阈值范围外,则证明至少有一组定位结果不可靠,该定位结果存在异常或PPP未收敛。在系统间交叉验证方法中,阈值通常设置为PPP精度的2倍。
随着GNSS的快速发展,特别是BDS和Galileo已基本完成全球卫星组网,加上BDS-3与GPS、Galileo之间卫星信号频率的共通,可极大便利不同系统间组合PPP[5-7]。为全面客观分析系统间交叉验证方法,采用全球均匀分布的MGEX观测站数据对比分析不同系统组合方式PPP的精度和收敛速度,并在静态、仿动态、海上动态定位模式下验证该方法用于检核PPP质量的有效性。
1 静态系统间交叉验证选取20个全球均匀分布、可同时接收BDS/GPS/Galileo/GLONASS信号的MGEX观测站(图 1)的GNSS数据,对比分析不同系统组合方式的静态PPP性能。数据采集时间为2019-12-22~28,即doy356~362,采样间隔为30 s,采用消电离层组合函数模型,卫星截止高度角设置为10°,采用GFZ网平差结果作为MGEX测站的坐标“真值”。

|
图 1 MGEX观测站分布 Fig. 1 Distribution of the MGEX stations |
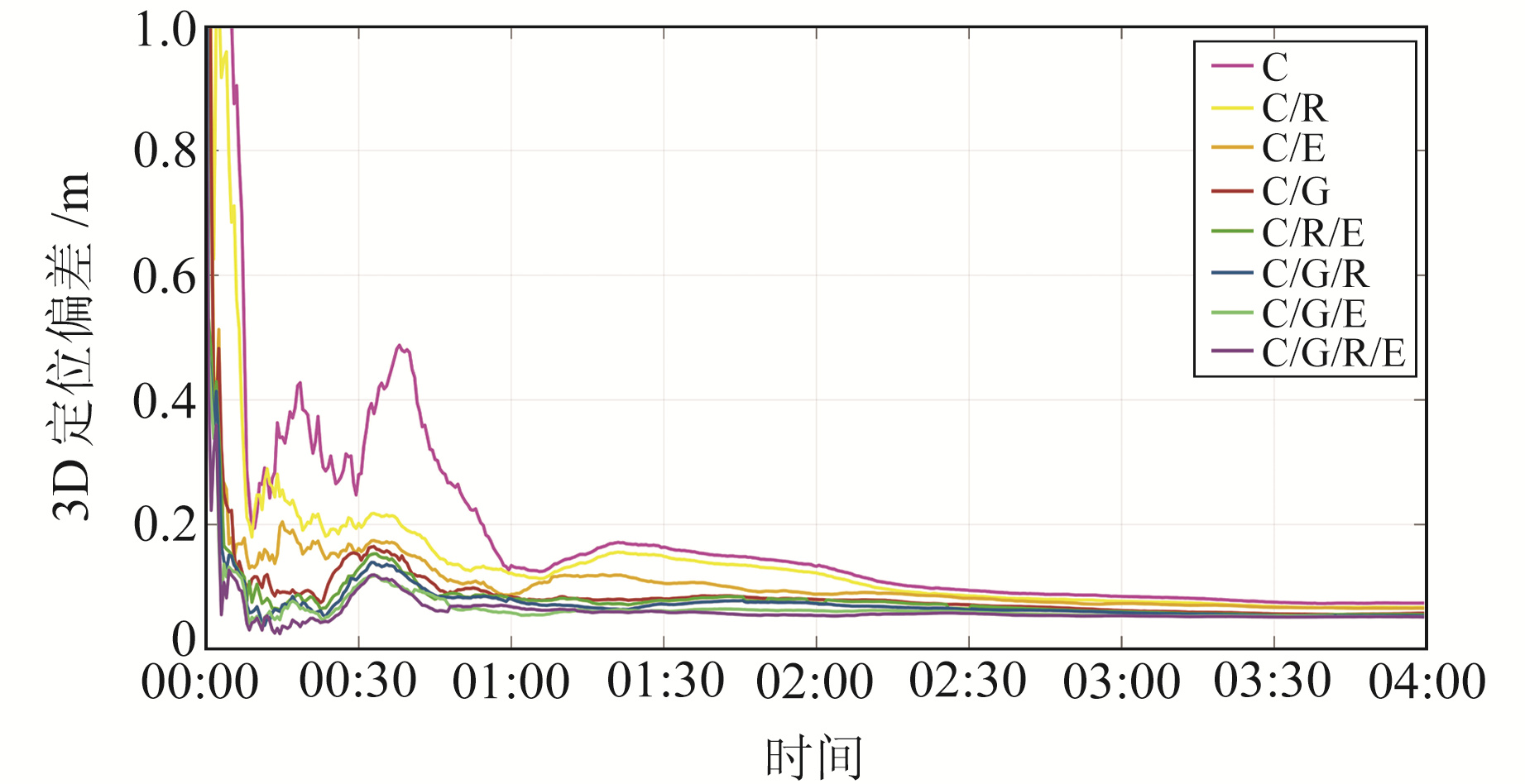
以WUH2测站doy360数据为例,图 2为不同系统组合PPP的位置偏差时间序列图,图中,C代表BDS,G代表GPS,R代表GLONASS,E代表Galileo(下同)。为便于数据统计分析,位置偏差取PPP结果与测站真值坐标间差值的绝对值。从图 2可以看出,相较于其他7种组合PPP,单BDS PPP的精度较差,尤其是在定位初始(PPP未收敛)阶段。随着PPP的收敛,8种PPP精度间的差值逐渐减小。
|
图 2 WUH2测站静态PPP的位置偏差时间序列 Fig. 2 Time series of position bias of static PPP at WUH2 station |
表 1为doy360所有MGEX测站收敛后的定位偏差均值。由表 1可知,相较于其他7种组合,单BDS PPP的位置平均偏差明显偏大。这是因为,在亚太地区,BDS GEO卫星的精密星历和钟差的精度相对较低,同时受限于GEO卫星的轨道类型,卫星空间几何变化较为缓慢;在亚太以外地区,BDS的可见卫星数相对较少。在PPP初期阶段,单系统定位的卫星观测量明显少于多系统,卫星空间几何构型和鲁棒性也都相对较差,导致单BDS PPP精度低于其他7种组合。组合系统的数目越多,定位精度相对越高;组合系统的数目相同时,不同系统组合PPP精度相近。
|
|
表 1 所有测站收敛后静态PPP位置偏差均值 Tab. 1 Average bias of static PPP of all stations after convergence |
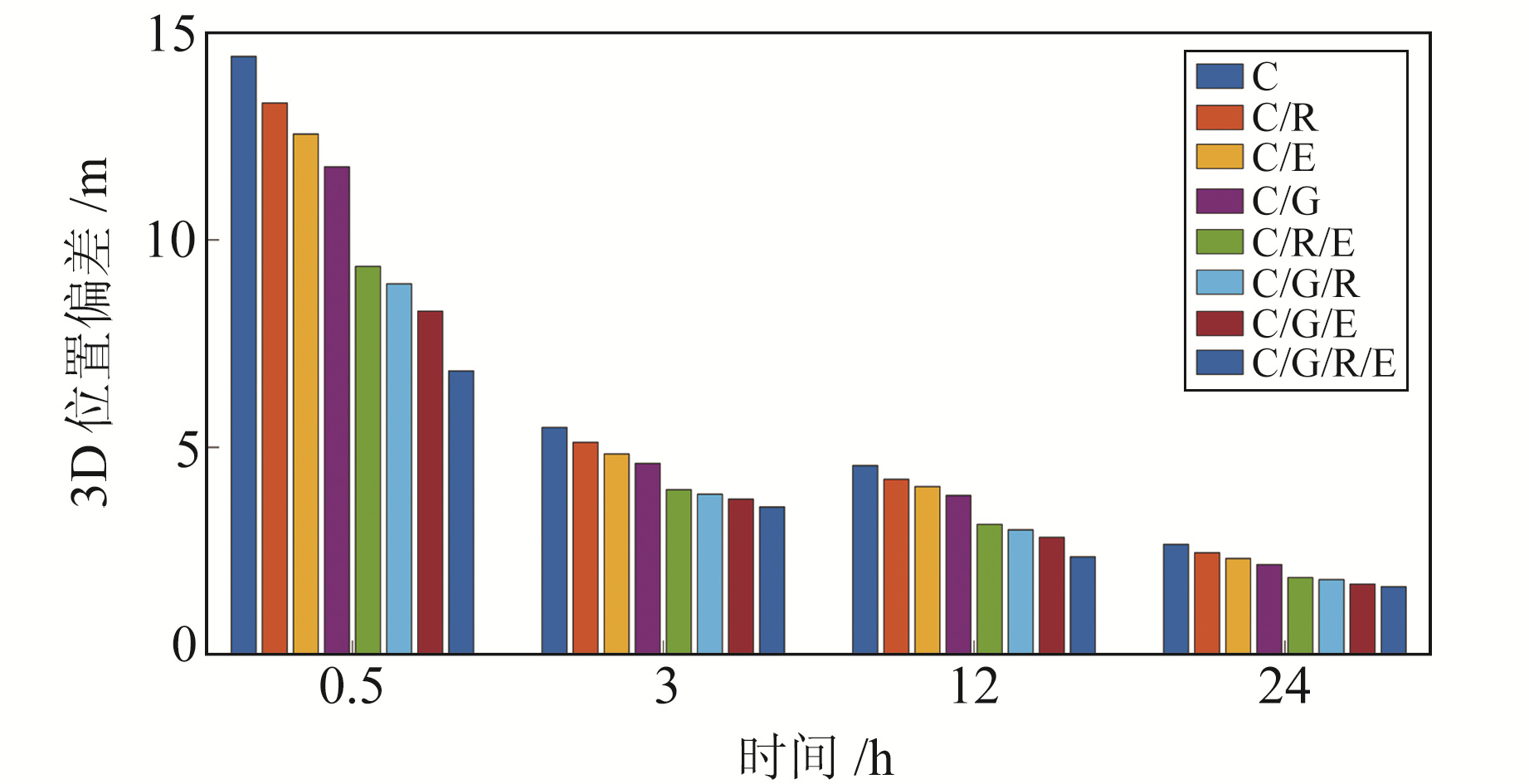
为便于分析PPP精度随时间的变化规律,给出doy360所有MGEX测站在不同时间段的PPP偏差均值(图 3)。由图 3可知,在定位阶段前半小时,相较于其他7种组合,单BDS PPP的位置偏差均值明显偏大;随着PPP逐渐收敛,不同系统组合PPP的位置偏差均值基本趋于一致。
|
图 3 不同时段PPP位置偏差均值统计 Fig. 3 Average position bias of PPP in different periods |
为系统分析PPP精度的变化规律,给出所有MGEX测站doy356~362不同系统组合PPP的位置偏差RMS值(表 2)。由表 2可知,8种不同组合方式PPP的位置偏差RMS处于同一水平,但由于误差改正模型精度相对较低,导致单BDS PPP的位置偏差RMS最大,定位精度最低。
|
|
表 2 所有MGEX测站静态PPP位置偏差RMS Tab. 2 RMS of position bias of static PPP of all MGEX stations |
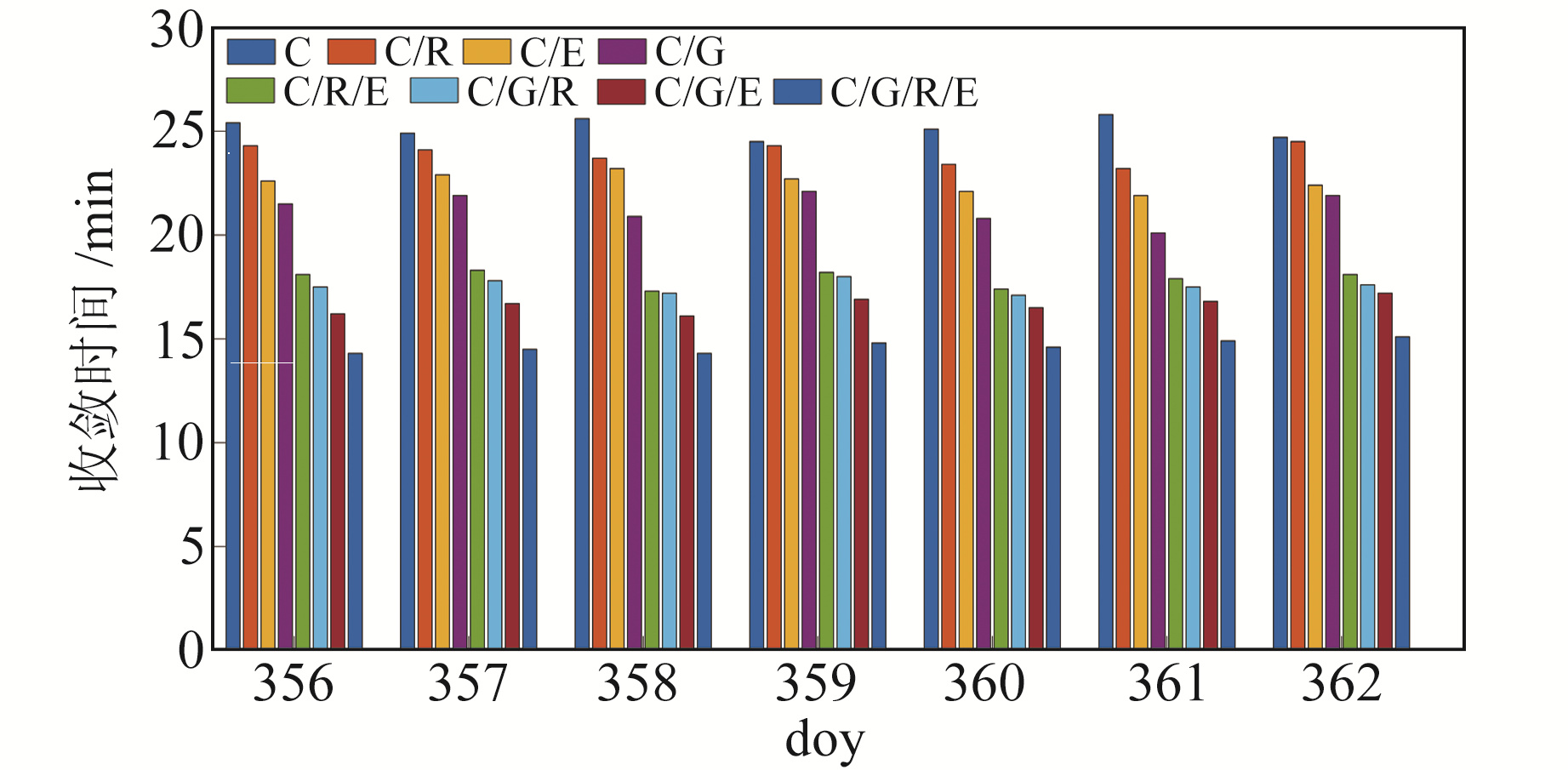
PPP性能指标主要包括精度和收敛速度。为分析不同系统组合PPP的收敛速度,给出20个MGEX测站在doy356~362的静态PPP平均收敛时间(图 4)。本文约定,N、E、U方向的位置偏差均小于10 cm,且保持5 min以上,才认定PPP达到收敛。由图 4可知,相较于其他7种组合,单BDS PPP的收敛时间最长、收敛速度最慢;系统组合的数目越多,PPP的收敛时间越短、收敛速度越快。这是因为BDS的卫星空间几何结构变化较慢,导致其PPP的收敛时间较长。
|
图 4 所有MGEX测站静态PPP收敛时间 Fig. 4 Convergence time of static PPP of all MGEX stations |
表 3为所有MGEX测站在doy356~362期间7种组合方式静态PPP的平均收敛时间相对于单BDS PPP的平均收敛时间的减少率。由表 3可知,多系统PPP的收敛时间小于单系统。在8种组合方式中,C/G/R/E的收敛速度最快,相比于单BDS PPP,收敛时间减少41.77%。
|
|
表 3 7种组合方式静态PPP平均收敛时间相对于单BDS静态PPP平均收敛时间的减少率 Tab. 3 Decrement of average convergence time of static PPP for seven combinations compared with single BDS |
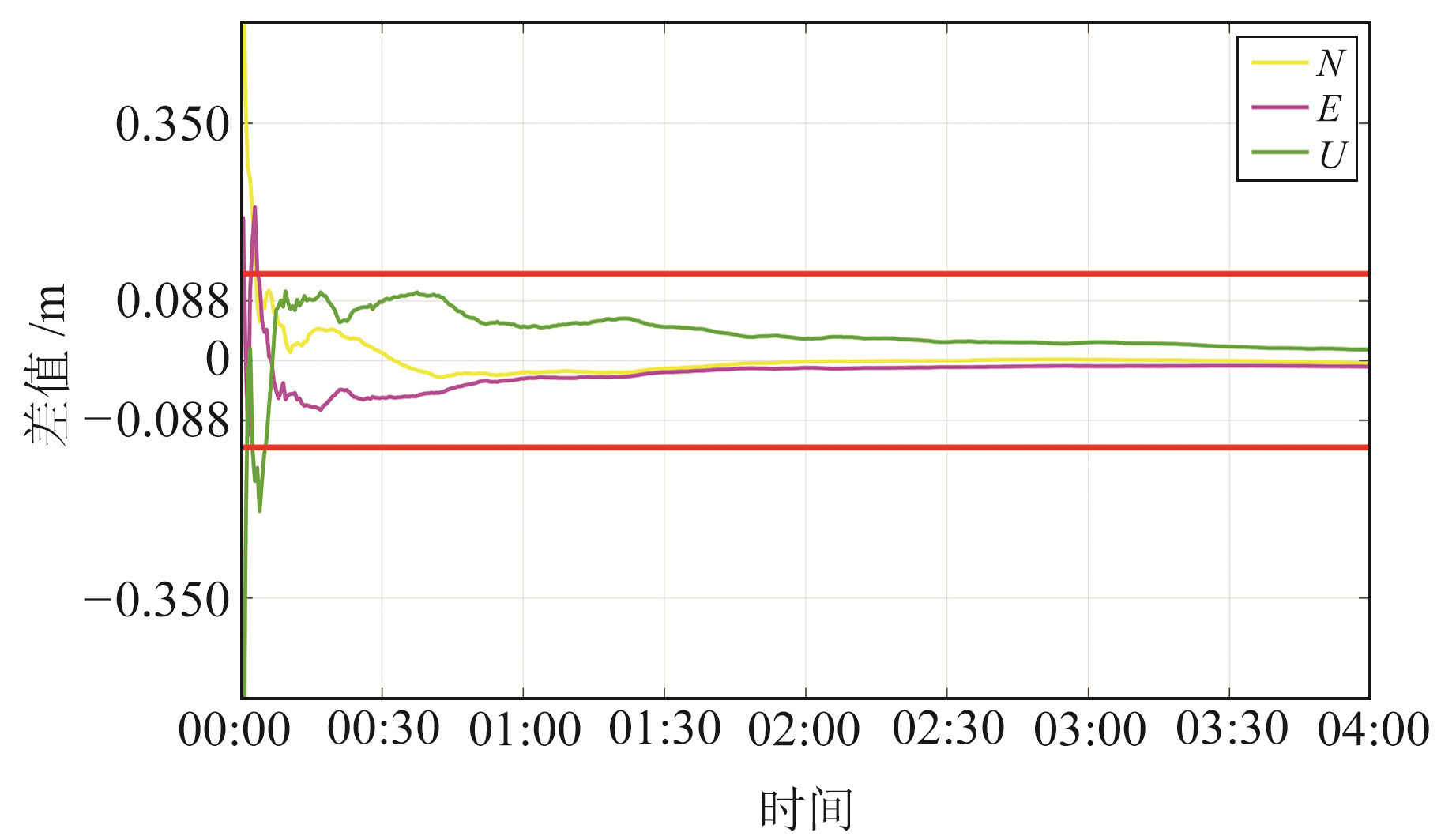
通过实验数据可知,C/G/R/E组合方式PPP的精度和收敛速度均最优,因此系统间交叉验证实验采用最优的C/G/R/E PPP结果与最差的单BDS PPP结果进行比较检核。以WUH2测站为例,C/G/R/E静态PPP精度为0.044 m,检核阈值设置为0.088 m。图 5为BDS与C/G/R/E静态PPP的差值。由图 5可知,除PPP的前期收敛阶段外,BDS与C/G/R/E静态PPP在N、E、U方向的差值均小于阈值0.088 m,表明系统间交叉验证方法在静态PPP质量检核中具有可行性和有效性。
|
图 5 BDS与C/G/R/E静态PPP交叉验证 Fig. 5 Cross validation of BDS and C/G/R/E static PPP |
仿动态PPP实验采用与静态PPP实验相同的数据,在仿动态PPP中,测站坐标视为随机游走过程进行估计,过程噪声的方差设置为10 000 m2。
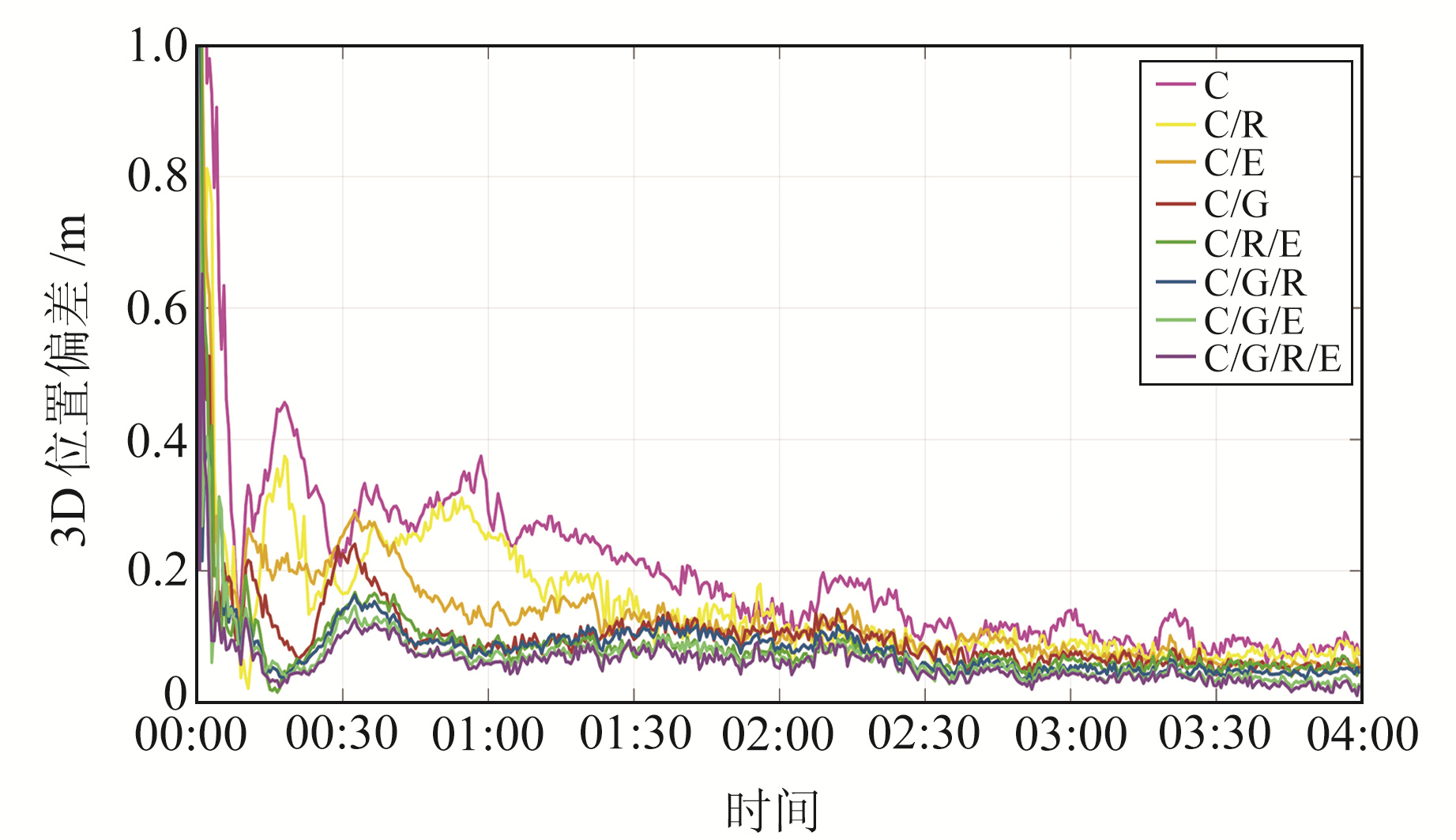
以WUH2测站doy360为例,图 6为不同系统组合仿动态PPP的位置偏差时间序列。由图 6可知,相比于其他7种组合,单BDS仿动态PPP的位置偏差较大,特别是在定位初始阶段(PPP未收敛)。但随着PPP的收敛,不同系统组合PPP的精度水平趋于一致。
|
图 6 WUH2测站仿动态PPP的位置偏差时间序列 Fig. 6 Time series of position bias of pseudo-dynamic PPP at WUH2 station |
为全面分析不同系统组合PPP的精度,给出所有MGEX测站doy356~362仿动态PPP的位置偏差RMS(表 4)。由表 4可知,单BDS仿动态PPP的精度低于其他7种组合;组合系统的数目越多,仿动态PPP精度越高,其中C/G/R/E仿动态PPP的精度最高,但不同系统组合PPP精度的差值较小。受可见卫星数目、卫星几何星座、精密星历精度、误差改正模型精度等因素影响,单BDS仿动态PPP精度相对较低。
|
|
表 4 所有MGEX测站仿动态PPP位置偏差RMS Tab. 4 RMS of position bias of pseudo-dynamic PPP of all MGEX stations |
图 7为MGEX测站doy356~362仿动态PPP的平均收敛时间,表 5为所有MGEX测站在doy356~362期间7种组合方式仿动态PPP的平均收敛时间相对于单BDS PPP的平均收敛时间的减少率。由图 7和表 5可知,在仿动态PPP中,相比于其他7种组合,单BDS PPP的收敛时间最长、收敛速度最慢;组合系统的数目越多,收敛时间越短、收敛速度越快。这可能是因为BDS GEO卫星空间几何变化较慢、系统可见卫星数目较少。在8种仿动态组合方式中,C/G/R/E PPP的收敛时间最短,相比于单BDS减小51.98%。仿动态定位模式下多系统组合对PPP的收敛速度的提高程度大于静态定位模式。

|
图 7 MGEX测站仿动态精密单点定位收敛时间 Fig. 7 Convergence time of pseudo-dynamic PPP of MGEX stations |
|
|
表 5 7种组合方式仿动态PPP平均收敛时间相对于单BDS仿动态PPP平均收敛时间的减少率 Tab. 5 Decrement of average convergence time of pseudo-dynamic PPP for seven combinations compared with single BDS |
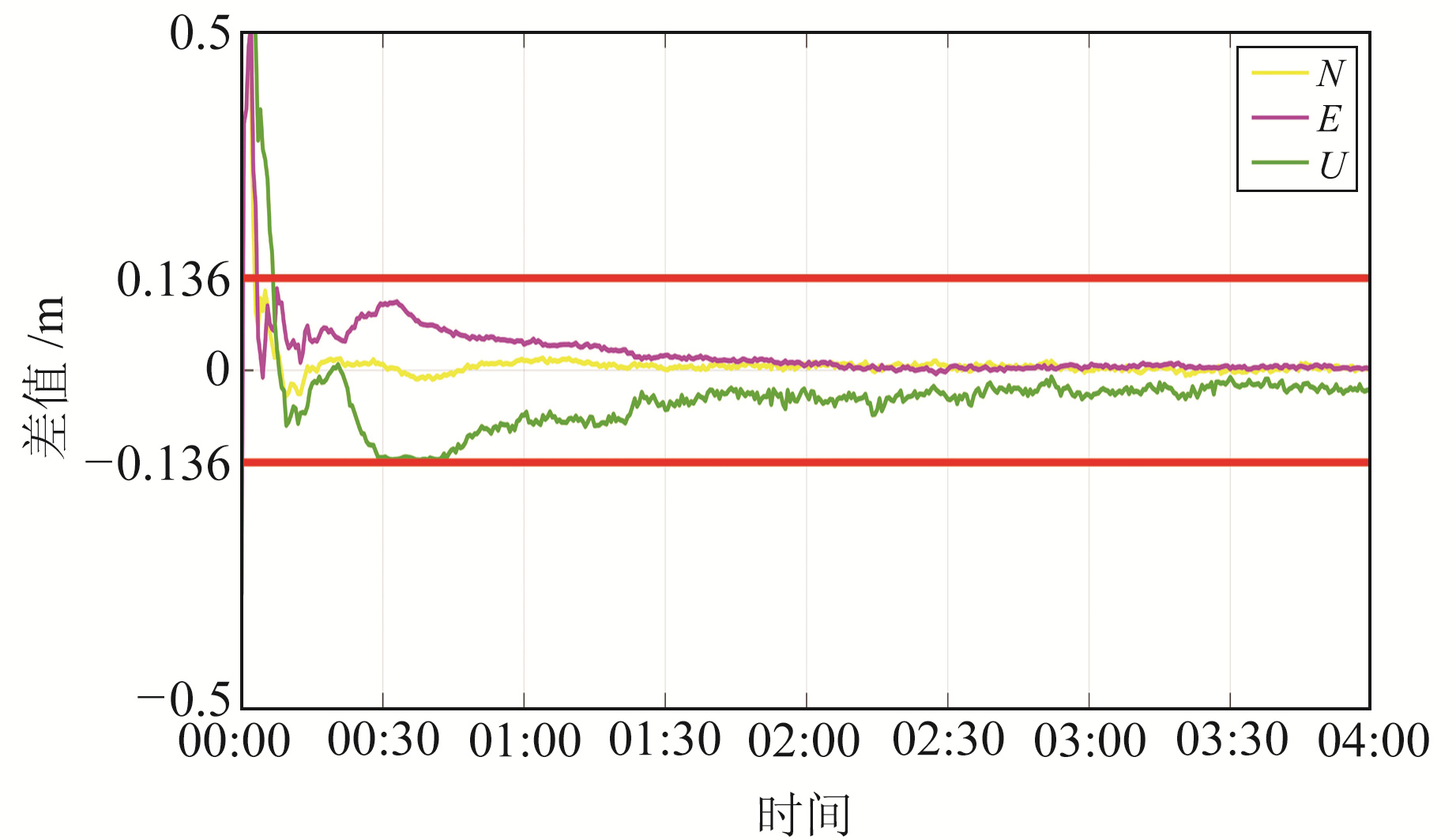
通过实验数据可知,在不同系统组合方式中,C/G/R/E PPP的精度和收敛速度均最优,因此仿动态系统间交叉验证实验采用最优的C/G/R/E PPP结果与最差的单BDS PPP结果进行比较检核。以WUH2测站为例,C/G/R/E仿动态PPP精度为0.068 m,检核阈值设置为0.136 m。图 8为单BDS与C/G/R/E仿动态PPP的差值。由图 8可知,除PPP前期收敛阶段外,单BDS与C/G/R/E仿动态PPP在N、E、U方向的差值均小于阈值0.136 m,表明系统间交叉验证方法在仿动态PPP质量检核中具有可行性和有效性。
|
图 8 BDS与C/G/R/E仿动态PPP交叉验证 Fig. 8 Cross validation of BDS and C/G/R/E pseudo-dynamic PPP |
海上动态系统间交叉验证实验中,仍采用单BDS与C/G/R/E PPP进行数据检核。
实验地点设置在江苏省盐城市大丰港附近海域。采用华测GPS500型号测量天线,该天线具有抗多径扼流圈,可有效减小多路径对定位精度的影响。在测量船上架设2根测量天线,采用司南板卡GNSS接收机,数据采集日期为2018-08-09 01:30~05:25,采样间隔为1 s。
在静态和仿动态PPP实验中,均采用已知的高精度测站坐标作为真值,将解算的测站结果与真值进行比较来分析评估算法性能。但海上测量环境缺乏已知的高精度测站坐标,同时也难以获取高精度测站坐标作为实验参照值。当RTK的流动站与基准站之间的距离在15 km范围内,RTK的定位精度可以达到cm级[7]。因此,将RTK定位结果作为海上动态精密单点定位的参照值。将船上的测量天线通过功分器连接2块司南定位板卡,定位模式分别设置为动态PPP和RTK,将船上RTK定位模式设置为流动站,同时在江苏省盐城市大丰港码头岸边架设基准站。
将测量船RTK定位结果作为“真值”,动态C/G/R/E PPP精度为0.31 m,系统间交叉验证阈值设置为0.62 m,图 9为海上动态单BDS PPP与C/G/R/E PPP结果的差值。由图 9可知,除在动态PPP前期收敛阶段外,单BDS与C/G/R/E PPP在N、E、U方向的差值均小于阈值0.62 m,表明系统间交叉验证方法在海上动态PPP质量检核中具有可行性和有效性。

|
图 9 海上动态BDS与C/G/R/E PPP交叉验证 Fig. 9 Cross validation of BDS and C/G/R/E marine dynamic PPP |
本文基于全球分布的MGEX测站实测数据,对8种不同系统组合PPP的精度和收敛速度进行分析。结果表明,相比于单BDS,组合系统PPP的精度更高、收敛速度更快;组合系统的数目越多,PPP的精度越高、收敛速度越快。
采用系统间交叉验证方法检核PPP质量,实验数据表明,在静态、仿动态和海上动态PPP中,除PPP初期收敛阶段外,不同系统组合PPP的差值均小于阈值,表明在静态、仿动态、海上动态PPP模式中,系统间交叉验证方法均可有效检验PPP的质量。系统间交叉验证方法不要求测量具有复现性,即不需要多台GNSS接收机同时接收到相同的观测数据,但需要对原始观测数据进行2次或以上不同系统组合的定位解算,然后对定位结果进行差运算来检核定位质量,是一种便利的海上PPP的质量检核方法。
| [1] |
张小红, 李盼, 左翔. 固定模糊度的精密单点定位几何定轨方法及结果分析[J]. 武汉大学学报: 信息科学版, 2013, 38(9): 1009-1013 (Zhang Xiaohong, Li Pan, Zuo Xiang. Kinematic Precise Orbit Determination Based on Ambiguity-Fixed PPP[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1009-1013)
(  0) 0) |
| [2] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453 (Zhang Baocheng, Ou Jikun, Yuan Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-Receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453)
(  0) 0) |
| [3] |
杨元喜. 弹性PNT基本框架[J]. 测绘学报, 2018, 47(7): 893-898 (Yang Yuanxi. Resilient PNT Concept Frame[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 893-898)
(  0) 0) |
| [4] |
周锋, 徐天河. GPS/BDS/Galileo三频精密单点定位模型及性能分析[J]. 测绘学报, 2021, 50(1): 61-70 (Zhou Feng, Xu Tianhe. Modeling and Assessment of GPS/BDS/Galileo Triple-Frequency Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(1): 61-70)
(  0) 0) |
| [5] |
金波文, 王慧, 刘玉龙, 等. 中国沿海海洋站GNSS坐标时间序列噪声模型的建立与分析[J]. 大地测量与地球动力学, 2020, 40(5): 476-481 (Jin Bowen, Wang Hui, Liu Yulong, et al. Establishment and Analysis of GNSS Coordinate Time Series Noise Model for Coastal Tide Stations in China[J]. Journal of Geodesy and Geodynamics, 2020, 40(5): 476-481)
(  0) 0) |
| [6] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[J]. 测绘学报, 2020, 49(7): 938 (Zhou Feng. Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(7): 938)
(  0) 0) |
| [7] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2016 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2016)
(  0) 0) |
2. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China;
3. School of Natural Resources and Surveying, Nanning Normal University, 175 East-Mingxiu Road, Nanning 530001, China
 2021, Vol. 41
2021, Vol. 41


