2. 中国地质大学(武汉)地理与信息工程学院,武汉市锦程街68号,430076
国际GNSS监测评估系统(iGMAS)提供的超快速钟差预报产品精度较低,一定程度上限制了北斗实时精密导航定位的应用。同时,随着BDS-3的建成,对其超快速卫星钟差进行精密建模和高精度预报对于维持BDS系统时间同步及满足实时动态精密单点定位的需求等具有重要意义[1]。国内外学者提出一系列钟差预报的模型和方法,包括谱分析模型(SA)[2]、灰色模型(GM)[2]、卡尔曼滤波及其优化模型[3]、附加周期和神经网络补偿的钟差预报模型[4]、基于粒子群优化核极限学习机的钟差预报算法[5]、T-S模糊神经网络钟差预测法[6]、小波神经网络模型[7]及其相关的组合预报模型[8-10]等。这些模型和算法都是利用神经网络或机器学习方法,从原始钟差数据或基本钟差模型拟合残差数据出发进行模型训练的,得到的最终钟差预报效果虽有所提升,但仍存在一些不足:1)没有考虑卫星钟差数据之间的相关性,且未能充分利用钟差数据的先验信息;2)模型参数的选取较为困难,算法复杂度较高。针对这些问题,本文从卫星钟差数据的相关性出发,提出一种基于EM算法优化相关向量机(relevance vector machine,RVM)的BDS卫星超快速钟差预报算法。
1 RVM钟差预报模型RVM基本原理参见文献[11],本文不再赘述。
1.1 EM算法求解RVM模型超参数在计算权值后验概率过程中,部分超参数会趋于无穷大,相应的权值会趋近0,其余超参数会趋于有限值,与之对应的非零权重钟差数据称为相关向量,体现了钟差数据之间的相关性。根据p(α, σ2|t)∞p(t | α, σ2)p(α)p(σ2),RVM模型的预测问题转变为采取有效的超参数求解方法以最大化超参数的边缘似然函数p(t | α, σ2)问题。
| $ \begin{array}{*{20}{c}} {p\left( {\mathit{\boldsymbol{t}}|\mathit{\boldsymbol{a}},{\sigma ^2}} \right) = \int {p\left( {\mathit{\boldsymbol{t}}|\mathit{\boldsymbol{\omega }},{\sigma ^2}} \right)} p\left( {\mathit{\boldsymbol{\omega }}|{\bf{a}}} \right){\rm{d}}\mathit{\boldsymbol{\omega }} = }\\ {{{\left( {2{\rm{ \mathit{ π} }}} \right)}^{ - \frac{N}{2}}}|\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}{|^{ - \frac{1}{2}}}{\rm{exp}}\left\{ { - \frac{{{\mathit{\boldsymbol{t}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{ - 1}}\mathit{\boldsymbol{t}}}}{2}} \right\}} \end{array} $ | (1) |
式中,ω为RVM的权值向量,Ω =σ2 I + ΦA -1 Φ T。
采用迭代法对式(1)求解,进而获取α和σ2的最优解。迭代计算过程中的模型超参数α和方差σ2采用αinew和(σ2)new表示,最终的最优解记为αMP和σMP2:
| $ a_i^{{\rm{new}}} = \frac{{{\gamma _i}}}{{\mu _i^2}},{\left( {{\sigma ^2}} \right)^{{\rm{new}}}} = \frac{{\left\| {{\bf{t}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\bf{ \pmb{\mathit{ μ}} }}} \right\|}}{{N - \sum\limits_{i = 1}^N {{\gamma _i}} }} $ | (2) |
式中,γi=1-αiΣii,μi为第i个后验权值的均值,Σii为权值后验方差矩阵第i个对角线元素。
对于一组钟差数据x*,其对应输出概率分布为p(t* | t, αMP, σMP2)=N(t* | t, σ2 *),相应的预测值与预测方差为:
| $ \left\{ {_{\sigma _*^2 = \sigma _{{\rm{MP}}}^2 + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{{\left( {{x_*}} \right)}^{\rm{T}}}{\boldsymbol{\Sigma}} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_*}} \right)}^{{t_*} = {\mathit{\boldsymbol{\mu }}^{\rm{T}}}\mathit{\Phi }\left( {{x_*}} \right)}} \right. $ | (3) |
式(3)在迭代计算过程中需要进行矩阵的求逆计算,以更新模型超参数α和σ2。当钟差训练样本较大时,运算量会急剧增加,同时出现奇异矩阵,无法进行求逆计算。为保证预测结果的可靠性,采用EM算法迭代更新α和σ2。基于EM迭代的RVM模型训练算法如下:
1) 对RVM模型的参数ω和σ2进行初始化。
2) 根据当前ω k和(σ-2)k估计ω k+1和E(ωω T):
| $ \left\{ {_{E\left( {\mathit{\boldsymbol{\omega }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}} \right) = \left( {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^k} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^k}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{\psi }}^k}} \right) + \mathit{\boldsymbol{\omega }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}}^{{\mathit{\boldsymbol{\omega }}^{k + 1}} = {{\left( {{\sigma ^{ - 2}}} \right)}^k}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^k} - {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^k}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{\psi }}^k}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}t}} \right. $ | (4) |
式中,B = Φψ k Φ T+(σ2) I,ψ k=diag[(ω0k)2(ω1k)2 …(ωNk)2]。
3) 利用步骤2)得到的ω k+1更新方差(σ2)k+1:
| $ \begin{array}{*{20}{l}} {{{\left( {{\sigma ^2}} \right)}^{k + 1}} = }\\ {\frac{{{\mathit{\boldsymbol{t}}^{\rm{T}}}\mathit{\boldsymbol{t}} - 2{\mathit{\boldsymbol{t}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot {{\left( {{\mathit{\boldsymbol{\omega }}^{k + 1}}} \right)}^{\rm{T}}} + {\rm{trace}}\left[ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}E\left( {\mathit{\boldsymbol{\omega }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right]}}{N}} \end{array} $ | (5) |
4) 判断收敛条件
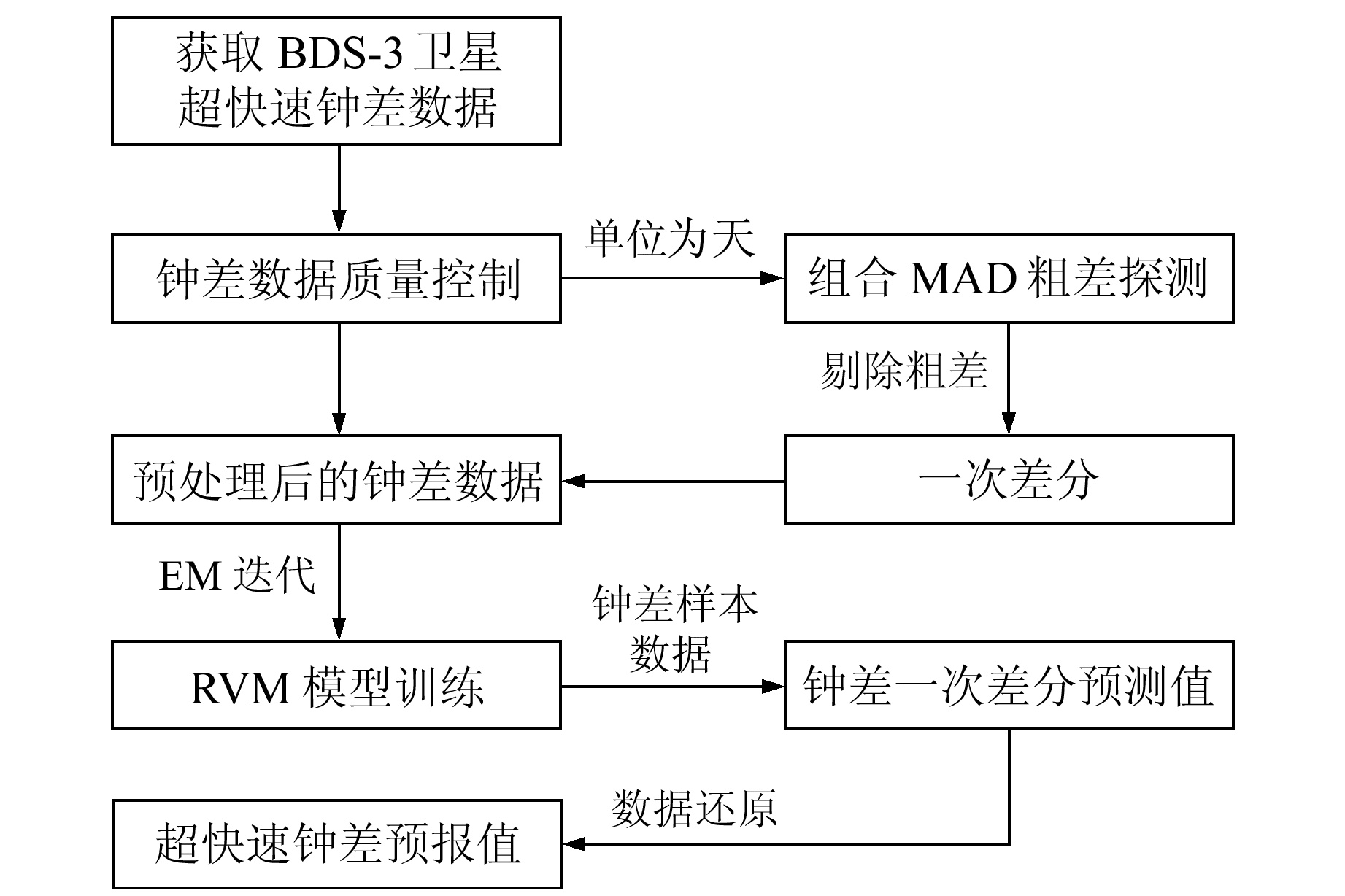
基于RVM模型算法的卫星超快速钟差预报具体流程(图 1)为:
|
图 1 RVM模型算法超快速钟差预报流程 Fig. 1 Flow chart of ultra-rapid clock offset prediction based on RVM algorithm |
1) 利用组合MAD法[12]预处理超快速钟差数据,剔除粗差与钟跳等异常值。
2) 为减弱钟差序列趋势项的影响[7],将钟差数据进行一次差分处理,得到一组有效数字位数减少且数值较小的序列。
3) 将钟差一次差分数据作为RVM模型的训练样本,利用EM算法通过式(4)和式(5)进行迭代,求取RVM模型的超参数α和σ2,进而输出最优的RVM预测模型。
4) 给定钟差一次差分数据样本x*,通过优化的RVM预测模型得到样本数据的预测值t*,最后将预报结果还原得到相应的钟差预报值。
2 算例分析iGMAS中心提供的超快速钟差包括观测部分(ISU-O)和预报部分(ISU-P),各占24 h。ISU-O钟差是通过对多个iGMAS中心解算的钟差进行综合加权得到的,精度约为1 ns;ISU-P钟差是基于前1 d的ISU-O钟差外推预报得到的,精度较低。本文采用iGMAS中心的实测BDS-3超快速钟差数据,选取8颗BDS-3卫星作为代表进行钟差预报分析,卫星信息如表 1所示。
|
|
表 1 BDS-3卫星相关信息 Tab. 1 Relevant information of BDS-3 satellites |
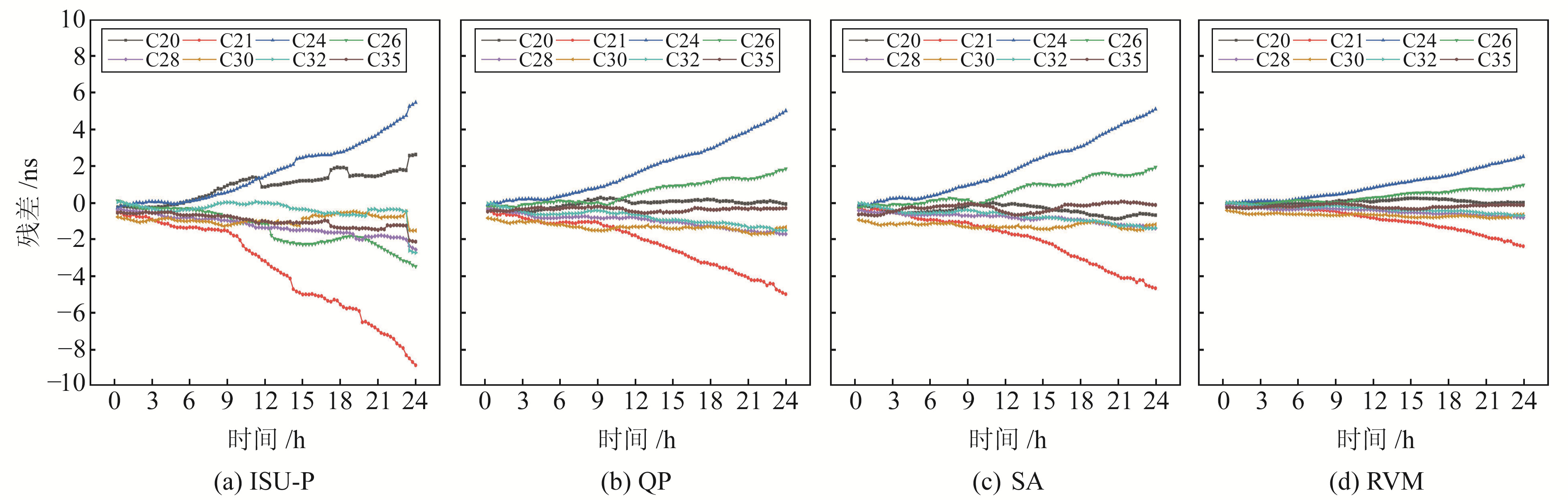
为分析本文RVM模型钟差预报算法的效果,采用QP模型、SA模型和ISU-P钟差产品作为对比,其中SA模型采用加入北斗MEO卫星钟差数据前2个主显著周期项进行钟差预报(主显著周期项为12 h和6 h)[13]。选取高斯核函数作为RVM钟差预报模型的核函数,并利用交叉验证法进行模型训练[11]。图 2为ISU-P钟差产品和采用3种模型使用2021-02-13数据预报2021-02-14钟差的预报残差。
|
图 2 不同预报模型BDS-3卫星钟差预报残差序列 Fig. 2 Clock offset prediction residual sequence of BDS-3 satellites using different prediction models |
从图 2可以看出:1)ISU-P钟差产品随着预报时间的推移累积预报误差很大,预报精度衰减很快,精度有待进一步提高;2)QP模型与SA模型的钟差预报精度略优于ISU-P钟差产品,两者预报结果差别不大;3)SA模型加入了钟差数据的前2个主周期项,改善了部分卫星钟差在预报过程中周期性系统误差的积累,发散程度有所减小,但提升效果并不明显,由此可见BDS-3卫星钟差数据的周期特性误差并不显著;4)RVM模型的预报精度最高,误差曲线最收敛,超快速钟差预报稳定性更好。综上,EM算法优化的RVM钟差预报模型可更为准确地拟合出钟差数据中的非线性特征,从而取得较好的超快速钟差预报效果。
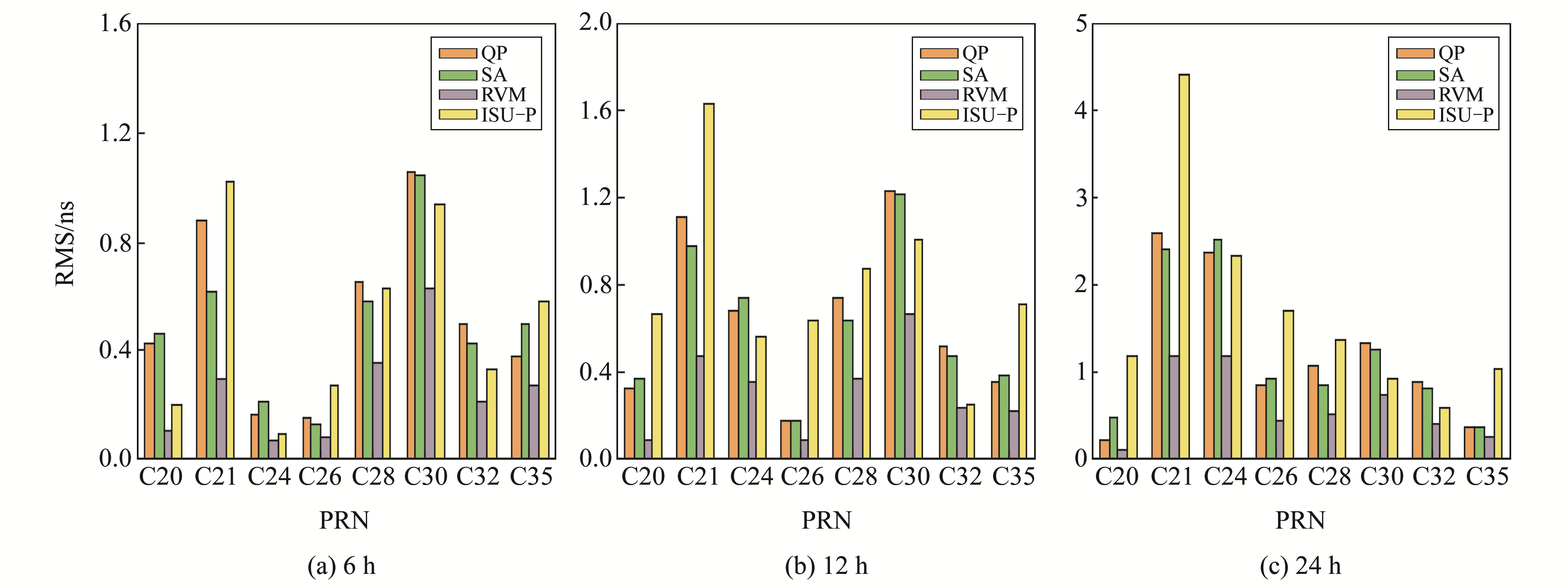
2.2 多天算例为更好地验证本文RVM模型进行钟差预报的普适性,采用2021-02-13~19共7 d的BDS-3超快速钟差数据进行实验分析,选取均方根误差(RMS)作为钟差预报精度的评定标准,预报结果如表 2和图 3所示。
|
|
表 2 不同预报模型一周预报结果平均精度统计 Tab. 2 Average precision statistics of one-week forecast results using different prediction models |
|
图 3 不同预报模型BDS-3卫星钟差预报精度统计 Fig. 3 Statistics of BDS-3 satellites clock offset prediction accuracy using different prediction models |
由表 2和图 3可以看出:1)随着预报时长的增加,4种预报模型的超快速钟差预报精度都有所下降,但ISU-P产品精度下降最快,降低幅度最为显著,可见当前阶段超快速钟差预报产品精度很低,难以满足实时精密单点定位的需求;2)QP模型与SA模型的钟差预报精度相当;3)RVM模型预报精度与稳定性均优于其他3种预报模型;4)在短期6 h超快速钟差预报下,RVM模型BDS-3钟差预报精度优于0.62 ns,能够满足北斗高精度实时PNT服务。
为了分析BDS-3卫星钟差的预报效果与星载钟类型的关系,表 3统计了不同星载钟类型钟差数据预报的平均精度。表 4给出了RVM模型较其他3种模型预报精度的提升率。
|
|
表 3 不同星载钟类型钟差预报的平均精度 Tab. 3 Average accuracy of clock offset prediction for different satellite clocks |
|
|
表 4 RVM模型较其他3种模型精度提升率 Tab. 4 Accuracy improvement rate of the RVM algorithm compared with other three models |
由表 3~4可以看出:1)在进行12 h钟差预报时,BDS-3卫星铷钟和氢钟的钟差预报精度相当,但在预报24 h钟差数据时,BDS-3卫星氢钟的预报精度明显更优,可见BDS-3搭载的新一代氢钟稳定性更强,性能优于同期的铷钟。2)对于6 h、12 h和24 h预报,RVM模型预报BDS-3卫星钟差数据的平均精度均优于0.61 ns;与ISU-P、QP模型和SA模型相比,RVM模型预报24 h的BDS-3卫星钟差精度分别提升64.1%、50.0%和49.2%,验证了RVM模型在BDS-3超快速钟差预报中的可行性。
3 结语针对当前BDS-3钟差预报产品无法满足实时高精度PNT服务需求的问题,提出一种基于EM算法优化RVM的BDS-3超快速钟差预报算法。利用iGMAS中心提供的实测BDS-3超快速钟差数据进行单天和多天预报实验,验证RVM模型在卫星钟差预报中的可行性,同时得出以下结论:
1) BDS-3超快速钟差数据进行一次差分后,数据的有效数字位数减少,一定程度上消除了钟差序列趋势项的影响,有利于更准确地拟合预测模型。
2) RVM模型采用高斯核函数,具有较强的局部学习与全局泛化能力,能够很好地对超快速钟差数据进行刻画。
3) 对比4种模型24 h钟差预报的误差曲线发现,RVM模型精度最高,误差曲线最收敛,稳定性最好。可见EM算法优化的RVM钟差预报模型可更准确地拟合钟差数据中的非线性特征,从而取得较好的超快速钟差预报效果。
4) 对于6 h、12 h和24 h预报,RVM模型预报BDS-3卫星钟差数据的平均精度均优于0.61 ns;与ISU-P、QP模型和SA模型相比,RVM模型预报24 h的BDS-3卫星钟差精度分别提升了64.1%、50.0%、49.2%。
致谢: 感谢iGMAS数据中心提供产品支持。
| [1] |
杨玉锋, 彭勇, 刘梦晗, 等. BDS-3在轨卫星钟性能评估与分析[J]. 导航定位学报, 2021, 9(1): 53-60 (Yang Yufeng, Peng Yong, Liu Menghan, et al. Performance Evaluation and Analysis of BDS-3 On-Orbit Satellite Clocks[J]. Journal of Navigation and Positioning, 2021, 9(1): 53-60)
(  0) 0) |
| [2] |
郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州: 信息工程大学, 2006 (Guo Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2006)
(  0) 0) |
| [3] |
Lou Y D, Liu Y, Shi C, et al. Precise Orbit Determination of Beidou Constellation: Method Comparison[J]. GPS Solutions, 2016, 20(2): 259-268 DOI:10.1007/s10291-014-0436-y
(  0) 0) |
| [4] |
黄观文, 崔博斌, 张勤, 等. 附加周期和神经网络补偿的实时钟差预报模型[J]. 宇航学报, 2018, 39(1): 83-88 (Huang Guanwen, Cui Bobin, Zhang Qin, et al. Real-Time Clock Offset Prediction Model with Periodic and Neural Network Corrections[J]. Journal of Astronautics, 2018, 39(1): 83-88)
(  0) 0) |
| [5] |
李文涛, 边少锋, 任青阳, 等. 基于粒子群优化核极限学习机的北斗超快速钟差预报[J]. 宇航学报, 2019, 40(9): 1080-1088 (Li Wentao, Bian Shaofeng, Ren Qingyang, et al. Kernel Extreme Learning Machine Based on Particle Swarm Optimization for Prediction of Beidou Ultra-Rapid Clock Offset[J]. Journal of Astronautics, 2019, 40(9): 1080-1088)
(  0) 0) |
| [6] |
王旭, 柴洪洲, 王昶. 卫星钟差预报的T-S模糊神经网络法[J]. 测绘学报, 2020, 49(5): 580-588 (Wang Xu, Chai Hongzhou, Wang Chang. T-S Fuzzy Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(5): 580-588)
(  0) 0) |
| [7] |
王宇谱, 吕志平, 陈正生, 等. 一种新的钟差预处理方法及在WNN钟差中长期预报中的应用[J]. 武汉大学学报: 信息科学版, 2016, 41(3): 373-379 (Wang Yupu, Lü Zhiping, Chen Zhengsheng, et al. A New Data Preprocessing Method for Satellite Clock Bias and Its Application in WNN to Predict Medium-Term and Long-Term Clock Bias[J]. Geomatics and Information Science of Wuhan University, 2016, 41(3): 373-379)
(  0) 0) |
| [8] |
Zhao Q L, Wang C, Guo J, et al. Precise Orbit and Clock Determination for Beidou-3 Experimental Satellites with Yaw Attitude Analysis[J]. GPS Solutions, 2017, 22(1): 1-13
(  0) 0) |
| [9] |
黄飞江, 陈演羽, 李廷会, 等. 基于灰色模型和混沌时间序列的卫星钟差预测算法[J]. 电子学报, 2019, 47(7): 1416-1424 (Huang Feijiang, Chen Yanyu, Li Tinghui, et al. A Satellite Clock Bias Prediction Algorithm Based on Grey Model and Chaotic Time Series[J]. Acta Electronica Sinica, 2019, 47(7): 1416-1424 DOI:10.3969/j.issn.0372-2112.2019.07.004)
(  0) 0) |
| [10] |
陈演羽, 李廷会, 黄飞江, 等. 基于混沌时间序列的GPS卫星钟差预测算法[J]. 仪器仪表学报, 2018, 39(4): 115-122 (Chen Yanyu, Li Tinghui, Huang Feijiang, et al. GPS Satellite Clock Bias Prediction Algorithm Based on Chaotic Time Series[J]. Chinese Journal of Scientific Instrument, 2018, 39(4): 115-122)
(  0) 0) |
| [11] |
雷亚国, 陈吴, 李乃鹏, 等. 自适应多核组合相关向量机预测方法及其在机械设备剩余寿命预测中的应用[J]. 机械工程学报, 2016, 52(1): 87-93 (Lei Yaguo, Chen Wu, Li Naipeng, et al. A Relevance Vector Machine Prediction Method Based on Adaptive Multi-Kernel Combination and Its Application to Remaining Useful Life Prediction of Machinery[J]. Journal of Mechanical Engineering, 2016, 52(1): 87-93)
(  0) 0) |
| [12] |
崔博斌. GNSS卫星钟时频特性及预报算法研究[D]. 西安: 长安大学, 2018 (Cui Bobin. Research on Time-Frequency Characteristics and Prediction Algorithm of GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2018)
(  0) 0) |
| [13] |
毛亚, 王潜心, 胡超, 等. BDS-3卫星钟差特性分析[J]. 武汉大学学报: 信息科学版, 2020, 45(1): 53-61 (Mao Ya, Wang Qianxin, Hu Chao, et al. Analysis of the Characterization for BDS-3 Satellite Clock Error[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 53-61)
(  0) 0) |
2. School of Geography and Information Engineering, China University of Geosciences, 68 Jincheng Street, Wuhan 430076, China
 2021, Vol. 41
2021, Vol. 41


