GNSS坐标时间序列中除了有信号外，还包含噪声与粗差。对噪声的研究主要集中于最优噪声模型的构建^[1-3]和噪声分量估计^[4-5]。粗差探测算法主要有3σ法^[6]、DIA(detection，identification and adaptation)算法^[7]和基于四分位距统计量IQR(inter-quartile range)准则的算法^[8]。无论是噪声估计还是粗差探测方法，均依赖于谐波模型获得的残差序列的分析，而谐波模型仅简单地将GNSS坐标时间序列描述成线性信号、常振幅的季节性信号以及噪声的线性组合。已有研究表明，由于基准站对全球气候以及环境负载等的不规则响应导致GNSS坐标时间序列中的季节性形变信号的振幅是时变的^[9]，因此基于谐波模型获得的残差序列并非是真实的残差。针对该不足，本文提出一种基于奇异谱分析(SSA)的GNSS坐标时间序列粗差探测和噪声估计算法，并通过模拟数据和实测数据的对比验证算法的有效性。

1 传统谐波模型

GNSS基准站连续坐标时间序列中蕴含着丰富的信号与噪声。其中信号包含线性信号与非线性信号，线性信号代表基准站由构造应力导致的构造运动，一般以速度场形式表示；非线性信号主要表现为由环境负载导致的测站季节性位移。噪声则包含白噪声与有色噪声。一般以谐波模型来描述GNSS坐标时间序列：

$ \begin{aligned} y\left(t_{i}\right)=& a+b t_{i}+\sum\limits_{k=1}^{2} c_{k} \sin \left(2 k {\rm{ \mathit{ π} }} t_{i}\right)+\\ & d_{k} \cos \left(2 k {\rm{ \mathit{ π} }} t_{i}\right)+e\left(t_{i}\right) \end{aligned} $

(1)

式中，y(t_i)为t_i历元时刻的基准站坐标，a、b为测站初始位置和速度，c_k、d_k(k=1, 2)为年和半年周期振幅，e(t_i)为观测误差。若顾及所有观测历元t_i(i=1, 2, …, N)，则式(1)可写为：

$ \boldsymbol{y}=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{e} $

(2)

式中，y、e ∈R^N×1为观测值及其误差向量，A∈R^N×6为系数矩阵，x∈R^6×1为未知参数。各变量的构成为：

$ \boldsymbol{y}=\left[\begin{array}{llll} y\left(t_{1}\right) & y\left(t_{2}\right) & \cdots & y\left(t_{N}\right) \end{array}\right]^{\mathrm{T}} $

$ \boldsymbol{A}=\left[\begin{array}{cccccc} 1 & t_{1} & \sin \left(2 {\rm{ \mathit{ π} }} t_{1}\right) & \cos \left(2 {\rm{ \mathit{ π} }} t_{1}\right) & \sin \left(4 {\rm{ \mathit{ π} }} t_{1}\right) & \cos \left(4 {\rm{ \mathit{ π} }} t_{1}\right) \\ 1 & t_{2} & \sin \left(2 {\rm{ \mathit{ π} }} t_{2}\right) & \cos \left(2 {\rm{ \mathit{ π} }} t_{2}\right) & \sin \left(4 {\rm{ \mathit{ π} }} t_{2}\right) & \cos \left(4 {\rm{ \mathit{ π} }} t_{2}\right) \\ \cdots && & \cdots& & \cdots \\ 1 & t_{N} & \sin \left(2 {\rm{ \mathit{ π} }} t_{N}\right) & \cos \left(2 {\rm{ \mathit{ π} }} t_{N}\right) & \sin \left(4 {\rm{ \mathit{ π} }} t_{N}\right) & \cos \left(4 {\rm{ \mathit{ π} }} t_{N}\right) \end{array}\right] $

$ \boldsymbol{x}=\left[\begin{array}{llllll} a & b & c_{1} & d_{1} & c_{2} & d_{2} \end{array}\right]^{\mathrm{T}} \quad \boldsymbol{e}=\left[\begin{array}{llll} e\left(t_{1}\right) & e\left(t_{2}\right) & \cdots & e\left(t_{{N}}\right) \end{array}\right]^{\mathrm{T}} $

则参数的最小二乘估值为：

$ \hat{\boldsymbol{x}}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{\varSigma}_{y}^{-1} \boldsymbol{A}\right)^{-1}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{\varSigma}_{y}^{-1} \boldsymbol{y}\right) $

(3)

式中，Σ_y为观测值的方差-协方差阵。由式(3)可知，要求得最优估值，需已知观测值的协方差阵。目前公认的最优噪声模型为白噪声+闪烁噪声的组合，因此需要估计各个噪声的噪声分量，可采用方差分量估计方法确定。

2 基于SSA的GNSS坐标时间序列粗差探测与噪声估计 2.1 SSA基本原理

对于时间序列{y₁, y₂, …, y_N}，首先选择一个合适的窗口L，将其进行滞后排列：

$ \boldsymbol{Y}=\left[\begin{array}{cccc} y_{1} & y_{2} & \cdots & y_{L} \\ y_{2} & y_{3} & \cdots & y_{L+1} \\ \vdots & \vdots & \ddots & \vdots \\ y_{K} & y_{K+1} & \cdots & y_{N} \end{array}\right] $

(4)

式中，K=N-L+1，Y∈R^K×L为滞后矩阵。其方差-协方差阵为C=Y^TY，对其进行奇异值分解：

$ \boldsymbol{C}=\boldsymbol{V} \boldsymbol{\varLambda} \boldsymbol{V}^{\mathrm{T}} $

(5)

式中，Λ∈R^L×L为对角阵，其对角元λ_k(1≤k≤L)为C的奇异值，V =(v₁, v₂, …, v _L)为正交阵，v_k为第k个特征向量。可通过V和Y确定主成分矩阵：

$ \boldsymbol{A}=\boldsymbol{V} \boldsymbol{Y} $

(6)

A的第k个行向量被称为第k个主成分，其第i个元素可由式(7)计算：

$ a_{k, i}=\sum\limits_{j=1}^{L} y_{i+j-1} v_{k, j}, 1 \leqslant i \leqslant N-L+1 $

(7)

式中，v_{k, j}为v_k的第j个元素。由第k个主成分可重构第k个分量：

$ y_{i}^{k}=\left\{\begin{array}{l} \frac{1}{i} \sum\limits_{j=1}^{i} a_{k, i-j+1} v_{k, j}, 1 \leqslant i \leqslant L-1 \\ \frac{1}{L} \sum\limits_{j=1}^{L} a_{k, i-j+1} v_{k, j}, L \leqslant i \leqslant N-L+1 \\ \frac{1}{N-i+1} \sum\limits_{j=i-N+L}^{L} a_{k, i-j+1} v_{k, j}, \\ \ \ \ \ N-L+2 \leqslant i \leqslant N \end{array}\right. $

(8)

则原序列y_i可表示成：

$ y_{i}=\sum\limits_{k=1}^{N} y_{i}^{k}, 1 \leqslant i \leqslant N $

(9)

2.2 粗差探测

已有大量研究表明，GNSS坐标时间序列中的粗差主要反映在其噪声(残差)中，因此可直接对噪声序列进行粗差探测。为避免残留信号对粗差探测的干扰，需将信号与噪声进行有效分离。经SSA处理后，GNSS坐标时间序列已被分解为若干能量不等的分量，其中能量较高(轨迹矩阵对应分量的特征值较大)的表示低频信号，能量较低(轨迹矩阵对应分量的特征值较小)的表示高频噪声。本文采用特征值比例法进行信噪分离，取总能量占比90%以上的特征值对应的重构分量作为信号s，剩下的分量作为噪声ε。

原坐标时间序列的粗差大都反映在ε中，将其中的元素进行升序排列。考虑到GNSS坐标时间序列的精度随历元而变化，采用开窗IQR准则进行粗差探测，其判定准则为：

$ \left|\varepsilon_{i}-\operatorname{med}\left(\varepsilon_{i-L / 2}, \varepsilon_{i+L / 2}\right)\right|>c \cdot \operatorname{IQR}\left(\varepsilon_{i-L / 2}, \varepsilon_{i+L / 2}\right) $

(10)

式中，ε_i为ε的第i个分量，med(·)为求中位数算子，IQR(·)为求四分位距算子，L为窗口长度(一般取182)，c为比例因子(一般取3)。因基于IQR准则的粗差探测有较强的边缘效应，式(10)仅适用于序列中部的粗差探测，对于序列两端的粗差探测效果较差。本文对式(10)进行改进，对于边缘数据适当降低c值，将边缘数据非边缘化，则有：

$ \left\{\begin{array}{l} \left|\varepsilon_{i}-\operatorname{med}\left(\varepsilon_{i-L / 2}, \varepsilon_{i+L / 2}\right)\right|>d \cdot \\ \ \ \operatorname{IQR}\left(\varepsilon_{i-L / 2}, \varepsilon_{i+L / 2}\right), \\ \ \ \ \ 1<i<L \text { 或 } N-L<i<N \\ \left|\varepsilon_{i}-\operatorname{med}\left(\varepsilon_{i-L / 2}, \varepsilon_{i+L / 2}\right)\right|>c \cdot \\ \ \ \operatorname{IQR}\left(\varepsilon_{i-L / 2}, \varepsilon_{i+L / 2}\right), \quad \text { 其他 } \end{array}\right. $

(11)

式中，d=c/3。对残差序列ε进行遍历，以当前值为中心，构建窗口序列，当满足准则(11)时，即认为当前历元观测值为粗差。

2.3 噪声分量估计

当粗差被剔除后，噪声序列已较为干净。为获得准确的形变信息，还需确定各噪声的方差分量，以获得准确的噪声模型。记剔除粗差后的坐标序列和噪声序列分别为y′和ε ′，按§2.1方法构建A′，并求其最小二乘估值$\mathit{\boldsymbol{\hat x}}$′。按式(12)生成新的坐标序列数据：

$ \boldsymbol{y}^{\prime \prime}=\boldsymbol{A}^{\prime} \hat{\boldsymbol{x}}^{\prime}+\boldsymbol{\varepsilon}^{\prime} $

(12)

式中，y″表示生成的新序列。考虑到式(12)严格满足Gauss-Markov模型，因此可采用LS_VCE方法估计噪声分量：

$ \hat{\boldsymbol{\sigma}}=\boldsymbol{N}^{-1} \boldsymbol{L} $

(13)

式中，${\bf{ \pmb{\mathit{\hat σ}} }} = {\left[ {\hat \sigma _w^2\;\;\;\hat \sigma _f^2} \right]^{\rm{T}}}$为待估噪声方差分量，其中$\hat \sigma _w^{}$和$\hat \sigma _f^{}$分别为白噪声和闪烁噪声的振幅因子，N和L分别为一个二维方阵和向量，其构成为：

$ \begin{aligned} &n_{i j}=\frac{1}{2} \operatorname{tr}\left(\boldsymbol{Q}_{i} \boldsymbol{\varSigma}_{y}^{-1} \boldsymbol{P}_{A}^{\perp} \boldsymbol{Q}_{j} \boldsymbol{\varSigma}_{y}^{-1} \boldsymbol{P}_{A}^{\perp}\right) ,\\ &\quad i, j=1,2 \\ &l_{j}=\frac{1}{2} \hat{\boldsymbol{e}}^{\mathrm{T}} \boldsymbol{\varSigma}_{y}^{-1} \boldsymbol{Q}_{i} \boldsymbol{Q}_{y}^{-1} \hat{\boldsymbol{e}} \end{aligned} $

(14)

式中，$\sum\nolimits_y = \sigma _w^2{{\bf{Q}}_1} + \sigma _f^2{{\bf{Q}}_2}$，Q₁为白噪声的协方差阵(单位阵)，Q ₂为闪烁噪声的协方差阵(具体构造方式见文献[5])，${\bf{P}}_A^ \bot = {{\bf{I}}_m} - {{\bf{A}}^\prime }{\left( {{{\bf{A}}^\prime }^{\rm{T}}\sum\nolimits_y^{ - 1} {{{\bf{A}}^\prime }} } \right)^{ - 1}}{{\bf{A}}^\prime }^{\rm{T}}\sum\nolimits_y^{ - 1} {} $，$\mathit{\boldsymbol{\hat e = P}}_A^ \bot \mathit{\boldsymbol{y}} $"。由于式(13)中N和L中均含有未知噪声分量，因此需迭代求解。

3 算例分析 3.1 模拟数据

为了验证本文算法的正确性，采用模拟的坐标时间序列数据进行验证。模拟策略同文献[9]，即认为GNSS坐标时间序列由3个部分组成：

$ y\left(t_{i}\right)=s_{1}\left(t_{i}\right)+s_{2}\left(t_{i}\right)+\varepsilon\left(t_{i}\right) $

(15)

式中，s₁(t_i)=a+bt_i为线性信号，s₂(t_i)= $ \sum\limits_{k = 1}^2 {} $(c_k+e(t_i))sin(2kπt_i)+(d_k+e(t_i))cos(2kπt_i)为时变季节性信号，e(t_i)=fe^gsin(t_i)为变振幅因子，表 1为模拟所用的参数。为验证粗差探测算法的有效性，采用文献[8]的策略对其模拟粗差。图 1为模拟的坐标时间序列。

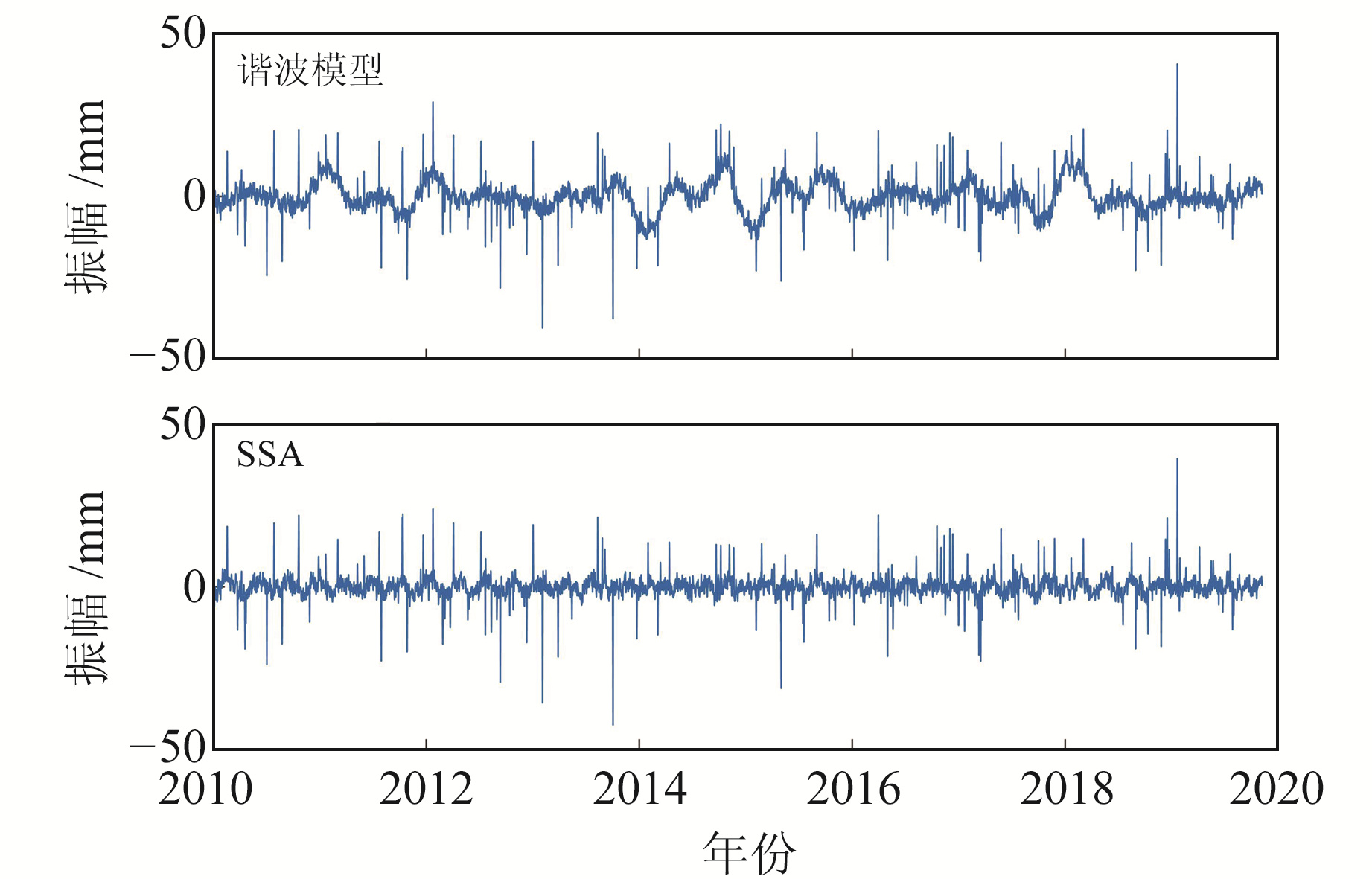
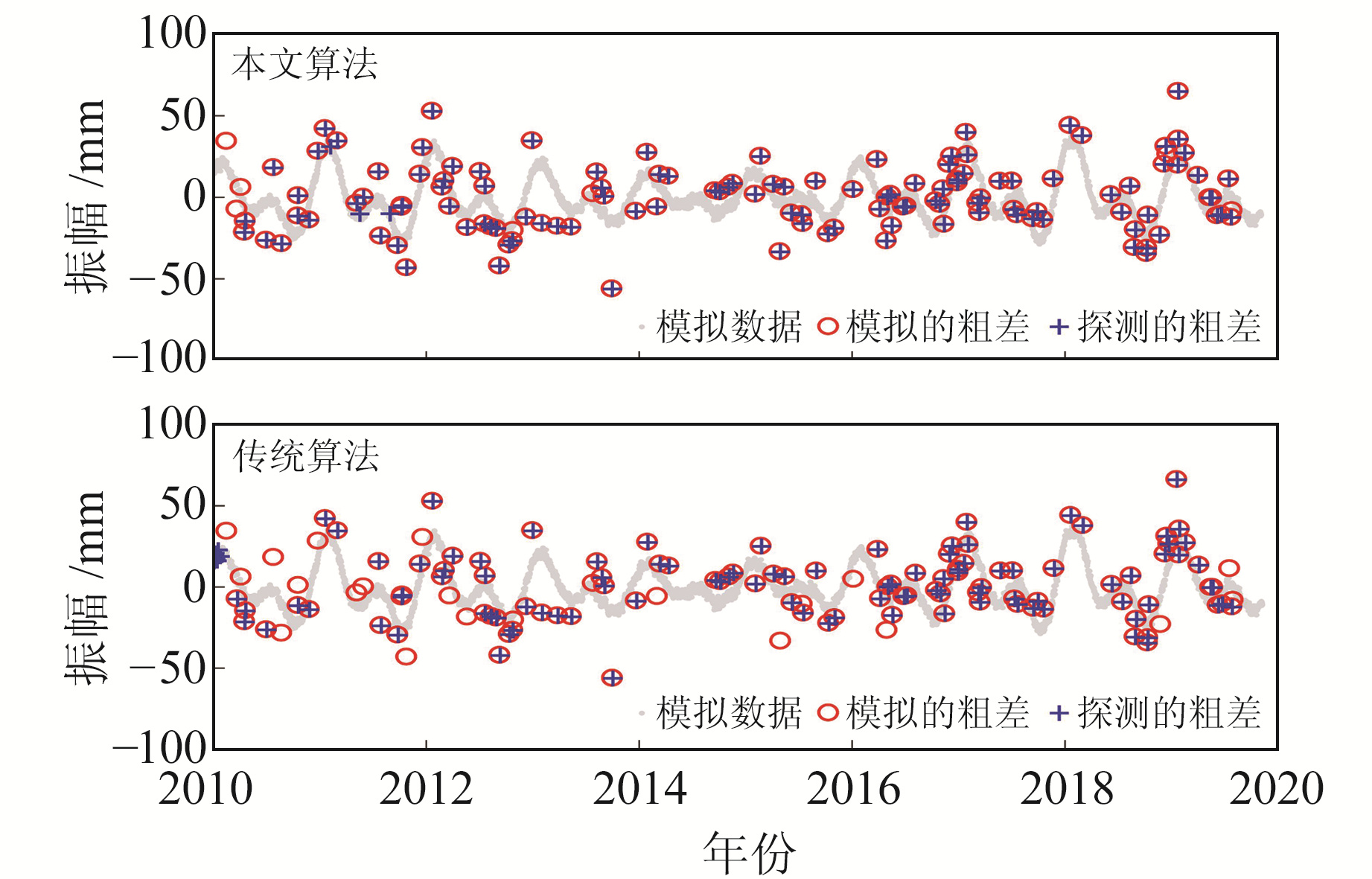
采用SSA对模拟的坐标时间序列进行分析，窗口长度取365。根据SSA原理构建轨迹矩阵，并求其协方差阵的特征值，结果见图 2。由图可见，前4个特征值占总特征值的91%，因此可选择前4个特征值对应的RC作为信号，剩余RC作为噪声。图 3和图 4分别为SSA和谐波模型分离出的信号与噪声，显然SSA提取出的信号更能反映出时间序列的真实非线性变化，其残差也相对较为平稳；而谐波模型仅能粗略地描述时间序列，其残差中仍然含有部分信号。此外，原始序列中的粗差大都传递至残差中。分别采用传统算法和本文算法探测残差中的粗差，结果见图 5。可以看出，传统算法仅能探测到83%的粗差，而本文算法可探测到94%的粗差。

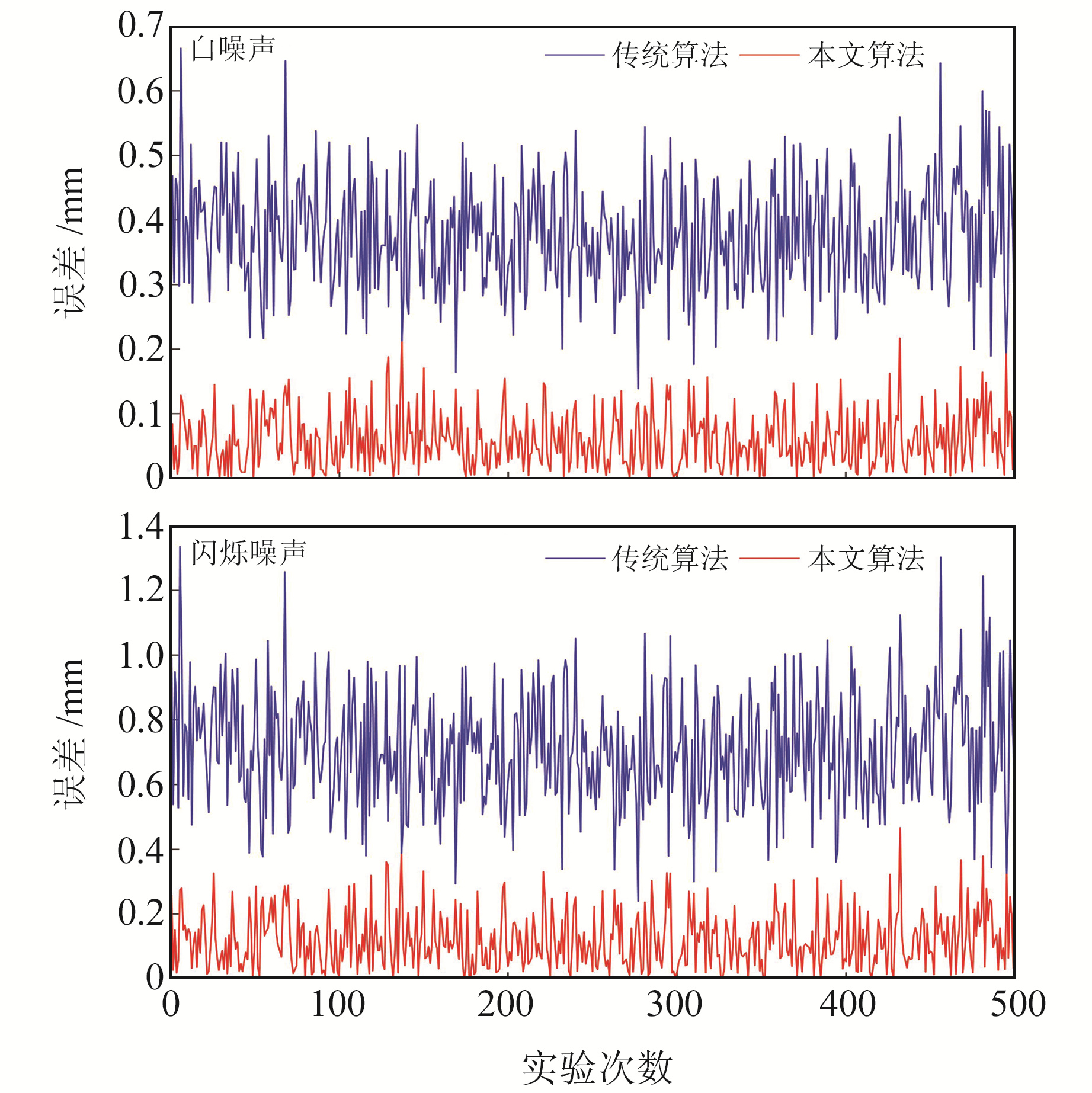
将粗差从原始坐标时间序列中剔除，可获得干净的坐标序列数据。分别采用传统算法和本文算法对其噪声分量进行估计，其中传统算法估计的噪声分量为2.63 mm($ {\hat \sigma _w}$)和3.51 mm(${\hat \sigma _f} $)，本文算法估计的噪声分量为1.92 mm(${\hat \sigma _w} $)和2.84 mm(${\hat \sigma _f} $)。显然，本文算法估计的噪声分量更接近模拟真值。模拟500次实验，每次实验均按上述策略随机生成时间序列，分别采用本文算法和传统算法估计噪声分量，统计每次实验噪声分量估值与真值的绝对误差(图 6)。可以看出，本文算法估计的噪声分量估值的绝对误差小于传统算法，其中传统算法估计的噪声分量与真值的平均偏差为0.38 mm(${\hat \sigma _w}$)和0.79 mm(${\hat \sigma _f} $)，本文算法则为0.06 mm(${\hat \sigma _w} $)和0.18 mm(${\hat \sigma _f} $)。

3.2 实测数据

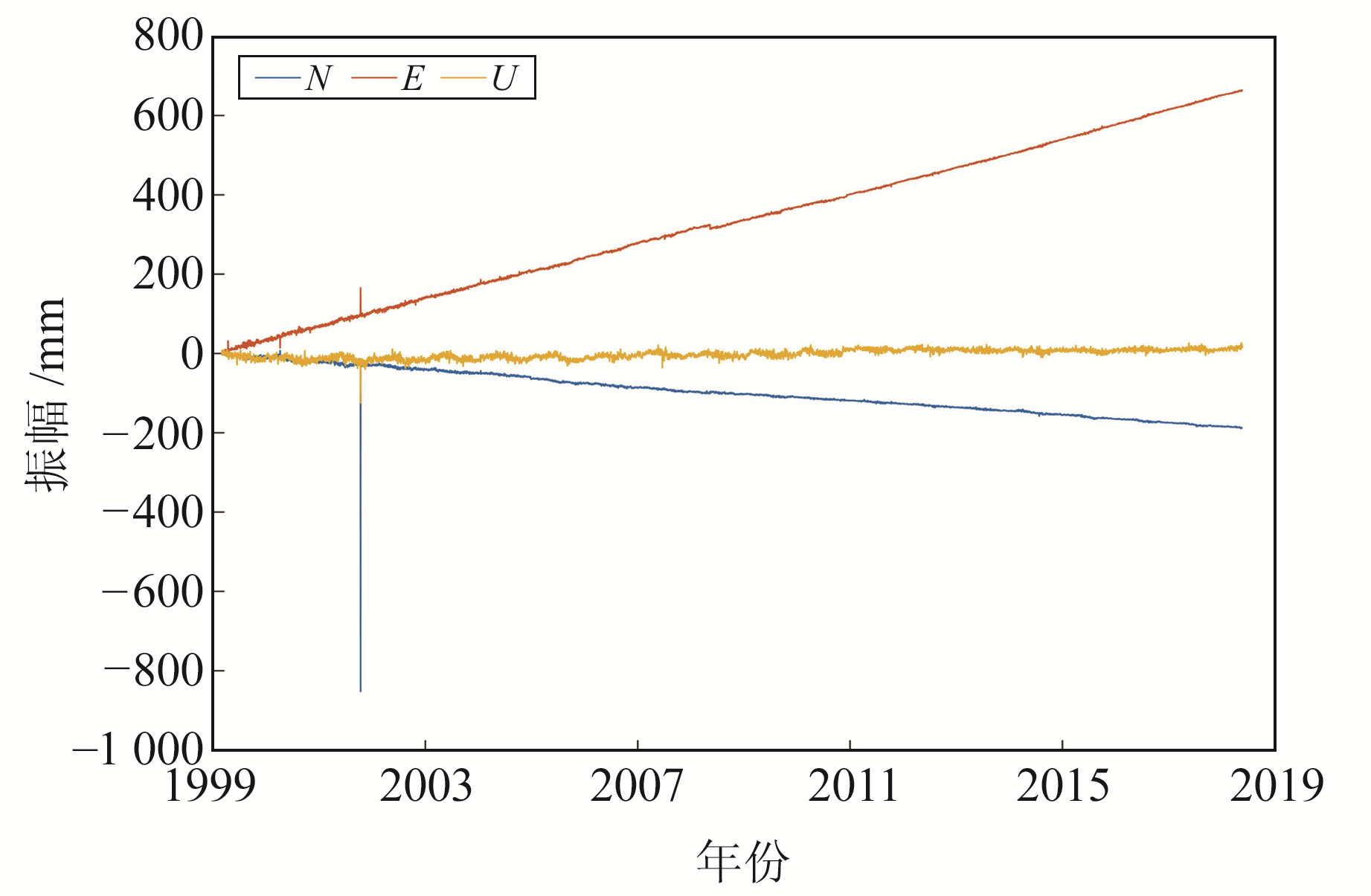
为进一步验证本文算法的有效性，选取陆态网络提供的10个基准站观测数据进行分析。所有数据可通过中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn/)获取，表 2为各站点的相关信息。以LUZH站为例，图 7为其1999~2019年的连续观测坐标序列，其中含有大量的粗差，必须剔除。分别采用SSA和谐波模型对去趋势后的坐标序列进行信噪分离，图 8为3个方向轨迹矩阵协方差阵的特征值及其占总特征值之比。由图可知，N方向前3个特征值之和占总特征值之比达90.88%，E方向前5个特征值之和占总特征值之比达90.05%，U方向前10个特征值之和占总特征值之比达90.03%。由此可确定，信号分量和噪声分量的分界层分别为3(N)、5(E)和10(U)。2种算法估计的信号如图 9所示。可以看出，传统谐波模型仅能粗略地描述GNSS坐标时间序列，特别是对于水平方向的坐标序列，其拟合度较差；而SSA不受正弦波的假定约束，它从时间序列的动力重构出发，能自适应地提取出时间序列的信号，因此其能较好地描述GNSS坐标时间序列的非线性变化。

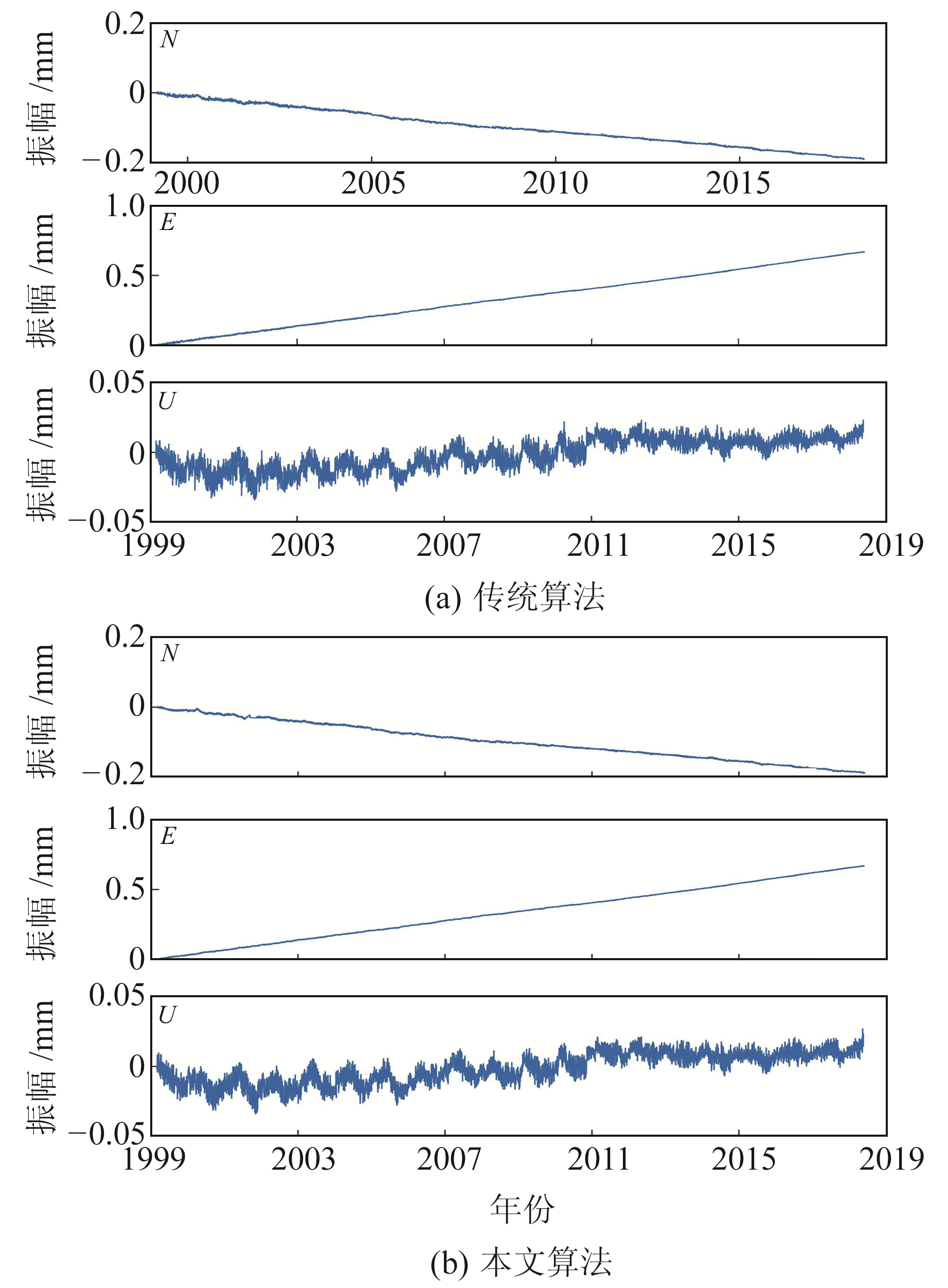
将信号从原坐标序列中去除，分别采用本文算法和传统算法对残差序列进行粗差探测，图 10为2种算法探测粗差剔除后的坐标序列。由图可见，采用本文算法处理后的坐标时间序列中几乎没有粗差，序列整体较为干净；而采用传统算法处理后的坐标时间序列仍存在一些小粗差(如1999~2003年)，这主要是因为谐波模型对该时段的拟合效果较差。分别采用2种算法估计坐标时间序列中的噪声分量，结果如表 3所示。从结果来看，传统算法估计的噪声分量略大于本文算法。

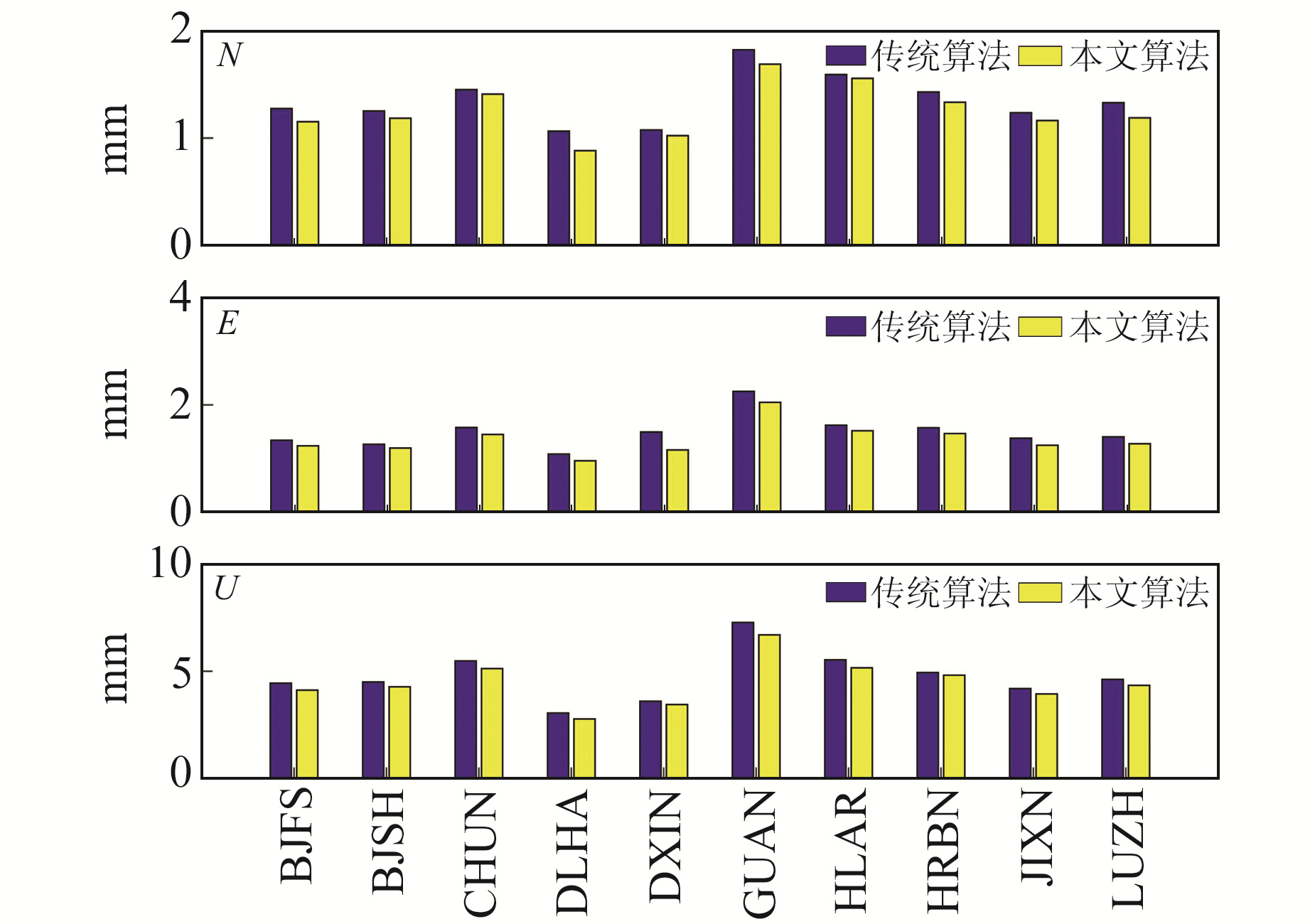
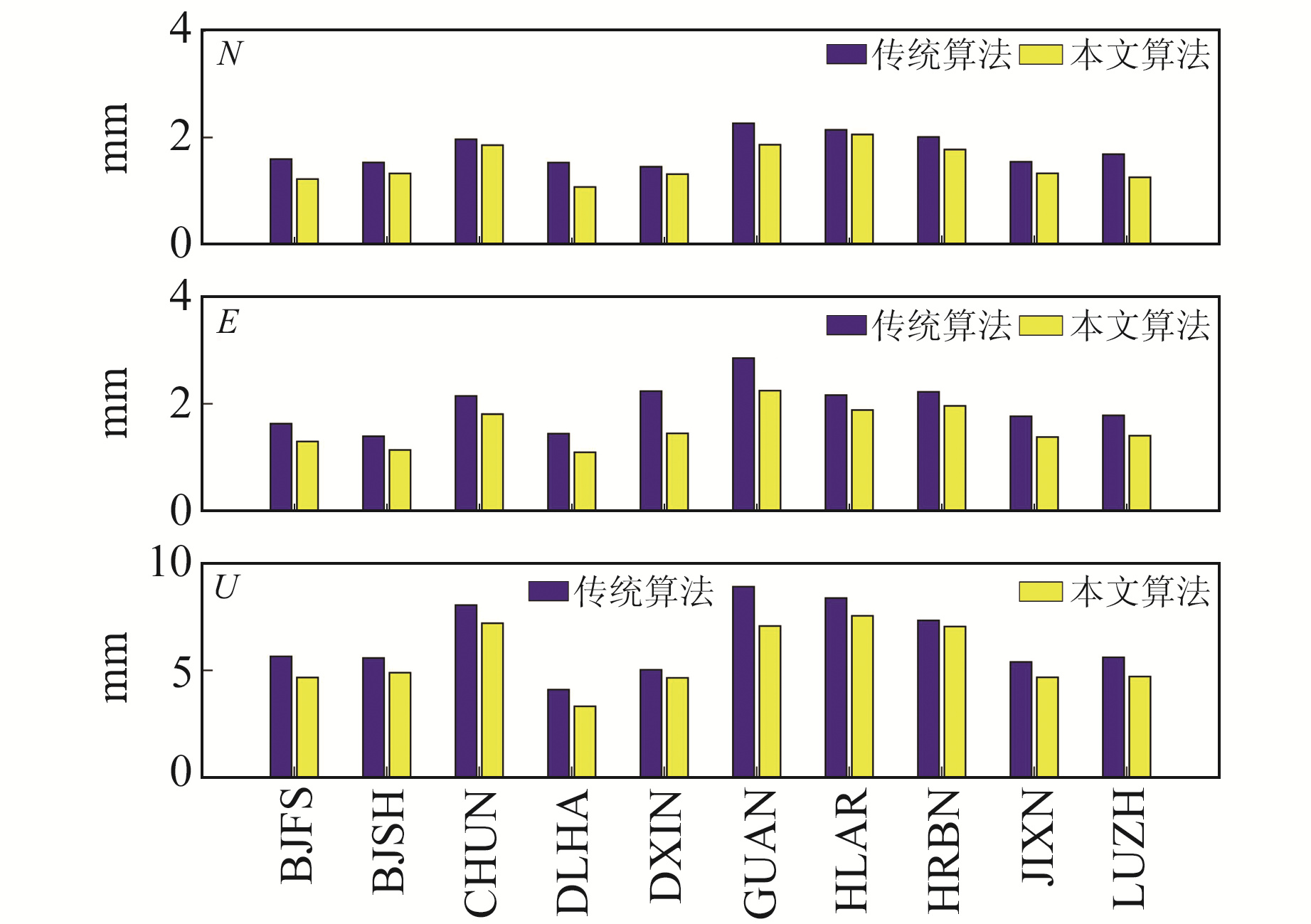
分别采用2种算法对10个基准站进行粗差探测和噪声分量估计，图 11为2种算法探测的粗差占总数据的比例。由图可知，采用传统算法探测到的粗差比例要低于本文算法，其10个站的平均比例分别为1.57%(N)、1.55%(E)和1.54%(U)；而本文算法所探测到的粗差平均比例为4.76%(N)、4.74%(E)和2.33%(U)。此外，高程方向的噪声强度远大于水平方向，这与文献[10]中的结论一致。图 12和图 13分别为估计的白噪声和闪烁噪声分量估值。从结果来看，本文算法估计的噪声强度均小于传统算法。对于N方向，本文算法估计的平均噪声分量分别为1.26 mm(${\hat \sigma _w} $)和1.50 mm(${\hat \sigma _f} $)，传统算法估计的平均噪声分量分别为1.35 mm(${\hat \sigma _w} $)和1.77 mm(${\hat \sigma _f} $)；对于E方向，本文算法估计的平均噪声分量分别为1.36 mm(${\hat \sigma _w} $)和1.57 mm($ {\hat \sigma _f}$)，传统算法估计的平均噪声分量分别为1.50 mm(${\hat \sigma _w} $)和1.96 mm(${\hat \sigma _f} $)；对于U方向，本文算法估计的平均噪声分量分别为4.47 mm(${\hat \sigma _w} $)和5.58 mm($ {\hat \sigma _f}$)，传统算法估计的平均噪声分量分别为4.77 mm(${\hat \sigma _w} $)和6.40 mm(${\hat \sigma _f} $)。准确地获取噪声序列是粗差探测和噪声估计的前提。由于谐波模型的局限性，其拟合得到的噪声序列呈非平稳特性，影响IQR统计量的计算，导致粗差探测准确率较低；此外，在进行噪声分量估计时，其中残留的非线性信号也会被误当成噪声而导致噪声分量被高估。

4 结语

由于多种因素的影响，GNSS坐标时间序列受到各类噪声和粗差的污染。为了能够更加精确地估计地壳形变信号，需将其中混有的粗差进行有效地识别、剔除并且对噪声进行准确的建模。以往进行粗差探测和噪声估计的算法大都是基于谐波模型进行构建的，然而谐波模型难以精确地描述GNSS坐标时间序列的非线性变化，进一步影响算法的性能。本文提出一种基于SSA的GNSS坐标时间序列粗差探测和噪声估计算法，并采用模拟实验对算法进行验证。实验结果表明，相比于传统算法，本文算法的粗差探测成功率更高，且估计的噪声分量与真值更为接近。陆态网络实测数据分析结果表明，高程方向时间序列噪声强度要高于水平方向，且闪烁噪声的振幅要高于白噪声。此外，由于谐波模型不正确的模型假设导致所获得的残差序列中仍含有部分信号，进一步导致其估计的噪声振幅略高于本文算法。