2. 长江三峡勘测研究院有限公司(武汉),武汉市光谷创业街99号,430074;
3. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079
GNSS长期坐标时间序列可以反映测站的运动趋势,对于地壳运动及动力学研究至关重要。国内外众多学者已对GNSS坐标时间序列的噪声特性进行过分析。Mao等[1]、Williams等[2]和Zhang等[3]认为,不论是全球还是区域分布的测站,其坐标时间序列的噪声模型主要表现为闪烁噪声+白噪声(FN+WN)的组合。李昭等[4]对11个IGS基准站近15 a的坐标序列进行分析,证明中国区域IGS基准站的噪声模型存在多样性,主要表现为FN+WN和带通幂律噪声加白噪声(BPPL+WN)。张风霜[5]的研究表明,FN+WN或幂律噪声+白噪声(PL+WN)为云南地区GNSS各坐标分量的最优噪声模型。
虽然以上学者对GNSS坐标时间序列的噪声模型进行了详细分析,但是并未研究环境负载对噪声特性的影响,而环境负载是GNSS信号呈现周期性变化的主要原因[6]。因此,本文选取云南省25个GNSS观测站长时间的坐标序列,计算相应的环境负载位移,采用多种不同的噪声组合模型来分析环境负载改正前后云南省区域GNSS坐标时间序列的噪声特性变化。
1 数据来源 1.1 GNSS数据本文采用中国大陆构造环境监测网络(简称陆态网络)云南省25个GNSS测站2010~2017年的坐标时间序列,站点的空间分布如图 1所示。采用GAMIT/GLOBK 10.4同时解算所有GNSS观测数据,获得每日松弛解,然后通过GLOBK采用7参数转换的方法将松弛解约束到ITRF框架下,具体解算策略可参考陆态网络数据处理手册。

|
图 1 测站分布 Fig. 1 Distribution of the stations |
环境负载主要指水文负载(HYDL)、非潮汐大气负载(NTAL)和非潮汐海洋负载(NTOL)等,根据弹性负载理论[7]可以计算地球上任意点环境负载所引起的地壳形变。本文采用美国宇航局(National Aeronautics and Space Administration, NASA)全球模型与同化办公室(Global Modeling and Assimilation Office, GMAO)提供的环境负载模型产品进行双三次插值得到所有站点的负载形变,其中水文负载模型产品采用MERRA-2(modern-era retrospective analysis for research and applications, version 2),模型分辨率为0.625°×0.5°×1 h;非潮汐大气负载模型产品采用GEOS-FPIT,模型分辨率为0.625°×0.5°×3 h×72层;非潮汐海洋负载模型产品采用由GFZ(German Research Centre for Geosciences) 提供数据计算得到的OMCT05(ocean model for circulation and tides)。插值后平均,得到日均负载位移量,与GNSS时间序列的时间分辨率统一。
2 数据分析方法 2.1 噪声分析方法采用极大似然估计分析噪声时间序列。该方法假设GNSS坐标时间序列由函数模型和随机噪声组成,其参数模型为[3]:
| $ \begin{array}{*{20}{c}} {x\left( t \right) = a + bt + {s_1}\sin \left( {2{\rm{ \mathsf{ π} }}t} \right) + {c_1}\cos \left( {2{\rm{ \mathsf{ π} }}t} \right) + }\\ {{s_2}\sin \left( {4{\rm{ \mathsf{ π} }}t} \right) + {c_2}\cos \left( {4{\rm{ \mathsf{ π} }}t} \right) + \sum\limits_{i = 1}^{{n_I}} {{h_i}} H\left( {t - {t_1}} \right) + }\\ {\sum\limits_{j = 1}^{{n_J}} {{a_j}} \ln \left( {1 + \left( {t - {t_j}} \right)/{T_J}} \right) + {v_t}} \end{array} $ | (1) |
式中,x(t)为t历元测站坐标序列日解,a为起始时刻测站位置,b为速度项,s1、c1、s2、c2为年周期和半年周期项系数,hi为由于天线或天线罩更换引起的跳变,nI为跳变的次数,ti为跳变历元,H为Heaviside阶梯函数,跳变前其值为0,跳变历元其值为0.5,跳变后其值为1,为地震跳变的次数,aj为测站的震后变形幅值,tj、TJ分别为地震历元和震后弛豫效应时间,TJ一般取值为1 a,vt为噪声项,可表示不同噪声或者噪声组合。
一般认为,FN+WN是描述GNSS坐标时间序列噪声的最佳模型,但是不少学者发现GNSS坐标时间序列中也包含有随机游走噪声(RW)、一阶高斯-马尔科夫噪声(FOGM)等[4, 8]。为了更加全面、系统地分析环境负载对噪声特性的影响,本文选取闪烁噪声加白噪声(FN+WN)、一阶高斯-马尔科夫噪声加白噪声(FOGM+WN)、幂律噪声加白噪声(PL+WN)、随机游走噪声、闪烁噪声加白噪声(RW+FN+WN)和随机游走噪声加白噪声(RW+WN)模型,应用Hector[9]软件进行分析。
2.2 噪声模型评价准则根据极大似然估计准则,时间序列的对数值随着组合噪声模型v的变化而变化,数值越大表明模型越优。但研究发现,不能单纯地认为对数值越大对应的噪声模型越优,因为其值越大表示模型中的参数也越多。为确定最优噪声组合模型,采用贝叶斯信息准则(BIC)[10]添加惩罚因子,BIC最小表示最优。贝叶斯信息准则定义如下:
| $ {\rm{BIC = }}k\ln - 2\ln L $ | (2) |
式中,k为总模型参数,N为坐标时间序列总历元数,lnL为模型对应的极大似然值。
3 结果与分析 3.1 环境负载改正前的最优噪声模型采用极大似然估计及其评价准则对云南省25个GNSS测站的坐标时间序列进行上述5种噪声组合模型的噪声分析,得到75组环境负载改正前的最优噪声组合模型,结果如表 1所示。
|
|
表 1 环境负载改正前后坐标时间序列最优噪声模型 Tab. 1 Optimal noise model of coordinate time series before and after environmental loading correction |
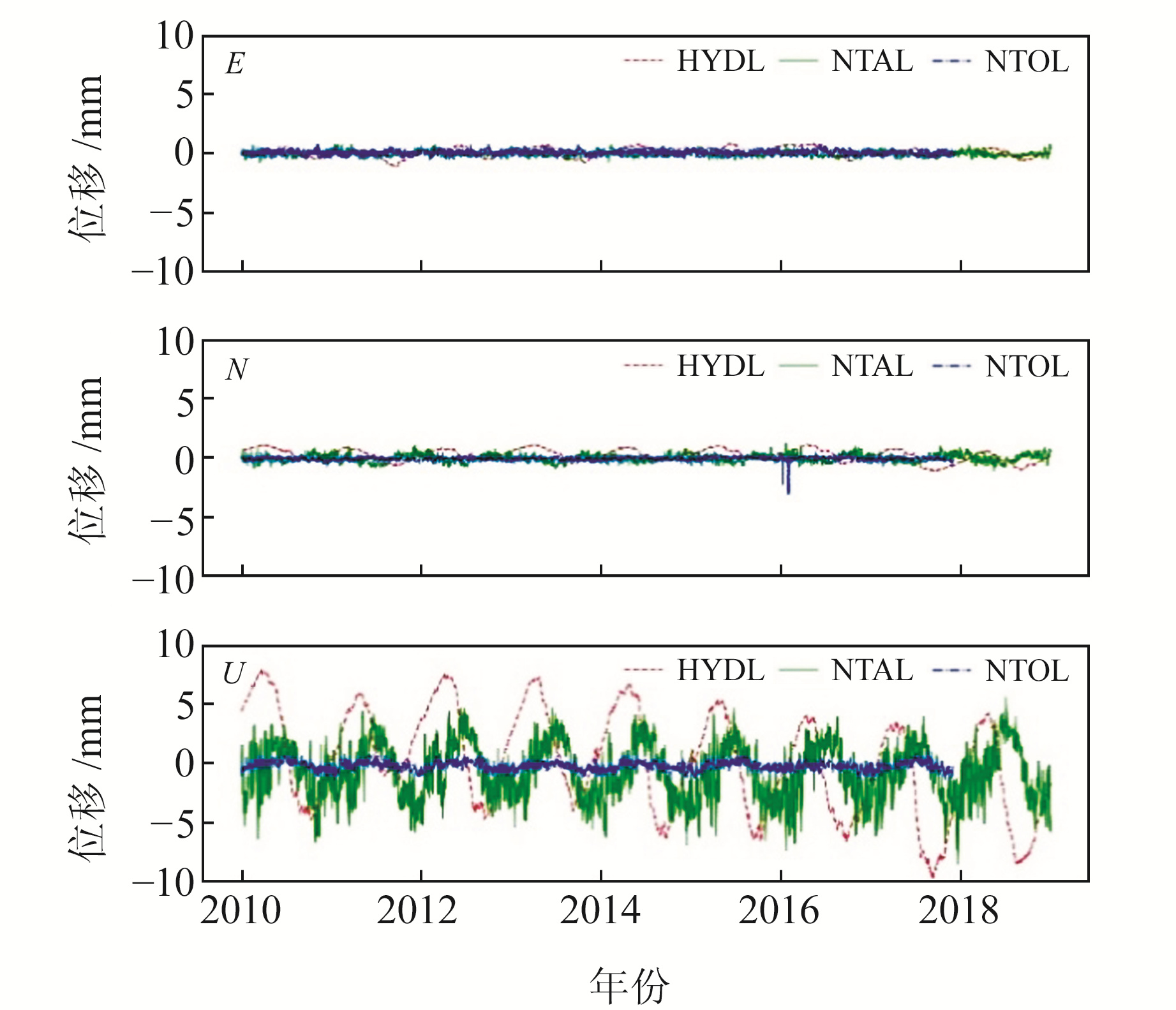
环境负载是引起GNSS测站季节性变化的主要因素。基于NASA公开的全球环境负载格网产品,采用双三次插值计算陆地水文负载、非潮汐大气负载及非潮汐海洋负载对测站E、N、U分量造成的位移,图 2为YNDC站计算结果。将相应的位移从GNSS坐标时间序列中扣除后,再采用极大似然估计进行上述噪声组合分析,即得到环境负载改正后的最优噪声组合模型。
|
图 2 环境负载造成YNDC站的位移 Fig. 2 The displacements caused by environmental loading at YNDC station |
由图 2可知,YNDC站水文负载产生的位移明显大于非潮汐大气负载和非潮汐海洋负载,并且在3个方向上都呈现出很强的周期性。
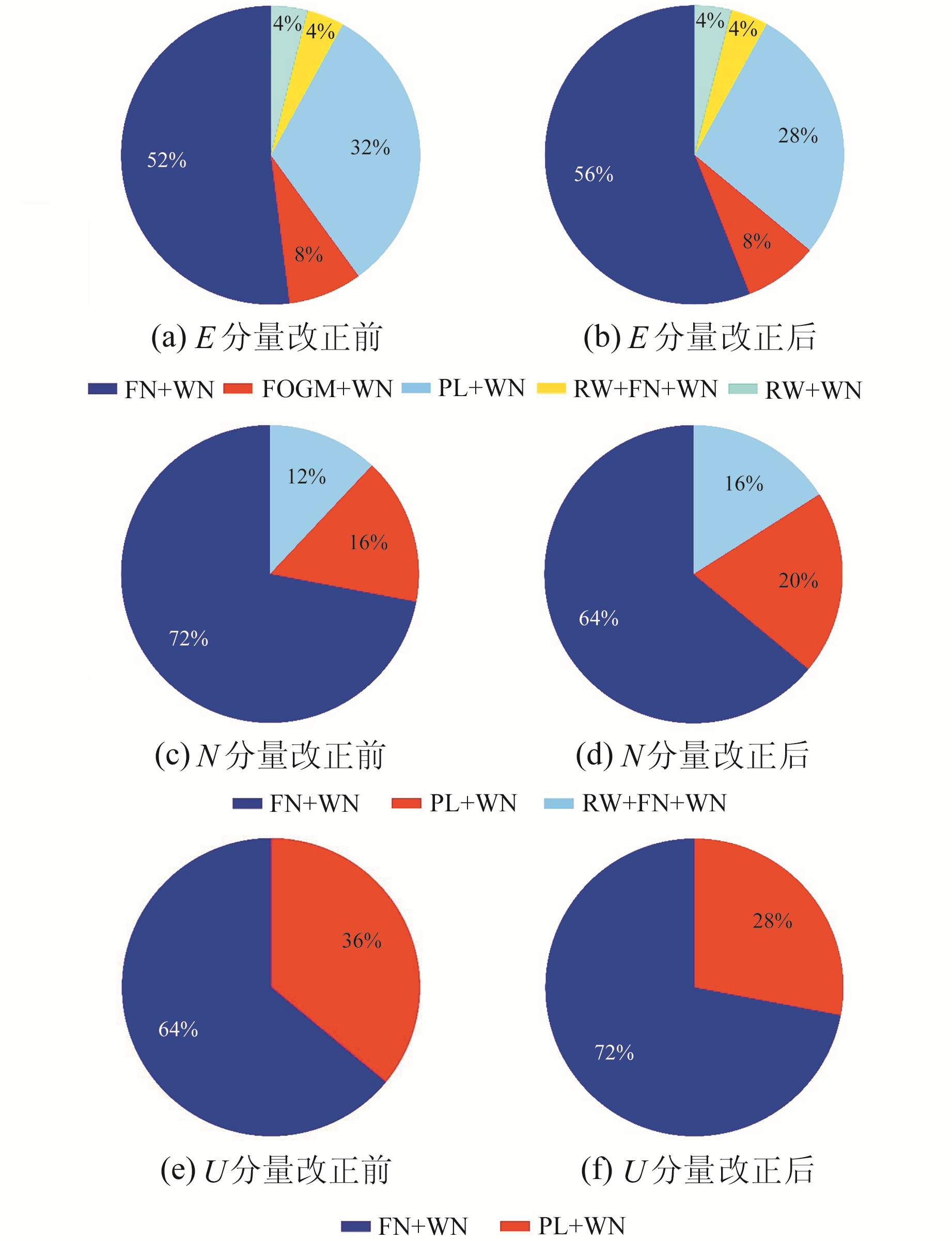
图 3为环境负载改正前后最优噪声比例分布图。可以看出,E、N、U分量的噪声模型并不完全相同,5种噪声模型中,N、U分量分别没有表现出FOGM+WN、RW+WN和FOGM+WN、RW+FN+WN、RW+WN。总体来看,噪声模型所占比例最大的均为FN+WN,E、N、U分量改正前比例分别为52%、72%、64%;改正后比例分别为56%、64%、72%。可见,加入环境负载改正后并没有大范围改变测站的最优噪声模型,仅有部分测站的最优噪声模型有所改变,如YNHZ站E分量的最优噪声模型由PL+WN变为FN+WN。究其原因,可能是对于大部分测站而言,环境负载改正并没有掩盖或者凸显出某一种噪声特性,而在某些特定测站的负载形变却能够让原本被湮没的信号显现出来,这与测站周围的地理环境有关。
|
图 3 环境负载改正前后坐标时间序列的最优噪声组合模型分布 Fig. 3 Distribution of the best noise models of coordinate time series before and after environmental loading correction |
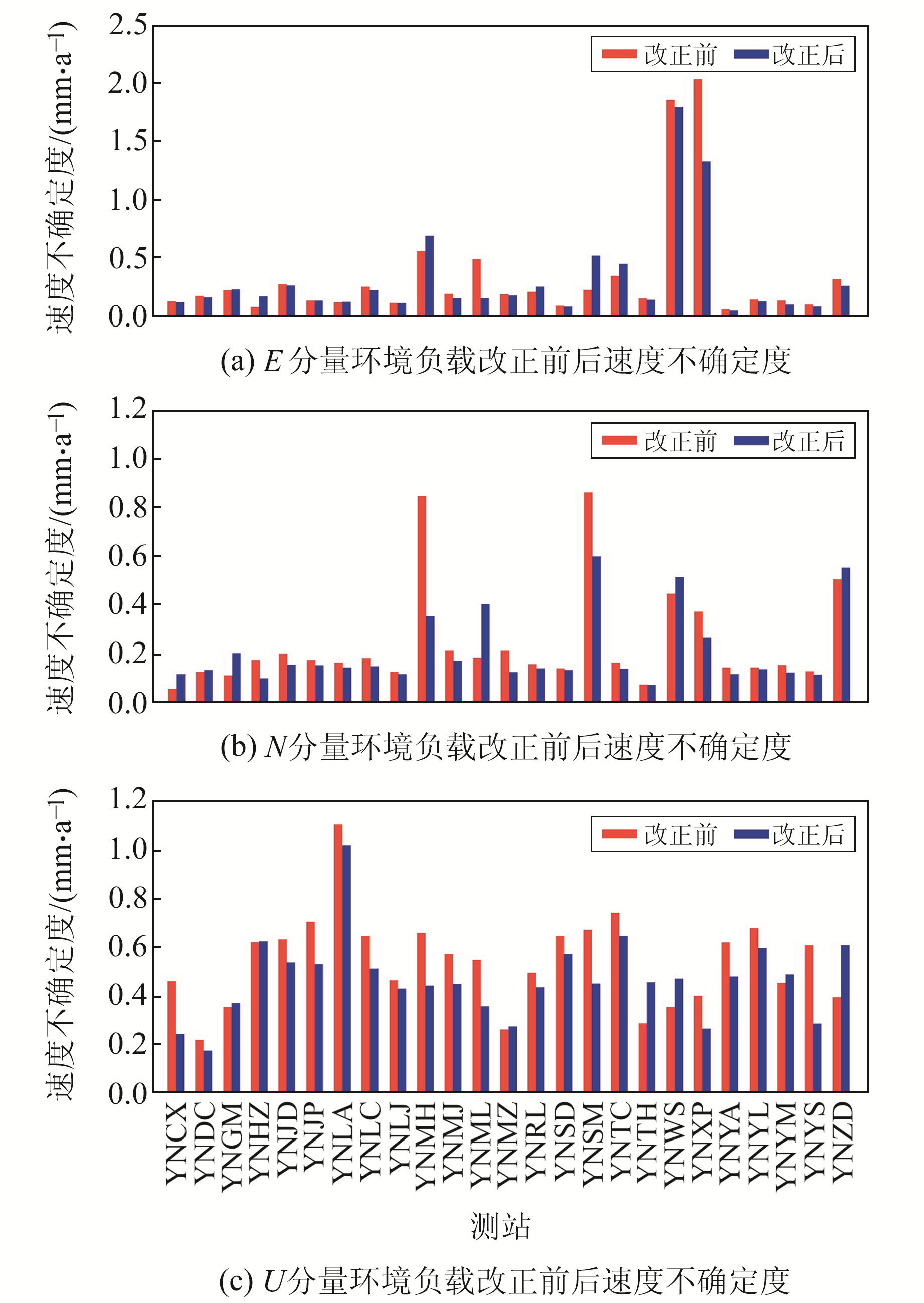
测站速度及其不确定度对地壳形变的影响至关重要。以表 1计算的最优噪声模型为准,以式(1)计算环境负载改正前后各测站的速度及其不确定度。根据计算结果,在环境负载改正前后速度项几乎无差异,故只进行速度不确定度差异的讨论,速度不确定度计算结果如图 4所示。
|
图 4 环境负载改正前后的速度不确定度 Fig. 4 Velocity uncertainty before and after environmental loading correction |
由图 4可以看出,在正确构建噪声模型的基础上,环境负载改正能够明显降低速度不确定度,其中U分量变化最大,E、N分量次之。采用加入环境负载改正后建立的最优噪声模型估计各测站的速度不确定度,对于E、N、U分量,分别有72%、80%、68%的测站的速度不确定度减小。在YNML站,E分量速度不确定度甚至降低2/3,YNMH站N分量及YNYS站U分量均降低超过1/2。但有部分测站的速度不确定度不降反升,如YNZD站U分量变大1/2,这可能与GNSS数据预处理不完全、仍存在系统误差有关。由此可以得出,环境负载改正能够影响测站的速度不确定度,在保证噪声模型正确的前提下提高速度估值的精度。
4 结语本文采用极大似然方法及BIC准则确定了云南省陆态网络25个测站的最优噪声模型,大部分测站3个分量的最优噪声模型表现为FN+WN,其次为PL+WN,少数测站表现为FOGM+WN、RW+FN+WN及RW+WN。通过计算分析得出,环境负载形变会在一定程度上影响测站坐标时间序列的噪声特性,改变其最优噪声模型。同时,环境负载改正能够减小测站的速度不确定度,提高速度估值的精度,在进行高精度地壳形变分析及研究时需顾及此项改正。
需要指出的是,本文采用的GNSS坐标时间序列是从2010年开始的,可能无法分析到某些长周期的形变信号,使结果带有一定的局限性。
| [1] |
Mao A L, Harrison C G A, Dixon T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B2): 2797-2816 DOI:10.1029/1998JB900033
(  0) 0) |
| [2] |
Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
(  0) 0) |
| [3] |
Zhang J, Bock Y, Johnson H, et al. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18035-18055 DOI:10.1029/97JB01380
(  0) 0) |
| [4] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [5] |
张风霜. 有色噪声模型下云南地区GPS基准站速度与周期估计[J]. 地震研究, 2016, 39(3): 410-420 (Zhang Fengshuang. Estimation on Velocity and Cycle of GPS Reference Stations in Yunnan Area Based on the Colored Noise Models[J]. Journal of Seismological Research, 2016, 39(3): 410-420)
(  0) 0) |
| [6] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052 (Wang Min, Shen Zhengkang, Dong Danan. Effects of Non-Tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045-1052)
(  0) 0) |
| [7] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [8] |
李斐, 马超, 张胜凯, 等. 南极半岛地区GPS坐标时间序列噪声分析及形变模式初探[J]. 地球物理学报, 2016, 59(7): 2402-2412 (Li Fei, Ma Chao, Zhang Shengkai, et al. Noise Analysis of the Coordinate Time Series of the Continuous GPS Station and the Deformation Patterns in the Antarctic Peninsula[J]. Chinese Journal of Geophysics, 2016, 59(7): 2402-2412)
(  0) 0) |
| [9] |
Bos M S, Fernandes R M S, Williams S D P, et al. Fast Error Analysis of Continuous GNSS Observations with Missing Data[J]. Journal of Geodesy, 2013, 87(4): 351-360 DOI:10.1007/s00190-012-0605-0
(  0) 0) |
| [10] |
Schwarz G. Estimating the Dimension of a Model[J]. Annals of Statistics, 1978, 6(2): 461-464
(  0) 0) |
2. Changjiang Three Gorges Survey Institute Co Ltd (Wuhan), 99 Guangguchuangye Street, Wuhan 430074, China;
3. GNSS Research Centre, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2021, Vol. 41
2021, Vol. 41


