2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
当无线电信号通过对流层时,传播路径会发生弯曲而产生对流层延迟,这种延迟无法通过双频改正的方法消除[1],需要采用模型改正法消除。天顶对流层延迟(zenith total delay, ZTD)由天顶静力学延迟(zenith hydrostatic delay, ZHD)和天顶湿延迟(zenith wet delay, ZWD)组成。随着大气再分析资料积分计算的对流层延迟在GNSS精密定位和GNSS大气反演中的广泛应用,提高对流层延迟信息的精度具有重要意义。
大气再分析资料的格网点高程与探空站、GNSS站等用户位置高程不一致,且ZTD/ZWD在垂直方向的变化远大于水平方向,因此ZTD/ZWD垂直剖面模型是实现高精度对流层格网产品空间插值的关键。部分学者基于二次多项式、负指数函数或高斯函数构建对流层垂直剖面模型[2-7],所得的区域或全球对流层延迟垂直剖面模型具有各自的优势,但仍然存在时空分辨率低、所需参数较多、部分区域适用性较差等不足,中国区域高精度、高分辨率、实时ZTD和ZWD垂直剖面模型仍然缺乏。
本文利用高时空分辨率的MERRA-2再分析资料积分计算的分层ZTD、ZWD剖面信息,基于负指数函数表达ZTD、ZWD垂直剖面,详细分析ZTD、ZWD高程缩放因子的时空分布特性,为构建中国区域高精度ZTD、ZWD垂直剖面模型提供参考。
1 数据来源MERRA-2是由美国宇航局(NASA)推出的高时空分辨率再分析资料(https://goldsmr4.gesdisc.eosdis.nasa.gov/data/MERRA2),可提供地表气象参数和分层气象参数,水平分辨率均为0.5°×0.625°(纬度×经度),分层气象参数的垂直分辨率为72层和42层标准气压层。本文选取42层分层数据,地表气象参数的时间分辨率为1 h,分层气象参数的时间分辨率为6 h。因需同时用到地表气象参数和分层气象参数,为统一时间分辨率,地表气象参数采样率取6 h。根据MERRA-2大气再分析资料提供的分层数据,通过积分法可得到ZTD、ZWD在每个格网点的垂直剖面,表达式如下[8]:
| $ e=\frac{\mathrm{Sh} \cdot P}{0.622} $ | (1) |
| $ N=\frac{k_{1}(P-e)}{T}+\frac{k_{2} e}{T}+\frac{k_{3} e}{T^{2}} $ | (2) |
| $ N_{\mathrm{w}}=\frac{k^{\prime}{ }_{2} e}{T}+\frac{k_{3} e}{T^{2}} $ | (3) |
| $ \mathrm{ZTD}=10^{-6} \int_{h_{\mathrm{L}}}^{h_{\mathrm{top}}} N \mathrm{d} H $ | (4) |
| $ \mathrm{ZWD}=10^{-6} \int_{h_{\mathrm{L}}}^{h_{\mathrm{top}}} N_{\mathrm{w}} \mathrm{d} H $ | (5) |
| $ \mathrm{ZTD}=\mathrm{ZHD}+\mathrm{ZWD} $ | (6) |
式中,e为水汽压(单位hPa),Sh为比湿,P为大气压(单位hPa),N为总折射率,Nw为湿折射率,T为温度(单位K),H为高程(单位km),hL为大气资料积分计算的最底层高度,htop为大气积分资料积分计算的最顶层高度,k1=77.604 K/Pa、k2=64.79 K/Pa、k3=375 463 K2/hPa、k′2=22.97 K/Pa为常数系数。
由于大气再分析资料MERRA-2顶层还有残余大气,需要利用Saastamoinen模型计算残余大气延迟值,并将其附加到格网点每一层的积分结果上。对流层层顶的对流层湿延迟较小,可忽略不计,因此仅计算ZHD即可:
| $ \begin{gathered} \mathrm{ZHD}_{\text {Saas }}= \\ \frac{0.002\ 276\ 7 P_{\text {top }}}{1-0.002\ 667 \cos (2 \varphi)-0.000\ 000\ 28 h_{\text {top }}} \end{gathered} $ | (7) |
式中,Ptop为对流层顶层大气压(单位hPa),φ为纬度,ZHDSaas为利用Saastamoinen模型计算的MERRA-2层顶的残余ZHD值。为便于积分计算,对式(4)和式(5)进行离散化:
| $ \begin{gathered} \mathrm{ZTD}=10^{-6} \int_{h_{\mathrm{L}}}^{h_{\mathrm{top}}} \mathrm{Nd} H= \\ 10^{-6} \sum\limits_{1}^{n} N_{i} \cdot \Delta H_{i}+\mathrm{ZHD}_{\text {Saas }} \end{gathered} $ | (8) |
| $ \mathrm{ZWD}=10^{-6} \int_{h_{\mathrm{L}}}^{h_{\mathrm{top}}} N_{\mathrm{w}} \mathrm{d} H=10^{-6} \sum\limits_{1}^{n} N_{\mathrm{w} i} \cdot \Delta H_{i} $ | (9) |
式中,Ni、Nwi和ΔHi分别为第i层的大气总折射率、湿折射率和大气厚度,n为积分大气层数。
Huang等[9]利用全球无线电探空数据和国际全球导航卫星系统服务的精确ZTD产品对大气再分析资料MERRA-2得到的ZTD和ZWD的性能进行评估。结果表明,全球范围的MERRA-2再分析资料得到的ZTD和ZWD值在中国区域具有较高的精度和较好的稳定性,因此可将MERRA-2再分析资料作为中国区域ZTD/ZWD垂直剖面格网模型构建的数据源。本文选取2014~2016年70°~135°E、15°~55°N范围内MERRA-2大气再分析分层数据及对应的地表数据进行积分计算,得到该范围内各格网点ZTD、ZWD的垂直剖面资料。
2 ZWD、ZTD高程缩放因子获取用二次项、高斯函数表示ZTD、ZWD在垂直方向的变化[2-7],用指数函数表示ZTD、ZWD与高程之间的关系[4, 6-7]:
| $ \operatorname{ZTD}(h)=a_{1} \cdot \mathrm{e}^{b_{1} \cdot h} $ | (10) |
| $ \operatorname{ZWD}(h)=a_{2} \cdot \mathrm{e}^{b_{2} \cdot h} $ | (11) |
式中,e为自然对数的底数,h为高程,ZTD(h)、ZWD(h)分别为高程h处的ZTD、ZWD值,a1、a2、b1、b2为模型参数。
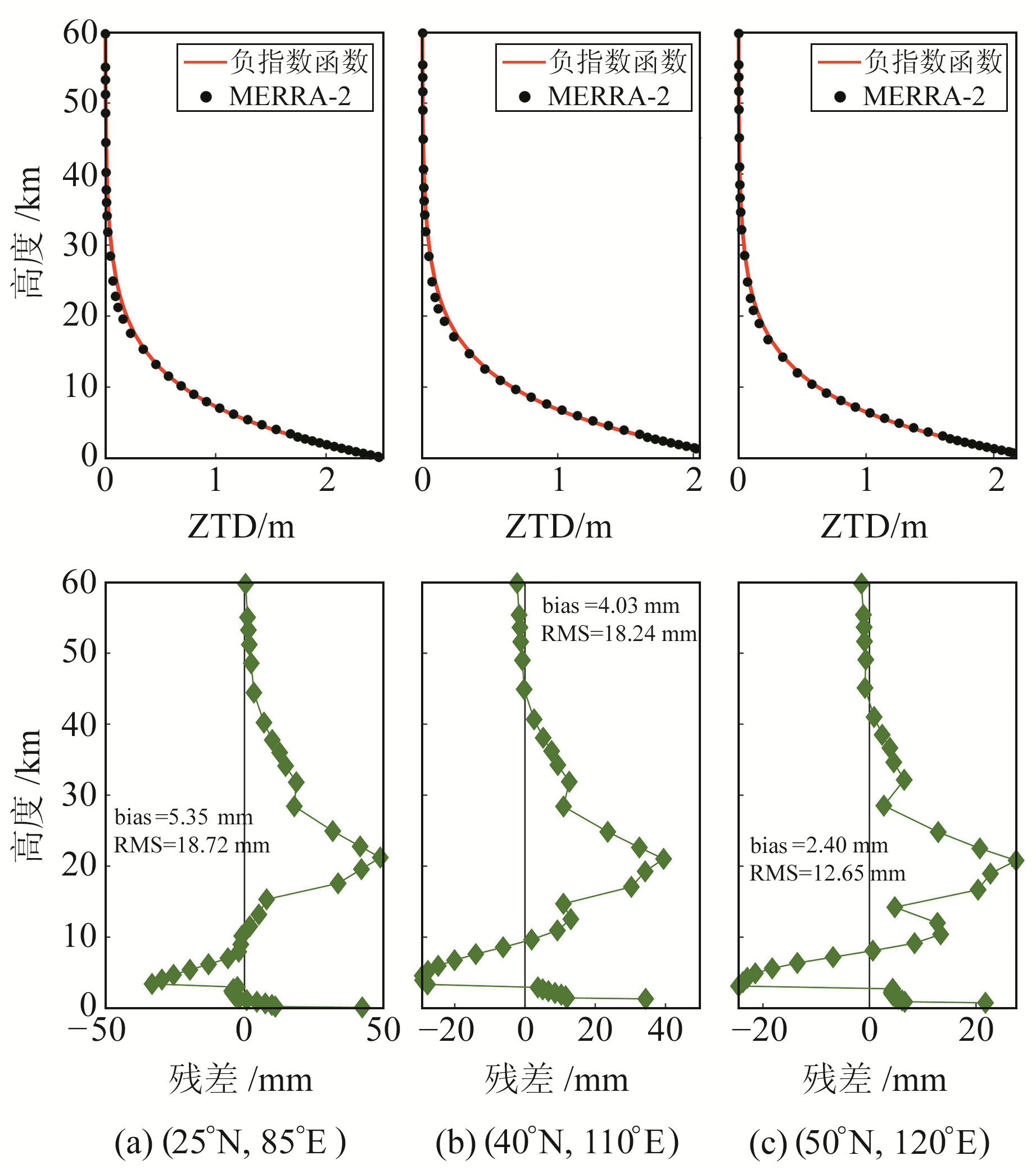
为进一步验证指数函数的适用性,选取2015-01-01 00:00(UTC)中国区域3个具有代表性的MERRA-2格网点,根据式(1)~(9)分别积分计算不同等压层面的ZTD、ZWD信息,并通过负指数函数分别对ZTD、ZWD进行拟合,结果如图 1和图 2所示。
|
图 1 ZTD值在高程上的变化与指数函数拟合结果及其拟合残差 Fig. 1 The changes of ZTD values with elevation and fitting results of exponential function and fitting residual |

|
图 2 ZWD值在高程上的变化与指数函数拟合结果及其拟合残差 Fig. 2 The change of ZWD value with elevation and fitting results of exponential function and fitting residual |
从图 1和图 2可以看出,利用负指数函数可较好地表达ZTD、ZWD在高程上的变化,ZTD拟合偏差在5.35 mm以内,拟合RMS误差在18.72 mm以内,ZWD拟合偏差在1.99 mm以内,拟合RMS误差在8.25 mm以内,表现出较高的拟合精度,因此可采用负指数函数来表达ZTD、ZWD的垂直剖面。位置A、B处的ZTD、ZWD可分别用式(12)~(15)表示,通过推导可得式(16)和式(17):
| $ \mathrm{ZTD}_{A}=a_{1} \cdot \mathrm{e}^{b_{1} \cdot H_{A}} $ | (12) |
| $ \mathrm{ZTD}_{B}=a_{1} \cdot \mathrm{e}^{b_{1} \cdot H_{B}} $ | (13) |
| $ \mathrm{ZWD}_{A}=a_{2} \cdot \mathrm{e}^{b_{2} \cdot H_{A}} $ | (14) |
| $ \mathrm{ZWD}_{B}=a_{2} \cdot \mathrm{e}^{b_{2} \cdot H_{B}} $ | (15) |
| $ \mathrm{ZTD}_{A}=\mathrm{ZTD}_{B} \cdot \mathrm{e}^{b_{1}\left(H_{A}-H_{B}\right)} $ | (16) |
| $ \mathrm{ZWD}_{A}=\mathrm{ZWD}_{B} \cdot \mathrm{e}^{b_{2}\left(H_{A}-H_{B}\right)} $ | (17) |
式中,ZTDA、ZTDB、ZWDA、ZWDB分别为位置A、B处ZTD、ZWD值,HA、HB分别为位置A、B处高程。由于b1、b2较小,为方便表示,对式(16)和式(17)进行改写:
| $ \mathrm{ZTD}_{t} =\mathrm{ZTD}_{r} \cdot \mathrm{e}^{\left(-\frac{H_{t}-H_{r}}{H_{s}}\right)} $ | (18) |
| $ \mathrm{ZWD}_{t} =\mathrm{ZWD}_{r} \cdot \mathrm{e}^{\left(-\frac{H_{t}-H_{r}}{H_{w}}\right)} $ | (19) |
式中,ZTDt和ZWDt分别为目标高程Ht处ZTD和ZWD值,ZTDr和ZWDr分别为参考高程Hr处ZTD和ZWD值,Hs和Hw分别为ZTD和ZWD的高程缩放因子(单位km)。本文中参考高程处ZTD、ZWD值为利用MERRA-2地表气象参数计算得到的ZTD、ZWD值,目标高程处ZTD、ZWD值为利用MERRA-2分层气象参数计算得到的ZTD、ZWD值,最终可得到Hs和Hw。
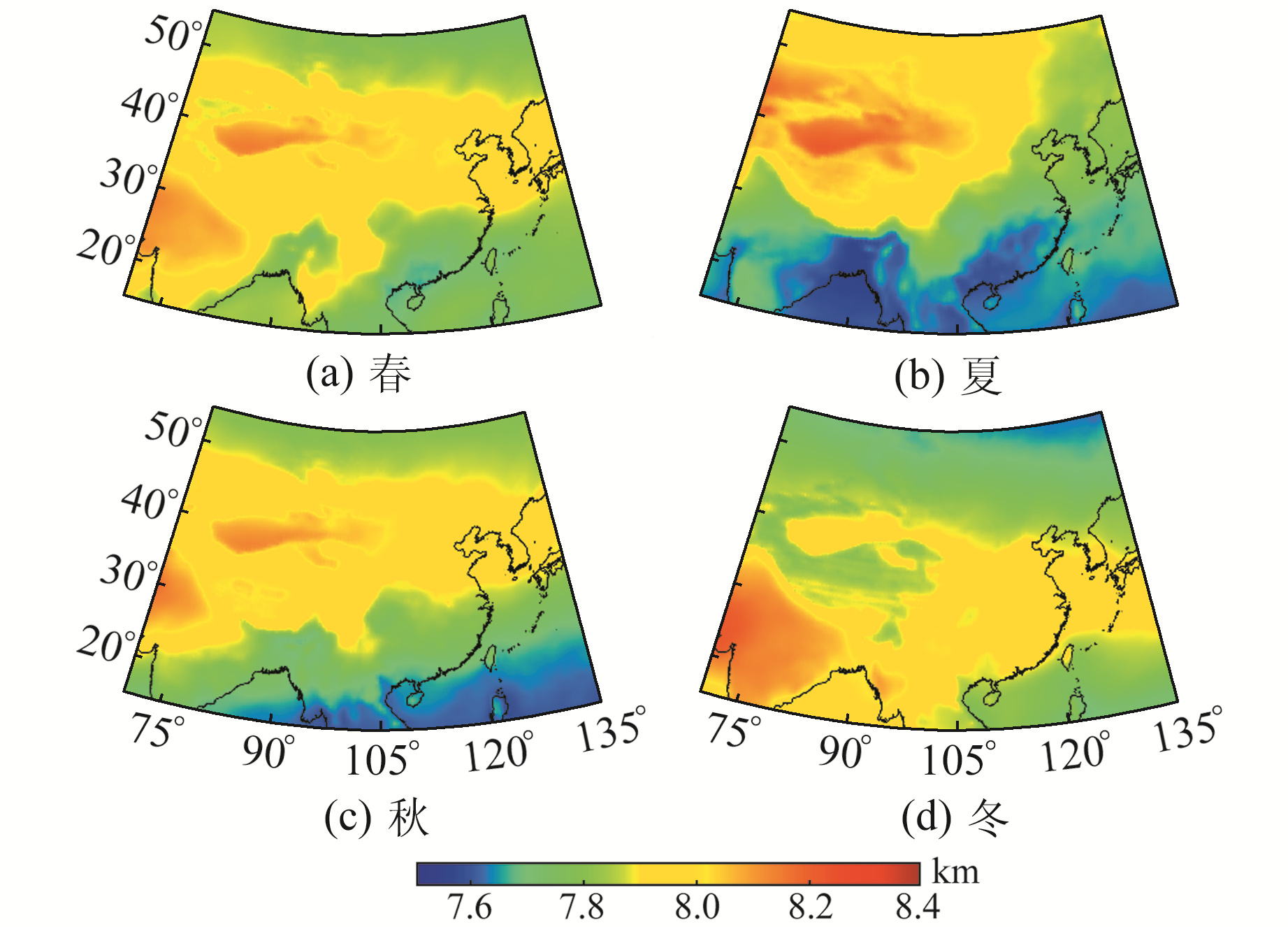
3 ZWD、ZTD高程缩放因子的时空特性分析图 3和图 4分别为2015年不同季节ZTD、ZWD高程缩放因子在中国区域的分布情况。从图 3可以看出,ZTD高程缩放因子最小值7.55 km出现在低纬度地区,最大值8.23 km出现在西部地区。春季和秋季ZTD高程缩放因子分布状况相似,且秋季低纬度地区季均ZTD高程缩放因子较小;夏季ZTD高程缩放因子最大值出现在40°~50°N附近,呈现向低纬度区域减小的趋势;冬季ZTD高程缩放因子最大值出现在20°~30°N附近,呈现向中纬度区域减小的趋势。从4季尺度来看,中纬度地区ZTD高程缩放因子先增大后减小,而低纬度地区先减小后增大。由图 4可知,ZWD高程缩放因子最小值、最大值均出现在低纬度地区,最小值为1.35 km,最大值为3.21 km。春季和秋季ZWD高程缩放因子分布状况相似,且秋季低纬度地区季均ZWD高程缩放因子较小;夏季和冬季ZWD高程缩放因子呈现相反的分布趋势,夏季最大值出现在20°~30°N和40°N附近,呈现向中纬度区域减小的趋势,冬季最大值出现在30°~40°N附近,呈现向低纬度区域减小的趋势。由图 3(b)可知,青藏高原地区(20°00′~39°47′N,73°19′~104°47′E)ZTD高程缩放因子与其附近地区相比存在明显差异;图 4(b)中青藏高原地区ZWD高程缩放因子与其附近地区相比也相对较小,这可能是由于青藏高原平均海拔在4 000 m以上、夏季温度低于其他地区的缘故。由图 4可知,从春季到夏季,中国区域ZWD高程缩放因子呈现增大的趋势,而从夏季至冬季呈现减小的趋势。值得注意的是,40°N附近、75°~105°E区域(即塔里木盆地)ZTD、ZWD高程缩放因子全年均处于较大值,可能是由于该区域位于内陆,且为非季风性气候,受地形因素影响,全年较干旱。
|
图 3 2015年中国区域ZTD高程缩放因子季均值分布 Fig. 3 Distribution of seasonal mean value of ZTD height scale factor in China in 2015 |

|
图 4 2015年中国区域ZWD高程缩放因子季均值分布 Fig. 4 Distribution of seasonal mean value of ZWD height scale factor in China in 2015 |
综上分析可知,ZTD、ZWD高程缩放因子均呈现一定的季节性分布差异,我国南北跨纬度较大,气温呈现一定的差异,因此可推断ZTD、ZWD高程缩放因子的分布与地理位置有关,且具有季节性。ZTD、ZWD高程缩放因子的时空分布存在差异,因此需分别构建模型。
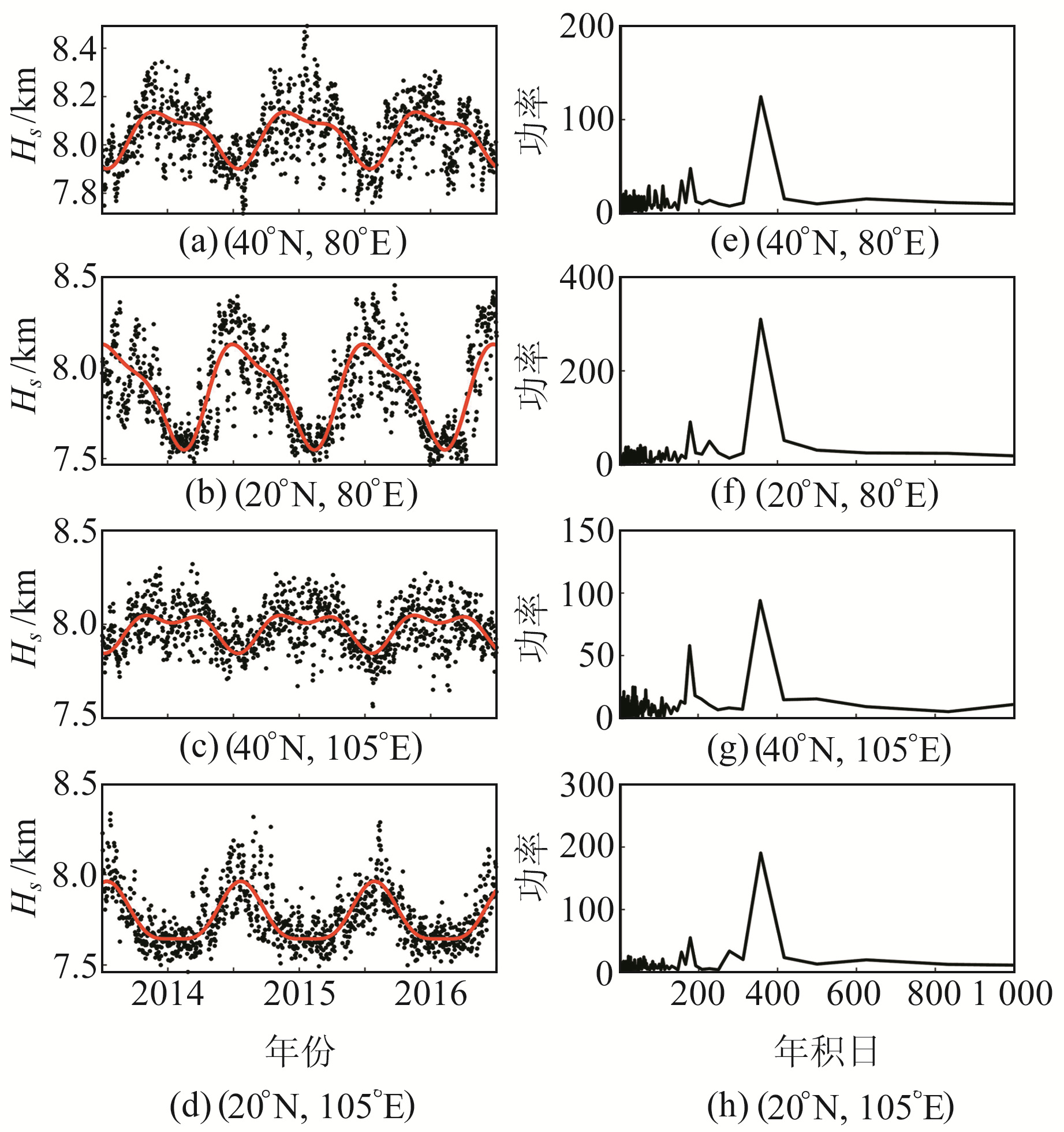
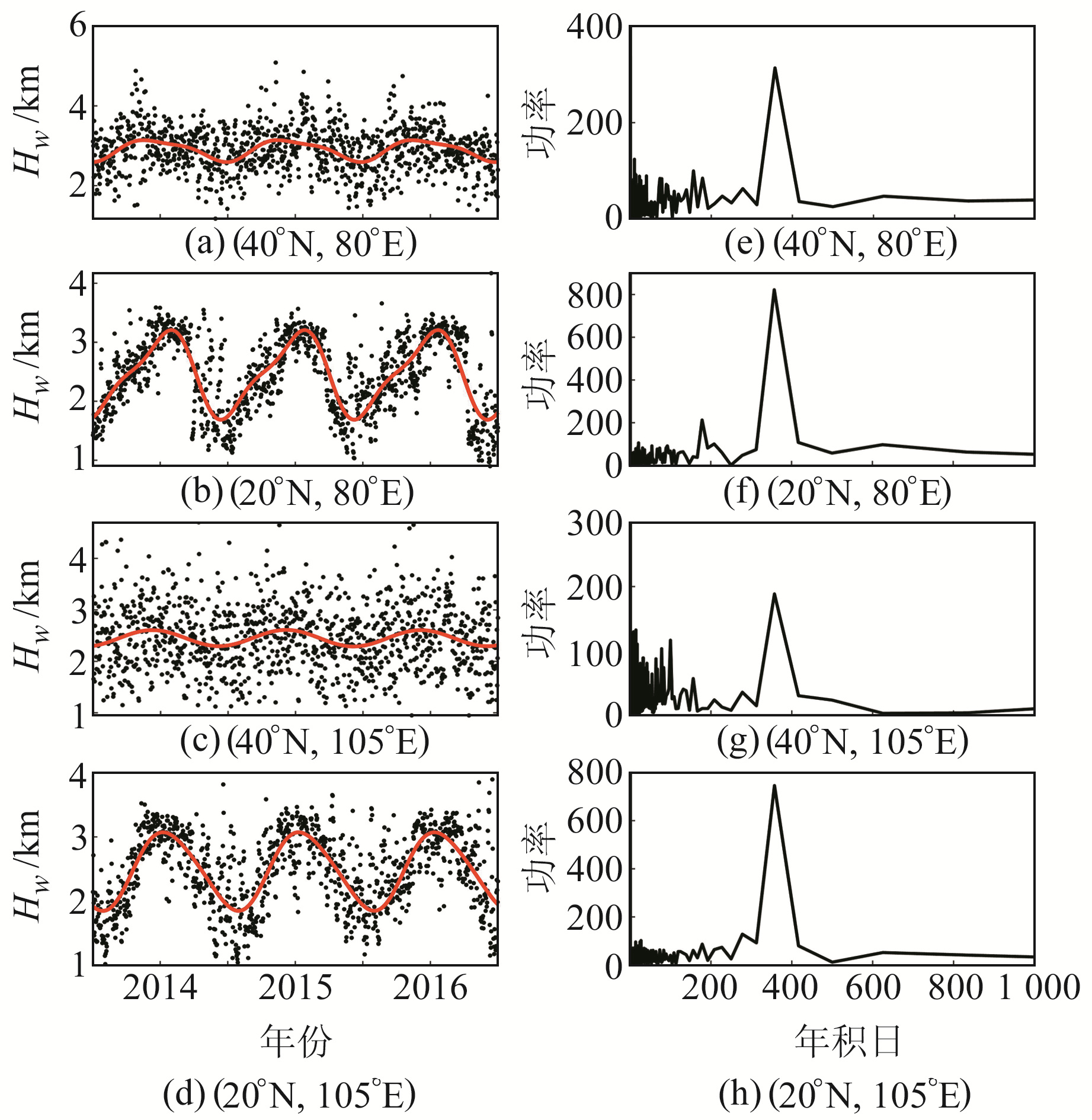
对流层延迟具有显著的年周期和半年周期变化,为探究ZTD、ZWD高程缩放因子是否具有周期性,本文随机选取4个格网点进行分析,图 5和图 6为其Hs、Hw时间序列及傅里叶频谱分析。
|
图 5 ZTD高程缩放因子时间序列及傅里叶频谱分析 Fig. 5 Time series and Fourier spectrum analysis of ZTD height scale factor |
|
图 6 ZWD的高程缩放因子的时间序列及傅里叶频谱分析 Fig. 6 Time series and Fourier spectrum analysis of ZWD height scale factor |
由图 5可知,Hs时间序列在中国区域呈现出明显的年周期和半年周期特性,波动范围为7.4~8.5km,变化范围相对稳定;相对于另外3个格网点,格网点(20°N, 80°E)表现出更为明显的年周期和半年周期特性。
由图 6可知,Hw在中国区域也表现出显著的年周期和半年周期特性,尤其在格网点(20°N, 80°E)和格网点(20°N, 105°E)处;在格网点(40°N, 80°E)处Hw变化范围相对较大,为1.5~6 km,另外3个格网点Hw变化范围相对较小,为1~4 km。
分别计算2014~2016年中国区域MERRA-2再分析资料计算的每个格网点Hs、Hw的年均值、年周期振幅及半年周期振幅值,以进一步分析Hs、Hw在中国区域的分布特性,结果见图 7和图 8。
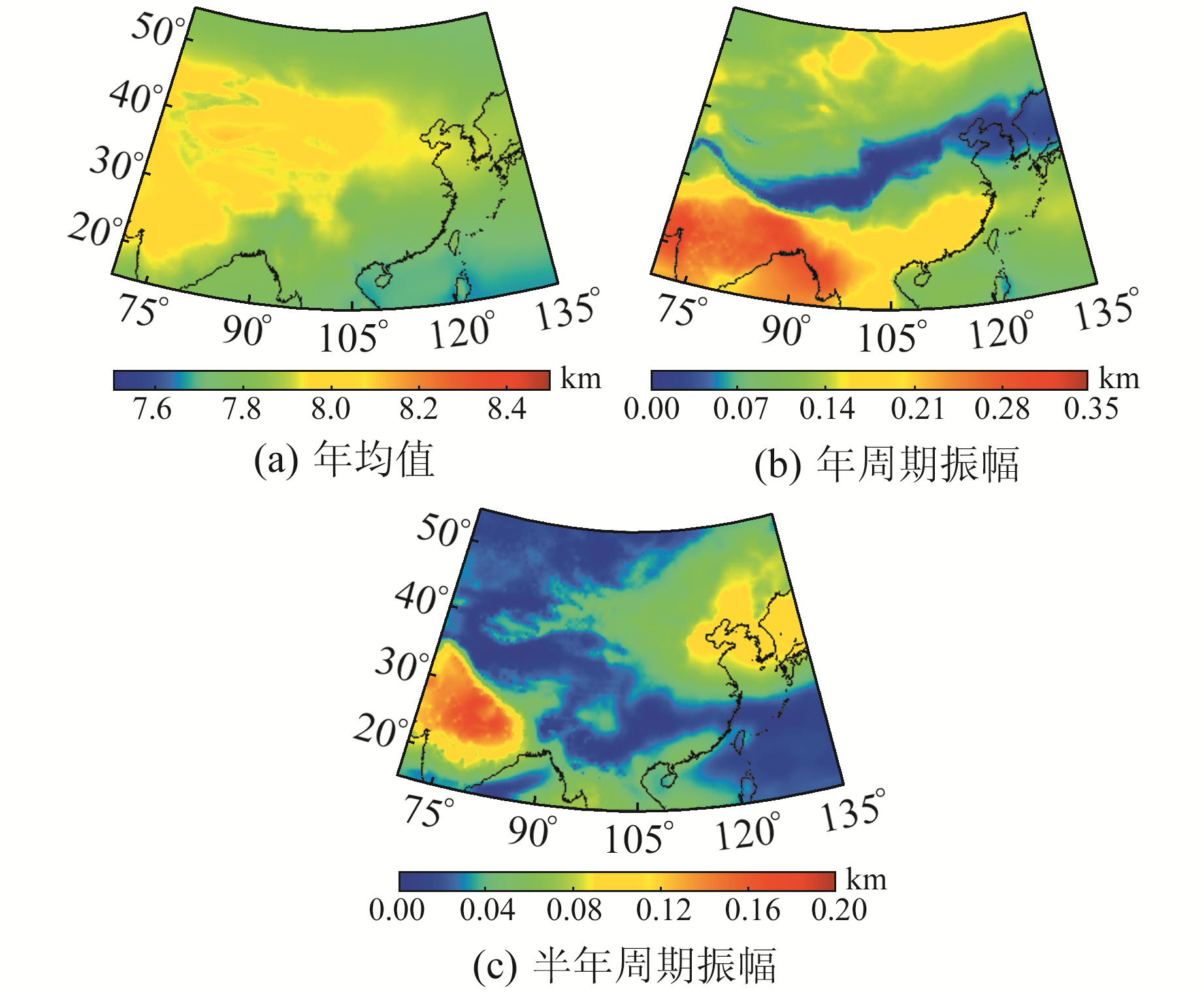
|
图 7 ZTD高程缩放因子年均值、年周期振幅、半年周期振幅 Fig. 7 The annual mean value, annual periodic amplitude, and semi-annual periodic amplitude of the ZTD height scale factor |
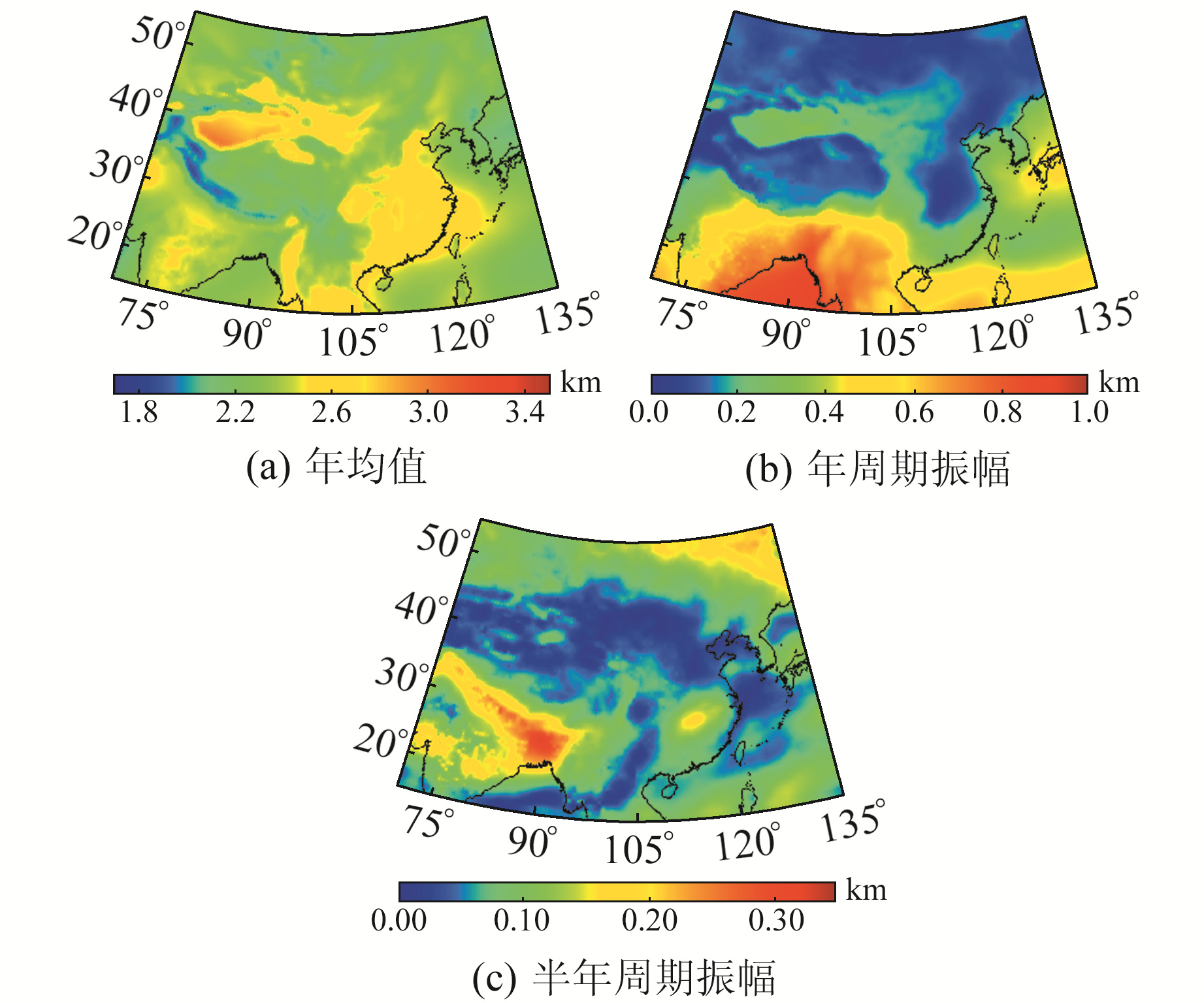
|
图 8 ZWD高程缩放因子年均值、年周期振幅、半年周期振幅 Fig. 8 The annual mean value, annual periodic amplitude, and semi-annual periodic amplitude of the ZWD height scale factor |
由图 7可知,Hs在中国西部到中部的三角形区域存在较大的年均值,可能是由于该地区以高原为主,平均海拔在4 000 m以上,地形起伏较大。年周期振幅在中纬度地区较小,从中纬度地区向西南部、东北部呈现增大趋势,且低纬度地区西南部数值较大。可能是由于中国低纬度地区属于亚热带季风气候,水汽变化较其他区域大,进而导致Hs的年周期振幅较大。中国西南地区和东北地区存在相对较大的半年周期振幅,西南地区数值较大,而西北地区至东南地区半年周期振幅较小。
由图 8可知,Hw在中国西北部和东南部存在较大的年均值,其中,中国西北部为塔里木盆地,处于非季风区,位于内陆,终年受大陆气团控制,冬季严寒,夏季高温,常年少雨;而中国西南部处于非季风区,位于沿海地区,该区域包含温带季风气候和亚热带季风气候,受冬夏季风交替控制,水汽充足,冬季寒冷干燥,夏季高温多雨。由此可见,ZWD高程缩放因子受多种因素影响。年周期振幅在纬度上表现为由低纬度向高纬度逐渐递减,低纬度地区存在较大值,中纬度地区存在较小值。可能是由于中国低纬度地区属于亚热带季风气候,水汽变化较其他区域大,进而导致Hw的年周期振幅较大。中国西南部和东北部存在相对较大的半年周期振幅。
综上,为保证ZTD、ZWD垂直剖面模型的精度,在构建中国区域ZTD、ZWD垂直模型时需顾及Hs、Hw的年周期和半年周期变化。
利用皮尔逊相关性分析法分析Hs、Hw的年均值与经纬度的相关性,结果见表 1。由表 1可知,Hs与经度呈负相关,相关性显著,与纬度呈正相关,相关性显著;Hw与经度相关性弱,与纬度呈负相关,相关性显著;Hs与Hw呈正相关。
|
|
表 1 相关性分析 Tab. 1 Correlation analysis |
针对中国区域缺乏实时、高时空分辨率的ZTD、ZWD垂直剖面模型,本文利用2014~2016年MERRA-2再分析数据,基于负指数函数,详细分析ZTD、ZWD高程缩放因子在中国区域的时空分布特性。结果表明:
1) 夏季Hs最大值出现在40°~50°N附近,呈现向低纬度区域减小的趋势;冬季Hs最大值出现在20°~30°N附近,呈现向中纬度地区减小的趋势。
2) Hs在中国西部到中部的三角形区域存在较大的年均值,中纬度地区先增大后减小,而低纬度地区先减小后增大,Hs年周期振幅、半年周期振幅具有显著的空间分布特性。
3) Hw的最值出现在低纬度地区,夏季Hw最大值出现在20°~30°N附近及40°N附近,呈现向中纬度区域减小的趋势;冬季Hw最大值出现在30°~40°N附近,呈现向低纬度地区减小的趋势。
4) Hw在中国区域西北部和东南部存在较大的年均值,Hw的年周期振幅、半年周期振幅也具有显著的空间分布特性。
综上可知,在构建中国区域ZTD、ZWD垂直剖面模型时需顾及Hs、Hw的年周期、半年周期特性,且Hs、Hw都与经纬度具有一定的相关性。研究结果可为ZTD、ZWD垂直剖面模型的构建提供参考。在后续工作中可进一步研究构建中国区域ZTD、ZWD垂直剖面模型,以实现高精度的对流层格网产品空间插值。
| [1] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2016 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2016)
(  0) 0) |
| [2] |
宋淑丽, 朱文耀, 陈钦明, 等. 中国区域对流层延迟改正模型(SHAO)的初步建立[C]. 中国卫星导航学术年会, 北京, 2010 (Song Shuli, Zhu Wenyao, Chen Qinming, et al. Preliminary Establishment of Regional Troposphere Delay Correction Model in China[C]. China Satellite Navigation Conference, Beijing, 2010)
(  0) 0) |
| [3] |
李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57(15): 1317-1325 (Li Wei, Yuan Yunbin, Ou Jikun, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(15): 1317-1325)
(  0) 0) |
| [4] |
黄良珂, 刘立龙, 姚朝龙, 等. 基于区域CORS网精密天顶对流层延迟建模方法研究[J]. 大地测量与地球动力学, 2013, 33(6): 141-144 (Huang Liangke, Liu Lilong, Yao Chaolong, et al. Modeling for Precise Zenith Tropospheric Delay Based on Regional CORS Network[J]. Journal of Geodesy and Geodynamics, 2013, 33(6): 141-144)
(  0) 0) |
| [5] |
毛健, 朱长青, 郭继发. 一种新的全球对流层天顶延迟模型[J]. 武汉大学学报: 信息科学版, 2013, 38(6): 684-688 (Mao Jian, Zhu Changqing, Guo Jifa. A New Global Zenith Tropospheric Delay Model[J]. Geomatics and Information Science of Wuhan University, 2013, 38(6): 684-688)
(  0) 0) |
| [6] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227 (Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227)
(  0) 0) |
| [7] |
姚宜斌, 胡羽丰, 余琛. 一种改进的全球对流层天顶延迟模型[J]. 测绘学报, 2015, 44(3): 242-249 (Yao Yibin, Hu Yufeng, Yu Chen. An Improved Global Zenith Tropospheric Delay Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 242-249)
(  0) 0) |
| [8] |
Thayer G D. An Improved Equation for the Radio Refractive Index of Air[J]. Radio Science, 1974, 9(10): 803-807 DOI:10.1029/RS009i010p00803
(  0) 0) |
| [9] |
Huang L K, Guo L J, Liu L L, et al. Evaluation of the ZWD/ZTD Values Derived from MERRA-2 Global Reanalysis Products Using GNSS Observations and Radiosonde Data[J]. Sensors, 2020, 20(22): 6440 DOI:10.3390/s20226440
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2021, Vol. 41
2021, Vol. 41


