地震反应谱是地震工程研究中的一项重要内容,通过研究单自由度震动体系下质点的运动情况来描述地震条件下结构的最大动力反应[1-2]和地震动的频谱特性。反应谱在强震监测计算分析中既可反映局部场地的地震强度特征,又可用来估算地震作用下工程结构的受力情况,大量的反应谱计算结果还可应用于结构抗震设计。因此,采用有效的方法提高反应谱的精度和计算效率具有重要意义。
反应谱的计算方法主要集中在时域和频域两个维度。频域计算方法的基本原理是在频域计算地震动和传递函数傅里叶频谱的乘积[3],然后通过傅里叶逆变换得到时间域的反应谱,需要已知频域内精确的传递函数[4]以及完整的地震记录来完成计算,其中长周期反应谱的计算精度受地震记录长度影响较大,因此频域不适合进行实时快速反应谱计算。反应谱时域计算方法一直为研究重点,其基本原理是以地震反应量所表述的动力平衡方程来寻找数字滤波器传递函数或递归公式[5]。时域计算方法有Duhamel逐步积分法、Newmark-β方法[6]、精确解法(ASM)[7]和Z变换方法[8]等,这些方法的计算精度主要受假定时间步长内加速度的特定分布形式所制约[9]。
本文基于单自由度体系运动方程推导计算地震反应谱的一般表达形式,并从传递函数的形式和滤波系数入手,推导用于计算反应谱的递推表达式,然后结合已有研究提出的满足高频和低频收敛条件对应的独立积分常数即可计算得到反应谱结果。
1 单自由度震动体系原理当地面以一定加速度运动时,单自由度震动体系的运动方程为[2]:
| $ \ddot{u}+2\xi \omega \dot{u}+{{\omega }^{2}}u=-{{\ddot{u}}_{g}}\left( \text{t} \right) $ | (1) |
令
定义时间加权函数W(t)为:
| $ W\left( t \right)\text{=1+}{{w}_{1}}{\mathit{\Gamma}} \text{+}{{w}_{2}}{{{\mathit{{\mathit{\Gamma}}}} }^{2}}\text{+}{{w}_{3}}{{{\mathit{\Gamma}} }^{3}} $ | (2) |
式中,
对u、
| $ u={{u}_{n}}+{{{\mathit{\Lambda}} }_{1}}{{\dot{u}}_{n}}\tau +{{{\mathit{\Lambda}} }_{2}}{{\ddot{u}}_{n}}{{\tau }^{2}}+{{{\mathit{\Lambda}} }_{3}}\frac{{{{\ddot{u}}}_{\text{n+1}}}-{{{\ddot{u}}}_{n}}}{\Delta t}{{\tau }^{3}} $ | (3) |
| $ \dot{u}={{\dot{u}}_{n}}+{{{\mathit{\Lambda}} }_{4}}{{\ddot{u}}_{n}}\tau +{{{\mathit{\Lambda}} }_{5}}\frac{{{{\ddot{u}}}_{\text{n+1}}}-{{{\ddot{u}}}_{n}}}{\Delta t}{{\tau }^{2}} $ | (4) |
| $ \ddot{u}={{\ddot{u}}_{n}}+{{{\mathit{\Lambda}} }_{6}}\frac{{{{\ddot{u}}}_{\text{n+1}}}-{{{\ddot{u}}}_{n}}}{\Delta t}\tau $ | (5) |
| $ f={{f}_{n}}+{{\dot{f}}_{n}}\tau $ | (6) |
式中,Λ1、Λ2、Λ3、Λ4、Λ5、Λ6为一系列自由参数。
将式(1)代入式(2)可得:
| $ \int_{0}^{\Delta t}{W\text{(}\ddot{u}+2\xi \omega \dot{u}+{{\omega }^{2}}u-}f\text{)d}t=0 $ | (7) |
将u、
| $ \begin{align} & {{{\ddot{u}}}_{n}}+{{{\mathit{\Lambda}} }_{6}}{{W}_{1}}\text{(}{{{\ddot{u}}}_{\text{n+1}}}-{{{\ddot{u}}}_{n}}\text{)}+2\xi \omega \text{(}{{{\dot{u}}}_{n}}+{{{\mathit{\Lambda}} }_{4}}{{W}_{1}}{{{\ddot{u}}}_{n}}\Delta t+ \\ & \ \ \ {{{\mathit{\Lambda}} }_{5}}{{W}_{2}}\text{(}{{{\ddot{u}}}_{\text{n+1}}}-{{{\ddot{u}}}_{n}}\text{)}\Delta t\text{)}+{{\omega }^{2}}\text{(}{{{\dot{u}}}_{n}}+{{{\mathit{\Lambda}} }_{1}}{{W}_{1}}{{{\dot{u}}}_{n}}\Delta t+ \\ & {{{\mathit{\Lambda}} }_{2}}{{W}_{2}}{{{\ddot{u}}}_{n}}\Delta t+{{{\mathit{\Lambda}} }_{3}}{{W}_{3}}\text{(}{{{\ddot{u}}}_{\text{n+1}}}-{{{\ddot{u}}}_{n}}\text{)}\Delta {{t}^{2}}\text{)}={{f}_{n}}+{{W}_{1}}{{{\dot{f}}}_{n}}\Delta t \\ \end{align} $ | (8) |
式中,
| $ {{u}_{n+1}}={{u}_{n}}+{{{\mathit{\lambda}} }_{1}}{{\dot{u}}_{n}}\Delta t+{{\lambda }_{2}}{{\ddot{u}}_{n}}\Delta {{t}^{2}}+{{\lambda }_{3}}\text{(}{{\ddot{u}}_{\text{n+1}}}-{{\ddot{u}}_{n}}\text{)}\Delta {{t}^{2}} $ | (9) |
| $ {{\dot{u}}_{n=1}}={{\dot{u}}_{n}}+{{\lambda }_{4}}{{\ddot{u}}_{n}}\Delta t+{{\lambda }_{5}}\text{(}{{\ddot{u}}_{\text{n+1}}}-{{\ddot{u}}_{n}}\text{)}\Delta t $ | (10) |
将式(9)和式(10)代入式(8)可得:
| $ {{\mathit{\boldsymbol{d}}}_{n+1}}={\mathit{\boldsymbol{A}}}{{\mathit{\boldsymbol{d}}}_{n}}+{{\mathit{\boldsymbol{L}}}_{n}} $ | (11) |
式中,
| $ \mathit{\boldsymbol{A}} = \left[ \begin{array}{l} 1 - {\lambda _3}{\kern 1pt} {A_{{\rm{31}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _1} - {\lambda _3}{\kern 1pt} {A_{32}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _2} - {\lambda _3}{\kern 1pt} {A_{33}}{\kern 1pt} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _5}{\kern 1pt} {A_{{\rm{31}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 - {\lambda _5}{\kern 1pt} {A_{{\rm{32}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _4} - {\lambda _5}{\kern 1pt} {A_{33}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_{{\rm{31}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_{32}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_{{\rm{33}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \end{array} \right], $ |
| $ {{\mathit{\boldsymbol{L}}}_n} = \frac{1}{D}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( \begin{array}{l} {\lambda _3}\Delta {t^2}\left[ {\left( {1 - {W_1}} \right)} \right]{f_n} + {W_1}{f_{n + 1}}\\ {\lambda _5}\Delta {t^2}\left[ {\left( {1 - {W_1}} \right)} \right]{f_n} + {W_1}{f_{n + 1}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta {t^2}\left[ {\left( {1 - {W_1}} \right)} \right]{f_n} + {W_1}{f_{n + 1}} \end{array} \right) $ |
A和Ln中变量可整理为:
| $ {A_{31}}{\kern 1pt} {\kern 1pt} = {\Omega ^2}/D, {A_{32}}{\kern 1pt} {\kern 1pt} = \left( {2\xi \Omega + {{\mathit{\Lambda}} _1}{W_1}{\Omega ^2}} \right)/D $ |
| $ {A_{{\rm{33}}}} = 1 - {\rm{(}}1 + 2{{\mathit{\Lambda}} _4}{W_1}\xi \Omega + {{\mathit{\Lambda}} _2}{W_2}{\Omega ^2}{\rm{)}}/D $ |
| $ D = {{\mathit{\Lambda}} _6}{W_1} + 2{{\mathit{\Lambda}} _5}{W_2}\xi \Omega + {{\mathit{\Lambda}} _3}{W_3}{\Omega ^2}, \Omega = \omega {\kern 1pt} \Delta t $ |
在Z变换域中输入、输出和传递函数的形式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Y\left( Z \right) = \\ \frac{{{B_{\rm{1}}} + {B_{\rm{2}}}{z^{ - {\rm{1}}}} + {B_{\rm{3}}}{z^{ - {\rm{2}}}} + {B_{\rm{4}}}{z^{ - {\rm{3}}}} + \cdots + {B_{{n_b} + {\rm{1}}}}{z^{ - {n_b}}}}}{{{\rm{1}} + {A_{\rm{1}}}{z^{ - {\rm{1}}}} + {A_{\rm{2}}}{z^{ - {\rm{2}}}} + {A_{\rm{3}}}{z^{ - {\rm{3}}}} + \cdots + {A_{{n_a} + {\rm{1}}}}{z^{ - {n_a}}}}} \end{array} $ | (12) |
式中,na为反馈滤波器阶数;nb为前馈滤波器阶数。可将式(12)表示为差分方程:
| $ \begin{array}{l} y\left( m \right) = {B_{\rm{1}}}x\left( m \right) + {B_{\rm{2}}}x\left( {m - {\rm{1}}} \right) + \cdots + \\ \;\;\;\;\;{B_{{n_b} + {\rm{1}}}}x\left( {m - {n_b}} \right) - {A_{\rm{1}}}y\left( {m - {\rm{1}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots + {B_{{n_a} + {\rm{1}}}}y\left( {m - {n_a}} \right) \end{array} $ | (13) |
根据Zhou等[10]提出的思路,构造3阶反馈滤波器系数和4阶前馈滤波器系数,令[1, -A1, A2, -A3]、[B1, B2, B3, B4] 为2组滤波器系数,其中A1、A2、A3、B1、B2、B3、B4分别由式(11)中矩阵A中元素得到:
| $ {A_1} = \mathit{\boldsymbol{I}} :\mathit{\boldsymbol{A}}, {A_2} = \frac{1}{2}\left( {A_1^2{\kern 1pt} {\kern 1pt} - \mathit{\boldsymbol{A}}:\mathit{\boldsymbol{A}}} \right), {A_3} = {\rm{det}}\mathit{\boldsymbol{A}} $ |
| $ {B_1} = \Delta {t^2}{\lambda _3}{W_1}/D $ |
| $ \begin{array}{l} {B_2} = \Delta {t^2}\left[ {{\lambda _3}{\rm{(}}1 - {W_1}{\rm{)}} - {\rm{(}}{A_{22}}{\kern 1pt} + {A_{{\rm{33}}}}{\kern 1pt} {\rm{)}}{\kern 1pt} {\lambda _3}{W_1}{\kern 1pt} + } \right.\\ {\kern 1pt} \left. {\;\;\;\;\;\;\;{A_{12}}{\kern 1pt} {\kern 1pt} {\lambda _5}{W_1}{\kern 1pt} + {A_{13}}{\kern 1pt} {\kern 1pt} {W_1}} \right]/D \end{array} $ |
| $ \begin{array}{l} {B_3} = \Delta {t^2}\lambda \left[ { - {\rm{(}}{A_{22}} + {A_{33}}{\rm{)(}}1 - {W_1}{\rm{)}}{\lambda _3} + } \right.{\kern 1pt} \\ \;\;\;\;\;\;\;{A_{12}}{\kern 1pt} {\kern 1pt} {\lambda _5}{\rm{(}}1 - {W_1}{\rm{)}} + {A_{13}}{\rm{(}}1 - {W_1}{\rm{)}} + \\ \;\;\;\;\;\;\;{\rm{(}}{A_{22}}{\kern 1pt} {A_{{\rm{33}}}} - {A_{{\rm{23}}}}{A_{{\rm{32}}}}{\kern 1pt} {\rm{)}}{\kern 1pt} {\lambda _3}{W_1} - {\rm{(}}{A_{12}}{\kern 1pt} {A_{{\rm{33}}}} - \\ \left. {\;\;\;\;\;\;\;{A_{{\rm{13}}}}{A_{{\rm{32}}}}{\kern 1pt} {\rm{)}}{\kern 1pt} {\lambda _5}{W_1}{\rm{ + (}}{A_{12}}{\kern 1pt} {A_{{\rm{23}}}} - {A_{{\rm{13}}}}{A_{{\rm{22}}}}{\kern 1pt} {\rm{)}}{\kern 1pt} {W_1}} \right]/D \end{array} $ |
| $ \begin{array}{l} {B_4} = \Delta {t^2}\lambda \left[ {{\rm{(}}{A_{22}}{\kern 1pt} {A_{{\rm{33}}}} - {A_{{\rm{23}}}}{A_{{\rm{32}}}}{\rm{)(}}1 - {W_1}{\rm{)}}{\lambda _3} - } \right.\\ \;\;\;\;\;\;\;{\rm{(}}{A_{12}}{\kern 1pt} {A_{{\rm{33}}}} - {A_{{\rm{13}}}}{A_{{\rm{32}}}}{\kern 1pt} {\rm{)}}{\kern 1pt} {\lambda _5} - {\rm{(}}1 - {W_1}{\rm{)}} + \\ \;\;\;\;\;\;\;\left. {{\rm{(}}{A_{12}}{\kern 1pt} {A_{{\rm{23}}}} - {A_{{\rm{13}}}}{A_{{\rm{22}}}}{\kern 1pt} {\rm{)}}{\kern 1pt} {\rm{(}}1 - {W_1}{\rm{)}}} \right]/D \end{array} $ |
| $ y{\rm{(}}m{\rm{)}} = {B_1}x{\rm{(}}m{\rm{)}} + {z_1}{\rm{(}}m - 1{\rm{)}} $ | (14) |
| $ {z_1}{\rm{(}}m{\rm{)}} = {B_2}x{\rm{(}}m{\rm{)}} + {z_2}{\rm{(}}m - 1{\rm{)}} - {A_1}y{\rm{(}}m{\rm{)}} $ | (15) |
| $ {z_2}{\rm{(}}m{\rm{)}} = {B_3}x{\rm{(}}m{\rm{)}} + {z_3}{\rm{(}}m - 1{\rm{)}} - {A_2}y{\rm{(}}m{\rm{)}} $ | (16) |
| $ {z_3}\left( m \right) = {B_4}x\left( m \right) - {A_3}y\left( m \right) $ | (17) |
滤波系数A1、A2、A3、B1、B2、B3、B4中λ1、λ2、λ3、λ4、λ5、Λ1、Λ2、Λ3、Λ4、Λ5、Λ6、w1、w2、w3系数可根据文献[11]中提出的高频和低频收敛条件得到,结合给定条件和初始地面加速度、速度及位移等数据,通过式(14)可求得位移反应谱Sd,再利用式(10)即可得到速度反应谱Sv。最后将已经求出的位移反应u(Sd) 和速度反应
为验证本文方法的计算精度,采用由2个频率合成的正弦简谐波f(t)作为单自由度震动体系的系统输入,如式(18)和式(19)所示,其中采样频率为200 Hz,时长为30 s,f1=0.5 Hz,f2=2.0 Hz。设置反应谱阻尼比为5%,周期为0~4 s,时间间隔为0.02 s,分别利用LRFM方法、Duhamel逐步积分法、Newmark-β方法和精确解法(ASM)[12]计算得到反应谱结果,并以ASM方法作为对比验证另外3种方法的相对误差:
| $ \begin{array}{l} f\left( t \right) = {\rm{sin}}(2{\rm{ \mathsf{ π} }} \times {f_1} \times t) + {\rm{sin}}(2{\rm{ \mathsf{ π} }} \times {f_2} \times t), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left[ {8, 15} \right] \end{array} $ | (18) |
| $ f\left( t \right) = 0, t \in \left[ {0, 8} \right)\;或\; t \in\; \left( {15, 30} \right) $ | (19) |
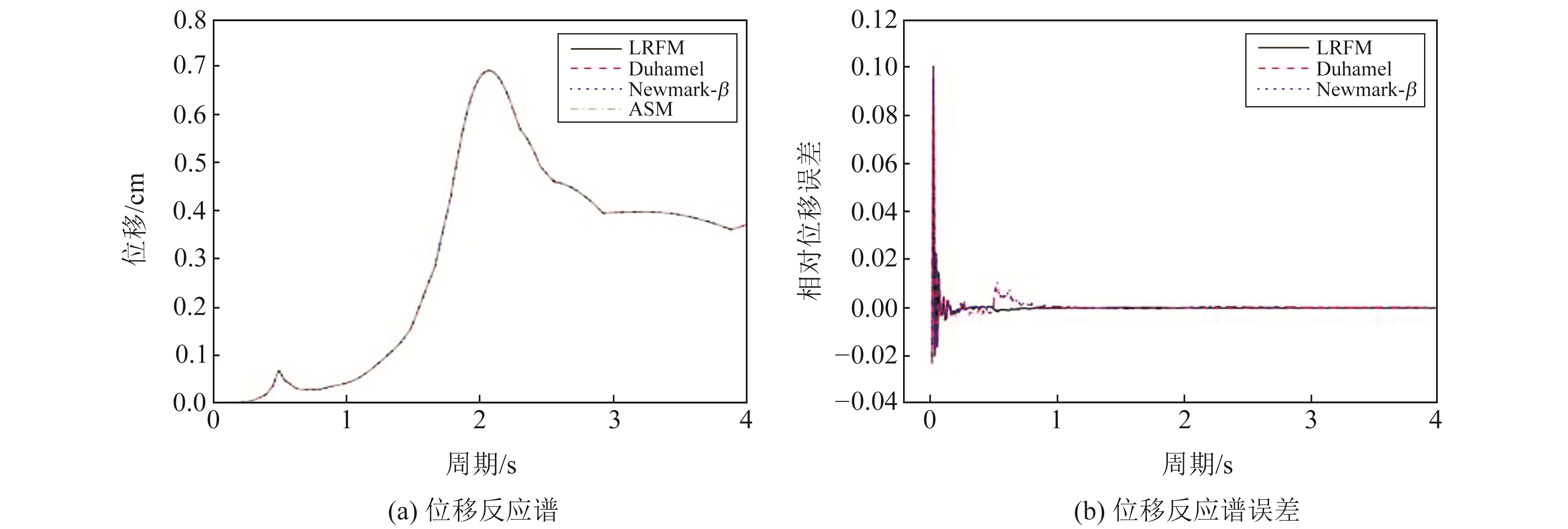
采用4种方法计算得到的位移反应谱如图 1(a)所示,从图中可以看出,4种方法计算得到的曲线形态一致,均反映出输入周期在0.5 s和2 s处的模拟地震动信息。位移反应谱的相对误差(图 1(b))结果显示,LRFM方法、Duhamel逐步积分法和Newmark-β方法在周期0~1 s内均存在一定误差,在周期2~4 s内误差较小,在0.5 s处具有明显突变;LRFM方法在周期0~1 s内的相对误差结果优于Duhamel逐步积分法和Newmark-β方法,且整体误差波动较小。
|
图 1 位移反应谱计算结果及误差 Fig. 1 The calculation results and errors of the displacement response spectrum |
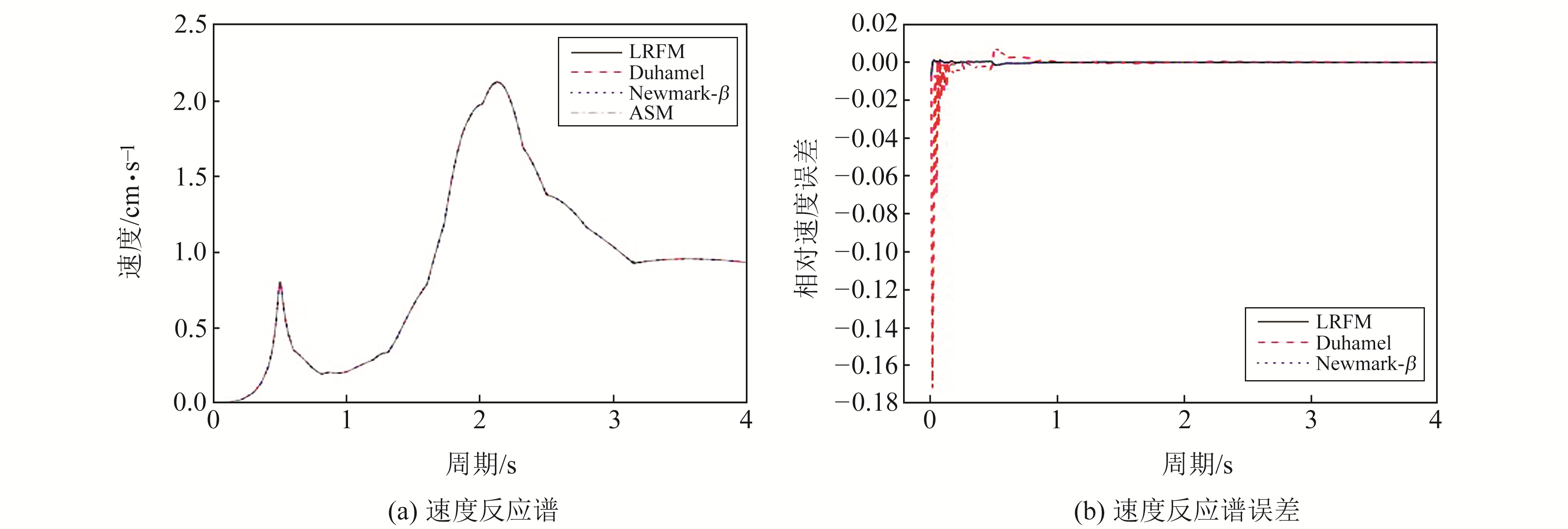
利用合成数据计算得到的速度反应谱和误差结果如图 2所示,从图中可以看出,4种方法计算得到的速度反应谱曲线几乎完全重合,其中Duhamel逐步积分法的相对误差在短周期0~1 s内跳动较大,最大达到18%;而Newmark-β方法和LRFM方法的整体误差较小,基本可达到ASM方法的计算效果。
|
图 2 速度反应谱计算结果及误差 Fig. 2 The calculation results and errors of the velocity response spectrum |
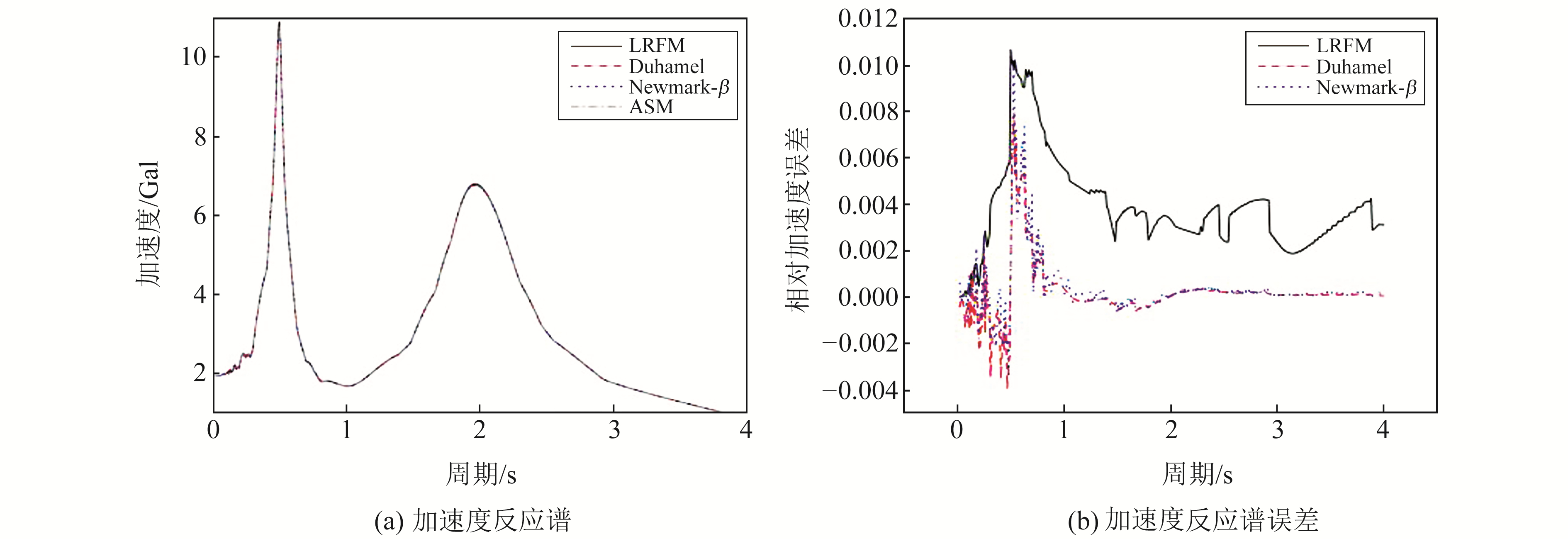
图 3为4种方法计算得到的加速度反应谱和误差结果,从图中可以看出,4种方法计算的加速度反应谱曲线仅在个别峰值点存在突变,而LRFM方法、Duhamel逐步积分法及Newmark-β方法的相对误差均小于2%,3种方法的相对误差均集中在短周期部分。LRFM方法的相对误差基本呈线性正相关变化,而Duhamel逐步积分法和Newmark-β方法的相对误差在正负方向来回震荡,且在0.5 s处存在突变。
|
图 3 加速度反应谱计算结果及误差 Fig. 3 The calculation results and errors of the acceleration response spectrum |
通过对合成数据的计算结果进行分析可知,LRFM方法的计算精度和稳定性优于Duhamel逐步积分法和Newmark-β方法,在位移最大值处的误差较小,而加速度反应谱的计算误差整体略大于另外2种方法,但相对误差小于2%,计算结果满足精度要求。
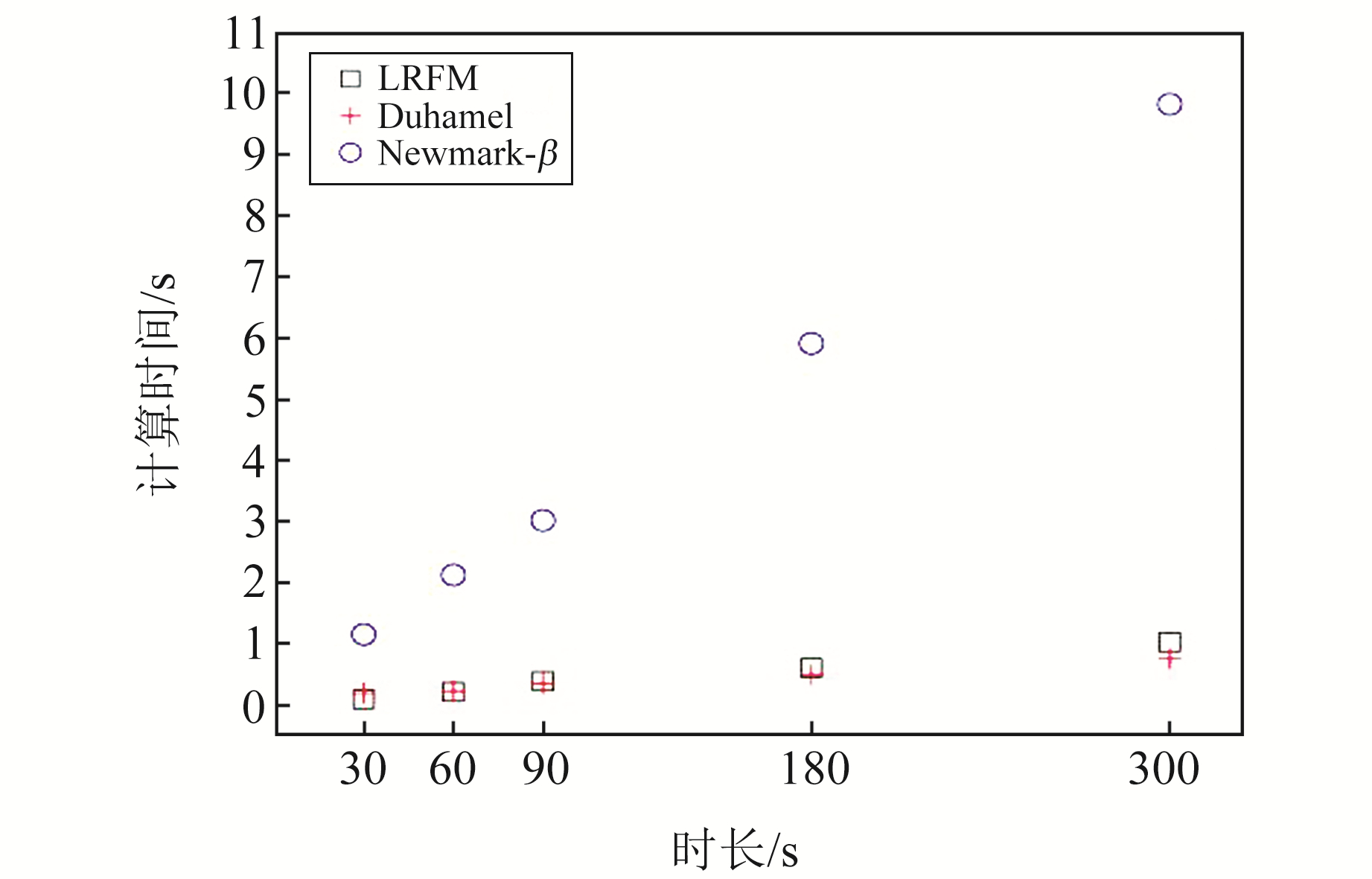
3.2 计算效率分析在计算地震反应谱时,为获得更充分的反应谱信息,一般选取输入时长较长的强震动记录,特别是在计算强震动条件下的加速度反应谱时,强震动记录时长可达300 s以上,因此会产生大量强震动记录,如果反应谱计算耗时太长,将不利于反应谱的进一步分析。为对比分析LRFM方法、Duhamel逐步积分法和Newmark-β方法的计算效率,利用式(18)作为系统输入,合成数据计算时长分别设置为30 s、60 s、90 s、180 s和300 s,采样频率为200 Hz,各方法的计算耗时如图 4所示。由图可知,Newmark-β方法的计算耗时明显大于另外2种方法,且随着时长的增加,计算耗时呈现线性变化,在300 s处计算耗时接近10 s;LRFM方法和Duhamel逐步积分法的整体耗时在1 s以内,两者的计算效率基本相当,且显著优于Newmark-β方法。
|
图 4 反应谱计算耗时对比 Fig. 4 Comparison of the response spectrum calculation time |
随着我国强震动监测台站的增加,强震及大地震发生后可获取数量多且持续时间长的强震动记录,如2008年汶川地震发生后,仅四川省数字强震台网获得的主震记录就接近400条,大部分纪录的持续时间为150~160 s[13], 最长超过300 s, 因此选取合适的方法快速计算得到反应谱以评估场地的地震强度特征或工程结构的受力情况尤为重要。本文提出的LRFM方法的计算效率显著优于目前普遍采用的Newmark-β方法, 可快速高效地得到计算结果。
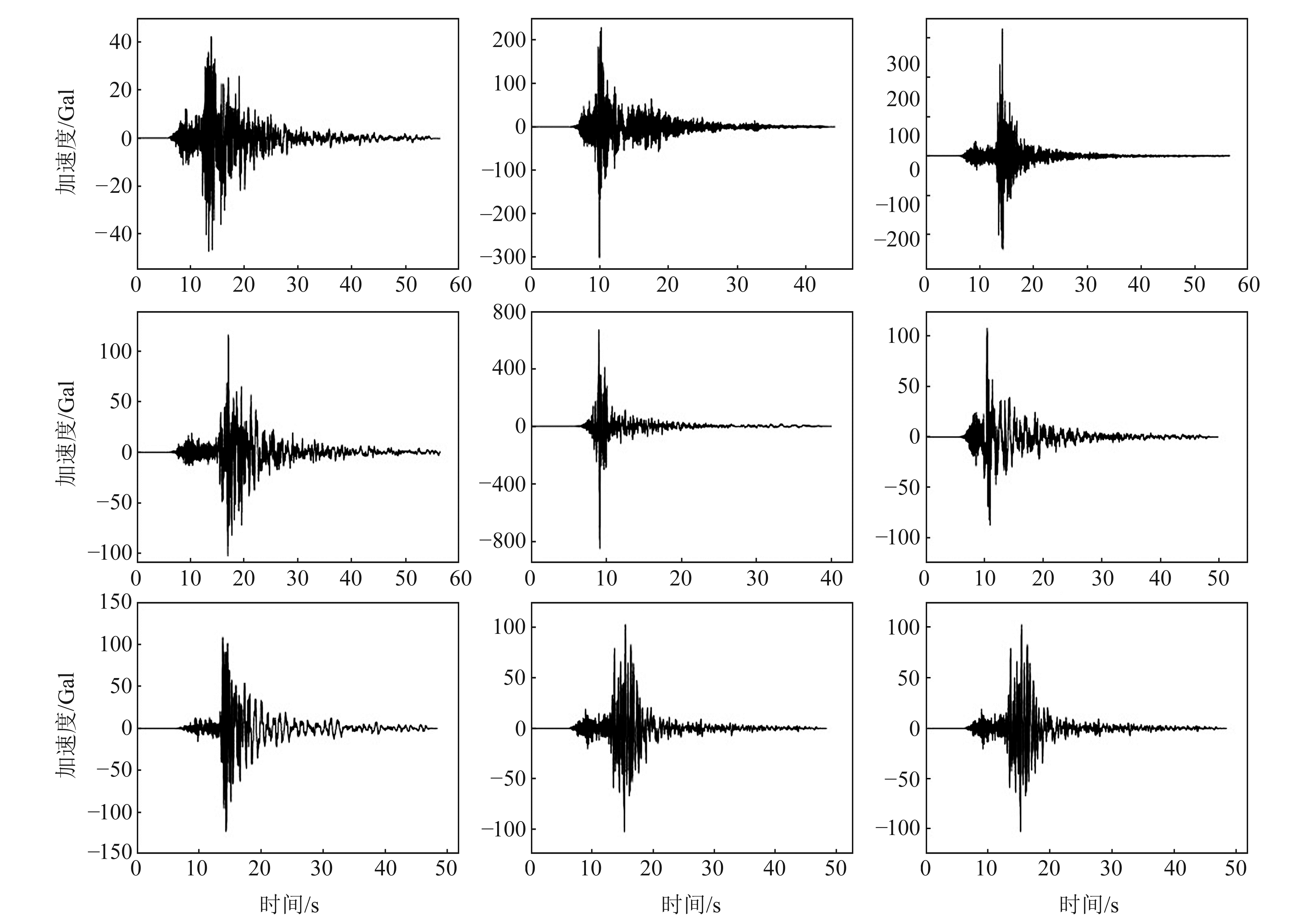
4 实际数据分析计算为验证LRFM方法计算实际强震动记录反应谱的效果,选取ESM强震数据库收录的SNO、PCB、FOC、TLN、AMT、MSCT、CLF、FOS共8个台站记录的2016-08-24意大利ML6.0地震强震波形数据,具体参数见表 1,采样频率均为200 Hz。选取的强震动记录震中距为8.5~57.50 km,PGA为47.13~850.80 Gal,卓越周期范围为0.06~0.56 s,这些记录可基本反映该地震的强震动特征,计算得到的反应谱能够代表在该地震作用下不同位置的地面运动,可以很好地验证LRFM方法对实际强震动记录反应谱的计算效果。计算反应谱的阻尼系数选取5%、10%、20%,自振周期为0~4 s,时间间隔为0.02 s,选取的强震记录时程曲线如图 5所示。本文选取的强震记录具有一般性,主频可基本覆盖从低频到高频不同范围的信息。
|
|
表 1 强震动记录参数 Tab. 1 The seismic recording parameters of strong motion |
|
图 5 地震动加速度时程 Fig. 5 The ground motion acceleration |
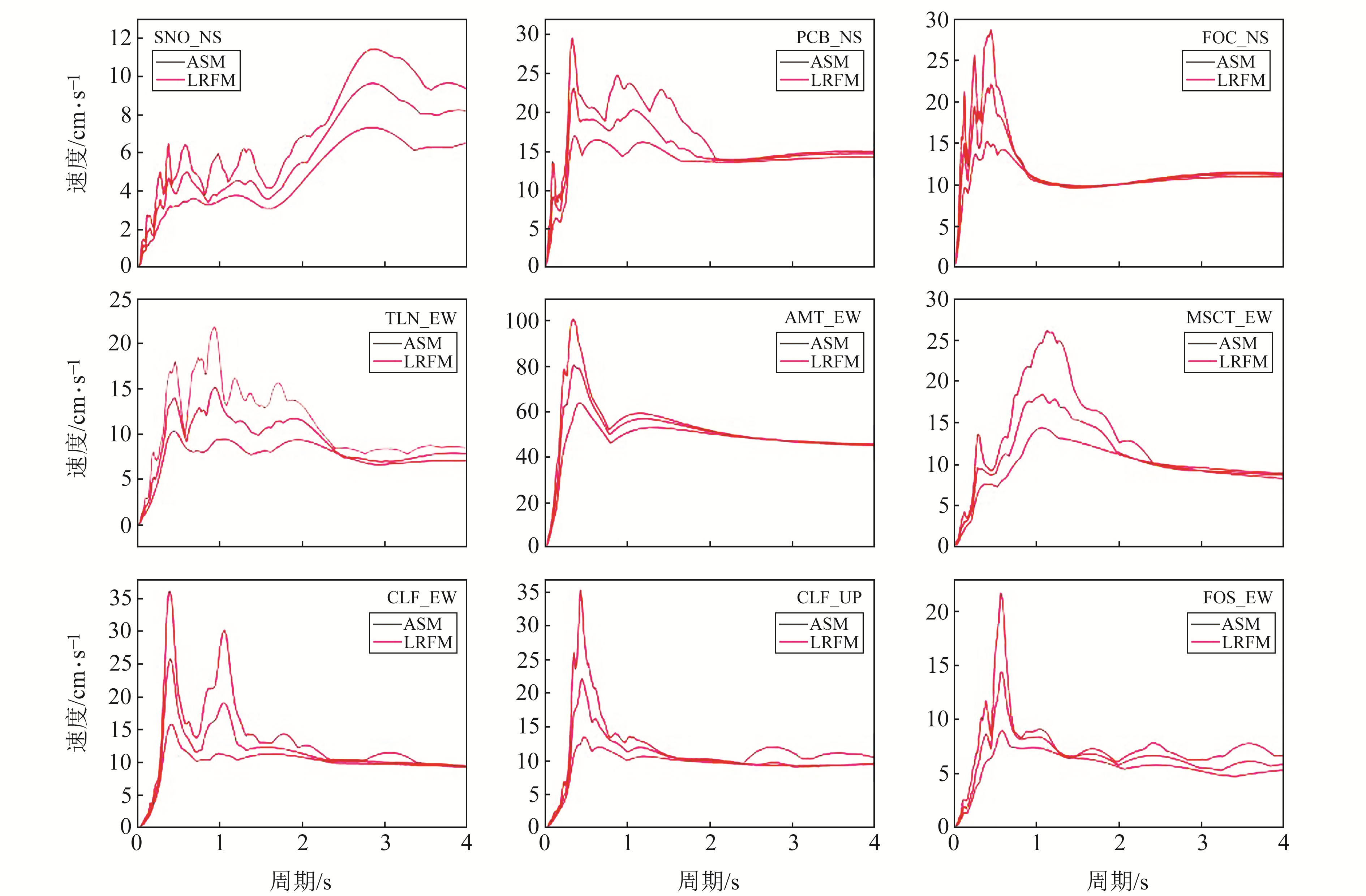
以ASM方法的计算结果作为参照,验证LRFM方法计算实际强震动数据反应谱的效果,另外由于不同方法计算得到的位移反应谱误差相差较小,因此本文仅分析速度反应谱和加速度反应谱的计算结果。图 6为采用LRFM方法和ASM方法计算9条强震记录得到的速度反应谱结果,除个别台站在周期0~1.0 s之间局部极大值处与ASM方法存在极小偏差外,2种方法的速度反应谱曲线形态几乎一致,均反映出不同阻尼条件下速度反应谱的变化趋势。由此说明,LRFM方法能够达到ASM方法的计算精度,与§3.1得出的结论一致。
|
图 6 不同台站速度反应谱计算结果 Fig. 6 The calculation results of velocity response spectrum of different stations |
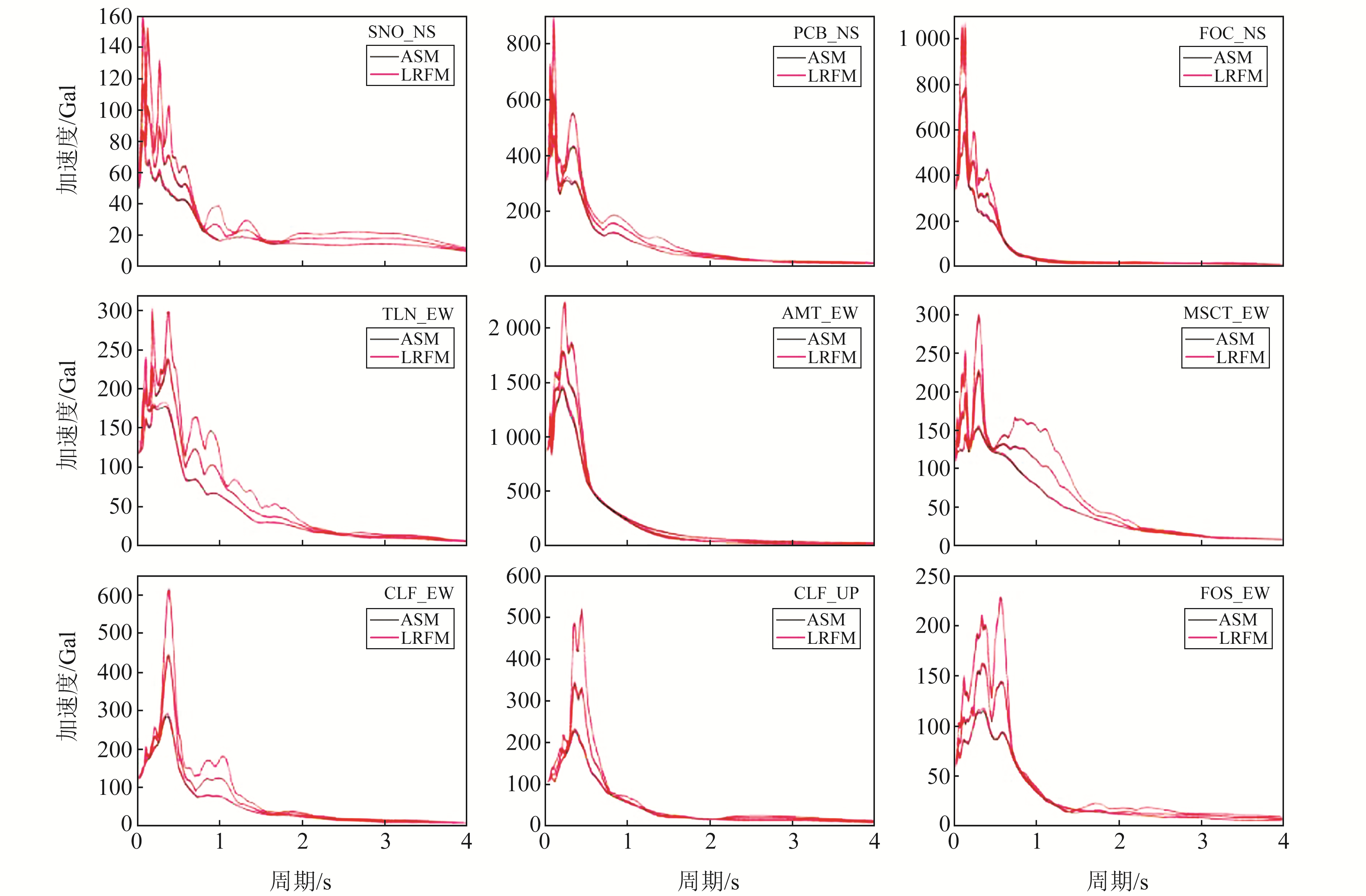
图 7为采用LRFM方法和ASM方法计算不同强震记录的加速度反应谱,从图中可以看出,与ASM方法相比,LRFM方法的计算误差主要集中在周期0~1.0 s之间,且随着阻尼的增大,误差逐渐增大;5%和10%阻尼计算结果的曲线形态与ASM方法基本重合,在极值点处存在极小误差,基本可忽略;20%阻尼的计算结果在曲线局部与ASM方法的计算结果偏差较大,其中最大误差均出现在曲线极大值或局部极大值处,特别是计算得到的加速度反应谱在卓越周期对应的曲线相邻位置存在局部极大值时,相邻区域内LRFM方法的计算结果与ASM方法出现一定分离,如TLN台EW方向的加速度反应谱计算结果。但从整体计算精度来看,LRFM方法对于不同台站强震动记录加速度反应谱的计算结果可以满足计算精度的要求。
|
图 7 不同台站加速度反应谱计算结果 Fig. 7 The calculation results of acceleration response spectrum of different stations |
本文将线性递推滤波算法(LRFM)应用于地震反应谱计算中,对比分析不同方法计算合成数据和实际强震动记录的结果,得出以下结论:
1) LRFM方法计算合成数据得到的反应谱精度和稳定性显著优于Duhamel逐步积分法,略优于Newmark-β方法。与ASM方法相比,LRFM方法计算位移、速度和加速度反应谱的误差均小于2%,满足精度要求。
2) LRFM方法的计算效率与Duhamel逐步积分法相当,且显著优于目前普遍采用的Newmark-β方法,因此对于快速处理强震及大地震产生的数量多且持续时间长的强震动记录具有重要意义。
3) 对于实际强震动记录数据的处理效果,LRFM方法与ASM方法计算的速度反应谱结果一致。
4) 与ASM方法相比,LRFM方法计算得到实际强震动加速度反应谱结果产生的误差主要集中在周期0~1.0 s之间,且随着阻尼的增大误差逐渐增大,但计算结果总体满足精度要求。
5) 针对不同卓越周期和频谱范围的实际强震动记录,采用LRFM方法均可得到可靠的计算结果,稳定性和适用性较好。
综上所述,本文提出的LRFM方法计算耗时短,结果精度高,优于目前普遍采用的Newmark-β方法,可作为一种快速、高效的反应谱计算方法。
| [1] |
Chopra A K. Elastic Response Spectrum: A Historical Note[J]. Earthquake Engineering and Structural Dynamics, 2007, 36(1): 3-12 DOI:10.1002/eqe.609
(  0) 0) |
| [2] |
Clough R W, Penzien J. Dynamics of Structures[M]. New York: McGraw-Hill Companies Inc, 1993
(  0) 0) |
| [3] |
大崎顺彦. 地震动的谱分析入门[M]. 北京: 地震出版社, 2008 (Ohsaki Yorihiko. Introduction to Spectral Analysis of Ground Motion[M]. Beijing: Seismological Press, 2008)
(  0) 0) |
| [4] |
金星, 马强, 李山有. 四种计算地震反应数值方法的比较研究[J]. 地震工程与工程振动, 2003, 23(1): 18-30 (Jin Xing, Ma Qiang, Li Shanyou. Comparison of Four Numerical Methods for Calculating Seismic Response of SDOF System[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(1): 18-30 DOI:10.3969/j.issn.1000-1301.2003.01.004)
(  0) 0) |
| [5] |
蒋甫玉, 高丽坤. 基于余弦变换的地震动反应谱计算方法[J]. 工程力学, 2011, 28(2): 49-56 (Jiang Fuyu, Gao Likun. Calculation of Earthquake Response Spectra by Cosine Transform[J]. Engineering Mechanics, 2011, 28(2): 49-56)
(  0) 0) |
| [6] |
Newmark N M. A Method of Computation for Structural Dynamics[J]. Journal of the Engineering Mechanics Division, 1959, 85(3): 67-94 DOI:10.1061/JMCEA3.0000098
(  0) 0) |
| [7] |
Nigam N C, Jennings P C. Calculation of Response Spectra from Strong-Motion Earthquake Records[J]. Bulletin of the Seismological Society of America, 1969, 59(2): 909-922 DOI:10.1785/BSSA0590020909
(  0) 0) |
| [8] |
Lee V W. Efficient Algorithm for Computing Displacement, Velocity and Acceleration Responses of an Oscillator to Arbitrary Ground Motion[J]. Soil Dynamics and Earthquake Engineering, 1990, 9(6): 288-300 DOI:10.1016/S0267-7261(05)80015-6
(  0) 0) |
| [9] |
梅雨辰, 李鸿晶, 孙广俊. 基于微分求积原理的地震反应谱计算方法[J]. 地震工程与工程振动, 2017, 37(5): 25-37 (Mei Yuchen, Li Hongjing, Sun Guangjun. A Method of Seismic Response Spectrum Calculation by the Differential Quadrature Rule[J]. Earthquake Engineering and Engineering Vibration, 2017, 37(5): 25-37)
(  0) 0) |
| [10] |
Zhou X, Tamma K K. Design, Analysis, and Synthesis of Generalized Single Step Single Solve and Optimal Algorithms for Structural Dynamics[J]. International Journal for Numerical Methods in Engineering, 2004, 59(5): 597-668 DOI:10.1002/nme.873
(  0) 0) |
| [11] |
Papazafeiropoulos G, Plevris V, Papadrakakis M. A Generalized Algorithm Framework for Non-Linear Structural Dynamics[J]. Bulletin of Earthquake Engineering, 2017, 15(1): 411-441 DOI:10.1007/s10518-016-9974-8
(  0) 0) |
| [12] |
谢礼立, 于双久. 强震观测与分析原理[M]. 北京: 地震出版社, 1982 (Xie Lili, Yu Shuangjiu. Principle of Strong Motion Observation and Analysis[M]. Beijing: Seismological Press, 1982)
(  0) 0) |
| [13] |
周荣军, 赖敏, 余桦, 等. 汶川MS8.0地震四川及邻区数字强震台网记录[J]. 岩石力学与工程学报, 2010, 29(9): 1 850-1 858 (Zhou Rongjun, Lai Min, Yu Hua, et al. Strong Motion Records of Wenchuan MS8.0 Earthquake from Digital Strong Earthquake Networks in Sichuan and Its Neighbouring Regions[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1 850-1 858)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

