地震预测是世界性的科学难题,地球内部的不可见性制约着人们对地震发生的构造环境、震源及孕震过程中震源区和邻近区应力状态与介质特征的认识[1]。目前,我国地震前兆观测手段主要是在地表或浅井进行被动观测,如地磁、地电、地应力、地形变等,对于地震的预测仍处于经验预测阶段。为探索地震预测的新途径,我国发射了张衡一号电磁监测实验卫星,以推进立体地震观测体系的建立。要实现地震的物理预报,就必须以定量的动力建模为基础,以获得监测区域结构、物性和状态的透明模型为前提,以实时获取区域地震和前兆关键物理量的四维数据为条件,通过高性能的计算平台对海量数据进行处理及对地震孕育、发生过程进行模拟计算[2]。对地下结构变化进行主动探测,取得地下介质的动态变化信息,研究其与地震孕育、发生的关系,是地震预测研究的新思路[3]。采用人工可控震源对地下介质进行主动观测是一项尖端的地球探测技术,包括信号产生、地球内部传播、远端地面接收、信号提取和信号解释等[4-7],目前我国采用精密可控震源向地壳发射线性调频信号,其能够从莫霍面反射回地面,水平传播距离可达200 km[8]。本文全面介绍了精密可控震源的设计原理和结构以及发出信号的参数估计方法。
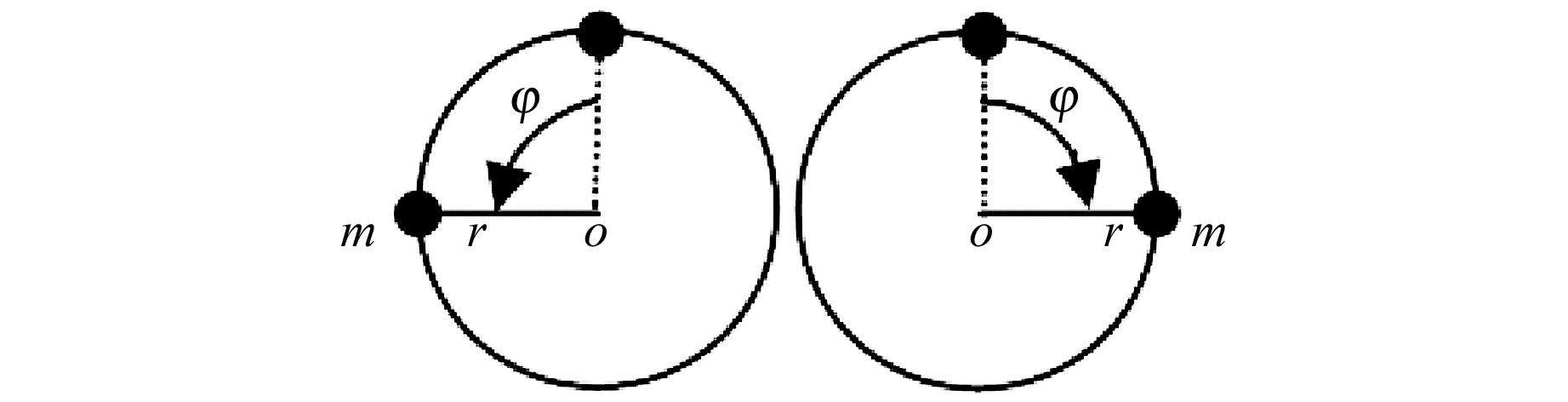
1 精密可控震源的原理及结构 1.1 输出力设计原理一个质量为m的物体围绕圆心作圆周运动,物体因运动方向或速度发生改变而产生离心力,该力的方向由圆心指向物体质心。在旋转半径r保持不变的情况下,物体从一个位置旋转到另外一个位置时(图 1),其相对于原位置会旋转一个角度φ。
|
图 1 两个离心力合成示意图 Fig. 1 Diagram of two centrifugal force synthesis |
当旋转频率f(t) 随时间线性变化时,物体旋转角度也随时间发生变换,旋转角度可表示为φ(t),此时离心力在x轴和y轴的分量分别为:
| $ \begin{matrix} {{F}_{x}}(t)=\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}mr{{f}^{2}}(t)\sin (\varphi (t)) \\ {{F}_{y}}(t)=\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}mr{{f}^{2}}(t)\cos (\varphi (t)) \\ \end{matrix} $ | (1) |
当2个离心力完全相向或背向对称时,相位相差180°,而在2个圆心的连线方向,离心力相互抵消,即
| $ {{F}_{x}}=0 $ | (2) |
当2个离心力完全垂直于圆心的连线方向时,离心力叠加后产生的合力为:
| $ {{F}_{y}}(t)=\text{8}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}mr{{f}^{2}}(t)\cos (\varphi (t)) $ | (3) |
从式(3)可以看出,精密可控震源发出信号的频率随时间而变化,振幅也随频率而改变,因此精密可控震源发出的信号是调频又调幅的双调信号。
本文根据上述2个离心力的合成与抵消原理设计精密可控震源,主要包括机械转动系统、伺服控制系统、运行控制系统和发射平台4个部分。
1.2 机械转动系统机械转动系统是精密可控震源产生合成离心力的关键部分,由2个完全相同的独立偏心轮构成(图 2(a)),其中偏心轮的水平安装方向完全一致,由2台伺服电机分别对偏心轮进行同步驱动,转动方向相反,相位差为180°,向地面输出垂直向下的合力。由式(1)和式(3)可以看出,合力大小是单个偏心轮旋转时的2倍,为保证运行安全,将2个偏心轮密封在金属仓内,并喷涂金属漆以免氧化生锈(图 2(b))。由于偏心轮及其支撑固定结构均由金属铁加工而成,其质量m和旋转半径r均不会随时间和环境而变化。

|
图 2 精密可控震源 Fig. 2 Controlled accurate seismic source |
机械设计的偏心轮质量为436.628 kg,等效旋转半径为0.125 m。根据式(3)可知,当精密可控震源工作频率为4 Hz时,垂直方向输出的离心合力约为6.89×104 N;工作频率为10 Hz时,输出的离心合力约为4.31×105 N,两者相差6.25倍。
1.3 伺服控制系统伺服控制系统由驱动增量型旋转编码器、伺服控制器和外围主回路部件构成,其中编码器提供电机位置的实时反馈信号,伺服控制器和外围主回路共同通过编程方式实现对电机位置、转速、加速度和输出转矩的高性能控制。
增量型编码器是利用光电转换原理将增量位移转换成脉冲信号,分别输出A、B、Z相3组脉冲信号,其中A、B相为每转2 048个脉冲,可以确定电机的实时位置和速度,脉冲相位差为90°,可判断旋转方向;Z相为每转1个脉冲,用于基准点定位。在伺服控制系统中,通过对分辨率为2 048 P/R编码器输出的脉冲信号进行逻辑处理,得到更高分辨率为8 192 P/R。编码器信号的输出方式采用RS-422线驱动输出,具有高速响应和良好的抗噪性能,适用于恶劣环境和长距离传输,编码器平均寿命可在几万小时以上。
1.4 运行控制系统运行控制系统主要包括2个部分:控制单元和信号采集系统。运行控制系统是一个与北斗或GPS同步授时的精密信号源,通过内部CPU输出高精度的线驱动脉冲序列和方向控制信号,同时将电机编码器的实时状态进行解析,得到精密可控震源的实时运转信息,并通过人机交互软件设置精密可控震源的运行参数。控制单元内部时钟模块的频率为10 MHz,CPU频率达到60 MHz,授时误差小于500 ns。控制单元可输出单频和线性调频2种脉冲序列,输出频率的绝对精度小于1×10-6 Hz,通过RS-232接口进行偏心轮运转控制和实时状态监视。
在距离精密可控震源10 m处安装一套短周期地震数据采集系统,实时采集存储精密可控震源的输出信号,监控精密可控震源输出信号的质量,同时也作为精密可控震源输出的标准信号。
1.5 发射平台在硬土层上挖掘长6 m、宽4 m、深1.3 m的方坑,并在坑内浇注长5 m、宽3 m、高1 m的钢筋混凝土平台(图 3)。在浇注钢筋混凝土平台时,在钢筋上安装长5 m、宽3 m、厚50 mm的钢板,钢板上安装44根直径为48 mm的地脚螺栓,确保精密可控震源系统准确固定在发射平台上,以提高精密可控震源能量传递的效率[9-10]。

|
图 3 精密可控震源发射平台 Fig. 3 Launch platform of CASS |
1976-07-28唐山地震和2008-05-12汶川地震等破坏性较大的地震均发生在地壳内,需要精密可控震源从地表向地下发射的信号穿过地壳到达莫霍面(大陆平均厚度约为33 km)后再反射回地面,才能带回孕震区的变化信息。大部分地震计的观测频带范围为0.016 7~50 Hz,地震数据采集器和地震计的自噪声在10 Hz后会急剧增加,精密可控震源发出的线性调频信号经过地下介质的衰减作用后,只有频率相对较低才能传播到较远的区域[11]。由式(3)可以看出,精密可控震源输出力的大小与旋转频率的平方成正比,精密可控震源在低频段激发的能量较低,因此对远端地震台站接收到的信号进行多次叠加可以提高信噪比,有利于提取精密可控震源发出的信号。本文将精密可控震源的工作频率设置在4~10 Hz,运行时间设置为300 s。
2 调频参数估计方法对于线性调频信号而言,Wigner-Ville变换可使其能量集中在时频面中一条直线上,因此对线性调频信号的检测就转化为时频面上的直线检测,将Wigner-Ville分布与Hough变换相结合,适用于线性调频信号的检测和估计[12]。对线性调频信号进行Wigner-Hough变换,将信号从时域变换为由频率和调频速率组成的参数空间域,然后在该参数空间域进行检测和估计[13]。信号x(t)的Wigner-Ville分布可定义为[14]:
| $ {{W}_{x}}(t, f)=\int_{-\infty }^{+\infty }{x(t+}\frac{\tau }{2}){{x}^{*}}(t-\frac{\tau }{2})\mathop{\text{e}}^{-j2\text{ }\!\!\pi\!\!\text{ }f\tau }\text{d}\tau $ | (4) |
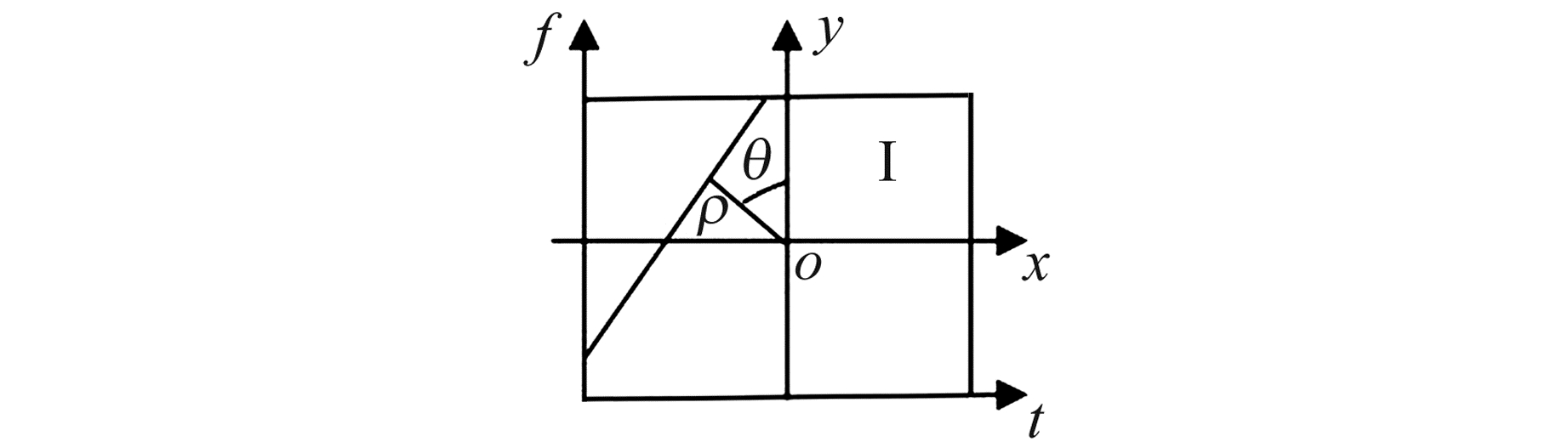
Hough变换专门用于检测图像中的直线,坐标原点o位于图像I中心(图 4),若图像大小为N×L,用(t, f)表示在图像中的位置,则:
| $ x\text{=}t-\frac{N}{\text{2}} $ | (5) |
| $y\text{=}f-\frac{L}{\text{2}}$ | (6) |
|
图 4 Hough变换 Fig. 4 Hough transform |
Hough变换用极坐标可表示为:
| $x\cos \theta +y\sin \theta =\rho $ | (7) |
式中,ρ为过原点垂直于直线的垂线长度,θ为垂直轴与该垂线的夹角。
对于图像I中每个像素点(x, y),经Hough变换后对应(ρ,θ)面内一条正弦曲线,其幅度对应像素点(x, y)的强度,因此对于图像I中所有像素点,经Hough变换后在(ρ,θ)面内对应一束交织在一起的正弦函数[15]。如果图像I中部分像素点高度集中在一条直线上,在(ρ,θ)面内必有一个尖峰对应该直线的参数,则初始频率f0和调频速率k与ρ及θ的关系为[16]:
| $ {{f}_{0}}=\rho /\sin \theta $ | (8) |
| $k=-\cos \theta $ | (9) |
最大输出力为4.31×105 N的精密可控震源在四川芦山运行的结果表明其发出信号的互相关系数均在0.99以上[17],在河北沽源试运行的结果显示其发出信号的互相关系数也都在0.99以上[18],因此精密可控震源发出的信号具有较高的重复性,与传统的炸药震源相比具有显著而独特的优点[19]。
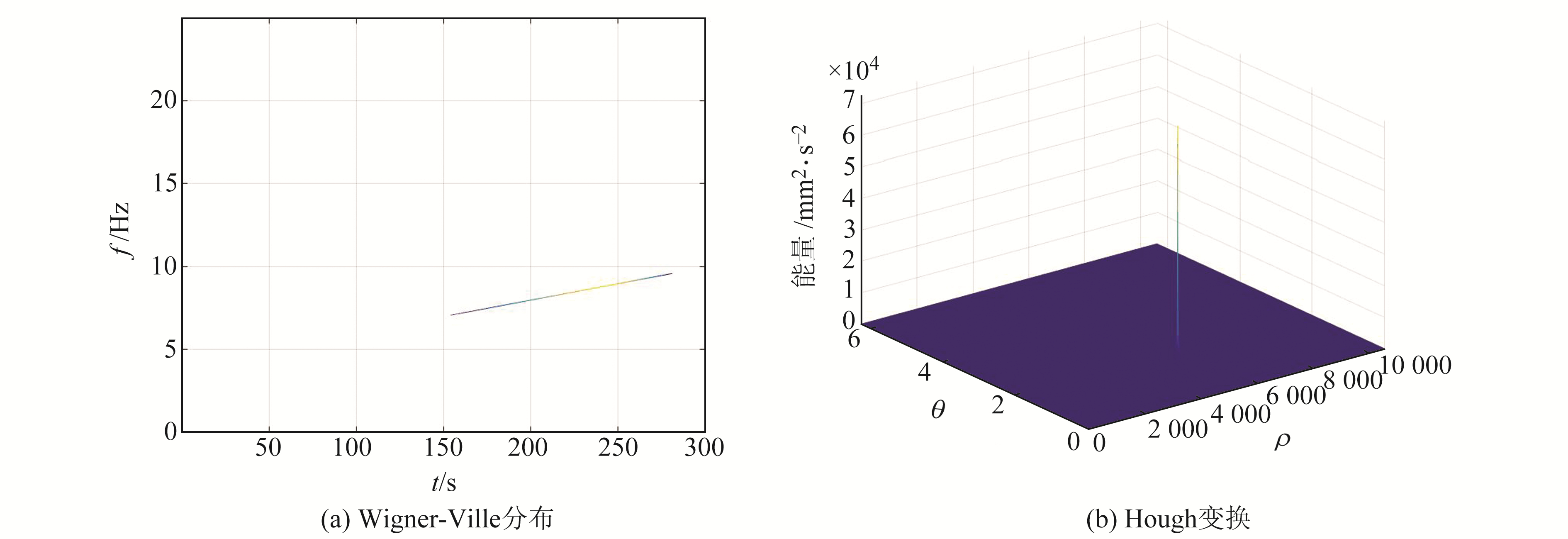
3.2 初始频率和调频速率由式(4)可知,Wigner-Ville分布为二次变换,在计算时对计算机的资源消耗较大,因此将采样率由200 Hz降至50 Hz,采用4~10 Hz带通滤波后再对其进行Wigner-Ville分布分析和Hough变换,结果见图 5。
|
图 5 精密可控震源信号分析 Fig. 5 The analysis of CASS signal |
从图 5(a)可以看出,精密可控震源发出的信号在Wigner-Ville分布的时频面上仅有一条直线,且频率f随时间t的增加而线性增加,说明该信号为线性调频信号。从图 5(b)可以看出,经过Hough变换后,在(ρ,θ)面上仅有一个突出尖峰,说明精密可控震源只发出一组线性调频信号,这有利于识别经地壳内不同深度反射到地面的信号。
从Hough变换后的参数中确定波峰坐标(ρ,θ),根据式(8)和式(9)估计得到初始频率和调频速率,结果见表 1。
|
|
表 1 调频参数 Tab. 1 Frequency modulation parameter |
由于理想的线性调频信号的Wigner-Ville分布为冲激函数,但有限长的线性调频信号的Wigner-Ville分布呈背鳍状,在估算过程中使用300 s的数据,且考虑到计算资源已将采样率降为50 Hz,因此估算的初始频率和调频速率与理论参数略有差异,重复性高就不会影响信号在地下走时变化的长期观测。
4 结语基于2台伺服电机驱动2个偏心轮相向旋转而产生垂直向下的离心合力,既可保证精密可控震源对周围环境无破坏,又使其输出信号的形态高度一致。偏心轮的质量和旋转半径不会随时间和环境而变化,精密可控震源系统的机械特性也不会改变,唯一影响输出信号特性的只有偏心轮的转动参数,而转动参数可受到精确控制,因此通过精密控制震源系统而发射的线性调频信号特征明确,并且具有高度可重复性。
炸药等震源在瞬间输出大功率的脉冲信号,对环境具有较大的破坏性,而精密可控震源向地面长时间输出小功率线性调频信号,对环境无破坏。通过北斗精确授时,精密可控震源的运行时间、频率、调频速率及运行周期数均由系统精确控制,合理设置调频参数和运行时间,避开地震数据采集器、地震计和地球的自噪声干扰频段,有利于信号叠加和提高信噪比。精密可控震源输出的线性调频信号在时频面内呈现聚集性,而地球自噪声杂乱无章,且无聚集性,两者容易分辨和提取。
将精密可控震源固定在活断层附近长期重复运行,并在四周布设北斗高精度授时的地震观测设备,重复接收精密可控震源信号通过不同深度分界面反射到地面的P波、S波及首波等,实现对地壳介质分层的长期主动观测。由于精密可控震源和接收信号的地震观测台站的位置已知和不变,通过分析相同路径上波速的变化规律和时空演化特征,构建地下地震云图,可为研究地震发生前后地壳的物理变化特征及其他前兆观测信息提供科学依据。
致谢: 感谢梁鸿森研究员提供的帮助。
| [1] |
崔仁胜, 孙安辉, 王洪体, 等. 用于龙门山断裂南段深部介质探测的精密可控震源[J]. 中国地震, 2016, 32(2): 426-437 (Cui Rensheng, Sun Anhui, Wang Hongti, et al. The Controlled Accurate Seismic Source for Exploration of Deep Medium below South Part of the Longmenshan Fault Zone[J]. Earthquake Research in China, 2016, 32(2): 426-437 DOI:10.3969/j.issn.1001-4683.2016.02.026)
(  0) 0) |
| [2] |
石耀霖, 孙云强, 罗纲, 等. 关于我国地震数值预报路线图的设想: 汶川地震十周年反思[J]. 科学通报, 2018, 63(19): 1 865-1 881 (Shi Yaolin, Sun Yunqiang, Luo Gang, et al. Roadmap for Earthquake Numerical Forecasting in China——Reflection on the Tenth Anniversary of Wenchuan Earthquake[J]. Chinese Science Bulletin, 2018, 63(19): 1 865-1 881)
(  0) 0) |
| [3] |
陈颙, 朱日祥. 设立"地下明灯研究计划"的建议[J]. 地球科学进展, 2005, 20(5): 485-489 (Chen Yong, Zhu Rixiang. Proposed Project of "Underground Bright Lump"[J]. Advance in Earth Science, 2005, 20(5): 485-489 DOI:10.3321/j.issn:1001-8166.2005.05.001)
(  0) 0) |
| [4] |
Alekseev A S, Chichinin I S, Korneev V A. Powerful Low-Frequency Vibrators for Active Seismology[J]. Bulletin of the Seismological Society of America, 2005, 95(1): 1-17 DOI:10.1785/0120030261
(  0) 0) |
| [5] |
Niu F L, Silver P G, Daley T M, et al. Preseismic Velocity Changes Observed from Active Source Monitoring at the Parkfield SAFOD Drill Site[J]. Nature, 2008, 454(7 201): 204-208
(  0) 0) |
| [6] |
Ikuta R, Yamaoka K. Temporal Variation in the Shear Wave Anisotropy Detected Using the Accurately Controlled Routinely Operated Signal System(ACROSS)[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B9)
(  0) 0) |
| [7] |
Silver P G, Daley T M, Niu F L, et al. Active Source Monitoring of Cross-Well Seismic Travel Time for Stress-Induced Changes[J]. Bulletin of the Seismological Society of America, 2007, 97(1B): 281-293 DOI:10.1785/0120060120
(  0) 0) |
| [8] |
Li Z W, You Q Y, Ni S D, et al. Waveform Retrieval and Phase Identification for Seismic Data from the CASS Experiment[J]. Pure and Applied Geophysics, 2013, 170(5): 815-830 DOI:10.1007/s00024-012-0585-2
(  0) 0) |
| [9] |
李琴, 张凯, 黄志强, 等. 精密可控震源隔振系统参数优化设计[J]. 工程设计学报, 2018, 25(2): 180-187 (Li Qin, Zhang Kai, Huang Zhiqiang, et al. Parameter Optimization Design for Vibration Isolation System of Accurately Controlled Routinely Operated Seismic Source[J]. Chinese Journal of Engineering Design, 2018, 25(2): 180-187 DOI:10.3785/j.issn.1006-754X.2018.02.008)
(  0) 0) |
| [10] |
宋澄, 冯静, 戴仕贵, 等. 大岗山库区主动震源探测系统性能及其影响因素[J]. 中国地震, 2016, 32(2): 417-425 (Song Cheng, Feng Jing, Dai Shigui, et al. The Performance of Monitoring System of Accurately-Controlled Routinely-Operated Seismic Source in the Dagangshan Reservoir Area and Its Affecting Factors[J]. Earthquake Research in China, 2016, 32(2): 417-425 DOI:10.3969/j.issn.1001-4683.2016.02.025)
(  0) 0) |
| [11] |
陈颙, 李宜晋. 地震波雷达研究展望: 用人工震源探测大陆地壳结构[J]. 中国科学技术大学学报, 2007, 37(8): 813-819 (Chen Yong, Li Yijin. Seismic Wave Radar Research: Using Active Source to Detect Continental Crust Structure[J]. Journal of University of Science and Technology of China, 2007, 37(8): 813-819 DOI:10.3969/j.issn.0253-2778.2007.08.002)
(  0) 0) |
| [12] |
Barbarossa S. Analysis of Multicomponent LFM Signals by a Combined Wigner-Hough Transform[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1 511-1 515 DOI:10.1109/78.388866
(  0) 0) |
| [13] |
刘建成, 王雪松, 肖顺平, 等. 基于Wigner-Hough变换的径向加速度估计[J]. 电子学报, 2005, 33(12): 2 235-2 238 (Liu Jiancheng, Wang Xuesong, Xiao Shunping, et al. Radial Acceleration Estimation Based on Wigner-Hough Transform[J]. Acta Electronica Sinica, 2005, 33(12): 2 235-2 238)
(  0) 0) |
| [14] |
张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998 (Zhang Xianda, Bao Zheng. Non-Stationary Signal Analysis and Processing[M]. Beijing: National Defense Industry Press, 1998)
(  0) 0) |
| [15] |
胡昌华, 夏启兵, 周涛, 等. 基于MATLAB的系统分析与设计——时频分析[M]. 西安: 西安电子科技大学出版社, 2002 (Hu Changhua, Xia Qibing, Zhou Tao, et al. System Analysis and Design Based on MATLAB——Time Frequency Analysis[M]. Xi'an: Xidian University Press, 2002)
(  0) 0) |
| [16] |
于凤芹, 曹家麟. 基于时频重排-霍夫变换的雷达回波信号检测[J]. 现代雷达, 2005, 27(2): 40-42 (Yu Fengqin, Cao Jialin. Detection for Multi-Target Radar Echo Signals Based on Time-Frequency Reassignment-Hough Transform[J]. Modern Radar, 2005, 27(2): 40-42 DOI:10.3969/j.issn.1004-7859.2005.02.012)
(  0) 0) |
| [17] |
刘明辉, 彭朝勇, 周银兴, 等. 芦山震中区上地壳剖面二维波速结构模型反演[J]. 地球物理学进展, 2016, 31(1): 69-78 (Liu Minghui, Peng Chaoyong, Zhou Yinxing, et al. Inversion of 2-D Velocity Structure Model of Upper Crust Section in the Lushan Epicentral Region[J]. Progress in Geophysics, 2016, 31(1): 69-78)
(  0) 0) |
| [18] |
刘明辉, 周银兴, 彭朝勇, 等. 用能量累积法检测地震波雷达信号[J]. 地球物理学报, 2015, 58(4): 1 259-1 268 (Liu Minghui, Zhou Yinxing, Peng Chaoyong, et al. Using the Method of Accumulating Energy for Detecting Seismic Wave Radar Signal[J]. Chinese Journal of Geophysics, 2015, 58(4): 1 259-1 268)
(  0) 0) |
| [19] |
杨光亮, 朱元清. 可控震源在深部地壳探测中的应用[J]. 大地测量与地球动力学, 2007, 27(5): 72-75 (Yang Guangliang, Zhu Yuanqing. Application of Vibrator on Deep Crust Structure Exploration[J]. Journal of Geodesy and Geodynamics, 2007, 27(5): 72-75)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

