2. 云南省麻栗坡民族中学,云南省文山州文麻路193号,663600
地震地磁数据预处理是地磁数据挖掘和地震预报预测的首要工作[1]。地磁观测数据属于时间序列,其计算方法要求数据序列连续完整,因此对缺失数据进行插值是前兆数据应用前必须进行的预处理工作[2]。国内外对缺失值进行插值处理的方法较多,如回归法、最近邻域替代法、人工填补法和期望值最大化法等[3-5]。武艳强等[6]利用三次样条插值方法对时间序列中数据缺失较多等问题展开研究;杨登科[7]采用拉格朗日插值等6种方法对时间序列的插值效果进行对比。
在实际地磁偏角观测工作中,由于地磁观测数据[8-10]种类众多,往往会出现单点缺失和连续多点缺失的现象,而现有的数据插值方法在地磁观测数据的插值应用中存在诸多局限性。目前针对地磁偏角数据插值方法的研究较少,本文根据地磁数据的记录特点,将时间序列模型[11-12]应用于地磁数据缺失处理。将ARMA预测模型[13-14]用于地磁数据的插值处理,可为地磁观测数据预处理提供一种可行的方法。
1 插值方法插值法是数据预处理的重要方法,在数据分析和数据挖掘中发挥着重要作用。常见的插值法有均值插值、线性插值等,不同方法的适用性也不同,如均值插值适用于原始数据方差较小、序列趋于平稳的数据,而本文所采用的地磁观测数据属于非平稳数据;线性插值为直线拟合运算,适用于趋势性较小的数据。但在处理连续多点缺失的数据时,上述方法的插值效果均不理想。本文尝试将ARMA模型预测方法应用于地磁序列插值。
1.1 均值插值均值插值就是计算数据的平均值并代替原始数据中的缺失部分,假设求解Ti和Ti+1之间任意一点T,则直接取T为Ti和Ti+1的平均值。对于数据集data=[45.20, 26.21, 42.10, NaN, NaN, NaN, 52.20, 32.52],Python可调用均值mean()函数计算均值,利用自带fillna()函数进行mean插值计算,计算方法如下:
| $ \text { data }=\text { data. fillna(data. mean( ) ) } $ | (1) |
线性插值是通过已知量来求解两者之间的未知量,由于其为直线拟合,适合处理较为平缓的数据。在Python中可用interpolate()函数进行线性运算,利用fillna()函数进行interpolate插值,计算方法如下:
| $ \text { data }=\text { data. fillna(data. interpolate }(\text { ) ) } $ | (2) |
或
| $ \text { data } \left.=\text { data. interpolate(method }=\text { 'linear '}\right) $ | (3) |
本文尝试将ARMA模型作为插值方法引入到地磁观测数据插值预处理中。将缺失数据作为时间序列预测数据,利用缺失序列之前的数据预测缺失数据,插值效果较好。
ARMA模型作为一种时间序列经典模型,由自回归模型(AR)和移动平均模型(MA)组合而成,其结构为:
| $\begin{gathered} x_{t}=\varphi_{0}+\varphi_{1} x_{t-1}+\varphi_{2} x_{t-2}+\cdots+\varphi_{p} x_{t-p}+ \\ \varepsilon_{t}-\theta_{1} \varepsilon_{t-1}-\theta_{2} \varepsilon_{t-2}-\cdots-\theta_{q} \varepsilon_{t-q} \end{gathered} $ | (4) |
式中,随机变量Xt的取值xt不仅与前p期的序列值有关,还与前q期的随机扰动有关,p为自回归模型阶数,q为移动平均模型阶数。
ARMA(p, q)模型预测步骤如下。
1) 非白噪声检验:使用Python自带函数库statsmodels中acorr_ljungbox函数进行检验,若p值小于显著性水平α,则该序列为非白噪声,具备建模分析价值。
2) 平稳性检验:使用Python自带函数库statsmodels中adfuller函数进行检验,也可通过地磁序列的自相关函数(ACF)和偏自相关函数(PACF)来确定序列是否平稳,若不平稳可使用差分方法使数据序列达到平稳,进而确定模型阶数(p、q值)。
3) 估计:对模型参数进行评估。
4) 预测:利用拟合模型进行预测分析。
为验证利用ARMA模型对地磁数据进行插值的可行性和有效性,将常用的均值插值、线性插值的插值结果作为参照,与ARMA模型的插值结果进行对比研究。
2 地磁数据插值实验设计 2.1 前期地磁数据处理ARMA模型要求数据序列必须为平稳数据,对于地磁观测数据而言,数据序列由各种趋势、周期和随机干扰组合而成,因此在建立ARMA模型之前需要去除数据中的趋势和周期成分。通过分析地磁偏角观测数据模型,可将地磁数据的曲线形态分为三类:1)随机干扰;2)地球背景场或太阳辐射周期;3)周期或趋势成分。由于地震仪器所处的台站和自然环境不同,其记录的地磁数据均包含不同形态的趋势和周期成分。
去除趋势或周期、地球背景场或太阳辐射周期最简单的方法是对地磁观测序列进行差分处理。对于多数观测序列而言,一阶差分即可去除大部分干扰成分,使数据序列达到平稳,若一阶差分数据仍未达到平稳,可进行多次差分。对大量观测数据序列进行统计分析发现,约92.43%的地磁观测数据序列为非平稳状态,经过一阶差分后,96.78%的非平稳序列均可达到平稳[1]。在对地磁偏角进行处理时发现,为了使观测数据趋于平稳化,对观测数据进行二阶差分,非平稳数据基本可达到平稳化。
2.2 地磁插值实验方法设计 2.2.1 非震异常数据数量≤10为比较ARMA模型与其他插值方法的插值效果,选取完整的地磁观测数据序列,人为构造缺失数据。数据缺失点包括单点缺失和连续多点缺失,本文设计的连续多点缺失为2~10点缺失,利用3种不同的插值方法对缺失数据序列进行插值处理。选择缺失值之前的400个数据点作为ARMA模型的基础,并确定参数最佳的ARMA模型,然后将预测值作为缺数填补结果。采用标准误差作为评价指标,标准误差越小,插值效果越优。标准误差计算公式如下:
| $ \sigma=\sqrt{\sum\limits_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2} / n} $ | (5) |
式中,n为缺值个数,xi为插值结果,yi为实际观测值。
2.2.2 插值实验及分析选取地磁偏角D数据,对地磁数据各种缺失情况进行插值实验,步骤如下:
1) 在地磁偏角数据中选取10个位置点作为缺失数据的起始点。
2) 依据起始点连续构造n(n取值1~10,分别对应10种缺失情况)对缺失数据序列进行差分处理。
3) 采用3种不同方法进行插值处理。
4) 利用式(5)计算3种不同方法的标准误差。
表 1为实验结果,从表中可以看出,3种插值方法中ARMA预测插值法的插值效果较好,其次为线性插值法和均值插值法。图 1为3种插值方法的平均标准误差曲线,从图中可以看出,在不同缺失值情况下,3种方法的标准误差曲线趋势表明,随着缺失值个数的增加,插值结果与实际值的标准误差也在增加,且不同插值方法标准误差的增长速度有所不同,相比于线性插值和ARMA预测插值,均值插值标准误差的增长速度最快;ARMA预测插值的效果最好,其标准误差最小,标准误差曲线的变化幅度小于其他方法。
|
|
表 1 三种不同插值方法在不同缺失条件下的平均标准误差 Tab. 1 The mean standard errors of three different interpolation methods under different missing conditions |

|
图 1 不同缺失值个数情况下不同插值方法的平均标准误差比较 Fig. 1 Comparison of mean standard errors of different interpolation methods under different numbers of missing values |
图 2为不同单点缺失位置3种插值方法对应的标准误差变化曲线,从图中可以看出,ARMA预测插值相比于其他2种方法的标准误差更小。

|
图 2 不同单点缺失位置3种方法对应的平均标准误差变化曲线 Fig. 2 Variation curve of mean standard errors of three interpolation methods corresponding to different single point missing positions |
为了能够更加直观地说明3种插值方法插值效果的差异,本文以2008-05-12汶川地震北京台的秒采样数据为例,给出磁偏角D在连续缺失10个数值时3种插值方法的插值效果(图 3)。
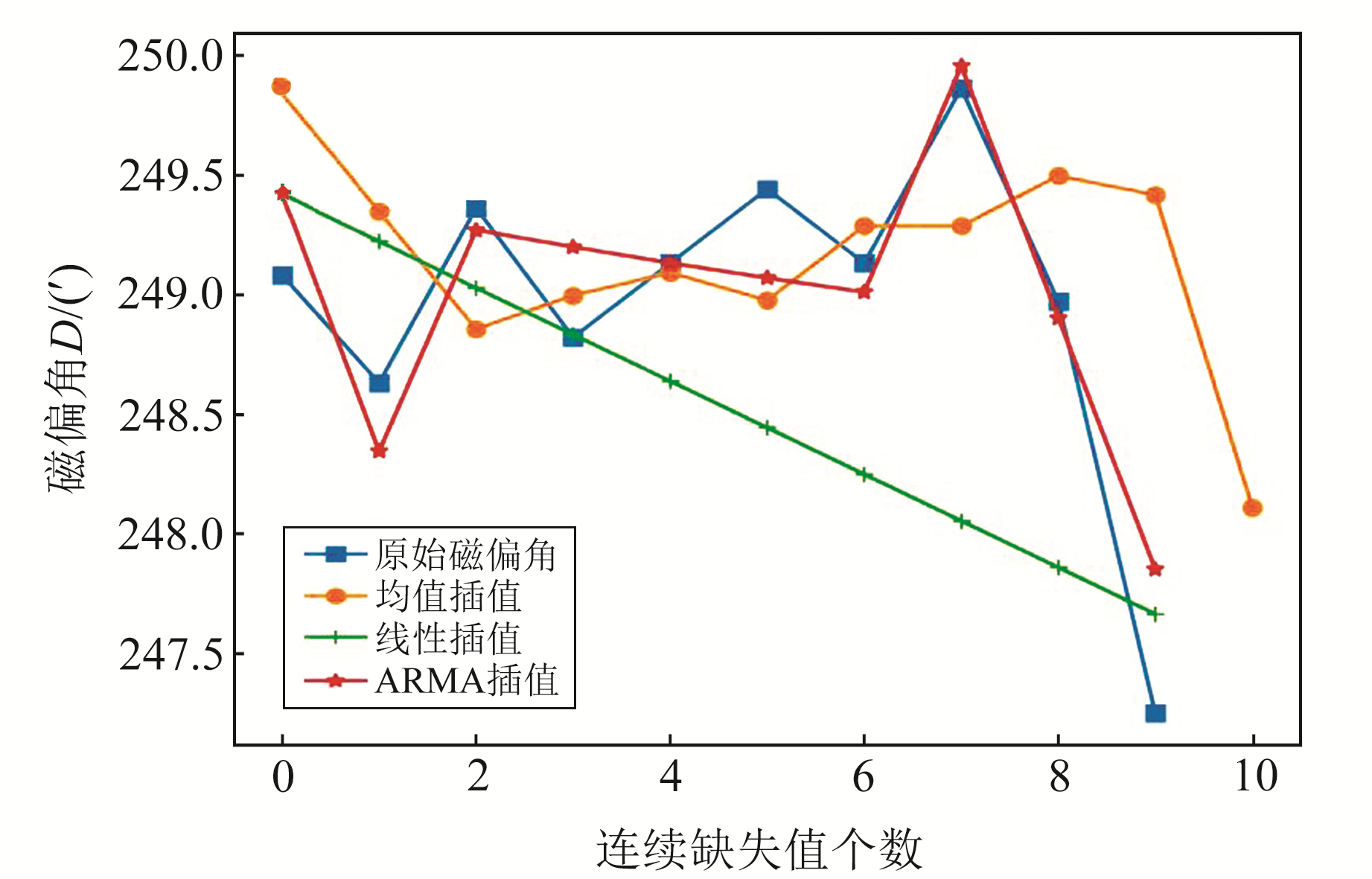
|
图 3 连续缺失10个数值的插值情况 Fig. 3 Interpolation with 10 continuous missing values |
实验表明,在均值插值、线性插值和ARMA预测插值中,ARMA模型的插值效果最优。本文以2017-08-08九寨沟地震满洲里地震台连续缺失10个数值的地磁偏角秒数据为例进行数据拟合,结果如图 4所示。
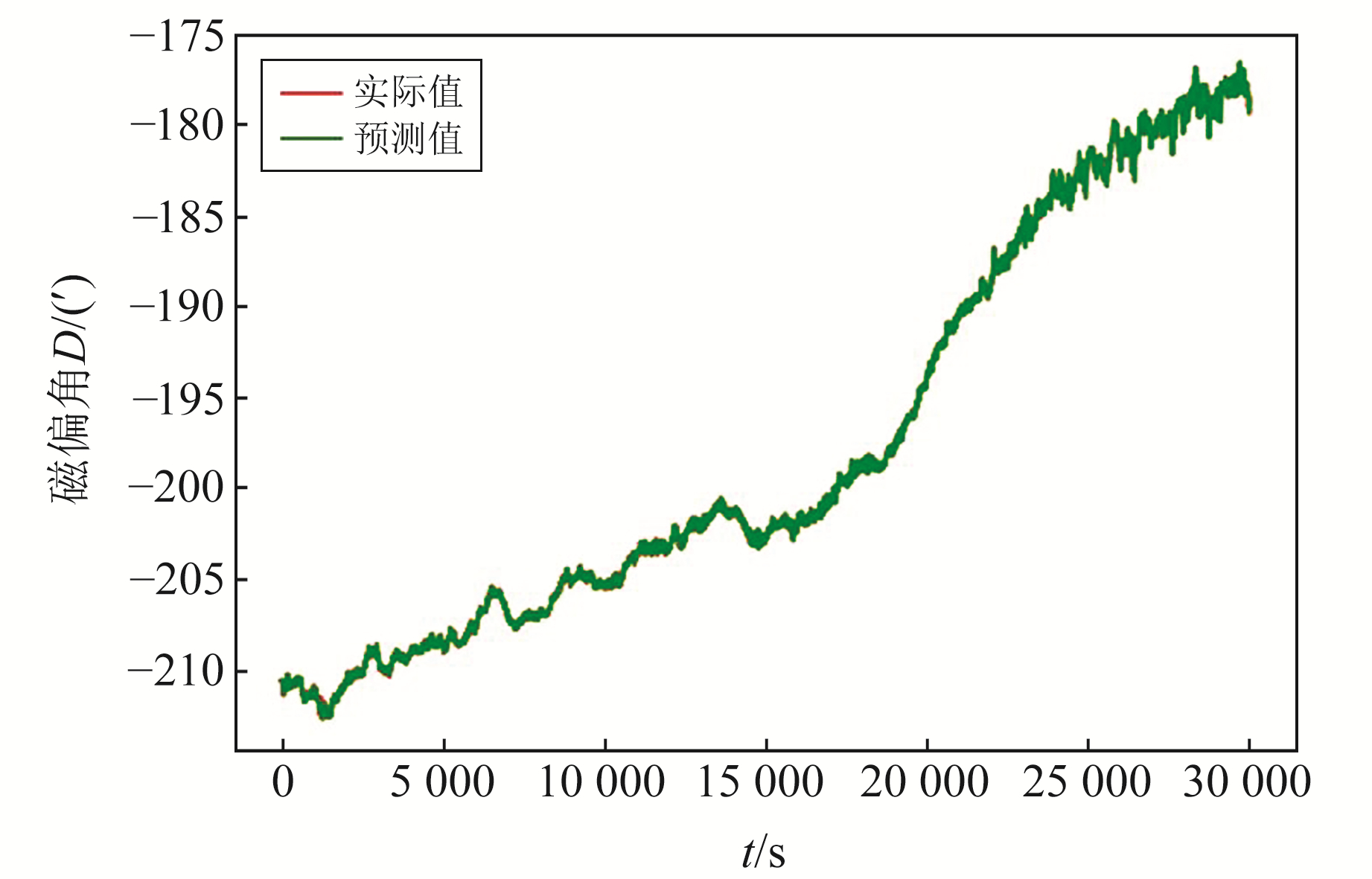
|
图 4 九寨沟地震满洲里地震台连续缺失10个数值的地磁偏角秒数据ARMA模型拟合 Fig. 4 ARMA model fitting for the geomagnetic declination second data with 10 continuous missing values of Jiuzhaigou earthquake at Manzhouli seismic station |
综上分析可知,不同插值方法对不同缺失情况的插值效果各不相同,表现为曲线形态特征存在差异。ARMA预测插值法的标准误差较小,且该模型中插值数据与实际观测值拟合度高,而均值插值和线性插值会改变数据原始趋势,因此ARMA插值对地磁偏角D数据的处理效果相对较好。
2.2.3 非震异常数据数量>10在数据缺失较多时不应采用插值方法,而应直接删除。但本文研究的地磁数据属于时间序列数据,为了后期可检测到数据异常点,本文采用统一合理值来代替大量缺失数据和非震异常数据。非震异常数据指地震仪器记录错误或未记录到的数据,其一般为多个连续数值88 888.0或99 999.0,或者为多个连续的小于99 999.0且远大于正常地磁峰值的数值。由于地磁由多个变化缓慢的磁场组成,其数值为随时间变化的时间序列,不可能出现多个连续相同且远大于正常峰值的数值。因此,该部分数值与真实值无相关性,会对地磁的趋势信息造成不可恢复的影响。但这部分数据是时间序列的一部分,而时间序列中每个数值所在的时间点也是重要信息,因此应用合理的数值代替该部分数据,有利于保持时间序列的完整性。处理这些数据的算法如下:
1) 遍历1 d内所有的地磁偏角D数据,统计数值为88 888.0、99 999.0及其以上数值的个数,若个数小于10,采用§2.2.1算法进行插值;若个数大于10,则采用邻域值进行代替,直到出现正常值。
2) 遍历1 d内所有的地磁偏角D数据,若数值出现0或“NaN”的个数小于10,采用§2.2.1算法进行插值;若个数大于10,则采用邻域值进行代替,直到出现正常值。
3) 遍历1 d内所有的地磁偏角D数据,若重复数值出现的个数小于10,采用§2.2.1算法进行插值;若个数大于10,则采用邻域值进行代替,直到出现正常值。
以2008-05-12汶川地震满洲里台站作为测试台站,其缺数中88 888.0、99 999.0、0和”NaN”个数大于10,数据为地磁偏角D的1 d秒采样数据,结果如图 5所示。

|
图 5 汶川地震满洲里台站多种缺数大于10 Fig. 5 Various missing number of the Wenchuan earthquake at Manzhouli seismic station are greater than 10 |
由于包含远大于正常值的数值88 888.0和99 999.0,从图 5中无法看出数据走势,该部分数据对于后期数据异常分析并不重要,但对异常时间点分析必不可少,因此本文采用邻域值代替该部分数据(图 6)。邻域代替属于就近代替,其数值差距较小,因此处理后的数据和原始数据相差较小。该处理过程是为了保证地磁序列的时序连贯性,并不会对后续分析产生影响。
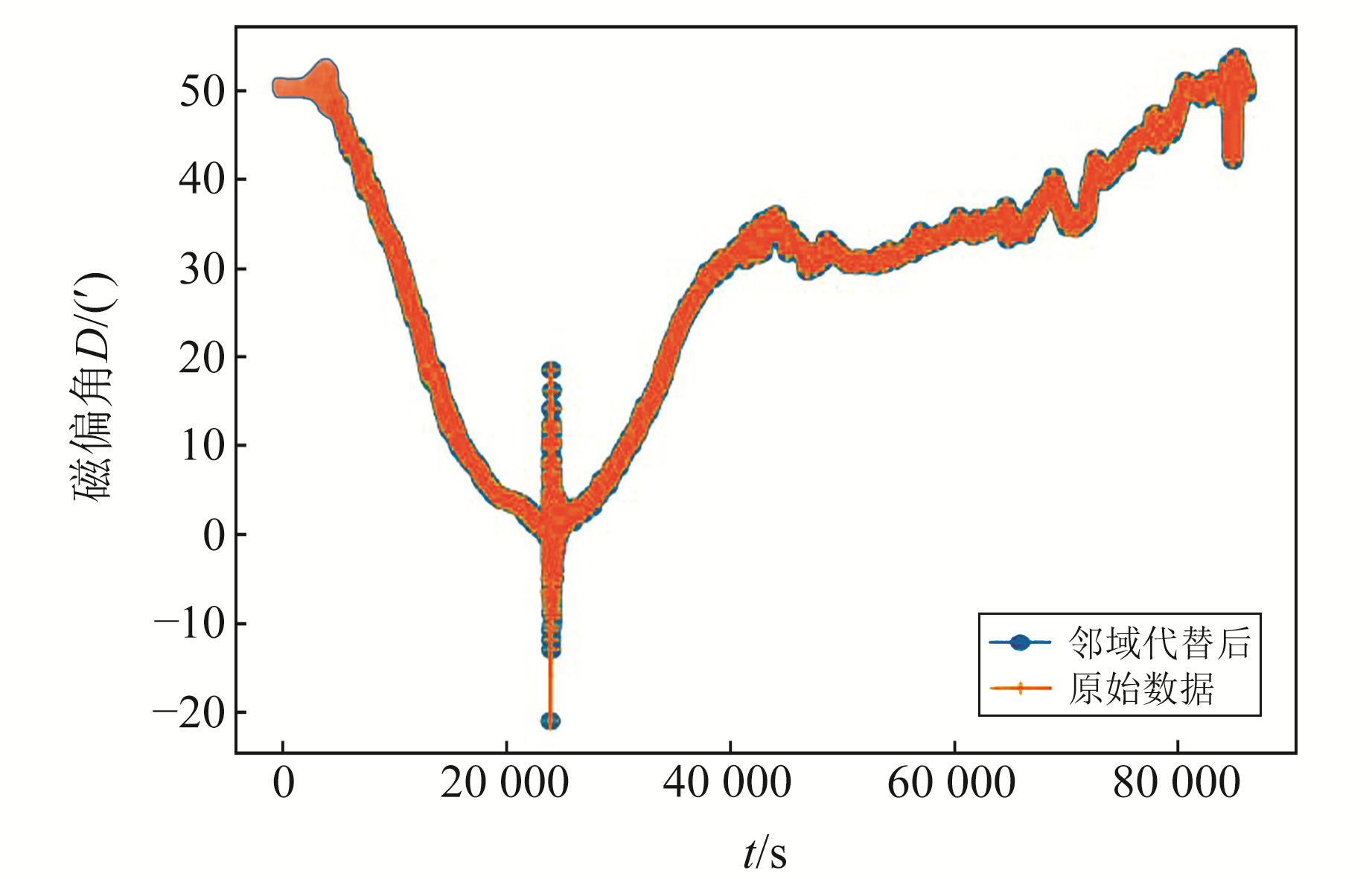
|
图 6 邻域值代替缺失数据拟合图 Fig. 6 Fitting graph of neighborhood values instead of missing data |
为了处理地震仪器记录的非震异常数据,本文将ARMA模型用于数据插值处理,并与均值插值、线性插值的实验效果进行对比分析,得到以下结论:
1) 无论是单点插值还是连续多点插值(2~10个),ARMA模型的插值效果均优于均值插值和线性插值。
2) ARMA模型能够较好地保持实际观测序列的曲线形态,而均值插值和线性插值会改变其形态。
3) 均值插值适用于方差小、稳定性好的数据;线性插值适用于曲线形态较为平坦的序列;ARMA模型适用于规律性变化、干扰较小的序列。
4) ARMA模型属于外插值法,采用该模型进行预测时需要建模,因此与均值插值和线性插值相比耗时较多。由于存在较多的历史数据作为参考,即使在多点缺失情况下,ARMA的预测效果仍高于其他两种方法。
5) ARMA模型有望在电磁学领域数据预处理中发挥作用。
| [1] |
张聪聪. 地震前兆观测数据异常检测方法研究[D]. 北京: 中国地震局地壳应力研究所, 2015 (Zhang Congcong. Research on the Detection Method of Abnormal Observation Data of Earthquake Precursor[D]. Beijing: Institute of Crustal Dynamics, CEA, 2015)
(  0) 0) |
| [2] |
韩凯旋. 地震前兆异常时间序列识别研究[D]. 石家庄: 河北师范大学, 2020 (Han Kaixuan. Research on Time Series Recognition of Earthquake Precursory Anomalies[D]. Shijiazhuang: Hebei Normal University, 2020)
(  0) 0) |
| [3] |
Pigott T D. A Review of Methods for Missing Data[J]. Educational Research and Evaluation, 2001, 7(4): 353-383 DOI:10.1076/edre.7.4.353.8937
(  0) 0) |
| [4] |
Taylor J M G, Cooper K L, Wei J T, et al. Use of Multiple Imputation to Correct for Nonresponse Bias in a Survey of Urologic Symptoms among African-American Men[J]. American Journal of Epidemiology, 2002, 156(8): 774-782
(  0) 0) |
| [5] |
张聪聪, 王秀英. 前兆观测异常数据检测方法研究[J]. 震灾防御技术, 2014, 9(增): 615-621 (Zhang Congcong, Wang Xiuying. Study on the Detecting Method of Abnormal Earthquake Precursor Observation Data[J]. Technology for Earthquake Disaster Prevention, 2014, 9(S): 615-621)
(  0) 0) |
| [6] |
武艳强, 黄立人. 时间序列处理的新插值方法[J]. 大地测量与地球动力学, 2004, 24(4): 43-47 (Wu Yanqiang, Huang Liren. A New Interpolation Method in Time Series Analyzing[J]. Journal of Geodesy and Geodynamics, 2004, 24(4): 43-47)
(  0) 0) |
| [7] |
杨登科. 不同插值方法对GPS时间序列的影响分析[J]. 全球定位系统, 2019, 44(5): 66-69 (Yang Dengke. Influences of Different Interpolation Methods on GPS Time Series[J]. GNSS World of China, 2019, 44(5): 66-69)
(  0) 0) |
| [8] |
毕金孟, 马永, 马朝晖. 徐庄子地震台地磁观测干扰因素剖析[J]. 地震地磁观测与研究, 2020, 41(2): 130-137 (Bi Jinmeng, Ma Yong, Ma Zhaohui. An Analysis of the Disturbance Factors of Geomagnetic Observation at Xuzhuangzi Seismic Station[J]. Seismological and Geomagnetic Observation and Research, 2020, 41(2): 130-137)
(  0) 0) |
| [9] |
Dobrovolsky M, Kudin D, Krasnoperov R. Unified Geomagnetic Database from Different Observation Networks for Geomagnetic Hazard Assessment Tasks[J]. Data Science Journal, 2020, 19(1)
(  0) 0) |
| [10] |
Tong X, Zhou J Q, Liu Z, et al. Analysis of Power Supply Interference of Geomagnetic Second Data Observation—Take Changli Seismic Station as an Example[J]. Earthquake Research in China, 2020, 34(2): 240-254
(  0) 0) |
| [11] |
贾澎涛, 何华灿, 刘丽, 等. 时间序列数据挖掘综述[J]. 计算机应用研究, 2007, 24(11): 15-18 (Jia Pengtao, He Huacan, Liu Li, et al. Overview of Time Series Data Mining[J]. Application Research of Computers, 2007, 24(11): 15-18)
(  0) 0) |
| [12] |
何书元. 应用时间序列分析[M]. 北京: 北京大学出版社, 2003 (He Shuyuan. Applied Time Series Analysis[M]. Beijing: Peking University Press, 2003)
(  0) 0) |
| [13] |
李瑞莹, 康锐. 基于ARMA模型的故障率预测方法研究[J]. 系统工程与电子技术, 2008, 30(8): 1 588-1 591 (Li Ruiying, Kang Rui. Research on Failure Rate Forecasting Method Based on ARMA Model[J]. Systems Engineering and Electronics, 2008, 30(8): 1 588-1 591)
(  0) 0) |
| [14] |
兰华, 廖志民, 赵阳. 基于ARMA模型的光伏电站出力预测[J]. 电测与仪表, 2011, 48(2): 31-35 (Lan Hua, Liao Zhimin, Zhao Yang. ARMA Model of the Solar Power Station Based on Output Prediction[J]. Electrical Measurement and Instrumentation, 2011, 48(2): 31-35)
(  0) 0) |
2. Malipo Ethnic Middle School of Yunnan Province, 193 Wenma Road, Wenshan 663600, China
 2021, Vol. 41
2021, Vol. 41


