2. 中国地质大学(武汉)地球物理与空间信息学院地球内部多尺度成像湖北省重点实验室,武汉市鲁磨路388号,430074;
3. 中国地质大学(武汉)地质过程与矿产资源国家重点实验室,武汉市鲁磨路388号,430074
将标量磁力仪测量的总磁场强度T的大小减去主磁场T0的大小,即可得到总磁场强度异常(ΔT)。在实际数据处理与正反演及定量解释时,往往将ΔT近似为磁力异常矢量Ta在主磁场方向的投影分量Tap[1-3],此时ΔT就和其他分量异常一样,与场源的磁化强度大小呈简单的线性关系,而与主磁场T0无直接关系,并且在场源外部空间满足拉普拉斯方程,从而具备调和性质,进而可以简化其数据处理、正反演与定量解释过程。但当Ta幅值较大时,这种近似将会产生较大误差。针对此误差,部分学者[4-7]分别提出利用实测ΔT数据计算投影分量Tap的最优化方法、等效源方法、迭代方法,并且其理论模型的实验和实际应用均表明,在高磁环境下考虑将ΔT近似为Tap的误差具有必要性。
但上述关于ΔT与Tap之间差异性问题的相关研究均是针对局部磁力异常在笛卡尔直角坐标系中完成,而对于区域乃至全球性中、长波长ΔT与Tap磁力异常之间的差异程度、分布规律及影响因素研究尚未见到相关报道。因此,本文基于全球地磁场球谐模型,从不同波长范围与不同观测高度探讨将ΔT近似为Tap的误差的全球分布特征,旨在为全球岩石圈磁场模型的应用以及基于地面、航空与卫星ΔT数据构建区域乃至全球岩石圈磁力异常场模型提供参考资料。
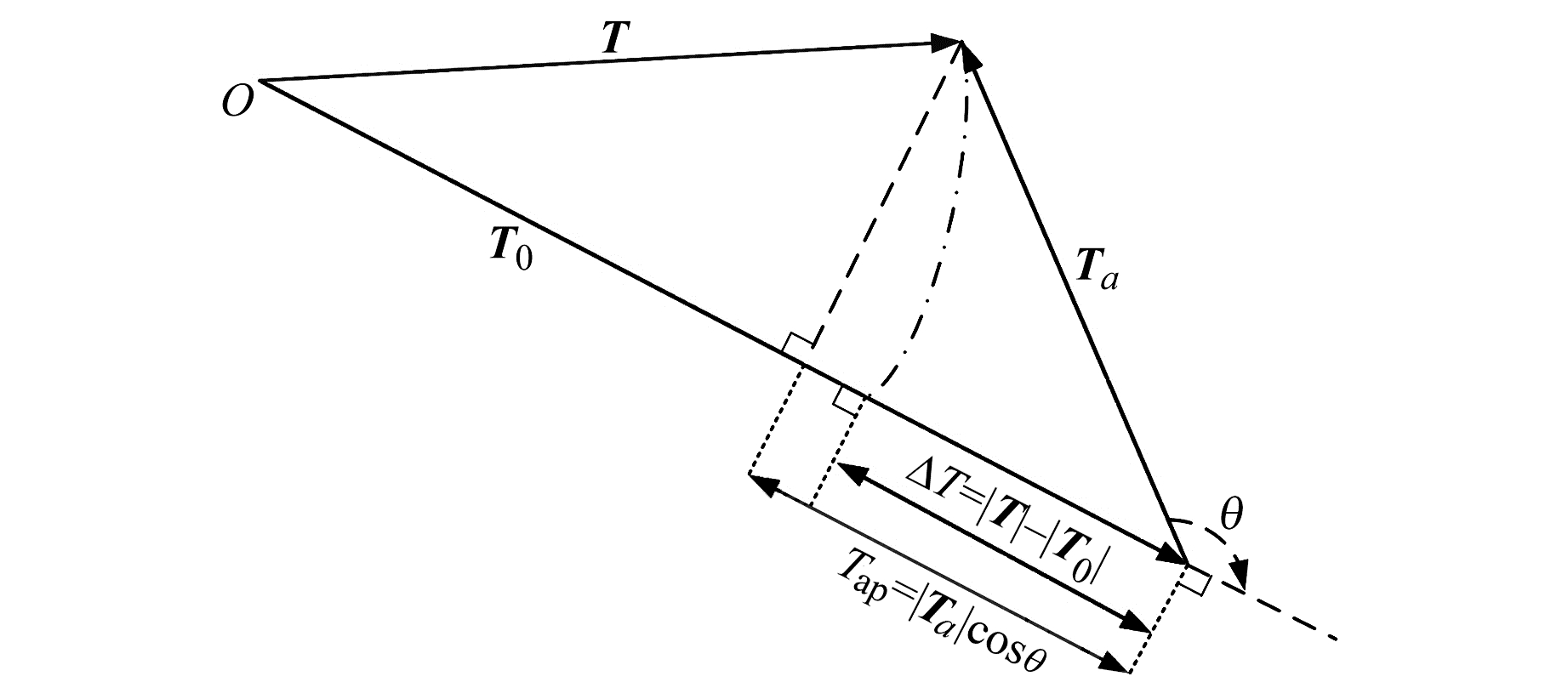
1 ΔT与Tap差异性的理论分析如图 1所示,总磁场强度异常(ΔT)为总磁场强度(T)的大小与主磁场强度(T0)的大小之差,Tap为磁力异常矢量(Ta)在主磁场方向的投影分量,即
| $ \begin{gathered} \Delta T=|\boldsymbol{T}|-\left|\boldsymbol{T}_{0}\right| \end{gathered} $ | (1) |
| $T_{\mathrm{ap}}=\left|\boldsymbol{T}_{a}\right| \cos \theta $ | (2) |
|
图 1 ΔT、Ta与Tap之间的关系示意图 Fig. 1 Relationship diagram between ΔT, Ta and Tap |
式中,θ为T0与Ta之间的夹角,其计算公式为:
| $ \theta=\arccos \frac{\boldsymbol{T}_{0} \cdot \boldsymbol{T}_{a}}{\left|\boldsymbol{T}_{0}\right|\left|\boldsymbol{T}_{a}\right|} $ | (3) |
根据文献[8]理论进行推导,ΔT与Tap之间的差异E为:
| $ E=\Delta T-T_{\mathrm{ap}}=\frac{\left|\boldsymbol{T}_{a}\right|^{2}-(\Delta T)^{2}}{2\left|\boldsymbol{T}_{0}\right|} $ | (4) |
由于ΔT≤|Ta|,因此误差E≥0。分析式(4)可知,当ΔT为0时,误差E达到最大值,即
| $ E_{\max }=\left|\boldsymbol{T}_{a}\right|^{2} /\left(2\left|\boldsymbol{T}_{0}\right|\right) $ | (5) |
此时,|T|与|T0|等长且与|Ta|形成等腰三角形,T0与Ta之间的夹角θ′为:
| $ \theta^{\prime}=\pi-\arccos \frac{\left|\boldsymbol{T}_{a}\right|}{2\left|\boldsymbol{T}_{0}\right|} $ | (6) |
袁晓雨等[8]认为,误差E与测点和场源之间的相对位置密切相关,误差比例最大的测点位于磁力异常矢量Ta接近垂直于主磁场T0的区域,随着Ta值增大,误差按照近似指数关系迅速增大,且误差最大值的极值主要分布在中纬度地区,对应的磁力异常矢量Ta与主磁场T0的夹角主要分布在90°~120°范围内。但上述关于误差E的幅值大小与空间分布特征以及影响因素的部分结论是基于局部平面直角坐标系的理论模型所获得,可能与实际情况存在偏离。另外,对于不同的波长范围与观测高度,误差E的幅值大小及其变化规律是构建与应用全球岩石圈磁场模型的重要因素。因此,需要从实际情况出发,采用全球岩石圈磁场模型研究误差E的幅值大小与空间分布特征以及影响因素。
2 基于全球岩石圈磁场模型的ΔT与Tap及其差异计算方法为分析实际情况下ΔT与Tap之间的差异性特征,本节给出基于全球岩石圈磁场模型计算相关物理量的方法。
主磁场与岩石圈磁场分别起因于地球外核磁流体运动与岩石圈磁性结构,两者共同组成地磁场的内源场,在地球表面及其以上空间,可以将内源场的磁位表示为球谐级数展开形式。根据展开式可以计算球面局部指北直角参考系(x轴指北、y轴指东、z轴指向地心)中的磁场三分量(X、Y与Z),其无奇异性球谐计算表达式参见文献[9]。为避免地球扁率的影响,所有解算点位坐标与参考坐标系分别为基于WGS84参考椭球的大地坐标(大地纬度B、大地经度L、大地高度H)与椭球面局部指北坐标系,坐标与矢量旋转方法参见文献[10]。
根据地磁场的球谐能量谱特征[11],一般将地磁场球谐展开式中1~15阶作为主磁场,而将16阶及其以上部分作为岩石圈磁场。因此,将相应阶数范围的球谐系数代入球谐表达式中,可计算出主磁场三分量(X0、Y0与Z0)、岩石圈磁场三分量(ΔX、ΔY与ΔZ)与总磁场三分量(X、Y与Z),进而可得到| T |、|T0|、ΔT、|Ta|、Tap:
| $ \begin{gathered} |\boldsymbol{T}|=\sqrt{X^{2}+Y^{2}+Z^{2}} \end{gathered} $ | (7a) |
| $ \left|\boldsymbol{T}_{0}\right|=\sqrt{X_{0}^{2}+Y_{0}^{2}+Z_{0}^{2}} $ | (7b) |
| $ \Delta T=\sqrt{X^{2}+Y^{2}+Z^{2}}-\sqrt{X_{0}^{2}+Y_{0}^{2}+Z_{0}^{2}} $ | (7c) |
| $ \begin{gathered} \left|\boldsymbol{T}_{a}\right|=\sqrt{\Delta X^{2}+\Delta Y^{2}+\Delta Z^{2}} \end{gathered} $ | (7d) |
| $ T_{\mathrm{ap}}=\Delta X \frac{X_{0}}{T_{0}}+\Delta Y \frac{Y_{0}}{T_{0}}+\Delta Z \frac{Z_{0}}{T_{0}} $ | (7e) |
将式(7)代入式(4)与式(5)即可分别得到将ΔT近似为Tap的误差E与最大误差Emax,将式(7)代入式(3)即可得到T0与Ta之间的夹角θ为:
| $ \theta=\arccos \frac{X \cdot \Delta X+Y \cdot \Delta Y+Z \cdot \Delta Z}{\left|\boldsymbol{T}_{0} \boldsymbol{T}_{a}\right|} $ | (8) |
采用EMM2017地磁场模型计算与分析实际情况下ΔT与Tap之间的差异性特征。该模型由最新的EMAG2v3[12]全球总磁场强度异常2′×2′网格数据通过球谐展开获得,最高展开阶数达790阶次,同时包含2000~2022年期间1~15阶主磁场及其长期变化。因此,采用该模型1~15阶、16~790阶分别作为主磁场与岩石圈磁场。
3.1 ΔT与Tap之间差异的大小与分布特征首先采用EMM2017(16~790阶)计算得到参考椭球面上的总磁场强度异常(ΔT)、ΔT与Tap之差(图 2))。从图中可以看出,ΔT与Tap之差均为非负值,说明ΔT≥Tap,这与理论分析结论一致。此外,该差异在全球大部分地区均低于2 nT,仅在部分区域存在较大值。

|
图 2 ΔT及其与Tap之间的差异分布 Fig. 2 Distribution of ΔT and its difference with Tap |
由表 1可以看出,对于参考椭球面与5 km高度面上16~790阶的岩石圈磁场,该差异的最大值分别可达248.5 nT与120.2 nT。由于目前地面与航空磁测的精度均远高于该差异,因此在图 2(b)所示差异性较大地区的实际地面与航空ΔT数据处理、正演与反演时不能忽略该差异。此外,随着全球岩石圈磁场模型展开阶数的增高与计算高度的降低,ΔT与Tap之差的差异性会更加显著,这说明在构建或应用高阶全球岩石圈磁场模型时需要考虑该差异,但对于卫星高度的ΔT磁力异常数据则无需考虑。
|
|
表 1 ΔT、Tap及两者之间的差异 Tab. 1 ΔT, Tap and their differences |
由式(4)可知,误差E与|T0|、|Ta|和ΔT均存在关系。图 3(a)与3(b)分别为采用EMM2017解算参考椭球面上的磁力异常模量|Ta|(16~790阶)与主磁场强度模量之倒数(1/|T0|)(1~15阶)。对比图 2(b)与图 3可以明显看出,误差E主要受|Ta|大小影响,而受主磁场强度|T0|影响很弱,并且误差E未表现出随纬度而变化的分布特征。

|
图 3 |Ta|与1/|T0|分布 Fig. 3 Distribution of |Ta| and 1/|T0| |
图 4(a)为误差E(≥2.0 nT)与|Ta|2之间的统计关系图,从图中可以看出,在整体趋势上误差E与|Ta|2近似满足线性关系(蓝色虚线)。图 4(b)为E(≥2.0 nT)与|Ta|2/2|T0|之间的统计关系图,从图中可以看出,采用式(5)计算的误差E确实为误差最大值Emax(红色虚线)。对比图 4(a)与4(b)也可以看出,误差E受主磁场强度T0影响很弱,而图中偏离直线的点受ΔT大小影响。进一步基于图 2和图 3中ΔT、|Ta|与误差E之间空间分布的相关性可知,误差E受|Ta|影响最大、ΔT次之、|T0|最弱。

|
图 4 误差E与|Ta|2、|Ta|2/2|T0|的统计关系 Fig. 4 Statistical correlations between the error E and |Ta|2, | Ta|2/2|T0| |
根据式(5),采用EMM2017地磁场模型(16~790阶)计算得到Emax分布,结果如图 5(a)所示。对比图 5(a)与图 2(b)可以看出,两者在空间分布上具有较好的一致性,两者差异见图 5(b)。从图中可以看出,Emax幅度大于实际误差,因此采用式(5)计算E会过高估计误差,但计算得到的结果一方面可以作为误差估计的上限,另一方面可以用于判断误差较大的区域。

|
图 5 Emax及其与实际误差E之间的差异分布 Fig. 5 Distribution of Emax and its difference with E |
从式(4)也可以看出,在将Tap近似为实际ΔT数据进行磁力异常三分量与模量转换处理时,为减小误差E,可以引入Ta趋近于ΔT的约束条件。通过表 1也可以看出,在统计意义上,|Ta|与ΔT的幅值比较接近,但这仅对磁力异常矢量的大小进行约束,并未约束其矢量方向,因此后文将分析误差E与磁力异常矢量Ta方向之间的关系。
根据式(8),采用EMM2017地磁场模型计算得到θ分布,结果如图 6(a)所示。对比图 6(a)与图 2(b)可以看出,误差E与夹角θ无相关性。根据式(6),采用EMM2017地磁场模型计算得到θ′分布,结果如图 6(b)所示,从图中可以看出,误差E与夹角θ′具有明显的对应关系,即当E较小时,θ′接近90°;而当E较大时,θ′逐渐增大(本次计算中夹角θ′未超过95°)。由式(6)可知,θ′受控于磁力异常模量|Ta|与主磁场强度模量|T0|之比值,这说明在对总磁场强度异常数据ΔT进行转换处理或磁场建模时,为减小将Tap近似为ΔT的误差,可以对磁力异常矢量的方向进行约束,即要求磁力异常矢量与主磁场垂直的分量的幅度较小。这点从图 1也可以看出,即欲使误差E最小,则要求磁力异常矢量Ta与主磁场T0方向平行。

|
图 6 T0与Ta之间的夹角θ分布以及当ΔT为0时T0与Ta之间的夹角θ′分布 Fig. 6 Distribution of angle θ between T0 and Ta and angle θ′ between T0 and Ta when ΔT is zero |
Lesur等[13]在利用全球总磁场强度异常汇编ΔT数据反演岩石圈磁场球谐模型系数时采用了上述磁力异常矢量的方向约束,并且认为引入该约束是为压制Backus效应[14]。但根据上述分析,本文认为该约束应该是为减小将Tap近似为ΔT的误差,而非压制Backus效应。实际上,所谓Backus效应,即由标量磁场值反演磁场矢量具有多解性;而Tap方向即主磁场方向,为磁力异常矢量在主磁场方向的投影。因此,Backus效应和Tap与ΔT的差异性为两个不同的问题。现今根据ΔT可以精确计算Tap[4-7],因此在利用总磁场强度异常ΔT数据反演构建岩石圈磁场模型时,无需引入磁力异常矢量的大小或方向约束。
4 结语本文采用全球地磁场模型EMM2017分别计算得到不同波长范围和不同高度的ΔT与Tap及两者差异E的全球分布,进而分析该差异的幅值大小与空间分布特征以及影响差异性的因素,得到以下结论:
1) 对不同波长范围与不同高度情况下误差E的幅值大小与空间分布特征进行分析,可为构建与应用岩石圈磁场模型时是否需要考虑ΔT与Tap之间的差异性提供判断依据。
2) 在实际情况下,误差E受|Ta|影响最大、ΔT次之、|T0|最弱,并且误差E未表现出随纬度而变化的分布特征,与T0和Ta之间的夹角也无相关性。
3) 为压制ΔT与Tap之间的差异性,可以引入|Ta|趋近于ΔT的约束条件,也可以将磁力异常矢量与主磁场垂直分量的幅度最小化作为约束,但目前研究表明,无论是等效源方法、最优化方法还是迭代方法均能够基于ΔT精确计算Tap,因此在利用总磁场强度异常ΔT数据反演构建岩石圈磁场模型时,无需对磁力异常矢量的大小或方向进行约束。
致谢: EMM2017全球地磁场模型来源于https://www.ngdc.noaa.gov/geomag/EMM/,在此表示衷心感谢!
| [1] |
Blakely R J. Potential Theory in Gravity and Magnetic Applications[M]. Cambridge: Cambridge University Press, 1995
(  0) 0) |
| [2] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005 (Guan Zhining. Geomagnetic Field and Magnetic Exploration[M]. Beijing: Geological Publishing House, 2005)
(  0) 0) |
| [3] |
Hinze W J, Frese R R B, Saad A H. Gravity and Magnetic Exploration: Principles, Practices, and Applications[M]. Cambridge: Cambridge University Press, 2013
(  0) 0) |
| [4] |
Zhen H X, Li Y Y, Yang Y S. Transformation from Total-Field Magnetic Anomaly to the Projection of the Anomalous Vector onto the Normal Geomagnetic Field Based on an Optimization Method[J]. Geophysics, 2019, 84(5): J43-J55 DOI:10.1190/geo2018-0671.1
(  0) 0) |
| [5] |
孙石达, 杜劲松, 陈超, 等. 基于等效源的总强度磁异常非线性处理方法[J]. 地球物理学报, 2020, 63(1): 351-361 (Sun Shida, Du Jinsong, Chen Chao, et al. Nonlinear Equivalent Source Method for Transformation and Inversion of Total-Field Magnetic Anomaly[J]. Chinese Journal of Geophysics, 2020, 63(1): 351-361)
(  0) 0) |
| [6] |
Yang J H, Liu S, Hu X Y. Inversion of High-Amplitude Magnetic Total Field Anomaly: An Application to the Mengku Iron-Ore Deposit, Northwest China[J]. Scientific Reports, 2020, 10(1)
(  0) 0) |
| [7] |
胡正旺, 杜劲松, 孙石达, 等. 基于磁异常ΔT计算投影分量ΔTPro的迭代算法[J]. 石油地球物理勘探, 2021, 56(3): 645-658 (Hu Zhengwang, Du Jinsong, Sun Shida, et al. An Iterative Algorithm for Calculating Component ΔTPro from Magnetic Anomaly ΔT[J]. Oil Geophysical Prospecting, 2021, 56(3): 645-658)
(  0) 0) |
| [8] |
袁晓雨, 姚长利, 郑元满, 等. 强磁性体ΔT异常计算的误差分析研究[J]. 地球物理学报, 2015, 58(12): 4 756-4 765 (Yuan Xiaoyu, Yao Changli, Zheng Yuanman, et al. Error Analysis of Calculation of Total Field Anomaly Due to Highly Magnetic Bodies[J]. Chinese Journal of Geophysics, 2015, 58(12): 4 756-4 765)
(  0) 0) |
| [9] |
Du J S, Chen C, Lesur V, et al. Non-Singular Spherical Harmonic Expressions of Geomagnetic Vector and Gradient Tensor Fields in the Local North-Oriented Reference Frame[J]. Geoscientific Model Development, 2015, 8(7): 1 979-1 990 DOI:10.5194/gmd-8-1979-2015
(  0) 0) |
| [10] |
胡正旺, 杜劲松, 陈超. 大地水准面起伏对国际地磁参考场计算的间接影响[J]. 大地测量与地球动力学, 2018, 38(3): 260-262 (Hu Zhengwang, Du Jinsong, Chen Chao. Indirect Impact of Geoid Undulation on Calculation of International Geomagnetic Reference Field[J]. Journal of Geodesy and Geodynamics, 2018, 38(3): 260-262)
(  0) 0) |
| [11] |
Lowes F J. Mean-Square Values on Sphere of Spherical Harmonic Vector Fields[J]. Journal of Geophysical Research, 1966, 71(8): 2 179 DOI:10.1029/JZ071i008p02179
(  0) 0) |
| [12] |
Meyer B, Chulliat A, Saltus R. Derivation and Error Analysis of the Earth Magnetic Anomaly Grid at 2 Arc Min Resolution Version 3(EMAG2v3)[J]. Geochemistry, Geophysics, Geosystems, 2017, 18(12): 4
(  0) 0) |
| [13] |
Lesur V, Hamoudi M, Choi Y, et al. Building the Second Version of the World Digital Magnetic Anomaly Map(WDMAM)[J]. Earth, Planets and Space, 2016, 68(1)
(  0) 0) |
| [14] |
Backus G E. Non-Uniqueness of the External Geomagnetic Field Determined by Surface Intensity Measurements[J]. Journal of Geophysical Research, 1970, 75(31): 6 339-6 341 DOI:10.1029/JA075i031p06339
(  0) 0) |
2. Hubei Subsurface Multi-Scale Imaging Key Laboratory, Institute of Geophysics and Geomatics, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China;
3. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China
 2021, Vol. 41
2021, Vol. 41


