2. 中国科学技术大学地球和空间科学学院,合肥市金寨路96号,230026;
3. 中南大学地球科学与信息物理学院,长沙市麓山南路932号,410083
地球重力场是地球内部、地表及外部空间物质分布与地球本身旋转运动信息的综合反映,其一般随空间、时间不同而发生变化。地震孕育与发生过程中伴随着地壳形变和质量迁移,在地表或外部空间引起相关重力变化,因此地球重力场时间变化观测是地震监测研究的重要手段之一。
1966年邢台地震之后,我国重力监测工作经过数十年的建设与完善,逐步形成由86个连续重力台(秒或分钟采样)、105个绝对重力点、约4 000个相对重力点组成的中国地震重力监测网(图 1),对我国中长期强震预测具有重要作用[1]。

|
图 1 中国地震重力监测网 Fig. 1 Gravity monitoring network of China |
中国大陆重力时变监测已经历3个主要发展阶段。第1阶段为1966~1997年,称为局域观测阶段。由于缺乏高精度绝对观测,该阶段以相对观测或测量为主,重力仪均采用弹簧式。第2阶段为1998~2009年,称为中国大陆观测阶段。由于引进高精度绝对观测,可初步实现中国大陆的联网观测。第3阶段为2010年至今,称为中国大陆整体观测阶段。该期间已开展华北、南北带等区域测网的整合与统一,形成了一定规模的中国大陆整体重力观测网(图 1),遵循“边观测、边预报、边研究”的基本策略,通过总结获得强震前典型重力变化图像,并对一系列6.0级以上地震进行了较为成功的中期预测[1-3]。
1966~1997年期间,在华北、南北地震带和部分构造活动带的局部区域,通过多年重复测量[4-5],总结得到一些有意义的、反映与孕震相关的部分“前兆”信息。海城地震前,震中西侧盖县点-东荒地测段重力变化较大[6],出现了可靠的重力变化前兆信息;唐山地震前,重力加速演变过程显著[7]。通过研究滇西实验场重力网资料,初步得到包括丽江7.0级等地震孕育过程的相关信息[8-10],发现地震往往发生在正、负异常区变换带的零线附近[8]。丽江地震前,震中南部的滇西实验场网存在近南北向的正负变换梯度带[1](图 2(a)),而震中北部缺乏测网,造成该梯度带观测不完整。在潮汐与地震相关性方面,主要开展固体潮触发机制研究[11]。如松潘7.2级地震前半年潮汐因子表现为显著低值,可能与区域介质密度降低或弹性模量变化有关[12]。

|
图 2 7次强震前典型重力变化 Fig. 2 Typical gravity changes before 7 strong earthquakes |
1998~2009年期间,绝对控制测量的引入开启了中国大陆联网观测时代,全国流动重力观测成果在地震会商中崭露头角。该阶段对汶川地震进行了一定程度的中期预测[2],震例分析认为其与震前重力梯度带密切相关[13-14]。利用区域网资料,对部分5~6级地震进行了较好的中期预报,如2000-06-06景泰5.9级地震[15],并对2001年昆仑山口西8.1级地震相关重力变化进行了总结[16-17]。
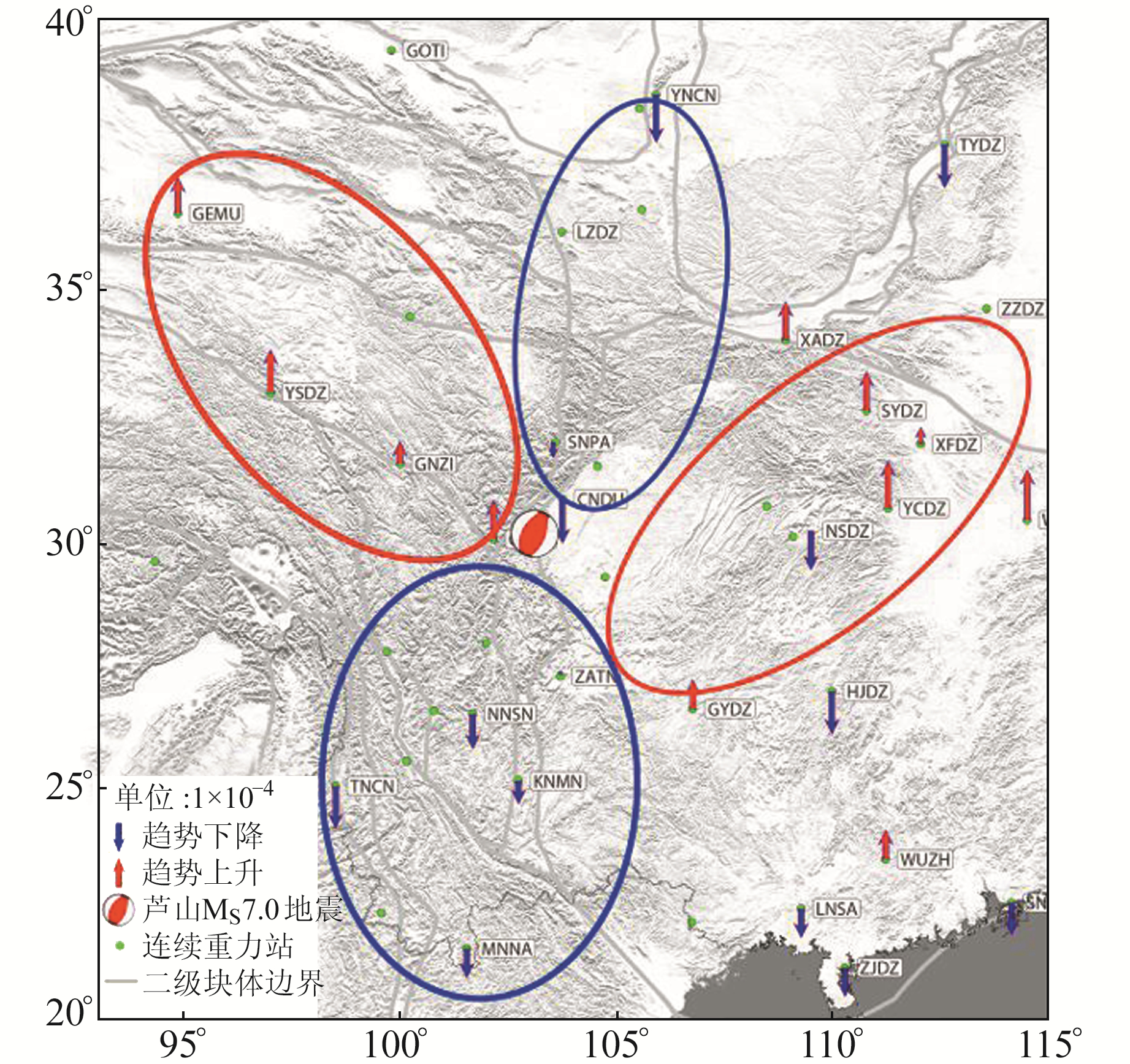
2010年至今,随着区域网与中国大陆联测网的逐步整合,重力测量成果在地震形势判定和年度地震会商中发挥着重要作用。姚安6.0级、芦山7.0级、门源6.4级、呼图壁6.2级、九寨沟7.0级地震等均在震前进行了较好的中期预测,其中,首次发现姚安地震前半年差分变化图像存在以震中为中心的四象限图像(图 2(b)),这与震源机制解具有一致性,由此提出闭锁剪力模式及其数值研究[3, 18]。震例检验表明[19],震前重力梯度变化和四象限特征(图 2)已成为中期地震危险的基本判据与指标[20]。芦山地震前1个月,区域潮汐因子趋势变化呈四象限分布(图 3),地震发生在四象限中心附近,可用闭锁剪力模式进行解释[21],即震前震源区双力偶闭锁剪力的持续作用可能造成区域介质参数(变形或质量规则迁移)扰动,进而引起潮汐因子规则扰动。
|
图 3 芦山地震前M2波潮汐因子变化趋势空间分布 Fig. 3 Spatial distribution of variation trend of M2 wave tidal factor before the Lushan earthquake |
近年来利用震例经验对一系列M6.0以上地震进行了较为成功的中期预测[1, 20, 22]。利用中国大陆重力观测网进行地震监测预报实践表明,强震前展现的具有预报意义的重力变化分布梯度带或四象限展布特征可称为典型重力变化。表 1为具有代表性的7次强震的典型重力变化,从表中可以看出,震前典型重力变化特征与震前观测时段、测网点位空间分布、变化幅值空间差异(数据处理成果、插值成图技术)等密切相关。但由于震例有限,很难得到典型重力变化特征的定量表述或规律。因此,在利用重力场动态图像进行地震预测时,采用震例经验总结的地震预测指标[20, 22]在指导震级或地点预测时往往具有较大的不确定性。值得注意的是,芦山地震前潮汐因子变化趋势也呈现正负四象限分布特征,且异常空间范围是流动重力动态变化异常范围的近10倍,可能是因为连续重力观测站的精度比流动重力联测高1个数量级。而潮汐因子主要与地球介质弹性参数变化相关,这正好也说明震前在来自NW向的推覆或剪切力持续作用下不仅能造成区域质量迁移,也能造成介质弹性参数的变化或扰动。从这方面来说,重力变化梯度带、四象限和潮汐因子变化四象限分布在力源上具有统一性,仅在表现形式上有所差异。
|
|
表 1 强震前典型重力场变化特征参数 Tab. 1 The characteristic parameters of typical gravity changes before strong earthquakes |
现代地震学理论认为,构造型地震源于地壳深处,介质应力应变能量积累到一定程度会造成剪切破裂,震源破裂可用双力偶模型进行表示,但震前是否一直存在双力偶机制仍未获证实。
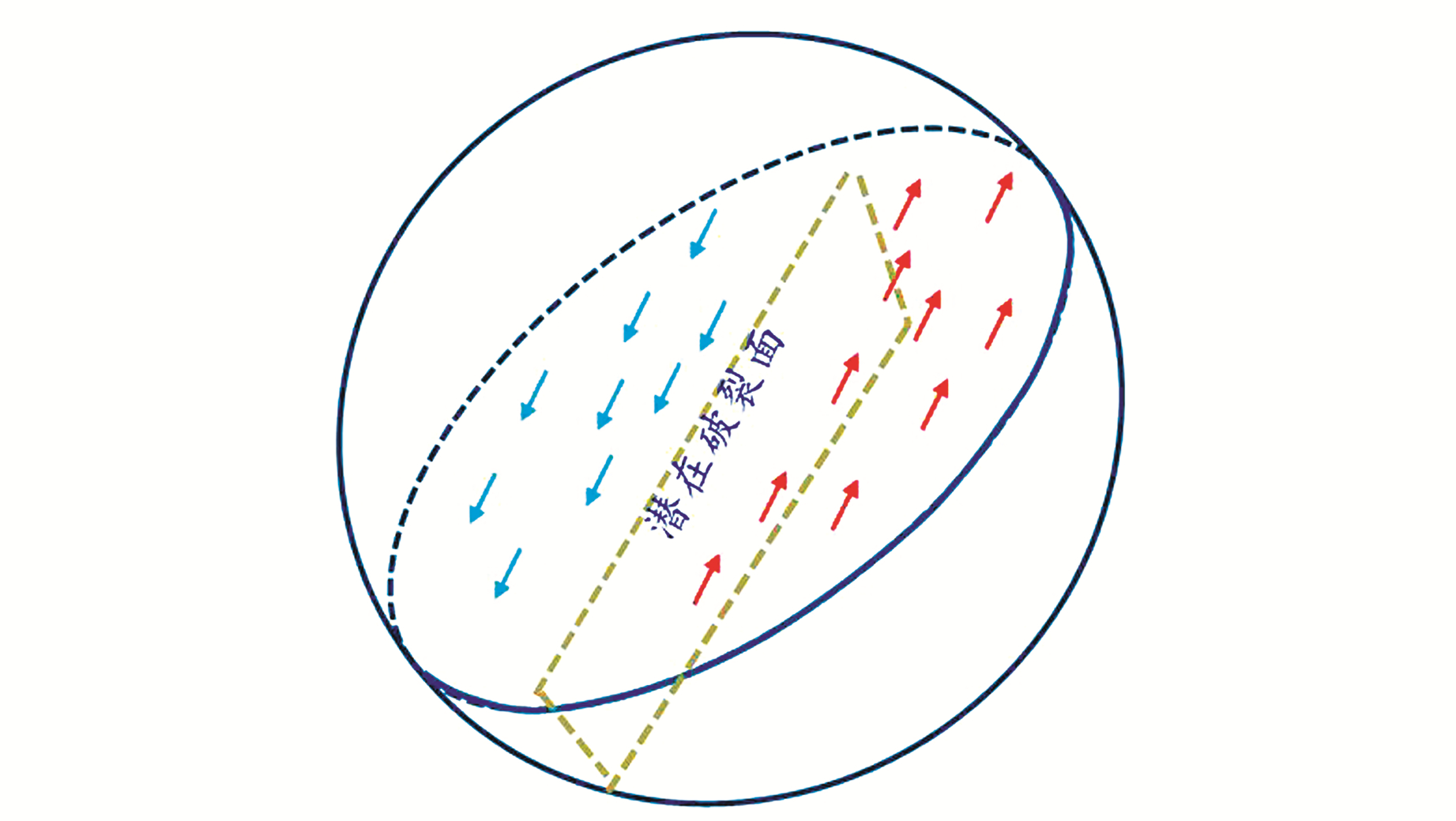
闭锁剪力模式[3]认为,地震破裂前震源孕育区存在闭锁剪力,孕震源区在外围动力作用下存在一定大小、优势方向明显的剪应力及在其作用下形成的与之关联的剪应变;由于该优势剪应力及其剪应变未超过岩体破裂阈值,震前(临震)孕震源区处于“闭锁”或相对稳定状态。该认识与目前以追踪应力应变积累(即能量)进行地震预测的传统思路不同,或许可为地震震源追踪与预测提供新的思考方向或途径。闭锁剪力的演化发展决定了地震破裂是否发生以及发生后的震级、破裂性质与规模。如何构造闭锁剪力或获取相关信息是地震数值预测的关键,“闭锁剪力”模型可用孕震源椭球进行描述(图 4):
|
图 4 孕震源椭球简化示意图 Fig. 4 Simplified diagram of seismogenic source ellipsoid |
1) 孕震源椭球表示闭锁剪力的作用范围,闭锁剪力具有双力偶特征,长轴与较大闭锁剪力的一组中心线一致,最大椭圆截面为其中心面;短轴与另一组闭锁剪力的中心线一致,最小椭圆截面为其中心面。
2) 孕震源能力的大小拟采用孕震矩或相应的矩震级进行表示。定量地震学理论表明,构造性震源可用双力偶模型来表示,弹性介质的双力偶震源中剪力与位错具有等效性[23],地震矩ME可表示为ME=μEAEUE,式中,μE为破裂时岩石剪切模量,AE为破裂面积,UE为破裂位移(即位错),该力矩称为“破裂矩”。为此将这些概念推广到孕震情形,闭锁剪力的力矩ML(称为“孕震矩”)也可表示成类似形式:ML=μLALUL,此时μL为孕震时岩石剪切模量,AL为孕震剪力面积(最大椭圆截面面积),UL为等效位移。由于孕震时震源处于闭锁状态(尽管存在剪力),等效位移UL实际不存在。假设在闭锁剪力作用下,孕震源及其周围物质会产生相应的变形或迁移运动,孕震源附近的重力场也将发生变化,比如前述强震前观测到的典型重力变化。因此,可将孕震区中存在的“闭锁剪力”视为“等效位错”,“剪力闭锁”效应引起的重力变化也可视作由此“等效位错”所产生,则孕震区中闭锁剪力的计算问题可转化为计算弹性介质中相应的“地震位错”,从而可用ML来评估孕震能力的大小。与孕震矩对应的矩震级换算可采用地震矩公式[24]MW=
3) 参考同震位错理论结果[25],强震前在孕震源存在的双力偶闭锁剪力的持续作用下,走滑型力偶会在地表引起四象限重力变化,倾滑型力偶会在地表引起二象限(梯度带)重力变化。
2.2 孕震源参数确定根据闭锁剪力模式,利用定量地震学震源理论,构建地震孕育发生的统一“剪力”模型,并借鉴位错理论[25]计算等效位错(U1, U2, U3)引起的地表重力变化Δg:
| $ $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta g\left( {{x_1}, {x_2}} \right) = \\ f\left( {{x_1}, {x_2}, 0;{U_1}, {U_2}, {U_3}, L, W, {\rm{dep}}, \delta , \varphi , X, Y} \right) = \\ \;\;\rho G\left[ {{U_1}{S_g}\left( {\xi , \eta } \right) + {U_2}{D_g}\left( {\xi , \eta } \right) + {U_3}{T_g}\left( {\xi , \eta } \right)} \right] \end{array}$ $ |
式中,U1、U2、U3分别为等效位错的走滑、倾滑和拉张分量;x1和x2为地表观测点;L、W、dep、δ、φ、X、Y分别为等效矩形位错面的长度、宽度、顶部埋深、倾角、走向方位角及地表投影的中心水平x、y分量坐标,即等效位错的几何分量;参量的具体含义可参见文献[18, 25]。
上式也是基于典型重力变化反演等效位错的正演模型。等效位错的几何分量可由典型重力变化特征来确定,黄浩哲等[18]给出走滑型等效位错几何分量的确定方法,倾滑型等效位错几何分量的确定方法也类似。等效位错几何分量确定后,即可利用该式选择适当方法反演等效位错量U1、U2、U3。考虑到地表观测的典型重力变化往往受到各种观测噪声干扰及剪力模型偏离的影响,反演方法可选择具有抗差的稳健-贝叶斯最小二乘算法[10, 18]。
2.3 算例实验通过震例总结发现,强震前典型重力场变化表现为正负四象限(如2009年姚安MS6.0、2013年芦山MS7.0潮汐因子、2016年门源MS6.4和呼图壁MS6.2地震)或高梯度带分布(如1996年丽江MS7.0、2008年汶川MS8.0、2013年芦山MS7.0和2017年九寨沟MS7.0地震),分别对应走滑型和倾滑型地震。本文基于这两种典型重力场变化,利用上述闭锁剪力模式定量反演计算孕震源的各种参数。
2.3.1 走滑型算例以2009年姚安MS6.0地震为例进行计算。根据地表重力变化与地震断层几何尺寸的关系[18, 26],“等效位错”长度L为“等效位错”一侧的正负极值点之间的距离,如图 2(b)中L为58.1 km;宽度W根据断层长宽比经验关系[27]取29.05 km;“等效位错”位置(X, Y)位于震前重力变化四象限图形的对称中心(100.94°E,25.51°N);走向φ为西侧正极值点与南侧负极值点之间连线与正北方向的夹角313.6°;倾角δ与孕震源两侧重力变化极值之间的比值密切相关,通过模拟分析比值0.769 2对应δ为84.8°;埋深dep与关于孕震源两侧对称的正负极值点之间的距离和同侧正负极值点之间距离的比值密切相关,通过模拟分析比值1.989 6对应dep为13.5 km。
基于表 2给出的孕震源几何参数,利用稳健-贝叶斯最小二乘反演算法,对姚安地震前2008-10~2009-02地表重力变化进行反演,得到孕震源“等效位错”的力学参数(表 3)。由反演的模型参数计算其对应的孕震能量为M=μ A=8.11×1017N ·m (其中μ取3×1010Pa),对应矩震级为MW5.9,比美国USGS给出的震级MW5.7稍大;震中位置与USGS给出的结果(101.105°E, 25.55°N)基本一致,说明该方法对走滑型地震震中位置以及震级的预估较为准确。
|
|
表 2 姚安MS6.0地震前孕震源“等效位错”的主要几何参数 Tab. 2 The main geometric parameters of the "equivalent dislocation" of the seismogenic source before the Yao'an MS6.0 earthquake |
|
|
表 3 姚安MS6.0地震孕震源力学参数反演结果 Tab. 3 The inversion results of the seismogenic source mechanical parameters of the Yao'an MS6.0 earthquake |
以2008年汶川MS8.0地震为例进行计算。同样根据地表重力变化特征(图 2(d))取梯度带长度580 km作为“等效位错”L值,宽度W为290 km;“等效位错”位置(X, Y)位于梯度带正负转换处的中心位置(104.2°E,30.1°N);走向φ为梯度带与正北方向的夹角310°;倾角δ与孕震源两侧重力变化极值之间的比值密切相关,通过模拟分析比值0.864对应δ为87°;埋深dep与孕震源两侧正负极值点之间的距离和“等效位错”长度之间的比值密切相关,通过模拟分析比值2.08对应dep为14 km。
基于表 4给出的孕震源几何参数,对汶川地震前1998~2007年地表重力变化进行反演,获得孕震源“等效位错”的力学参数(表 5)。由反演的模型参数计算其对应的孕震能量为M=μUA=1.32×1021N ·m (其中μ取3×1010Pa),对应矩震级为MW8.02,比美国USGS给出的震级MW7.9稍大,说明地震孕育的能量在主震时未完全释放,导致后续余震较多。震源位置与USGS给出的结果(103.24°E,31.0°N)相差约110 km,这可能与震源的表示方式不同有关。本文给出的位置为震源的几何中心,而USGS给出的震中为震源初始破裂位置,且汶川地震主要表现为单侧破裂,起始破裂位置与断层中心位置不一致。整体来看,该方法对倾滑型地震震中位置以及震级的预估也较为准确。
|
|
表 4 汶川MS8.0地震前孕震源“等效位错”的主要几何参数 Tab. 4 The main geometric parameters of the "equivalent dislocation" of the seismogenic source before the Wenchuan MS8.0 earthquake |
|
|
表 5 汶川MS8.0地震孕震源力学参数反演结果 Tab. 5 The inversion results of the seismogenic source mechanical parameters of the Wenchuan MS8.0 earthquake |
1) 重力变化与地震孕育。地震孕育与发生过程伴随着地壳形变和质量迁移变化,从而会在地表或外部空间引起相关重力变化,因此可利用地表观测的重力变化来研究地震孕育过程。早期研究受到重力测网分辨率及网形限制,主要是通过震源附近单点或测线的重力变化来研究震源,能粗略得到地震孕育的重力加速过程[6-7]。随着重力观测精度的提高、绝对重力仪的引进以及测网网形的优化,可以从面上更精细地了解地震孕育的重力场变化信息。部分学者[1, 4, 20, 22]通过震例总结给出典型强震前的重力变化特征(表 1):重力变化正负四象限分布、高梯度带、潮汐参数正负四象限分布以及重力变化量值与震级大小对应关系等。这些研究对认识地震孕育与发生过程发挥着重要作用,但以此作为地震预测指标具有一定的不确定性:流动重力变化与测网观测时段、测点空间分布、变化幅值空间差异等具有密切关系;潮汐因子异常空间范围是流动重力典型变化范围的近10倍。目前在“以场求源”的道路上仍然处于场源经验关系中,急需合适的物理模型向场源物理关系迈进。
2) 地震孕育的闭锁剪力模式。基于重力变化,部分学者曾提出多种地震孕育模式,如扩容膨胀模式[28]、形变与质量迁移模式[29]和震质中模式[30]等,这些模型分别能在一些地震解释中起到很好的效果,但很难适用于所有地震。为解释姚安6.0级地震震前出现的重力场四象限图像,申重阳等[3]定性提出闭锁剪力模式,认为震源孕育区存在闭锁剪力和在其作用下形成的与之关联的剪应变,且在未超过岩体破裂阈值前处于闭锁或相对稳定状态。本文进一步细化闭锁剪力模式的双力偶特性,并参考位错理论给出其等效位错的表现形式和数值计算方式,提出利用典型重力变化图像进行地震数值预测的方法。强震前在孕震源存在的双力偶闭锁剪力的持续作用下,走滑型力偶会在地表引起四象限重力变化,倾滑型力偶会在地表引起二象限(梯度带)重力变化,定量建立了震前重力变化与孕震源之间的关系。
3) 闭锁剪力模式的映震效果。基于闭锁剪力模式的等效位错表示方式,本文分别对震前走滑型四象限重力变化图像和倾滑型二象限高梯度带重力变化图像进行建模和反演,得到孕震源的主要参数。从结果来看,对于走滑型的姚安MS6.0地震,孕震源位置和能量大小的预估均较为准确;破裂走向的预估结果与震源机制解结果存在约20°的差异,这可能主要与测点分布不均及测点间距(80~100 km)较大导致重力变化图像绘制出现偏转有关。对于倾滑型的汶川MS8.0地震,预估的震级比USGS给出的结果稍大,说明地震孕育的能量在主震时未完全释放;震源位置与USGS给出的结果相差约1°,这可能与震中的表示方式不同有关(本文为预估震源的几何中心,而其他研究结果为震源初始破裂位置);预估的破裂走向与USGS震源机制解结果(202°)相差108°,两者走向近乎垂直,说明倾滑型孕震源的实际破裂走向有可能为共轭双力偶模型中的另外一对。
上述分析表明,基于闭锁剪力模式的数值预估方法对走滑型和倾滑型地震的震级预测较为有效,同时可给出未来地震的地点和类型,可作为地震危险性分析和强震预测的有效手段。
致谢: 十分感谢众多重力观测研究人员长期的坚持不懈与艰苦努力。
| [1] |
申重阳, 祝意青, 胡敏章, 等. 中国大陆重力场时变监测与强震预测[J]. 中国地震, 2020, 36(4): 729-743 (Shen Chongyang, Zhu Yiqing, Hu Minzhang, et al. Time-Varying Gravity Field Monitoring and Strong Earthquake Prediction on the Chinese Mainland[J]. Earthquake Research in China, 2020, 36(4): 729-743)
(  0) 0) |
| [2] |
祝意青, 梁伟锋, 徐云马. 重力资料对2008年汶川MS8.0地震的中期预测[J]. 国际地震动态, 2008(7): 36-39 (Zhu Yiqing, Liang Weifeng, Xu Yunma. Medium-Term Prediction of MS8.0 Earthquake in Wenchuan, Sichuan by Mobile Gravity[J]. Recent Developments in World Seismology, 2008(7): 36-39 DOI:10.3969/j.issn.0253-4975.2008.07.006)
(  0) 0) |
| [3] |
申重阳, 谈洪波, 郝洪涛, 等. 2009年姚安MS6.0地震重力场前兆变化机理[J]. 大地测量与地球动力学, 2011, 31(2): 17-22 (Shen Chongyang, Tan Hongbo, Hao Hongtao, et al. Mechanism of Precursory Gravity Change before Yaoan MS6.0 Earthquake in 2009[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 17-22)
(  0) 0) |
| [4] |
许厚泽, 王谦身, 陈益惠. 中国重力测量与研究的进展[J]. 地球物理学报, 1994, 37(增1): 339-352 (Xu Houze, Wang Qianshen, Chen Yihui. The Progress of the Gravity Survey and Research in China[J]. Acta Geophysica Sinica, 1994, 37(S1): 339-352)
(  0) 0) |
| [5] |
贾民育, 詹洁晖. 中国地震重力监测体系的结构与能力[J]. 地震学报, 2000, 22(4): 360-367 (Jia Minyu, Zhan Jiehui. The Structure and Ability of the China Seismological Gravity Monitoring System[J]. Acta Seismologica Sinica, 2000, 22(4): 360-367 DOI:10.3321/j.issn:0253-3782.2000.04.004)
(  0) 0) |
| [6] |
卢造勋, 方昌流, 石作亭, 等. 重力变化与海城地震[J]. 地球物理学报, 1978, 21(1): 1-8 (Lu Zaoxun, Fang Changliu, Shi Zuoting, et al. Variation of the Gravity Field and the Haicheng Earthquake[J]. Acta Geophysica Sinica, 1978, 21(1): 1-8)
(  0) 0) |
| [7] |
李瑞浩, 黄建梁, 李辉, 等. 唐山地震前后区域重力场变化机制[J]. 地震学报, 1997, 19(4): 399-407 (Li Ruihao, Huang Jianliang, Li Hui, et al. The Mechanism of Regional Gravity Changes before and after Tangshan Earthquake[J]. Acta Seismologica Sinica, 1997, 19(4): 399-407)
(  0) 0) |
| [8] |
贾民育, 邢灿飞, 孙少安, 等. 滇西重力变化的二维图像及其与5级(MS)以上地震的关系[J]. 地壳形变与地震, 1995, 15(3): 9-19 (Jia Minyu, Xing Canfei, Sun Shaoan, et al. Two-Dimension Pictures of Gravity Change in Western Yunnan and Their Relations to the Earthquake MS>5.0[J]. Crustal Deformation and Earthquake, 1995, 15(3): 9-19)
(  0) 0) |
| [9] |
孙少安, 项爱民, 李辉. 滇西和北京区域重力场演化及其与地震关系的探讨[J]. 地震, 1999, 19(1): 97-106 (Sun Shaoan, Xiang Aimin, Li Hui. Research on Evolution of Western Yunnan and Beijing Regional Gravity Fields and Their Relationship with Earthquake[J]. Earthquake, 1999, 19(1): 97-106 DOI:10.3969/j.issn.1000-3274.1999.01.014)
(  0) 0) |
| [10] |
申重阳, 李辉, 付广裕. 丽江7.0级地震重力前兆模式研究[J]. 地震学报, 2003, 25(2): 163-171 (Shen Chongyang, Li Hui, Fu Guangyu. Study on a Gravity Precursor Mode of Lijiang Earthquake with MS=7.0[J]. Acta Seismologica Sinica, 2003, 25(2): 163-171 DOI:10.3321/j.issn:0253-3782.2003.02.006)
(  0) 0) |
| [11] |
李瑞浩, 孙和平, 陈冬生, 等. 重力潮汐观测资料的改正和异常背景值的显示问题[J]. 地震学报, 1991, 13(2): 259-269 (Li Ruihao, Sun Heping, Chen Dongsheng, et al. On the Correction to Observation of Gravity Tides and the Indication of Gravity Anomaly[J]. Acta Seismologica Sinica, 1991, 13(2): 259-269)
(  0) 0) |
| [12] |
徐纪人. 潮汐因子变化与1976年松潘地震[J]. 地壳形变与地震, 1983(4): 38-43 (Xu Jiren. Tidal Factors Change and the Songpan Earthquake in 1976[J]. Crustal Deformation and Earthquake, 1983(4): 38-43)
(  0) 0) |
| [13] |
申重阳, 李辉, 孙少安, 等. 重力场动态变化与汶川MS8.0地震孕育过程[J]. 地球物理学报, 2009, 52(10): 2547-2557 (Shen Chongyang, Li Hui, Sun Shaoan, et al. Dynamic Variations of Gravity and the Preparation Process of the Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2009, 52(10): 2547-2557 DOI:10.3969/j.issn.0001-5733.2009.10.013)
(  0) 0) |
| [14] |
祝意青, 徐云马, 吕弋培, 等. 龙门山断裂带重力变化与汶川8.0级地震关系研究[J]. 地球物理学报, 2009, 52(10): 2538-2546 (Zhu Yiqing, Xu Yunma, Lü Yipei, et al. Relations between Gravity Variation of Longmenshan Fault Zone and Wenchuan MS8.0 Earthquake[J]. Chinese Journal of Geophysics, 2009, 52(10): 2538-2546 DOI:10.3969/j.issn.0001-5733.2009.10.012)
(  0) 0) |
| [15] |
祝意青, 陈兵, 张希, 等. 景泰5.9级地震前后的重力变化研究[J]. 中国地震, 2001, 17(4): 356-363 (Zhu Yiqing, Chen Bing, Zhang Xi, et al. Gravity Variation Research before and after Jingtai MS=5.9 Earthquake[J]. Earthquake Research in China, 2001, 17(4): 356-363 DOI:10.3969/j.issn.1001-4683.2001.04.004)
(  0) 0) |
| [16] |
祝意青, 王双绪, 江在森, 等. 昆仑山口西8.1级地震前重力变化[J]. 地震学报, 2003, 25(3): 291-297 (Zhu Yiqing, Wang Shuangxu, Jiang Zaisen, et al. Gravity Variation before Kunlun Mountain Pass Western MS8.1 Earthquake[J]. Acta Seismologica Sinica, 2003, 25(3): 291-297 DOI:10.3321/j.issn:0253-3782.2003.03.007)
(  0) 0) |
| [17] |
李辉, 申重阳, 孙少安, 等. 中国大陆近期重力场动态变化图像[J]. 大地测量与地球动力学, 2009, 29(3): 1-10 (Li Hui, Shen Chongyang, Sun Shaoan, et al. Dynamic Gravity Change in Recent Years in China Continent[J]. Journal of Geodesy and Geodynamics, 2009, 29(3): 1-10)
(  0) 0) |
| [18] |
黄浩哲, 申重阳, 谈洪波, 等. 姚安MS6.0地震典型重力前兆孕震模型量化研究[J]. 大地测量与地球动力学, 2019, 39(4): 351-355 (Huang Haozhe, Shen Chongyang, Tan Hongbo, et al. Quantitative Research on the Seismic Model of Typical Gravity Precursors in Yao'an MS6.0 Earthquake[J]. Journal of Geodesy and Geodynamics, 2019, 39(4): 351-355)
(  0) 0) |
| [19] |
祝意青, 闻学泽, 孙和平, 等. 2013年四川芦山MS7.0地震前的重力变化[J]. 地球物理学报, 2013, 56(6): 1887-1894 (Zhu Yiqing, Wen Xueze, Sun Heping, et al. Gravity Changes before the Lushan, Sichuan, MS=7.0 Earthquake of 2013[J]. Chinese Journal of Geophysics, 2013, 56(6): 1887-1894)
(  0) 0) |
| [20] |
祝意青, 申重阳, 张国庆, 等. 我国流动重力监测预报发展之再思考[J]. 大地测量与地球动力学, 2018, 38(5): 441-446 (Zhu Yiqing, Shen Chongyang, Zhang Guoqing, et al. Rethinking the Development of Earthquake Monitoring and Prediction in Mobile Gravity[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 441-446)
(  0) 0) |
| [21] |
黄雅, 申重阳, 韦进, 等. 2013年芦山7.0级地震前重力固体潮参数时空变化研究[J]. 大地测量与地球动力学, 2020, 40(2): 165-169 (Huang Ya, Shen Chongyang, Wei Jin, et al. Temporal and Spatial Variation of Gravity Tide Parameters before the Lushan M7.0 Earthquake in 2013[J]. Journal of Geodesy and Geodynamics, 2020, 40(2): 165-169)
(  0) 0) |
| [22] |
胡敏章, 郝洪涛, 李辉, 等. 地震分析预报的重力变化异常指标分析[J]. 中国地震, 2019, 35(3): 417-430 (Hu Minzhang, Hao Hongtao, Li Hui, et al. Quantitative Analysis of Gravity Changes for Earthquake Prediction[J]. Earthquake Research in China, 2019, 35(3): 417-430 DOI:10.3969/j.issn.1001-4683.2019.03.001)
(  0) 0) |
| [23] |
Burridge R, Knopoff L. Body Force Equivalents for Seismic Dislocations[J]. Bulletin of the Seismological Society of America, 1964, 54(6A): 1875-1888 DOI:10.1785/BSSA05406A1875
(  0) 0) |
| [24] |
Kanamori H. The Energy Release in Great Earthquakes[J]. Journal of Geophysical Research, 1977, 82(20): 2981-2987 DOI:10.1029/JB082i020p02981
(  0) 0) |
| [25] |
Okubo S. Gravity and Potential Changes Due to Shear and Tensile Faults in a Half-Space[J]. Journal of Geophysical Research: Solid Earth, 1992, 97(B5): 7137-7144 DOI:10.1029/92JB00178
(  0) 0) |
| [26] |
谈洪波, 申重阳, 李辉. 断层位错引起的地表重力变化特征研究[J]. 大地测量与地球动力学, 2008, 28(4): 54-62 (Tan Hongbo, Shen Chongyang, Li Hui. Characteristics of Surface Gravity Changes Caused by a Fault or Faults Dislocation[J]. Journal of Geodesy and Geodynamics, 2008, 28(4): 54-62)
(  0) 0) |
| [27] |
燕乃玲, 李辉, 申重阳. 丽江地震前后重力场变化的有限矩形位错模型分析[J]. 地震学报, 2003, 25(2): 172-181 (Yan Nailing, Li Hui, Shen Chongyang. Analyses on Gravity Variation before and after the Lijiang Earthquake Based on a Finite Rectangular Dislocation Model[J]. Acta Seismologica Sinica, 2003, 25(2): 172-181 DOI:10.3321/j.issn:0253-3782.2003.02.007)
(  0) 0) |
| [28] |
Nur A. Matsushiro, Japan, Earthquake Swarm: Confirmation of the Dilatancy-Fluid Diffusion Model[J]. Geology, 1974, 2(5): 217-221 DOI:10.1130/0091-7613(1974)2<217:MJESCO>2.0.CO;2
(  0) 0) |
| [29] |
陈运泰, 顾浩鼎, 卢造勋. 1975年海城地震与1976年唐山地震前后的重力变化[J]. 地震学报, 1980, 2(1): 21-31 (Chen Yuntai, Gu Haoding, Lu Zaoxun. Variations of Gravity before and after the Haicheng Earthquake, 1975 and the Tangshan Earthquake, 1976[J]. Acta Seismologica Sinica, 1980, 2(1): 21-31)
(  0) 0) |
| [30] |
Kuo J T, Sun Y F. Modeling Gravity Variations Caused by Dilatancies[J]. Tectonophysics, 1993, 227(1-4): 127-143 DOI:10.1016/0040-1951(93)90091-W
(  0) 0) |
2. School of Earth and Space Sciences, University of Science and Technology of China, 96 Jinzhai Road, Hefei 230026, China;
3. School of Geosciences and Info-Physics, Central South University, 932 South-Lushan Road, Changsha 410083, China
 2021, Vol. 41
2021, Vol. 41


