GRACE-FO卫星是美国航空航天局(NASA)和德国地学中心(GFZ)联合研制的、继GRACE卫星后的新一代编队卫星。两颗GRACE-FO(GRACE-C与GRACE-D)卫星于2018-05-22发射,运行在高度约为491.5 km、轨道倾角为89°的近极地轨道上,并且在同一轨道上相距约220 km。为了得到高精度的卫星轨道和地球重力场模型,GRACE-FO卫星搭载星载GPS接收机、高精度K波段测距系统(KBR,K-band ranging)、卫星激光测距系统(SLR,satellite laser ranging)、恒星相机(SCA,star camera assembly)以及其他器件[1]。其中,两颗GRACE-FO卫星搭载的TriG接收机,最多能够同时跟踪16颗GPS卫星,观测值的采样频率可达到1 Hz。KBR提供的两颗卫星之间的高精度距离信息(10 μm以内)不仅能够用于恢复重力场,也能够用于检验并改善卫星轨道精度。星跟踪器(star trackers)的测量数据可用于确定卫星姿态,从而使加速度计数据从星固系旋转到惯性参照系。此外,不同于GRACE卫星搭载的单向星间测距系统(inter-satellite ranging system),GRACE-FO使用激光干涉测距系统(LRI,laser ranging interferometer),这意味着其能够进一步评估LRI在编队卫星中测距的表现与性能,同时为未来空间重力测量任务的改进奠定基础[2-3]。重力场、地球水体变化及大气模型等产品的获得均需要建立在高精度卫星轨道的基础上,因此对GRACE-FO卫星进行精密定轨研究具有重要意义。
由于GPS卫星能够提供连续、全弧段、高精度的跟踪观测值,自星载GPS技术在TOPEX/Poseidon任务成功应用以来,已逐渐成为低轨卫星精密轨道确定(POD,precise orbit determination)的重要技术手段,并成功应用于大量低轨卫星计划中。研究表明,利用GPS星载观测值,基于简化动力学的定轨方法,CHAMP卫星能够实现亚dm级的定轨精度[4]。对于GRACE卫星,Kang等[5]结合力学模型对其进行动力学定轨分析,结果表明,径向、切向和法向轨道精度分别达到1.0 cm、2.5 cm、2.5 cm。李建成等[6]使用一种改进的星载GPS非差数据质量控制技术以及大型法方程快速求解算法,得到GRACE-A卫星单天非差运动学轨道的径向精度为3~4 cm,GRACE-B卫星为3~5 cm。对于GRACE-FO卫星,Xia等[7]对其星载GPS接收机观测数据的质量以及相位中心变化(PCV)模型和姿态对GRACE-FO的影响进行分析,使用名义姿态得到的运动学轨道在径向、切向和法向上的精度分别为1.17 cm、1.54 cm与1.32 cm。Kang等[8]对GPS非差和双差观测值进行GRACE-FO卫星简化动力学定轨的差异进行分析,结果表明,非差策略的KBR残差为6 mm、双差为9 mm,均能得到三维精度优于2 cm的轨道。
在对低轨卫星进行模糊度固定方面,张小红等[9]利用全球IGS跟踪站的数据,计算得到各卫星的相位偏差产品,进而对GRACE卫星进行固定PPP整数模糊度的事后精密定轨,结果表明,固定解比浮点解定轨精度高20%~50%。Montenbruck等[10-11]利用CNES/CLS发布的整数相位钟产品固定星间单差模糊度,使得Swarm和Sentinel-3卫星的简化动力学轨道相比于浮点解定轨精度提升30%~50%。张强[12]对Jason-3和HY-2A卫星进行精密定轨研究并分析固定星间单差模糊度的效果,结果表明固定模糊度能够显著改善轨道切向的精度。此外,Allende-Alba等[13]进一步证明,利用固定星间单差模糊度可以提高低轨卫星编队的相对定位精度。
本文基于GARCE-FO星载GPS数据,解算2019年年积日277~290的简化动力学轨道;得到简化动力学的浮点解轨道后,对星间单差模糊度进行固定,分析固定模糊度参数对卫星轨道精度的影响;同时通过相位残差分析、重叠弧段比较、参考轨道比较及KBR检验来评估解算轨道的精度。
1 卫星定轨基本原理 1.1 简化动力学定轨简化动力学定轨法是一种在动力学模型中引入随机过程参数的定轨方法。该方法将几何法与动力法有机结合起来,在精密定轨过程中将伪随机参数和轨道初始状态等参数同时进行估计,可以获得低轨卫星质心的位置和速度。简化动力学定轨与动力学定轨的区别在于:简化动力学通过在动力学模型中引入一个假想力(伪随机脉冲),并将这个假想力与其他参数一起估计。假想力可用径向、切向和法向加速度表示[12]:
| $ {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{r}}} = \frac{\mathit{\boldsymbol{r}}}{{\left| \mathit{\boldsymbol{r}} \right|}}, {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{T}}} = {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{N}}} \times {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{R}}}, {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{N}}} = \frac{{\mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{v}}}}{{\left| {\mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{v}}} \right|}} $ |
式中,er、eT、eN分别为径向、切向、法向经验加速度,r、v分别为低轨卫星的位置矢量和速度矢量。简化动力学定轨中引入伪随机脉冲参数的最大优点是可以有效吸收动力学模型误差与未被模型化的误差,简化所需的先验经验力学模型的数量及精度,从而提高低轨卫星简化动力学定轨精度。
1.2 单站模糊度固定方法本文基于UPD方法[14]进行实验,UPD指初始相位或硬件延迟等导致模糊度无法固定的未标定的相位延迟(uncalibrated phase delay),同时存在于卫星端和接收机端。接收机端UPD可通过星间单差消除,因此通常提到的UPD为卫星端UPD的小数部分,称为相位小数周偏差(fractional cycle bias, FCB)。非差无电离层组合模糊度可分解为宽巷模糊度和窄巷模糊度,宽巷模糊度在几天甚至一个月内变化十分稳定,而窄巷模糊度在一小段时间内变化也十分稳定,因此可以使用合适的地面网将卫星端宽巷和窄巷小数部分进行标定。在标定宽巷和窄巷UPD后,即可固定单站模糊度。
2 数据来源与定轨策略本文使用GFZ提供的GRACE-FO卫星的双频GPS接收机观测数据和姿态文件(ftp://isdcftp.gfz-potsdam.de/grace-fo),并选取2019-10-04~10-17(年积日277~290)共14 d的数据。参考轨道由GFZ提供,采样间隔为1 s,轨道精度优于2 cm[3, 15],将其作为定轨结果的对比对象。此外,采样间隔为30 s的钟差以及5 min的GPS精密星历由CODE(center for orbit determination in Europe)提供,通过拉格朗日插值方法可将其内插至1s。具体解算策略与误差模型见表 1。
|
|
表 1 解算策略 Tab. 1 Solution strategy |
将卫星每个面板上的太阳辐射压力以吸收、漫反射和镜面反射的形式在可见光波长范围内进行参数化,并通过Milani模型[16]和锥形地球阴影模型进行计算。同时,每90 min估算一次大气阻力的整体比例因子Cd,将其作为分段常数,初始值为2.2,设置为松约束。同样,每隔90 min将沿切向和法向的附加经验加速度估计为分段常数,而地球反照压力由于幅度较小未通过特定模型进行校正,并且据推测会被经验加速度所吸收。
实验采用最小二乘批处理方法进行解算,解算弧段长度为24 h。对于随机模型,实验中定权方法为高度角加权,截止高度角为0°,伪距观测值和相位观测值的权比为1/1 000。对于模糊度固定,利用由全球164个IGS站计算得到的FCB产品[14]改正卫星端硬件延迟,将不存在周跳、连续观测时间大于8 min的观测弧段组成星间单差观测值来消除接收机端FCB,并使用判别函数法[17]依次固定每个独立的星间单差宽巷、窄巷模糊度,设置宽巷模糊度阈值为0.25周、窄巷为0.15周。通过迭代方法获得固定解,当模糊度固定率不再提高时停止迭代,最后使用经验模糊度检查方法剔除错误固定的模糊度后得到最终的固定解。
3 简化动力学轨道解算 3.1 单天轨道精度分析为分析定轨精度,将固定模糊度后的轨道与浮点解轨道同GFZ提供的事后精密科学轨道(PSO)进行对比。以2019-10-10(年积日283)为例,GRACE-C卫星简化动力学解算结果(浮点解与固定解)在径向(R)、切向(T)和法向(N)的轨道残差如图 1和表 2所示。

|
图 1 GRACE-C和GRACE-D卫星轨道固定解和浮点解与PSO差异 Fig. 1 The orbit difference between PSO and ambiguity-float and ambiguity-fixed of GRACE-C and GRACE-D satellites |
|
|
表 2 GRACE-C卫星与PSO差异统计 Tab. 2 Statistics of the difference between GRACE-C orbit and PSO |
使用卫星端FCB产品固定低轨卫星的模糊度参数,其中宽巷模糊度固定率为99%,窄巷固定率为94%。固定模糊度可以显著增强观测模型的强度,并能有效分离模糊度和其他相关参数以及混入其中的相位误差,使坐标参数更为精确[12]。由图 1和表 2可知,GRACE-C卫星浮点解和固定解轨道与PSO差异值的RMS在R方向上分别分9.8 mm和7.6 mm、T方向上分别为18.9 mm和8.3 mm、N方向上分别为9.5 mm和7.5 mm,固定模糊度后轨道误差在R、T、N方向上分别减少22.4%、56.1%、21.1%。
从图 1可以看出,简化动力学轨道在N方向比R、T方向更稳定,与PSO相比差异浮动较小。3个方向上存在较明显的周期性与相关性,初始历元和结束历元轨道与PSO差异较大,主要原因为轨道积分对两端力学参数的约束较小,存在边界效应。从单天轨道结果可以看出,固定模糊度能够提高轨道精度,在切向上改善最为明显。
3.2 多天轨道精度分析为综合评价简化动力学固定模糊度参数后GRACE-FO卫星的定轨精度,解算2019-10-04~10-17(年积日277~290)共14 d的星载GPS数据。选取部分结果,从相位残差的RMS值、重叠弧段比较、参考轨道比较以及KBR数据检验4个方面分析评价简化动力学轨道的精度。
3.2.1 载波相位残差分析载波相位残差包含平差过程中模型的误差以及未能模型化的误差,能够反映简化动力学中力学模型的准确度。当所采用的动力学模型和观测数据的质量及其预处理结果都很理想时,观测值残差就接近观测噪声水平[18]。采用消电离层组合(LC)对GRACE-FO卫星GPS观测数据进行处理,得到简化动力学定轨结果,计算单天LC载波相位残差RMS,表 3(单位mm)为年积日277~283的处理结果。
|
|
表 3 GRACE-FO卫星LC载波相位残差RMS值 Tab. 3 The RMS values of LC carrier phase residual of GRACE-FO satellite |
从表 3可以看出,GRACE-C与GRACE-D卫星经过简化动力学定轨并固定模糊度后的相位无电离层组合观测值残差的RMS值在9.5~11.5 mm之间;浮点解残差的RMS值相对稳定,在7.7~8.4 mm之间。出现该现象的原因为固定模糊度可以显著增强观测模型的强度,并有效分离模糊度和其他相关参数以及混入其中的相位误差,从而使得相位残差不可避免地增大[12]。上述分析说明,实验选取的简化动力学模型与实际情况一致性较好,解算策略能够较好地探测周跳并处理粗差。两颗GRACE-FO卫星的运行环境基本相同,其相位残差也基本一致。
3.2.2 重叠弧段比较选取2019-10-09~10-11的观测数据,将每天24 h的数据分为两个弧段进行计算。第一个弧段为00:00:00~14:59:59,第二个弧段为15:00:00~23:59:59,定轨弧长为15 h,两个弧段中存在6 h的重叠数据。将两次定轨结果在重叠弧段轨道进行比较,能够反映GRACE-FO卫星简化动力学轨道的内符合精度。重叠弧段差值的RMS统计结果见表 4。
|
|
表 4 重叠弧段残差RMS值 Tab. 4 The RMS values of overlapping arc residual |
从表 4可以看出,GRACE-FO卫星简化动力学浮点解轨道重叠弧段的RMS在R方向上为3.3~12.3 mm,T方向上为5.7~9.9 mm,N方向上为1.8~8.4 mm;固定解轨道在R方向上为3.7~9.4 mm,T方向上为1.9~5.5 mm,N方向上为3.0~4.9 mm。其中T方向改进最为明显,精度改善40%以上。固定模糊度并不一定都能改善3个方向的内符合精度,如年积日283的R方向与年积日284的N方向,固定模糊度后RMS反而增大,但在三维精度上均有所提升。整体来说,固定模糊度能够明显提升轨道的内符合精度,且浮点解在三维上重叠弧段的精度均大于1 cm,而固定解能保持在1 cm以内。
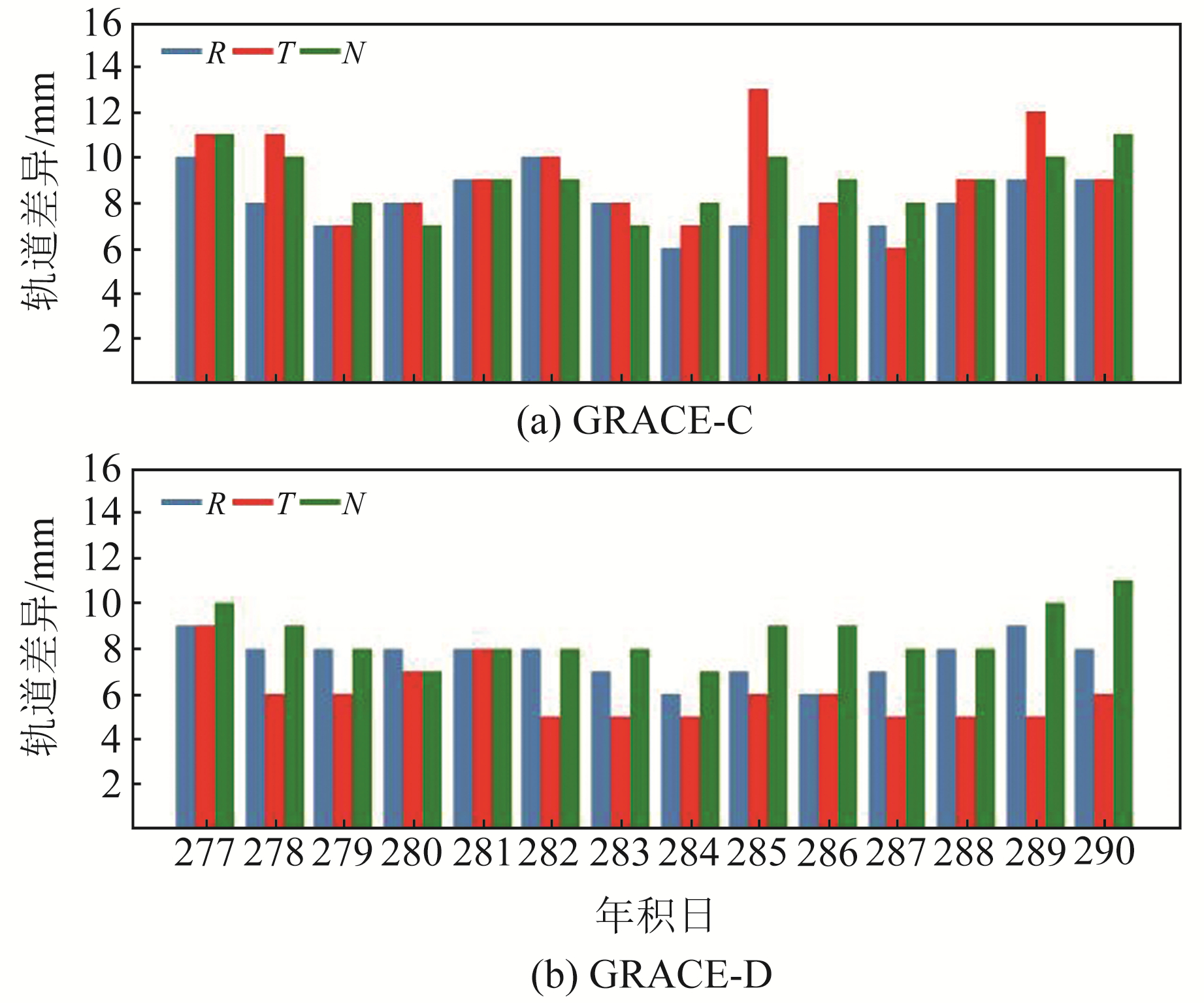
3.2.3 参考轨道比较将2019-10-04~10-17的固定解简化动力学轨道与GFZ发布的科学轨道进行对比,GRACE-FO卫星在R、T、N方向上轨道差异的RMS值统计结果如图 2所示。其中GRACE-C卫星在14 d内R、T、N方向上轨道差异的RMS均值分别为8.1 mm、9.1 mm和9.0 mm,GRACE-D卫星分别为7.6 mm、6.0 mm和8.5 mm。从图 2可以看出,大多数时候N方向上轨道精度相对更高,且GRACE-D卫星的简化动力学轨道精度优于GRACE-C卫星。总体来说,两颗卫星的定轨结果在各方向上无明显差异,且与参考轨道符合较好。
|
图 2 GRACE-C和GRACE-D卫星简化动力学轨道与PSO产品差异 Fig. 2 The difference between PSO and reduced-dynamic orbits of GRACE-C and GRACE-D satellites |
K波段测距系统(KBR)是GRACE-FO卫星上搭载的关键科学仪器,可以在两颗卫星之间进行双单向测距,采样间隔为5 s,测距精度可达到10 μm[7]。该距离信息不仅可以用于地球重力场恢复,也可以用于GRACE卫星的精密轨道确定与检核。表 5(单位mm)为去除KBR观测数据中的模糊度偏差后[19],GRACE-FO卫星简化动力学轨道与KBR观测数据残差的RMS均值。从表中可以看出,固定解单天轨道的KBR残差RMS值小于等于9 mm,相比于浮点解的10.7 mm改善20~40%,表明固定模糊度后简化动力学轨道的外符合精度得到提升,且两颗卫星之间的距离精度可达到1 cm以内。
|
|
表 5 KBR残差RMS值 Tab. 5 The RMS values of KBR residual |
本文使用简化动力学方法,通过GRACE-FO卫星上星载GPS接收机的观测数据,对其进行精密定轨研究。同时对GPS载波相位观测值进行模糊度固定,进一步分析固定模糊度后卫星的轨道精度。通过观测值残差分析、重叠弧段比较、参考轨道比较以及KBR检验4种方法对轨道精度进行综合评估,得到以下结论:
1) 固定模糊度参数后能够提高GRACE-FO卫星的轨道外符合精度。以GFZ提供的事后精密轨道作为参考,固定模糊度后R、T、N方向上GRACE-C轨道精度分别提升22.4%、56.1%、21.1%。
2) 通过重叠弧段比较可以看出,固定模糊度后GRACE-FO卫星的3D-RMS值均在1 cm以内,内符合精度达到cm级。
3) 固定模糊度参数会使载波相位无电离组合观测值的残差增大2 mm左右,且GRACE-C与GRACE-D卫星的相位残差基本一致。
4) KBR检验结果显示,固定解轨道经KBR星间数据检验后的残差在9 mm以内,浮点解在10.7 mm以内,表明两颗卫星的轨道相对稳定。
以上结论表明,固定模糊度参数能够提升低轨卫星的轨道精度,同时可有效分离其他相关参数以及混入其中的相位误差,具有重要的科学应用价值。
| [1] |
Tapley B D, Bettadpur S, Watkins M, et al. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9)
(  0) 0) |
| [2] |
Case K, Kruizinga G L H, Wu S C. GRACE Level 1B Data Product User Handbook[Z]. Pasadena: Jet Propulsion Laboratory, 2010
(  0) 0) |
| [3] |
Wen H Y, Kruizinga G L H, Paik M, et al. Gravity Recovery and Climate Experiment Follow-On(GRACE-FO) Level-1 Data Product User Handbook[Z]. Pasadena: Jet Propulsion Laboratory, 2019
(  0) 0) |
| [4] |
Ijssel J, Visser P, Rodriguez E P. Champ Precise Orbit Determination Using GPS Data[J]. Advances in Space Research, 2003, 31(8): 1889-1895 DOI:10.1016/S0273-1177(03)00161-3
(  0) 0) |
| [5] |
Kang Z G, Tapley B, Bettadpur S, et al. Precise Orbit Determination for the GRACE Mission Using only GPS Data[J]. Journal of Geodesy, 2006, 80(6): 322-331 DOI:10.1007/s00190-006-0073-5
(  0) 0) |
| [6] |
李建成, 张守建, 邹贤才, 等. GRACE卫星非差运动学厘米级定轨[J]. 科学通报, 2009, 54(16): 2355-2362 (Li Jiancheng, Zhang Shoujian, Zou Xiancai, et al. Precise Orbit Determination for GRACE with Zero-Difference Kinematic Method[J]. Chinese Science Bulletin, 2009, 54(16): 2355-2362)
(  0) 0) |
| [7] |
Xia Y W, Liu X, Guo J Y, et al. On GPS Data Quality of GRACE-FO and GRACE Satellites: Effects of Phase Center Variation and Satellite Attitude on Precise Orbit Determination[J]. Acta Geodaetica et Geophysica, 2021, 56(1): 93-111 DOI:10.1007/s40328-020-00324-2
(  0) 0) |
| [8] |
Kang Z, Bettadpur S, Nagel P, et al. GRACE-FO Precise Orbit Determination and Gravity Recovery[J]. Journal of Geodesy, 2020, 94(9) DOI:10.1007/s00190-020-01414-3
(  0) 0) |
| [9] |
张小红, 李盼, 左翔. 固定模糊度的精密单点定位几何定轨方法及结果分析[J]. 武汉大学学报: 信息科学版, 2013, 38(9): 1009-1013 (Zhang Xiaohong, Li Pan, Zuo Xiang. Kinematic Precise Orbit Determination Based on Ambiguity-Fixed PPP[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1009-1013)
(  0) 0) |
| [10] |
Montenbruck O, Hackel S, Ijssel J, et al. Reduced Dynamic and Kinematic Precise Orbit Determination for the Swarm Mission from 4 Years of GPS Tracking[J]. GPS Solutions, 2018, 22(3)
(  0) 0) |
| [11] |
Montenbruck O, Hackel S, Jäggi A. Precise Orbit Determination of the Sentinel-3A Altimetry Satellite Using Ambiguity-Fixed GPS Carrier Phase Observations[J]. Journal of Geodesy, 2018, 92(7): 711-726 DOI:10.1007/s00190-017-1090-2
(  0) 0) |
| [12] |
张强. 采用GPS与北斗的低轨卫星及其编队精密定轨关键技术研究[D]. 武汉: 武汉大学, 2018 (Zhang Qiang. Research on the Key Technologies of Precise Orbit Determination for Low Earth Orbit Satellites and Their Formation Using GPS and BDS[D]. Wuhan: Wuhan University, 2018)
(  0) 0) |
| [13] |
Allende-Alba G, Montenbruck O, Hackel S, et al. Relative Positioning of Formation-Flying Spacecraft Using Single-Receiver GPS Carrier Phase Ambiguity Fixing[J]. GPS Solutions, 2018, 22(3)
(  0) 0) |
| [14] |
Ge M, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning(PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399 DOI:10.1007/s00190-007-0187-4
(  0) 0) |
| [15] |
Kornfeld R P, Arnold B W, Gross M A, et al. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission[J]. Journal of Spacecraft and Rockets, 2019, 56(3): 931-951 DOI:10.2514/1.A34326
(  0) 0) |
| [16] |
Milani A, Nobili A M, Farinella P. Non-Gravitational Perturbations and Satellite Geodesy[J]. Bristol: Adam Hilger Ltd, 1987
(  0) 0) |
| [17] |
Ge M, Gendt G, Dick G, et al. A New Data Processing Strategy for Huge GNSS Global Networks[J]. Journal of Geodesy, 2006, 80(4): 199-203 DOI:10.1007/s00190-006-0044-x
(  0) 0) |
| [18] |
张兵兵, 聂琳娟, 吴汤婷, 等. SWARM卫星简化动力学厘米级精密定轨[J]. 测绘学报, 2016, 45(11): 1278-1284 (Zhang Bingbing, Nie Linjuan, Wu Tangting, et al. Centimeter Precise Orbit Determination for SWARM Satellite via Reduced-Dynamic Method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1278-1284 DOI:10.11947/j.AGCS.2016.20160284)
(  0) 0) |
| [19] |
田英国, 郝金明, 刘伟平, 等. 利用KBR数据检核GRACE卫星精密轨道[J]. 测绘科学技术学报, 2014, 31(6): 580-583 (Tian Yingguo, Hao Jinming, Liu Weiping, et al. Checking the GRACE Satellite Orbit Precision Using the KBR Data[J]. Journal of Geomatics Science and Technology, 2014, 31(6): 580-583 DOI:10.3969/j.issn.1673-6338.2014.06.007)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41

