2. 东华理工大学勘察设计研究院,江西省抚州市学府路56号,344000;
3. 同济大学测绘与地理信息学院,上海市四平路1239号,200092
大地测量领域中部分解算模型如GPS快速定位[1-2]、大地测量反演[3-4]以及重力场向下延拓[5-6]等均存在病态问题。当模型病态时,常规的最小二乘解受系数阵的小奇异值影响而精度较低。为获得稳定、可靠的参数估值,部分学者提出一系列有偏估计,如Tikhonov正则化法[7]和TSVD(truncated singular value decomposition)正则化法[8]。当处理病态问题需同时顾及系数矩阵误差时,即病态总体最小二乘模型的解算,是当前测量数据处理研究的热点之一。Fierro等[9]基于广义奇异值分解(generalized singular value decomposition, GSVD)导出病态总体最小二乘问题的截断奇异值法; 葛旭明等[10]基于狭义正则化原理,推导出病态总体最小二乘问题的广义正则化解法; 孙同贺等[11]将Tikhonov正则化和TV正则化有效结合, 提出一种混合正则化解法; 文献[12-13]利用平差参数之间的相互独立性作为先验约束条件,导出病态总体最小二乘问题的虚拟观测值解法。然而,目前已有的病态总体最小二乘问题解法几乎全是在等权条件下推导得到的,对于观测值和系数阵精度不同的情形,缺少实用的解法。王乐洋等[14]将变量误差模型(errors-in-variables, EIV)线性化并用岭估计法解算病态加权总体最小二乘问题,由于线性化过程中舍去二阶项,估值的精度受到影响。在实际测量过程中,观测值除含有偶然误差外,往往还受到粗差的影响。当观测数据中含有粗差时,会极大影响参数估值,因此有必要研究病态总体最小二乘问题的抗差解法。目前有关抗差估计的研究多集中于最小二乘估计(least squares, LS)或总体最小二乘估计(total least squares, TLS), 鲜有关于病态加权总体最小二乘问题的抗差估计研究。本文首先建立病态加权总体最小二乘模型的正则化准则, 构建拉格朗日极值函数,利用Euler-Lagrange必要条件导出病态加权总体最小二乘模型的正则化解;在此基础上,针对观测值中的粗差,提出一种基于中位数法的病态加权总体最小二乘模型的正则化抗差解法。
1 等权病态总体最小二乘模型的正则化解常用的变量误差模型(errors-in-variables, EIV)可表示为[15-16]:
| ${\boldsymbol{y}} - {{\boldsymbol{e}}_y} = ({\boldsymbol{A}} - {{\boldsymbol{E}}_A}){\boldsymbol{x}}$ | (1) |
式中,y∈Rm和A∈Rm×n分别为观测向量和系数矩阵;ey∈Rm和EA∈Rm×n分别为观测向量和系数矩阵的误差;m、n分别表示观测值个数和未知参数个数。其随机模型为:
| $ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_y}}\\ {{{\boldsymbol{e}}_A}} \end{array}} \right]\sim \left( {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right]}&{\sigma _{\rm{0}}^{\rm{2}}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{Q}}_y}}&{}\\ {}&{{{\boldsymbol{Q}}_A}} \end{array}} \right]} \end{array}} \right) $ | (2) |
式中,eA=vec(EA), vec(·)为矩阵拉直算子;Qy和QA分别为观测向量和系数矩阵元素的协因数阵,等权情形下均取单位阵;σ02为单位权方差。当系数阵病态时,观测向量和系数矩阵中元素值的微小误差会导致参数估值的巨大波动,为获得稳定的参数估值,需对参数施加正则化约束。根据Tikhonov正则化原理,建立等权病态总体最小二乘模型的正则化准则:
| $ {\boldsymbol{e}}_y^{\rm{T}}{{\boldsymbol{e}}_y} + {\boldsymbol{e}}_A^{\rm{T}}{{\boldsymbol{e}}_A} + \alpha {{\boldsymbol{x}}^{\rm{T}}}{\boldsymbol{x}} = \min $ | (3) |
式中,α为正则化参数。根据式(3)可导出参数估值的迭代计算式:
| ${\boldsymbol{\hat x}} = {({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}} + b{{\boldsymbol{I}}_n})^{ - 1}}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{y}}$ | (4) |
式中,
为不失一般性且顾及观测值和系数阵的协因数阵可记为:
| ${{\boldsymbol{Q}}_y}{\boldsymbol{ = P}}_y^{ - 1}{\boldsymbol{, }}{{\boldsymbol{Q}}_A} = {{\boldsymbol{Q}}_0} \otimes {{\boldsymbol{Q}}_{\boldsymbol{x}}}$ | (5) |
式中,Q0=P0-1, Qx=Px-1,则式(3)可改写为:
| $ {\boldsymbol{e}}_y^{\rm{T}}{{\boldsymbol{P}}_y}{{\boldsymbol{e}}_y} + {\boldsymbol{e}}_A^{\rm{T}}({{\boldsymbol{P}}_0} \otimes {{\boldsymbol{P}}_{\boldsymbol{x}}}){{\boldsymbol{e}}_A} + \alpha {{\boldsymbol{x}}^{\rm{T}}}{\boldsymbol{x}} = \min $ | (6) |
式(6)即为病态加权总体最小二乘模型的正则化准则,由此可建立拉格朗日极值函数:
| $ \begin{array}{l} \varPhi ({{\boldsymbol{e}}_y}, {{\boldsymbol{e}}_A}, {\boldsymbol{\lambda }}, {\boldsymbol{x}}) = {\boldsymbol{e}}_y^{\rm{T}}{{\boldsymbol{P}}_y}{{\boldsymbol{e}}_y} + {\boldsymbol{e}}_A^{\rm{T}}({{\boldsymbol{P}}_0} \otimes {{\boldsymbol{P}}_{\boldsymbol{x}}}){{\boldsymbol{e}}_A} +\\ \alpha {{\boldsymbol{x}}^{\rm{T}}}{\boldsymbol{x}} + 2{{\boldsymbol{\lambda }}^{\rm{T}}}({\boldsymbol{y}} - {\boldsymbol{Ax}} - {{\boldsymbol{e}}_y} + ({{\boldsymbol{x}}^{\rm{T}}} \otimes {{\boldsymbol{I}}_n}) \cdot {{\boldsymbol{e}}_A}) \end{array} $ | (7) |
式中,λ为联系数向量。将式(7)分别对各变量进行求导并令其为0,则:
| $ \frac{1}{2}\frac{{\partial \varPhi }}{{\partial {{\boldsymbol{e}}_y}}} = {\boldsymbol{Q}}_y^{ - 1}{{\boldsymbol{\tilde e}}_y} - {\boldsymbol{\hat \lambda }} = {\rm{0}} $ | (8a) |
| $ \frac{1}{2}\frac{{\partial \varPhi }}{{\partial {{\boldsymbol{e}}_A}}} = ({\boldsymbol{Q}}_0^{ - 1} \otimes {\boldsymbol{Q}}_{\boldsymbol{x}}^{ - 1}){{\boldsymbol{\tilde e}}_A} + ({\boldsymbol{\hat x}} \otimes {{\boldsymbol{I}}_n}){\boldsymbol{\hat \lambda }} = {\rm{0}} $ | (8b) |
| $ \frac{1}{2}\frac{{\partial \varPhi }}{{\partial {\boldsymbol{\hat \lambda }}}} = {\boldsymbol{y}} - {\boldsymbol{A\hat x}} - {{\boldsymbol{\tilde e}}_y} + ({{\boldsymbol{\hat x}}^{\rm{T}}} \otimes {{\boldsymbol{I}}_n}){{\boldsymbol{\tilde e}}_A} = {\rm{0}} $ | (8c) |
| $ \frac{1}{2}\frac{{\partial \varPhi }}{{\partial {\boldsymbol{\hat x}}}} = \alpha {\boldsymbol{\hat x}} - {{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{\hat \lambda }} + {\boldsymbol{\tilde E}}_A^{\rm{T}}{\boldsymbol{\hat \lambda }} = {\rm{0}} $ | (8d) |
由式(8a)和(8b)可得:
| ${{\boldsymbol{\tilde e}}_y} = {{\boldsymbol{Q}}_y}{\boldsymbol{\hat \lambda }}$ | (9a) |
| ${{\boldsymbol{\tilde e}}_A} = - ({{\boldsymbol{Q}}_0}{\boldsymbol{\hat x}} \otimes {{\boldsymbol{Q}}_{\boldsymbol{x}}}){\boldsymbol{\hat \lambda }}$ | (9b) |
| ${{\boldsymbol{\tilde E}}_A} = - {{\boldsymbol{Q}}_x}{\boldsymbol{\hat \lambda }}{{\boldsymbol{\hat x}}^{\rm{T}}}{{\boldsymbol{Q}}_0}$ | (9c) |
将式(9)代入式(8c)可得:
| ${\boldsymbol{\hat \lambda }} = {\left( {{{\boldsymbol{Q}}_y} + ({{{\boldsymbol{\hat x}}}^{\rm{T}}}{{\boldsymbol{Q}}_0}{\boldsymbol{\hat x}}){{\boldsymbol{Q}}_{\boldsymbol{x}}}} \right)^{ - 1}}({\boldsymbol{y}} - {\boldsymbol{A\hat x}})$ | (10) |
将式(10)代入式(8d)可得:
| $\begin{array}{l} - {{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{\hat \lambda }} = {{\boldsymbol{A}}^{\rm{T}}}{\left( {{{\boldsymbol{Q}}_y} + ({{{\boldsymbol{\hat x}}}^{\rm{T}}}{{\boldsymbol{Q}}_0}{\boldsymbol{\hat x}}){{\boldsymbol{Q}}_{\boldsymbol{x}}}} \right)^{ - 1}}({\boldsymbol{A\hat x}} - {\boldsymbol{y}})=\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\boldsymbol{\tilde E}}_A^{\rm{T}}{\boldsymbol{\hat \lambda }} - \alpha {\boldsymbol{\hat x}} \end{array}$ | (11) |
式中,
| $ {{\boldsymbol{A}}^{\rm{T}}}{\left( {{{\boldsymbol{Q}}_y} + ({{{\boldsymbol{\hat x}}}^{\rm{T}}}{{\boldsymbol{Q}}_0}{\boldsymbol{\hat x}}){{\boldsymbol{Q}}_{\boldsymbol{x}}}} \right)^{ - 1}}({\boldsymbol{A\hat x}} - {\boldsymbol{y}}) = {{\boldsymbol{Q}}_0}{\boldsymbol{\hat x}}\hat v - \alpha {\boldsymbol{\hat x}} $ | (12) |
通过推导可知,病态加权总体最小二乘模型的正则化解为:
| ${\boldsymbol{\hat x}} = {({{\boldsymbol{A}}^{\rm{T}}}{{\boldsymbol{Q}}_{\boldsymbol{l}}}{\boldsymbol{A}} - \hat v{{\boldsymbol{Q}}_0} + \alpha {{\boldsymbol{I}}_n})^{ - 1}}{{\boldsymbol{A}}^{\rm{T}}}{{\boldsymbol{Q}}_{\boldsymbol{l}}}{\boldsymbol{y}}$ | (13) |
式中,
| $\hat \sigma = \frac{{{\boldsymbol{\tilde e}}_y^{\rm{T}}{{\boldsymbol{Q}}_y}{{{\boldsymbol{\tilde e}}}_y} + {\boldsymbol{\tilde e}}_A^{\rm{T}}{{\boldsymbol{Q}}_A}{{{\boldsymbol{\tilde e}}}_A}}}{{m - n}}$ | (14) |
现考虑等权情形,即取Qy=Im, Q0=In, Qx=Im,则:
| $\begin{array}{c} {{\boldsymbol{Q}}_{\boldsymbol{l}}} = {(1 + {{{\boldsymbol{\hat x}}}^{\rm{T}}}{\boldsymbol{x}})^{ - 1}}{{\boldsymbol{I}}_m}\\ {\boldsymbol{\hat \lambda }} = {(1 + {{{\boldsymbol{\hat x}}}^{\rm{T}}}{\boldsymbol{x}})^{ - 1}}({\boldsymbol{y}} - {\boldsymbol{A\hat x}})\\ \hat v = {(1 + {{{\boldsymbol{\hat x}}}^{\rm{T}}}{\boldsymbol{x}})^{ - 2}}{({\boldsymbol{y}} - {\boldsymbol{A\hat x}})^{\rm{T}}}({\boldsymbol{y}} - {\boldsymbol{A\hat x}}) \end{array}$ | (15) |
将式(15)代入式(13)可得:
| ${\boldsymbol{\hat x}} = {\left( {{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}} + (\alpha - \hat v)(1 + {{{\boldsymbol{\hat x}}}^{\rm{T}}}{\boldsymbol{\hat x}}){{\boldsymbol{I}}_n}} \right)^{ - 1}}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{y}}$ | (16) |
式中,
当观测数据受到粗差污染时,参数估值必定会受粗差影响,严重时甚至会偏离真值。选取迭代法是应用较为广泛的抗差估计方法之一,其基本思想是根据参数估值的残差,利用等价权函数重构观测值的权重,并利用新的权值对参数估值进行迭代求解。对于病态加权总体最小二乘模型,利用式(13)求得正则化解后,由式(9a)和(9b)获得观测向量和系数矩阵元素的改正值,利用等价权函数对其重新定权,以IGG权函数为例:
| $ {{\bar P}_i} = \left\{ \begin{array}{l} {P_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {{{\hat e}_i} \le a} \right|\\ {P_i}a{\rm{/}}\left| {{{\hat v}_i}} \right|\;\;\;\;\;\;\;\;\;a < \left| {{{\hat e}_i}} \right| \le b\\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b < \left| {{{\hat e}_i}} \right| \end{array} \right. $ | (17) |
式中,Pi为观测值的权重;Pi为等价权;
本文提出一种基于中位数法的病态加权总体最小二乘模型的正则化抗差解法。对于模型(1), 共有m个观测值和n(n < m)个未知参数,故共可确定Cmn组参数估值:
| ${\boldsymbol{\hat X}} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{\hat X}}}_1}}& \cdots &{{{{\boldsymbol{\hat X}}}_{C_m^n}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\hat x_1^1}& \cdots &{\hat x_{C_m^n}^1}\\ \vdots &{}& \vdots \\ {\hat x_1^n}& \cdots &{\hat x_{C_m^n}^n} \end{array}} \right]$ | (18) |
式中,
| ${{\boldsymbol{\hat X}}_{\rm{med}}} = {\left[ {\begin{array}{*{20}{c}} {{\rm{med}}({{\hat x}^1})}& \cdots &{{\rm{med}}({{\hat x}^n})} \end{array}} \right]^{\rm{T}}}$ | (19) |
将式(19)代入式(9a)和(9b)可得观测向量和系数矩阵的误差向量分别为
| $\begin{array}{l} {\rm{med}}({{{\boldsymbol{\hat e}}}_y}) = \sqrt {{\rm{med}}(\left[ {(\begin{array}{*{20}{c}} {\hat e_y^1{)^2}}& \cdots &{{{(\hat e_y^n)}^2}} \end{array}} \right])} \\ {\rm{med}}({{{\boldsymbol{\hat e}}}_A}) = \sqrt {{\rm{med}}(\left[ {(\begin{array}{*{20}{c}} {\hat e_A^1{)^2}}& \cdots &{{{(\hat e_A^n)}^2}} \end{array}} \right])} \end{array}$ | (20) |
由绝对误差中位数与中误差的关系可知, 观测向量和系数矩阵元素的中误差分别为
第一类Fredholm积分方程为典型的病态问题,其基本形式为:
| $z(y) = \int_a^b {K(x, y)f(x){\rm{d}}x} $ | (21) |
式中,K(x, y)为核函数,f(x)为真值函数,分别取为:
| $\begin{array}{l} K(x, y) = \frac{{1.0}}{{1.0 + 100{{(y - x)}^2}}}\\ f(x) = \frac{{\exp ({\beta _1}) + \exp ({\beta _2})}}{{10.9550408}} - 0.052130913 \end{array}$ | (22) |
式中,
| $ \begin{array}{l} z({y_i}) = \frac{1}{2}\Delta x\sum\limits_{j = 1}^{50} {[K({x_j},{y_i})f({x_j}) + } \\ \;\;\;\;\;\;\;\;\;K({x_{j + 1}},{y_i})f({x_{j + 1}})] \end{array} $ | (23) |
其可改写成一般的线性模型。对系数阵模拟随机误差eA~N(0, σ02I), σ0取0.001,I为单位阵;对观测值模拟随机误差ey~N(0, σ02Qy),Qy为观测值的协因数阵,假设其是对角元素为0.5、非对角元素为0.2的对称方阵。以均值为0、单位权中误差为6σ0的正态分布模拟得到一组数据序列,剔除其中小于3σ0的数据,将剩余数据作为粗差随机添加到原始观测值中。分别采用最小二乘法(LS)、总体最小二乘法(TLS)、正则化加权总体最小二乘法(regularized weighted total least squares, RWTLS,以下简称正则化解)及其抗差解法(robust regularized weighted total least squares, RRWTLS,以下简称正则化抗差解)估计参数及其均方根误差(RMSE):
| $RMSE = \sqrt {\frac{{{{({\boldsymbol{\hat X}} - {\boldsymbol{\bar X}})}^{\rm{T}}}({\boldsymbol{\hat X}} - {\boldsymbol{\bar X}})}}{n}} $ | (24) |
式中,
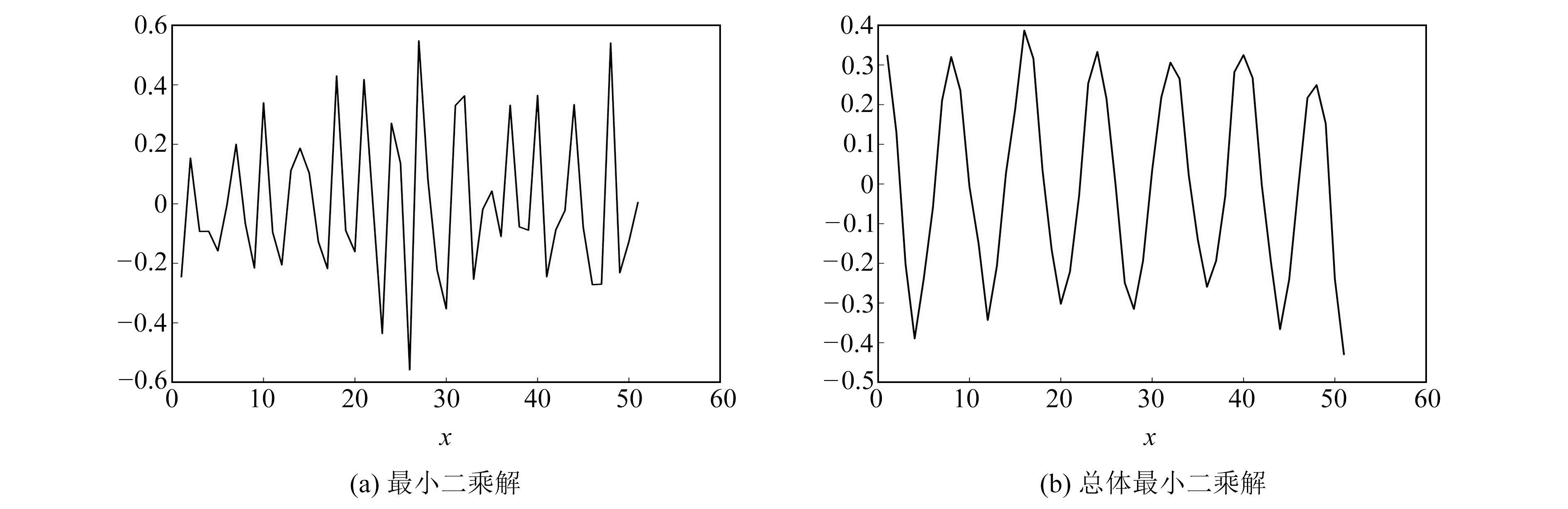
|
图 1 最小二乘解和总体最小二乘解 Fig. 1 Least squares solution and total least squares solution |
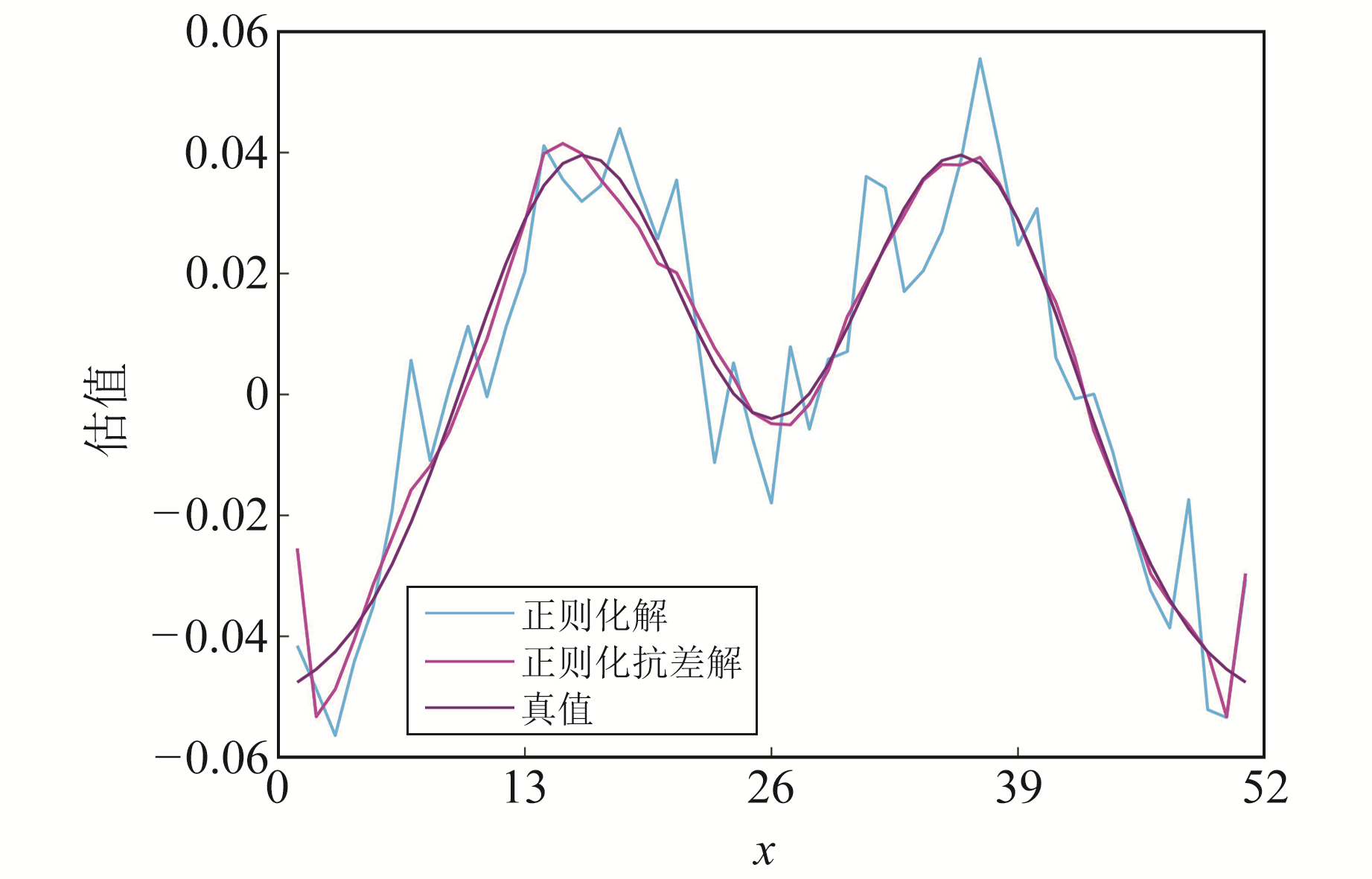
|
图 2 正则化解、正则化抗差解与真值对比 Fig. 2 Comparison between regularized solution, regularized robust solution and true values |
模拟500次实验,每次实验均采用相同策略模拟随机误差和粗差,分别采用4种算法估计参数及其RMSE,结果见图 3。由图可知,受病态性以及粗差影响,最小二乘解和总体最小二乘解的精度最差,其平均RMSE分别为0.137 3和0.407 7;正则化解可顾及系数阵的病态性及误差,其精度较最小二乘解和总体最小二乘解有较大提升,平均RMSE为0.006 0;正则化抗差解可顾及粗差的影响,通过等价权函数重构权阵,能有效抵御粗差的影响,其精度最高,平均RMSE为0.002 3。
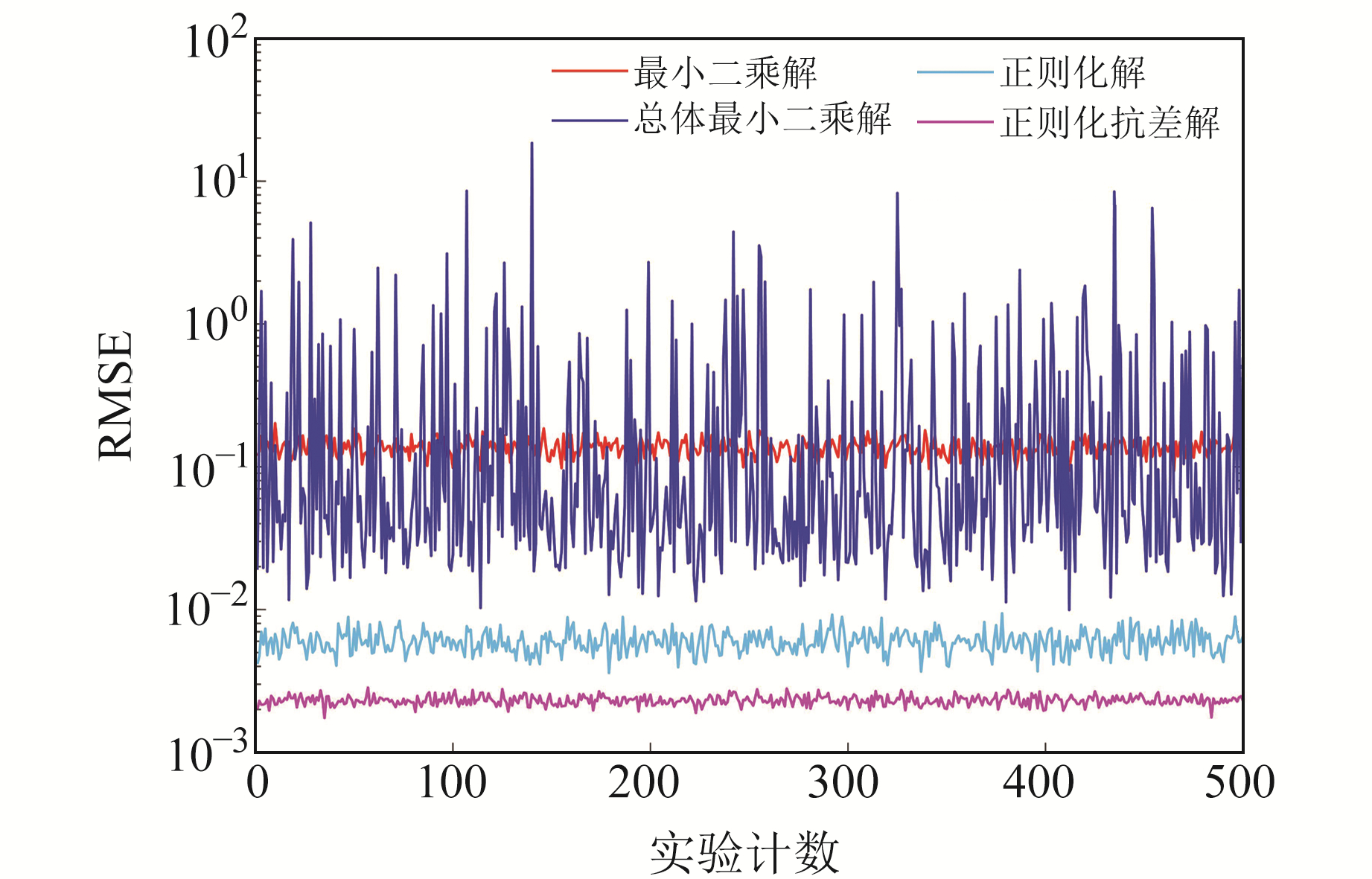
|
图 3 不同算法500次实验获得估值的RMSE Fig. 3 The root mean square error of parameter estimation of four algorithms for 500 experiments |
模拟一个病态测边网算例,该算例中共有9个坐标已知点和2个坐标未知点。其中,已知点与未知点的距离观测值已经给定(表 1),图 4为点位二维平面分布图。2个未知点位之间的观测距离为13.107 8 m,其真实三维坐标分别为(0, 0, 0)和(7, 10, -5), 要求通过已知的距离观测值组建误差方程来求解未知点坐标。
|
|
表 1 控制点坐标及距离观测值 Tab. 1 The coordinates and distance observations of control points |
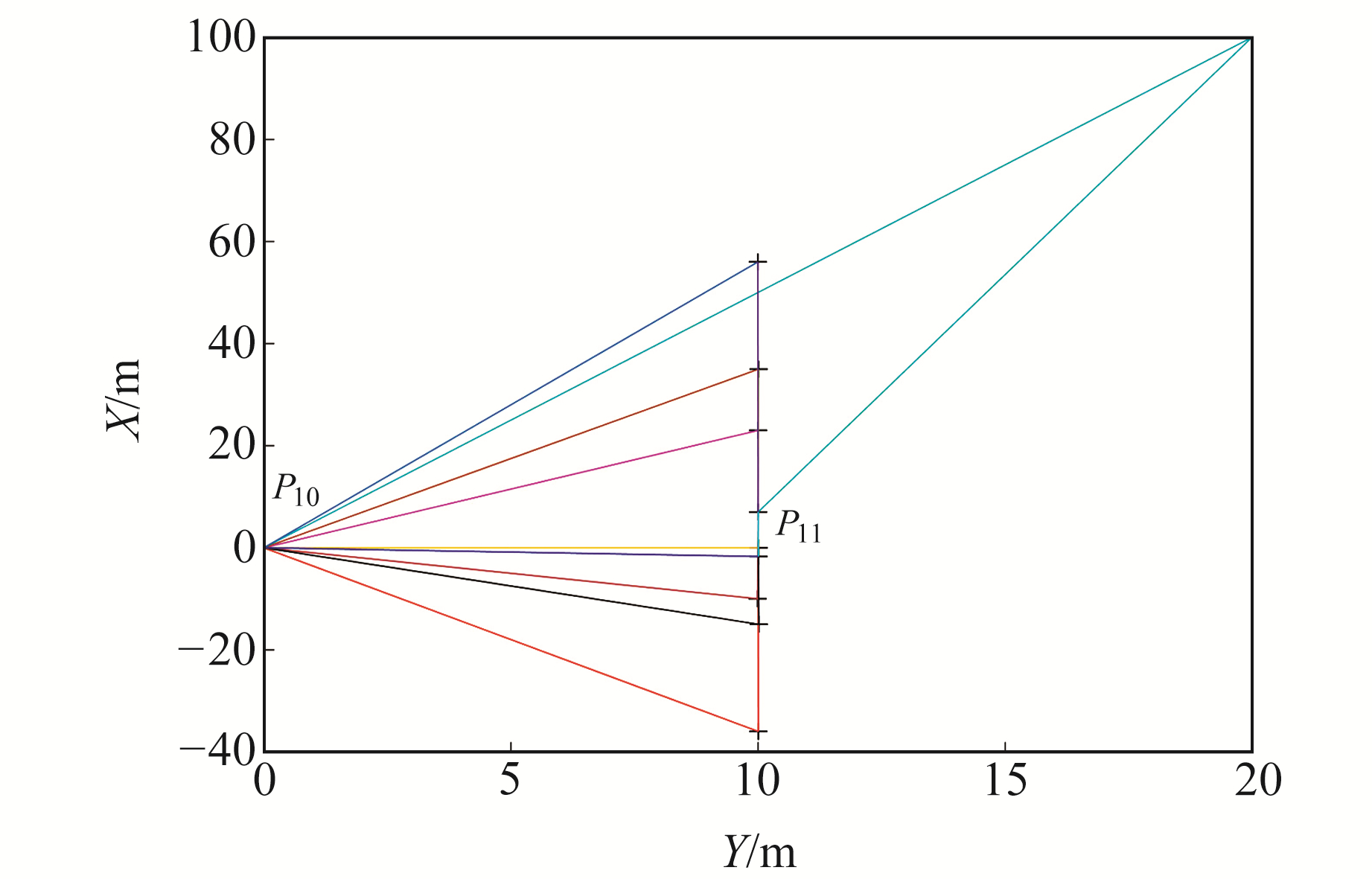
|
图 4 空间测边网平面点位分布 Fig. 4 The point position distribution of the space net in XY plane |
在该算例中,法矩阵的条件数为4.585 1×103,存在病态性。将1号点x坐标和2号点y坐标混入4~5 dm粗差,其余点坐标混入1~2 cm随机误差。与数值算例相同,分别采用4种算法估计参数,表 2为不同算法获得的参数估值及其RMSE。由表可知,最小二乘解和总体最小二乘解受模型病态性和粗差影响,其精度较低,RMSE分别为4.573 8和10.876 3。从结果来看,总体最小二乘解受病态性和粗差的影响更加严重;正则化解可同时顾及系数阵和观测值的误差,并且可通过正则化参数削弱模型的病态性,其精度相比最小二乘解和总体最小二乘解有较大提升,RMSE为0.745 7;正则化抗差解在正则化解的基础上,利用等价权函数有效削弱粗差的影响,因此精度最高,RMSE为0.250 2。
|
|
表 2 不同算法获得的参数估值及其RMSE Tab. 2 The parameter estimation and RMSE of different algorithms |
当变量误差模型的系数阵存在病态时,常规的最小二乘解和总体最小二乘解均不再适用。本文基于Tikhonov正则化原理,通过构建拉格朗日函数导出病态加权总体最小二乘模型的正则化解。当观测值和系数阵的权阵均取单位阵时,本文公式退化为等权病态总体最小二乘模型的正则化解。在此基础上,进一步提出基于中位数法的病态加权总体最小二乘模型的正则化抗差解法,该方法能够自适应地对观测值和系数矩阵元素进行分类定权,可提高等价权函数的有效性。算例分析结果表明,本文提出的正则化解法能够较好地处理病态加权总体最小二乘问题,并且当模型混入粗差时,正则化抗差解法能够自适应地重构权阵以抵御粗差的影响,得到较为稳定且可靠的参数估值。
| [1] |
Li B F, Shen Y Z, Feng Y M. Fast GNSS Ambiguity Resolution as an Ill-Posed Problem[J]. Journal of Geodesy, 2010, 84(11): 683-698 DOI:10.1007/s00190-010-0403-5
(  0) 0) |
| [2] |
Pan S G, Gao W, Wang S L, et al. Analysis of Ill Posedness in Double Differential Ambiguity Resolution of BDS[J]. Survey review, 2014, 46(339): 411-416 DOI:10.1179/1752270614Y.0000000121
(  0) 0) |
| [3] |
顾勇为, 归庆明, 张璇, 等. 大地测量与地球物理中病态性问题的正则化迭代解法[J]. 测绘学报, 2014, 43(4): 331-336 (Gu Yongwei, Gui Qingming, Zhang Xuan, et al. Iterative Solution of Regularization to Ill-Conditioned Problems in Geodesy and Geophysics[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 331-336)
(  0) 0) |
| [4] |
Fu H Q, Wang C C, Zhu J J, et al. Estimation of Pine Forest Height and Underlying DEM Using Multi-Baseline P-Band PolInSAR Data[J]. Remote Sensing, 2016, 8(10): 820 DOI:10.3390/rs8100820
(  0) 0) |
| [5] |
Save H, Bettadpur S, Tapley B D. Reducing Errors in the GRACE Gravity Solutions Using Regularization[J]. Journal of Geodesy, 2012, 86(9): 695-711 DOI:10.1007/s00190-012-0548-5
(  0) 0) |
| [6] |
Freeden W, Schreiner M. Spaceborne Gravitational Field Determination by Means of Locally Supported Wavelets[J]. Journal of Geodesy, 2005, 79(8): 431-446 DOI:10.1007/s00190-005-0482-x
(  0) 0) |
| [7] |
Tikhonov A N, Goncharsky A V, Stepanov V V, et al. Numerical Methods for the Solution of Ill-Posed Problems[M]. Dordrecht: Springer Netherlands, 1995
(  0) 0) |
| [8] |
Xu P L. Truncated SVD Methods for Discrete Linear Ill-Posed Problems[J]. Geophysical Journal International, 1998, 135(2): 505-514 DOI:10.1046/j.1365-246X.1998.00652.x
(  0) 0) |
| [9] |
Fierro R D, Golub G H, Hansen P C, et al. Regularization by Truncated Total Least Squares[J]. SIAM Journal on Scientific Computing, 1997, 18(4): 1223-1241 DOI:10.1137/S1064827594263837
(  0) 0) |
| [10] |
葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377 (Ge Xuming, Wu Jicang. Generalized Regularization to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372-377)
(  0) 0) |
| [11] |
孙同贺, 闫国庆. 病态总体最小二乘的混合正则化算法[J]. 大地测量与地球动力学, 2017, 37(4): 390-393 (Sun Tonghe, Yan Guoqing. A Hybrid Regularization Algorithm to Ill-Posed Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 390-393)
(  0) 0) |
| [12] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
| [13] |
Wang L Y, Wen G S, Zhao Y W. Virtual Observation Method and Precision Estimation for Ill-Posed Partial EIV Model[J]. Journal of Surveying Engineering, 2019, 145(4)
(  0) 0) |
| [14] |
王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报: 信息科学版, 2010, 35(11): 1346-1350 (Wang Leyang, Xu Caijun, Lu Tieding. Ridge Estimation Method in Ill-Posed Weighted Total Least Squares Adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1346-1350)
(  0) 0) |
| [15] |
王彬, 李建成, 高井祥, 等. 抗差加权整体最小二乘模型的牛顿-高斯算法[J]. 测绘学报, 2015, 44(6): 602-608 (Wang Bin, Li Jiancheng, Gao Jingxiang, et al. Newton-Gauss Algorithm of Robust Weighted Total Least Squares Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 602-608)
(  0) 0) |
| [16] |
Xu P L, Liu J N, Shi C. Total Least Squares Adjustment in Partial Errors-in-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
2. Institute of Survey and Design, East China University of Technology, 56 Xuefu Road, Fuzhou 344000, China;
3. College of Surveying and Geo-Informatics, Tongji University, 1239 Siping Road, Shanghai 200092, China
 2021, Vol. 41
2021, Vol. 41

