2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
在高楼密集林立的城市峡谷中,因为建筑物对于卫星信号的反射、衍射和遮挡等产生多路径误差,使得移动终端定位精度不理想或者无法进行定位[1]。针对城市峡谷中过街方向上定位精度低的问题,Groves[2]提出阴影匹配(shadow matching,SM)算法,该算法可以识别出人行横道和街道。随后,Wang[3]改进阴影匹配的打分模板,过街精度提高9.4%。Wang[4]又利用阴影匹配/卡尔曼滤波、阴影匹配/粒子滤波组合算法提高了定位精度,但在沿街方向上改变不大[5-6]。对于这个问题,胡辉等[7-9]提出粒子滤波的高分值加权改进算法,还提出SM/粒子滤波自适应加权组合算法和EKF的GPS/SM组合定位算法,对定位精度都有显著改善。但在这些研究中,用于判断卫星信噪比可见性的信噪比阈值对所有卫星均采用固定单一值,而不同星座卫星的最小接收功率设计不同,且不同卫星信号到达接收机穿过的大气状况不同,通常状况下的信噪比值也会有所差别,所以对所有卫星采用同一阈值显然会增加卫星可见性判断错误的概率。针对此问题,本文提出采用动态阈值阴影匹配法(dynamic threshold shadow matching,DTSM)来提高卫星可见性判断的准确性,进而提高移动终端的GNSS定位精度。
1 动态阈值阴影匹配算法阴影匹配算法原理是以依据信噪比判定标准获得的卫星可见性为参考基准,对接收机在城市峡谷中的可能位置(搜索范围)上依据已有3D建筑模型和卫星方位角、仰角等信息获得的卫星空间可见性进行评分,所有可能位置中评分(可见性匹配度)最高者作为接收机定位位置。传统算法定位步骤为:
1)进行移动终端初始化定位。通过GNSS接收机获取单点定位结果,得到精度较低的P0点位置信息,将P0点设为可能位置的搜索原点。
2)设定搜索区域。以P0点为中心设定搜索区域,通常情况下可以设置为圆形或者矩形,搜索半径可根据不同终端的定位精度设为10~50 m。
3)预测搜索区域内每个候选位置的卫星可见性。在每个候选位置上,通过卫星坐标和候选位置坐标计算该时刻卫星方位角和高度角,同时结合周围建筑物的三维模型判定该候选位置上的卫星可见性。
4)依据信噪比判断卫星可见性。一般认为,接收机直接接收到卫星信号时其SNR值较高,当接收的是经过建筑物衍射和反射的卫星信号,则SNR值会变低。设定一定的信噪比阈值作为判断标准,当信噪比低于阈值时则判定卫星不可见,否则为可见。
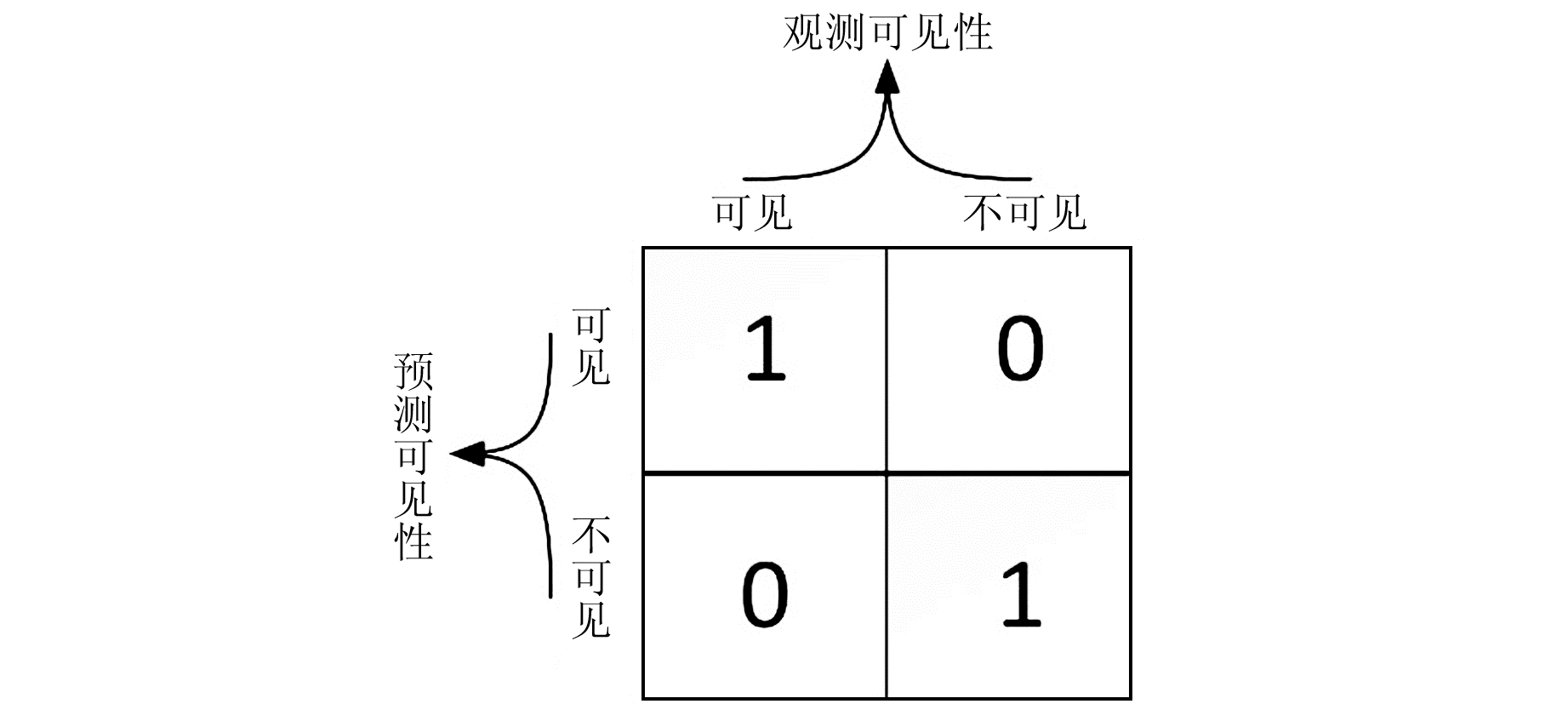
5)候选位置评分。对比步骤3)、4)评估卫星可见度预测值和观测值之间的匹配度,匹配较好的候选位置将被赋予更高的权重。计算候选位置分为两个阶段。首先,利用评分方案,根据预测和观测到的可见度,利用打分模板(图 1),给每颗卫星打分。
|
图 1 打分模板示意图 Fig. 1 Schematic diagram of scoring template |
每个候选位置的总体得分为:
| $ {f_{{\rm{pos}}}}(j) = \sum\limits_{i = 1}^n {{f_{{\rm{sat}}}}(i, j)} $ | (1) |
式中,
6)定位解算。由打分方案可知,在卫星预测和观测准确的情况下,高分值所在的侯选位置更接近真实位置,通常高分侯选位置不止一个,则取坐标均值作为阴影匹配的定位结果。
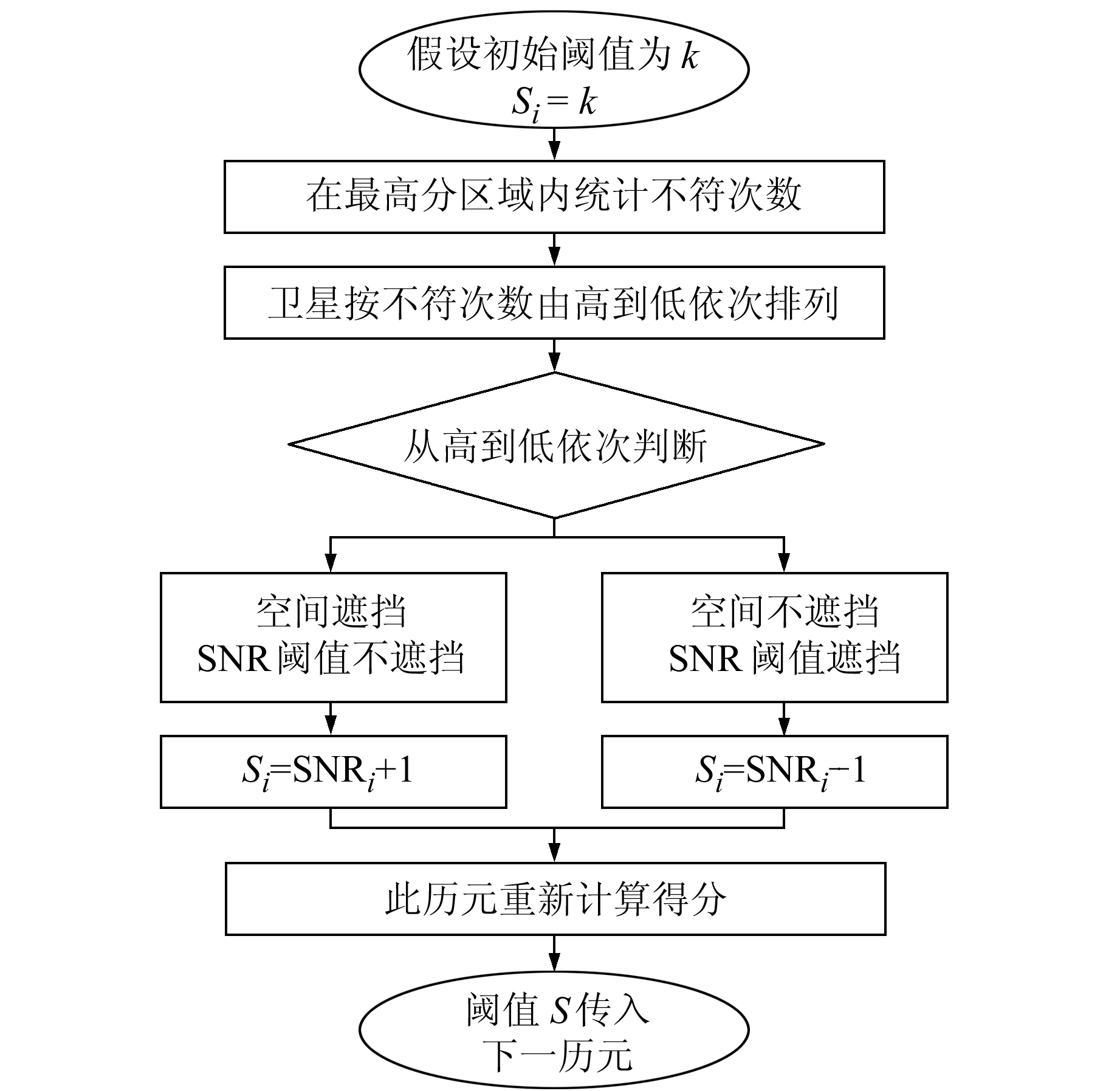
在实际运算过程中,传统方法通过卫星的信噪比经验阈值来判定卫星的可见性不够准确,因为同为可见或同为遮挡的不同卫星,其SNR值由于信号穿过大气/云层的不同也会存在差异,采用相同阈值会有误判的可能。在高分值区域内,如果阈值设置正确,理论上当搜索位置与实际观测位置一致时,预测可见性与观测可见性将完全一致,但实际上每历元的候选位置中通常不存在满分位置,据此本文提出在每个历元中找到可使最优区域产生满分的一组动态阈值,阈值组随时间继承,直至因非满分再进行局部阈值改变。动态阈值算法计算流程如图 2所示,具体步骤为:
|
图 2 动态阈值流程图 Fig. 2 Dynamic threshold flow chart |
1)首先设定初始阈值组为k(
2)在该历元中最高分区域内统计每个候选位置上预测可见性与观测可见性不符的卫星,设分差为d,全部不符卫星数为
3)选择不符卫星中出现次数由高到低的前d颗卫星;
4)依据卫星预测可见性对d颗卫星依次改进SNR阈值Si:
① 依据几何关系判断遮挡,SNR阈值判断不遮挡
| $ {S_i} = {\rm{SN}}{{\rm{R}}_i} + 1 $ | (2) |
② 依据几何关系判断不遮挡,SNR阈值判断遮挡
| $ {S_i} = {\rm{SN}}{{\rm{R}}_i} - 1 $ | (3) |
5)重新进行搜索区域内的候选位置打分,根据打分最高区域计算改正后点位,将阈值组传入下一历元。
2 实验分析本次实验采用某品牌智能手机作为接收机,同时使用RTK完成对实验区域周围的建筑物的测量,包括建筑物各个角点测量以及楼层高度测量,以此建立的三维模型。实验区域位于桂林理工大学雁山校区7A、7B、6B、6C四栋楼之间的过道,峡谷总长为130 m,宽度为16 m,进行静态模式测量。
实验中同时采用RTK测定坐标。由于RTK获得的坐标精度远高于手机定位后的坐标精度,因此将其作为分析实验精度的参考值。数据采集时间为2020-05-10 14:13~14:36,采样间隔1 s。以3 s时刻采集的坐标数据为例,用采集的坐标作为中心建立20 m×20 m的矩阵搜索区域,候选区域边长为0.5 m,共1 600个候选区域。
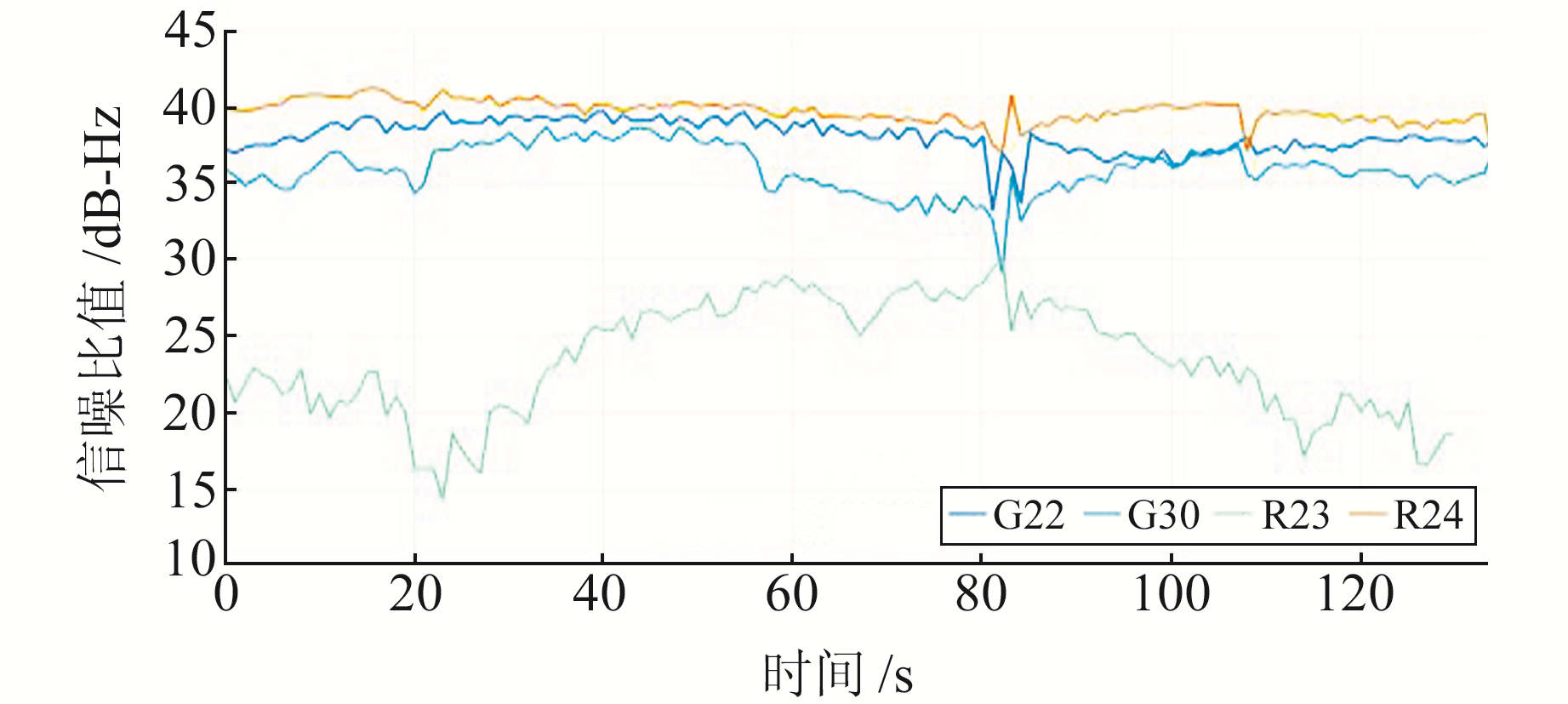
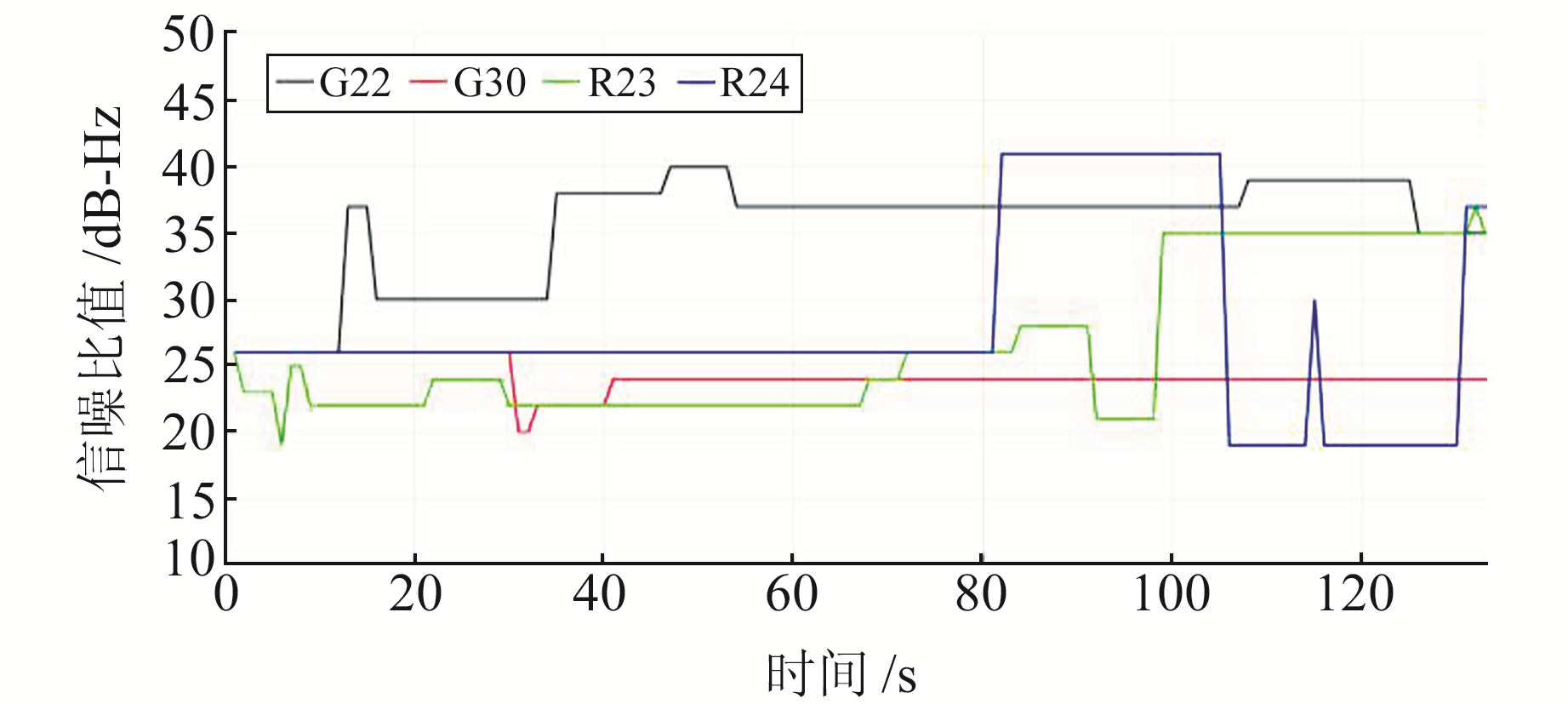
在整个观测的过程中部分卫星信噪比值变化如图 3所示,可以很明显地看出,卫星信噪比数值在每个历元均会发生波动,不同卫星信噪比所处区间有较大差异。为了避免采用单一阈值可能造成的卫星可见性的误判,引入动态阈值来减弱这种影响(图 4),对每颗卫星在不同历元均采用动态阈值后,阈值与相应卫星的信噪比区间有较好的对应,对于单颗卫星,其SNR值波动不大的情况下阈值变化也非常稳定。
|
图 3 卫星信噪比值变化 Fig. 3 Variation of satellite SNR |
|
图 4 卫星动态阈值 Fig. 4 Satellite dynamic threshold |
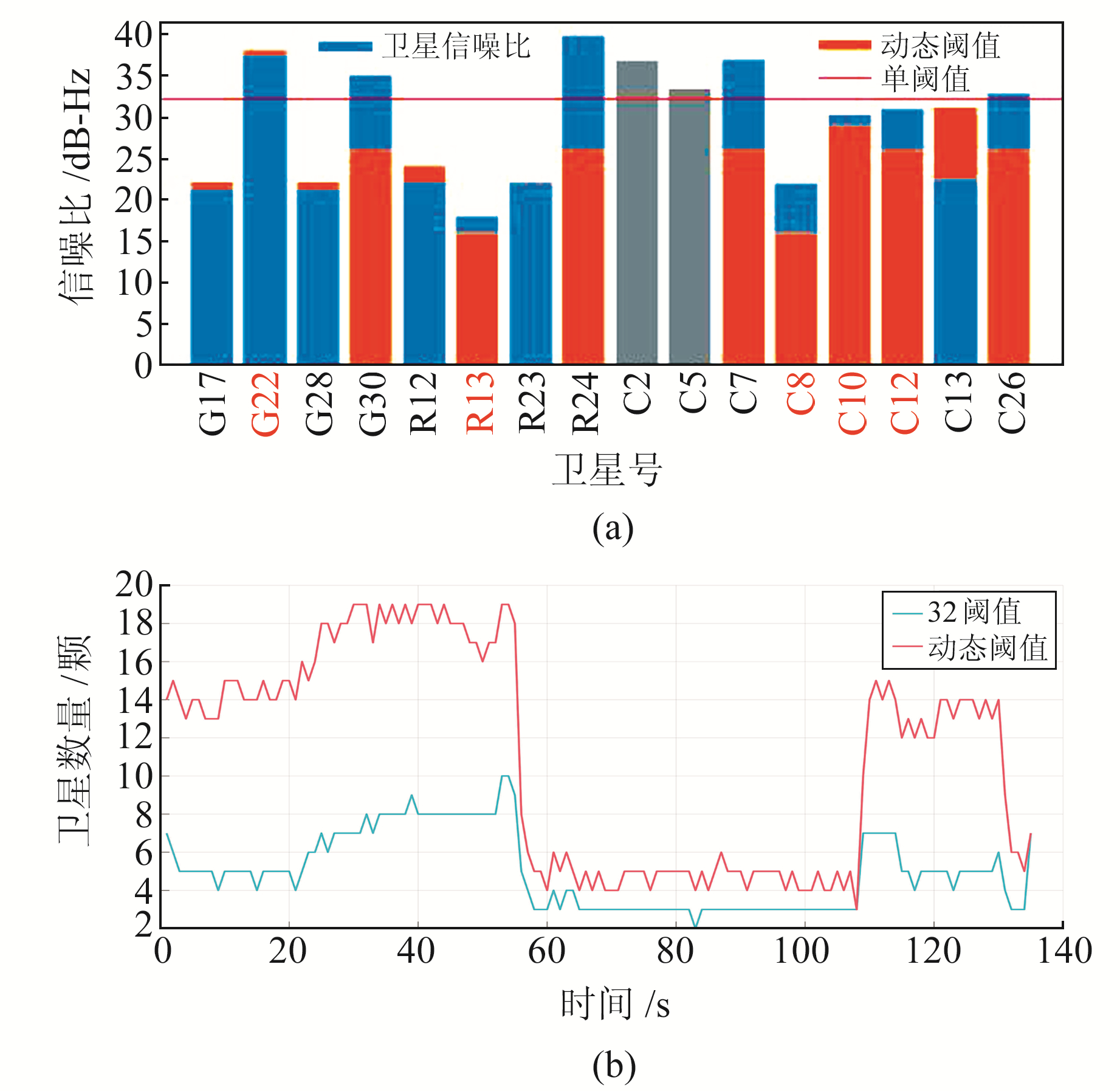
根据文献[7],基于高分值加权的改进阴影匹配定位算法研究中推荐使用38作为单阈值,本文中所采集数据信噪比值偏低,经验证后采用32作为单阈值。以3 s时刻为例,手机原始观测接收到16颗卫星的信号,每颗卫星的信噪比值如图 5(a)所示,灰色标记的卫星为5°截止角过滤掉的卫星,不参与匹配过程。图中红色横线为单阈值(32阈值),橘黄色部分为该时刻从上一时刻继承及本时刻改进后的动态阈值,可以看出,采用动态阈值后与单一阈值时相比对于卫星可见性的判断差异明显,红色字体的卫星为采用动态阈值后可见性发生变化的卫星。图 5(b)显示了每历元采用单阈值和动态阈值判断的卫星可见性与SNR判断一致的卫星个数(得分)。
|
图 5 依据32阈值、动态阈值判断第3 s的卫星可见性及与SNR判断一致卫星个数(得分)随时间的变化 Fig. 5 The satellite visibility of the 3 s time according to 32 threshold and dynamic threshold and the variation of satellite number consistent with SNR judgment |
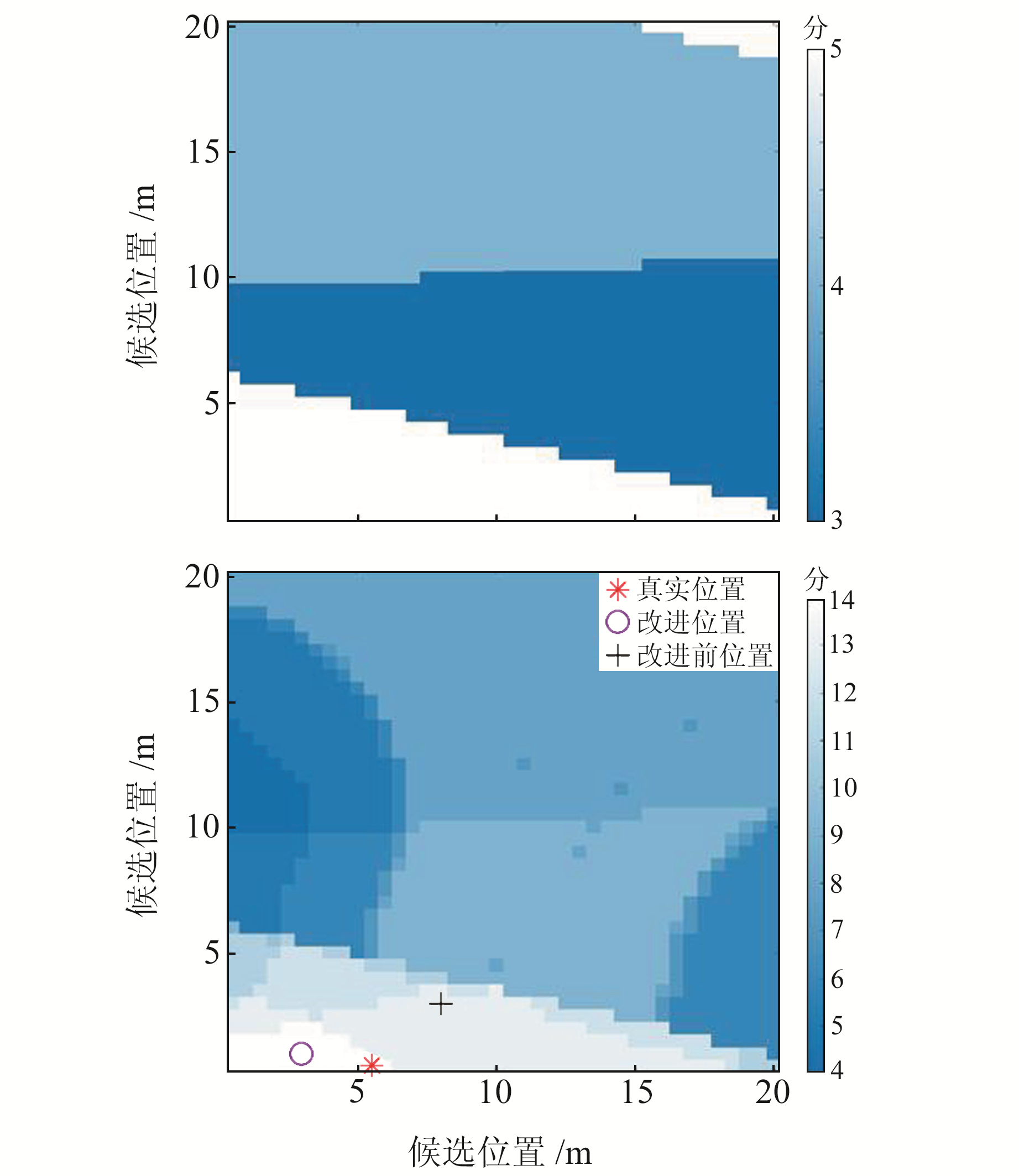
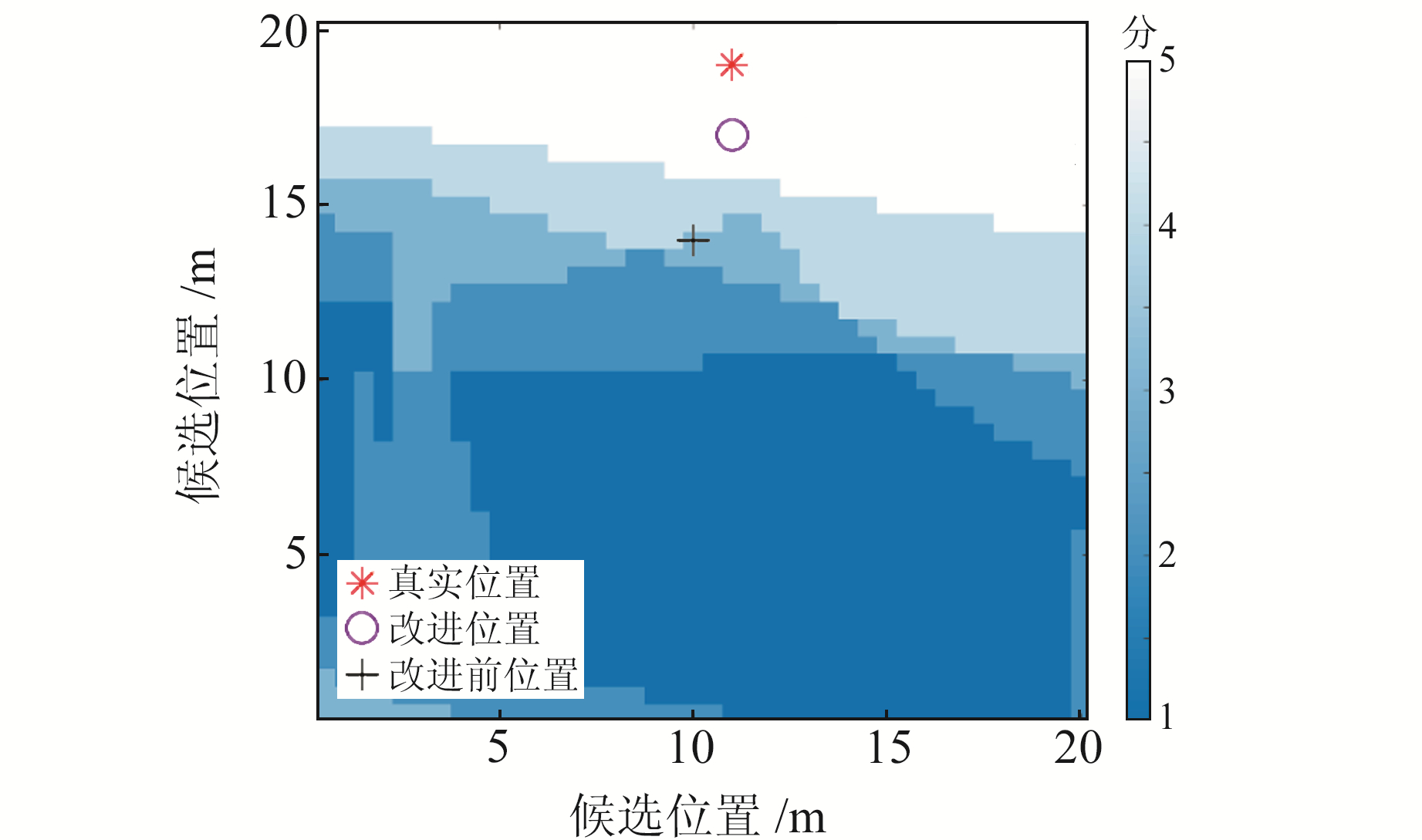
图 6为分别依据单一阈值法和动态阈值法进行阴影匹配计算后的得分如图 6所示,单一阈值时搜索区域中最高得分的位置数量较多,采用邻近点KNN-SM算法得出的位置精度会有所偏差,通过动态阈值处理后原高分区域内出现了分化,出现了相对单一阈值的更高分区域,面积相对变小,计算出的点位位置变得相对更加精确。图 6中,红色“*”代表真实位置粉色,“o”代表动态阈值阴影匹配计算位置,黑色“+”代表 32阈值时阴影匹配的计算位置。可以看出,动态阈值时较32单阈值时匹配结果有明显的精度提升。对比可知,第3 s时刻动态阈值算法改正值相较于32阈值在点位误差上降低了1.08 m,相比于原始观测值降低了8.37 m。如图 7所示,在第96 s时刻动态阈值改进后的点位误差比32阈值的SM算法降低3.46 m,定位精度有较大的提升。
|
图 6 32阈值和动态阈值下第3 s打分图 Fig. 6 Scoring diagram at the 3 s time under 32 threshold and dynamic threshold |
|
图 7 第96 s动态阈值打分图 Fig. 7 Scoring diagram of dynamic threshold at the 96 s time |
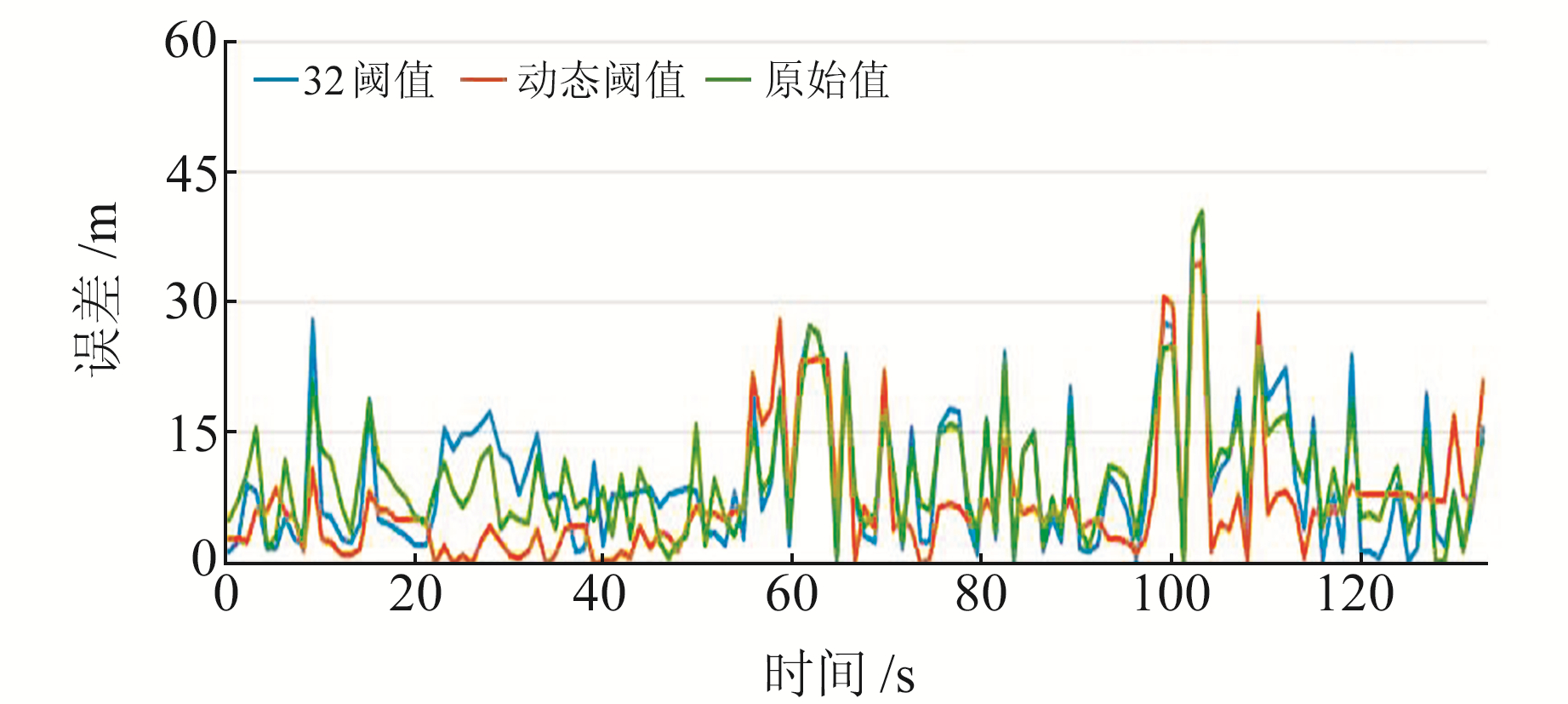
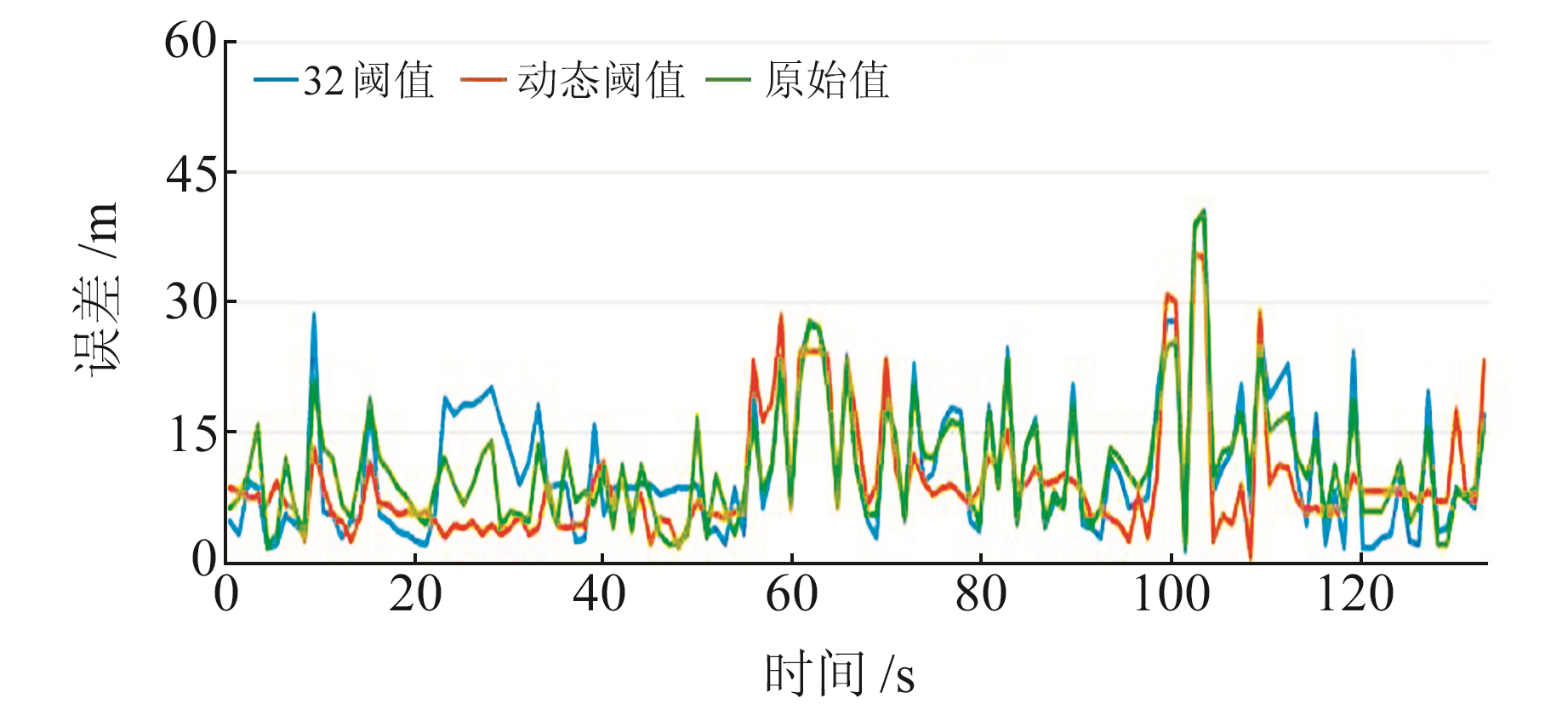
对实验中采用不同算法所获得的点位误差进行分析发现,动态阈值法相对于单阈值法(32阈值)和原始观测值在过街方向上都有一定程度的改进(图 8),点位误差也有一定程度的改善(如图 9)。然而,也存在部分位置改进效果不好甚至变差的情况,为该时段卫星数量较少所致。卫星数越少动态阈值所能改正的卫星阈值的数量越少,同样单阈值时能使用的卫星也就越少,导致误差增大,改正效果不理想。
|
图 8 过街方向平均绝对误差 Fig. 8 MAE in crossing direction |
|
图 9 点位误差 Fig. 9 Point error |
从整体上来看,动态阈值法(DTSM)相对于32阈值的阴影匹配(SM)算法计算精度有所改进,动态阈值相比于固定阈值,点位平均绝对值误差(mean absolute error,MAE)降低约15.1%,均方根误差(root mean square error,RMSE)降低约14.9%。在过街方向上,动态阈值MAE相对于固定阈值降低约26.7%,RMSE降低约19.7%,相对于原始值MAE降低约28.9%,RMSE降低约16.4%。
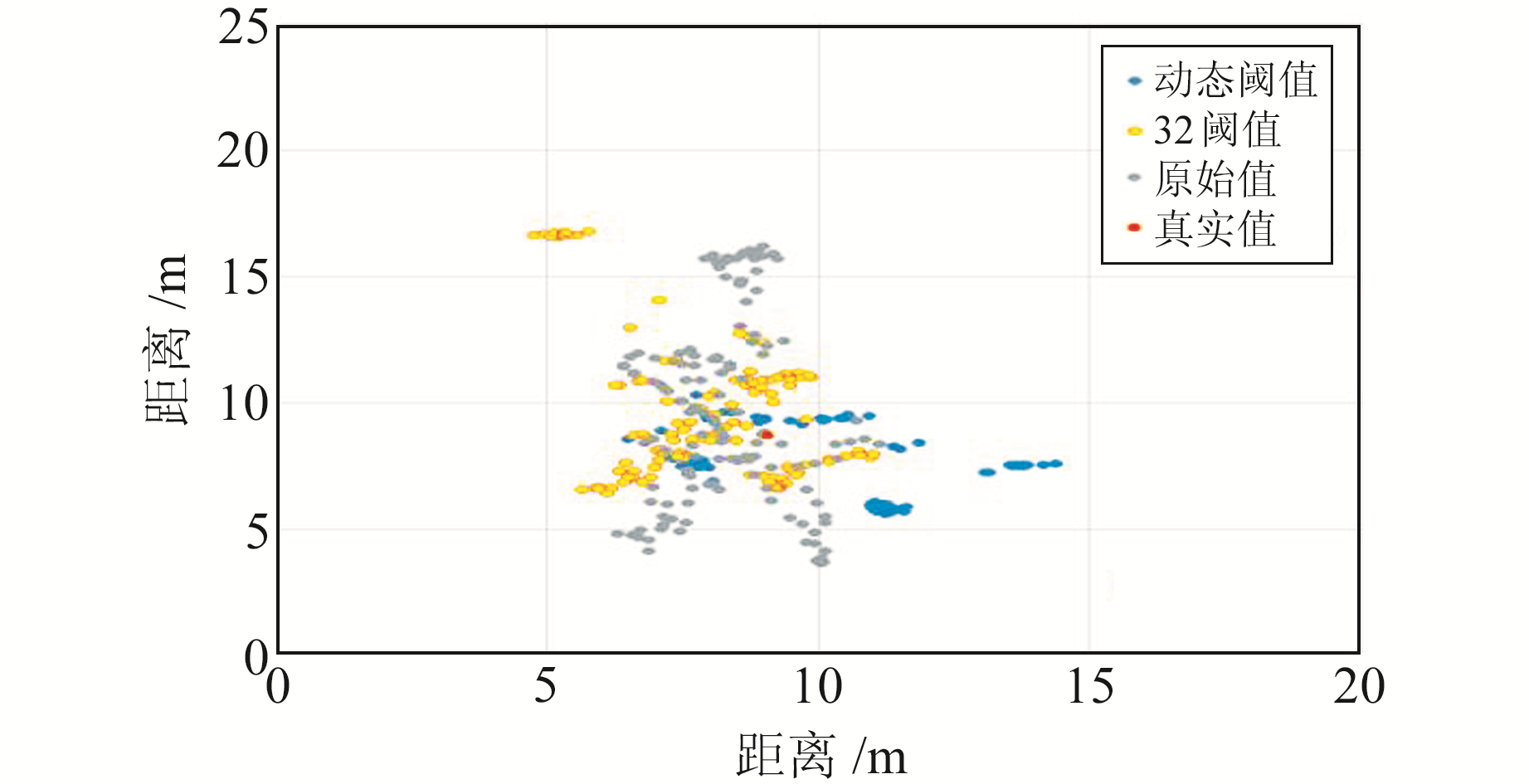
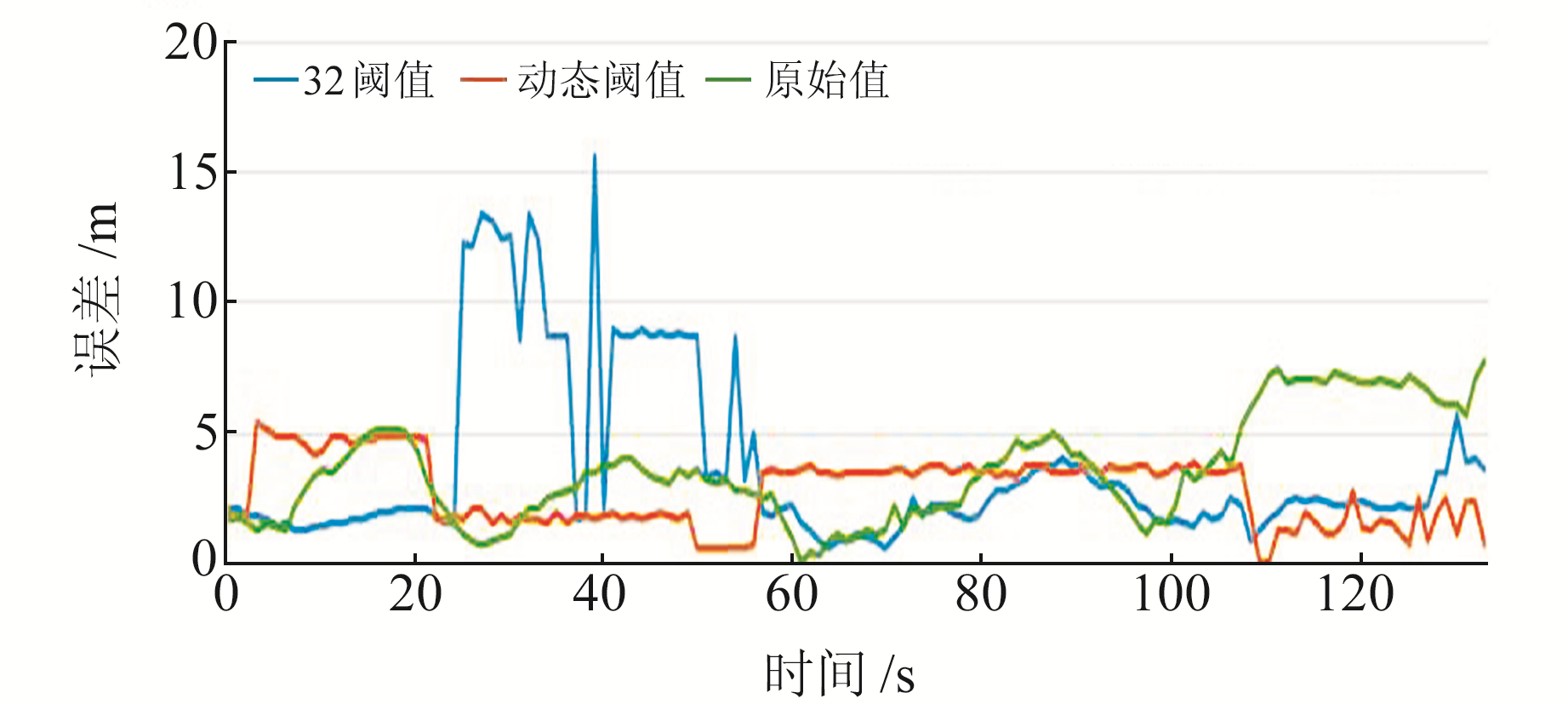
对原始观测值进行卡尔曼滤波(KF)后再进行阴影匹配,采用动态阈值和32阈值计算的坐标点如图 10所示,卡尔曼滤波后采用动态阈值阴影匹配(KF+DTSM)的RMSE为3.09 m,相比于卡尔曼滤波的4.09 m降低24.4%。图 11为不同方法的点位误差,动态阈值相比于其他两种方法更加稳定,卡尔曼滤波的MAE为4.77 m,KF+32阈值SM的MAE为4.58 m,KF+DTSM的MAE为3.55 m。KF+DTSM相比于KF在误差上降低1.22 m,精度提升25.6%;相比于KF+32阈值SM降低1.03 m,精度提升22.4%。实验中不同算法的点位误差统计见表 1。
|
图 10 点位分布 Fig. 10 Point distribution |
|
图 11 加入卡尔曼滤波后的点位误差对比 Fig. 11 Comparison of point error after adding Kalman filter |
|
|
表 1 不同算法点位误差统计 Tab. 1 Point error statistics of different algorithms |
阴影匹配算法对于城市峡谷中智能移动设备GNSS导航定位的精度有一定提升,但采用单一阈值进行卫星可见性判断时会增加部分卫星误判的可能,针对此问题,本文提出采用动态阈值法进行卫星可见性判断,在每个历元进行卫星的几何判断可见性与信噪比判断可见性的一致性分析,采用动态阈值使一致性最大,从而改进阴影匹配算法的定位精度。实验分析表明,相对于单一阈值法,动态阈值阴影匹配算法对于手机GNSS定位结果的改正效果更加明显,点位精度更加稳定。在实验中也发现,初始定位精度对算法的有效性有较大影响,初始定位利用卡尔曼滤波处理后再进行动态阈值阴影匹配,精度会有明显的改进,原因可能为初始定位偏离真实值太远后,搜索区域无法覆盖到真实值,进而导致算法改进不理想。沿街方向上由于直视信号较好,其定位更准确,阴影匹配的改进效果不够理想。
| [1] |
徐龙威, 刘晖, 张明, 等. 不同截止高度角多模GNSS组合单点定位性能分析[J]. 大地测量与地球动力学, 2015, 35(6): 987-991 (Xu Longwei, Liu Hui, Zhang Ming, et al. Performance Assessment of Multi-GNSS Single Point Positioning with Different Cut-Off Elevation Angles[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 987-991)
(  0) 0) |
| [2] |
Groves P D. Shadow Matching: A New GNSS Positioning Technique for Urban Canyons[J]. Journal of Navigation, 2011, 64(3): 417-430 DOI:10.1017/S0373463311000087
(  0) 0) |
| [3] |
Wang L, Groves P D, Ziebart M K. Smartphone Shadow Matching for Better Cross-Street GNSS Positioning in Urban Environments[J]. Journal of Navigation, 2015, 68(3): 411-433 DOI:10.1017/S0373463314000836
(  0) 0) |
| [4] |
Wang L, Groves P, Ziebart M. Urban Positioning on a Smartphone: Real-Time Shadow Matching Using GNSS and 3D City Models[C]. International Technical Meeting of the Satellite Division of the Institute of Navigation, 2013
(  0) 0) |
| [5] |
Wang L, Groves P D, Ziebart M K. GNSS Shadow Matching: Improving Urban Positioning Accuracy Using a 3D City Model with Optimized Visibility Scoring Scheme[J]. Navigation, 2013, 60(3): 195-207 DOI:10.1002/navi.38
(  0) 0) |
| [6] |
Groves P D, Wang L, Ziebart M. Shadow Matching: Improved GNSS Accuracy in Urban Canyons[J]. GPS World, 2012, 23(2): 14-18
(  0) 0) |
| [7] |
夏景平, 胡辉, 颜瑜军, 等. 基于高分值加权的改进阴影匹配定位算法研究[J]. 全球定位系统, 2017, 42(6): 1-8 (Xia Jingping, Hu Hui, Yan Yujun, et al. Improved Shadow Matching Positioning Algorithm Based on High Score Weighting[J]. GNSS World of China, 2017, 42(6): 1-8)
(  0) 0) |
| [8] |
胡辉, 欧敏辉, 颜瑜军. 阴影匹配/粒子滤波自适应加权组合定位算法[J]. 探测与控制学报, 2016, 38(4): 82-87 (Hu Hui, Ou Minhui, Yan Yujun. Shadow Matching/Particle Filter Adaptive Weighted Integrated Localization Algorithm[J]. Journal of Detection & Control, 2016, 38(4): 82-87)
(  0) 0) |
| [9] |
胡辉, 颜瑜军, 欧敏辉. 一种基于EKF的GPS/SM组合定位算法[J]. 全球定位系统, 2016, 41(2): 7-13 (Hu Hui, Yan Yujun, Ou Minhui. A Novel GPS/SM Integrated Positioning Algorithm Based on EKF[J]. GNSS World of China, 2016, 41(2): 7-13)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2021, Vol. 41
2021, Vol. 41


