2. 南宁师范大学北部湾环境演变与资源利用教育部重点实验室, 南宁市明秀东路175号,530001;
3. 南宁师范大学广西地表过程与智能模拟重点实验室,南宁市明秀东路175号,530001
卫星测高技术起初是为研究海洋环境所研制的,在全球海平面、冰川监测等领域得到了广泛应用。近年来,众多学者逐渐将其应用于内陆水体水位变化监测[1-5],但对于地形复杂且水面宽度不大的河流来说,卫星测高的精度有待提升。主要提升方法包括:1)对各种改正参数进行优化,如电离层延迟校正、对流层干湿分量改正及地球物理项改正;2)通过波形重跟踪算法提高卫星至河流表面距离的观测精度。很多学者针对近海海域及内陆湖泊的水位监测进行了算法改进,例如基于子波形的波形重跟踪算法[6]、基于主波峰的波形重跟踪算法[7]、多子波多权重阈值重跟踪算法[8]等,但在应用于河流水位监测时的精度还有进一步提升的空间。
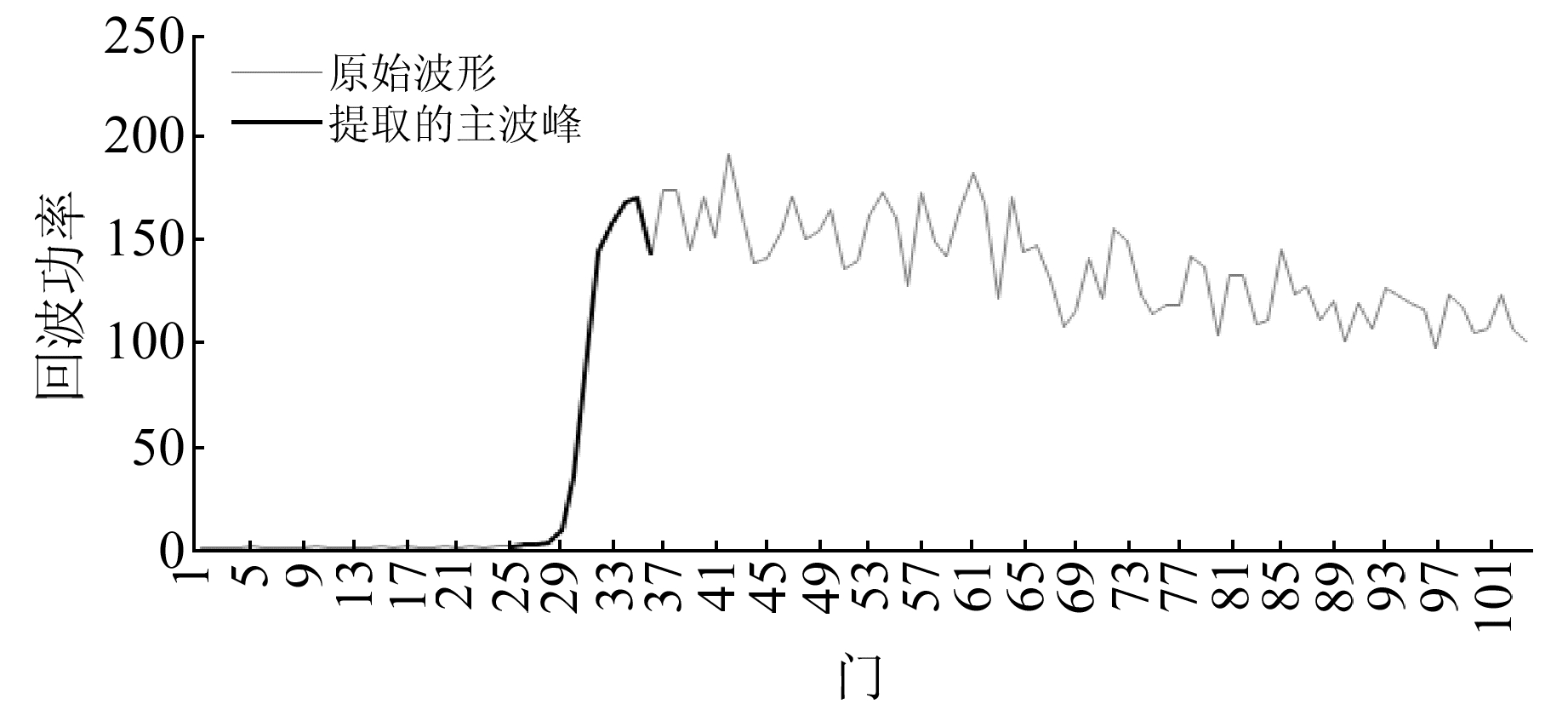
寻找主波峰是波形重跟踪算法中的关键和难点(图 1)。由于受陆地反射效应引起的卫星测高回波波形的污染,卫星测高精度均受限于湖泊及河流区域。但相比湖泊水位观测,河流水体反射的回波波形更为复杂,在寻找主波峰时更易受噪声影响。其次,同一卫星轨道在不同时期的回波波形复杂多变,以一种算法难以适应整个水位监测时期的精度。为此,本文针对河流水体,在基于主波峰波形重跟踪算法[7]的基础上提出一种基于主波峰波形的自适应重跟踪算法(AMWRT),并以长江中游河段为研究区,利用水文站日平均实测水位数据对其进行精度检验。
|
图 1 主波峰提取示意图 Fig. 1 Schematic diagram of the extraction of the primary wave peak |
长江中游位于湖北省中南部(111°45′~ 114°16′E,29°26′~31°10′N),流经宜昌市至湖口县,全长955 km,流域面积约68万km2,洞庭湖水系(四水流域)、汉江分别位于长江中游的南北两岸。长江经过的湖北省西部地区两侧多为高山,流水容易汇集,加上河道弯曲,导致洪水宣泄不畅,极易溃堤成灾[9]。因此,精准监测长江中游水位变化,对于防汛抗旱、调蓄能力评估等具有重要的指导意义。本文研究区选择长江中游的枝城水文站附近河道(图 2),沿坡两岸地理环境较为复杂,分布有植被及建筑物等。

|
图 2 研究区位置 Fig. 2 Location of the studied area |
Jason-2卫星波形地球物理数据(SGDR)来源于法国国家空间研究中心的卫星海洋学存档数据中心(https://www.aviso.altimetry.fr/en/home.html),时间范围选取2008-07~2016-07(cycle001~cycle302)。SGDR数据包含20 Hz的波形数据、卫星地面距离数据和一些质量控制字段及地球物理校正数据。Jason-2卫星每运行一个完整的周期就会有254条pass, 重访周期为10 d,经过长江中游枝城水文站附近的轨迹为pass12。枝城水文站实测日平均数据(2008-07~2009-12) 来源于长江水利委员会(http://www.cjw.gov.cn),宜昌气象站日降水量数据来源于国家气象数据共享服务平台(https://data.cma.cn)。
2 研究方法 2.1 波形重跟踪算法卫星测高波形是雷达脉冲信号回波功率的几何表示,与测高仪观测距离存在函数关系,且与反射表面的散射性质有关[6]。测高卫星自南半球向北半球运转,当卫星轨道从海洋经过内陆水域时,接收到的测高回波波形由规则低噪声逐渐向不规则强噪声过渡。测高回波波形大致有规则波形(图 3(a))、尖锥波形(图 3(b))、复杂波形(图 3(c))3种模式,其中规则波形是海洋回波波形的主要表现形式,形状近似于规则的布朗模型且波形前缘噪声很小;尖锥波形、复杂波形则是内陆水体回波波形的主要表现形式。当卫星同一轨迹的不同时期经过内陆水域时,回波会以2种形式出现,可以看到复杂波形的前缘噪声很大且出现多个波峰。

|
图 3 不同区域内的卫星测高波形 Fig. 3 Satellite altimetry waveforms in different areas |
通过重跟踪算法对卫星测高波形进行模拟,找到波形上升前缘的中点,其与Jason-2卫星预设跟踪门(值为32)之间的差值为距离改正值,最后对卫星至水体表面的距离进行重新修正即为波形重跟踪。当前波形重跟踪算法在寻找内陆水体复杂波形的前缘中点时面临困难,为此本文构建了一种基于主波峰的自适应波形重跟踪算法(AMWRT)对卫星测高波形进行重跟踪,并与较为经典的重心偏移法(OCOG)[6]及10%、20%、50%三种不同阈值水平的阈值法(threshold)[10]进行对比。
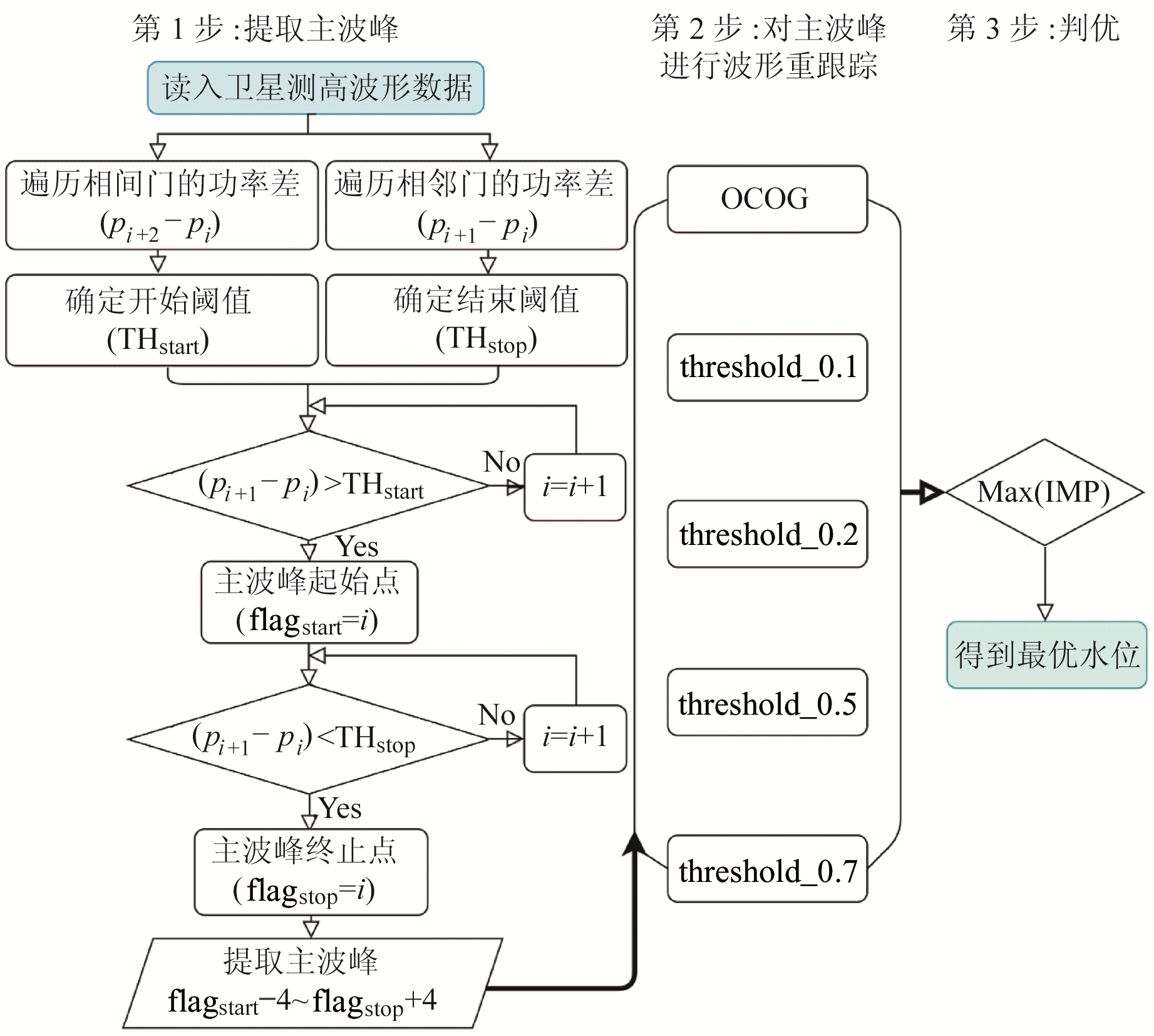
AMWRT算法具体包括3个步骤(图 4)。
|
图 4 AMWRT算法流程 Fig. 4 Flow chart of AMWRT algorithm |
1) 提取主峰波形[11]:
| $ d_{1}^{i}=p_{i+1}-p_{i} $ | (1) |
| $ d_{2}^{i}=p_{i+2}-p_{i} $ | (2) |
| $ \begin{gathered} T H_{\text {start }}=\sqrt{\frac{(N-2) \sum\limits_{i=1}^{N-2}\left(d_{2}^{i}\right)^{2}-\left(\sum\limits_{i=1}^{N-2} d_{2}^{i}\right)^{2}}{(N-2)(N-3)}} \end{gathered} $ | (3) |
| $ \begin{gathered} \mathrm{TH}_{\text {stop }}=\sqrt{\frac{(N-1) \sum\limits_{i=1}^{N-2}\left(d_{1}^{i}\right)^{2}-\left(\sum\limits_{i=1}^{N-2} d_{1}^{i}\right)^{2}}{(N-1)(N-2)}} \end{gathered} $ | (4) |
式中,d1i为相邻跟踪门所对应的功率差,d2i为相间跟踪门所对应的功率差,THstar为主波峰标记开始点的阈值,THstop为主波峰标记结束点的阈值。以整个波形数据相邻、相间跟踪门功率差序列确定主波峰提取的开始阈值(THstart)和结束阈值(THstop),当d1i首次大于THstart时,标记i门为主波峰起始点;当d1i小于THstop时,标记该i门为主波峰的终止点。将找到的主波峰前后各增加4个跟踪门,形成完整的主波峰波形。由于河流类型的波形较为复杂,波形前缘热噪声出现起伏,可通过适当调整开始阈值以减少波形前缘噪声的影响。
2) 对主波峰进行波形重跟踪,即对上述提取的主波峰波形进行OCOG和threshold法10%、20%、50%及70%四种不同阈值水平的波形重跟踪。
3) 以IMP评判指标对上述同一时期波形重跟踪算法获得的水位值进行判优:
| $ \mathrm{IMP}=\frac{\sigma_{\mathrm{raw}}-\sigma_{\mathrm{re}}}{\sigma_{\mathrm{raw}}} \times 100 \% $ | (5) |
式中,σraw为波形重跟踪前水位的标准差,σre为波形重跟踪后水位的标准差,IMP值越大则表明测高点瞬时水位值之间的差值越小。以IMP最大值的波形重跟踪算法得到的结果作为AMWRT算法的结果。
2.2 卫星测高数据获取河流水位使用Jason-2卫星数据20 Hz的SGDR波形数据,根据上述波形重跟踪算法,计算获得改正后的观测距离(Ran)。河流自由水面的高程[12]计算公式为:
| $ H = {\rm{Alt}}-{\rm{Ran}}-{\rm{Hei}}-\Delta {\rm{CCor}} $ | (6) |
式中,H为河流水位高程,Alt为测高仪的椭球高,Ran为雷达高度计至水面的观测距离,Hei为大地基准面相对于参考椭球面的高度,ΔCCor为各项观测误差修正。由于河流的面积较小,与海洋相比受海潮、逆气压、高频风压力和压力反馈等的影响很小,可忽略[13]。ΔCCor计算公式为:
| $ \Delta {\rm{CCor}} = {\rm{Wet}} + {\rm{Dry}} + {\rm{Iono}} + {\rm{Solid}} + {\rm{Pol}} $ | (7) |
式中,Wet为湿对流层修正,Dry为干对流层修正,Iono为电离层修正,Solid为固体潮修正,Pol为极潮修正。
利用雷达测高工具箱BRAT(basic radar altimetry toolbox)软件对SGDR数据进行以下处理:1)提取出河流范围内的所有点;2)保证测高仪所观测的高度有效;3)对各修正项数值范围进行有效设定[14],确保各项改正数据在有效范围内;4)提取波形数据。
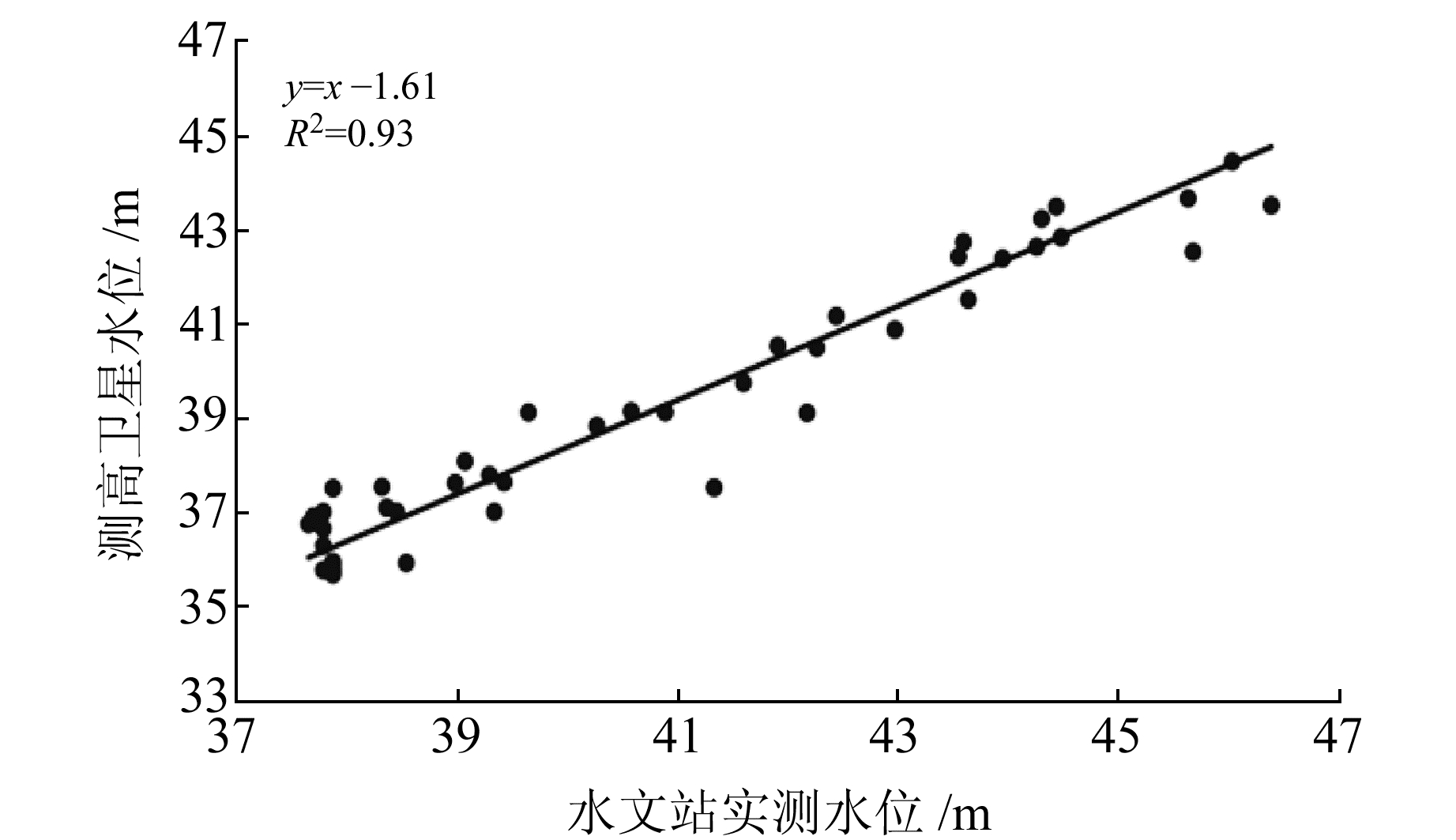
2.3 水位高程基准转换利用AMWRT算法对测距值进行重新修正,通过水位计算公式获得瞬时水位。利用连续优质点数据质量筛选办法[3]对瞬时水位进行数据筛选,然后取水位均值,获得区域内某一时期的卫星测高水位。由于卫星测高水位(基于EGM96大地水准面)与枝城水文站实测水位(基于吴淞水系水准面)的基准面不同,为进行对比分析,需要获取垂直基准偏差[10]。对卫星测高水位与实测水位进行线性拟合(拟合斜率为1),将卫星测高水位归算至枝城水文站基准面下,结果如图 5所示,可以看出,二者具有很强的相关性。由拟合方程可知,EGM96大地水准面比吴淞水系水准面起点高1.61 m。
|
图 5 卫星测高水位与实测水位散点对比 Fig. 5 Comparison of the scatter points of the water level measured by satellite and the hydrological station |
Jason-2卫星测高数据经6种重跟踪算法(AMWRT算法中threshold_0.7(即阈值水平为70%,下同)仅针对特殊波形,故未考虑)处理后,获得长江中游2008-07~2009-12的瞬时水位。AMWRT算法在该时期的平均水位为40.79 m,与实测水位40.81 m最为接近,threshold_0.1、threshold_0.2、threshold_0.5及GDR (原数据自带的重跟踪算法)、OCOG法获得的平均水位依次为41.15 m、40.89 m、40.25 m、40.20 m、40.13 m。
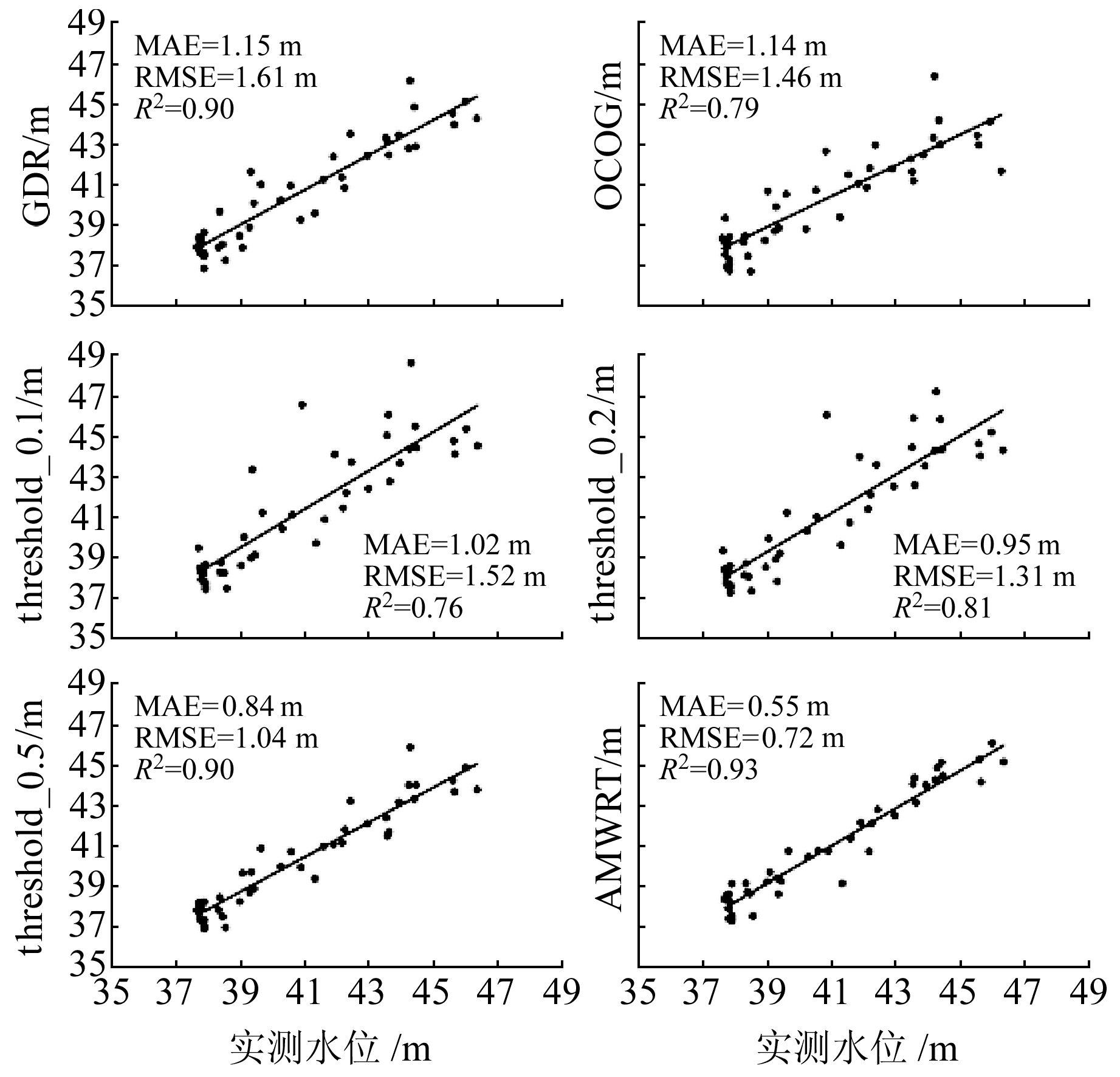
月内长江中游日平均水位变化较大,最低水位为39.43 m,最高水位为44.31 m,变化幅度可达4.88 m。图 6显示,不同波形重跟踪算法获得的水位在变化趋势上与实测水位高度一致,二者拟合系数在0.73~0.93之间,但均出现了不同程度的偏离(图 7)。与实测水位相比,除AMWRT算法外,其他算法在2008-11-08得到的水位均被不同程度地高估(图 6红色方框),其原因在于该时期岸边地物目标距离卫星更近,使得回波波形中陆地反射信号在波形中占主导地位,形成的第1个上升强回波容易被经典重跟踪算法认为是水体反射形成的回波,从而形成误差。

|
图 6 测高与实测月水位对比 Fig. 6 Comparison of height measurement and gauged monthly water level |
|
图 7 卫星测高与实测日平均水位对比 Fig. 7 of height measurement and average gauged water level |
图 7显示了OCOG法及threshold法在10%、20%和50% 阈值水平下得到的卫星测高水位与枝城水文站日平均水位的对比,可以看出,其精度差异较大,MAE介于0.55~1.41 m之间,RMSE介于0.72~1.61 m之间。GDR算法获取的卫星测高水位MAE为1.15 m,表明在长江中游区域对波形数据进行重跟踪十分必要。就threshold法而言,相对于其他阈值水平,50%阈值水平的重跟踪算法的精度改善效果更好,MAE为0.845 m,RMSE为1.04 m。相比于经典算法,AMWRT算法表现最好,获得的河流水位精度最高,MAE为0.55 m,RMSE为0.72 m。
不同波形重跟踪算法得到的水位与实测水位的偏差对比如表 1所示,可以看出,在最大、最小差值变化幅度中,经典的重跟踪算法得到的水位与实测水位偏离较大,而AMWRT算法得到的水位偏差都较为稳定。就绝对平均误差而言,除AMWRT算法外,其他重跟踪算法的精度都在1 m左右,其原因可能在于,典型的重跟踪算法在复杂的内陆水域往往会被卫星测高波形前缘的热噪声所影响,从而导致寻找波形上升前缘的位置与实际位置产生较大的偏离。由于AMWRT算法对主波峰的开始阈值进行了调整,可以减少回波波形上升前缘的热噪声对波形重跟踪结果的影响,故AMWRT算法表现最好。
|
|
表 1 波形重跟踪算法精度分析 Tab. 1 Comparison of accuracy improvement of data screening methods |
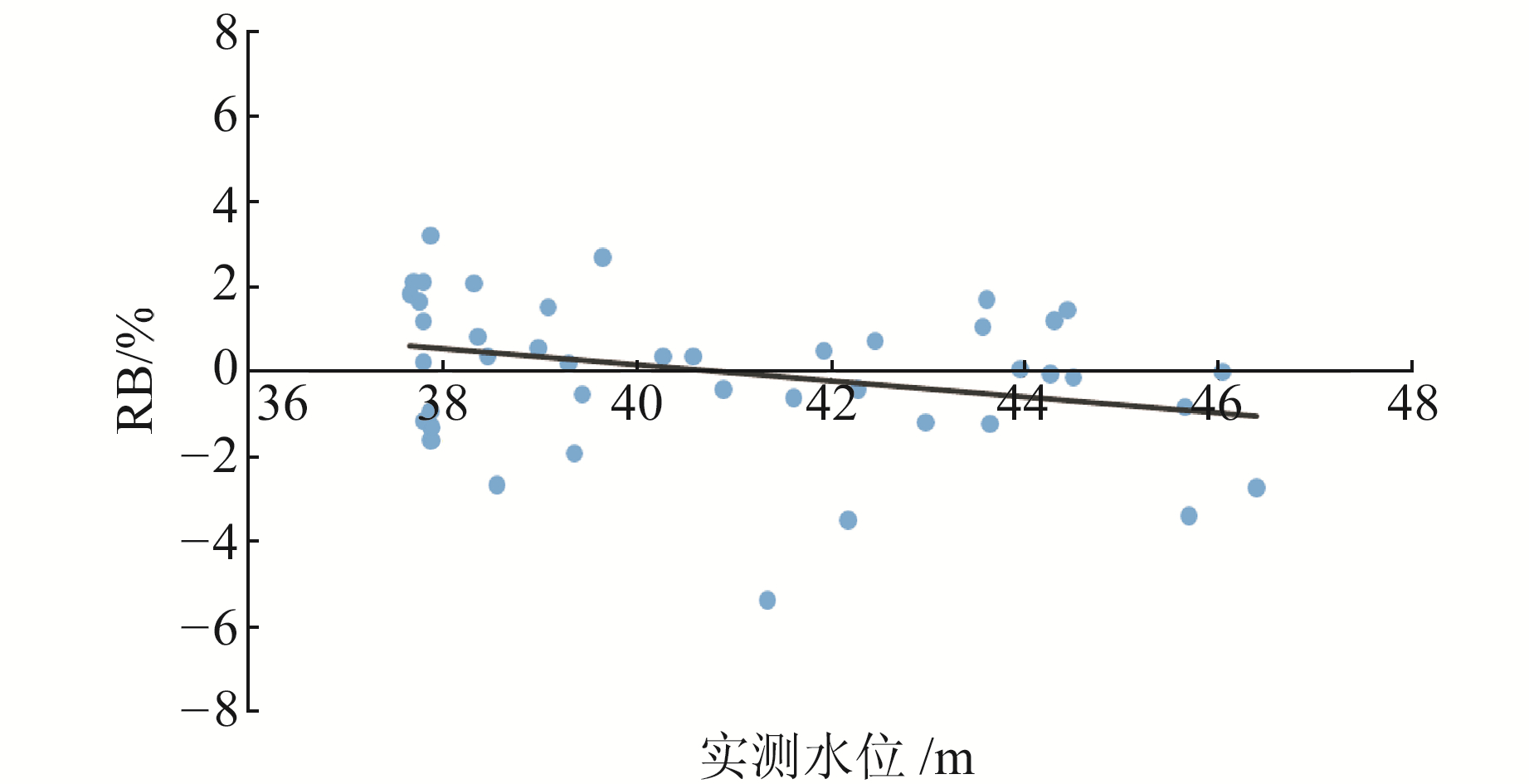
AMWRT算法获得的长江中游水位MAE在0.55 m左右波动,如图 8所示,随着实测水位的降低,卫星测高水位的相对误差(RB)随之升高。其原因在于:1)受长江中游周围地形的影响,河流水位降低会导致反射波的上升前缘之前和之后都容易出现回波,且由于岸边物体的反射率与水体发射率不同,波形中多个波峰的强度也不同;2)雷达高度计的脚印大小与卫星高度、反射面坡度及粗糙度有关。Jason-2测高卫星中心脚印点的直径约为2~4 km[15],而与平坦宽阔海域相比,长江中游河流宽度较小,当河流水位较低时,探测区水域均质性降低,测高回波中陆地污染影响增强,导致河流的测高卫星回波更为复杂。在进行波形重追踪时,会出现难以正确找到波形上升前缘的情况,故降低了卫星测高数据的精度。
|
图 8 卫星测高水位误差随实测水位变化 Fig. 8 Changes of the error of height measurement with the gauged water level |
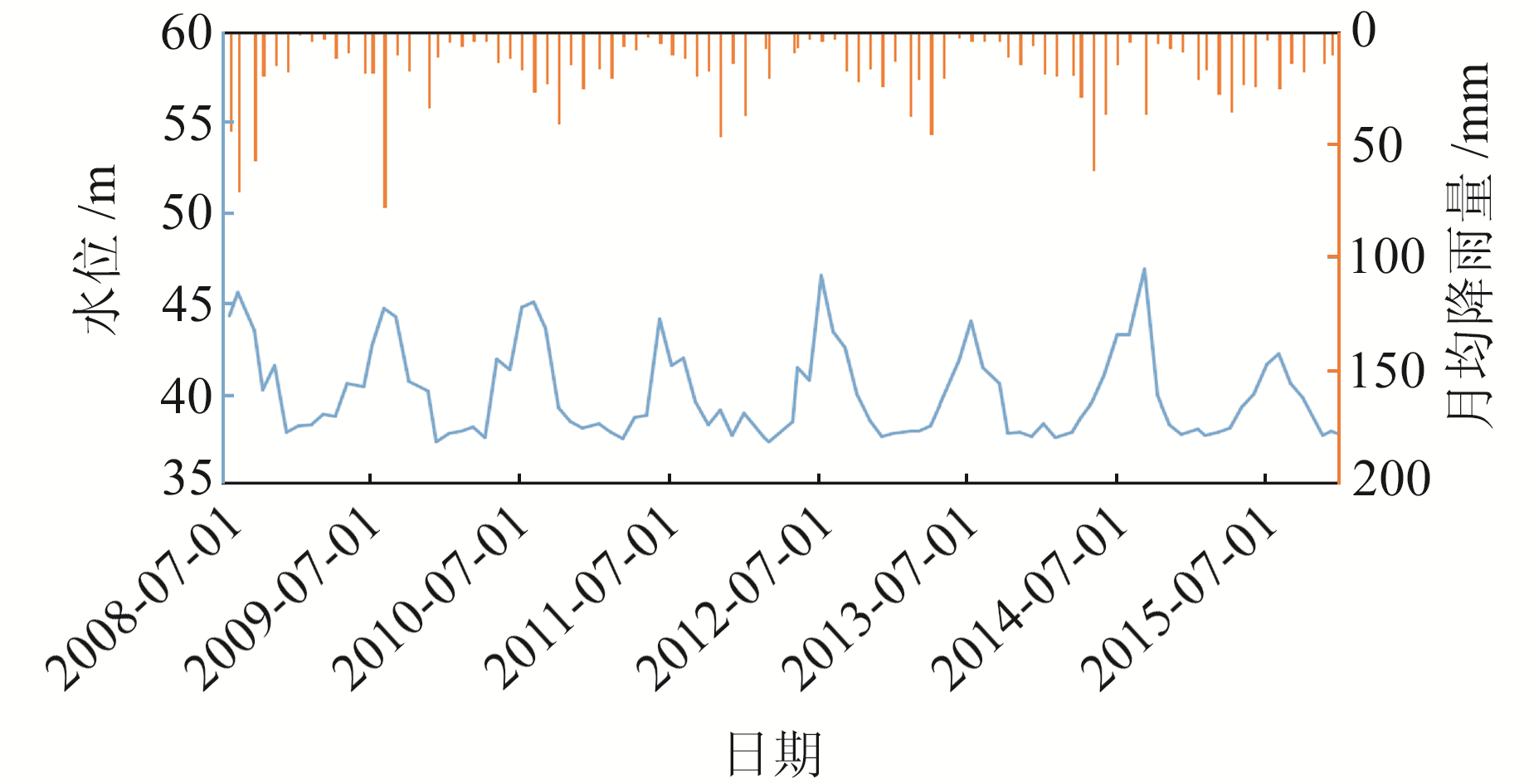
将AMWRT算法与数据质量等级筛选方法[3]相结合,计算2008-07~2016-08月平均水位序列。如图 9所示,长江中游月平均降雨量与水位都有明显的季节性特征,二者呈正相关关系,相关系数为0.18,并通过了显著性水平检验。长江中游水位变化较为剧烈,可能在一定程度上受降雨量的影响。由2008~2016年月平均水位变化可知,年内最高水位在降水集中期(7~8月),最低水位在11月至次年4月。
|
图 9 卫星测高水位与月降水对比 Fig. 9 Comparison of satellite height measurement water level and monthly precipitation |
在长江中游的水位监测中,AMWRT算法在卫星测高精度方面取得了不错的效果,其MAE为0.55 m,RMSE为0.72 m,与经典波形重跟踪算法中表现最好的threshold_0.5(MAE为0.84 m,RMSE为1.04 m)相比提高了30%。河流周边复杂的地形地物及水位较低时水域均质性差均会导致复杂波形的出现,而AMWRT算法在处理较为复杂的波形数据时比其他重跟踪算法表现更好。王红等[14]基于Jason-2卫星GDR数据获得的水位在相关分析中的相关系数达0.93,而本文利用AMWRT重跟踪算法对波形进行重跟踪,结果与实测水位的相关系数达0.96。就卫星测高水位的精度提升而言,原数据自带的重跟踪算法与其他算法相比表现最差,说明波形重跟踪算法对数据精度的提升具有重要意义。另外,由于数据筛选方法的不同,最终结果也会出现一定的差异。从本文算法的应用效果来看,AMWRT算法在表面宽度不大的河流区域的表现优于经典重跟踪算法。
由于卫星测高技术主要应用于宽阔的海洋及冰川区域,测高卫星在内陆水体的监测精度有待提升。而本文研究仅考虑了部分误差校正,且由卫星摄动影响产生的轨道误差会影响卫星测高数据的最终精度。但由于卫星测高技术的优点明显,对于偏远且缺乏水位资料的地区而言,建立长时间水位变化序列仍具有重要意义。本文算法是否适用于不同区域类型的水位监测,后续需结合不同区域河流及多种卫星测高数据进行进一步检验。
5 结语本文利用Jason-2卫星SGDR数据进行波形重跟踪,结合数据筛选方法提升卫星测高数据的精度,获取2008-07~2016-09水位变化序列,分析了长江中游水位变化与降雨量的关系,并基于实测水位数据对不同的波形重跟踪算法进行精度评价。主要结论如下:
1) 基于Jason-2卫星SGDR数据集中的GDR数据得到的水位与实测水位相比,在长时间水位序列变化上趋势一致,但GDR数据自带的重跟踪算法获得的水位在精度改善效果上仍有待提升,其MAE为1.15 m,RMSE为1.61 m。
2) AMWRT算法相较于其他重跟踪算法表现最好,MAE为0.55 m,RMSE为0.72 m;而经典的重跟踪算法threshold_0.5的MAE为0.84 m,RMSE为1.04 m。
3) 长江中游的月平均水位与降雨量有一定的相关性,且年内月平均水位变化较大。
| [1] |
程鹏飞, 文汉江, 刘焕玲, 等. 卫星大地测量学的研究现状及发展趋势[J]. 武汉大学学报: 信息科学版, 2019, 44(1): 48-54 (Cheng Pengfei, Wen Hanjiang, Liu Huanling, et al. Research Situation and Future Development of Satellite Geodesy[J]. Geomatics and Information Science of Wuhan University, 2019, 44(1): 48-54)
(  0) 0) |
| [2] |
褚永海, 李建成, 姜卫平, 等. 利用Jason-1数据监测呼伦湖水位变化[J]. 大地测量与地球动力学, 2005, 25(4): 11-16 (Chu Yonghai, Li Jiancheng, Jiang Weiping, et al. Monitoring of Water Level Variations of Hulun Lake with Jason-1 Altimetric Data[J]. Journal of Geodesy and Geodynamics, 2005, 25(4): 11-16)
(  0) 0) |
| [3] |
文京川, 赵红莉, 蒋云钟, 等. 卫星测高数据筛选方法研究——以Jason-3数据和洪泽湖为例[J]. 南水北调与水利科技, 2018, 16(3): 194-200 (Wen Jingchuan, Zhao Hongli, Jiang Yunzhong, et al. Research on the Quality Screening Method for Satellite Altimetry Data——Take Jason-3 Data and Hongze Lake as an Example[J]. South-to-North Water Transfers and Water Science and Technology, 2018, 16(3): 194-200)
(  0) 0) |
| [4] |
Silva J S D, Calmant S, Seyler F, et al. Water Levels in the Amazon Basin Derived from the ERS-2 and ENVISAT Radar Altimetry Missions[J]. Remote Sensing of Environment, 2010, 114(10): 2160-2181 DOI:10.1016/j.rse.2010.04.020
(  0) 0) |
| [5] |
Boergens E, Dettmering D, Schwatke C, et al. Treating the Hooking Effect in Satellite Altimetry Data: A Case Study along the Mekong River and Its Tributaries[J]. Remote Sensing, 2016, 8(2): 91 DOI:10.3390/rs8020091
(  0) 0) |
| [6] |
常晓涛, 李建成, 郭金运, 等. 一种多前缘多阈值的波形重构算法[J]. 地球物理学报, 2006, 49(6): 1629-1634 (Chang Xiaotao, Li Jiancheng, Guo Jinyun, et al. A Multi-Leading Edge and Multi-Threshold Waveform Retracker[J]. Chinese Journal of Geophysics, 2006, 49(6): 1629-1634 DOI:10.3321/j.issn:0001-5733.2006.06.008)
(  0) 0) |
| [7] |
赵云, 廖静娟, 沈国状, 等. 卫星测高数据监测青海湖水位变化[J]. 遥感学报, 2017, 21(4): 633-644 (Zhao Yun, Liao Jingjuan, Shen Guozhuang, et al. Monitoring the Water Level Changes in Qinghai Lake with Satellite Altimetry Data[J]. Journal of Remote Sensing, 2017, 21(4): 633-644)
(  0) 0) |
| [8] |
CNES, EUMETST, JPL, et al. OSTM/Jason-2 Products Handbook[EB/OL]. http://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_j2.pdf, 2017
(  0) 0) |
| [9] |
张志杰, 谢欢, 童小华, 等. 星载激光测高全波形数据处理技术研究进展[J]. 测绘科学, 2019, 44(12): 168-178 (Zhang Zhijie, Xie Huan, Tong Xiaohua, et al. Research Progress of Full Waveform Processing Technology of Satellite Laser Altimetry[J]. Science of Surveying and Mapping, 2019, 44(12): 168-178)
(  0) 0) |
| [10] |
袁翠. 基于雷达高度计的内陆水体应用研究[D]. 北京: 中国科学院大学, 2017 (Yuan Cui. Applied Research on Radar Altimetry over Inland Waters[D]. Beijing: University of Chinese Academy of Sciences, 2017)
(  0) 0) |
| [11] |
Deng X, Featherstone W E, Hwang C, et al. Estimation of Contamination of ERS-2 and Poseidon Satellite Radar Altimetry Close to the Coasts of Australia[J]. Marine Geodesy, 2002, 25(4): 249-271 DOI:10.1080/01490410214990
(  0) 0) |
| [12] |
李景刚, 李纪人, 阮宏勋, 等. Jason-2卫星测高数据在陆地水域水位变化监测中的应用——以南洞庭湖为例[J]. 自然资源学报, 2010, 25(3): 502-510 (Li Jinggang, Li Jiren, Ruan Hongxun, et al. Application of Jason-2 Altimetry Data in Monitoring of Continental Water Level Fluctuations: A Case Study in South Dongting Lake, China[J]. Journal of Natural Resources, 2010, 25(3): 502-510)
(  0) 0) |
| [13] |
何飞, 刘兆飞, 姚治君. Jason-2测高卫星对湖泊水位的监测精度评价[J]. 地球信息科学学报, 2020, 22(3): 494-504 (He Fei, Liu Zhaofei, Yao Zhijun. Evaluation of the Monitoring Accuracy of Lake Water Level by the Jason-2 Altimeter Satellite[J]. Journal of Geo-Information Science, 2020, 22(3): 494-504)
(  0) 0) |
| [14] |
王红, 孙福宝, 杨涛, 等. Jason-2卫星测高数据在长江中游水位监测中的应用[J]. 三峡生态环境监测, 2018, 3(3): 48-54 (Wang Hong, Sun Fubao, Yang Tao, et al. Application of Jason-2 Satellite Altimetry Data to Water Level Monitoring in the Middle Reaches of the Yangtze River[J]. Ecology and Environmental Monitoring of Three Gorges, 2018, 3(3): 48-54)
(  0) 0) |
| [15] |
赵云. 雷达高度计数据中国主要湖泊水位变化监测方法研究[D]. 北京: 中国科学院大学, 2017 (Zhao Yun. Method of Monitoring Water Level Change of Main Lakes in China with Radar Altimeter Data[D]. Beijing: University of Chinese Academy of Sciences, 2017)
(  0) 0) |
2. Key Laboratory of Beibu Gulf Environment Change and Resources Use, Ministry of Education, Nanning Normal University, 175 East-Mingxiu Road, Nanning 530001, China;
3. Guangxi Key Laboratory of Earth Surface Processes and Intelligent Simulation, Nanning Normal University, 175 East-Mingxiu Road, Nanning 530001, China
 2021, Vol. 41
2021, Vol. 41


