2. 北方信息控制研究院集团有限公司,南京市将军大道528号,211153;
3. 同济大学测绘与地理信息学院,上海市四平路1239号,200092
周跳探测与修复是利用GNSS载波相位观测值进行高精度定位的重要基础[1]。邹璇等[2]提出基于历元间单差观测值的单频周跳探测与修复方法,但该方法易受异常卫星数量的影响;Li等[3]采用低阶多项式约束位置参数实现了单频数据的周跳探测;Blewitt[4]提出用于周跳探测的TurboEdit方法,具有能单站探测和探测效率高等特点,被广泛使用;张小红等[5]通过构建阈值模型改进了TurboEdit算法,提高了周跳探测的精度。多频观测值可形成具有波长更长、电离层延迟和噪声影响更小等特性优良的组合观测值,有利于提高周跳探测与修复的性能。在三频周跳探测方法研究中,李金龙等[6]基于3个线性无关的三频伪距相位组合进行周跳探测与修复,当历元间电离层延迟变化量可忽略时,该方法可探测和修复所有周跳;黄令勇等[7]和吕伟才等[8]提出一种联合2个无几何相位组合和1个伪距相位组合共同进行周跳探测与修复的方法,具有较好的探测与修复效果。
BDS-3四频数据的出现带来了新的机遇和挑战,研究表明,四频数据有利于提高模糊度固定成功率,周跳探测与修复则是准确进行该工作的重要前提[9-10]。相较于双频和三频数据,四频数据理论上可形成更多更小电离层延迟和更少观测噪声影响的组合观测值,有利于提高周跳探测与修复的性能,但鲜有学者对BDS-3四频数据的实时周跳探测与修复方法进行研究。
本文通过探讨三频和四频条件下的高质量组合,提出一种联合3个无几何相位组合和1个伪距相位组合的实时周跳探测与修复方法,并采用不同观测条件下的实测数据,通过人为加入周跳组合的方式来验证该方法的有效性,以期得到有益结论。
1 四频无几何相位组合假设α、β、γ、δ是组合系数,令α+β+γ+δ=0,四频无几何相位组合观测值为:
| $ \begin{gathered} \alpha \lambda_{1} \varphi_{1}(t)+\beta \lambda_{2} \varphi_{2}(t)+\gamma \lambda_{3} \varphi_{3}(t)+\delta \lambda_{4} \varphi_{4}(t)= \\ -\eta I_{1}(t)+\lambda_{C} N_{C}(t)+\varepsilon_{C}(t) \end{gathered} $ | (1) |
式中,λi、φi分别为相应频点的载波波长和相位观测值;
| $ \begin{gathered} D(t)=\alpha \lambda_{1} \Delta \varphi_{1}(t)+\beta \lambda_{2} \Delta \varphi_{2}(t)+\gamma \lambda_{3} \Delta \varphi_{3}(t)+ \\ \delta \lambda_{4} \Delta \varphi_{4}(t)=-\eta \Delta I_{1}(t)+\alpha \lambda_{1} \Delta N_{1}(t)+ \\ \beta \lambda_{2} \Delta N_{2}(t)+\gamma \lambda_{3} \Delta N_{3}(t)+\delta \lambda_{4} \Delta N_{4}(t)+\Delta \varepsilon_{C}(t) \end{gathered} $ | (2) |
由于式(2)仅受-ηΔI1(t)和ΔεC(t)的影响,因此应尽可能地满足
| $ \sigma_{\alpha \beta \gamma_{\delta}}=\sqrt{2} \sqrt{\left(\alpha \lambda_{1}\right)^{2}+\left(\beta \lambda_{2}\right)^{2}+\left(\gamma \lambda_{3}\right)^{2}+\left(\delta \lambda_{4}\right)^{2}} \sigma_{\varphi} $ | (3) |
式中,σφ为原始相位观测值的观测误差,设置为0.01周,采用4σαβγδ作为周跳探测阈值。
2 无几何相位组合系数的确定为使无几何相位组合受较小的电离层延迟和观测噪声影响,本文选择在[-5, 5]整数范围内进行组合系数的挑选[11]。为探讨四频数据带来的优势,根据组合观测值的电离层延迟和观测噪声等条件挑选较优组合,本文将电离层延迟放大系数|η| < 0.2和观测噪声σ < 0.03的组合视为高质量组合。经统计,三频和四频条件下的高质量组合数分别为28个和288个,可以发现,频率数越多高质量组合越多,周跳探测中可供选择的探测组合也越多。
为探讨理论上的最优组合,表 1给出三频和四频条件下电离层延迟和观测噪声相对最小的高质量组合信息。可以发现,四频高质量组合相较于三频具有更小的电离层延迟和观测噪声影响,因此当频率数增多时,周跳探测和减弱电离层延迟影响的性能理论上应该更好。
|
|
表 1 三频和四频条件下最优高质量组合相关信息 Tab. 1 The best high-quality combination and information of triple-frequency and four-frequency |
基于组合观测理论值的周跳探测方法存在不敏感周跳组合的现象[12],尽管部分无几何相位组合观测噪声相对较小,但仅能对2个或3个频点进行周跳探测,无法探测仅在其他频点发生的周跳,不敏感周跳组合数较多。因此,令组合系数满足αβγδ≠0以减少不敏感周跳组合数。表 2为挑选的部分较优的无几何相位组合信息,其中第4列为各组合10周内的不敏感周跳组合数。
|
|
表 2 无几何相位组合及其电离层延迟放大系数和观测噪声 Tab. 2 The ionospheric delay coefficient and observation noise of the geometry-free phase combination |
显然,表 2中的无几何相位组合均存在不敏感周跳组合,但不同组合间的不敏感周跳组合及数量不同。为减少不敏感周跳组合数及利于进行周跳修复,挑选3个线性无关的无几何相位组合(表 3),其中第2列为各探测组合100周内的不敏感周跳组合数。
|
|
表 3 探测组合的不敏感周跳组合数 Tab. 3 The number of detection combination insensitive cycle slip group |
由表 3可知,联合3个无几何相位组合共同进行周跳探测时,100周内的周跳均可被探测。因此,选取无几何相位组合(1, -2, 3, -2)、(2, -1, -3, 2)和(2, -4, 3, -1)进行周跳探测,原因是其具有最小的电离层延迟和观测噪声影响,周跳探测的性能理论上应该最好。由于四频无几何相位组合最多仅能构成3个线性无关的探测组合,为能实时修复周跳大小,选择加入1个四频伪距相位组合。
3 四频伪距相位组合假设(a,b,c,d)和(i,j,k,m)分别为伪距相位组合和载波相位组合观测值的组合系数,四频伪距相位组合观测值的整周模糊度为:
| $ \begin{gathered} N_{i j k m}(t)=\varphi_{i j k m}(t)-\frac{P_{a b c d}(t)}{\lambda_{i j k m}}- \\ \frac{\eta_{i j k m}+\eta_{a b c d}}{\lambda_{i j k m}} I_{1}(t)+\varepsilon(t) \end{gathered} $ | (4) |
式中,I1(t)为B1C频点上的电离层延迟,Nijkm(t)为伪距相位组合观测值的整周模糊度,φijkm(t)和Pabcd(t)分别为相位和伪距组合的观测值,λijkm为相位组合观测值的波长,ηijkm和ηabcd分别为φijkm(t)和Pabcd(t)的电离层延迟放大系数,ε(t)为伪距相位组合观测值的观测噪声。当周跳发生时,伪距相位组合观测值历元间差分的周跳探测量为:
| $ \begin{aligned} &D(t)=\Delta N_{i j k m}(t)=\Delta \varphi_{i j k m}(t)- \\ &\frac{\Delta P_{a b c d}(t)}{\lambda_{i j k m}}-K_{i j k m} \Delta I_{1}(t)+\Delta \varepsilon(t) \end{aligned} $ | (5) |
式中,Kijkm=(ηijkm+ηabcd)/λijkm,可知周跳探测主要与电离层延迟放大系数及历元间电离层延迟变化量有关,ΔI1值较小,当组合系数(a,b,c,d)和(i,j,k,m)使Kijkm足够小时,电离层延迟KijkmΔI1可忽略不计。由误差传播定律可知,伪距相位组合观测值的观测噪声为:
| $ \begin{gathered} \sigma_{i j k m}=\sqrt{2} \times \\ \sqrt{\left(i^{2}+j^{2}+k^{2}+m^{2}\right) \sigma_{\varphi}^{2}+\frac{\left(a^{2}+b^{2}+c^{2}+d^{2}\right)}{\lambda_{i j k m}^{2}} \sigma_{P}^{2}} \end{gathered} $ | (6) |
式中,σφ为原始相位观测值的观测噪声,设置为0.01周;σP为伪距观测值的观测噪声,为探讨不同伪距观测噪声下的周跳探测灵敏度,σP分别设置为0.3 m、0.6 m和1 m。本文取4σijkm为周跳探测阈值,σijkm越小,周跳探测灵敏度越高。为尽可能减小σijkm,应减小a2+b2+c2+d2,增大λijkm,因此令a=b=c=d=1/4以使伪距组合观测值噪声最小。表 4为挑选的部分超宽巷及电离层延迟和观测噪声影响较小的伪距相位组合。
|
|
表 4 伪距相位组合及其电离层延迟放大系数和观测噪声 Tab. 4 The ionospheric delay coefficient and observation noise of thecode-phase combination |
可以发现,不同组合的电离层延迟放大系数及不同伪距观测噪声影响下的周跳探测灵敏度均不同。组合(-1, 2, -4, 3)的电离层延迟放大系数较大,但波长相对较长,抗伪距观测噪声能力更强,即不同伪距观测噪声下的σijkm变化幅度较小。当探测到某历元发生周跳时,周跳浮点值可联立方程求解得到:
| $ \underbrace{\left[\begin{array}{l} L_{1} \\ L_{2} \\ L_{3} \\ L_{4} \end{array}\right]}_{\boldsymbol{L}}=\underbrace{\left[\begin{array}{cccc} \alpha_{1} \lambda_{1} & \beta_{1} \lambda_{2} & \gamma_{1} \lambda_{3} & \delta_{1} \lambda_{4} \\ \alpha_{2} \lambda_{1} & \beta_{2} \lambda_{2} & \gamma_{2} \lambda_{3} & \delta_{2} \lambda_{4} \\ \alpha_{3} \lambda_{1} & \beta_{3} \lambda_{2} & \gamma_{3} \lambda_{3} & \delta_{3} \lambda_{4} \\ i & j & k & m \end{array}\right]}_{\boldsymbol{A}} \underbrace{\left[\begin{array}{c} \Delta N_{1} \\ \Delta N_{2} \\ \Delta N_{3} \\ \Delta N_{4} \end{array}\right]}_{\boldsymbol{X}} $ | (7) |
| $ \begin{gathered} \boldsymbol{X}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P L} \end{gathered} $ | (8) |
| $ \begin{gathered} \boldsymbol{D}_{X}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}\right)^{-1} \end{gathered} $ | (9) |
式中,L为组合观测值矩阵,A为组合系数矩阵,X为周跳值矩阵,P为权阵,原始载波相位和伪距观测值的观测噪声分别设置为0.01周和0.3 m。由于组合系数矩阵A为满秩矩阵,因此式(8)也可表示为:
| $ \boldsymbol{X}=\boldsymbol{A}^{-1} \boldsymbol{L} $ | (10) |
利用式(10)解算得到周跳浮点值后,可采取直接取整方法,但该方法可能会受观测噪声等的影响导致修复不准确。由式(10)可知,在矩阵求逆中,周跳修复的稳定性也与组合系数矩阵的条件数有关,条件数越小周跳修复越稳定,因此选择组合系数矩阵条件数相对最小及电离层延迟影响较小的伪距相位组合(-1, 1, 1, -1)。同时,采用整数最小二乘降相关平差(least square ambiguity decorrelation adjustment,LAMBDA)方法进行搜索并确定周跳整数值。
4 实验验证与结果分析 4.1 实验1实验选取BDS-3两种类型卫星相同观测时段的四频实测数据,其中C33为MEO卫星,C38为IGSO卫星,接收机类型为Trimble Alloy接收机,采样间隔为1 s。为验证本文四频实时周跳探测与修复方法的有效性,并充分考虑各种可能出现的周跳组合,选择在两颗卫星实测数据中每隔5个历元人为加入随机周跳组合,具体如(0, 0, 0, 1),(0, 0, 0, 2),……,(6, 6, 6, 6), 共计2 058个周跳组合。
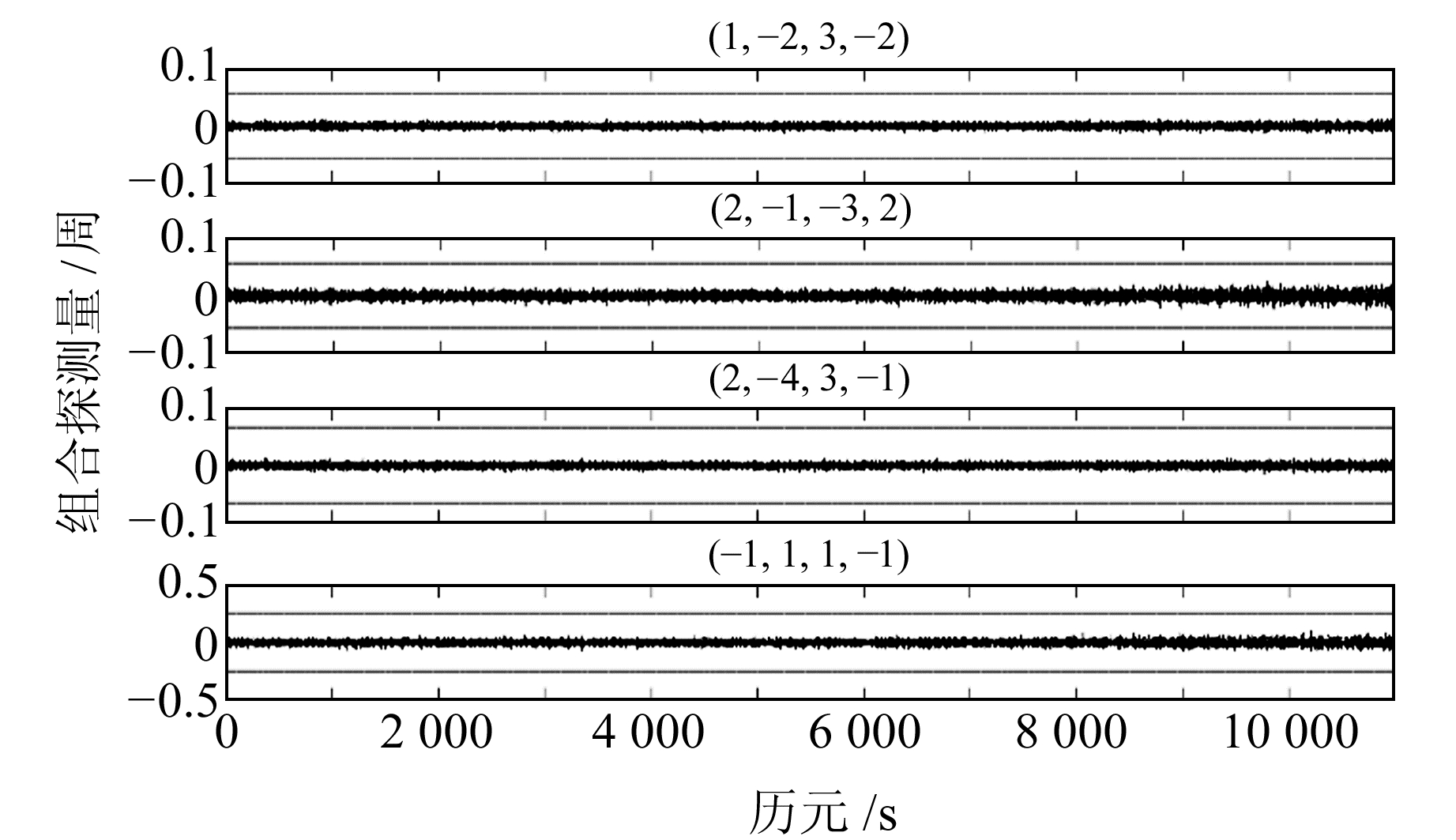
对人为加入周跳组合前后的周跳探测序列进行对比分析,图 1为C33号卫星未加入周跳组合时的探测序列,其中上下两条虚线表示相应探测组合的周跳探测阈值。当未加入周跳组合时,4种探测组合的周跳探测序列为一条在一定范围内变化的曲线,且均未超出相应阈值,表明无周跳发生。此外,伪距相位组合的观测噪声明显大于无几何相位组合,原因是伪距相位组合引入了观测噪声较大的伪距观测值。C38号卫星未发生周跳时的探测序列与此类似,不再赘述。
|
图 1 C33号卫星未加入周跳时的探测序列 Fig. 1 The detection results of the satellite C33 when no cycle slip occurs |
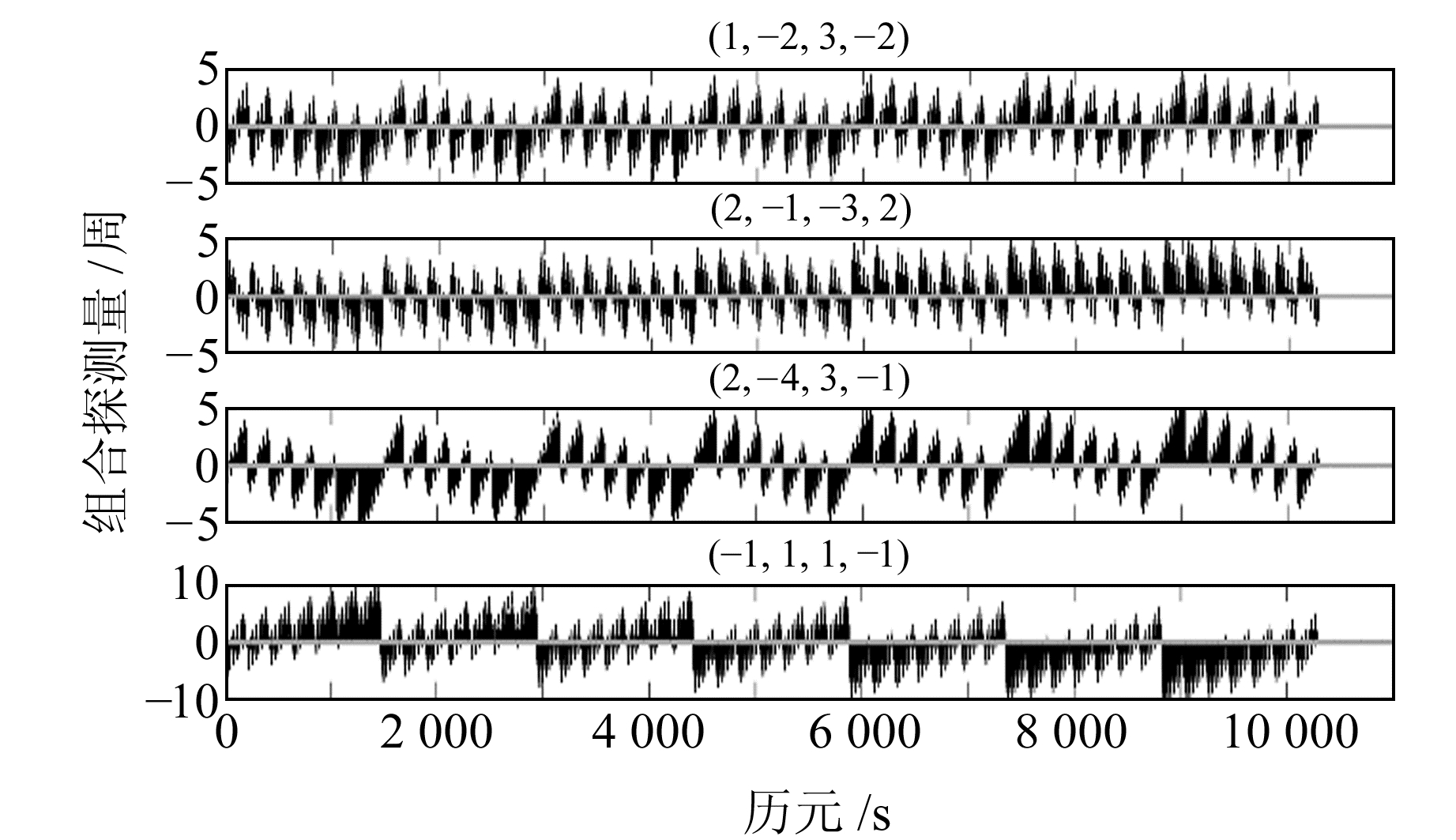
限于篇幅,本文仅给出加入周跳组合后C33号卫星的周跳探测序列,具体见图 2。可以发现,当某历元加入周跳后,其周跳探测量会发生明显变化并超出相应探测阈值,表明该历元发生了周跳。经统计,C33和C38号卫星四频数据中所有人为加入的周跳均可被探测。此外,对两颗卫星分别采用直接取整方法和LAMBDA搜索方法的周跳实时修复成功率进行对比(表 5),可以发现,C33和C38号卫星采用直接取整方法的周跳修复成功率分别为92.03%和91.11%;而LAMBDA搜索方法可实时修复所有周跳,原因是采用直接取整方法会受到观测噪声等的影响导致部分周跳修复不准确。
|
图 2 C33号卫星加入周跳时的探测序列 Fig. 2 The detection results of the satellite C33 when cycle slip occurs |
|
|
表 5 实时周跳探测与修复成功率 Tab. 5 The real-time cycle slip detection and repair success rate |
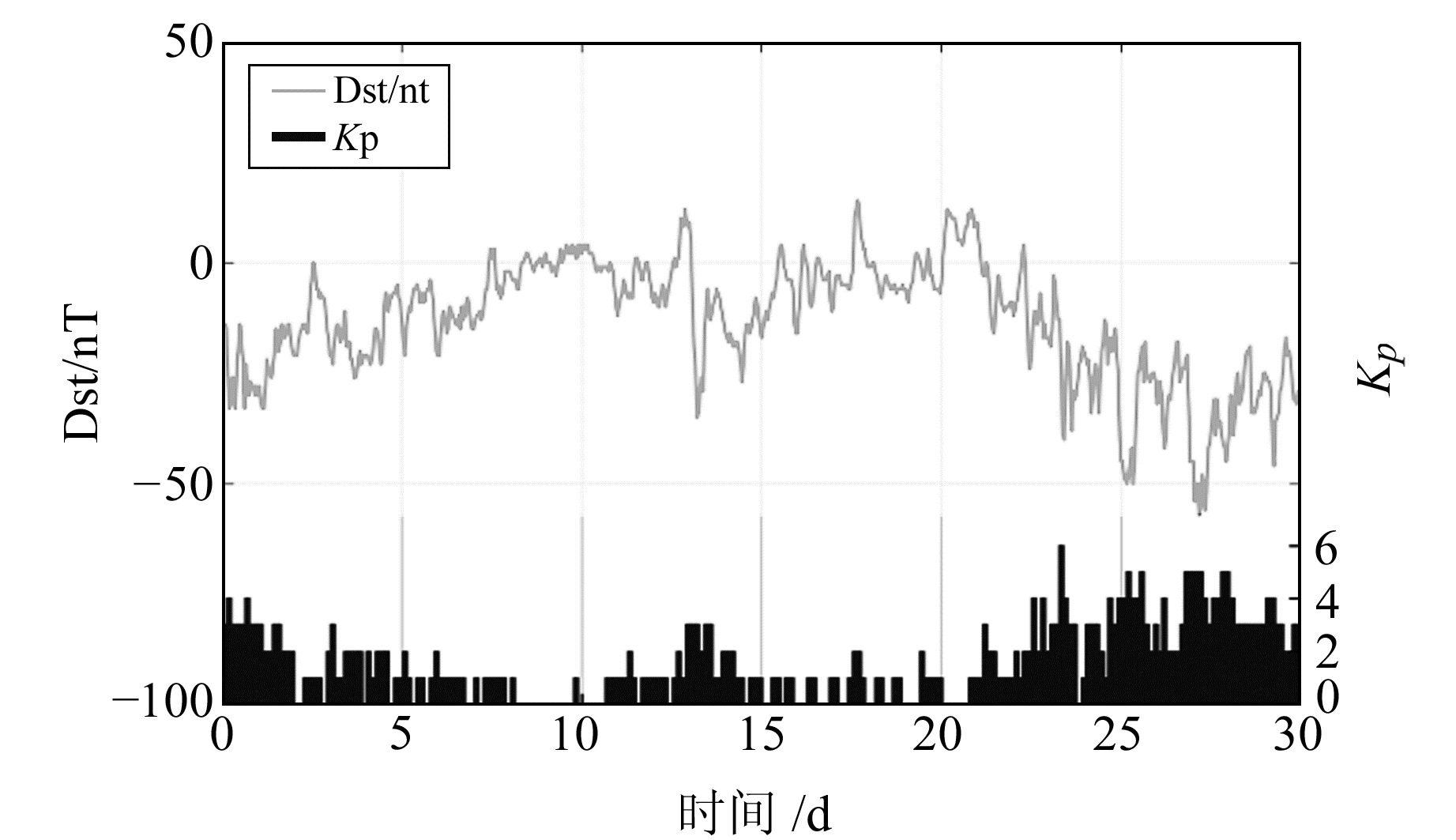
为进一步验证本文四频实时周跳探测与修复方法在电离层活跃期和低采样率条件下的有效性,选取MGEX测站SGOC(6.89°N, 79.87°E)的实测数据,数据采样间隔为30 s。图 3为2020-09的Dst和KP指数时间序列,可以看出,09-28当日Dst指数在大部分时间段小于-50 nT,KP指数之和为35,可知当日地磁活动剧烈且有磁暴发生。选择2020-09-28当日C27号(MEO)卫星四频实测数据进行实验。
|
图 3 Dst和KP指数时间序列 Fig. 3 The time series of the Dst index and the KP index |
由于SGOC测站的原始观测数据中未发生周跳且观测时段有限,本文采取每隔50个历元随机加入周跳组合的方式来验证该方法的有效性,共计8个小周跳和7个大周跳组合。
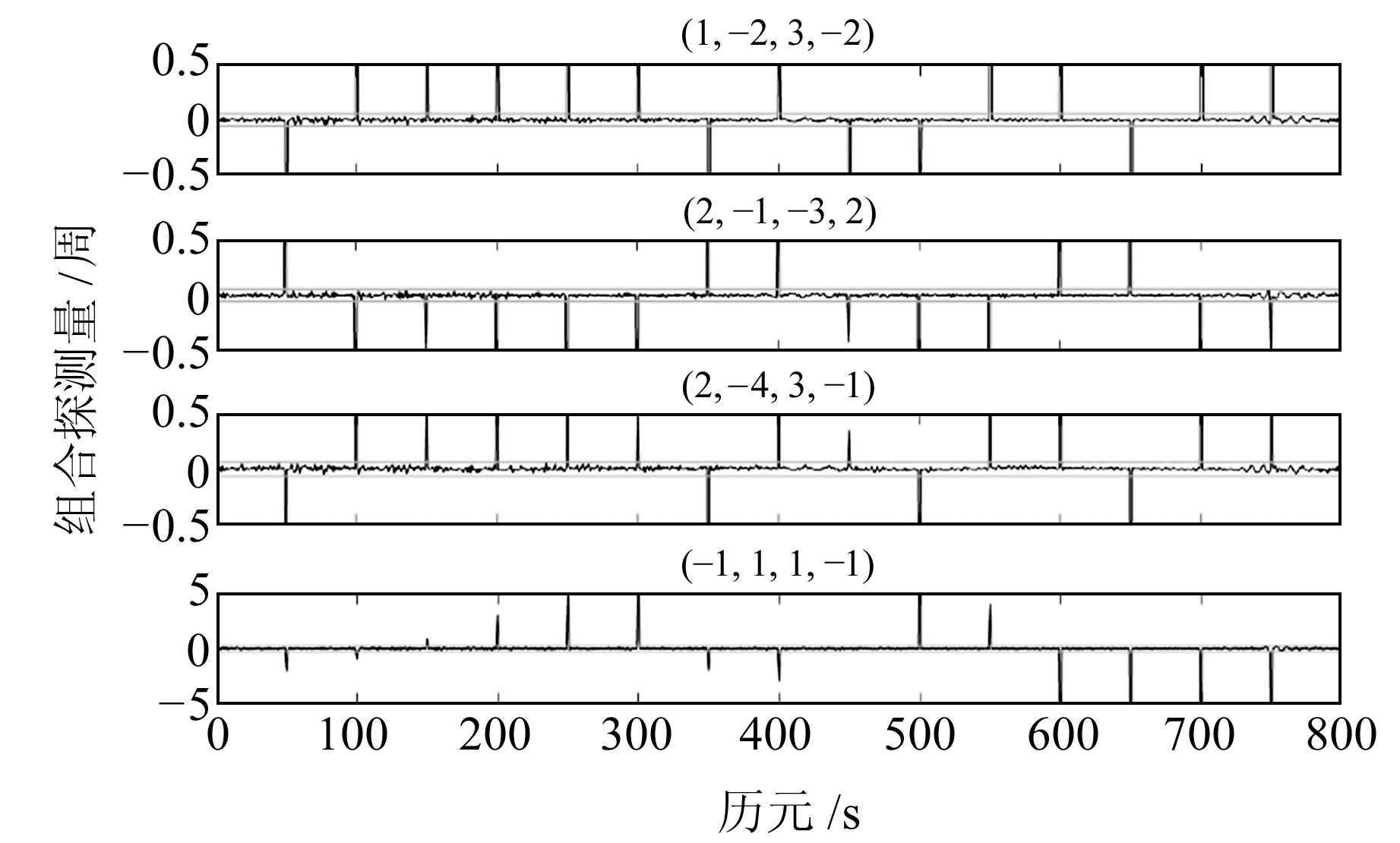
图 4为C27号卫星人为加入所有周跳组合后的探测序列,可以看出,周跳发生时的探测量将超过相应探测阈值。经统计,所有加入的周跳组合均可被实时探测。此外,进一步对周跳探测结果进行实时修复,由表 6可知,相应历元的周跳修复值与模拟值完全一致,表明所有加入的周跳组合均可被实时探测与修复。因此,在电离层活跃期或低采样率的条件下,联立无几何相位组合(1, -2, 3, -2)、(2, -1, -3, 2)、(2, -4, 3, -1) 和伪距相位组合(-1, 1, 1, -1) 可准确进行四频数据的实时周跳探测与修复。
|
图 4 C27号卫星加入周跳时的探测序列 Fig. 4 The detectionresults of the satellite C27 when cycle slip occurs |
|
|
表 6 C27号卫星周跳探测量与修复结果 Tab. 6 The cycle slip detection and repair results of the satellite C27 |
北斗三号卫星四频数据带来了电离层延迟和观测噪声影响相对较小的组合观测值,本文联立了3个四频无几何相位组合(1, -2, 3, -2)、(2, -1, -3, 2)、(2, -4, 3, -1) 共同进行四频数据的实时周跳探测,相较于三频数据,四频组合观测值具有更小的电离层延迟影响,有利于提高周跳探测与修复的性能;再加入1个四频伪距相位组合(-1, 1, 1, -1) 以构成4个线性无关的探测组合,联立以上组合共同进行周跳探测,并采用LAMBDA搜索方法进行周跳实时修复。结果表明,该方法可实时探测与修复所有人为加入的周跳,修复结果与周跳模拟值完全一致。
| [1] |
Li B F, Qin Y N, Liu T X. Geometry-Based Cycle Slip and Data Gap Repair for Multi-GNSS and Multi-Frequency Observations[J]. Journal of Geodesy, 2019, 93(3): 399-417 DOI:10.1007/s00190-018-1168-5
(  0) 0) |
| [2] |
邹璇, 李宗楠, 陈亮, 等. 一种历元间差分单站单频周跳探测与修复方法[J]. 武汉大学学报: 信息科学版, 2017, 42(10): 1406-1410 (Zou Xuan, Li Zongnan, Chen Liang, et al. A New Cycle Slip Detection and Repair Method Based on Epoch Difference for a Single-Frequency GNSS Receiver[J]. Geomatics and Information Science of Wuhan University, 2017, 42(10): 1406-1410)
(  0) 0) |
| [3] |
Li B F, Liu T X, Nie L W, et al. Single-Frequency GNSS Cycle Slip Estimation with Positional Polynomial Constraint[J]. Journal of Geodesy, 2019, 93(9): 1781-1803 DOI:10.1007/s00190-019-01281-7
(  0) 0) |
| [4] |
Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 DOI:10.1029/GL017i003p00199
(  0) 0) |
| [5] |
张小红, 曾琪, 何俊, 等. 构建阈值模型改善TurboEdit实时周跳探测[J]. 武汉大学学报: 信息科学版, 2017, 42(3): 285-292 (Zhang Xiaohong, Zeng Qi, He Jun, et al. Improving TurboEdit Real-Time Cycle Slip Detection by the Construction of Threshold Model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 285-292)
(  0) 0) |
| [6] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722 (Li Jinlong, Yang Yuanxi, Xu Junyi, et al. Real-Time Cycle Slip Detection and Repair Based on Code-Phase Combinations for GNSS Triple-Frequency Un-Differenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722)
(  0) 0) |
| [7] |
黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768 (Huang Lingyong, Song Lijie, Wang Yan, et al. Beidou Triple-Frequency Geometry-Free Phase Combination for Cycle-Slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768)
(  0) 0) |
| [8] |
吕伟才, 高井祥, 严超, 等. 北斗三频载波伪距组合观测值的周跳探测算法研究[J]. 大地测量与地球动力学, 2020, 40(2): 117-122 (Lü Weicai, Gao Jingxiang, Yan Chao, et al. Research on Cycle Slip Detection Algorithm for Beidou Triple-Frequency Carrier Pseudorange Combination[J]. Journal of Geodesy and Geodynamics, 2020, 40(2): 117-122)
(  0) 0) |
| [9] |
Zhang Z T, Li B F, He X F, et al. Models, Methods and Assessment of Four-Frequency Carrier Ambiguity Resolution for Beidou-3 Observations[J]. GPS Solutions, 2020, 24(4): 1-12 DOI:10.1007/s10291-020-01011-z
(  0) 0) |
| [10] |
章浙涛, 李博峰, 何秀凤. 北斗三号多频相位模糊度无几何单历元固定方法[J]. 测绘学报, 2020, 49(9): 1139-1148 (Zhang Zhetao, Li Bofeng, He Xiufeng. Geometry-Free Single-Epoch Resolution of BDS-3 Multi-Frequency Carrier Ambi-Guities[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1139-1148)
(  0) 0) |
| [11] |
Huang L, Lu Z, Zhai G, et al. A New Triple-Frequency Cycle Slip Detecting Algorithm Validated with BDS Data[J]. GPS Solutions, 2015, 20(4): 1-9
(  0) 0) |
| [12] |
刘柳, 吕志伟, 戴琦, 等. 利用三频数据组合探测不敏感周跳[J]. 武汉大学学报: 信息科学版, 2019, 44(3): 392-397 (Liu Liu, Lü Zhiwei, Dai Qi, et al. Using Triple-Frequency Data Combination to Detect Insensitive Cycle-Slip[J]. Geomatics and Information Science of Wuhan University, 2019, 44(3): 392-397)
(  0) 0) |
2. Northern Information Control Research Institute Group Co Ltd, 528 Jiangjun Road, Nanjing 211153, China;
3. College of Surveying and Geo-Informatics, Tongji University, 1239 Siping Road, Shanghai 200092, China
 2021, Vol. 41
2021, Vol. 41

