BDS网络RTK的核心问题是准确固定参考站间的整周模糊度^[1]。由于大气延迟误差与距离具有强相关性，将残余的大气延迟误差与参考站间整周模糊度进行分离较为困难。参考站间三频整周模糊度解算一直是学者研究的热点问题，Feng^[2]提出一种基于综合噪声的最小弱电离层组合三频几何模糊度解算策略；Li等^[3]提出了一种长距离参考站间整周模糊度解算方法；张小红等^[4]研究了短基线和长基线条件下3个最优BDS三频整数线性组合；Chen等^[5]综合利用无几何和无电离层模型实现了参考站间三频整周模糊度的固定；高猛等^[6]利用整周模糊度之间的线性关系实现了BDS三频整周模糊度的固定；祝会忠等^[7]研究了一种顾及大气误差的参考站间载波相位整周模糊度解算方法；Dai等^[8]利用已固定整周模糊度的卫星辅助解算了低高度角卫星整周模糊度；邓健等^[9]提出了一种参考站间低高度角卫星部分整周模糊度快速解算方法；高猛等^[10]利用固定整周模糊度卫星的大气延迟误差和整周模糊度之间的线性关系，实现了低高度角卫星整周模糊度固定。本文提出一种BDS参考站间低高度角卫星三频整周模糊度解算方法，该方法利用双差整周模糊度之间的线性关系，结合无电离层组合确定高高度角卫星双差整周模糊度，并建立双差电离层延迟误差空间线性模型，以削弱低高度角卫星的电离层延迟误差，最后将固定整周模糊度的高高度角卫星双差载波相位观测方程作为约束条件，搜索确定低高度角卫星双差整周模糊度。

1 BDS参考站间三频整周模糊度的确定 1.1 参考站间双差超宽巷/宽巷整周模糊度确定

假设参考站u、v的同步观测卫星为p、q，利用伪距观测值和载波相位观测值的MW组合可计算B2-B3双差超宽巷整周模糊度为：

$ \begin{gathered} \Delta \nabla N_{u v,23}^{p q}=\left(\frac{\Delta \nabla \varPhi_{u v,3}^{p q}}{\lambda_{3}}-\frac{\Delta \nabla \varPhi_{u v, 2}^{p q}}{\lambda_{2}}\right)- \\ \frac{f_{3}-f_{2}}{f_{3}+f_{2}}\left(\frac{\Delta \nabla P_{u v, 3}^{p q}}{\lambda_{3}}+\frac{\Delta \nabla P_{u v, 2}^{p q}}{\lambda_{2}}\right) \end{gathered} $

(1)

式中，P为测码伪距，Φ为载波相位，$ \Delta \nabla $为双差标志，上标p和q为卫星的PRN，下标u和v为参考站接收机，λ为波长，f为频率，N为整周模糊度。

B1-B2和B1-B3双差宽巷整周模糊度的整数线性关系为：

$ \Delta \nabla N_{u v,23}^{p q}=\Delta \nabla N_{u v,12}^{p q}-\Delta \nabla N_{u v,13}^{p q} $

(2)

将B1-B2和B1-B3双差宽巷组合载波相位观测方程作差之后为：

$ \begin{gathered} \Delta \nabla \varPhi_{u v, 12}^{p q}-\Delta \nabla \varPhi_{u v, 13}^{p q}=-\lambda_{12} \Delta \nabla N_{u v,12}^{p q}+ \\ \lambda_{13} \Delta \nabla N_{u v, 13}^{p q}+\left(\mu_{13}-\mu_{12}\right) \frac{\Delta \nabla \kappa_{u v}^{p q}}{f_{1}^{2}} \end{gathered} $

(3)

式中，$ \frac{{\Delta \nabla \kappa _{uv}^{pq}}}{{f_1^2}} $为B1频段观测值受到的双差一阶电离层延迟误差；μ₁₂和μ₁₃为一阶电离层延迟误差放大系数，二者较为接近，对于中长基线(小于等于100 km)可忽略残余电离层延迟误差对整周模糊度的影响。联合式(2)和式(3)，根据最小二乘参数估计方法，可估计B1-B2和B1-B3双差宽巷整周模糊度，之后利用LAMBDA算法搜索并确定双差宽巷整周模糊度。

1.2 参考站间高高度角卫星双差整周模糊度确定

B1-B2双差整周模糊度之间的整数线性关系为：

$ \Delta \nabla N_{u v, 12}^{p q}=\Delta \nabla N_{u v, 1}^{p q}-\Delta \nabla N_{u v, 2}^{p q} $

(4)

B1-B2双差无电离层组合载波相位观测方程为：

$ \begin{aligned} \Delta \nabla \varPhi_{u v,\mathrm{LC}}^{p q} =& \Delta \nabla \rho_{u v}^{p q}+\Delta \nabla T_{u v}^{p q}+\frac{\lambda_{1} \lambda_{2}^{2}}{\lambda_{2}^{2}-\lambda_{1}^{2}} \Delta \nabla N_{u v,1}^{p q}-\\ &{\frac{\lambda_{1}^{2} \lambda_{2}}{\lambda_{2}^{2}-\lambda_{1}^{2}} \Delta \nabla N_{u v, 2}^{p q}}+\Delta \nabla \varepsilon_{\varPhi, \mathrm{LC}} \end{aligned} $

(5)

式中，下标LC为BDS的B1-B2无电离层组合。双差对流层延迟误差$ \Delta \nabla $T_uv^pq的干分量延迟误差$ \Delta \nabla $T_{dry, uv}^pq可通过模型进行改正，湿分量延迟误差$ \Delta \nabla $T_{wet, uv}^pq可用相对天顶对流层湿分量延迟误差RZTD_{wet, uv}表示。联合式(4)和式(5)，对双差整周模糊度和相对天顶对流层湿分量延迟误差进行参数估计，最后利用LAMBDA算法确定双差整周模糊度。

高高度角卫星B1、B2的双差整周模糊度固定之后，双差电离层延迟误差为：

$ \begin{array}{c} \Delta \nabla I_{u v}^{p q}=\frac{\Delta \nabla \kappa_{u v}^{p q}}{f_{1}^{2}}=\frac{1}{\mu_{2}-\mu_{1}}\left(\Delta \nabla \varPhi_{u v, 1}^{p q}-\Delta \nabla \varPhi_{u v, 2}^{p q}+\right. \\ \lambda_{1} \Delta \nabla N_{u v,1}^{p q}-\lambda_{2} \Delta \nabla N_{u v, 2}^{p q} \end{array} $

(6)

参考站间高高度角卫星双差电离层延迟误差确定之后，双差电离层延迟误差的线性模型为：

$ \Delta \nabla I_{u v}^{p q}=a_{0}+a_{1} \Delta B+a_{2} \Delta L $

(7)

式中，a₀、a₁和a₂为参考站间双差电离层延迟误差空间线性模型的拟合系数，ΔB为参考站u上双差卫星的电离层穿刺点纬差，ΔL为参考站u上双差卫星的电离层穿刺点经差，$ \Delta \nabla $I为双差电离层延迟误差。利用高高度角卫星，可计算得到双差电离层延迟误差空间线性模型拟合系数，进一步计算低高度角卫星所受到的双差电离层延迟误差。

1.3 参考站间低高度角卫星双差整周模糊度确定

根据式(7)计算改正参考站间低高度角卫星受到的电离层延迟误差。假定在历元i，参考站u、v同步观测到m+1颗高高度角卫星和n+1颗低高度角卫星，将固定整周模糊度的高高度角卫星B1双差载波相位观测方程作为低高度角卫星B1双差载波相位观测方程的约束条件，可得双差载波相位观测方程为：

$ \boldsymbol{L}_{*}(i)=\boldsymbol{H}_{*}(i) \boldsymbol{X}_{*}(i) $

(8)

其中，

$ \boldsymbol{H}_{*}(i)=\left[\begin{array}{cc} {\bf{0}}_{m} & \boldsymbol{\varTheta}_{m} \\ -\lambda_{1} \cdot \boldsymbol{I}_{n} & \boldsymbol{\varTheta}_{n} \end{array}\right] $

$ \boldsymbol{X}_{*}(i)=\left[\begin{array}{llll} {\Delta \nabla} N_{u v, 1}^{1} & \cdots & \Delta \nabla N_{u v, 1}^{n} & \mathrm{RZTD}_{\mathrm{wet}, u v} \end{array}\right]^{\mathrm{T}} $

$ \boldsymbol{L}_{*}(i)=\left[\begin{array}{llllll} l_{u v, 1}^{1} & \cdots & l_{u v, 1}^{m} & \dot{l}{}_{u v, 1}^{1} & \cdots & \dot{l}{}_{u v, 1}^{n} \end{array}\right]^{\mathrm{T}} $

$ \boldsymbol{\varTheta}_{m}=\left[\begin{array}{lll} M_{u}^{1} & \cdots & M_{u}^{m} \end{array}\right]^{\mathrm{T}} $

$ \boldsymbol{\varTheta}_{n}=\left[\begin{array}{lll} M_{u}^{1} & \cdots & M_{u}^{n} \end{array}\right]^{\mathrm{T}} $

$ \begin{gathered} l_{u v, 1}^{m}=\Delta \nabla \varPhi_{u v, 1}^{m}-\Delta \nabla \rho_{u v}^{m}-\Delta \nabla T_{\mathrm{dry}, u v}^{m}+ \\ \mu_{1} \frac{\Delta \nabla \kappa_{u v}^{m}}{f_{1}^{2}}+\lambda_{1} \Delta \nabla N_{u v, 1}^{m}-\mu_{1} \Delta \nabla I_{u v}^{m} \end{gathered} $

$ \begin{gathered} \dot{l}_{u v, 1}^{n}=\Delta \nabla \varPhi_{u v, 1}^{n}-\Delta \nabla \rho_{u v}^{n}-\Delta \nabla T_{\mathrm{dry}, u v}^{n}+ \\ \mu_{1} \frac{\Delta \nabla \kappa_{u v}^{n}}{f_{1}^{2}}-\mu_{1} \Delta \nabla I_{u v}^{n} \end{gathered} $

式中，0_m为m维零矩阵，I_n为n维单位矩阵，$ \Delta \nabla $I为参考站间双差电离层延迟误差空间线性模型计算的双差电离层延迟误差，l和$\dot l $分别为高高度角卫星和低高度角卫星B1双差载波相位观测方程对应的常数项。

2 算例与分析

采用2018年doy061的CORS数据进行测试，采样间隔为1 s，卫星截止高度角为15°，观测历元为28 800 s。图 1给出了CORS站的分布情况，其中A站到B站的距离为130 km，B站到C站的距离为113 km，C站到A站的距离为118 km。

低高度角卫星双差组合C04-C06和C07-C06参考站间B2-B3双差超宽巷整周模糊度N₂₃的单历元值和平均值计算结果如图 2所示。从图 2可以看出，由于双差超宽巷整周模糊度的波长较长，低高度角卫星双差超宽巷整周模糊度可以直接取整确定。

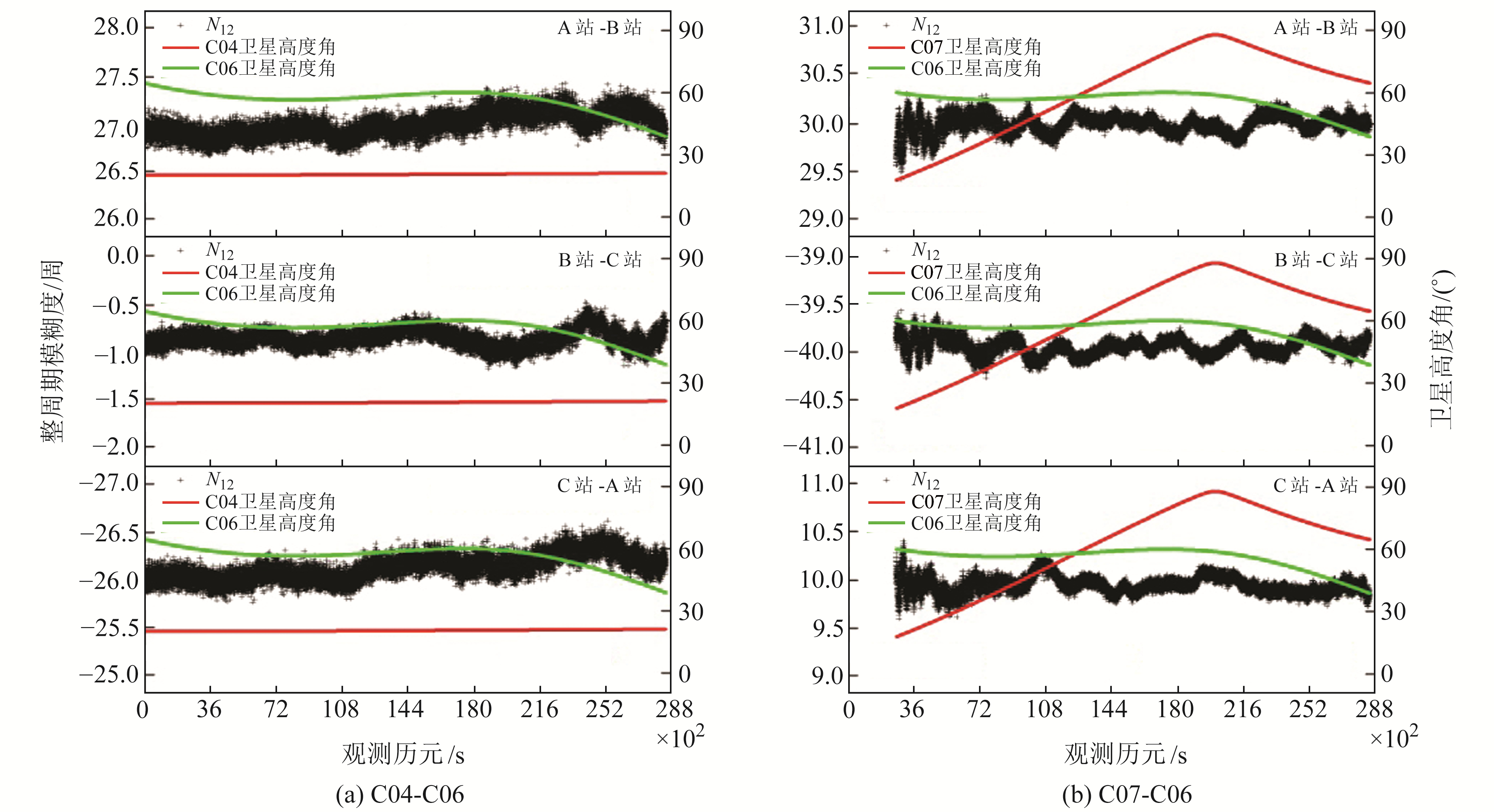
图 3给出低高度角卫星双差组合C04-C06和C07-C06的B1-B2双差宽巷整周模糊度N₁₂的浮点解和卫星高度角变化时间序列。由C04-C06和C07-C06的B1-B2双差宽巷整周模糊度N₁₂浮点解变化时间序列可知，直接取整即可准确固定B1-B2双差宽巷整周模糊度。

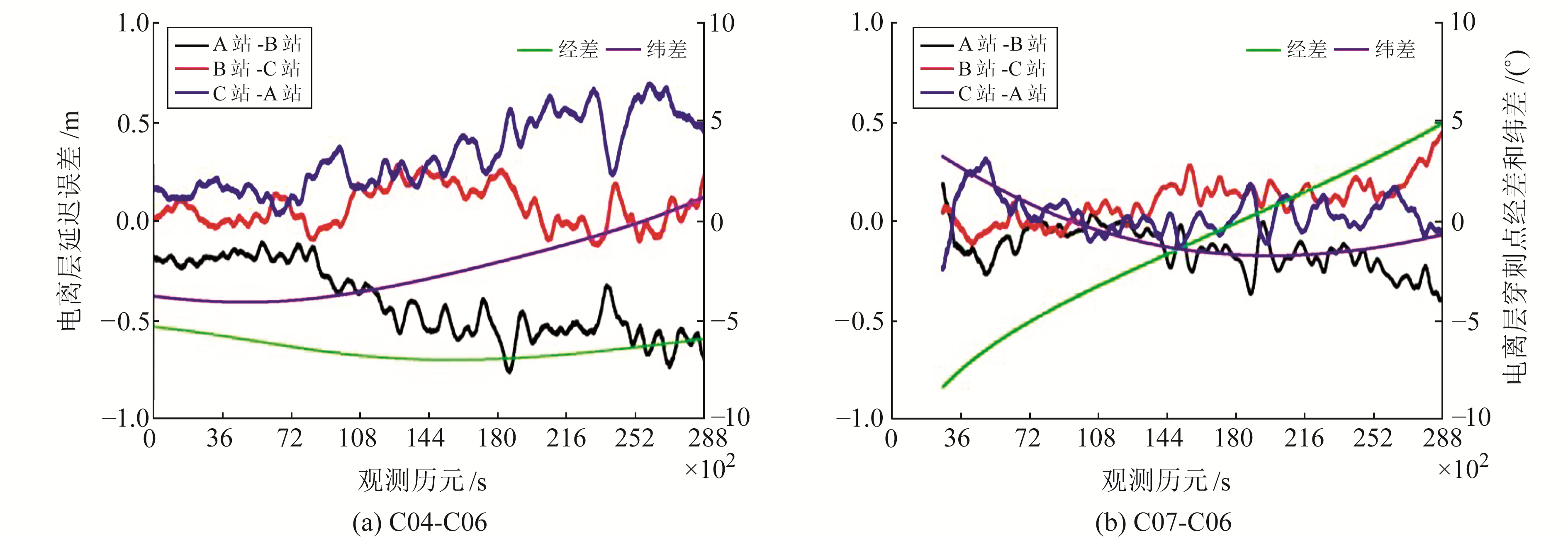
图 4给出利用双差电离层延迟误差空间线性模型计算的低高度角卫星双差组合C04-C06和C07-C06的B1载波相位观测值所受的双差电离层延迟误差和对应电离层穿刺点经纬度差值。由图可见，双差电离层延迟误差随双差卫星电离层穿刺点经差和纬差的变化而变化。

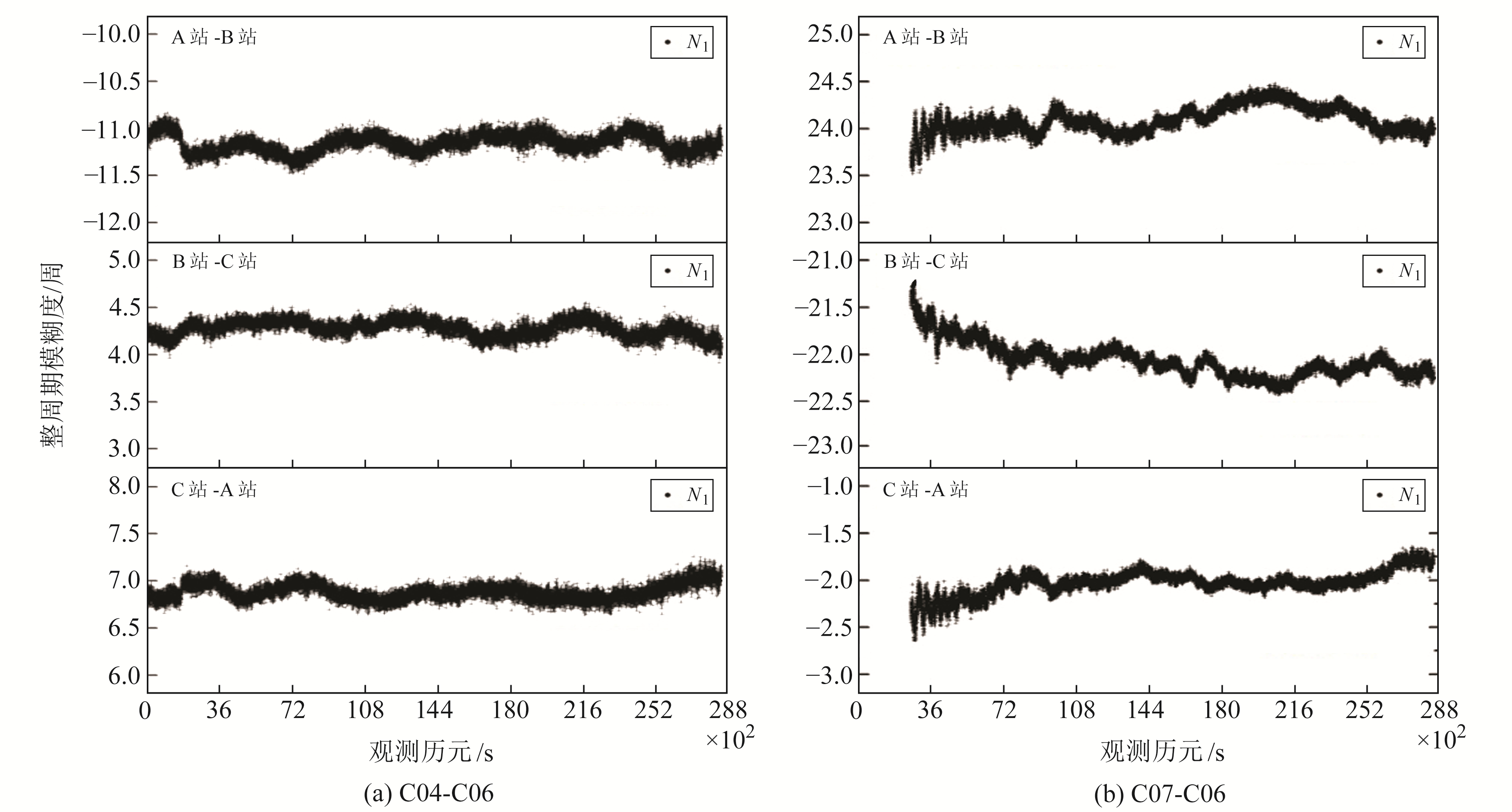
图 5给出低高度角卫星双差组合C04-C06和C07-C06的B1双差整周模糊度N₁浮点解。由图可见，低高度角双差组合C04-C06的双差整周模糊度浮点解与其整周模糊度准确值之间的差值小于0.5周，新升起卫星C07-C06的双差整周模糊度浮点解在卫星捕获开始阶段与其整周模糊度准确值之间的差值稍大于0.5周，利用LAMBDA算法可较准确地固定B1双差整周模糊度。

3 结语

本文利用超宽巷整周模糊度长波长的优势确定双差超宽巷整周模糊度，根据双差宽巷组合观测值与对应电离层延迟误差较接近的特点确定双差宽巷整周模糊度，利用无电离层组合模型解算高高度角卫星双差整周模糊度；然后根据建立的参考站间双差电离层延迟误差空间线性模型，实现对低高度角卫星电离层延迟误差的削弱；最后联合固定双差整周模糊度的高高度角卫星和低高度角卫星双差载波相位观测方程进行参数估计，搜索确定低高度角卫星的双差整周模糊度。