全球导航卫星系统(global navigation satellite system, GNSS)作为空间大地测量的主要技术手段之一,已被广泛应用于地球内部动力学机制、板块运动和地壳形变监测等研究[1]。目前,中国大陆构造环境监测网络(陆态网络)已建成由近300个GNSS基准站和2 000多个GNSS流动站构成的观测网络[2]。由于受数据处理策略、钟差、电离层延迟、对流层延迟和多路径效应等因素的影响,解算得到的GNSS垂向坐标时间序列存在误差,从而影响GNSS定位的精度和可靠性,导致某些地球物理现象出现错误解释[3]。因此,对GNSS垂向坐标时间序列进行降噪研究具有非常重要的科学意义和现实意义[4]。
目前用于GNSS坐标时间序列分解的方法主要有小波[5]、经验模态分解[6]及STL(seasonal-trend decomposition procedure based on LOESS)[7]等,其中小波和经验模态分解方法侧重于去噪分析,而STL方法主要用于季节性变化的提取,较少涉及去噪效果分析[8]。本文采用LOESS方法对GNSS垂向坐标时间序列进行降噪分析,并对其有效性及降噪效果进行验证和评价。
1 LOESS原理及降噪方法 1.1 LOESS方法基本原理LOESS是一种基于局部回归分析的非参数降噪方法[7],与线性回归、多项式回归等方法相比,该方法未对预测点进行限制,而是直接基于数据进行分析。该方法需要预先设置一个窗口,根据窗口内的点计算拟合点的拟合值,具体过程如下:
1) 对坐标时间序列中第1个点(x1, y1)进行拟合,此时窗口位于坐标时间序列的最左端,计算对应窗口内所有点相对于(x1, y1)的权重,通过加权最小二乘进行二次多项式拟合,得到回归曲线并计算得到拟合后的点(x1,
2) 设(xk, yk)为窗口在最左端时的中心点,重复步骤1),对(x1, y1)到(xk, yk)进行拟合,此时窗口位置固定,但从点(xk+1, yk+1)开始需要以拟合点为中心移动窗口位置,并逐个计算各点的拟合值,参与拟合值计算的仍为窗口内所有点。
3) 当窗口移动到坐标时间序列的最右端时,与最左端的情况类似,此时窗口中心点(xm-k+1, ym-k+1)到右端点(xm, ym)(m为坐标时间序列的总长度)均采用同一窗口内的所有点进行拟合。
4) 通过上述步骤对坐标时间序列中所有点进行拟合,将拟合后的点连接成完整的LOESS回归曲线,该曲线即为降噪后的坐标时间序列。
该方法的关键在于设置窗口宽度,经过多次实验,本文将窗宽设置为75。关于窗口内所有点权重的计算,可通过窗口内各点与拟合点的距离进行确定,该距离指X轴方向上的距离。随着距离的增加,权重减小,因此需要采用三次权重函数进行转化:
| $ W\left( u \right) = \left\{ \begin{array}{l} {(1 - {u^3})^3}, {\rm{ }}0 \le u < 1\\ 0, u \ge 1 \end{array} \right. $ | (1) |
此时还需要确定距离拟合点最远的点,并计算最大距离,对其他距离进行归一化处理,从而确定各点的权重:
| $ {\upsilon _i}\left( x \right) = W\left( {\frac{{|{x_i} - x|}}{{\Delta \left( x \right)}}} \right) $ | (2) |
式中,x为拟合点横坐标,xi为窗口内某点的横坐标,Δ(x)为最远点与拟合点之间的距离,υi(x)为该点相对于x的权重。
当目标模型为非线性模型时,局部加权回归算法相对于线性回归算法更合适,该算法选择窗口内的点而不是全部点进行回归。加权最小二乘法的目标函数为:
| $ J\left( \mathit{\boldsymbol{\theta }} \right) = \sum\limits_i {{\upsilon _i}\left( x \right){{({y_i} - {\mathit{\boldsymbol{\theta }}^{\rm{T}}}{x_i})}^2}} $ | (3) |
式中,J(θ)为损失函数,(xi, yi)为窗口内某点,θ为最佳回归系数。
利用最小二乘原理,进一步对加权后的损失函数J(θ)求偏导,即可求得最佳回归系数θ,最终得到加权回归曲线及拟合点(x,
用LOESS方法对陆态网络289个测站的垂向坐标时间序列进行降噪分析,具体流程如下:1)降噪前先剔除坐标时间序列中的粗差;2)用LOESS方法对剔除粗差后的序列进行降噪处理,得到降噪后的坐标时间序列及噪声序列;3)确定噪声模型,并利用极大似然估计(MLE)方法解算GNSS坐标时间序列谐波模型对应的各项运动参数;4)检验降噪后噪声序列的自相关性和降噪前后各指标的显著性;5)综合数学指标和GNSS测站运动模型参数对降噪结果进行评价。技术路线如图 1所示。
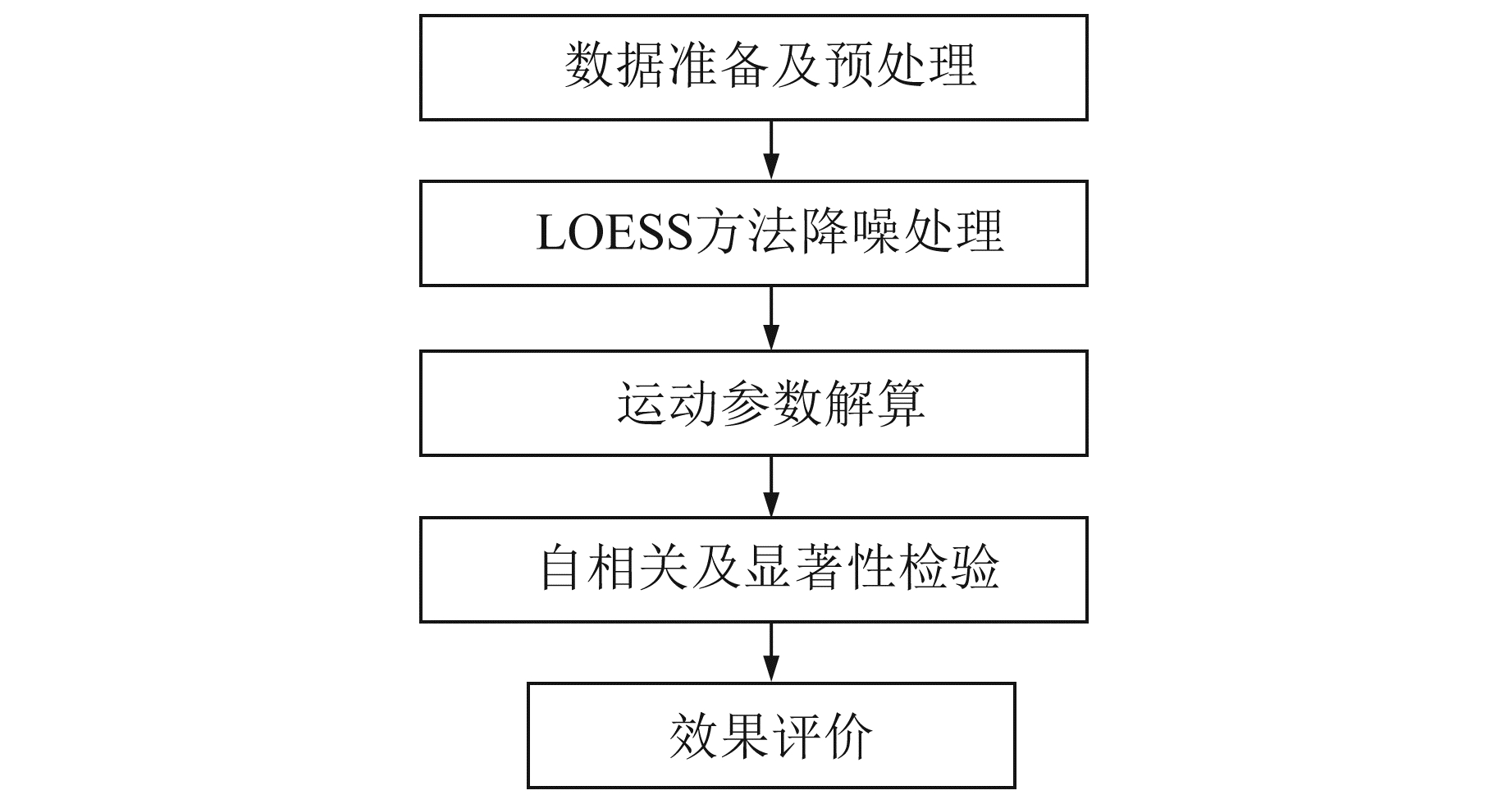
|
图 1 技术路线 Fig. 1 Technical road |
考虑到坐标时间序列数据缺失的问题,本文采用陆态网络中289个GNSS基准站原始的垂向坐标时间序列进行降噪分析。GNSS坐标时间序列数据来源于中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn),数据处理方法与精度指标可参考该平台提供的说明文档(ftp://ftp.cgps.ac.cn/doc/processing_manual.pdf)。
2.2 数据预处理由于受各种外界因素的影响,原始数据中含有一定的粗差,在分析前需要对序列中的粗差进行探测与剔除。本文采用IQR方法[9]消除GNSS原始坐标时间序列中的异常值。
3 算例及结果分析 3.1 算例分析采用§1.1的方法对选取的289个GNSS站进行降噪处理。为验证LOESS方法对GNSS坐标时间序列降噪的可靠性,以XJHT站为例进行说明,图 2为XJHT站原始坐标时间序列、降噪后时间序列及噪声序列。由表 1可知,XJHT站垂向坐标时间序列降噪后的信噪比达48.47 dB,降噪效果较好,标准差减小了1.11 mm,白噪声和闪烁噪声分别从1.81 mm、11.27 mm·a-0.25降至0.01 mm、2.40 mm·a-0.25,表明序列中包含的噪声明显降低,速度不确定度从0.48 mm·a-1降至0.10 mm·a-1。
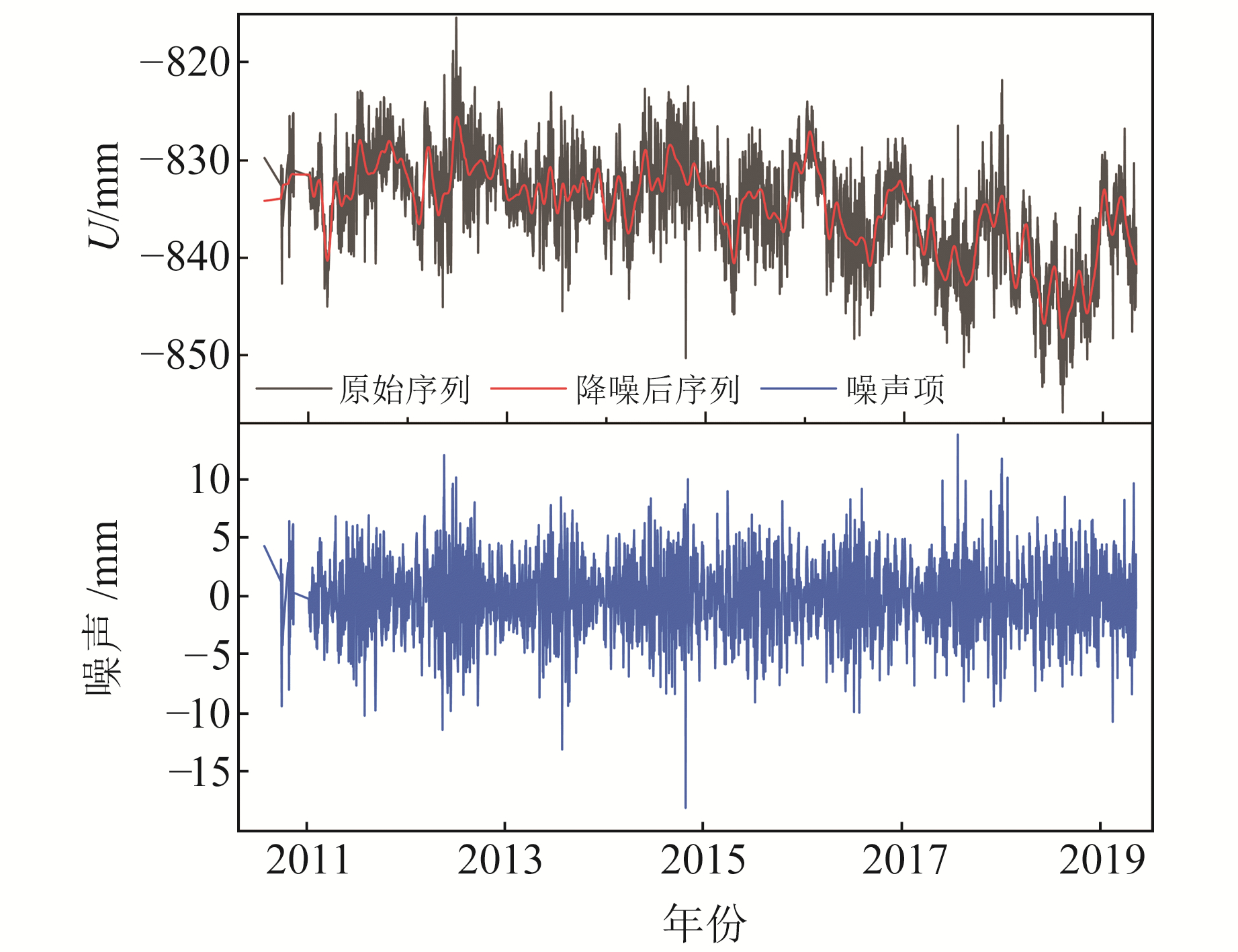
|
图 2 XJHT站垂向GPS原始坐标时间序列、降噪后时间序列和噪声项 Fig. 2 Vertical GPS original coordinate time series, time series after noise reduction and noise items of XJHT station |
|
|
表 1 XJHT站降噪前后评价指标 Tab. 1 Evaluation index of XJHT station before and after noise reduction |
为进一步分析降噪后噪声序列是否存在自相关性,本文采用Durbin-Watson(DW)检验对降噪后的噪声序列进行自相关性检验。DW检验是一种检验序列自相关性的方法[10],采用该方法对各测站降噪后的噪声序列进行检验可得到检验统计量。由判断准则可知,若DW值约为2,即可推断序列完全不相关。
采用§1.1的方法对289个GNSS站的垂向坐标时间序列进行降噪处理后,对噪声序列进行DW自相关性检验,结果如图 3所示。结果表明,DW平均值为1.64±0.19(n=289),其中78%介于1.50~2.10之间,表明采用LOESS方法进行降噪处理后,各测站的噪声序列不存在自相关性,可进行后续的评价工作。
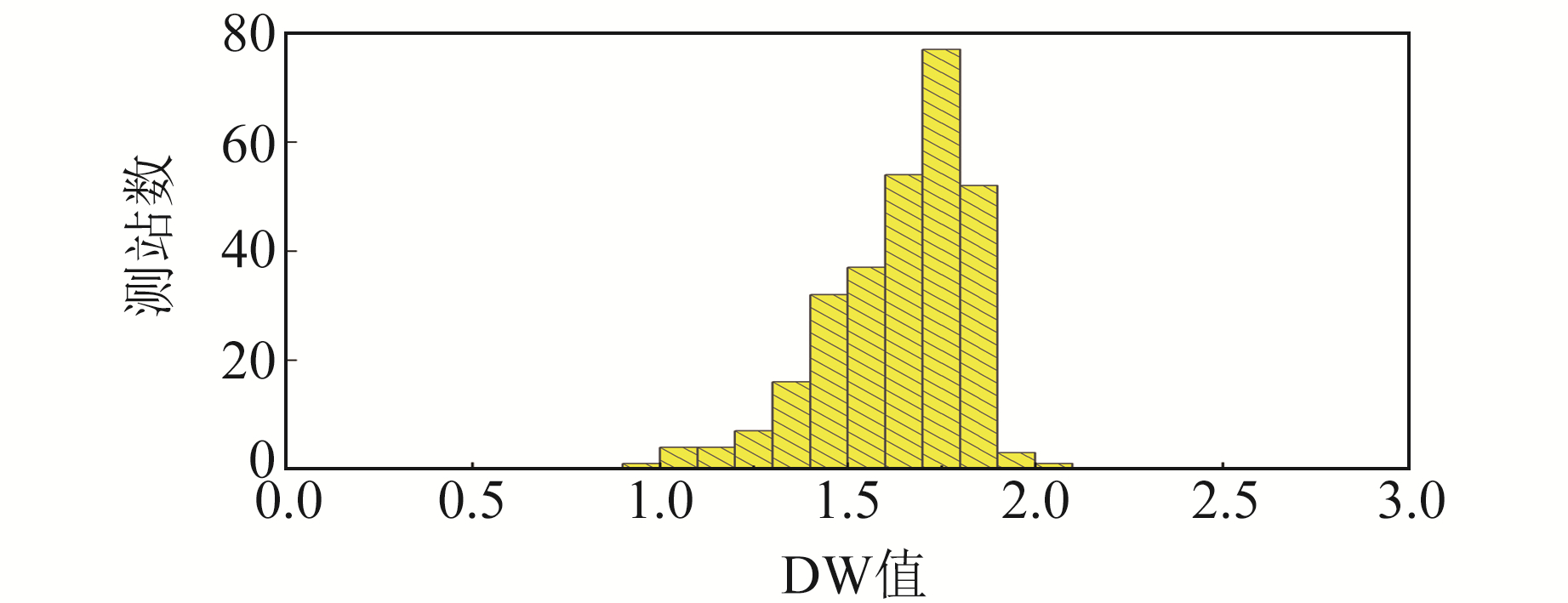
|
图 3 DW检验结果 Fig. 3 DW test results |
本文采用以下4种指标来定量评价LOESS方法对GNSS坐标时间序列降噪的可靠性和效果:1)信噪比(signal-noise ratio, SNR);2)标准差(standard deviation, STD);3)白噪声(white noise, WN)和闪烁噪声(flicker noise, FN);4)速度不确定度。
3.3.1 信噪比SNR计算公式可表示为:
| $ \mathrm{SNR}=10 \log \left\{\frac{\sum\limits_{n=0}^{N-1} S_{n}^{2}}{\sum\limits_{n=0}^{N-1}\left(S_{n}-\hat{S}_{n}\right)^{2}}\right\} $ | (4) |
式中,Sn为原始序列,
研究表明[11],白噪声(WN)和闪烁噪声(FN)组成的噪声模型(WN+FN)是GNSS垂向坐标时间序列的最优噪声模型,因此本文采用WN+FN噪声模型。
作为常用的GNSS坐标时间序列分析软件,Hector软件采用极大似然估计方法求解GNSS测站的运动模型参数:
| $ \begin{aligned} x(t)=& \sum\limits_{i=0}^{n_{P}} p_{i}\left(t-t_{R}\right)^{i}+\sum\limits_{j=1}^{n_{J}} b_{j} H\left(t-t_{j}\right)+\\ & \sum\limits_{k=1}^{n_{F}} s_{k} \sin \left(\omega_{k} t\right)+c_{k} \cos \left(\omega_{k} t\right)+\\ & \sum\limits_{m=1}^{n_{M}} a_{k} \log \left(1+\left(t-t_{m}\right) / T_{m}\right) \end{aligned} $ | (5) |
式中,pi为nP次多项式系数,默认nP=1为线性趋势;H(t)为Heaviside阶跃函数,用于建模tj时刻发生的偏移量,振幅为bj;nF为用来模拟季节位移周期的频率数,GNSS坐标时间序列的年、半年变化振幅和频率分别为
参照文献[12-14]使用的指标,本文计算评价指标的改正率(correction rate, CR),以进一步分析评价LOESS方法对GNSS垂向坐标时间序列的降噪效果:
| $ {\rm{CR}} = \frac{{{I_{{\rm{before}}}} - {I_{{\rm{after}}}}}}{{{I_{{\rm{before}}}}}} \times 100 $ | (6) |
式中,Ibefore和Iafter分别为各评价指标在时间序列降噪前后的指标值,CR为正表示LOESS方法能够有效削弱GNSS垂向坐标时间序列中包含的噪声,CR值越大则表示降噪效果越明显。
3.4 降噪效果评价采用LOESS方法对各测站进行降噪,得到降噪后的时间序列及噪声部分,并计算降噪前后SNR、STD、噪声和速度不确定度等4个评价指标值,分析其变化情况。为验证降噪前后序列的各项指标是否存在显著性差异,本文采用非参数Wilcoxon秩和检验[15]对各项指标在降噪前后进行显著性检验,若检验结果中P值均小于0.05,则表明在95%的置信区间内,指标在降噪前后存在显著性差异。
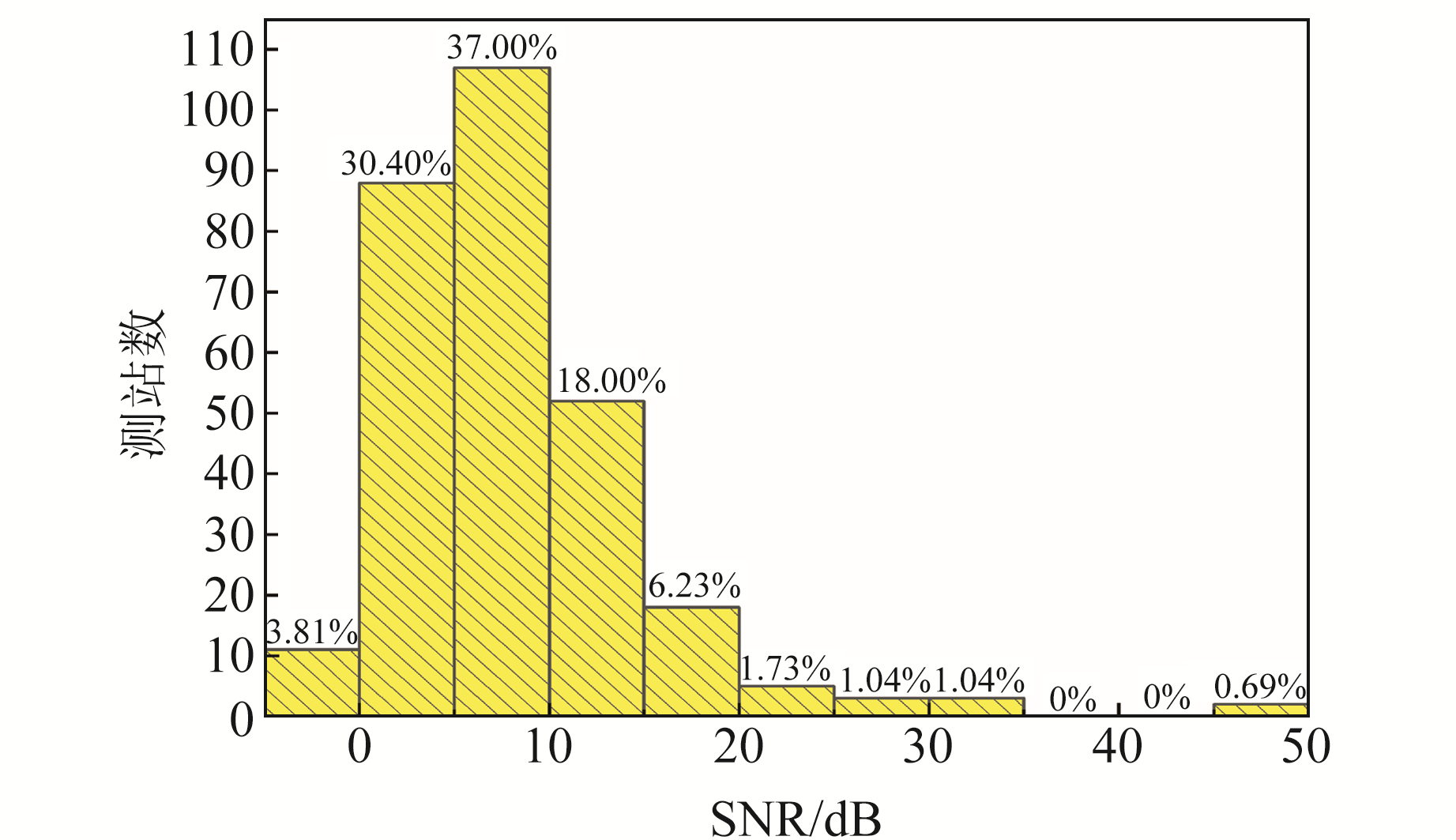
3.4.1 SNR与STD由式(4)可知,原始序列的SNR均为0。图 4为各测站坐标时间序列降噪后的信噪比,测站分布直方图如图 5所示。由图 4和5可知,垂直分量坐标时间序列降噪后的信噪比均较高,最高达48.47 dB,均值为8.14 dB,80%以上测站介于0~15 dB之间;部分测站的信噪比为负,其原因可能为使用LOESS方法降噪时设置的窗宽较小。结果表明,采用LOESS方法进行降噪后信噪比总体有显著提高。
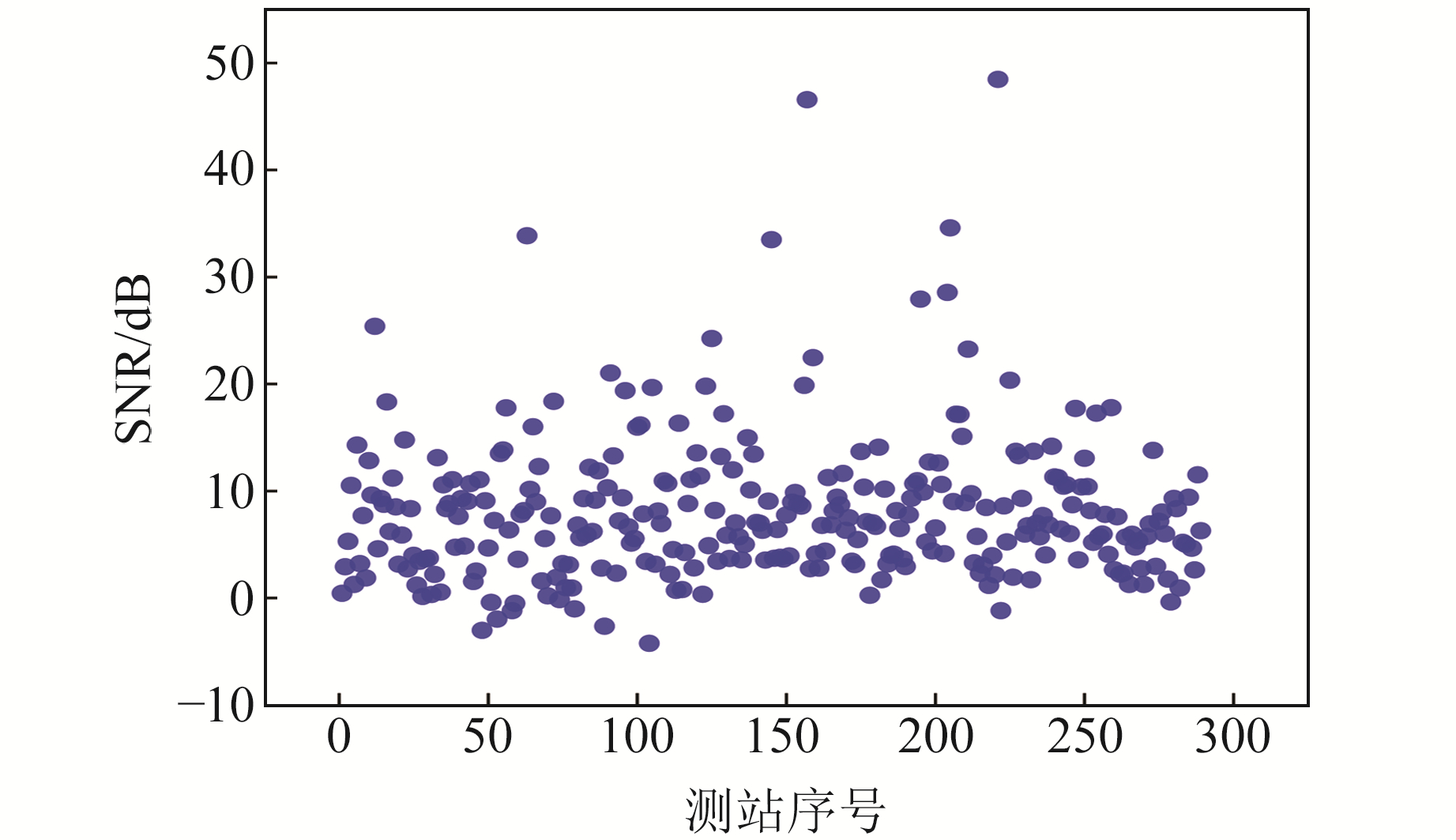
|
图 4 各测站坐标时间序列降噪后的信噪比 Fig. 4 Signal-to-noise ratio after noise reduction in coordinate time series of each station |
|
图 5 降噪后信噪比的测站分布 Fig. 5 Distribution of stations for signal-to-noise ratio after noise reduction |
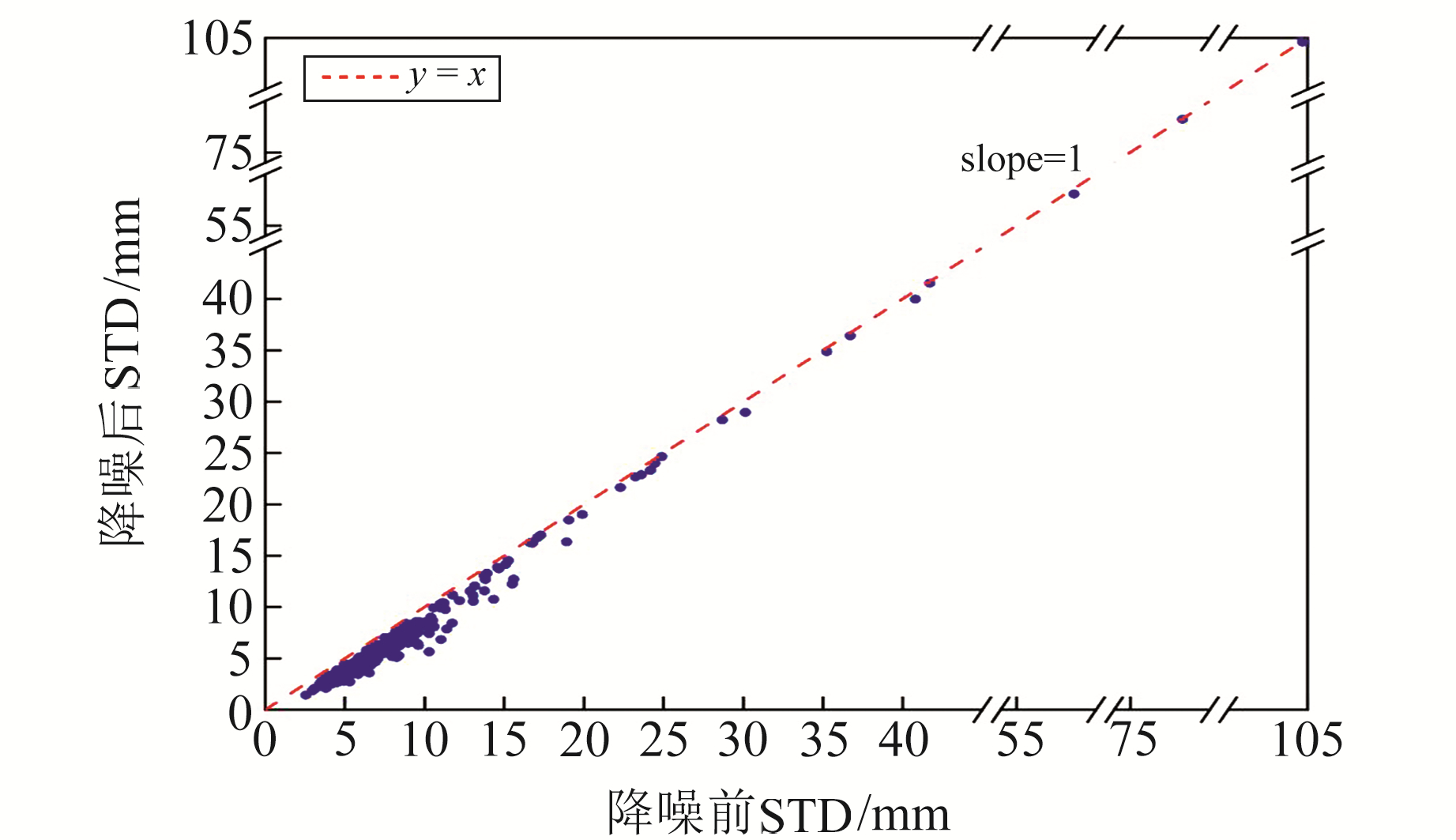
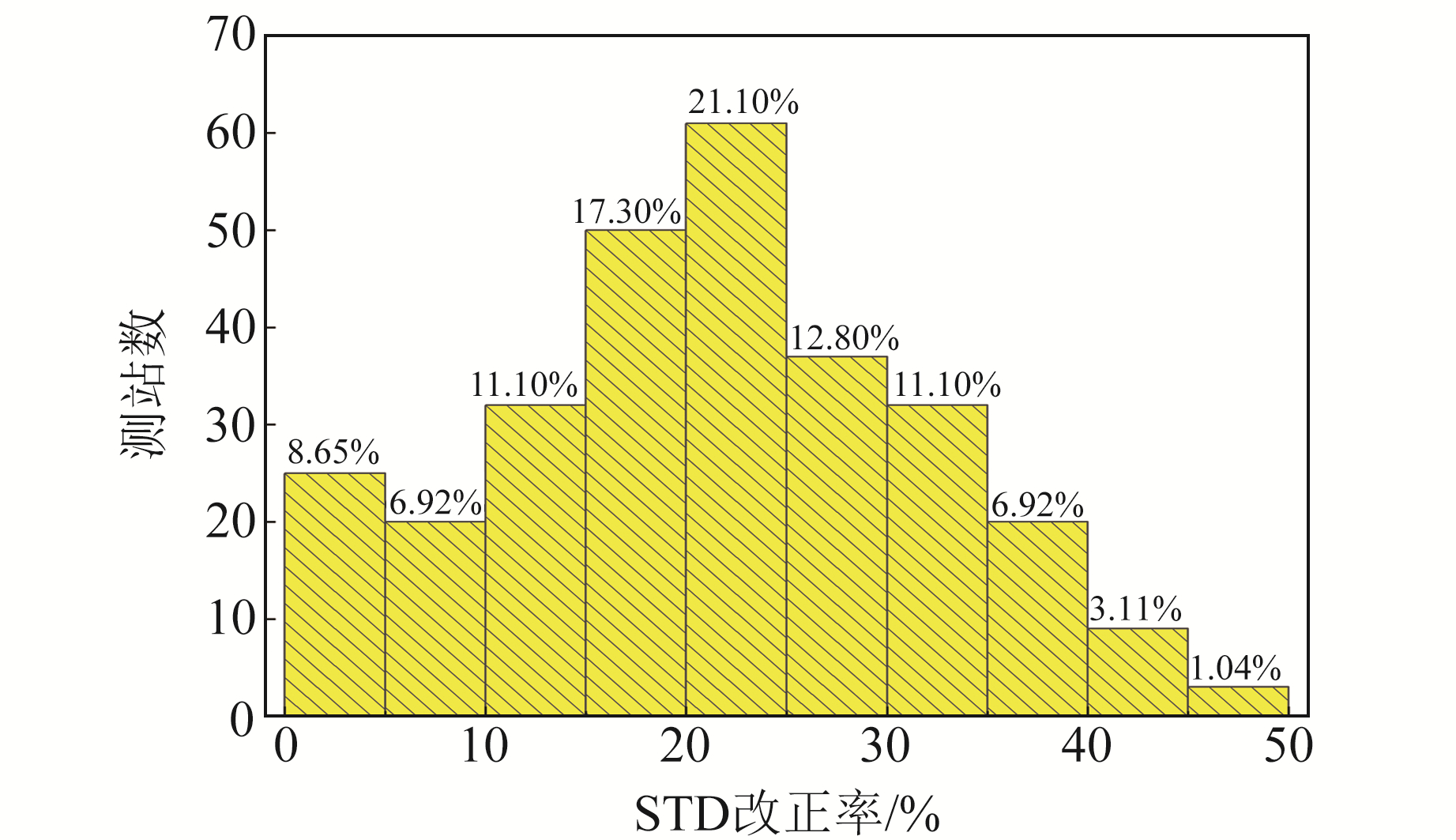
图 6为各测站垂向坐标时间序列降噪前后的标准差变化,标准差改正率的测站分布情况如图 7所示。由图 6可知,采用LOESS方法降噪后的STD均有所减小,平均减小21.35%,最高减小48.77%,且Wilcoxon检验表明,降噪前后标准差具有显著性差异(p < 0.05, n=289)。由图 7可知,22%的测站改正率介于30%~50%之间,34%的测站改正率介于20%~30%之间,因此采用LOESS方法能够显著降低时间序列的标准差。
|
图 6 降噪前后各测站序列的标准差 Fig. 6 The standard deviation of each station series before and after noise reduction |
|
图 7 标准差改正率的测站分布 Fig. 7 Distribution of stations for correction rate of standard deviation |
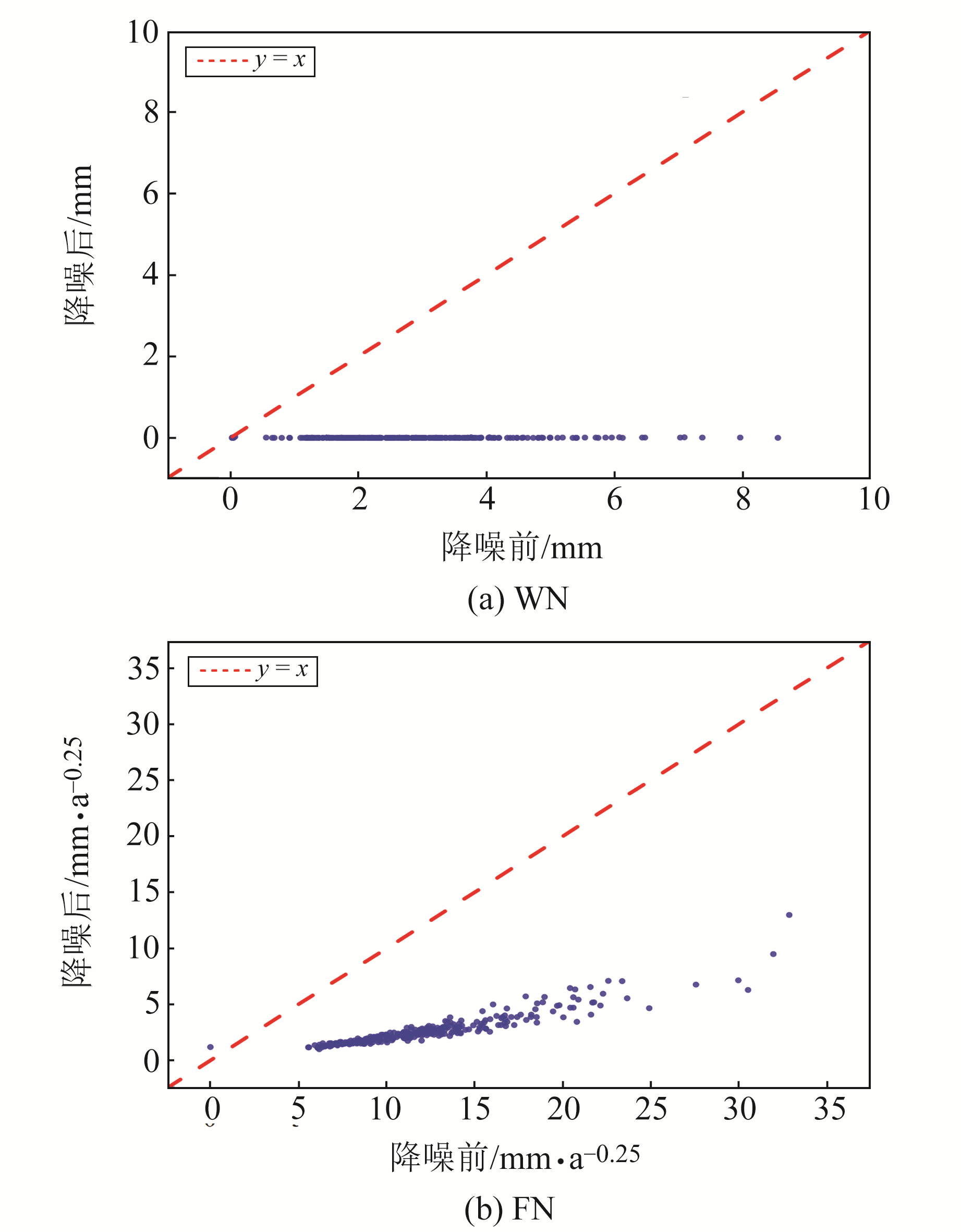
图 8(a)和8(b)分别为各测站垂向坐标时间序列降噪前后白噪声和闪烁噪声变化情况,2种噪声改正率的测站分布情况分别见图 9(a)和9(b)。由图 8(a)可知,降噪后序列的噪声均明显降低,特别是白噪声均降低至0.03 mm以下,且Wilcoxon检验表明,降噪前后序列的白噪声具有显著性差异(p < 0.05, n=289)。由图 9(a)可知,94.81%的测站白噪声改正率在95%以上。从图 8(b)可以看出,闪烁噪声降低至0~5 mm·a-0.25范围内,改正率最低为68.35%,最高为85.28%,且Wilcoxon检验表明,降噪前后序列的闪烁噪声具有显著性差异(p < 0.05, n=289)。由图 9(b)可知,约34%的测站闪烁噪声改正率在80%~86%之间,约64%的测站在70%~80%之间。结果表明,LOESS方法可有效降低时间序列中的噪声,其中HNCS站FN由0变为1.20 mm·a-0.25,其原因可能是该测站的噪声并不符合WN+FN噪声模型,而降噪会将非整数谱指数幂律噪声PL变成FN。
|
图 8 降噪前后各测站坐标时间序列的白噪声和闪烁噪声 Fig. 8 White noise and flicker noise of coordinate time series of each station before and after noise reduction |

|
图 9 白噪声和闪烁噪声改正率的测站分布 Fig. 9 Distribution of stations for correction rate of white noise and flicker noise |
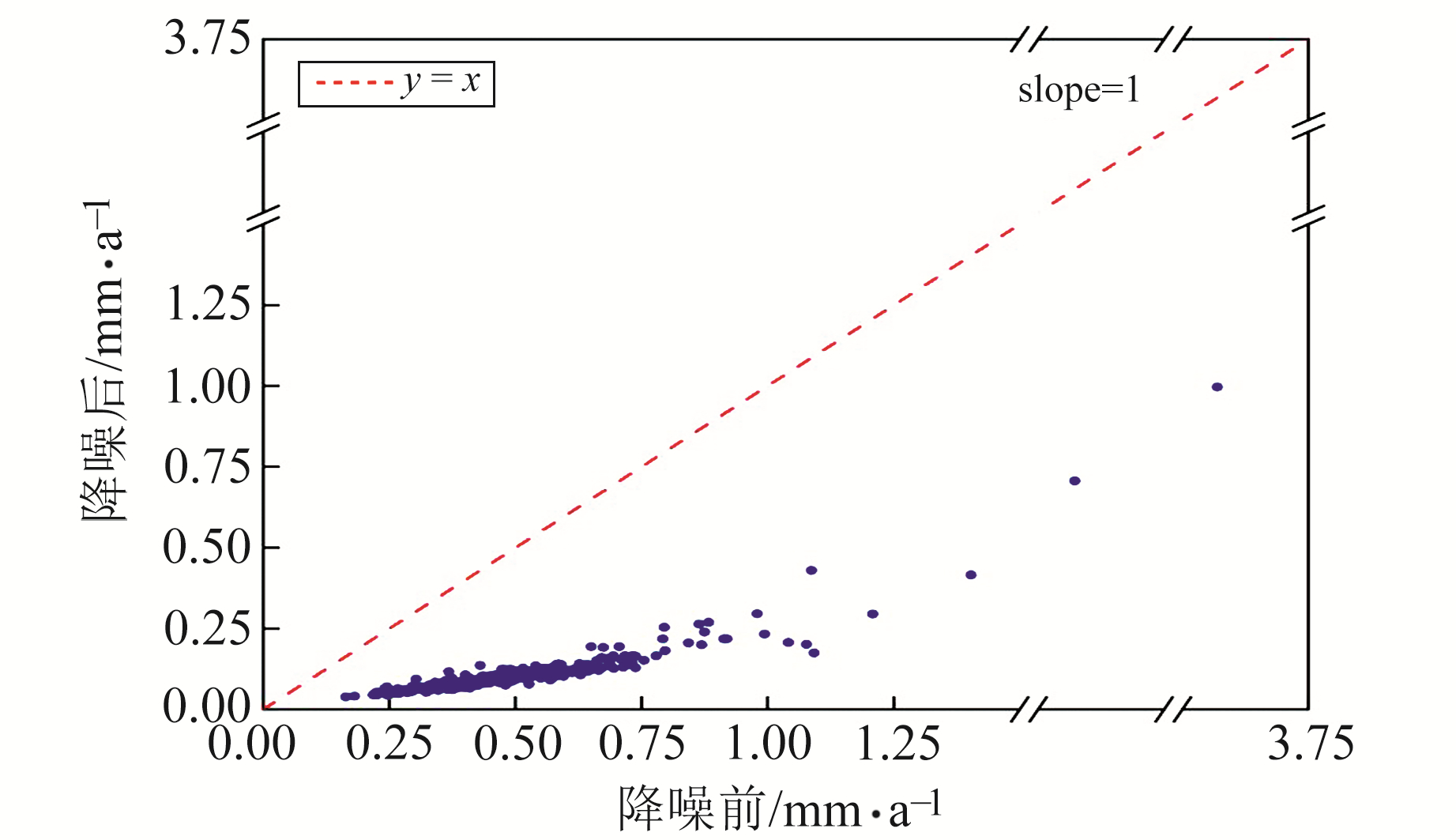
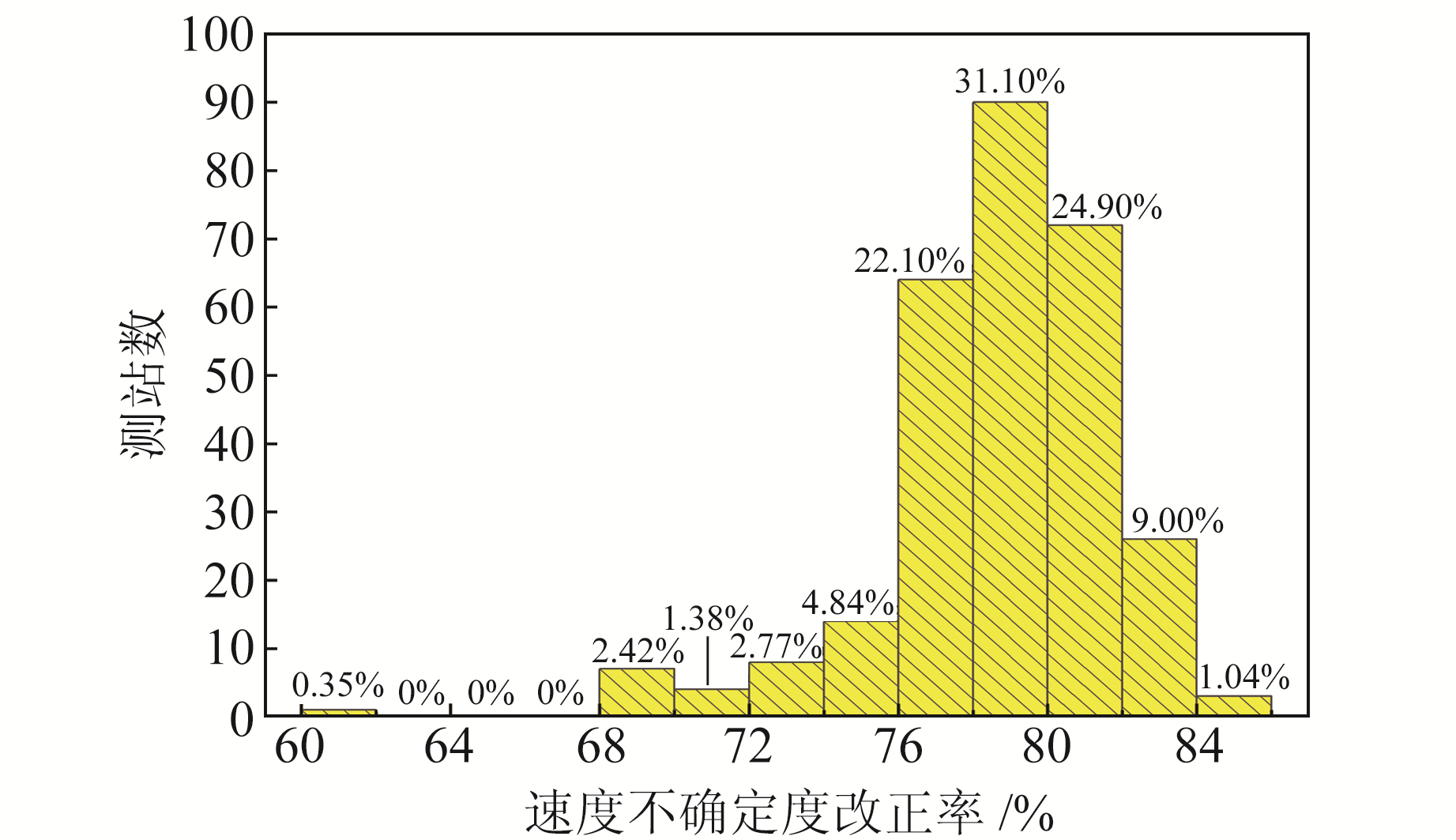
图 10为各测站垂向坐标时间序列降噪前后的速度不确定度,其改正率的测站分布情况如图 11所示。由图 10可知,降噪后速度不确定度也明显降低,平均改正率为78.68%,且Wilcoxon检验表明,降噪前后序列的速度不确定度具有显著性差异(p < 0.05, n=289)。由图 11可知,35%的测站改正率在80%以上,63%的测站改正率在70%~80%之间。分析表明,LOESS方法可显著降低序列的速度不确定度。
|
图 10 降噪前后各测站坐标时间序列的速度不确定度 Fig. 10 The speed uncertainty of coordinate time series of each station before and after noise reduction |
|
图 11 速度不确定度改正率的测站分布 Fig. 11 Distribution of stations for correction rate of speed uncertainty |
本文将LOESS方法引入GNSS垂向坐标时间序列的降噪研究中,并使用数学指标、统计检验和GNSS测站运动模型参数进行效果分析,结果表明,LOESS方法可有效提高GNSS原始坐标时间序列的精度。
分析表明,降噪后信噪比均值提高至8.14 dB,最高达48.47 dB;标准差平均减小1.38 mm,平均改正率为21.35%,最高达48.77%。对于降噪后的序列,白噪声和闪烁噪声均值分别由2.685 mm、12.415 mm·a-0.25降至0.006 mm、2.723 mm·a-0.25,平均改正率为78.63%;同时,速度不确定度得到明显改善,平均改正率达78.68%。
本文在以下方面仍需进一步研究:1)未将本文方法与其他降噪方法进行对比,以分析本文方法的优势和不足;2)本文直接采用了普遍认为的最佳噪声模型WN+FN,未考虑GNSS基准站复杂的噪声特性。
| [1] |
陈俊勇, 张鹏, 武军郦, 等. 关于在中国构建全球导航卫星国家级连续运行站系统的思考[J]. 测绘学报, 2007, 36(4): 366-369 (Chen Junyong, Zhang Peng, Wu Junli, et al. On Chinese National Continuous Operating Reference Station System of GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 366-369 DOI:10.3321/j.issn:1001-1595.2007.04.002)
(  0) 0) |
| [2] |
甘卫军, 李强, 张锐, 等. 中国大陆构造环境监测网络的建设与应用[J]. 工程研究——跨学科视野中的工程, 2012, 4(4): 324-331 (Gan Weijun, Li Qiang, Zhang Rui, et al. Construction and Application of Tectonic and Environmental Observation Network of Mainland China[J]. Journal of Engineering Studies, 2012, 4(4): 324-331)
(  0) 0) |
| [3] |
姚宜斌, 张顺, 孔建. GNSS空间环境学研究进展和展望[J]. 测绘学报, 2017, 46(10): 1 408-1 420 (Yao Yibin, Zhang Shun, Kong Jian. Research Progress and Prospect of GNSS Space Environment Science[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 408-1 420)
(  0) 0) |
| [4] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series Inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [5] |
Wu H, Li K, Shi W Z, et al. A Wavelet-Based Hybrid Approach to Remove the Flicker Noise and the White Noise from GPS Coordinate Time Series[J]. GPS Solutions, 2015, 19(4): 511-523 DOI:10.1007/s10291-014-0412-6
(  0) 0) |
| [6] |
鲁铁定, 钱文龙, 贺小星, 等. 一种确定分界IMF分量的改进EMD方法[J]. 大地测量与地球动力学, 2020, 40(7): 720-725 (Lu Tieding, Qian Wenlong, He Xiaoxing, et al. An Improved EMD Method for Determining Boundary IMF[J]. Journal of Geodesy and Geodynamics, 2020, 40(7): 720-725)
(  0) 0) |
| [7] |
Cleveland R B, Cleveland W S, McRae J E, et al. STL: A Seasonal-Trend Decomposition Procedure Based on Loess[J]. Journal of Official Statistics, 1990, 6(1): 3-73
(  0) 0) |
| [8] |
Isotta F, Martius O, Sprenger M, et al. Long-Term Trends of Synoptic-Scale Breaking Rossby Waves in the Northern Hemisphere between 1958 and 2001[J]. International Journal of Climatology, 2008, 28(12): 1 551-1 562 DOI:10.1002/joc.1647
(  0) 0) |
| [9] |
蔡晓军. 区域GPS坐标时间序列特性分析[D]. 西安: 长安大学, 2019 (Cai Xiaojun. Characteristic Analysis of Regional GPS Coordinate Time Series[D]. Xi'an: Chang'an University, 2019))
(  0) 0) |
| [10] |
刘明, 王永瑜. Durbin-Watson自相关检验应用问题探讨[J]. 数量经济技术经济研究, 2014, 31(6): 153-160 (Liu Ming, Wang Yongyu. Exploring in Durbin-Watson Autocorrelation Test[J]. The Journal of Quantitativeand Technical Economics, 2014, 31(6): 153-160)
(  0) 0) |
| [11] |
Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
(  0) 0) |
| [12] |
Blewitt G, Lavallée D. Effect of Annual Signals on Geodetic Velocity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B7)
(  0) 0) |
| [13] |
Bos M S, Bastos L, Fernandes R M S. The Influence of Seasonal Signals on the Estimation of the Tectonic Motion in Short Continuous GPS Time-Series[J]. Journal of Geodynamics, 2010, 49(3-4): 205-209 DOI:10.1016/j.jog.2009.10.005
(  0) 0) |
| [14] |
Klos A, Gruszczynska M, Bos M S, et al. Estimates of Vertical Velocity Errors for IGS ITRF2014 Stations by Applying the Improved Singular Spectrum Analysis Method and Environmental Loading Models[J]. Pure and Applied Geophysics, 2018, 175(5): 1 823-1 840 DOI:10.1007/s00024-017-1494-1
(  0) 0) |
| [15] |
周聪, 余晖, 傅刚. Wilcoxon秩和检验在热带气旋强度预报方法评定中的应用[J]. 大气科学学报, 2014, 37(3): 285-288 (Zhou Cong, Yu Hui, Fu Gang. Application of Wilcoxon Signed Rank Test in Evaluation of Tropical Cyclone Intensity Forecast[J]. Transactions of Atmospheric Sciences, 2014, 37(3): 285-288 DOI:10.3969/j.issn.1674-7097.2014.03.004)
(  0) 0) |
 2021, Vol. 41
2021, Vol. 41


